#if that doesn't suffice I'll replace the image

[ithroweggsatbillionaires]

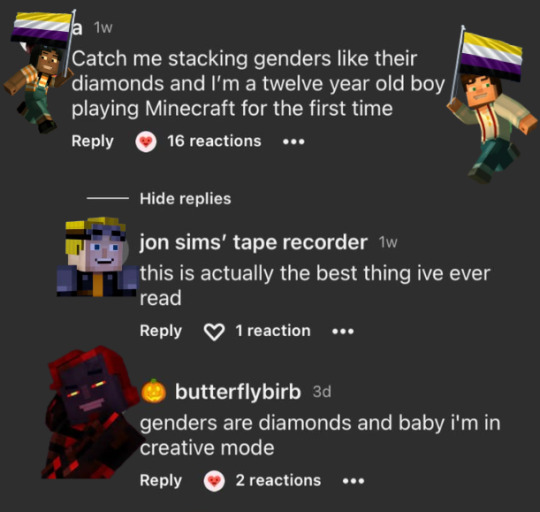
Disclaimers on that last part

I have not yet seen Season 2 and I based it on the impression I got from other posts

I thought the zesty Romeo image was real (see no.1)

The creator of zesty Romeo is "hero :)" or "ivorsblocksleeve" on Tiktok

[lilith-hazel-mathematics]

I'd like to add that there's a technical sense in which the result for determinants & polytopes is elementary, in that the result is captured by the power of Peano Arithmetic. So you for sure don't need the full power of measure theory. In particular it suffices to use the Peano-Jordan measure: the outer Jordan content of a compact set agrees exactly with the Lebesgue measure of that set. In any case, the Lebesgue outer measure is typically defined as follows.

The measure of a box is the product of its side lengths

A simple set is a countable disjoint union of boxes, and its measure is the sum of the measures of those boxes

The Lebesgue outer measure of a set is the infimum measure of any simple superset.

In the case of the Jordan measure, "countable union" is replaced by "finite union", but otherwise it's the same. It's a foundational theorem that the overlap in the above definitions is consistent: the infimum measure of the simple supersets of a box is exactly the product of that box's side lengths. Interestingly, to define measure, it suffices to only consider boxes & simple sets having rational coordinates. Critical to the Jordan measure however, there's only countably many simple sets having rational coordinates, since the Jordan measure only considers finite unions. Peano Arithmetic has no problem reasoning about finite lists of rational coordinates, and so the Jordan measure is definable over a conservative extension of Peano Arithmetic. For polytopes, they can be proved measurable using very elementary techniques, and in fact we won't need anything beyond the axioms of an ordered field. This is the sense in which the proof is elementary.

Okay, putting the technical stuff away, I'll just show you what the proof looks like.

-----

To fully prove the relationship between determinant and measure, it does suffice to handle the case of a box. If the matrix is diagonal, then the proof is trivial since the image of a box will be another box, and the measure of a box is easily computed. For a shear matrix transform, we partition our box into a large number of thin slices, thin along the dimension being sheared, and then approximate the image by similarly sized slices. As the width of those slices tends to zero, the measured approximation of the image will converge to the measure of the original box. This is satisfactory to us, since the determinant of the matrix for a shear is 1. Notice that that only required finite additivity and monotonicity, so the argument works for the Jordan measure. Finally, In the sense of elementary row operations, every invertible matrix can be expressed as a product between a diagonal matrix and a finite number of shear transforms. Consequently the claim extends to all invertible matrices by proxy of those simpler cases. For non-invertible matrices, we instead approximate the image by arbitrarily thin boxes to argue that the measure of the image will be zero. The claim is finally generalized to any measurable set by approximating it with simple sets.

The above proof doesn't require the comprehension axiom at all: the result holds for any set known to exist; which sets actually exist is a separate issue. It also doesn't need the completeness axiom either, for basically the same reason. The above result is proved for polytopes by demonstrating that they are actually measurable. First you'll want to show that the unit simplex is measurable, which is mostly demonstrated by partitioning the unit hypercube into a finite number of congruent simplices. Next, any arbitrary simplex is proved measurable as it's obtained from a linear transform of the unit simplex; the previous proof can be modified slightly to show that linear transforms preserve measurability. Lastly, each polytope can be partitioned into a finite number of simplices using a triangulation, from which we infer that every polytope is measurable.

Am I correct in assuming that if you want to rigorously derive formulas for calculating volumes of arbitrary n-dimensional polytopes (or to even formally define what a volume is in the first place) you need to get into measure theory? Or is there a simpler, more algebraic way that still leads to a fully formal and rigorous proof?

(I'm specifically interested in a rigorous proof that the correspondence between determinants of n x n matrices and volumes of n-parallelotopes spanned by the corresponding vectors continues to hold for arbitrary n)

[auspicious-voice]

OH GOD.

I was looking through my photos and I came across THIS fucking relic. It's from 2017, but the UTAUs in this picture (save for an early iteration of Mario) are all from 2014, AKA the year I first started using UTAU!

So I was thinking of talking about the four UTAUs in this post (and some with no designs whatsoever) while reminiscing over the past memories I made back then. With that being said, this will be under the #nostalgia tag whenever I collect old stuff related to my UTAU project. More under the cut!

The ASTRAloid Project

While I was developing Maria during my noob days as an UTAU user in 2014, I founded the ASTRAloid Project dedicated to her and any UTAU that I would make. I told my friends about this silly hobby and they got interested in the idea of making your own voicebank. So we all got together and made additional UTAUs for the ASTRAloid project. This was around the time when I first started working on Mario as a character and as voicebank.

Fast forward several months later, the ASTRAloid project was then disbanded since members of the project left either due to loss of interest or that they found it difficult to record an UTAU voicebank. I picked up the remaining pieces of this project and formed the FUWAutau Project, which would then feature Maria and Mario as its main UTAUs. It got some rebrands along the way up until I renamed it to AUSPICIOUS VOICE in 2022 - to reflect Maria and Mario in their current iteration.

Many of the character concepts my friends and I have drawn for the project have been lost to time. At least the art of them from 2017 survived! If I come across any more surviving materials, I'll update this post once in a while.

The Lost UTAUs of ASTRAloid

Aside from Maria and Mario, the remaining UTAUs of the now-defunct ASTRAloid project were left abandoned without a functioning voicebank. I lost contact with many of my friends down the line, but I still do get in touch with some of them.

I don't have the character concepts with me anymore, so everything I say about these UTAUs will come from my memory. Hopefully it'll suffice...

Murasaki Chou

Murasaki Chou is an UTAU created by leoriosexy. She's one of the first ASTRAloids made for the project aside from Maria. Her personality is very happy-go-lucky for the most part, and she has a butterfly motif.

The image of Chou I've shown above is her first design! leoriosexy gave her a new design back in 2021 to replace the old Crypton-inspired design.

We discussed when we should start developing Chou's voicebank, but life's been pretty busy, Maybe the time will come when Chou will receive a functional voicebank, and when she does, I'll go on covering duet songs with Chou and Maria LMAO

Anaki Williams

Anaki Williams is an UTAU created by one of my friends involved in the ASTRAloid project. His personality is well-reserved and polite.

Nothing much is known about Anaki, but I do remember he has blond hair and red eyes. I do wish I still have his original concept though because he has a really nice design...not to mention that I lost contact with his creator...

Gali

Gali is an UTAU created by one of my friends. Unfortunately I do not have much information on Gali, other than the fact that...she likes tacos??? She has a black-red colour scheme for the most part.

She was an OC way before she was an UTAU, and I drew her one time at some point...It was a Code Geass OC × canon fanart depicting her and Lelouch. I think this was back in 2013-2014, back when most of my friends were in their My Little Pony/Attack on Titan/Supernatural/Torchwood phases.

Teelato Kimura

Teelato Kimura is an UTAU created by one of my friends. She had fiery hair, blue eyes, and a long black-red coat...

I don't remember her character details correctly, but she's said to have a violent personality, and one of her likes include plants! She's holding a plant pot in her art.

Herschel

Now Herschel doesn't have any official character design or concept, but he's an UTAU created by one of my friends! He was also an OC before was an UTAU, much like Gali.

One character detail I know about Herschel was that he's a merman. Yup, that's about it.

The Future of the Scrapped ASTRAloid UTAUS...?

Chou has seen some new content in recent years such as artwork (and hopefully a new voicebank), but as for the rest of the ASTRAloid UTAUs, they're still abandoned to this day and in terms of voicebank development, they still have no voicebanks. I was thinking of adopting these scrapped UTAUs and release them under the "other" series or something like that. I'd love to breathe new life into these UTAUs, but that would mean getting into contact with friends whom I haven't talked to in years. I'll try and see if I can talk to them and ask them about their UTAUs, but for now, these UTAUs will likely remain abandoned until the end of time.

Anyways, thank you for reading! I love talking about my beginner days in using UTAU, and I hope to post more stuff like this in the future...if I can get my hands on old stuff I managed to salvage, that is. :)