jessecmckeown

[jessecmckeown]

I Stand Corrected

Desargue's Involution Theorem is about Involutions

And to put it in brief, given a Line and Four Points in General Position, the statement is that the family of conics passing through Those Four Points, via their intersections with The Line, define a Projective Involution Of The Line. There's a dual theorem about a Point and Four Lines, the family of conics tangent to Those Four Lines, et.c. Its possibly-strange-seeming statement emphasizes that the family of conics includes (we've mentioned this before) three degenerate quadratic curves, each a pair of lines.

One could, of course, do the algebra required; or, we might content ourselves with the observations: it's obvious that the relation: conic$\wedge$line$\mapsto$twoPoints is also reversible: point-On-Line$\mapsto$conicFromFivePoints$\mapsto$theOtherIntersection; and that that reversal is "Clearly" an involution; and the observation that all the relations defined are clearly algebraic, so What Else Is It Going To Be???

[jessecmckeown]

Oh, I have a geogebra online account.

[jessecmckeown]

It's not really operators on a Hilbert Space

That is, in the prototypical Quantum Theory defined by a Hamiltonian, viz the Harmonic Oscillator, the famous Hamiltonian isn't a complete operator on that space. It can't be a bounded operator, as it's got arbitrarily large singular values. You could restrict to A Subspace where the Hamiltonian is complete, but that rather changes things. The subspace itself won't be complete w.r.t the original Hilbert Norm; but the Hilbert Norm is also the definition of Born-Rule Probabilities. So... Someone someday will/has clean[ed] up the terminology and the conceptual framework... and that won't really fix everything, but it might be very healthy for everyone.

[jessecmckeown]

There are ever so many ways to argue

Monge and Apollonius

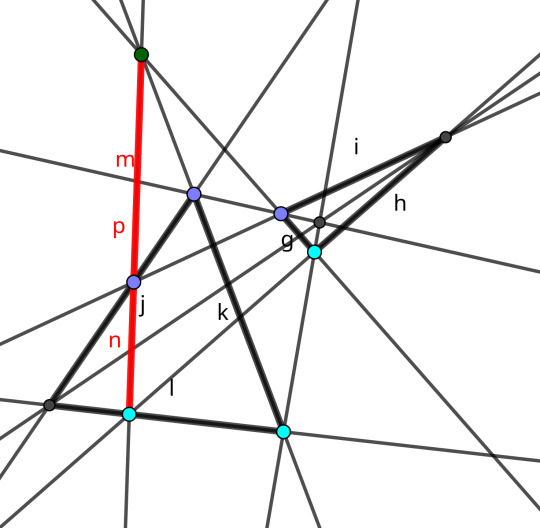
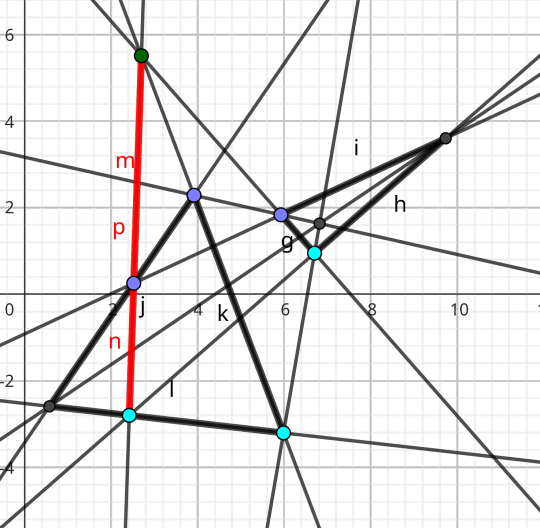
My grandmother's house was full of books. When I was still relatively small, I found in her basement a book my grandfather (d 1982) must have enjoyed, which I've surely mentioned here before, Triumph der Mathematik by Heinrich Dörrie, translated by David Antin as 100 Great Problems of Elementary Mathematics. It has heaps in it that you wouldn't often encounter anywhere else today, some for reasons you might guess ("Gauss' Altitude Problem", From the time intervals between the moments that three known stars attain the same altitude, determine the moments of the observations, the latitude of the observatory, and the altitude of the three stars. SOLUTION: ...) and some for reasons that I can't guess, but then my brain is wired up something funny.

Monge's Problem

is entry 31. Recall that plane circles are said to intersect normally or perpendicularly if their respective radius segments are perpendicular at the points of intersection.

Monge's problem in the book is then: given three (suitable) circles, describe a fourth that intersects normally with the given three. This happens to be impossible when the three circles intersect too closely, but the geometry is still interesting.

As it happens, the centres of circles normal to two given circles are colinear!

In the figure above, let the circles centred at $A$, $B$, $O$ have radii $a$, $b$, $o$, respectively; and let the right triangles have common leg $y$ and colinear legs $x$ and $z$, respectively. The wealth of right triangles then gives $$ x^2 + y^2 = a^2 + o^2 $$ and $$ z^2 + y^2 = b^2 + o^2, $$ so that $$ (x-z) (x+z) = x^2 - y^2 = a^2 - b^2, $$ the difference $x-y$ depends only on the circle radii $a$ and $b$, and the separation $x+y = |\overline{AB}|$.

The line so defined is sometimes called the "radical line" of the two circles, and if given THREE circles, their three radical lines intersect concurrently -- because if a constructed circle intersect both circles $\alpha$ and $\beta$ normally, and also both $\beta$ and $\gamma$ normally, then it intersects both $\alpha$ and $\gamma$ normally as well. This concurrence also makes it easy to find the radical line in the first place, because as it happens, the radical line of intersecting circles is also concurrent with their intersections. Is that a good exercise? Maybe that's a good exercise.

Tangencies

Two circles are tangent, of course, when they share a tangent line. This means if circles $A$ and $B$, say, are tangent at a point $P$, and third circle intersects $A$ normally at $P$, then it also intersects $B$ normally.

A trivial observation about a circle $X$ tangent to two given circles $A,C$, the centre of $X$ is the same distance from $A$ as from $C$--just as trivially, this means the locus of circle centres tangent to both $A$ and $B$ is probably a hyperbola, unless it's an ellipse, as when $A$ surrounds $B$; HOWEVER! because the common tangent lines of $A$ and $X$, and of $B$ and $X$ are both tangent to $X$, it follows that also their intersection is the same distance from both tangencies -- in other words, that the tangencies are also intersections of $A$ and $B$ with a common normal circle.

We'll combine this with one other useful observation about normally-intersecting circles:

(I'm so terribly sorry that Geogebra makes labels so awkward. I could tug them around, but there are limits to its utility) Drawing any line ($h$, in yellow and red and blue) through one of the intersection points ($B$) defines the bases of two isosceles triangles ($ABD$ and $CBE$); because the circles intersect normally, the base angles of the red and blue triangles are complementary; and because the base angles at $D$ and $E$ are respectively congruent, they are still complementary and so are the adjacent angles of a right triangle. Let's draw some Isosceles triangles into the previous picture.

Because of that right triangle, we can describe the relation of the two tangency points quite neatly, in terms of the line $ST$ joining the centres of $A$ and $C$: they subtend chords from $S$ and $T$, respectively that extend to intersect on the radical line.

These Correspondences be Projective

Given THREE circles, as already discussed, there are three, concurrent radical lines, and so one can chase the tangency points, as in the last figure, around the three circles; usually, we won't end up in the same place we started...

So, starting at point $T$ on circle $a$ (who picks these names?? Why aren't the choices consistent from one figure to the next????) in brown lines we relate it to a compatible point on circle $b$, and in yellow lines relate that to a compatible point on circle $c$, and finally with the green lines relate it to $T'$, again on circle $a$. Each monochrome map is a construction called a perspective map of "ray pencils", and the colour-changing maps are congruences of ray pencils (what's a "ray pencil"? Dörrie is vague on this point -- he is writing as a historian as much as anything, and his sources predate the Everything Is A Set heresy. For us, it's a set of lines through one point). Because the individual maps are all projective(geometry) (They preserve cross-ratios, nothing to do with lifting diagrams) their composite (oh! it's a category after all!) is again projective and as it happens, Dörrie also includes an entry on finding the FixedPoints of such a map! That's a construction by Steiner. It's not bad.

I've also drawn in red the circle through the first three points of this construction, but you can probably tell that it does a little bit more; and figuring why is probably a good Exercise; also, figuring that, since it does do that bit more, the particular projectivity constructed is even an involution. (There's something else in the same part of Dörrie's book, called "Desargues' involution theorem", but what HE means by "involution"... I'll have to read it again.)

So we put these things together and, well, here's a sample construction of an Appolonius tritangent circle:

the black circles are given -- we've suppressed the construction of their three radical lines, but other than that all needed lines and their useful intersections are shown. The bold maroon circle is one of the eight that are tangent to all three given circles. The blue circle is needed to find the fixedpoints of the composite involution on the circle $c$.

Commentary

If we're being strict Euclideans (Socratic Euclideans... cf. his remarks on the solved Delian Problem) then actually, the construction shown above has several shortcuts in it --- it is missing several construction arcs and lines. The geogebra "midpoint" primitive is used a good few times, and so is "circle through three points". Perhaps you notice, about this construction (or any lengthy construction...) It's more than a bit messy. The lines cluster together in awkward ways. They're often nearly parallel. You can imagine that, if you tried to do this by hand, it'd be very difficult even keeping track of Which Line Was Which, and drawing them with sufficient precision would be a Chore.

Now, this isn't the solution that Dörrie chose to showcase in his book --- that was Gergonne's solution, which is a good one, too. I've assembled this method because Gergonne's Approach also uses Monge's Radical Lines (so they're going to be on your page anyway) and to show how much more they do than just locate Normal Circles.

Here is Gergonne's solution, allowing ourselves roughly equivalent shortcutting. I'll let you decide if it's tidier. Here is how Dörrie summarizes Gergonne's construction:

The line is the "Similarity axis" of the given circles, the subject of d'Alembert+Monge's theorem, and it's not an accident that it is also the Radical Axis of the two constructed circles.

Perhaps I might blether on a few more posts about this stuff.

[jessecmckeown]

More to say about these, soon

[jessecmckeown]

To tidily quarter a given angle in place, draw two circles with a common radius

[jessecmckeown]

there, that's better....

[jessecmckeown]

The same configuration, highlighted in two different ways. Puzzle: How Many Desargues-Homologous pairs in one diagram?

[jessecmckeown]

If this is happening in salt water, and the drinks are alcoholic, they will also float away; just turn the cups upside-down! (Where are you keeping the ice, anyway???)

i had a dream i worked in an underwater restaurant and people kept ordering ice in their drinks and then getting mad at me when it would float away. and i’d tell them beforehand that the ice would float away & they’d be like lol no that’s not how it works just give me the ice. I’m fighting customer service battles never seen before

[jessecmckeown]

It's Not $\Pi$ day

I've not had enough time to do maths properly for the past... well, quite a long while, actually, but in particular I got myself a REAL JOB in INDUSTRY, in fact as a welder, which takes up twelve or thirteen hours most days (ten of them are spent Working)... Anyways, I'd Like To Let the Tau Fans Know Something about Circles in Industry.

Nobody measures the radius of an Industrial Circle. Never. Radii are not a Thing. It's Diameters, if possible, that we measure, and if a circle is Unfinished, we compare it with a template. At least, most of the time. I imagine a Machinist working at a Lathe may well consider truly radial measurements, but we don't have any genuine lathes in our plant, and that's Just Fine.

And the Reason that no-one measures the Radius of an Industrial Circle is because it's basically impossible. You see, to measure the radius, you have to locate the center. This is, of course, doable in principle, but pretty much a waste of time, because the center is located at the intersection of DIAMETERS. And if you have a diameter, you may as well measure THAT.

Some Caveats: the principal method of producing one of our Industrial Circles is by rolling (that is, incrementally locally bending) some material beyond its elastic/plastic transition. Sometimes it's feasible to do this end-to-end and then check: have I closed a circle? sometimes this is not feasible, and instead the ends of the material to be bent circlewise must be first matched to a template. But there are other ways --- with a lathe, for instance, one may cut both external and internal circles. One will have a decent estimate of the radial location of the cutter, but you'll still measure a diameter. But SOMETIMES, particularly in preparing the templates we have mentioned (sometimes to cut out holes to admit other industrial circles passage), we will draw a circle using a compass, and then cut along the lign. This is the ONLY case in which the radius is more easily known than the diameter, and it's when we LEAST care about the circumference produced. For the compassed circles we most use, the center is promptly thrown away, because it would make the template too large and unwieldy.

That is all, you may now return to your what-have-you.

[jessecmckeown]

Whence Fabulous Faulhaber?

should I promise not to make this a habit?

Dear Mr. Haran, I'm grateful to you and correspondent Eischen (and Conway) for putting the name of Faulhaber on a calculation which heretofore I'd only known quoted, without attribution, by Heinrich Dörrie in Triumf der Mathematik---(which I've only read in translation). However, I'm most frustrated that neither Dörrie nor Eischen give any satisfying motivation for why the postulate should work.

For bystanders still catching up, this postulate is that if one defines a sequence of numbers $B_k$ "by expanding" $$(B-1)^{k+1} = B^{k+1}$$ and transcribing exponents to subscripts... one finds that the differences $$ (n + B)^{k+1} - B^{k+1} $$ similarly treated are equal to cumulative power sums, $$(k+1) \sum_{j \leq n} j^k$$

So the calculation is doable. My Beef is Dilemmimorphic: Either the notational abuse of $(n + B)^k$ suggests that $B$ should be Some Kind Of Linear Operator, in which case what is it? Or else there's an Amazing Coincidence being Overlooked!

It's a comparative Triviality that the power sums $\sum_1^N n^k$ should be polynomials of $N$, and that the leading term be $\frac{1}{k+1} N^{k+1}$ , so indeed it is perfectly reasonable to consider coefficients $B_{k,j}$ defined by $$ \sum_1^N n^k = \frac{1}{k+1} \sum \binom{k+1}{j} B_{k,j} N^{k+1-j} $$ BUT WHY SHOULD WE ASSUME that in fact $B_{k,j}$ depends only on $j$? That's STAGE MAGIC, and the fact that indeed it somehow works does not explain "where it comes from" (Eischen's favourite phrase on the matter).

So, in my customary way of starting with the actual problem and throwing at it what seems to me the minimum of thought, let's first explicate that "comparative triviality": the sequence of polynomials $p_k(j) = \binom{j+k}{j}$ are integral generators for the Integral-valued polynomials, and are recursively definable as iterated cumulative sums of the constant polynomial $p_0 \equiv 1$: $$\binom{j+k+1}{j} = \binom{j+k}{j} + \binom{j+k}{j-1}$$. Hence, cumulative sums of any polynomial, written in the binomial basis, can be obtained just by incrementing: $$\sum_{j=1}^N \sum a_n p_n(j) = \sum a_n p_{n+1}(N)$$

Next, cumulative sums are themselves defined by induction: $"\sum_{j=1}^0" P(j) = 0$ and $\sum_{j=1}^{N+1} P(j) = P(N+1) + \sum_{j=1}^N P(j)$, or said differently, by the Difference equation $$ SP(N+1) - SP(N) = P(N+1).$$ In other words we are trying to solve the Difference Equations $$ S_k(N) - S_k(N-1) = N^k,$$ but in the basis of Monomials $N^j$ instead of Binomials $p_j(N)$.

The binomial theorem, $$ (x+y)^k = \sum \binom{k}{j} x^{k-j} y^j $$ makes the Taylor-MacLaurin formula a Theorem for polynomials $$ (x+y)^k = \sum y^j \frac{1}{j!} \frac{d^j}{dx^j} x^k $$ which is fruitfully abbreviated $$ P(x+y) = e^{y\\, d/dx} P(x) $$ the Backwards Difference, then, is similarly $$ P(x) - P(x-1) = (1 - e^{- d/dx}) P(x) $$

Shall we say, The kernel of the Backward Difference is reasonably well understood? The differential operator is the retract of the Integral operator $\int_0$, so the Taylor-MacLaurin formula provides us also a section for the Forward Difference operator, $$ 1-e^{-x} = \frac{d}{dx} + A\frac{d^2}{dx^2} $$ where, for now, the main point is that the unbounded-degree differential operator $A$ commutes with $d/dx$, so that, for example $$ (1 - e^{-d/dx}) \left(\int_0 \sim dx - A + A^2 \frac{d}{dx} - A^3\frac{d^2}{dx^2} + - \cdots \right) P(x) = P(x)$$

Of course, there are various paths to the power series, other than via expansion of the powers of $A$, but there is a (Laurent) power series $$ \frac{1}{1-e^{-t}} = \frac{1}{2}\coth(\frac{t}{2})+\frac{1}{2} = \frac{1}{t} + \sum \frac{B_j}{j!} t^{j-1} $$ where $B_j$ are the faBulous Bernoulli numbers.

In any case, applied to simple powers, $$ \left( \int_0 \sim dx + \frac{1}{2} + \sum_{j=2}^{\infty} \frac{B_j}{j!} \frac{d^{j-1}}{dx^{j-1}} \right) x^k = \frac{1}{k+1} x^{k+1} + \sum_{j=1}^{k} \frac{k!}{j!(k-j+1)!} x^{k-j+1} B_j \\\\ {} = \frac{1}{k+1} \sum_{j=0}^{k} \binom{k+1}{j} B_j x^{k+1-j} $$ Finally, the power sum polynomials $S_k$ vanish both at zero (formally an empty sum) and at $-1$ (since $S_k(0) - S_k(-1) = 0^k$), so that in particular, $$ \sum_{j=0}^k \binom{k+1}{j} B_j (-1)^{k-j} = 0$$ THAT'S WHERE THIS IS COMING FROM.

[jessecmckeown]

Silly Question: What Is the Binomial Theorem?

by which I mean: it's obviously not "Pascal's" "Triangle"; That is: it's not just the fact that (in commutative algebra) there are "binomial coefficients"; nor even that, for reasons of applicable combinatorics, the binomial coefficients get to be called "en-choose-kay". If anything is The Binomial Theorem, it's the coincidence of the binomial coefficients and certain fractions involving factorials. And while I'm as happy as the next fellow to agree that the number of subsets of a given size out of a set of the given size is equal to the number of permutations of the whole set modulo the permutations that fix the prefix/suffix partition at a fixed index... there are still more ways to interpret that equation than "precommutative terms in an algebraic expression, modulo the commutativity relations". That is, once we've decided that there ARE Binomial Coefficients, and that they are Integers, we can choose any argument that gives us those integers, even if it doesn't look like it need give integers. The underlying combinatorics, even, may be identitical, but where we apply them doesn't have to be "the terms of an algebraic expression". In other words, we can read the Binomial Theorem as saying $$ \frac{(a+b)^n}{n!} = \sum_{k+l=n} \frac{a^k}{k!}\frac{b^l}{l!} $$ just as well as anything else; and we can construe the left hand side as the volume of an $n$-simplex with axes $(a+b)$, and the right hand side similarly as a sum of suitable products of simplices. So I wrote a p3/java sketch to see what that looks like. Incidentally, I've often told myself that I write code that is basically terrible to maintain. Can't seem to break those habits...

Oh. You wanted an argument. Yes. Of Course. The volume of a Euclidean $k$-simplex containing an orthonormal basis among its edges is $1/k!$, because a $k$-dimensional cube can be subdivided into $k!$ of them with lower-dimensional overlaps, because an indexed set of $k$ real numbers also has a natural partial-ordering --- $\leq$. Generalizing to a $k$-simplex with $k$ orthogonal edges of lengths $a$, $b$, or $(a+b)$ are straightforward enough. Partitioning! Let's focus on an interior point of an orthogonal $n$-simplex with edges of length $(a+b)$; that is, $\leq$ is a total order on its coordinates. We might as well be looking at $$ 0 \lt x_1 \lt x_2 \lt \dots \lt x_n \lt (a+b) $$ But there are furthermore $n+1$ possible comparisons of each $x_j$ with $a$! Videlicet, $$ 0 \lt x_1 \lt \dots \lt x_k \lt a \lt x_{k+1} \lt \dots \lt x_n \lt a+b $$ That is, comparing coordinates with $a$ gives a natural partition of the simplex into products of simplices: an orthogonal $k$-simplex of size $a$ and an orthogonal $(n-k)$-simplex of size $b$, hurrah! It's not meant to be a profound; but last year I just wanted to show some high-school students that the binomial theorem could be really geometrical, as well as algebraic.

[jessecmckeown]

Theta the Magical

So, these Elliptic Curve things --- It's become very natural, post-Asteroids™ to think of "Torus" as $\mathbb{C}/\mathbb{Z}^2$, and so a function on an elliptic curve is "the same as" a doubly-periodic function on $\mathbb{C}$; it breaks some of the symmetry of this picture, but there is something marvelous that happens when one views the Torus instead as the quotient of a Cyllinder and --- because $\exp$ teaches us how to view $\mathbb{C}^\times$ as a cyllinder --- considers functions on a Torus as functions on $\mathbb{C}^\times$ with a discrete scaling-invariance. Let $ 0 \lt |q| \lt 1 $, and for a warm-up, verify that the product $$ R_q(z) = \prod_{n\in\mathbb{N}} (1 + q^{2n+1} z) $$ is absolutely convergent, with zeros $-\frac{1}{q^{2n+1}}$, and has a nice scaling property: $$ R_q(z/q^2) = \frac{q+z}{q} R_q(z) $$ Check that similarly, $$ R_q(\frac{q^2}{z}) = \frac{z}{q+z} R_q(\frac{1}{z}) $$ so that the product $$ \Theta(q,z) = R_q(z) R_q(1/z) $$ has an even nicer scaling property, $$ \Theta(q,z/q^2) = \frac{z}{q} \Theta(q,z) $$ and the fraction, even better: $$\Psi(q,z) = \frac{\Theta(q,z)}{\Theta(q,-z)} = - \frac{\Theta(q,q^2z)}{\Theta(q,-q^2z)} = \Psi(q,z/q^4) $$ Furthermore, for straight-forward reasons, $\Theta(q,z)$ has critical points at $z=\pm 1$ so that the fraction $\Psi(q,z)$ has critical points at even powers of $q$, $z = q^{2m}$ All of the preceding should be Routine. As the title of this post is meant to suggest, what we've called $\Theta$ is more like the star of this show than is $\Psi$, although it's not really the famous $\theta$... we'll get to $\theta$ in a minute. And the genuine star $\theta$ will give us the same $\Psi$, in some sense. The way $\Theta$ is defined, it should also have a very good Laurent Series Expansion, but (here's the trick) for now we're only going to worry about the second variable: $$ \Theta(q,z) = \sum_{n\in\mathbb{Z}} a_n(q) z^n $$ because the scaling property from above, $$ \sum_{n\in\mathbb{Z}} a_n(q) (z/q^2)^n = \frac{z}{q} \sum_{n\in\mathbb{Z}} a_n(q) z^n $$ is telling us that $$ q^{2n-1} a_{n-1}(q) = a_n(q) $$ so that, inductively, $$ a_n(q) = q^{n^2} a_0(q) .$$ It follows that $\Psi(q,z)$ can alternatively be written $$ \Psi(q,z) = \frac{\sum_{n\in\mathbb{Z}} q^{n^2} z^n }{\sum_{n\in\mathbb{Z}} (-1)^n q^{n^2} z^n }$$ and the first bit of magic is this: we really have no right to expect that any Laurent series defined by a nice-looking product should be so very sparse in any of its variables, but only square powers of $q$ need appear in this fraction-of-series representation of $\Psi$. The Really Magical $\theta$ then is defined to be this sparse series $$\theta(q,z) = \sum_{n\in\mathbb{Z}} q^{n^2} z^n $$ But that's just a hint of the Magic!

The basic Critical Points of $\theta(q,z)$, $z=\pm 1$, tells us we should particularly consider the series, also called $\theta(q) = \sum_{n\in\mathbb{Z}} q^{n^2} $, as well as the particular product $$ \Theta(q,1) = \prod (1+q^{2n+1})^2 $$ There is a Curious Relation one may exploit: $$ \Theta(q,1) \Theta(q,-1) = \prod_\mathbb{N} (1+q^{2n+1})^2(1 - q^{2n+1})^2 = \prod_\mathbb{N} (1-(q^2)^{2n+1})^2 = \Theta(q^2,-1) .$$ If nothing else, this suggests we should also consider the product $$ \theta(q) \theta(-q) = \left(\sum_\mathbb{Z} q^{n^2}\right) \left(\sum_\mathbb{Z} (-q)^{n^2}\right) $$ about which, some observations: if $m+n$ is odd, then we have some cancellation, or more precisely: $$q^{m^2}(-q)^{n^2} + q^{n^2}(-q)^{m^2} = ((-1)^n+(-1)^m) q^{m^2} q^{n^2} $$ which means that only terms with $m$ and $n$ of the same parity contribute; and $m$ and $n$ being of the same parity means exactly that there is a unique solution $m = a + b; n= a-b$: $$ \theta(q) \theta(-q) = \sum_{\mathbb{Z}^2} (-1)^{a-b} q^{(a+b)^2} q^{(a-b)^2} = \sum_{\mathbb{Z}^2} (-q^2)^{a^2} (-q^2)^{b^2} = (\theta(-q^2))^2 .$$ Significant "Hmmm...", Number 1. Of course, the terms with $m=n$ only turn up once each, as $(-1)^m q^{2m^2}$; but $m=n$ is a special case of $m\equiv_2 n$ Moving on, comparing the two relations by means of $a_0(q) \theta(q) = \Theta(q,1)$, $$ \theta(-q^2)^2 = \theta(q)\theta(-q) = \frac{1}{a_0(q)^2} \Theta(q,1)\Theta(q,-1) = \frac{1}{a_0(q)^2} \Theta(q^2,-1) = \frac{a_0(q^2)}{a_0(q)^2} \theta(-q^2) $$ or $$ \frac{1}{a_0(q)^2} = \frac{1}{a_0(q^2)} \theta(-q^2) = \frac{1}{a_0(q^2)^2} \Theta(q^2,-1) $$ From here, it's easy to check that $\lim_{q\to 0} a_0(q) = 1,$ and so $$ \frac{1}{a_0(q)} = \prod_{n\in\mathbb{N}} (1 - q^{2(n+1)}) $$ or, more famously known as the Jacobi Triple Product Identity, $$ \prod_{n=1}^\infty (1-q^{2n}) (1-q^{2n-1}z)(1-q^{2n-1}z^{-1}) = \sum_{n\in\mathbb{Z}} q^{n^2} (-z)^n $$ ... talk about Excessively Sparse $q$-Series! There must, of course, be a nice pictographable combinatorial argument for this analytic result. Ask Professor Polster. We've had one Significant "Hmmm...", wherein we found ourselves looking at $\theta(-q^2)^2 = \sum_{\mathbb{Z}^2} (-1)^{(a+b)} q^{2(a^2+b^2)}$; Those signums, of course, look a tad irksome; it'd be nice if we could drop them, but keep the cancellation; but that's Not Too Bad Either. The cancellation we had was from $(-1)^m + (-1)^n$, but we get the same zeroness with $1+(-1)^{m+n}$, in which the nonzero terms are all $2$. In Short: $$ 2 \sum_{a,b:\mathbb{Z}} q^{2(a^2+b^2)} = \sum_{m,n:\mathbb{Z}} (1 + (-1)^{m+n}) q^{m^2+n^2} = \theta(q)^2 + \theta(-q)^2 $$ and THIS (Significant "Hmmm..." Number 2) is the Start of the Real Magic of Theta the Magical: $$ \theta(q^2)^2 = \frac{\theta(q)^2+\theta(-q)^2}{2} \qquad \theta(-q^2)^2 = \sqrt{\theta(q)^2\theta(-q)^2} $$ $$ \operatorname{AGM}\big(\theta(q)^2,\theta(-q)^2\big) = 1 $$

[jessecmckeown]

from the MIT AI Lab memo "HAKMEM"...

[jessecmckeown]

Landen Pt. 5: the notorious stuff

Let us Name some Maps. "The" "Landen" transform, $v\mapsto \frac{1}{\sqrt{k}} \frac{2v}{1+v^2} $ is a double-cover of the elliptic curve $y^2=\sqrt{(k-x^2)(1-kx^2)}$ by the elliptic curve $u^2=\sqrt{(l-v^2)(1-lv^2)}$, where $$ l = L(k) = \frac{k^2}{(1+\sqrt{1-k^2})^2} ;$$ which defines $L$, one of our Important Named Maps. Similarly, the transposition $v \mapsto \frac{1-v}{1+v}$ is an isomorphism of whatever elliptic curve $y^2=\sqrt{(k-x^2)(1-kx^2)}$ and $u^2=\sqrt{(r-v^2)(1-rv^2)}$ with $$ r = T(k) = \left(\frac{1-\sqrt{k}}{1+\sqrt{k}}\right)^2 $$ which defines $T$, another Important Named Map. About two and half Pt.s ago, we pointed out that $L(v)^2 + L(T(v))^2 = 1$, a Curious Circumstance Indeed.

Among Elliptic Integrals $$ \int_a^b \frac{Q(x)}{\sqrt{P(x)}} dx $$ the Periods get a lot of attention, which correspond (roughly) to choosing $a,b$ to be (adjacent) roots of $P$. It doesn't look like it, but the [quarter] periods commonly known as $E(k)$ and $K(k)$ are, in the arrangement of things from Pt 4, easily written $$ E(k) = \int_0^{\sqrt{k}} \sqrt{\frac{1-kx^2}{k-x^2}} dx \\\\ K(k) = \int_0^{\sqrt{k}} \frac{1}{\sqrt{(1-kx^2)(k-x^2)}} dx $$ and the calculation we described but didn't do also gives us the lovely relations $$ E(k) = \frac{2}{1+l} E(l) - (1-l) K(l) \\\\ K(k) = (1+l) K(l) $$ where $$ k = \frac{2\sqrt{l}}{1+l} $$ Nice as those relations are, it's even nicer to write them like this: $$ E(l) = \frac{1+l}{2} E\left(\frac{2\sqrt{l}}{1+l}\right) + \frac{1-l}{2} K\left(\frac{2\sqrt{l}}{1+l}\right)$$ $$ K(\sqrt{1-l^2}) = \frac{2}{1+l}K\left(\frac{1-l}{1+l}\right) $$ which, on multiplying, gives us the Curious Equation $$ E(l)K(\sqrt{1-l^2}) = E\left(\frac{2\sqrt{l}}{1+l}\right) K\left(\frac{1-l}{1+l}\right) + \frac{1-l}{1+l} K\left(\frac{2\sqrt{l}}{1+l}\right) K\left(\frac{1-l}{1+l}\right) $$ or, in terms of our Named Maps, $$ E(L k) K(L T k) = E(k) K(L L T k) +(LL Tk) K(k) K( LL T k) $$ about which we note: the elliptic products on both sides involve complementary arguments. Continuing, this arrangement also makes it easier to deduce the (equivalent) $$ E(LLTk) K(k) = E(LTk)K(Lk) + (L k) K(LTk)K(Lk) $$ which, added to the original, also gives us $$ E(Lk)K(LTk) + K(Lk)E(LTk) + (Lk)K(LTk)K(Lk) \\\\ = \\\\ E(LLTk)K(k) + K(LLTk)E(k) + (LLTk) K(k)K(LLTk) $$ From here, it is a simple "Exercise" to check that the very symmetric expression $$ E(Lk)K(LTk) + K(Lk)E(LTk) - K(Lk)K(LTk) $$ is invariant under replacement of $k$ with $L k$. At this point, the following should be easy calculations: $$ E(0)=K(0)=\pi/2 $$ $$ E(1) = 1 $$ $$ K(k) - E(k) \lt k^2 K(k) $$ $$ K(1 - k) \underset{k\to 0}{\sim} \log\frac{1}{k} $$ $$ \lim_{k\to 0} \left[ E(k)K(\sqrt{1-k^2}) + E(\sqrt{1-k^2})K(k) - K(\sqrt{1-k^2})K(k)\right] = \frac{\pi}{2} $$ BUT! Since $L^n k$ tends to $0$, and since the subject of the limit is invariant under $k\mapsto L k$, it follows that $$ E(k)K(\sqrt{1-k^2}) + E(\sqrt{1-k^2})K(k) - K(\sqrt{1-k^2})K(k) = \frac{\pi}{2} $$ for all $k$. Other folk derive that lovely equation by differentiating with respect to $k$... other smart folk. I don't think I could have made that approach look any prettier than this one here.

[jessecmckeown]

Landen Pt 4. More Integrands!

It's easier with a well-understood Computer Algebra Assistant, but, well... But that's very Woostery of me, starting in the wrong place. One develops a conviction that the simple maps representing double-covers of elliptic curves are "the right" way to think about Landen Transforms, and then you get lost looking for "the right" way to understand the next trick in these terms. It's easy to get lost. If we choose to norrmalize our Elliptic Curves in terms of the modulus $k$ as defined by $y^2 = (k-x^2)(1-kx^2)$, then writing in terms of $x$ there are roughly two globally-available double-covering maps... one could say there's only one, up to twists and re-orientations, but ... I digress. There's the Möbius-translated squaring map $$ x\mapsto \frac{x^2 - \lambda}{1-\lambda x^2} \tag{Sq1}$$ and there is the conjugate of this map by the transposition $u\mapsto \frac{1-u}{1+u}$, which one calculates is $$ x\mapsto \rho \frac{2x}{1+x^2} \tag{Sq2} $$ The particular relations between $\rho,\lambda,k$ will depend on whether one is mapping from or to the curve with modulus $k$. In one sense, it does not matter whether we now use $\mathrm{Sq1}$ or $\mathrm{Sq2}$; however, the algebra is much simpler using $\mathrm{Sq2}$, or specifically, substitutions $$ x = \frac{1}{\sqrt{k}} \frac{2u}{1+u^2} $$ which is a double cover mapping to a curve with modulus $k$, from one with modulus... something that you can work out if you really must. Well, we already know what happens to our favourite measure, $$ \frac{dx}{\sqrt{(k-x^2)(1-kx^2)}} $$ when pulling-back along this substitution, $$ \frac{dx}{\sqrt{(k-x^2)(1-kx^2)}} = \frac{du}{\sqrt{k^2u^2-(4-2k^2)u^2+k^2}} $$ (if you ask maxima to do this substitution, it'll ALMOST tell you that, except that it'll mention an extra pair of branch points at $u=\pm 1$ ... which I believe I've mentioned before...) So it's maybe a Good Idea to see what happens under this substitution to other elliptic integrands. How about this one: $$ \sqrt{\frac{1-kx^2}{k-x^2}} dx = \frac{1-kx^2}{\sqrt{(k-x^2)(1-kx^2)}} dx ?$$ They call that one "second kind". And the Answer, up to some Branching Considerations: $$ \frac{2(1-u^2)^2}{(1+u^2)^2\sqrt{(k^2u^2-(4-2k^2)u^2+k^2)}} $$ Hm. That may not look like Progress, but in fact It Is! The first opacity to overcome here is that the fraction we have acquired, $$\frac{2(1-u^2)^2}{(1+u^2)^2} $$ ... it really wants to be a Polynomial... let's do Partial Fraction decomposition. $$ \frac{2(1-u^2)^2}{(1+u^2)^2} = \frac{8}{(1+u^2)^2} - \frac{8}{1-u^2} + 2 $$ The second is: the conceit of this game is that we're now allowed to Integrate $\frac{1}{\sqrt{P(x)}}$. We also know how to differentiate. A perfectly good thing to Differentiate is $$ \sqrt{P(x)} $$! You can probably tell that this doesn't immediately help, so instead, differentiate products $$ \frac{x^m}{Q(x)} \sqrt{P(x)} $$ and in particular you find $$ \frac{d}{du} \frac{u\sqrt{k^2u^4-(4-2k^2)u^2+k^2}}{1+u^2} = \left(\frac{8}{(1+u^2)^2} -\frac{8}{1+u^2} +k^2 u^2+k^2\right)\frac{1}{\sqrt{k^2u^4-(4-2k^2)u^2+k^2}} $$ and this is great! The derivative and the transformed Second Kind Integrand have exactly proportional singularities, at least at $\pm i$, where they're new. Or, to put it differently, Landen-transforming the Second Kind Integrand gives a sum of another Second-Kind integrand, a First-kind integrand, and a derivative (whose integral we know trivially).

[jessecmckeown]

Landen Pt 3: double covers and duality ... and ...

... this one feels a little more I-don't-know-where-to-stop-ish... I hope you don't mind.

Any way, $\RR$eal elliptic curves (i.e. with $\RR$eal coefficients) have $\RR$eal duals, and while there isn't a "double one direction" map of one elliptic curve to itself, there's an elliptic curve that does receive such a map. Let's invent some confusing notation, and call the primary form of any given $\RR$eal Elliptic curve $E_{a,b}$ where $a$ and $b$ are suggestive names. The dual of $E_{a,b}$ will be $E_{b,a}$ and there's a double-covering map in one direction $E_{a,b} \to E_{a,2b} \sim E_{a/2,b}$ and a conjugate double-covering map in the other direction $E_{a,b} \to E_{2a,b} \sim E_{a,b/2}$. Let's say that $E_{a,b} \to E_{a,2b}$ is our "Squaring" map. Then the usual way to describe the Landen transforms is the other one; and so we want to describe the main parameter, call it $l$, of $E_{2a,b}$. But we know that the main parameters $l$ of $E_{2a,b}$, and $k$ of $E_{2a,2b}$ are related by $$ l^2 = \frac{4k}{(1+k)^2} $$ or equivalently $$ k = \frac{1-\sqrt{1-l^2}}{1+\sqrt{1-l^2}} = \frac{l^2}{(1+\sqrt{1-l^2})^2} $$ AND! $E_{a,b}$ and $E_{2a,2b}$ are isomorphic! So $$ l = \frac{2\sqrt{k}}{1+k} $$ is the relation we want anyways! The geometrically-sensitive among us will have noticed some Suspicious Fractions turning up ... well, all over the place. It really shouldn't be a surprise... a peripherally-centered inversion maps a circle onto a line... Well, anyways. With all the transformations to choose from and compose, it's easy to get lost. One would be excused for not immediately asking how to compare $E_{2a,b}$ and $E_{2b,a}$; we've just calculated the main parameter --- call it $k_{2a,b}$ --- for $E_{2a,b}$; From Fiddly Constants, we can also calulate $$ k_{2b,a} = \frac{2 \frac{1-\sqrt{k}}{1+\sqrt k} }{1 + \left(\frac{1-\sqrt{k}}{1+\sqrt{k}}\right)^2} = \left( \frac{1 - \frac{k}{1+\sqrt{1-k^2}}}{1 + \frac{k}{1+\sqrt{1-k^2}}}\right)^2 = \frac{1-k}{1+k}$$ from which the geometrically-sensitive among us will immediately remember $$ k_{2b,a}^2 + k_{2a,b}^2 = 1 $$ In the Elliptic Integration Liturature, this relationship is called complementarity, and would sometimes written $k_{2a,b} = k'_{2b,a}$, except that nobody else puts those subscripts there. Since we can use whatever values of $a$ we like, we can in fact write the same result a suggestive bunch of times: $$ k_{b,2^{n-1} a}^2 + k_{2^{n+1}a,b}^2 = 1 .$$