mancoub

[mancoub]

The Compelling Truth of the Universe

I'm really trying to make a point here. I'm not trying to go on a religious rant. Most people alive today and even in the history of personkind, have asked this fundamental question, "Where did it all come from?" If you have studied Science or even just observed the natural world, there is so much to the word "all." We aren't talking about the Earth and the World, People and Cities. We are also talking about Music, Mathematics, Language, Biology, Atoms, Computer Science. There are so many details and so much Truth to discover in the word, "all" in the question, "Where did it all come from?" Like Bertrand Russell writes about in "The History of Western Philosophy" That the Nile River would flood on a certain day of the year. So ancient people who studied the stars and made the first calendars, could tell farmers to plant all their crops and use all their stored seeds by a certain day, before the Nile River would flood. Back then, if you planted too early, you seeds would dry out and die. If you planted too late, your crops wouldn't come to harvest before the first of winter. It was a type of magic that eventually became agriculture and science. Even if these ancient stargazers would have tried to explain how they created a calendar with days, months, season, cycles, still those people would see it as magic and not as part of the "all" that is evidence of the detail and complexity of the world. Most people in the world, and throughout time, are stressed out by this question being unanswered. In a way, Scientist challenge themselves to hold onto that stress and anxiety of not knowing the answers. Most people can't hold onto this anxiety and seek a simple and inaccurate answer. "Where did it all come from?" Some find comfort in saying God made it all. This is a powerful belief that offers closure. It may offer closure but it also risks halting deeper inquiry. It takes a lifetime of effort to answer the unknown and just a moment to say that god made all of it. This stops most people from asking or probing for more resolution, more detail, more explanation to the natural follow-up question, "What is the nature of god?" Only scientists would pose this question in this way. Most people would say, "Well then, who created god?" which is kind of the same question, whoever created god, must have designed his nature. Most people believe that god has always existed. This belief is unprovable. But more importantly, it's a paradox, much like the universe itself. One of the natures of the universe is that it's paradoxical, we find paradoxes throughout this concept of "all." It's these paradoxes that I find to be the most compelling and truth aspect of the Universe, the reason I write this blog, the reason I get out of bed every day. I'm writing my own BigInt class and I'm testing by calculating the square root of 2 to more than 6,000 digits. With computers, this is a trivial thing. Before computers, there are books in ancient libraries, where monks calculated 5, 6, even 7 or more digits of the square root of two. This is part of the "all" that exists when you ask, "Where did it all come from?" It's this part of the "all" that has roots in "transcendentalism." We can calculate, to more and more precision, the digits of irrational numbers. We can say, "Where did it come from?" and the answer is "We don't know." and then follow it up with, "How much of it, can we know?" and we can get 5, 6, even 7 digits out of infinity, but we don't stop there. We build computers, and we build better algorithms, and we can get millions of digits of precision. We just can never get to god. No matter how hard we try, we will always fall short of infinity. And this is not to say that we should give up and just answer the question that god did it. No, Answering the question with an absolute is unfair to the nature of the universe which is paradoxical, infinite, and transcendental by nature. I want to answer the question, "Where did it all come from?" with "We may never know but we can always try to learn more."

[mancoub]

Back at it, Beltmatic

After reaching level 100 in the game Beltmatic, i was disapointed to learn that there are 1000 levels. The truth is that the game still brings me some joy and I've constantly been thinking up new strategies and algprithms to solve these factory machines quickly.

One of my first algorithms was based om square numbers which I must have used for dozens of levels. I quickly realized that finding two different numbers like 8x8 is harder than 4x16 because finding two 8's close together may be more difficult than finding a 4 and 16 close together.

As the target number grew past 1 million, I had to find new ways to blow-up numbers fast.

Exponetial opperations fit the bill but eith a predictable period of 2^n or 3^n... etc I found that just multiplying several large numbers was easier and more reliable to find.

As I'm developing new algorithms, I'm also making Javascript widgets to help with the math. Some of my code would stall my browser because of Big(O) and efficiency failure. That is until last night.

1. I start by creating an array of all primes less than or equal to my largest extractor.

2. Then I solve for smallest prime factors for N

2b. If I run out of primes, I end the cycle early, since one of the prime factors is larger than my max extractor.

3. Then I solve for N-1

4. I keep solving for N-c, until c is equal to my max extractor

Not only does this code run fast, I'm getting multiple solutions for x*y*z+a, event for N>2 mil

[mancoub]

Guess Sqrt Aprox

Stepwise Square Roots from Fractions

We know that the square root of 30 is between 5 and 6 because 30 is greater that 25 and 30 is less than 36.

If we write 5 as a fraction 5/1 and we consider that 30/5 is another sqrt approximation, then we get 5 and 6. Neither are exact but the average of the two is 11/2.

We can do this for all integers.

First guesses could be g= starting sqrt aprox based on, n= the number we are taking the square root of, a is the lower sqrt aprox where a^2 is less then n.

g=(a^2+n)/2a

2:1+2/1=3/2

3:1+3/1=4/2

5:2+5/2=9/4

6:2+6/2=10/4

7:11/4

8:12/4

10:19/6

(LowerA^2+x)/(LowerA*2)

x=2;A=1;(1+2)/2;sqrt2-aprox=-0.08

x=3;A=1;(1+3)/2;sqrt3-aprox=-0.26

x=4;sqrt4=2

x=5;A=2;(4+5)/4;-0.01

x=6;A=2;(4+6)/4;-0.05

x=7;A=2;(4+7)/4;-0.10

x=8;A=2;(4+8)/4;-0.17

x=9;sqrt9=3

x=10;A=3;(9+10)/6;-0.004

[mancoub]

Beltmatic and Factory Math

I've been playing this factory game called Beltmatic, which doesn't require any real math but the potential is there. All the nodes but 1's are inactive to start. You must build extractors on those nodes and combine them with operators to build numbers. For example, you have only 1's to start and once you unlock the addition operator, you can add 1 plus 1 to make 2's and now you can deliver 2's at the rate of your addition operators. The trick is to design multiple machines that combine to increase your rate of delivery well beyond the rate of your operators. You can also upgrade your rates by delivering numbers as a side quest with a soft cap at level 8 and then miniscule increases to their rates after that. There are several strategies that I've seen and read about on the forums, like: Calculators, Duplicators, Binary Operations, etc. If you want to feed some integers from an extractor node into a division operator to get out the same number twice, you could use the formula: Ex = n x (n + 1) + n If you have an Extractor Node for Ex, and an Extractor node for (n + 1), then you can use Division to make two outputs of n. Let's say I want to make a bunch of 7's n x (n + 1) + n 7 x (8) + 7 56 + 7 63 Then with your Division Operator take in 63 and divide by 8 to get 7 r7 If you are early in the game, you may not have 63's unlocked, so you will have to make them with 8 x 8 - 1 or 31 + 32 or even 21 x 3 or 15 + 16 + 16 + 16 The way you make the numbers are limitless. You can use any operator that you've unlocked and you can be as efficient or as inefficient as you'd like. But efficiency is nice. 3 / 2 = 1 r1 8 / 3 = 2 r2 15 / 4 = 3 r3 24 / 5 = 4 r4 35 / 6 = 5 r5 48 / 7 = 6 r6 63 / 8 = 7 r7 80 / 9 = 8 r8 99 / 10 = 9 r9 120 / 11 = 10 r10 143 / 12 = 11 r11 168 / 13 = 12 r12 195 / 14 = 13 r13 224 / 15 = 14 r14 255 / 16 = 15 r15 288 / 17 = 16 r16 323 / 18 = 17 r17 360 / 19 = 18 r18 399 / 20 = 19 r19 440 / 21 = 20 r20

But these are just the minimum numbers you need to get double the result. If you don't mind increasing your denominator by 1, you can then increase your numerator by n and do it all over again. 63 / 8 = 7 r7 (63 + 7) / (7 + 1 + 1) = 70 / 9 = 7 r7 For the example of 7, you could run this out to 19 (63 + 7 x 19) / (7 + 1 + 19) = 196 / 27 = 7 r7 To make 27, you just need 13 + 14 and to make 196 you just need 14 x 14. The efficiency comes when you recycle a single Extractor, in this case 14, to make all your secondary numbers by performing operations. You could even go to the extreme and make a storage of 1's by dividing 14 by 14 and then subtracting 14 - 1 Extractor 14 > Division (14, 14) > Storage 1's Extractor 14, Storage 1 > Subtraction (14, 1) > Storage 13's Extractor 14, Storage 13 > Addition (14, 13) > Storage 27's Extractor 14 > Multiplication (14, 14) > Storage 196's Storage 196, Storage 27 > Division (196, 27) > Storage 7's Compare that to an Extractor 2 Extractor 2 > Division (2, 2) > Storage 1's Extractor 2 > Multiplication > Storage 4's Extractor 2, Storage 1 > Addition (2, 1) > Storage 3's Storage 4, Storage 3 > Addition (4, 3) >Storage 7's Compare to Extractor 8 Extractor 8 > Division (8, 8) > Storage 1's Extractor 8, Storage 1 > Subtraction (8, 1) > 7's 7x3=21 21-2=19 19x19=361 21+2=23 23x23=529 21+7=28 28*28=784 361/10=36 r1 36/10=3 r6 3/10= 0 r3 529/10=52 r9 52/10=5 r2 5/10= 0 r5 784/10=78 r4 78/10=7 r8 7/10= 0 r7 11826x11826=139854276

[mancoub]

ChatGPT's modern dialog

Here’s a short modernized dialog inspired by Euthyphro, introducing Jean (a postmodernist) and Neil (a science advocate), with Socrates in his usual role of questioning:

Scene: Outside a courthouse in modern times. Socrates is standing with Jean and Neil.

Socrates: Ah, Jean, I see you are deep in thought. What brings you to this place today?

Jean: Socrates, I’m here to challenge the very idea of truth. You see, truth is nothing more than a construct. It is shaped by our perspectives, experiences, and the culture we live in. What is true for one may not be true for another.

Socrates: Fascinating. And so, you suggest there is no absolute truth? Merely many truths, each as valid as the next?

Jean: Exactly. Each of us carries our own truth. The world is a web of interpretations, and we are the spiders, spinning the threads as we see fit.

Socrates: Then, if I were to say the sun rises in the east, and another says it rises in the west, are both equally true?

Jean: Well, to you, the sun rises in the east. But for someone on the other side of the world, their experience may differ. Truth is subjective and contingent on the observer.

Neil: (chuckling) With all due respect, Jean, that’s an oversimplification. The sun’s movement, relative to the Earth, follows laws of physics that are the same for everyone, everywhere. Truth might be elusive, but it’s not entirely subjective. Through observation, testing, and critical thinking, we can refine our understanding of the world.

Socrates: Ah, Neil, you speak as one who believes in a truth that can be known, albeit gradually, through inquiry and evidence.

Neil: Absolutely. It’s not that everyone gets to create their own reality. We all exist in the same universe. While we may not know everything about it yet, scientific inquiry helps us get closer to a shared truth over time. It’s not subjective, it’s incremental. Take gravity, for instance. It doesn't matter where you're standing or how you interpret it—jump off a cliff, and gravity works the same for everyone.

Jean: (smiling) But Neil, science itself is constantly evolving. What we believed to be true a century ago is now outdated. You admit that your truths change with new discoveries. Doesn’t that make your truth just another story, albeit a more popular one?

Neil: (nodding) Science evolves, yes, but that doesn’t mean all truths are equally valid. Scientific knowledge builds on itself, getting more precise as we refine our methods and understand the universe better. It’s not about picking any truth you like—it’s about testing, refining, and getting closer to what’s real. Gravity isn’t just a story; it’s a fact that has withstood countless tests.

Socrates: (raising an eyebrow) Then, Neil, would you say that there is an absolute truth, though perhaps we cannot fully grasp it?

Neil: I believe so. There is an underlying reality, and while our understanding of it may never be perfect, we can get closer to it through careful observation and critical thought.

Jean: But why this obsession with getting closer to something you can never fully reach? Isn’t it more freeing to accept that truth is fluid, changing with the times, shaped by our experiences and perspectives?

Neil: Accepting that nothing is real leads to dangerous territory. If truth is fluid, as you suggest, how do we navigate the world? How do we build bridges, cure diseases, or send rockets into space? You may believe truth is subjective, but when you’re sick, you want a doctor who trusts in science, not someone who tells you their personal interpretation of disease.

Socrates: (smiling) So we return to the question of piety—or in our case, truth. Jean, you say that truth is relative, shaped by the mind of the observer. Neil, you argue that truth is something objective, though our understanding of it may evolve. But what if we cannot define truth without falling into contradiction, as our friend Euthyphro once did with piety?

Jean: Exactly, Socrates! Truth is a paradox—it changes, and the more we try to pin it down, the more it slips away.

Neil: I see your point, but paradoxes only exist because we haven’t figured things out yet. Look at quantum mechanics—it’s full of weird contradictions at first glance, but that doesn’t mean it’s unknowable. It means we need better models to explain it.

Socrates: And so, we come to a crossroads. Jean, you embrace the fluidity of truth, while Neil, you seek to approach it through refinement and knowledge. Perhaps both views have merit, for if truth is elusive, does that not give us a reason to continue searching, rather than resigning ourselves to either extreme?

Jean: I see where you're going with this. Perhaps the search for truth is the real pursuit, rather than truth itself.

Neil: I can agree with that, as long as we understand that some pursuits lead us closer to understanding reality, while others can lead us astray.

Socrates: (smiling) And so, the dialogue continues. Let us never cease in our questioning, for in that lies the true spirit of inquiry.

This modernized dialog retains the tension between relative truth and absolute truth, while framing the debate in contemporary terms: the postmodern relativism of Jean versus the scientific realism of Neil, with Socrates guiding the discussion as a neutral inquirer.

[mancoub]

Euthyphro and Truth of Piety

I've been thinking about Euthyphrho a lot lately. It's one of the most popular dialogs, written by Plato (depicted above) and it features Socrates as the main character.

The story goes like this, Socrates is standing outside of the courthouse, waiting to defend himself against charges for "corrupting the youth," when he runs into Euthyphrho, a lawyer for the state. Euthyphrho has a reputation for being a pious man and a virtuous lawyer. Euthyphrho is prosecuting his own father for murder and the facts have room for interpretation. Socrates challenges Euthyphrho to define Piety and Euthyphrho is unable to define it without a paradox or a self-referential-definition.

The word Piety and Virtue are such old-fashioned words. Today, we might use the term Ethical or Moral. There is also an ancient ideal of Divinity attributed to the Greek gods. This notion is somewhat foreign to a modern ethical society, since we all know how fickle the Greek gods were and so to describe them as Pious is difficult because their actions are often immoral and unethical and not Virtuous or Divine.

The other thing I've been thinking about is the approximation of Truth due to language. In this dialog, Socrates challenges Euthyphrho to define Piety and he says, "That which pleases the gods." When you define something using language this way, you open yourself to paradoxes and un-evaluable statements. What are the gods? Just the good ones? Even gods who are evil or spiteful? How do we know which gods to follow? In the end Euthyphrho's definition was flawed.

But I went on to think, all definitions are flawed in the same way. Definitions are not the thing they wish to define. In a physical world, we have real things that can be observed, tested, and evaluated. We can define these things in different ways with different observers having slightly different points of view. The thing itself is the Truth and things are not definitions. Any language definition would be an approximation of a thing that's True.

This gets more complicated when the thing you are trying to define is not part of the physical world. If you are trying to define a concept like Piety or Virtue, then you are talking about a concept that is moldable and not immutable. Any real attempt to define something that changes will never be exact, subject to a changing definition.

I think about this idea from time to time, that truth can be relative, especially truth based in terms. That our values as a society change and that there are similarities that span over the ages. Similarities that could be like Aristotle's Substance of things, which helps us understand what is Virtue and how our modern Morals are the same.

Fast forward my philosophical links to Jean Baudrillard who had the audacity to say that all true is relative and that every observer can choose. Because of Postmodernism, we now have a definition of truth that states, "Truth can be anything." While the dialog of Euthyphrho does lead to the inability to precisely define terms like Piety, I think that the jump in logic to then state that nothing can be known or that all truth is relative, is quite a stretch.

Today, we live in a world where a large group of society either believes a construct of truth and still others define their own truth, I feel that the missing puzzle piece is that there is still room for absolute Truth that more and more people ignore or deny.

And I'm not talking about religion, because I feel that religious truth falls into the category of constructed truth. It's Scientists who struggle to wrangle the definitions of the universe, to describe and define the attributes of observable things. And yet, these same Scientists are constantly changing their definitions based on their experiments to refine and change their definitions. This process sounds exactly the same as the refining and changing of definitions over time based on trends and changes in society.

So either Absolute Truth exists and can never be precisely defined or there is no such thing as Absolute Truth and you can choose your reality.

I know that we live in a world where people lean towards the second definition. They want to choose their illusion of reality. And in some ways we all fool ourselves, for emotional reasons, we define our reality so that we can bear to live in an uncertain world.

But I feel it's more complex than just choosing. There is a "real" reality out there, one that can be shared, one that challenge our illusions, critical thought and critical evaluations.

The answer is not to give up on the pursuit of Truth but to stay vigilant and to challenge those who are certain.

[mancoub]

Origami Math

There is an old technique I learned from an art teacher who was teaching proportionality on a canvas. He drew a rough square, then made a couple diagonals. Then he divided the square into half with a vertical line and drew all possible diagonals in them. It's a rough proof, especially when you consider that the lines are drawn by hand, but it still works for people trying to find thirds.

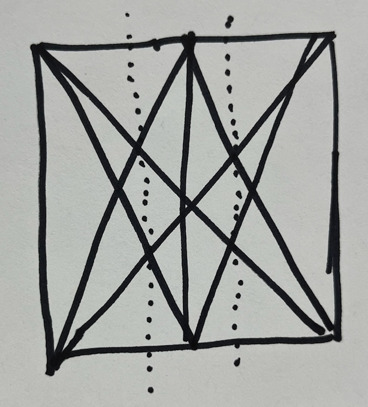
Years later, I found the same process outlined in more than one of my origami books from my childhood. I guess I was too busy looking at the diagrams to read the text.

The idea of finding divisions of a unit square is a compelling and useful pursuit. Some people guess, which can have surprising accuracy. Some people use a ruler, which also works. What I'd like to do is write a proof and create a process from that proof that can find any division, just by using origami.

The Math

For starters, the math is slope intercept form to find two functions and set them equal to each other.

If you extrapolate the above diagram, you can convert this to a function f(x) = mx +b, where f1(x) = (1/2)x and f2(x) = -x +1

f1(x) has a y-intercept of 0 and a slope of +(1/2)

f2(x) has a y-intercept of +1 and a slope of -1

f1(x) = (1/2)x

f2(x) = -x +1

Set the two formulas equal to each other and then solve for x.

x/2 = -x+1

(mul 2 on both sides), x = -2x + 2

(add 2x on both sides), 3x = 2

(div 3 on both sides), x = 2/3

Folding the left edge of the paper to the 2/3 mark will create a 1/3 crease in the unit square. You can also fold through the mark and when you plug this back in to solve for y, you find that it works both ways forming a 3x3 grid in the paper.

You can use 1/4 divisions of the unit square as a guideline to fold a diagonal with a slope of +(1/4), like this

Creating functions for the diagonals like we did before, you get:

f1(x) = (1/4)x

f2(x) = -x +1

Set them equal to solve for x.

x/4 = -x+1

(mul 4 on both sides), x = -4x + 4

(add 4x on both sides), 5x = 4

(div 5 on both sides), x = 4/5

Folding the left edge of the paper to the 4/5 mark will create a 2/5 crease in the unit square. Because there are eight creases to make a 5x5 grid, using the intersection as a guideline only, you will get 1/5 and 2/5 in both directions and then you will need to divide your 2/5 sections in half.

What may not be evident is that since quartering the paper is folding edge to edge to make even divisions for a power of 2, that there is another division of quarters that will also intersect the diagonal, but this time it intersects giving a different fractional part of the unit square. f(x) = (3/4)x. Set this equal to our unit diagonal and you get this:

3x/4 = -x+1

(mul 4 on both sides), 3x = -4x + 4

(add 4x on both sides), 7x = 4

(div 7 on both sides), x = 4/7

Since f(x) = (2/4)x reduces down to x/2, you don't need to repeat this one because we've already proved that it will divide the unit square into thirds.

If you study the sequence of formulas that we solved, you may see that a pattern emerges.

Our first set of formulas started with slope 1/2 and solved for 2/3

The second set of formulas used slope 1/4 and solved for 4/5

The last set of formulas had slope 3/4 and solved for 4/7

In each case, the new division of the unit square that we found, borrows the denominator from the guideline folds and places this in the numerator. Then it adds the numerator to the denominator to find the new denominator.

One can also state that all divisions less than 2 to the power of n has at least one guideline that can be calculated. So for 2^3, which is 8, you can find 1/7, 1/5, 1/3 and you don't have to find 1/6 because you can make that by starting with 1/3 and dividing by 2. You don't need to find 1/4 because it is a power of 2 and you don't have to solve for 1/1 because that is the unit square.

diagonals of long rectangles will intersect the unit diagonal

1/8 finds 8/9

2/8 (1/4) finds 4/5

3/8 finds 8/11

4/8 (1/2) finds 2/3

5/8 finds 8/13

6/8 (3/4) finds 4/7

7/8 finds 8/15

Going through this motley list of fractions, every denominator less than 2^4 can be seen except for 14, 12, 10, 8, 6, 4, 2, 1

We've already addresses most of these but let's explain

1/14 can be found by dividing 4/7

1/12 can be found by dividing 1/6

1/10 can be found by dividing 4/5

1/8 can be found by dividing 1/4

1/6 can be found by dividing 2/3

1/4 can be found by dividing 1/2

1/1 is the unit square.

[mancoub]

This weekend, I was challenged to diagram the 3 color weave for a 30 piece origami modular. This is a slightly challenging problem that comes to me intuitively. I've explained it to other intuitive folders and mathematicians with repeatable successes. However, I've been challenged to go one step further to document or diagram the "map" so that I will never have to "figure it out" again. Electra is an origami modular, folded from a square, published in Paul Jackson's book, "The Ultimate Papercraft and Origami Book" and attributed to Origami Artist David Mitchell.

Step 1

Fold a preliminary base with pre-creased blintzes and two cupboard pinches. When collapsing the preliminary base, put back two blintzes on opposite corners.

Step 2

Find the pinch guideline and fold a long diagonal from the bottom tip to the pinch. This causes the flap to go over the center vertical, which is required to create the pocket. Crease this on the right hand side of the front, flip the model over and crease the right hand side on the back. If you swap sides, and crease only on the left hand side, that's okay too, as long as you repeat on the left side from behind. Finally, inside reverse the long diagonal and find those two missing blintz pre-creases and put them back in place. This will make the basic unit which can make modular with nearly any multiple of 3. Unit count 12, 24, 30, 60, 90

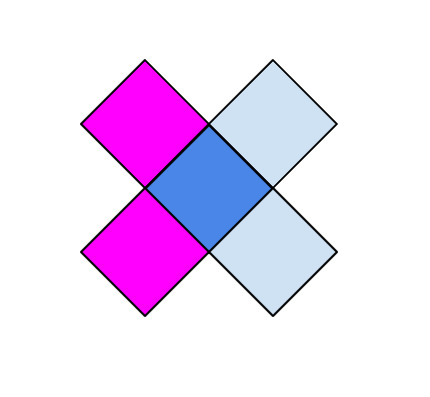
In this photo you can see a bright pink unit and two different shades of blue. Let's call them Pink, Blue, Light. The word light meaning a shortened version of "light blue."

In this photo overlay, you can see that the Blue units form a star pattern. This is my old method for both solving the color weave and also teaching it. But we can start from this photo to graph out a color map for 30 pieces with the central starting point being the five units in the lower front of this photo, "Pink, Light above a single Blue with Pink, Light below."

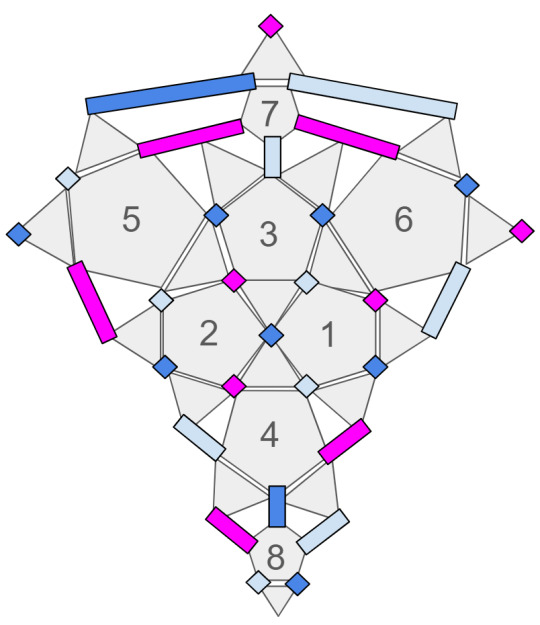
Hub 1 This is a starting form of five units in an X-shape. It can be defined as a Blue Hub, with the Blue in the center and has two Pink and two Light units attached. You can also say that the pattern is BPLPL. Meaning that the four units surrounding the center unit are mirrored Pink, Light. You can make three more units with these five colors: BPLLP, BLPLP, BLPPL.

Ring 1 Here is another way to identify five units, this time in a ring of five, also one of the polygon faces. The ring below is identified for it's single Pink with two Blue and two Light units. You can call this ring PBLBL. There is only one other ring that you can create with the same units: PLBLB.

Ring 2 Here is the second ring. LPBPB

Ring 3 Here is the third ring. PBLBL

Here is the whole 30 pieces mapped. Now this is just one mapping, and there should be a couple different ways to map this pattern over this polyhedron. However, there should only be two different ways to map it, once you have locked onto the first five pieces from "Hub 1"

[mancoub]

Triangular numbers and Primes continue

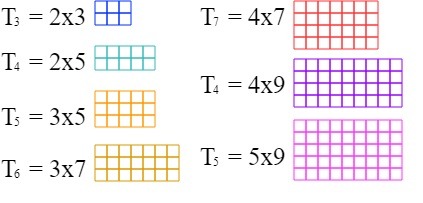
Starting with 2x3 and incrementing one factor by 2 and then alternating and incrementing by 1 we can create a pattern of product pairs thay give us the triangular numbers.

2x3 and 2x5 (four legs all primes)

3x5 and 3x7 (all primes)

4x7 and 4x9 (just one prime leg)

5x9 and 5x11 (two primes, three legs)

6x11 and 6x13 (two primes)

7x13 and 7x15 (two primes, three legs)

8x15 and 8x17 (one prime leg)

9x17 and 9x19 (two primes)

10x19 and 10x21 (one prime)

11x21 and 11x23 (all primes)

12x23 and 12x25 (one prime)

13x25 and 13x27 (one prime, two legs)

14x27 and 14x29 (two primes)

15x29 and 15x31 (two primes)

16x31 and 16x33 (one prime)

17x33 and 17x35 (one prime, two legs)

18x35 and 18x37 (one prime)

19x37 and 19x39 (two primes, three legs)

20x39 and 20x41 (one prime)

21x41 and 21x43 (two primes)

22x43 and 22x45 (one prime)

23x45 and 23x47 (two primes, three legs)

24x47 and 24x49 (one prime)

25x49 and 25x51 (no primes)

Here is where the primes dry up and relatively primes prevail. We have {5,5} and {7,7} and {3,7}l

Each line is n(2n-1) and n(2n+1) or 2n²±n

For factors of these triangular numbers that both legs are different by 2 they are always twin primes. For others where the shared factor is the same prime, there are a high number of third prime legs.

We can test this with primes

p|2p-1|2p+1

2|3|5

3|5|7

5|9|11

7|13|15

11|21|23

13|25|27

13 is the first prime where this pattern does not generate a new prime. But there is a high degree of new primes even if it's not everytime.

Even though it's clear that we can't predict primes in the factors for these triangular numbers it's really satisfying to say that all the factors generated using this pattern are relatively prime to each other.

n=53, 107=2x53+1

n=509, 1019=2x509+1

n=5003, 10007=2x5003+1

[mancoub]

Triangular numbers and Primes

Triangular numbers can be created by adding whole numbers in a series, like this 1+2+3+4+5

Algebraically, it can also be expressed as a quadratic equation (n(n+1))/2 or (n²+n)/2

Since prime numbers can never be the product of two or more numbers, it's fascinating to find a sequence using addition that creates non-prime numbers.

When it comes to triangular numbers, they can be expressed as a series of numbers added together or as a quadratic equation. This also means that they can never be prime. Additionally, there are patterns when they are products of two relatively prime numbers.

Starting with the third triangular number, 6, you can multiply together two primes 6=2x3

Expanding this new pattern the number 8 is the product of 2x4 and is not a triangular number. A requirement for triangular number is that they are the product of two relatively prime numbers. So either two prime numbers or two numbers that share no prime factors.

Following this pattern the next product to check is 2x5 which is 10 and since 2 and 5 share no common factors, this means that 10 is a triangular number and it is.

Once we find a new product, we increment the next factor as in 2. So 3x5 has no common factors and is confirmed to be a triangular number as well 15=3x5

Keep 3 and increment the next factor, 5 becomes 6 and you get 18=3x6 and we see that 3 and 6 share a common prime factor in 3 itself so 18 is not a triangular number and we increment again until we find one.

Next is 21=3x7 which has two prime factors and is our next triangular number.

We could just write them out like this

2x3 2x4 2x5 3x5 3x6 3x7 4x7 4x8 4x9

What we get is a new pattern where each new relatively prime pair is kept and the next number is dropped. Instead of calculating the next relatively prime pair, it's always every other one.

When 2 is the first factor we increment 3 which is Tri and 4 is not then 5 is Tri again.

Keeping 5 we increment 2 to 3 and so 3x5 is tri

Next we keep 3 and increment 5 to 6 which is not. Then 6 becomes 7 which is Tri again.

Drop 7 and increment 3 to 4 to get Tri again.

Then 4x8 is not Tri but 4x9 is Tri.

Grouping this way 2x3, 2x4, 2x5 the middle term pairs always share a common prime factor and the first and second term pairs are always relatively prime. Written this way

2x3, 2x4, 2x5 3x5, 3x6, 3x7 4x7, 4x8, 4x9 5x9, 5x10, 5x11 6x11, 6x12, 6x13 7x13, 7x14, 7x15 8x15, 8x16, 8x17

It's fascinating that we create a loop of counting numbers which are either prime or relatively prime to the first and third terms of the pairs.

[mancoub]

Classifying Triples

In my last post, I immediately noticed that number 3 (iii. comp hyp with no common factors) had already been found in (25,24,7)

Here are the first several triples with hypotenuse 101 or less, classified by the order of their multiple of prime hypotenuse with the Composite exceptions listed as COM

1P(5),(2.2),(3), 2P(2.5),(2.2.2),(2.3), 1P(13),(2.2.3),(5), 3P(3.5),(2.2.3),(3.3), 1P(17),(3.5),(2.2.2), 4P(2.2.5),(2.2.2.2),(2.2.3), >>COM<<(5.5),(2.2.2.3),(7), 5P(5.5)(2.2.5),(3.5) 2P(2.13),(2.2.2.3),(2.5), 1P(29),(3.7),(2.2.5), 6P(2.3.5),(2.2.2.3),(2.3.3), 2P(2.17),(2.3.5),(2.2.2.2), 7P(5.7),(2.2.7),(3.7), 1P(37),(5.7),(2.2.3), 3P(3.13),(2.2.3.3),(3.5), 8P(2.2.2.5),(2.2.2.2.2),(2.2.2.3), 1P(41),(2.2.2.5),(3.3), 9P(3.3.5),(2.2.3.3),(3.3.3), 2P(2.5.5),(2.2.2.2.3),(2.7), interesting, this is 2x our first COM 10P(2.5.5),(2.2.2.5),(2.3.5), 3P(3.17),(3.3.5),(2.2.2.3), 4P(2.2.13),(2.2.2.2.3),(2.2.5), 1P(53),(3.3.5),(2.2.7), 11P(5.11),(2.2.11),(3.11), 2P(2.29),(2.3.7),(2.2.2.5), 12P(2.2.3.5),(2.2.2.2.3),(2.2.3.3), 1P(61),(2.2.3.5),(11), >>COM<<(5.13),(3.3.7),(2.2.2.2), 5P(5.13),(2.2.3.5),(5.5), >>COM<<(5.13),(2.2.2.7),(3.11), 13P(5.13),(2.2.13),(3.13), 4P(2.2.17),(2.2.3.5),(2.2.2.2.2), 14P(2.5.7),(2.2.2.7),(2.3.7), 1P(73),(5.11),(2.2.2.2.3), 2P(2.37),(2.5.7),(2.2.2.3), 3P(3.5.5),(2.2.2.3.3),(3.7), 15P(3.5.5),(2.2.3.5),(3.3.5), 6P(2.3.13),(2.2.2.3.3),(2.3.5), 16P(2.2.2.2.5),(2.2.2.2.2.2),(2.2.2.2.3), 2P(2.41),(2.2.2.2.5),(2.3.3), >>COM<<(5.17),(2.2.3.7),(13), >>COM<<(5.17),(7.11),(2.2.3.3), 5P(5.17),(3.5.5),(2.2.2.5), 17P(5.17),(2.2.17),(3.17), 3P(3.29),(3.3.7),(2.2.3.5), 1P(89),(2.2.2.2.5),(3.13), 18P(2.3.3.5),(2.2.2.3.3),(2.3.3.3), 7P(7.13),(2.2.3.7),(5.7), 19P(5.19),(2.2.19),(3.19), 1P(97),(2.2.2.3.3),(5.13), 4P(2.2.5.5),(2.2.2.2.2.3),(2.2.7), 20P(2.2.5.5),(2.2.2.2.5),(2.2.3.5), 1P(101),(3.3.11),(2.2.5),

Seems like we might be able to find these COM numbers by taking prime hypotenuse triples and multiplying them to get the resulting composite hypotenuses.

5x5, (5.5),(2.2.2.3),(7)

5x13, (5.13),(3.3.7),(2.2.2.2) and  (5.13),(2.2.2.7),(3.11)

5x17, (5.17),(2.2.3.7),(13) and (5.17),(7.11),(2.2.3.3)

13x17, (13.17), (2.2.5.11),(3.7) and (13.17),(3.3.19),(2.2.5.7)

29x29, (29.29),(2.2.2.3.5.7),(41),

5x101, (5.101),(2.2.2.3.19),(7.31) and (5.101),(13.29),(2.2.2.2.3.7)

It looks like we have a consistent way to find triples that are relatively ]prime to each other by creating psudo-prime hypotenuses using triples with prime hypotenuses.

[mancoub]

Ordering Triples

I began sorting triples by using the maximum formula and listing them in order of small leg a.

a=3, N=3 b=4, (N²-1)/2, (9-1)/2, 8/2 c=5, (N²+1)/2, (9+1)/2, 10/2a=4, N=4 a=4, N=4 b=3, (N²-4)/4, (16-4)/4, 12/4 c=5, (N²+4)/4, (16+4)/4, 20/4 a=5, N=5 b=12, (N²-1)/2, (25-1)/2, 24/2 c=13, (N²+1)/2, (25+1)/2, 26/2 With new analysis, using a grid of squares minus squares, we have a new way to list sets of triples when ordering by hypotenuse instead of by legs. Ordering this way will still have entries with more than one triple, but sorting in this way may reveal new patterns to analyze.

{2516,9}, (5,4,3), [5] {100,64,36}, (10,8,6), [10], (2*5) {169,144,25}, (13,12,5), [13] {225,144,81}, (15,12,9), [15], (3*5) {289,225,64}, (17,15,8), [17] {400,256,144}, (20,16,12), [20], (2*2*5) {625,576,400,225,49}, (25,24,7), (25,20,15), [25], (5*5) {676,576,100}, (26,24,10), [26], (2*13) {841,441,400}, (29,21,20), [29] (900,576,324}, (30,24,18), [30], (2*3*5)

This list, when ordered by hypotenuse, gives a glimpse at the prime relationship with triples but also their relative prime(ness). In the above “small” set of triples, we have 5, 13, 17, 29, all of which have prime hypotenuse. Looking closer at the legs of these sets, they are relatively prime to each other. As for the remainder triples, they all have a common factor which is the same as saying that they exist as a lower order triple with a common factor, the same prime factor that has been multiplied to get the composite hypotenuse.

2*5=10 {5,4,3}*2 3*5=15 {5,4,3}*3 2*2*5=20 {5,4,3}*4 5*5=25 {5,4,3}*5 exception, 25 has two triples with a shared hypotenuse 5*5=25 {25,24,7} these are relatively prime to each other (5*5),(2*2*2*3),(7) 2*13=26 {13,12,5}*2 2*3*5=30 {5,4,3}*6

With composites listed above, we can look at prime hypotenuse

{5,4,3} {13,12,5} {17,15,8} {29,21,20} Each triple on this list is a set of relatively prime numbers. The exception is a non-prime hypotenuse of 25 will a triple consisting of relatively prime numbers.

In my mind, it would be interesting to find triples with the following properties

i. prime hypotenuse with composite legs that have a common factor ii. composite hypotenuse with composite legs that have no common factors iii, composite hypotenuse with legs that share a common factor that is not shared with the hypotenuse iv. even a composite hypotenuse that has largest prime factor where there is not a smaller triple with that prime hypotenuse

[mancoub]

Factors of Squares

After we discussed the Number Theory pattern with Difference of squares, I wanted to cycle through square factors in respect to the geometric functions below

N²-1²=1*2*p

N²-2²=2*2*p

N²-3²=3*2*p

N²-4²=4*2*p

N²-5²=5*2*p

Odd numbers have a simple progression, since the factors of each term is reduced to it’s lowest common factor, remove the x2 from the third term and you get the same number of triples as you have factors of N² lower than but not equal to N

N=9,N²=81,factors(81)={1,3,9,27,81}

End on 3

1:N²-1²=1*2*p,p=40

3:N²-3²=3*2*p,p=12

This makes a lot of sense since all odd values of N² will have an odd number of factors and the middle factor will always have a p value of 0. So the number of possible Triples for odd values of N will always be half of the factors of N². This checks out.

Even numbers have a different progression that I haven’t figured out. While the terms of the geometric functions are all factors of the square, you must skip over some of them, including 1, to find the correct p values. I’ve shown two examples below.

N=12,N²=144,factors(144)={1,2,3,4,6,8,9,12,16,18,24,36,48,72,144}

2:N²-2²=2*2*p,p=35

4:N²-4²=4*2*p,p=16

6:N²-6²=6*2*p,p=9

8:N²-8²=8*2*p,p=5

N=20,N²=400,factors(400)={1,2,4,5,8,10,16,20,25,40,50,80,100,200,400}

2:N²-2²=2*2*p,p=99

4:N²-4²=4*2*p,p=48

8:N²-8²=8*2*p,p=21

10:N²-10²=10*2*p,p=15

[mancoub]

Difference of Squares Triples, cont.

So, what I want to do is reconstruct or “find” the row in which the earliest appearance of a certain square number will be.

For the first case of 3, you start by squaring the number, so N² = 9

Then we cycle through patterns to find all the times that 9 shows up with a difference of squares relationship, starting with N = 1²+p*2

3² = 1² + p*2 p = 4 p² = 16

This relationship is very exciting, because it translates to the Triple Maximum formula of (N²-1)/2 Where N=3 you get (9-1)/2=4 but also (9+1)/2=5

So let’s take it to the next diagonal, with N = 2²+p*4

3² = 2² + p*4 p = 5/4

This appears to be a stopping point of sorts, where there are no integer solutions for this trajectory.

The full list would look something like this:

N = 1²+p*2, 9-1=2p, p=4 N = 2²+p*4, 9-4=4p, p=5/4 N = 3²+p*6, 9-9=6p, p=0 For N = 5, the list would look like this N = 1²+p*2, 25-1=2p, p=12 N = 2²+p*4, 25-4=4p, p=21/4 N = 3²+p*6, 25-9=6p, p=16/6 N = 4²+p*8, 25-16=8p, p=9/8 N = 5²+p*10, 25-25=10p, p=0 So to jump directly to N=20 you get a process that finds integers without relying on square root function. Also, I think this is an exhaustive algorithm, that finds all legs for any given N with a Big(O) of N

N = 1²+p*2, 400-1=2p, p=399/2 N = 2²+p*4, 400-4=4p, p=99 N = 3²+p*6, 400-9=6p, p=391/6 N = 4²+p*8, 400-16=8p, p=48 N = 5²+p*10, 400-25=10p, p=75/2 N = 6²+p*12, 400-36=12p, p=91/3 N = 7²+p*14, 400-49=14p, p=351/14 N = 8²+p*16, 400-64=16p, p=21 N = 9²+p*18, 400-81=18p, p=319/18 N = 10²+p*20, 400-100=20p, p=15 N = 11²+p*22, 400-121=22p, p=279/22 N = 12²+p*24, 400-144=24p, p=64/3 N = 13²+p*26, 400-169=26p, p=231/26 N = 14²+p*28, 400-196=28p, p=51/7 N = 15²+p*30, 400-225=30p, p=35/6 N = 16²+p*32, 400-256=32p, p=57/16 N = 17²+p*34, 400-289=34p, p=111/34 N = 18²+p*36, 400-324=36p, p=19/9 N = 19²+p*38, 400-361=38p, p=39/38 N = 20²+p*40, 400-400=40p, p=0 It seems that the coefficient of p divides evenly throughout the equations and could be taken further by finding all the factors of N²

Factors(400)=1,2,4,5,8,10,16,20,25,40,50,80,100,400

All of the coefficients are factors of the square. And for the factors that are coefficients that do not have integer solutions, like 10, the difference of square -25 is not divisible by 10 evenly, so I would guess that this is a requirement for finding triples. That the coefficient must be a factor of it’s own square and also a factor of N.

[mancoub]

Difference of Squares Triples

Looking at Number Theory’s answer to finding integer solutions to the Pythagorean Theorem gives us this relationship.

a² + b² = c² a =  u² - v² b = 2uv c = u² + v²

When I studied integer solutions without knowing this Number Theory relationship, I used to look for patterns using the Triple Maximums which is another square relationship. Namely N² + (N²-1)/2 = (N²+1)/2 (for odd values of N) also even values of N follow this formula  N² + (N²-4)/4 = (N²+4)/4

a² + b² = c² a² = N² b² =  (N²-1)/2 c² = (N²+1)/2

There are a few things that happens when you plot all the solutions using the Triple Maximums, you always get solutions for the large leg and the hypotenuse that are only different by 1 (for odds the difference is 1 and for evens it’s 2) This is great to get a repeatable pattern but the relationship between smaller leg and larger leg grows exponentially making them very large for larger values of N.

It should be said that you can multiply all the sides by a factor to get new solutions. When you are finding the Maximums, the three sides of the triple are considered relatively prime to each other. When you take a relatively prime triple and multiply them by a factor you get a solution that is no longer relatively prime (by definition).

Using the formula (N²-1)/2 with odd numbers, you can create several triples easily and even more when you multiple them by integers. (x1) 3, 4, 5 | (x2) 6, 8, 10 | (x3) 9, 12, 15 (x1) 5, 12, 13 | (x2) 10, 24, 26 | (x3) 15, 36, 26 (x1) 7, 24, 25 | (x2) 14, 48, 50 | (x3) 21, 72, 75

Another point of note is that when you follow this pattern for smaller numbers you get solutions where the N side is larger than the (N²-1)/2 side. These are always interesting but for most studies can be ignored or skipped over.

Next, you can make a table of “difference of squares” where the legs equal a² = c² - b² If the columns and rows of the table are all squares, then the table gets filled in with the difference of them, creating a reflection over the diagonal. When square solutions show up, you find all the possible integer triples.

What I find fascinating about this table and the relationships it exposes about the Number Theory representation for difference of Squares, is that there is an geometric pattern in the diagonals. For instances, the first diagonal, closest to the center (all zeros) is all odd numbers.

These diagonals follow this pattern

1: 1+2, 1+2+2 (1²+1*2) 2: 4+4, 4+4+4 (2²+2*2) 3: 9+6, 9+6+6 (3²+3*2) 4: 16+8, 16+8+8 (4²+4*2) 5: 25+10, 25+10+10 (5²+5*2)

[mancoub]

Back to Farey and, “Hey, what about Pi?”

So, someone recently asked my why I care so much about solving irrational numbers like the “Square Root of Two? I mean, it’s not as important as a number like Pi”

I answered, that the Farey Sequence is just a method for “rationally” pinpointing a specific irrational number. The caveat is that each iteration or cycle, you must be able to check and test your accuracy. With a number like Pi, we should be able to set a specific approximation to test each time. Additionally, methods like these can be performed manually, with pen and paper. This takes some of the mystique out of math and can make it more tangible and easier to teach. Plus, if you are a coder, it can lend alternative methods for faster calculations. But if you are like me, it’s just so cool.

Farey Sequence goes something like this:

1. Choose a numerator and denominator for the lower approximation 2. Choose Num and Den for upper approx. 3. Add both numerators to get a new numerator 4. Add both denominators to get a new denominator 5. Test to see if the new number is a closer lower approx. or an upper approx. 6. Substitute and repeat

When I was first introduced to Pi in grade school, my teacher told me that it was one of the most amazing numbers ever discovered, but she couldn’t tell me exactly why. She also stated that after hundreds of years of studying the number, we know that it goes on forever and that it is exactly 22/7. While she got most of the properties of Pi correct, and her “exact” number is a very good approximation, by definition, Pi is irrational and does not have an exact fractional representation. I guess this assessment can be seen as fair, since irrational numbers are out of the scope of most 4th grade classes.

Still, I would like to start with 3 and 4 as starting guesses, even though we could start with a guess much closer.

N1 = 3 D1 = 1 N2 = 4 D2 = 1 R1 = 7/2 (3.5)

Our result of Farey “Addition” is 7/2, which is unsurprisingly 3.5 and we know this is higher than Pi

N1 = 3 D1 = 1 N2 = 7 D2 = 2 R2 = 10/3 (3.333)

Also not surprising that we get 3+1/3, also higher

N1 = 3 D1 = 1 N2 = 10 D2 = 3 R3 = 13/4 (3.25) R4 = 16/5 (3.2) R5 = 19/6 (3.1666) R6 = 22/7 (3.142867)

After 6 iterations, we get the infamous 22/7, this is a whopping two decimals of precision and the smallest fraction approximation with numerator under 100. After one more iteration we get our first lower approximation 25/8 R7 = 25/8 (3.125)

N1 = 25 D1 = 8 N2 = 22 D2 = 7 R8 = 47/15 (3.1333) R9 = 69/22 (3.136)

Keep following this cycle until R22 and you get 333/106 (3.14150) and 355/113 (3.1415929) The later being the best approximation with numerator lower than 1000

So yeah, it works for irrational numbers that are also transcendental, with the caveat of being able to test the closeness of the approximation each cycle

[mancoub]

Patterns in Triples

I have always been a little fascinated with Pythagorean Triples.

The Pythagorean Theorem is such an extraordinarily simple formula.

a² + b² = c²

While this formula is great at generating Irrational numbers, 1² + 1²  = sqrt(2)², I wanted to explore some of the Number Theory that makes integer patterns.

For starters, there are an infinite number of triples where the difference between the legs is 1 and when the hypotenuse is also an integer, the average of the ratio between hypotenuse and leg is an approximation of the square root of 2.

n² + (n+1)² = c² where c/((2n+1)/2) is an integer ratio approximation for square root of 2 that gets better for larger numbers n. This has been the focus of my past several posts but when you follow this formula, you do get good decimal precision but the pattern grows very quickly and I find the smaller denominators more interesting. Interesting but for another post

[3,4,5] gives you 5/3.5 simplifies to 10/7 = 1.42

[20,21,29] gives you 29/20.5 simplifies to 58/41 = 1.41463

Instead of irrational ratios, I wanted to focus on other patterns. The first being the maximums in integer forms for every number n that is odd, where n² + (c-1)² = c² and even numbers m that are m² + (c-2)² = c² You can find c easily for odd numbers by taking (n²+1)/2 and for even numbers with (m²+4)/4

But what I’ve been finding so interesting are the in-between triples that are relatively prime legs, basically not factors of smaller triples, and also not maximums.

One way to go start sorting these triples is to start with n=3; [3,4,5]

Case n = 3

c = (n²+1)/2

c = (9+1)/2

c = 10/2

c = 5 (maximum)

Skipping Case 4 because it’s basically case 3 but with a smaller large leg ???

Case n = 5; [5,12,13] also a maximum

Case n = 6; [6,8,10] maximum and 2x [3,4,5]

This is our first even integer larger than 3 that’s not the special case n = 4 and we can see that (6²+4)/4 = 10 making this one also a maximum. But also a 2x [3,4,5] which makes it a multiple of a smaller triple.

Case n = 7; [7,24,25] (maximum)

Case n = 8; [8,15,17] (maximum)

When you look at [8,6,10] you could say this is part of Case n = 8 but since we can sort these by n being the smaller leg, you can ignore this one.

Case n = 9; 

This is the first case where there are multiple triples for a given integer.

[9,12,15]; 3x [3,4,5]

[9,40,41] (maximum)

You can continue finding all integer solutions where either the triple is a multiple of a smaller triple or where it fulfills the maximum formula until n = 20.

Case n = 20;

[20,21,29]; all relatively prime sides with no common factors

[20,48,52]; 4x [5,12,13]

[20,99,101]; (maximum)

You can also find triples using another Number Theory formula namely the difference of squares. I’m writing another post to discuss the proof for why this relationship works for all triples which is interesting in itself. But I wanted to end this post with the u and v values for this first smallest special case [20,21,29]

Number Theory relationship with difference of squares uses the following formulas to construct triples.

a² + b² = c²

a =  u² - v²

b = 2uv

c = u² + v²

When u = 5 and v = 2 you get

a = 25 - 4

a = 21

b = 2 * (5 * 2)

b = 20