mathingtime

[mathingtime]

geometry witch

(graph screencapped from http://demonstrations.wolfram.com/)

[mathingtime]

HEY. I first want to say that I love what you guys are doing! So hats off to you guys! Could you possibly tell where I can find notes for A level math P3 (Just complex numbers and vectors) but any help regarding that would be appreciated! Thanks!

Khan academy is always useful, wolfram might have something as wellBest of luck with your studiesAlso sorry for the late response

[mathingtime]

Do you have any experience/advice for H3 mathematics?

Sadly not, best of luck with your studies!

[mathingtime]

Comic day :) Have a great weekend ^_^

Break of Day by Nate Fakes

[mathingtime]

HOW TO NEVER FAIL MATH AGAIN

1) UNDERSTAND THE MATERIAL! Be able to apply the material you know to different types of problems and scenarios. Teachers like to throw students off with problems that only students who understand the material are able to solve.

2) ASK YOUR TEACHER FOR HELP! That’s why you teacher is there. If you are having trouble understanding a concept, having the lesson repeated or said in a different perspective may help.

3) DO YOUR HOMEWORK! Homework gives you a chance to practice your material. Similar problems on homework often show up on tests.

4) RE DO THE ANSWERS YOU GET WRONG ON HOMEWORK AND TESTS! This way you’ll be able to see where you went wrong and know not to make that mistake again.

5) SHOW YOUR WORK! Showing your work on tests and homework show your teacher that you understand the concept. Teachers may give you partial credit for an incorrect problem with your work showing that you understand the material even with a silly mistake.

[mathingtime]

I want to know more about Applied Mathematics, Can you help me?

We would love to help you! Sorry for the late response as this blog has been on break for summer.

There are quite a few branches of applied mathematics, but i'll use the A-level maths topic definitions of mechanics, statistics and decision.

Mechanics is a subject focused on forces and motion and applying mathematics to understand how these affect real world situations. It is closely linked to physics and engineering.

Statistics is the understanding of probability and percentages. It deals with how high the chances are of certain situations occuring including combiniations of numbers.

Decision maths is based on algorithms and using them to... well make decisions. Its quite close to ICT and probably the least mathematical area here.

Thank you for being patient and I hope your studies go well!

[mathingtime]

Uh hi, this may sound like a stupid question but I'm a 6th to 7th new algebra student. We were given this giant text book to do without any help. The textbook fails to describe how to do Equations with many solutions or no solution properly so if you could explain with this problem it would be very nice! 5(x-3) + 6 = 5x-9 (Tell whether each equation has one, zero, or infinitely many solutions

Sorry for the delay in response, this blog has been on a bit of a break over summer. Its quite alright to ask for help. I’m assuming you would need to multiply out the first bracket to find that 5x-15+6=5x-9This simplifies to 5x-9=5x-9This means that any value of x you input will result in a solution, therefore there are infintely many solutions.

For example if you put x=1 then it would be 5-9=-4

Best of luck with the rest of your studies! And again, sorry this is quite late

[mathingtime]

wrote up some math notes on my white board and added some chemistry and math notes to my wall 😊

[mathingtime]

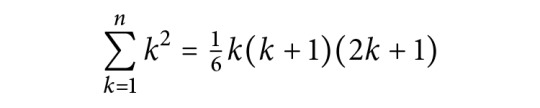
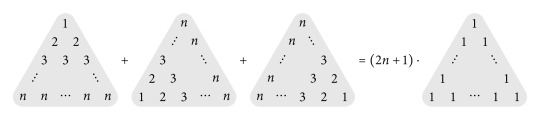
A very neat visual proof for the formula of the first n square numbers.

Correction: as pointed out by @othermaterial, the right-hand side of the formula should have variables n instead of k.

[mathingtime]

could you recommend some maths studyblrs to follow? :)

Hi,

@rebeccastudiesmaths is probably my favourite maths studyblr.

I also follow:@studylove, @mathmewishing, @thestudyingprocess, @mathbrain, @gingerlie-math

Studyblrs studying maths/further maths at A-level:@almost-an-economist, @astro-study, @bookssweatandtears, @bucketchemistry, @code-bug, @penandanotebook, @study-at-peace, @studyanise

Please reblog if you are a maths studyblr (I’m looking to follow more maths blogs myself!), thank you :)

[mathingtime]

Scans of the inside covers of Strang’s Calculus, which you can legally-download for free here from the MIT website. This is my all-time favorite math or physics textbook. Scanned it so I could cut and paste it into my new sketchbook, wanna try and make a ~cool artistic~ reference poster out of it, ‘cuz I’ve been real into that idea since I took notes about rings for the algebra midterm on a big piece of watercolor paper.

[mathingtime]

The 10 highest-paying jobs for math geeks.

[mathingtime]

What is Group Theory?

In math, a group is a particular collection of elements. That might be a set of integers, the face of a Rubik’s cube–which we’ll simplify to a 2x2 square for now– or anything, so long as they follow 4 specific rules, or axioms.

Axiom 1: All group operations must be closed, or restricted, to only group elements. So in our square, for any operation you do—like turn it one way or the other—you’ll still wind up with an element of the group. Or for integers, if we add 3 and 2, that gives us 1—4 and 5 aren’t members of the group, so we roll around back to 0, similar to how 2 hours past 11 is 1 o’clock.

Axiom 2: If we regroup the order of the elements in an operation, we get the same result. In other words, if we turn our square right two times, then right once, that’s the same as once, then twice. Or for numbers, 1 + 2 is the same as 2 + 1.

Axiom 3: For every operation, there’s an element of our ground called the identity. When we apply it to any other element in our group, we still get that element. So for both turning the square and adding integers, our identity here is 0. Not very exciting.

Axiom 4:  Every group element has an element called its inverse, also in the group. When the two are brought together using group’s addition operation, they result in the identity element, 0. So they can be thought of as cancelling each other out. Here 3 and 1 are each other’s inverses, while 2 and 0 are their own worst enemies.

So that’s all well and good, but what’s the point of any of it? Well, when we get beyond these basic rules, some interesting properties emerge. For example, let’s expand our square back into a full-fledged Rubik’s cube. This is still a group that satisfies all of our axioms, though now with considerably more elements, and more operations—we can turn each row and column of each face.

Each position is called a permutation, and the more elements a group has, the more possible permutations there are. A Rubik’s cube has more than 43 quintillion permutations, so trying to solve it randomly isn’t going to work so well. However, using group theory we can analyze the cube and determine a sequence of permutations that will result in a solution. And, in fact, that’s exactly what most solvers do, even using a group theory notation indicating turns.

From the TED-Ed Lesson Group theory 101: How to play a Rubik’s Cube like a piano - Michael Staff

Animation by Shixie

[mathingtime]

no thank you

[mathingtime]

What is Math?

Mathematics is everywhere and we all learned it at some point, but what is mathematics, really? A search on the internet will yield many different interpretations. According to Google, mathematics is “the abstract science of number, quantity, and space.” Here is a collection of how some of history’s greatest minds described mathematics.

An intellectual game “Mathematics is a game played according to certain simple rules with meaningless marks on paper.”—David Hilbert

“Pure mathematics is the world’s best game. It is more absorbing than chess, more of a gamble than poker, and lasts longer than Monopoly. It’s free. It can be played anywhere—Archimedes did it in a bathtub.”—Richard J. Trudeau

“Mathematics is about making up rules and seeing what happens.”—Vi Hart

“Mathematics is like checkers in being suitable for the young, not too difficult, amusing, and without peril to the state.”—Plato

“Mathematics is an independent world created out of pure intelligence.”—William Woods Worth

A tool for the sciences “Mathematics is the tool specially suited for dealing with abstract concepts of any kind and there is no limit to its power in this field.”—Paul Dirac

“Our physical world doesn’t have just some mathematical properties, it has only mathematical properties.”—Max Tegmark

“Mathematics serves as a handmaiden for the explanation of the quantitative situations in other subjects …”—H. F. Fehr

“In order to understand the universe, you must know the language in which it is written. And that language is mathematics.”—Galileo

A search for pattern, order, and structure “A mathematician, like a painter or poet, is a maker of patterns. If his patterns are more permanent than theirs, it is because they are made with ideas.”—G. H. Hardy

“Mathematics compares the most diverse phenomena and discovers the secret analogies that unite them.”—Joseph Fourier

“Go down deep enough into anything and you will find mathematics.”—Dean Schlicter

Logic and reasoning “All Mathematics is Symbolic Logic.”—Bertrand Russell

“Pure mathematics is, in its way, the poetry of logical ideas.” –Albert Einstein

“Mathematics is the supreme judge; from its decisions there is no appeal.“—Tobias Dantzig

Which do you believe best describes math?

[mathingtime]

From xkcd.com 

[mathingtime]

By  Illustrator Genevieve Womack