soanbaitap - Tumblr blog

soanbaitap · 4 years ago

Link

Bài viết này chúng ta cùng ôn lại công thức tính khoảng cách giữa 2 điểm, từ điểm tới đường thẳng, qua đó vận dụng giải một số bài tập minh họa để các em hiểu rõ cách vận dụng công thức tính này.

I. Công thức tính khoảng cách giữa 2 điểm

- Cho điểm A(xA; yA) và điểm B(xB; yB), khoảng cách giữa hai điểm này là:

AB =√(xB - xA)2 + (yB - yA)2

II. Công thức tính khoảng cách từ điểm tới đường thẳng

- Cho đường thẳng Δ: Ax + By + C = 0 và điểm M0(x0; y0). Khi đó khoảng cách từ điểm M0 đến đường thẳng Δ là:

d(M0;Δ) =|Ax0 + By0 + C|/√A2 + B2

- Khoảng cách từ điểm M0 đến đường thẳng Δ là độ dài của đoạn thẳng M0H (trong đó H là hình chiếu vuông góc của M0 lên Δ).

> Lưu ý: Trong trường hợp đường thẳng Δ chưa viết dưới dạng tổng quát thì đầu tiên ta cần đưa đường thẳng Δ về dạng tổng quát.

III. Tính khoảng cách giữa 2 điểm, từ điểm tới đường thẳng qua bài tập minh họa

* Ví dụ 1: Trong mặt phẳng Oxy cho điểm A(1;2) và điểm B(-3;4). Tính độ dài đoạn thẳng AB.

* Lời giải:

- Độ dài đoạn thẳng AB là khoảng cách giữa 2 điểm A,B ta có:

AB = √(-3 - 1)2 + (4 - 2)2 = √(16 + 4) = √20.

* Ví dụ 2: Tính khoảng cách từ điểm M(2;-1) đến đường thẳng (Δ): 3x + 4y + 7 = 0.

* Lời giải:

- Khoảng cách từ điểm M đến đường thẳng (Δ) là:

d(M;Δ) = |3.2 + 4.(-1) + 7|/√(32 + 42) = 9/5

* Ví dụ 3: Tính khoảng cách từ điểm A(0;1) đến đường thẳng (Δ): 4x + 3y = 12

* Lời giải:

- Đường thẳng (Δ): 4x + 3y = 12 ⇔ 4x + 3y - 12 = 0

- Khoảng cách từ điểm A đến (Δ) là:

d(A;Δ) = |4.0 + 3.(1) - 12|/√(42 + 32) = 3/5.

* Ví dụ 4: Tính khoảng cách từ điểm M(1;1) đến đường thẳng (Δ) có phương trình tham số: x = 3 + 3t và y = 2 + t.

* Lời giải:

- Ta cần đưa phương trình đường thẳng (Δ) về dạng tổng quát.

- Ta có: (Δ) đi qua điểm A(3;2) và có VTCP u(3;1) ⇒ VTPT n(1;-3)

⇒ Phương trình (Δ): 1.(x - 3) - 3(y - 2) = 0 ⇔ x - 3y + 3 = 0

⇒ Khoảng cách từ điểm M(1;1) đến (Δ) là:

d(M;Δ) = |1.1 - 3.(1) + 3|/√(12 + (-3)2) = 1/√10.

* Ví dụ 5: Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng (Δ): 4x - 3y + 25 = 0. Bán kính R của đường tròn (C) bằng:

* Lời giải:

- Do đường thẳng (Δ) tiếp xúc với đường tròn (C) nên khoảng cách từ tâm đường tròn đến đường thẳng (Δ) chính là bán kính R của đường tròn.

d(M;Δ) = R = |4.0 - 3.0 + 25|/√(42 + (-3)2) = 25/5 = 5.

* Ví dụ 6: Khoảng cách từ giao điểm của hai đường thẳng (d1): x - 3y + 4 = 0 và (d2): 2x + 3y - 1 = 0 đến đường thẳng ∆: 3x + y + 16 = 0 bằng:

* Lời giải:

- Trước hết ta cần tìm giao điểm của (d1) và (d2); từ đó tính khoảng cách từ giao điểm này tới (∆).

- Giả sử giao điểm của (d1) và (d2) là A thì tọa độ của A là nghiệm của hệ phương trình:

x - 3y + 4 = 0 và 2x + 3y - 1 = 0

Giải hệ được x = -1 và y = 1 ⇒ A(-1;1)

- Khoảng cách từ điểm A(-1;1) đến đường thẳng ∆: 3x + y + 16 = 0 là:

d(A;Δ) = |3.(-1) + 1.1 + 16|/√(32 + 12) = 14/√10

* Ví dụ 7: Trong mặt phẳng hệ tọa độ Oxy, cho tam giác ABC có A(1;1); B(0;3) và C(4;0).

a) Tính chiều dài đường cao AH (H thuộc BC).

b) Tính diện tích tam giác ABC

* Lời giải:

a) Tính chiều dài đường cao AH

- Chiều dài đường cao AH chính là khoảng cách từ A tới đường thẳng BC. Vì vậy ta cần viết phương trình dường thẳng BC từ đó tính khoảng cách từ A tới BC.

- PT đường thẳng BC: Đi qua B(0;3) và có CTCP BC(xC - xB; yC - yB) = (4;-3) nên VTPT là n(3;4).

⇒ PTĐT (BC) là: 3(x - 0) + 4( y - 3) = 0 ⇔ 3x + 4y - 12 = 0

⇒ chiều cao của tam giác kẻ từ đỉnh A chính là khoảng cách từ điểm A đến đường thẳng BC:

d(A;BC) = |3.1 + 4.1 - 12|/√(32 + 42) = 5/5 = 1.

b) Tính diện tích tam giác ABC.

- Ta có: SΔABC = (1/2).AH.BC

- Có độ dài BC là: BC = √(xC - xB)2 + (yC - yB)2 = √(4)2 + (-3)2 = √25 = 5

- Mà AH = d(A;BC) = 1 (theo câu a)

⇒ SΔABC = (1/2).AH.BC = (1/2).1.5 = 5/2 =2,5.

Cách tính khoảng cách giữa 2 điểm, khoảng cách từ điểm tới đường thẳng - Toán hình 10 được biên soạn theo sách mới nhất và Được hướng dẫn biên soạn bởi các thầy cô giáo dạy Giỏi tư vấn, nếu thấy hay hãy chia sẻ và comment để nhiều bạn khác học tập cùng.

#soanbaitap

#soanbaitap #giải bài tập #Cách tính khoảng cách giữa 2 điểm #khoảng cách từ điểm tới đường thẳng – T

0 notes

soanbaitap · 4 years ago

Link

Toán hình 10 Cách tính khoảng cách giữa hai đường thẳng song song

Thật vậy, nếu cho hai đường thẳng (d1) và (d2) song song với nhau. Khoảng cách hai đường thẳng này bằng khoảng cách từ một điểm bất kì thuộc đường thẳng này đến đường thẳng kia, tức là:

d(d1; d2) = d( A; d2) trong đó A là điểm bất kỳ thuộc đường thẳng d1.

* Để tính khoảng cách giữa hai đường thẳng song song ta thực hi��n như sau:

+ Bước 1: Đưa phương trình đường thẳng d1; d2 đã cho về dạng tổng quát.

+ Bước 2: Lấy một điểm A bất kì thuộc đường thẳng d1.

+ Bước 3: Tính khoảng cách từ điểm A đến đường thẳng d2.

+ Bước 4: Kết luận: d(d1;d2) = d(A;d2).

* Tính khoảng cách giữa hai đường thẳng qua các bài minh họa

* Ví dụ 1: Tính khoảng cách giữa hai đường thẳng d1: 2x - 3y - 12 = 0 và d2: 4x - 6y + 3 = 0:

* Lời giải:

- Xét vị trí tương đối của 2 đường thẳng d1 và d2 ta có:

2/4 = -3/-6 ≠ -12/3

⇒ Hai đường thẳng đã cho song song với nhau: d1 // d2.

- Ta lấy điểm A(3;-2) ∈ d1 khi đó khoảng cách từ điểm A tới d2 chính là khoảng cách giữa 2 đường thẳng d1 và d2.

d(d1;d2) = d(A;d2) = |4.3 - 6.(-2) + 3|/√(42 + (-6)2) = 27/√52.

* Ví dụ 2: Tính khoảng cách giữa hai đường thẳng song song d1: 6x - 8y + 3 = 0 và d2: 3x - 4y - 6 = 0.

* Lời giải:

- Xét vị trí tương đối của 2 đường thẳng d1 và d2 ta có:

6/3 = -8/-4 ≠ 3/-6

⇒ Hai đường thẳng d1, d2 đã cho song song với nhau: d1 // d2.

- Lấy điểm B(2;0) ∈ d2 khi đó khoảng cách từ điểm B tới d1 chính là khoảng cách giữa 2 đường thẳng d1 và d2.

d(d1;d2) = d(B;d1) = |6.2 - 8.0 + 3|/√(62 + 82) = 15/√100 = 15/10 = 3/2

> Lưu ý: Việc chọn 1 điểm thuộc đường thẳng d1 (hoặc d2) các em nên chọn giá trị x, y sao cho là số nguyên nhỏ (như 0; 1; -1; 2; -2) thỏa phương trình đường thẳng d1 (hoặc d2) để thuận tiện tính toán.

* Ví dụ 3: Tính khoảng cách giữa 2 đường thẳng d1: 7x + y - 3 và d2 có phương trình tham số: x = -2 + t và y = 2 - 7t.

* Lời giải:

- Ta cần đưa phương trình tham số của d2 về phương trình tổng quát:

d2: qua điểm A(-2;2) có VTCP u(1;-7) suy ra VTPT n(7;1)

⇒ Phương trình tổng quát của d2 là: 7(x + 2) + 1(y - 2) = 0 ⇔ 7x + y + 12 = 0

- Ta xác định vị trí d1 và d2, có: 7/7 = 1/1 ≠ -3/12 nên d1//d2

- Như vậy, giờ ta cần tính khoảng cách giữa hai đường thẳng song song d1: 7x + y - 3 và d2: 7x + y + 12 = 0.

- Ta lấy ngay điểm A(-2;2) ∈ d2. ta có:

d(d2;d1) = d(A;d1) = |7.(-2) + 1.2 - 3|/√(72 + 12) = 15/√50 = 3/√2 = 3√2/2.

* Ví dụ 4: Tập hợp các điểm cách đường thẳng ∆: 4x + 3y - 6 = 0 một khoảng bằng 1?

* Lời giải:

- Gọi điểm M (x ; y) là điểm cách đường thẳng ∆ một khoảng bằng 1. Như vậy ta có:

d(M; Δ) = 1 ⇔ |4x + 3y - 6|/√(42 + 32) = 1

⇔ |4x + 3y - 6| = 5 ⇔ 4x + 3y - 6 = 5 hoặc 4x + 3y - 6 = -5

⇔ 4x + 3y - 11 = 0 hoặc 4x + 3y - 1 = 0.

- Vậy tập hợp các điểm cách ∆ một khoảng bằng 1 là 2 đường thẳng: 4x + 3y - 11 = 0 và 4x + 3y - 1 = 0.

* Ví dụ 5: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d1: 6x + 8y - 20 = 0 và d2: 6x + 8y + 22 = 0 song song nhau. Viết phương trình đường thẳng Δ vừa song song và cách đều với d1; d2.

* Lời giải:

- Lấy điểm M (x; y) thuộc đường thẳng Δ, ta có:

d(M;d1) = d(M;d2) ⇔ |6x + 8y - 20|/√(62 + 82) = |6x + 8y + 22|/√(62 + 82)

⇔ |6x + 8y - 20| = |6x + 8y + 22|

⇔ 6x + 8y - 20 = 6x + 8y + 22 hoặc 6x + 8y - 20 = -(6x + 8y + 22)

⇔ -44 = 0 (vô lý) hoặc 12x + 16y + 2 = 0 hay 6x + 8y + 1 = 0

Vậy đường thẳng Δ: 6x + 8y + 1 = 0 song song và cách đều d1; d2

Toán hình 10 Cách tính khoảng cách giữa hai đường thẳng song song được biên soạn theo sách mới nhất và Được hướng dẫn biên soạn bởi các thầy cô giáo dạy Giỏi tư vấn, nếu thấy hay hãy chia sẻ và comment để nhiều bạn khác học tập cùng.

#soanbaitap

#soanbaitap #giải bài tập #Toán hình 10 Cách tính khoảng cách giữa hai đường thẳng song song

0 notes

soanbaitap · 5 years ago

Link

Ôn tập chương 1 hình học 9 là tâm huyết biên soạn của đội ngũ giáo viên dạy giỏi môn toán trên toàn quốc. Đảm bảo chính xác, dễ hiểu giúp các em hệ thống kiến thức toán 9 ôn tập chương 1 hình học và hướng dẫn giải bài tập ôn tập chương i hệ thực lượng giác tam giác vuông sgk để các em hiểu hơn.

Ôn tập chương 1 hình học 9 thuộc: CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG

I. Lý thuyết ôn tập chương 1 hình học 9

1. Hệ thức về cạnh và đường cao

Tam giác ABC vuông tại A, đường cao AH, ta có:

Chú ý: Diện tích tam giác vuông: S = (1/2)bc = (1/2)ah.

2. Tỉ số lượng giác của góc nhọn.

+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sinα.

+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu là cosα.

+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu là tanα.

+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu là cotα.

Hay sinα = AB/BC; cosα = AC/BC; tanα = AB/AC; cotα = AC/AB.

Tính chất:

+ Nếu α là một góc nhọn thì 0 < sinα < 1; 0 < cosα < 1; tanα > 0; cotα > 0.

Ta có: sin2α + cos2α = 1;

tanα.cotα = 1

+ Với hai góc nhọn α, β mà α + β = 90°.

Ta có: sinα = cosβ; cosα = sinβ; tanα = cotβ; cotα = tanβ.

Nếu hai góc nhọn α và β có sinα = sinβ hoặc cosα = cosβ thì α = β.

3. Hệ thức về cạnh và góc trong tam giác vuông.

Trong một tam giác vuông, mỗi cạnh góc vuông bằng:

+ Cạnh huyền nhân với sin góc đối hay nhân với côsin góc kề.

+ Cạnh góc vuông kia nhân với tan của góc đối hay nhân với cotg của góc kề.

b = a.sinB = a.cosC; c = a.sinC = a.cosB; b = c.tgB = c.cotgC; c = b.tgC = b.cotgC.

Chú ý: Trong một tam giác vuông nếu cho trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông) thì ta sẽ tìm được các yếu tố còn lại.

II. Toán 9 ôn tập chương 1 hình học - Hướng dẫn giải bài tập vận dụng sgk

Câu 1: Cho tam giác cân ABC có đáy BC = 2a , cạnh bên bằng b (b > a) .

a) Tính diện tích tam giác ABC

b) Dựng BKk ⊥ AC . Tính tỷ số

Lời giải

a) Gọi H là trung điểm của BC. Theo định lý Pitago ta có:

b) Ta có

Áp dụng định lý Pitago trong tam giác vuông AKB ta có:

Câu 2: Cho tam giác ABC với các đỉnh A, B, C và các cạnh đối diện với các đỉnh tương ứng là: a, b, c .

a) Tính diện tích tam giác ABC theo a, b , c

b) Chứng minh: a2 + b2 + c2 ≥ 4√3S

Lời giải

a) Ta giả sử góc A là góc lớn nhất của tam giác

ABC ⇒ B, C là các góc nhọn.

Suy ra chân đường cao hạ từ A lên BC là điểm H thuộc cạnh BC.

Ta có: BC = BH + HC.

Áp dụng định lý Py ta go cho các tam giác vuông AHB, AHC ta có:

AB2 = AH2 + HB2; AC2 = AH2 + HC2

Trừ hai đẳng thức trên ta có:

Áp dụng định lý Pitago cho tam giác vuông AHB

b) Từ câu a) ta có:

Dấu bằng xảy ra khi và chỉ khi tam giác ABC đều.

Câu 3: Biết sinα 5/13 . Tính cosα, tanα và cotα .

Lời giải

Xét Δ vuông tại A.

Câu 4: Biết sinα.cosα = 12/25. Tính sinα.cosα.

Lời giải

Biết sinα.cosα = 12/25. Để tính sinα.cosα ta cần tính sinα + cosα rồi giải phương trình với ẩn là sinα hoặc cosα.

Ta có:

Câu 5: Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H. Biết HD:HA = 1:2 . Chứng minh rằng tgB.tgC = 3 .

Lời giải

Câu 6: Cho tam giác ABC nhọn. Gọi a, b, c lần lượt là độ dài các cạnh đối diện với các đỉnh A, B, C. Chứng minh rằng:

Lời giải

Câu 7: Ở một cái thang đơn dài có ghi “để dảm bảo an toàn cần đặt thang sao cho tạo với mặt đất một góc α thì phải thỏa mãn 60° < α < 75° . Vậy phải đặt thang cách vật thang dựa khoảng bao nhiêu để đảm bảo an toàn?

Ta xem đề bài như hình vẽ trên

Khi đó: Khoảng an toàn nằm trong khoảng từ C đến D

Ta có:

BC = AC.cos75° = 3.cos75° ≃ 0,776 (m)

BD = ED.cos60° = 1,5 (m)

Vậy phải đặt thang cách vật dựa một đoạn l(m) thỏa mãn 0,776(m) < l < 1,5(m)

Câu 8: Cho tam giác ABC vuông tại B có BC = 20m,

. Một đường thẳng song song với BC cắt AB, AC lần lượt tại D, E. Biết BD = 5m . Tính độ dài AE là?

Câu 9: Tính diện tích tam giác ABC biết

bán kính đường tròn ngoại tiếp tam giác ABC là R .

Giả thiết có các góc có số đo đặc biệt, nhưng tam giác ABC là tam giác thường nên ta sẽ tạo ra tam giác vuông bằng cách.

Dựng các đường thẳng qua C, B lần lượt vuông góc với AC, AB . Gọi D là giao điểm của hai đường thẳng trên.

Khi đó tam giác ABD và ACD là các tam giác

vuông và 4 điểm A, B, C, D cùng nằm trên đường tròn đường kính AD = 2R .

Ta có:

Câu 10: Cho tam giác ABC với các đỉnh A, B, C và các cạnh đối diện với các đỉnh tương ứng là: a, b, c . Chứng minh rằng:

a) Dựng đường cao BH của tam giác ABC

Giả sử H thuộc cạnh AC .

Ta có: AC = AH + HC.

Áp dụng định lý

Pi ta go cho các tam giác vuông AHB, BHC ta có:

AB2 = AH2 + HB2, BC2 = BH2 + HC2

Trừ hai đẳng thức trên ta có:

Để chứng minh bài toán ta cần kết quả sau:

Từ đó ta suy ra: sin2α = 2sinα.cosα .

*) Xét tam giác ABC. Dựng đường cao BE ta có:

a) a2 = b2 + c2 - 2bccosA

b) Gọi D là chân đường phân giác trong góc A . Chứng minh:

Câu 11: Không dùng máy tính và bảng số hãy chứng minh rằng

III. Hướng dẫn giải bài tập ôn tập chương 1 hình học 9

Bài 33 trang 93 SGK Toán 9 Tập 1:

Chọn kết quả đúng trong các kết quả dưới đây:

a) Trong hình 41, sin α bằng:

b) Trong hình 42, sin Q bằng:

c) Trong hình 43, cos 30o bằng:

Lời giải:

a) Chọn C

b) Chọn D

c) Chọn C vì:

Bài 34 trang 93 SGK Toán 9 Tập 1:

a) Trong hình 44, hệ thức nào trong các hệ thức sau là đúng?

b) Trog hình 45, hệ thức nào trong các hệ thức sau không đúng ?

(A) sin2α + cos2α = 1

(B) sin α = cos β

Lời giải:

a) Chọn C

b) Chọn C sai

- Vì đẳng thức đúng phải là: cos β = sin(90o - β)

Bài 35 trang 94 SGK Toán 9 Tập 1:

Tỉ số giữa hai cạnh góc vuông của một tam giác vuông bằng 19: 28. Tìm các góc của nó.

Lời giải:

Kí hiệu góc như trên hình vẽ.

Tỉ số giữa hai cạnh góc vuông của một tam giác vuông là tg của góc nhọn này và là cotg của góc nhọn kia.

Giả sử α là góc nhọn của tam giác vuông đó.

Ta có:

=> α ≈ 34o10'

=> β ≈ 90o - 34o10' = 55o50'

(Lưu ý: Bạn cũng có thể sử dụng cotg để tính, nhưng cũng sẽ cho kết quả tương tự bởi vì tính chất lượng giác của 2 góc phụ nhau.)

Bài 36 trang 94 SGK Toán 9 Tập 1:

Cho tam giác có một góc bằng 45o. Đường cao chia một cạnh kề với góc đó thành các phần 20cm và 21 cm. Tính cạnh lớn trong hai cạnh còn lại (lưu ý có hai trường hợp hình 46 và hình 47).

Lời giải:

- Trường hợp hình 46: cạnh lớn trong hai cạnh còn lại được kí hiệu là x.

ΔHAB cân vì có ∠B = 45o

=> HA = HB = 20

Áp dụng định lí Pitago trong ΔHAC có:

x2 = AC2 = HA2 + HC2 = 202 + 212 = 841

=> x = 29 hay độ dài cạnh lớn trong hai cạnh còn lại là 29.

- Trường hợp hình 47: cạnh lớn trong hai cạnh còn lại được kí hiệu là y.

ΔH'A'B' cân vì có ∠B' = 45o

=> H'A' = H'B' = 21

Áp dụng định lí Pitago trong ΔH'A'B' có:

y2 = A'B'2 = H'A'2 + H'B'2 = 212 + 212 = 2.212

=> y = 21√2 ≈ 29,7 hay độ dài cạnh lớn trong hai cạnh còn lại là 29,7.

Bài 37 trang 94 SGK Toán 9 Tập 1:

Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.

a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.

b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nằm trên đường nào?

Lời giải:

a) Ta có: AB2 + AC2 = 62 + 4,52 = 7,52 = BC2

nên tam giác ABC vuông tại A. (đpcm)

=> ∠B = 37o

=> ∠C = 90o - ∠B = 90o - 37o = 53o

Mặt khác trong tam giác ABC vuông tại A, ta có:

=> AH = 3,6 cm

b) Gọi khoảng cách từ M đến BC là MK. Ta có:

Ta thấy SMBC = SABC khi MK = AH = 3,6 cm

Do đó để SMBC = SABC thì M phải nằm trên đường thẳng song song và cách BC một khoảng là 3,6 cm (có hai đường thẳng như trên hình).

Bài 39 trang 95 SGK Toán 9 Tập 1:

Tìm khoảng cách giữa hai cọc để căng dây vượt qua vực trong hình 49 (làm tròn đến mét)

Hình 49

Lời giải:

Kí hiệu như hình vẽ. Theo hệ thức giữa cạnh và góc của tam giác vuông:

Trong tam giác vuông ABC:

AB = AC tan 50o = 20.tan 50o = 23,83 m

=> BD = 20tan50o - 5 = 18,83 m

Trong tam giác vuông BHD:

Vậy khoảnh cách giữa hai cọc là 24,59 m.

Bài 40 trang 95 SGK Toán 9 Tập 1:

Tính chiều cao của cây trong hình 50 (làm tròn đến đề-xi-mét)

Hình 50

Lời giải:

Kí hiệu như hình vẽ.

Trong tam giác vuông ABC có:

BA = AC.tan35o = 30.tan35o ≈ 21 (m)

Chiều cao của cây là:

BH = BA + AH ≈ 21 + 1,7 ≈ 22,7 (m)

Vậy chiều cao của cây là 22,7 (m) (hoặc = 227 dm).

(Ghi chú: Bạn cũng có thể làm tắt hơn như sau:

Chiều cao của cây là:

BH = BA + AH = AC.tan35o + AH = 30.tan35o + 1,7 = 22,7 m)

Bài 42 trang 96 SGK Toán 9 Tập 1:

Ở một cái thang dài 3m người ta ghi: "Để đảm bảo an toàn khi dùng thang, phải đặt thang này tạo với mặt đất một góc có độ lớn từ 60o đến 70o". Đo góc thì khó hơn đo độ dài. Vậy hãy cho biết: Khi dùng thang đó chân thang phải đặt cách tường khoảng bao nhiêu mét để đảm bảo an toàn?

Lời giải:

Kí hiệu như hình vẽ.

Trong tam giác vuông ABC có:

AC = BC.cosC = 3.cosC

Vì phải đặt thang tạo với mặt đất một góc 60o đến 70o nên

60o ≤ ∠C ≤ 70o

=> cos 70o ≤ cosC ≤ cos 60o

=> 3.cos 70o ≤ 3.cosC ≤ 3.cos 60o

=> 1,03 ≤ AC ≤ 1,5

Vậy phải đặt chân thang cách tường từ 1,03 m đến 1,5 m.

Vào khoảng năm 200 trước Công Nguyên, Ơratôxten, một nhà toán học và thiên văn học Hi Lạp, đã ước lượng được "chu vi" của Trái Đất (chu vi đường Xích Đạo) nhờ hai quan sát sau:

1) Một ngày trong năm, ông ta để ý thấy Mặt Trời chiếu thẳng các đáy giếng ở thành phố Xy-en (nay gọi là At-xu-an), tức là tia sáng chiếu thẳng đứng.

2) Cùng lúc đó ở thành phố A-lếch-xăng-đri-a cách Xy-en 800km, một tháp cao 25m có bóng trên mặt đất dài 3,1m.

Từ hai quan sát trên, em hãy tính xấp xỉ "chu vi" của Trái Đất.

(Trên hình 51 điểm S tượng trưng cho thành phố Xy-en, điểm A tượng trưng cho thành phố A-lếch-xăng-đri-a, bóng của tháp trên mặt đất được coi là đoạn thẳng AB).

Hình 51

Lời giải:

Gọi c là chu vi Trái đất, góc ∠AOS = α. Ta có:

Vì các tia sáng chiếu thẳng đứng nên BC // SO do đó:

∠AOS = ∠ACB (so le trong)

Trong tam giác ABC vuông tại A có:

Vì ∠AOS = ∠ACB nên α = 7,07o

Vậy chu vi Trái đất là:

Ôn tập chương 1 hình học 9 được biên soạn bám sát chương trình sgk mới toán hình lớp 9. Được Soanbaitap.com tổng hợp và đăng trong chuyên mục giải toán 9 giúp các em tiện tra cứu và tham khảo để học tốt môn toán hình 9. Nếu thấy hay hãy comment và chia sẻ để nhiều bạn khác cùng học tập.

#soanbaitap

#soanbaitap #giải bài tập #Ôn tập chương I Hệ thức lượng giác trong tam giác vuông

0 notes

soanbaitap · 5 years ago

Link

Một số hệ thức về cạnh và đường cao trong tam giác vuông toán lớp 9 bài 1 giải bài tập là tâm huyết biên soạn của đội ngũ giáo viên dạy giỏi môn toán trên toàn quốc. Đảm bảo chính xác, dễ hiểu giúp các em nắm chắc kiến thức trong bài Một số hệ thức về cạnh và đường cao trong tam giác vuông lớp 9 và hướng dẫn giải bài tập sgk để các em hiểu hơn.

Bài 1. Một số hệ thức về cạnh và đường cao trong tam giác vuông thuộc: CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG

I. Lý thuyết về một số hệ thức về cạnh và đường cao trong tam giác vuông

1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền

Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông trên cạnh huyền.

Trong tam giác ABC vuông tại A ta có: b2 = a.b'; c2 = a.c'

2. Một số hệ thức liên quan đến đường cao

a) Định lý 1

Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của cạnh góc vuông trên cạnh huyền

Trong tam giác ABC vuông tại A ta có: h2 = b'.c'.

b) Định lý 2

Trong một tam giác vuông, tích của hai cạnh góc vuông bằng tích của cạnh huyền với đường cao tương ứng

Trong tam giác ABC vuông tại A ta có: a.h = b.c

c) Định lý 3

Trong tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.

Trong tam giác ABC vuông tại A ta có:

3. Ví dụ cụ thể

Câu 1: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB:AC = 3:4 và AB + AC = 21cm.

a) Tính các cạnh của tam giác ABC.

b) Tính độ dài các đoạn AH, BH, CH.

Hướng dẫn:

a) Theo giả thiết: AB:AC = 3:4, suy ra

Do đó AB = 3.3 = 9 (cm); AC = 3.4 = 12 (cm).

Tam giác ABC vuông tại A, theo định lý Py – ta – go ta có:

BC2 = AB2 + AC2 = 92 + 122 = 225, suy ra BC = 15cm

b) Tam giác ABC vuông tại A, ta có AH.BC = AB.AC, suy ra

AH2 = BH.HC. Đặt BH = x (0 < x < 9) thì HC = 15 - x, ta có:

(7,2)2 = x(15 - x) ⇔ x2 - 15x + 51,84 = 0 ⇔ x(x - 5,4) = 9,6(x - 5,4) = 0 ⇔ (x - 5,4)(x - 9,6) = 0 ⇔ x = 5,4 hoặc x = 9,6 (loại)

Vậy BH = 5,4cm. Từ đó HC = BC - BH = 9,6 (cm).

Chú ý: Có thể tính BH như sau:

AB2 = BH.BC suy ra

Câu 1: Cho tam giác cân ABC có đáy BC = 2a , cạnh bên bằng b (b > a) .

a) Tính diện tích tam giác ABC

b) Dựng BK ⊥ AC . Tính tỷ số

II. Hướng dẫn giải bài tập về một số hệ thức về cạnh và đường cao trong tam giác vuông lớp 9

Bài 1 trang 68 SGK Toán 9 Tập 1: Hãy tính x và y trong mỗi hình sau: (h.4a, b)

Hình 4

Lời giải:

- Hình a

Theo định lí Pitago ta có:

Áp dụng định lí 1 ta có:

- Hình b

Áp dụng định lí 1 ta có:

=> y = 20 - 7,2 = 12,8

Bài 2 trang 68 SGK Toán 9 Tập 1: Hãy tính x và y trong mỗi hình sau: (h.5)

Hình 5

Lời giải:

Áp dụng định lí 1 ta có:

Bài 3 trang 69 SGK Toán 9 Tập 1: Hãy tính x và y trong mỗi hình sau: (h.6)

Hình 6

Lời giải:

Áp dụng định lí Pitago ta có:

Áp dụng định lí 3 ta có:

Bài 4 trang 69 SGK Toán 9 Tập 1: Hãy tính x và y trong mỗi hình sau: (h.7)

Hình 7

Lời giải:

Theo định lí 2 ta có:

22 = 1.x => x = 4

Theo định lí 1 ta có:

y2 = x(1 + x) = 4(1 + 4) = 20

=> y = √20 = 2√5

Bài 5 trang 69 SGK Toán 9 Tập 1:

Trong tam giác vuông với các cạnh góc vuông có độ dài 3 và 4, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và độ dài các đoạn thẳng mà nó định ra trên cạnh huyền.

Lời giải:

ΔABC vuông tại A có AB = 3, AC = 4 và đường cao AH như trên hình.

Theo định lí Pitago ta có:

Mặt khác, AB2 = BH.BC (định lí 1)

Theo định lí 3 ta có: AH.BC = AB.AC

Bài 6 trang 69 SGK Toán 9 Tập 1:

Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 1 và 2. Hãy tính các cạnh góc vuông của tam giác này.

Lời giải:

ΔABC vuông tại A và đường cao AH như trên hình.

BC = BH + HC = 1 + 2 = 3

Theo định lí 1: AB2 = BH.BC = 1.3 = 3

=> AB = √3

Theo định lí 1: AC2 = HC.BC = 2.3 = 6

=> AC = √6

Vậy độ dài các cạnh góc vuông của tam giác lần lượt là √3 và √6.

Bài 7 trang 69 SGK Toán 9 Tập 1:

Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 1 và 2. Hãy tính các cạnh góc vuông của tam giác này.

Lời giải:

ΔABC vuông tại A và đường cao AH như trên hình.

BC = BH + HC = 1 + 2 = 3

Theo định lí 1: AB2 = BH.BC = 1.3 = 3

=> AB = √3

Theo định lí 1: AC2 = HC.BC = 2.3 = 6

=> AC = √6

Vậy độ dài các cạnh góc vuông của tam giác lần lượt là √3 và √6.

Bài 8 trang 70 SGK Toán 9 Tập 1:

Tìm x và y trong mỗi hình sau:

Lời giải:

a) Theo định lí 2 ta có:

x2 = 4.9 = 36 => x = 6

b) Vì đường cao chia cạnh huyền thành hai nửa bằng nhau nên nó đồng thời là đường trung tuyến. Mà trong tam giác vuông, đường tuyến bằng nửa cạnh huyền nên nên x = 2.

Theo định lí Pitago ta có:

Bài 9 trang 70 SGK Toán 9 Tập 1:

Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:

a) Tam giác DIL là một tam giác cân

b) Tổng

không đổi khi I thay đổi trên cạnh AB.

Lời giải:

a) Xét hai tam giác vuông ADI và CDL có:

AD = CD (cạnh hình vuông)

Nên ΔADI = ΔCDL (cạnh góc cuông và góc nhọn)

Suy ra DI = DL hay ΔDIL cân. (đpcm)

b) Trong tam giác DKL vuông tại D với đường cao DC. Theo định lí 4, ta có:

không đổi khi I thay đổi trên cạnh AB. (đpcm)

Một số hệ thức về cạnh và đường cao trong tam giác vuông toán lớp 9 bài 1 giải bài tập được biên soạn bám sát chương trình sgk mới toán hình lớp 9. Được Soanbaitap.com tổng hợp và đăng trong chuyên mục giải toán 9 giúp các em tiện tra cứu và tham khảo để học tốt môn toán hình 9. Nếu thấy hay hãy comment và chia sẻ để nhiều bạn khác cùng học tập.

#soanbaitap

#soanbaitap #giải bài tập #Bài 1. Một số hệ thức về cạnh và đường cao trong tam giác vuông

0 notes

soanbaitap · 5 years ago

Link

Hình vuông toán lớp 8 bài 12 giải bài tập được biên soạn từ đội ngũ giáo viên dạy giỏi môn toán trên toàn quốc đảm bảo chính xác, dễ hiểu giúp các em nắm được kiến thức trong bài hình vuông lớp 8 và hướng dẫn giải bài tập hình vuông lớp 8 sgk để các em hiểu rõ hơn.

Bài 12. Hình vuông thuộc: CHƯƠNG I. TỨ GIÁC

I. Lý thuyết về hình vuông

1. Hình vuông là gì ?

Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.

Tổng quát: ABCD là hình vuông ⇔

Nhận xét:

+ Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.

+ Hình vuông là hình thoi có bốn góc vuông.

+ Hình vuông vừa là hình chữ nhật vừa là hình thoi.

2. Tính chất hình vuông lớp 8

Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.

3. Dấu hiệu nhận biết hình vuông lớp 8

+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.

+ Hình thoi có một góc vuông là hình vuông.

+ Hình thoi có hai đường chéo bằng nhau là hình vuông.

Ví dụ: Cho tam giác ABC vuông tại A. Phân giác trong AD của góc A (D ∈ BC ). Vẽ DF ⊥ AC, DE ⊥ AB. Chứng minh tứ giác AEDF là hình vuông.

Hướng dẫn:

+ Xét tứ giác AEDF có Aˆ = Eˆ = Fˆ = 900

⇒ AEDF là hình chữ nhật . ( 1 )

Theo giả thiết ta có AD là đường phân giác của góc Aˆ

⇒ EADˆ = DAFˆ = 450.

+ Xét Δ AED có AEDˆ = 900; DAEˆ = 450 ⇒ EDAˆ = 450

⇒ Δ AED vuông cân tại E nên AE = ED ( 2 )

Từ ( 1 ),( 2 ) ⇒ AEDF là hình vuông (dấu hiệu 1 – mục 3)

II. Hình vuông lớp 8 - Hướng dẫn giải bài tập ví dụ

Bài 1: Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC.

a) Chứng minh rằng BI ⊥ AK.

b) Gọi E là giao điểm của BI và AK. Chứng minh rằng CE = AB.

Hướng dẫn:

Xét Δ BAI và Δ ADK có:

⇒ Δ BAI = Δ ADK ( c - g - c )

⇒ ABIˆ = DAKˆ (góc tương ứng bằng nhau)

Mà IAEˆ + EABˆ = 900 ⇒ ABIˆ + EABˆ = 900

+ Xét Δ ABE có EABˆ + ABEˆ + AEBˆ = 1800

⇒ AEBˆ = 1800 - ( ABEˆ + BAEˆ ) = 1800 - 900 = 900 hay AK ⊥ BI (đpcm)

+ Xét tứ giác EBCK có KEBˆ + EBCˆ + BCKˆ+ CKEˆ = 3600

⇒ EBCˆ + EKCˆ = 1800.

Mà AKDˆ + AKCˆ = 1800 nên EBCˆ = EKDˆ

+ Tứ giác EBCK nội tiếp nên BECˆ = BKCˆ

Mà BKCˆ = AKDˆ nên EBCˆ = BECˆ hay tam giác BEC cân tại C

⇒ CE = BC = AB (đpcm)

Bài 2: Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho MANˆ = 450. Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính:

a) Tính số đo KANˆ = ?

b) Chu vi tam giác MCN theo a.

Hướng dẫn:

a) Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được

⇒ Δ ABM = Δ ADK ( c - g - c )

Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:

⇒ KANˆ = A3ˆ + A4ˆ = A1ˆ + A3ˆ = 900 - 450 = 450

b) Đặt BM = DK = x thì KN = x + DN, MC = a - x, CN = a - DN

Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:

⇒ Δ AMN = Δ AKN ( c - g - c )

⇒ MN = KN (cạnh tương ứng bằng nhau)

Khi đó, chu vi của tam giác MCN là

MC + CN + MN = a - x + a - DN + x + DN = 2a.

III. Hướng dẫn trả lời câu hỏi bài tập sgk hình vuông toán lớp 8 bài 12

Trả lời câu hỏi Toán 8 Tập 1 Bài 12 trang 107:

Đường chéo của hình vuông có những tính chất gì ?

Lời giải

Hình vuông có tất cả các hình chữ nhật và hình thoi

⇒ Hai đường chéo của hình vuông có tính chất:

Hai đường chéo bằng nhau

Hai đường chéo cắt nhau tại trung điểm mỗi đường

Hai đường chéo vuông góc với nhau.

Trả lời câu hỏi Toán 8 Tập 1 Bài 12 trang 108:

Tìm các hình vuông trên hình 105.

Lời giải

- ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường ⇒ ABCD là hình bình hành

Hình bình hành ABCD có hai đường chéo bằng nhau ⇒ ABCD là hình chữ nhật

Hình chữ nhật ABCD có AB = BC ⇒ ABCD là hình vuông

- MNPQ có hai đường chéo cắt nhau tại trung điểm mỗi đường ⇒ MNPQ là hình bình hành

Hình bình hành MNPQ có hai đường chéo bằng nhau ⇒ MNPQ là hình chữ nhật

Hình chữ nhật MNPQ có MP ⊥ NQ tại O ⇒ MNPQ là hình vuông

- RSTU có 4 cạnh bằng nhau ⇒ RSTU là hình thoi

Hình thoi RSTU có một góc vuông ⇒ RSTU là hình vuông.

IV. Hướng dẫn giải bài tập sgk hình vuông toán lớp 8 bài 12

Bài 79 trang 108 SGK Toán 8 Tập 1:

a) Một hình vuông có cạnh bằng 3cm. Đường chéo của hình vuông đó bằng: 6cm, √18 cm, 5cm hay 4cm?

b) Đường chéo của một hình vuông bằng 2dm. Cạnh của hình vuông đó bằng:

Lời giải:

Gọi đường chéo của hình vuông có độ dài là a.

Áp dụng định lí Pi-ta-go ta có:

a2 = 32 + 32 = 18 suy ra a = √18 = 3√2

Vậy đường chéo của hình vuông đó bằng 3√2 (cm)

Gọi cạnh của hình vuông là a.

Áp dụng định lí Pi-ta-go ta có:

a2 + a2 = 22 ⇒ 2a2 = 4

⇒ a2 = 2 ⇒ a = √2

Vậy cạnh của hình vuông đó bằng √2 (dm).

Kiến thức áp dụng

+ Hình vuông có bốn góc vuông và bốn cạnh bằng nhau.

Bài 80 trang 108 SGK Toán 8 Tập 1:

Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông.

Lời giải:

+ Hình vuông cũng là hình bình hành nên nhận O là giao điểm của hai đường chéo là tâm đối xứng.

+ Hình vuông cũng là hình thoi nên nhận hai đường chéo AC và BD là các trục đối xứng.

+ Hình vuông cũng là hình thang cân nên nhận đường thẳng nối trung điểm các cặp cạnh đối diện là trục đối xứng.

Vậy hình vuông có 1 tâm đối xứng và 4 trục đối xứng như trên.

Kiến thức áp dụng

+ Hình bình hành nhận giao điểm của hai đường chéo là tâm đối xứng.

+ Hình thang cân nhận đường thẳng nối trung điểm hai cạnh đáy là trục đối xứng.

+ Hình thoi nhận hai đường chéo là hai trục đối xứng.

Bài 81 trang 108 SGK Toán 8 Tập 1:

Cho hình 106. Tứ giác AEDF là hình gì? Vì sao?

Lời giải:

Cách 1:

Tứ giác AEDF có EA // DF (cùng vuông góc AF)

DE // FA (cùng vuông góc AE)

⇒ AEDF là hình bình hành (theo định nghĩa)

Hình bình hành AEDF có đường chéo AD là phân giác của góc A

⇒AEDF là hình thoi.

Hình thoi AEDF có Â = 90º

⇒ AEDF là hình vuông.

Kiến thức áp dụng

+ Tứ giác có các cặp cạnh đối song song là hình bình hành

+ Hình bình hành có đường chéo là phân giác của một góc là hình thoi.

+ Hình thoi có một góc vuông là hình vuông.

Cách 2:

Tứ giác AEDF có EA // DF (cùng vuông góc AF)

DE // FA (cùng vuông góc AE)

⇒ AEDF là hình bình hành (theo định nghĩa)

Hình bình hành AEDF có Â = 90º

⇒ AEDF là hình chữ nhật.

Hình chữ nhật AEDF có AD là phân giác của Â

⇒ AEDF là hình vuông.

Kiến thức áp dụng

+ Tứ giác có các cặp cạnh đối song song là hình bình hành

+ Hình bình hành có một góc vuông là hình chữ nhật.

+ Hình chữ nhật có đường chéo là phân giác của một góc là hình vuông.

Bài 82 trang 108 SGK Toán 8 Tập 1:

Cho hình 107, trong đó ABCD là hình vuông. Chứng minh rằng tứ giác EFGH là hình vuông.

Lời giải:

* Do ABCD là hình vuông nên AB = BC = CD = DA.

Theo giả thiết ta có: AE = BF = CG = DH nên ta có:

AB – AE = BC – BF = CD – CG = DA – DH

⇔ BE = CF= DG = HA

* Xét các tam giác vuông AEH, BFE, CGF, DHG có:

AE= BF = CG = DH (giả thiết)

HA= BE = CF = DG (chứng minh trên)

⇒ ΔAEH = ΔBFE = ΔCGF = ΔDHG ( c.g.c)

Suy ra: HE = EF = FG = GH (các cạnh tương ứng)

* Tứ giác EFGH là hình thoi có 1 góc bằng 90o nên EFGH là hình vuông.

Kiến thức áp dụng

+ Tứ giác có bốn cạnh bằng nhau là hình thoi.

+ Hình thoi có một góc vuông là hình vuông.

Bài 83 trang 109 SGK Toán 8 Tập 1:

Các câu sau đúng hay sai?

a) Tứ giác có hai đường chéo vuông góc với nhau là hình thoi.

b) Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi.

c) Hình thoi là tứ giác có tất cả các cạnh bằng nhau.

d) Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.

e) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

Lời giải:

- Các câu a và d sai.

- Các câu b, c, e đúng.

Kiến thức áp dụng

Dấu hiệu nhận biết hình thoi:

+ Tứ giác có bốn cạnh bằng nhau.

+ Hình bình hành có hai đường chéo vuông góc với nhau.

Dấu hiệu nhận biết hình vuông:

+ Hình thoi có hai đường chéo bằng nhau là hình vuông.

+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

Bài 84 trang 109 SGK Toán 8 Tập 1:

Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.

a) Tứ giác AEDF là hình gì? Vì sao?

b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi?

c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông?

Lời giải:

a) Tứ giác AEDF là hình bình hành.

Vì có DE // AF, DF // AE (gt) (theo định nghĩa)

b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.

c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).

d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

Kiến thức áp dụng

+ Tứ giác có các cặp cạnh đối song song là hình bình hành

+ Hình bình hành có đường chéo là phân giác của một góc là hình thoi.

+ Hình bình hành có một góc vuông là hình chữ nhật.

+ Tứ giác vừa là hình thoi, vừa là hình chữ nhật thì là hình vuông.

Bài 85 trang 109 SGK Toán 8 Tập 1:

Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.

a) Tứ giác ADFE là hình gì? Vì sao?

b) Tứ giác EMFN là hình gì? Vì sao?

Lời giải:

a) E, F là trung điểm AB, CD ⇒ AE = EB = AB/2, DF = FC = CD/2.

Ta có: AB = CD = 2AD = 2BC

⇒ AE = EB = BC = CF = FD = DA.

+ Tứ giác ADFE có AE // DF, AE = DF

⇒ ADFE là hình bình hành.

Hình bình hành ADFE có Â = 90º

⇒ ADFE là hình chữ nhật.

Hình chữ nhật ADFE là hình chữ nhật có AE= AD

⇒ ADFE là hình vuông.

b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành

Do đó DE // BF

Tương tự: AF // EC

Suy ra EMFN là hình bình hành

Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.

Hình bình hành EMFN có M̂ = 90º nên là hình chữ nhật.

Lại có ME = MF nên EMFN là hình vuông.

Kiến thức áp dụng

+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

+ Hình bình hành có một góc vuông là hình chữ nhật.

+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

Bài 86 trang 109 SGK Toán 8 Tập 1:

Đố. Lấy một tờ giấy gấp làm tư rồi cắt chéo theo nhát cắt AB (h.108). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác nhận được là hình gì? Vì sao? Nếu ta có OA = OB thì tứ giác nhận được là hình gì?

Lời giải:

- Tứ giác nhận được theo nhát cắt của AB là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường v�� vuông góc với nhau.

- Nếu có thêm OA = OB thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông.

Kiến thức áp dụng

+ Hình bình hành có 2 đường chéo vuông góc với nhau là hình thoi.

+ Hình thoi có 2 đường chéo bằng nhau là hình vuông.

Hình vuông toán lớp 8 bài 12 giải bài tập do đội ngũ giáo viên giỏi toán biên soạn, bám sát chương trình SGK mới toán học lớp 8. Được Soanbaitap.com biên tập và đăng trong chuyên mục giải toán 8 giúp các bạn học sinh học tốt môn toán đại 8. Nếu thấy hay hãy comment và chia sẻ để nhiều bạn khác cùng học tập.

#soanbaitap

#soanbaitap #giải bài tập #Bài 12. Hình vuông

0 notes

soanbaitap · 5 years ago

Link

Hình chữ nhật toán lớp 8 bài 9 giải bài tập được biên soạn từ đội ngũ giáo viên dạy giỏi môn toán trên toàn quốc đảm bảo chính xác, dễ hiểu giúp các em nắm được kiến thức trong bài hình chữ nhật lớp 8 và hướng dẫn giải bài tập hình chữ nhật lớp 8 để các em hiểu rõ hơn.

Bài 9. Hình chữ nhật thuộc: CHƯƠNG I. TỨ GIÁC

I. Lý thuyết về hình chữ nhật

1. Hình chữ nhật là gì?

Hình chữ nhật là tứ giác có bốn góc vuông. Hình chữ nhật cũng là một hình bình hành và cũng là hình thang cân

Tổng quát: ABCD là hình chữ nhật ⇔ Aˆ = Bˆ = Cˆ = Dˆ = 900

2. Tính chất hình chữ nhật

Hình chữ nhật là có tất cả các tính chất của hình bình hành và hình thang cân.

Định lí: Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường

3. Dấu hiệu nhận biết hình chữ nhật

+ Tứ giác có ba góc vuông là hình chữ nhật.

+ Hình thang cân có một góc vuông là hình chữ nhật.

+ Hình bình hành có một góc vuông là hình chữ nhật.

+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

4. Áp dụng vào tam giác

+ Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.

+ Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.

Ví dụ: Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Chứng minh tứ giác AHCE là hình chữ nhật.

Hướng dẫn:

+ Trong Δ AHC vuông có I là trung điểm của AC

⇒ HE là đường trung tuyến của Δ AHC.

⇒ HI = 1/2AC = AI = IC.

Mà E đối xứng với H qua I ⇒ HI = IE.

Khi đó ta có HI = IE = AI = IC.

+ Xét Δ HCE có CI là đường trung tuyến ��ng với cạnh HE

mà CI = 1/2HE ⇒ Δ HCE vuông tại C.

Tương tự xét với Δ AHE,Δ AEC đều là các tam giác vuông tại A, E.

Xét tứ giác AHCE có EAHˆ = AHCˆ = HCEˆ = CEAˆ = 900

⇒ AHCE là hình chữ nhật.

5. Diện tích hình chữ nhật và chu vi hình chữ nhật

Diện tích hình chữ nhật được đo bằng độ lớn của bề mặt hình, là phần mặt phẳng ta có thể nhìn thấy của hình chữ nhật.

Diện tích hình chữ nhật được tính theo công thức chiều dài nhân chiều rộng.

Trong đó:

S là diện tích hình chữ nhật.

a là chiều dài hình chữ nhật.

b là chiều rộng hình chữ nhật.

Chu vi hình chữ nhật được tính bằng tổng độ dài các đường bao quanh hình, cũng chính là đường bao quanh toàn bộ diện tích.

Chu vi hình chữ nhật bằng 2 lần tổng của chiều dài và chiều rộng.

Trong đó:

P là chu vi hình chữ nhật.

a là chiều dài hình chữ nhật.

b là chiều rộng hình chữ nhật.

II. Toán 8 hình chữ nhật - hướng dẫn giải bài tập ví dụ sgk

Bài 1: Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Giải thích?

Hướng dẫn:

Tứ giác EFGH là hình chữ nhật.

Giải thích: Theo giả thiết ta có EF, GH lần lượt là đường trung bình của tam giác Δ ABC,Δ ADC

Áp dụng định lí đường trung bình vào hai tam giác ta được

Chứng minh tương tự: EH//FG//BD ( 2 )

Từ ( 1 ) và ( 2 ), tứ giác EFGH có hai cặp cạnh đối song song nên tứ giác EFGH là hình bình hành.

Gọi O là giao điểm của AC và BD, I là giao điểm của EF với BD.

Áp dụng tính chất của các góc đồng vị vào các đường thẳng song song ở trên và giả thiết nên ta có:

Hình bình hành EFGH có một góc vuông nên EFGH là hình chữ nhật.

Bài 2: Tìm giá trị của x từ các thông tin trên hình sau ?

Hướng dẫn:

Kẻ BH ⊥ CD, tứ giác ABHD có Aˆ = ABHˆ = BHDˆ = 900

⇒ Tứ giác ABHD là hình chữ nhật.

Áp dụng tính chất của hình chữ nhật ta có:

Ta có: CD = DH + HC ⇒ HC = CD - DH = 15 - 10 = 5( cm )

+ Xét Δ BCH, áp dụng định lý Py – ta – go ta có:

BC2 = HC2 + BH2 ⇒ BH2 = BC2 - HC2

⇒ BH = √ (BC2 - HC2) = √ (132 - 52) = 12( cm )

Do đó BH = AD = x = 12( cm ). Vậy x = 12

III. Hướng dẫn trả lời câu hỏi bài tập sgk toán lớp 8 bài 9 hình chữ nhật

Trả lời câu hỏi Toán 8 Tập 1 Bài 9 trang 97:

Chứng minh rằng hình chữ nhật ABCD trên hình 84 cũng là một hình bình hành, một hình thang cân.

Lời giải

- ABCD có các góc đối bằng nhau (đều là góc vuông) nên ABCD là hình bình hành

- ABCD là hình thang (vì AB // CD),

hai góc ở đáy: góc D = góc C ⇒ ABCD là hình thang cân

Trả lời câu hỏi Toán 8 Tập 1 Bài 9 trang 98:

Với một chiếc compa, ta sẽ kiểm tra được hai đoạn thẳng bằng nhau hay không bằng nhau. Bằng compa, để kiểm tra tứ giác ABCD có là hình chữ nhật hay không, ta làm thế nào?

Lời giải

- Ta kiểm tra các cặp cạnh đối xem chúng có bằng nhau không

Nếu các cặp cạnh đối bằng nhau ⇒ ABCD là hình bình hành

- Sau đó: Kiểm tra hai đường chéo xem chúng bằng nhau không

Nếu hai đường chéo bằng nhau ⇒ ABCD là hình chữ nhật

Trả lời câu hỏi Toán 8 Tập 1 Bài 9 trang 98: Cho hình 86:

a) Tứ giác ABDC là hình gì ? Vì sao ?

b) So sánh các độ dài AM và BC.

c) Tam giác vuông ABC có AM là đường trung tuyến ứng với cạnh huyền. Hãy phát biểu tính chất tìm được ở câu b) dưới dạng một định lý.

Lời giải

a) Tứ giác ABDC có hai đường chéo cắt nhau tại trung điểm mỗi đường ⇒ ABDC là hình bình hành

Hình bình hành ABDC có góc A vuông ⇒ ABDC là hình chữ nhật

b) Hình chữ nhật ABDC ⇒ AD = BC (hai đường chéo)

c) Định lí: Trong một tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền

Trả lời câu hỏi Toán 8 Tập 1 Bài 9 trang 98: Cho hình 87:

a) Tứ giác ABDC là hình gì ? Vì sao ?

b) Tam giác ABC là tam giác gì ?

c) Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Hãy phát biểu tính chất tìm được ở câu b) dưới dạng một định lý.

Lời giải

a) Tứ giác ABDC có hai đường chéo cắt nhau tại trung điểm mỗi đường ⇒ ABDC là hình bình hành

Hình bình hành ABDC có hai đường chéo bằng nhau ⇒ ABDC là hình chữ nhật

b) ABDC là hình chữ nhật ⇒ góc BAC = 90o

⇒ ΔABC là tam giác vuông tại A

c) Định lí: Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông.

IV. Hướng dẫn giải bài tập sgk toán lớp 8 bài 9 hình chữ nhật

Bài 58 trang 99 SGK Toán 8 Tập 1:

Điền vào chỗ trống, biết rằng a, b là độ dài của các cạnh, d là độ dài đường chéo của một hình chữ nhật.

a 5 .... √13 b 12 √6 .... d .... √10 7

Lời giải:

Trong hình chữ nhật ABCD ta luôn có

Do đó áp dụng định lý Py-ta-go ta có: d2 = a2 + b2.

Vậy :

- Cột thứ hai:

d2 = a2 + b2 = 52 + 122 = 25 + 144 = 169 nên d = 13

- Cột thứ ba:

a2 + b2 = d2 ⇒ a2 = d2 – b2 = (√10)2 – (√6)2 = 4 nên a = 2

- Cột thứ tư:

a2 + b2 = d2 ⇒ b2 = d2 – a2 = 72 – (√13)2 = 36 nên b = 6.

Vậy ta có bảng sau:

a 5 2 √13 b 12 √6 6 d 13 √10 7

Kiến thức áp dụng

Hình chữ nhật là tứ giác có bốn góc vuông.

Bài 59 trang 99 SGK Toán 8 Tập 1: Chứng minh rằng:

a) Giao điểm của hai đường chéo của hình chữ nhật là tâm đối xứng của hình chữ nhật đó.

b) Hai đường thẳng đi qua trung điểm hai cặp cạnh đối của hình chữ nhật là hai trục đối xứng của hình chữ nhật đó.

Lời giải:

Giả sử ABCD là hình chữ nhật. Gọi O là giao điểm của AC và BD.

Theo tính chất đường chéo của hình chữ nhật ta có; hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.

Vậy: OA = OC và OB= OD

Do đó, O là tâm đối xứng của hình chữ nhật đó.

Áp dung tính chất: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.

ABCD là hình chữ nhật

⇒ ABCD là hình thang cân (hai đáy AB và CD)

⇒ Đường thẳng đi qua trung điểm AB và CD là trục đối xứng ABCD.

Tương tự vậy: ABCD cũng là hình thang cân với hai đáy AD và BC

⇒ Đường thẳng đi qua trung điểm AD và BC là trục đối xứng của ABCD.

Vậy ta có điều phải chứng minh.

Kiến thức áp dụng

+ Hình chữ nhật là hình bình hành đặc biệt.

+ Hình chữ nhật là hình thang cân đặc biệt.

+ Hình bình hành có giao điểm của hai đường chéo là tâm đối xứng.

+ Hình thang cân nhận đường thẳng đi qua trung điểm hai đáy là trục đối xứng.

Bài 60 trang 99 SGK Toán 8 Tập 1:

Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có cạch góc vuông bằng 7cm và 24 cm.

Lời giải:

Gọi a là độ dài cạnh huyền của tam giác vuông.

Theo định lý Pi-ta-go ta có:

a2 = 72 + 242 = 625

⇒ a = 25cm

⇒ Độ dài trung tuyến ứng với cạnh huyền bằng: a/2 = 25/2 = 12,5 (cm).

Kiến thức áp dụng

+ Định lý Pitago: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

+ Định lý: Trong một tam giác vuông, độ dài đường trung tuyến ứng với cạnh huyền bằng một nửa độ dài cạnh huyền.

Bài 61 trang 99 SGK Toán 8 Tập 1:

Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Tứ giác AHCE là hình gì? Vì sao?

Lời giải:

I là trung điểm của AC ⇒ IA = IC.

E đối xứng với H qua I ⇒ IE = IH

⇒ AC ∩ HE = I là trung điểm của AC và HE

⇒ AHCE là hình bình hành (dấu hiệu nhận biết 4)

Lại có : Ĥ = 90º

⇒ AHCE là hình chữ nhật (đpcm).

Kiến thức áp dụng

+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.

+ Hình bình hành có một góc vuông là hình chữ nhật.

Bài 62 trang 99 SGK Toán 8 Tập 1: Các câu sau đúng hay sai?

a) Nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có đường kính là AB (h.88)

b) Nếu điểm C thuộc đường tròn có đường kính là AB (C khác A và B) thì tam giác ABC vuông tại C (h.89).

Lời giải:

a) Đúng

Gọi O là trung điểm của AB.

Ta có CO là trung tuyến ứng với cạnh huyền nên

⇒ OC = AB/2 = OA = OB.

⇒ A, B, C cùng thuộc đường tròn bán kính OA.

Tâm O là trung điểm của AB nên AB là đường kính.

Vậy C thuộc đường tròn đường kính AB.

b) Đúng

Gọi O là tâm đường tròn.

⇒ OA = OB = OC = R

AB là đường kính nên AB = 2R.

Tam giác ABC có CO là trung tuyến và CO = AB/2

⇒ ΔABC vuông tại C.

Kiến thức áp dụng

+ Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.

+ Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng một nửa cạnh ấy thì tam giác đó là tam giác vuông.

Bài 63 trang 100 SGK Toán 8 Tập 1: Tìm x trên hình 90

Lời giải:

* Kẻ BH vuông góc CD.

Xét tứ giác ABHD có:

=> Tứ giác ABHD là hình chữ nhật

=> AB = DH= 10 ( hình chữ nhật có các cạnh đối bằng nhau)

+ Suy ra: HC =DC- DH =15- 10= 5

+ Áp dụng định lí py- ta- go vào tam giác vuông BHC có:

BC2 = BH2 + HC2 ⇔ 132 = BH2 + 52

⇔ BH2 = 132 – 52 = 144

⇔ BH = 12

+ Do ABHD là hình chữ nhật nên AD= BH = 12

Vậy x= 12

Kiến thức áp dụng

+ Tứ giác có ba góc vuông là hình chữ nhật.

Bài 64 trang 100 SGK Toán 8 Tập 1:

Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.

Lời giải:

Vậy tứ giác EFGH là hình chữ nhật.

Kiến thức áp dụng

Tứ giác có ba góc vuông là hình chữ nhật.

Bài 65 trang 100 SGK Toán 8 Tập 1:

Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

Lời giải:

Ta có EB = EA, FB = FC (gt)

⇒ EF là đường trung bình của ΔABC

⇒EF // AC và EF = AC/2 (1)

HD = HA, GD = GC

⇒ HG là đường trung bình của ΔADC

⇒ HG // AC và HG = AC/2 (2)

Từ (1) và (2) suy ra EF // HG và EF = HG

⇒ Tứ giác EFGH là hình bình hành (*)

EA = EB, HA = HD ⇒ EH là đường trung bình của ΔABD ⇒ EH // BD.

Mà EF // AC, AC ⊥ BD

⇒ EH ⊥ EF ⇒ Ê = 90º (**)

Từ (*) và (**) suy ra EFGH là hình chữ nhật.

Kiến thức áp dụng

+ Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành.

+ Hình bình hành có một góc vuông là hình chữ nhật.

+ Đoạn thẳng nối hai trung điểm của hai cạnh của một tam giác là đường trung bình của tam giác. Đường trung bình của tam giác song song và bằng một nửa cạnh còn lại.

Bài 66 trang 100 SGK Toán 8 Tập 1:

Đố. Một đội công nhân đang trồng cây trên đoạn đường AB thì gặp chướng ngại vật che lấp tầm nhìn (h.92). Đội đã dựng các điểm C, D, E như trên hình vẽ rồi trồng cây tiếp trên đoạn đường EF vuông góc với DE. Vì sao AB và EF cùng nằm trên một đường thẳng?

Lời giải:

Tứ giác BCDE có:

BC // DE (vì cùng vuông góc với CD);

BC = DE

nên BCDE là hình bình hành ⇒ CD // BE.

Lại có :

⇒ AB // CD

⇒ EF // CD

Theo tiên đề Ơ-clit suy ra A, B, E, F thẳng hàng.

Hình chữ nhật toán lớp 8 bài 9 giải bài tập do đội ngũ giáo viên giỏi toán biên soạn, bám sát chương trình SGK mới toán học lớp 8. Được Soanbaitap.com biên tập và đăng trong chuyên mục giải toán 8 giúp các bạn học sinh học tốt môn toán đại 8. Nếu thấy hay hãy comment và chia sẻ để nhiều bạn khác cùng học tập.

#soanbaitap

#soanbaitap #giải bài tập #Bài 9. Hình chữ nhật

0 notes

soanbaitap · 5 years ago

Link

Đối xứng tâm toán lớp 8 bài 8 giải bài tập được biên soạn từ đội ngũ giáo viên dạy giỏi môn toán trên toàn quốc đảm bảo chính xác, dễ hiểu giúp các em nắm được kiến thức trong bài đối xứng tâm lớp 8 và hướng dẫn giải bài tập về đối xứng tâm lớp 8 để các em hiểu rõ hơn.

Bài 8. Đối xứng tâm thuộc: CHƯƠNG I. TỨ GIÁC

I. Lý thuyết về đối xứng tâm

1. Hai điểm đối xứng qua một điểm

Định nghĩa: Hai điểm gọi là đối xứng với nhau qua điểm I nếu I là trung điểm của đoạn thẳng nối hai điểm đó.

Hai điểm M và M' gọi là hai điểm đối xứng với nhau qua điểm I.

2. Hai hình đối xứng qua một điểm

Định nghĩa: Hai hình gọi là đối xứng với nhau qua điểm I nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua điểm I và ngược lại.

Điểm I gọi là tâm đối xứng của hai hình đó.

3. Hình có tâm đối xứng

Định nghĩa: Điểm I gọi là tâm đối xứng qua hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua điểm I cũng thuộc hình H.

Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.

Ví dụ: Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua A, F là điểm đối xứng với D qua C. Chứng minh:

a, AC // EF

b, Điểm E đối xứng với điểm F qua điểm B.

Hướng dẫn:

E là điểm đối xứng với D qua A ⇒ A là trung điểm của DE.

F là điểm đối xứng với D qua C ⇒ C là trung điểm của DF.

a) Xét Δ DEF có

⇒ AC là đường trung bình của Δ DEF.

⇒ AC // EF

b) AC là đường trung bình của tam giác Δ DEF

⇒ AC = 1/2EF

+ ABCD là hình bình hành

Mà DC = CF ⇒ AB = 1/2DF.

⇒ AB là đường trung bình của Δ DEF

Do đó B là trung điểm của EF hay E đối xứng với F qua B.

II. Toán 8 đối xứng tâm - Hướng dẫn giải bài tập ví dụ sgk

Bài 1: Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, F là điểm đối xứng với D qua C. Chứng minh rằng E đối xứng với F qua B.

Hướng dẫn:

Theo giả thiết ta có:

+ A là trung điểm của DE thì AD = AE ( 1 )

+ C là trung điểm của DF thì CD = CF ( 2 )

Ta có ABCD là hình bình hành nên AD//BC

⇒ AE//BC ( 3 ) và AD = BC ( 4 )

Từ ( 1 ), ( 4 ) ⇒ AE = BC ( 5 )

Từ ( 3 ) và ( 5 ), tứ giác ACBE có cặp cạnh đối song song và bằng nhau nên là hình bình hành.

Áp dụng tính chất và định nghĩa về hình bình hành ACBE ta được

Chứng minh tương tự, tứ giác ACBF là hình bình hành

Ta được:

Từ ( 6 ), ( 7 ) ⇒ E, B, F thẳng hàng và BE = BF do đó B là trung điểm của EF hay E đối xứng với F qua B.

Bài 2: Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox, C là điểm đối xứng với A qua Oy. Chứng minh B đối xứng với C qua O.

Hướng dẫn:

Vẽ AH ⊥ Ox, AK ⊥ Oy

Vẽ hai điểm B, C sao cho H, K lần lượt là trung điểm của AB, AC thì B là điểm đối x��ng với A qua Ox, C là điểm đối xứng với A qua Oy.

Vì O ∈ Ox, O ∈ Oy nên O đối xứng với O qua Ox, Oy.

Áp dụng tính chất của phép đối xứng ta được

Và

⇒ BOCˆ = {180^0}. (2)

Từ ( 1 ), ( 2 ) suy ra O là trung điểm của BC hay B đối xứng với C qua O.

III. Hướng dẫn giải bài tập sgk toán lớp 8 bài 8 đối xứng tâm

Trả lời câu hỏi Toán 8 Tập 1 Bài 8 trang 93:

Cho điểm O và điểm A. Hãy vẽ điểm A’ sao cho O là trung điểm của đoạn thẳng AA’.

Lời giải

Trả lời câu hỏi Toán 8 Tập 1 Bài 8 trang 94:

Cho điểm O và đoạn thẳng AB (h.75)

- Vẽ điểm A’ đối xứng với A qua O.

- Vẽ điểm B’ đối xứng với B qua O.

- Lấy điểm C thuộc đoạn thẳng AB, vẽ điểm C’ đối xứng với C qua O.

- Dùng thước để kiểm nghiệm rằng điểm C’ thuộc đoạn thẳng A’B’.

Lời giải

Điểm C’ thuộc đoạn thẳng A’B’

Trả lời câu hỏi Toán 8 Tập 1 Bài 8 trang 95:

Gọi O là giao điểm hai đường chéo của hình bình hành ABCD (h.79). Tìm hình đối xứng với mỗi cạnh của hình bình hành qua điểm O.

Lời giải

AB đối xứng với CD qua O

AD đối xứng với CB qua O

Trả lời câu hỏi Toán 8 Tập 1 Bài 8 trang 95:

Trên hình 80, các chữ cái N và S có tâm đối xứng, chữ cái E không có tâm đối xứng. Hãy tìm thêm một vài chữ cái khác (kiểu chữ in hoa) có tâm đối xứng.

Lời giải

Chữ H, I, X có tâm đối xứng

Trả lời câu hỏi Toán 8 Tập 1 Bài 8 trang 95:

Gọi O là giao điểm hai đường chéo của hình bình hành ABCD (h.79). Tìm hình đối xứng với mỗi cạnh của hình bình hành qua điểm O.

Lời giải

AB đối xứng với CD qua O

AD đối xứng với CB qua O

Trả lời câu hỏi Toán 8 Tập 1 Bài 8 trang 95:

Trên hình 80, các chữ cái N và S có tâm đối xứng, chữ cái E không có tâm đối xứng. Hãy tìm thêm một vài chữ cái khác (kiểu chữ in hoa) có tâm đối xứng.

Lời giải

Chữ H, I, X có tâm đối xứng

IV. Hướng dẫn giải bài tập đối xứng tâm toán lớp 8 bài 8 sgk

Bài 51 trang 96 SGK Toán 8 Tập 1:

Trong mặt phẳng tọa độ, cho điểm H có tọa độ (3; 2). Hãy vẽ điểm K đối xứng với H qua gốc tọa độ và tìm tọa độ của K.

Lời giải:

K đối xứng với H qua gốc tọa độ ⇔ O(0; 0) là trung điểm của KH.

Dựa vào hình biểu diễn ta có K(-3; -2).

Kiến thức áp dụng

Hai điểm được gọi là đối xứng nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.

Bài 52 trang 96 SGK Toán 8 Tập 1:

Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, gọi F là điểm đối xứng với D qua C. Chứng minh rằng E đối xứng với điểm F qua điểm B.

Lời giải:

Ta có: ABCD là hình bình hành nên AB //= CD, AD//=BC.

+ E đối xứng với D qua A

⇒ AE = AD

Mà BC = AD

⇒ BC = AE.

Lại có BC // AE (vì BC // AD ≡ AE)

⇒ AEBC là hình bình hành

⇒ EB //= AC (1).

+ F đối xứng với D qua C

⇒ CF = CD

Mà AB = CD

⇒ AB = CF

Mà AB // CF (vì AB // CD ≡ CF)

⇒ ABFC là hình bình hành

⇒ AC //= BF (2)

Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF

⇒ B là trung điểm EF

⇒ E đối xứng với F qua B

Kiến thức áp dụng

+ Hai điểm được gọi là đối xứng nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.

+ Hình bình hành có hai cạnh đối song song và bằng nhau.

+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

Bài 53 trang 96 SGK Toán 8 Tập 1:

Cho hình 82, trong đó MD // AB và ME // AC. Chứng minh rằng điểm A đối xứng với điểm M qua điểm I.

Lời giải:

Ta có: MD// AE (vì MD// AB)

ME // AD (vì ME // AC)

Nên AEMD là hình bình hành, I là trung điểm của DE nên I cũng là trung điểm của AM, do đó A đối xứng với M qua I.

Kiến thức áp dụng

+ Hai điểm được gọi là đối xứng nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.

+ Tứ giác có các cặp cạnh đối song song là hình bình hành.

+ Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Bài 54 trang 96 SGK Toán 8 Tập 1:

Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox, gọi C là điểm đối xứng với A qua Oy. Chứng minh rằng điểm B đối xứng với điểm C qua O.

Lời giải:

+ B đối xứng với A qua Ox

⇒ Ox là đường trung trực của AB

⇒ OA = OB (1)

+ C đối xứng với A qua Oy

⇒ Oy là đường trung trực của AC

⇒ OA = OC (2)

Từ (1) và (2) suy ra OB = OC (*).

+ Xét ΔOAC cân tại O (do OA = OC) có Oy là đường trung trực

⇒ Oy đồng thời là đường phân giác

Xét ΔOAB cân tại O có Ox là đường trung trực

⇒ Ox đồng thời là đường phân giác

⇒ B, O, C thẳng hàng (**)

Từ (*) và (**) suy ra O là trung điểm BC

⇒ B đối xứng với C qua O.

Kiến thức áp dụng

+ Hai điểm được gọi là đối xứng nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.

+ Hai điểm A và B được gọi là đối xứng nhau qua một đường thẳng d nếu d là đường trung trực của đoạn thẳng AB.

+ Trong một tam giác cân, đường trung tuyến xuất phát từ đỉnh cân đồng thời là các đường trung trực, phân giác và đường cao.

Bài 55 trang 96 SGK Toán 8 Tập 1:

Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các c��nh AB và CD theo thứ tự ở M và N. Chứng minh rằng điểm M đối xứng với điểm N qua O.

Lời giải:

+ ABCD là hình bình hành có O là giao điểm hai đường chéo

⇒ OB = OD.

+ ABCD là hình bình hành ⇒ AB // CD ⇒

(Hai góc SLT).

Hai tam giác BOM và DON có:

⇒ ΔBOM = ΔDON (g.c.g)

⇒ OM = ON

⇒ O là trung điểm của MN

⇒ M đối xứng với N qua O.

Kiến thức áp dụng

+ Hai điểm được gọi là đối xứng nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.

+ Hình bình hành có hai cạnh đối song song và hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Bài 56 trang 96 SGK Toán 8 Tập 1:

Trong các hình sau, hình nào có tâm đối xứng?

a) Đoạn thẳng AB (h.83a)

b) Tam giác đều ABC (h.83b)

c) Biển cấm đi ngược chiều (h.83c)

d) Biển chỉ hướng đi vòng tránh chướng ngại vật (h.83d)

Lời giải:

- Hình 83a có tâm đối xứng là trung điểm của đoạn thẳng AB

- Hình 83b không có tâm đối xứng

(Lưu ý: Trọng tâm đồng thời là trực tâm của tam giác đều ABC không phải tâm đối xứng của tam giác đó)

- Hình 83c có tâm đối xứng là tâm của hình tròn.

- Hình 83d không có tâm đối xứng.

Kiến thức áp dụng

Điểm O gọi là tâm đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua điểm O cũng thuộc hình H.

Bài 57 trang 96 SGK Toán 8 Tập 1:

Các câu sau đúng hay sai?

a) Tâm đối xứng của một đường thẳng là điểm bất kì của đường thẳng đó.

b) Trọng tâm của một tam giác là tâm đối xứng của tam giác đó.

c) Hai tam giác đối xứng với nhau qua một điểm thì có chu vi bằng nhau.

Lời giải:

a) Đúng, vì nếu lấy một điểm O bất kì trên đường thẳng thì nó chia đường thẳng đó thành hai và với bất kì một điểm M, trên tia này cũng luôn có một điểm M' đối xứng với nó qua O trên tia kia.

b) Sai,

Giả sử tam giác ABC có trọng tâm G.

Khi đó điểm A’ đối xứng với A qua G không nằm trong tam giác.

c) Đúng, vì hai tam giác đối xứng với nhau qua một điểm thì chúng bằng nhau.

Do đó chu vi của chúng bằng nhau.

Đối xứng tâm toán lớp 8 bài 8 giải bài tập do đội ngũ giáo viên giỏi toán biên soạn, bám sát chương trình SGK mới toán học lớp 8. Được Soanbaitap.com biên tập và đăng trong chuyên mục giải toán 8 giúp các bạn học sinh học tốt môn toán đại 8. Nếu thấy hay hãy comment và chia sẻ để nhiều bạn khác cùng học tập.

#soanbaitap

#soanbaitap #giải bài tập #Bài 8. Đối xứng tâm

0 notes

soanbaitap · 5 years ago

Link

Hình bình hành toán lớp 8 bài 7 giải bài tập được biên soạn từ đội ngũ giáo viên dạy giỏi môn toán trên toàn quốc đảm bảo chính xác, dễ hiểu giúp các em nắm được kiến thức trong bài hình bình hành lớp 8 và hướng dẫn giải bài tập về hình bình hành lớp 8 để các em hiểu rõ hơn.

Bài 7. Hình bình hành thuộc: CHƯƠNG I. TỨ GIÁC

I. Lý thuyết về hình bình hành

1. Định nghĩa hình bình hành

Hình bình hành là tứ giác có các cạnh đối song song

Tứ giác ABCD là hình bình hành ⇔

Chú ý đặc biệt: Hình bình hành là một hình thang đặc biệt (hình bình hành là hình thang có hai cạnh bên song song)

2. Tính chất hình bình hành

Định lí: Trong hình bình hành:

+ Các cạnh đối bằng nhau.

+ Các góc đối bằng nhau.

+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

3. Dấu hiệu nhận biết hình bình hành

+ Tứ giác có các cạnh đối song song là hình bình hành.

+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.

+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

+ Tứ giác có các góc đối bằng nhau là hình bình hành.

+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.

Ví dụ: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh BE = DF và ABEˆ = CDFˆ .

Hướng dẫn:

Xét tứ giác BEDF có

⇒ BEDF là hình bình hành

⇒ BE = DF (hai cạnh đối song song và bằng nhau)

Ta có: ABCD là hình bình hành nên BADˆ = BCDˆ ( 1 )

BEDF là hình bình hành nên BEDˆ = DFBˆ ( 2 )

Mà

Từ ( 2 ) và ( 3 ) ⇒ AEBˆ = DFCˆ ( 4 )

Xét Δ ABE có BAEˆ + AEBˆ + ABEˆ = 1800 (5)

Xét Δ DFC có DFCˆ + FCDˆ + FDCˆ = 1800 (5)

Từ ( 1 ), ( 4 ), ( 5 ) ⇒ ABEˆ = CDFˆ (đpcm)

4. Công thức tính diện tích hình bình hành và chu vi hình bình hành

Diện tích hình bình hành được đo bằng độ lớn của bề mặt hình, là phần mặt phẳng ta có thể nhìn thấy của hình bình hành.

Diện tích hình bình hành được tính theo công thức bằng tích của cạnh đáy nhân với chiều cao.

SABCD = a.h

Trong đó:

S là diện tích hình bình hành.

a là cạnh đáy của hình bình hành.

h là chiều cao, nối từ đỉnh tới đáy của một hình bình hành.

Chu vi hình bình hành được tính bằng tổng độ dài các đường bao quanh hình, cũng chính là đường bao quanh toàn bộ diện tích, bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.

Nói cách khác, chu vi hình bình hành là tổng độ dài của 4 cạnh. Công thức cụ thể như sau:

C = 2 x (a+b)

Trong đó:

C là chu vi hình bình hành.

a và b là cặp cạnh kề nhau của hình bình hành.

II. Hình bình hành toán 8 - giải bài tập ví dụ SGK

Bài 1: Cho hình bình hành ABCD có H, K lần lượt là các chân đường cao kẻ từ đỉnh A,C xuống BD.

a) Chứng minh AHCK là hình bình hành.

b) Gọi O là trung điểm của HK. Chứng minh A, O, C thẳng hàng.

Hướng dẫn:

a) Từ giả thiết ta có:

⇒ AH//CK. ( 1 )

Áp dụng tính chất về cạnh của hình bình hành và tính chất của các góc so le ta có:

⇒ Δ ADH = Δ CBK

(trường hợp cạnh huyền – góc nhọn)

⇒ AH = CK (cạnh tương tứng bằng nhau) ( 2 )

Từ ( 1 ) và ( 2 ) ta có tứ giác AHCK có cặp cạnh đối song song và bằng nhau là hình bình hành.

b) Áp dụng tính chất đường chéo của hình bình hành AHCK

Hình bình hành AHCK có hai đường chéo AC và HK cắt nhau tại trung điểm mỗi đường

Do O là trung điểm của HK nên O cũng là trung điểm của AC

⇒ A, O, C thẳng hàng.

Bài 2: Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AK, AI lần lượt tại M, N. Chứng minh rằng:

a) AK//CI

b) DM = MN = NB

Hướng dẫn:

a) Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:

Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.

b) Theo câu a, AICK là hình bình hành

⇒ AK//CI. Khi đó , ta có:

Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:

ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:

⇒ DM = MN = NB

III. Hướng dẫn trả lời câu hỏi bài tập sgk hình bình hành toán lớp 8 bài 7

Trả lời câu hỏi Toán 8 Tập 1 Bài 7 trang 90:

Các cạnh đối của tứ giác ABCD trên hình 66 có gì đặc biệt ?

Lời giải

Các cạnh đối của tứ giác ABCD bằng nhau và song song với nhau

(Nhận xét trang 70: Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau)

Trả lời câu hỏi Toán 8 Tập 1 Bài 7 trang 90:

Cho hình bình hành ABCD (h.67). Hãy thử phát hiện tính chất về cạnh, về góc, về đường chéo của hình bình hành đó.

Lời giải

- Các cạnh đối bằng nhau

- Các góc đối bằng nhau

- Hai đường chéo cắt nhau tại trung điểm mỗi đường

Trả lời câu hỏi Toán 8 Tập 1 Bài 7 trang 92:

Trong các tứ giác ở hình 70, tứ giác nào là hình bình hành? Vì sao ?

Lời giải

ABCD là hình bình hình vì có các cạnh đối bằng nhau

EFGH là hình bình hành vì có các góc đối bằng nhau

PQRS là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường

XYUV là hình bình hành vì có XV = YU và XV // YU

IV. Hướng dẫn giải bài tập sgk toán lớp 8 bài 6 hình bình hành

Bài 43 trang 92 SGK Toán 8 Tập 1:

Các tứ giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông ở hình 71 có là hình bình hành hay không?

Lời giải:

Cả ba tứ giác là hình bình hành

- Tứ giác ABCD là hình bình hành vì có AB // CD và AB = CD = 3 (dấu hiệu nhận biết 3)

- Tứ giác EFGH là hình bình hành vì có EH // FG và EH = FG = 3 (dấu hiệu nhận biết 3)

- Tứ giác MNPQ là hình bình hành vì có MN = PQ và MQ = NP (dấu hiệu nhận biết 2)

(Chú ý:

- Với các tứ giác ABCD, EFGH còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 2.

- Với tứ giác MNPQ còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 5.)

Kiến thức áp dụng

Dấu hiệu nhận biết hình bình hành:

Tứ giác ABCD là hình bình hành nếu thỏa mãn một trong các dấu hiệu sau đây:

1) AB // CD và AD // BC.

2) AB = CD và AD = BC.

3) AB // CD và AB = CD.

4) Â = Ĉ và B̂ = D̂

5) OA = OC và OB = OD (Với O = AC ∩ BD)

Bài 44 trang 92 SGK Toán 8 Tập 1:

Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF

Lời giải:

Cách 1:

+ ABCD là hình bình hành ⇒ AB = CD, AD = BC, Â = Ĉ.

+ E là trung điểm của AD ⇒ AE = AD/2

F là trung điểm của BC ⇒ CF = BC/2

Mà AD = BC (cmt) ⇒ AE = CF.

+ Xét ΔAEB và ΔCFD có: AB = CD, Â = Ĉ, AE = CF (cmt)

⇒ ΔAEB = ΔCFD (c.g.c)

⇒ EB = DF.

Cách 2:

ABCD là hình bình hành ⇒ AD//BC và AD = BC.

+ AD // BC ⇒ DE // BF

+ E là trung điểm của AD ⇒ DE = AD/2

F là trung điểm của BC ⇒ BF = BC/2

Mà AD = BC ⇒ DE = BF.

+ Tứ giác BEDF có:

DE // BF và DE = BF

⇒ BEDF là hình bình hành

⇒ BE = DF.

Kiến thức áp dụng

- Tính chất của hình bình hành:

+ Hai cạnh đối song song và bằng nhau

+ Hai góc đối bằng nhau.

ABCD là hình bình hành

- Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành

Tứ giác ABCD có: AB = CD, AD // CD ⇒ ABCD là hình bình hành

Bài 45 trang 92 SGK Toán 8 Tập 1:

Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

a) Chứng minh rằng DE // BF

b) Tứ giác DEBF là hình gì? Vì sao?

Lời giải:

a) Ta có:

+ ABCD là hình bình hành ⇒ AB // CD ⇒

(Hai góc đồng vị) (1)

+ DE là tia phân giác của góc D

Mà hai góc này ở vị trí đồng vị ⇒ DE // BF (đpcm)

b) Tứ giác DEBF có:

DE // BF (chứng minh ở câu a)

BE // DF (vì AB // CD)

⇒ DEBF là hình bình hành.

Kiến thức áp dụng

+ Hình bình hành có các cặp cạnh đối song song.

Tứ giác có các cặp cạnh đối song song là hình bình hành

ABCD là hình bình hành ⇔ AB // CD và AD//BC.

+ Hình bình hành có các góc đối bằng nhau.

ABCD là hình bình hành ⇒ Â = Ĉ và B̂ = D̂

Bài 46 trang 92 SGK Toán 8 Tập 1:

Các câu sau đúng hay sai?

a) Hình thang có hai cạnh đáy bằng nhau là hình bình hành

b) Hình thang có hai cạnh bên song song là hình bình hành

c) Tứ giác có hai cạnh đối bằng nhau là hình bình hành

d) Hình thang có hai cạnh bên bằng nhau là hình bình hành

Lời giải:

a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bằng nhau nên là hình bình hành theo dấu hiệu nhận biết 5

b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)

c) Sai.

Ví dụ tứ giác ABCD ở dưới có AB = CD nhưng không phải hình bình hành.

d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.

Bài 46 trang 92 SGK Toán 8 Tập 1:

Các câu sau đúng hay sai?

a) Hình thang có hai cạnh đáy bằng nhau là hình bình hành

b) Hình thang có hai cạnh bên song song là hình bình hành

c) Tứ giác có hai cạnh đối bằng nhau là hình bình hành

d) Hình thang có hai cạnh bên bằng nhau là hình bình hành

Lời giải:

a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bằng nhau nên là hình bình hành theo dấu hiệu nhận biết 5

b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)

c) Sai.

Ví dụ tứ giác ABCD ở dưới có AB = CD nhưng không phải hình bình hành.

d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.

Bài 48 trang 93 SGK Toán 8 Tập 1:

Tứ giác ABCD có E, F , G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

Lời giải:

+ E là trung điểm AB, F là trung điểm BC

⇒ EF là đường trung bình của tam giác ABC

⇒ EF // AC và EF = AC/2

+ H là trung điểm AD, G là trung điểm CD

⇒ HG là đường trung bình của tam giác ACD

⇒ HG // AC và HG = AC/2.

+ Ta có:

EF //AC, HG//AC ⇒ EF // HG.

EF = AC/2; HG = AC/2 ⇒ EF = HG

⇒ tứ giác EFGH là hình bình hành.

Kiến thức áp dụng

+ Đường trung bình là đoạn thẳng nối hai trung điểm của hai cạnh trong tam giác.

Đường trung bình song song và bằng một nửa cạnh còn lại.

ΔABC, AD = DB, AE = EC ⇒ DE // BC và DE = BC/2.

+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành (Dấu hiệu nhận biết 3)

ABCD có : AB // CD và AB = CD

⇒ ABCD là hình bình hành.

Bài 49 trang 93 SGK Toán 8 Tập 1:

Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:

a) AI // CK

b) DM = MN = NB

Lời giải:

a) + K là trung điểm của AB ⇒ AK = AB/2.

+ I là trung điểm của CD ⇒ CI = CD/2.

+ ABCD là hình bình hành

⇒ AB // CD hay AK // CI

và AB = CD ⇒ AB/2 = CD/2 hay AK = CI

+ Tứ giác AKCI có AK // CI và AK = CI

⇒ AKCI là hình bình hành.

b) + AKCI là hình bình hành

⇒ AI//KC hay MI//NC.

ΔDNC có: DI = IC, IM // NC ⇒ DM = MN (1)

+ AI // KC hay KN//AM

ΔBAM có: AK = KB, KN//AM ⇒ MN = NB (2)

Từ (1) và (2) suy ra DM = MN = NB.

Kiến thức áp dụng

+ Hình bình hành có hai cạnh đối song song.

+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

+ Đường thẳng đi qua trung điểm của một cạnh và song song với cạnh thứ hai thì đi qua trung điểm của cạnh còn lại.

Hình bình hành toán lớp 8 bài 7 giải bài tập do đội ngũ giáo viên giỏi toán biên soạn, bám sát chương trình SGK mới toán học lớp 8. Được Soanbaitap.com biên tập và đăng trong chuyên mục giải toán 8 giúp các bạn học sinh học tốt môn toán đại 8. Nếu thấy hay hãy comment và chia sẻ để nhiều bạn khác cùng học tập.

#soanbaitap

#soanbaitap #giải bài tập #Bài 7. Hình bình hành

0 notes

soanbaitap · 5 years ago

Link

Đối xứng trục toán lớp 8 bài 6 giải bài tập được biên soạn từ đội ngũ giáo viên dạy giỏi môn toán trên toàn quốc đảm bảo chính xác, dễ hiểu giúp các em nắm được kiến thức trong bài đối xứng trục lớp 8 và hướng dẫn giải bài tập về đối xứng trục lớp 8 để các em hiểu rõ hơn.

Bài 6. đối xứng trục thuộc: CHƯƠNG I. TỨ GIÁC

I. Toán 8 đối xứng trục phần lý thuyết

1. Hai điểm đối xứng qua một đường thẳng

Hai điểm được gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó

Quy ước: Nếu điểm B nằm trên đường thẳng d thì điểm đối xứng của B qua đường thẳng d cũng chính là điểm B.

2. Hai hình đối xứng qua đường thẳng

Hai hình gọi là đối xứng với nhau qua đường thẳng d nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng d và ngược lại.

Đường thẳng d gọi là trục đối xứng của hai hình đó.

3. Hình có trục đối xứng

Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H.

Ta nói rằng hình H có trục đối xứng.

Định lí: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang đó.

II. Toán 8 đối xứng trục - Hướng dẫn giải bài tập ví dụ SGK

Bài 1: Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Chứng minh rằng:

a) D đối xứng với E qua AH.

b) Δ ADC đối xứng với Δ AEB qua AH.

Hướng dẫn:

a) Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là đường phân giác của góc A.

Theo giả thiết ta có AD = AE nên Δ ADE cân tại A nên AH là đường trung trực của DE

⇒ D đối xứng với E qua AH.

b) Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là trung trực của BC.

⇒ B đối xứng với C qua AH, E đối xứng với D qua AH.

Mặt khác, ta có A đối xứng với A qua AH theo quy ước.

⇒ Δ ADC đối xứng với Δ AEB qua AH.

Bài 2: Cho Δ ABC có Aˆ = 500, điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC.

a) Chứng minh rằng AD = AE.

b) Tính số đo góc DAEˆ = ?

Hướng dẫn:

a) Theo giả thiết ta có:

+ D đối xứng với M qua AB.

+ E đối xứng với M qua AC.

+ A đối xứng với A qua AB, AC.

⇒ AD đối xứng với AM qua AB, AE đối xứng với AM qua AC.

Áp dụng tính chất đối xứng ta có:

⇒ AD = AE ⇒ (đpcm).

b) Theo ý câu a, ta có

+ A1ˆ đối xứng A2ˆ qua AB

+ A3ˆ đối xứng A4ˆ qua AC.

Áp dụng tính chất đối xứng trục, ta có:

⇒ A1ˆ + A4ˆ = A2ˆ + A3ˆ = Aˆ = 500 ⇒ DAEˆ = 2Aˆ = 1000.

Vậy DAEˆ = 1000.

III. Hướng dẫn trả lời câu hỏi sgk đối xứng trục toán lớp 8 bài 6

Trả lời câu hỏi Toán 8 Tập 1 Bài 6 trang 84:

Cho đường thẳng d và một điểm A không thuộc d. Hãy vẽ điểm A’ sao cho d là đường trung trực của đoạn thẳng AA’.

Lời giải

Trả lời câu hỏi Toán 8 Tập 1 Bài 6 trang 84:

Cho đường thẳng d và đoạn thẳng AB (h.51).

- Vẽ điểm A’ đối xứng với A qua d. - Vẽ điểm B’ đối xứng với B qua d. - Lấy điểm C thuộc đoạn thẳng AB, vẽ điểm C’ đối xứng với C qua d.

Lời giải

Trả lời câu hỏi Toán 8 Tập 1 Bài 6 trang 86:

Cho tam giác ABC cân tại A, đường cao AH (h.55). Tìm hình đối xứng với mỗi cạnh của tam giác ABC qua AH.

Lời giải

AB đối xứng với AC qua AH BC đối xứng với CB qua AH

Trả lời câu hỏi Toán 8 Tập 1 Bài 6 trang 86:

Mỗi hình sau có bao nhiêu trục đối xứng?

a) Chữ cái in hoa A (h.56a) b) Tam giác đều ABC (h.56b) c) Đường tròn tâm O (h.56c).

Lời giải

a) 1 trục đối xứng b) 3 trục đối xứng c) vô số trục đối xứng

IV. Hướng dẫn giải bài tập đối xứng trục toán lớp 8 bài 6 sgk

Bài 35 trang 87 SGK Toán 8 Tập 1:

Vẽ hình đối xứng với các hình đã cho qua trục d (h.58).

Lời giải:

Vẽ hình:

Bài 36 trang 87 SGK Toán 8 Tập 1:

Cho góc xOy có số đo 50o, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy.

a) So sánh các độ dài OB và OC

b) Tính số đo góc BOC

Lời giải:

a) + B đối xứng với A qua Ox

⇒ Ox là đường trung trực của AB

⇒ OA = OB (1)

+ C đối xứng với A qua Oy

⇒ Oy là đường trung trực của AC

⇒ OA = OC (2)

Từ (1) và (2) suy ra OB = OC (= OA)

b) + ΔOAC cân tại O có Oy là đường trung trực

⇒ Oy đồng thời là đường phân giác

+ ΔOAB cân tại O có Ox là đường trung trực

⇒ Ox đồng thời là đường phân giác

Kiến thức áp dụng

+ Hai điểm gọi là đối xứng nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.

+ M thuộc đường trung trực của đoạn thẳng AB ⇔ MA = MB

+ Trong tam giác cân, đường trung trực tại đỉnh cân đồng thời là đường phân giác.

Bài 37 trang 87 SGK Toán 8 Tập 1:

Tìm các hình có trục đối xứng trên hình 59.

Lời giải:

+ Hình a có hai trục đối xứng:

+ Hình b có một trục đối xứng

+ Hình c có một trục đối xứng

+ Hình d có một trục đối xứng

+ Hình e có một trục đối xứng

+ Hình g có năm trục đối xứng

+ Hình h không có trục đối xứng

+ Hình i có một trục đối xứng

Kiến thức áp dụng

Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H cũng thuộc hình H.

Bài 38 trang 88 SGK Toán 8 Tập 1:

Thực hành. Cắt một tấm bìa hình tam giác cân, một tấm bìa hình thang cân. Hãy cho biết đường nào là trục đối xứng của mỗi hình, sau đó gấp mỗi tấm bìa để kiểm tra lại điều đó.

Lời giải:

- ΔABC cân tại A có trục đối xứng là đường phân giác AH của góc BAC (đường này đồng thời là đường cao, đường trung trực, đường trung tuyến).

– Hình thang cân ABCD nhận đường thẳng đi qua trung điểm hai đáy HK làm trục đối xứng.

Bài 39 trang 88 SGK Toán 8 Tập 1:

a) Cho hai điểm A, B thuộc cùng một mặt phẳng có bờ là đường thẳng d (h.60). Gọi C là điểm đối xứng với A qua d. Gọi D là giao điểm của đường thẳng d và đoạn thẳng BC. Gọi E là điểm bất kì của đường thẳng d (E khác D).

Chứng minh rằng AD + DB < AE + EB.

b) Bạn Tú đang ở vị trí A, cần đến bờ sông d lấy nước rồi đi đến vị trí B (h.60). Con đường ngắn nhất mà bạn Tú nên đi là con đường nào?

Lời giải:

a) + A và C đối xứng qua d

⇒ d là trung trực của AC

⇒ AD = CD

⇒ AD + DB = CD + DB = CB (1)

+ E ∈ d ⇒ AE = CE

⇒ AE + EB = CE + EB (2)

+ CB < CE + EB (3)

Từ (1), (2), (3) ⇒ AD + DB < AE + EB

b) Vì với mọi E ∈ d thì AE + EB > AD + DB

Do đó con đường ngắn nhất bạn Tú nên đi là đường ADB.

Kiến thức áp dụng

+ A đối xứng với B qua đường thẳng d

⇔ d là đường trung trực của AB.

+ M thuộc đường trung trực của AB ⇔ MA = MB.

Bài 40 trang 88 SGK Toán 8 Tập 1:

Trong các biển báo giao thông sau đây, biển nào có trục đối xứng?

a) Biển nguy hiểm: đường hẹp hai bên (h.61a)

b) Biển nguy hiểm: đường giao thông với đường sắt có rào chắn (h.61b)

c) Biển nguy hiểm: đường ưu tiên gặp đường không ưu tiên bên phải (h.61c)

d) Biển nguy hiểm khác (d.61d)

Lời giải:

- Các biển báo ở hình a, b, d có trục đối xứng.

- Biển báo c không có trục đối xứng.

Bài 41 trang 88 SGK Toán 8 Tập 1:

Các câu sau đúng hay sai?

a) Nếu ba điểm thẳng hàng thì ba điểm đối xứng với chúng qua một trục cũng đường thẳng hàng.

b) Hai tam giác đối xứng với nhau qua một truc thì có chu vi bằng nhau.

c) Một đường tròn có vô số trục đối xứng.

d) Một đoạn thẳng chỉ có một trục đối xứng.

Lời giải:

a) Đúng

b) Đúng vì hai tam giác đối xứng nhau qua một trục thì bằng nhau nên chúng cũng có chu vi bằng nhau.

c) Đúng. Tất cả các đường thẳng đi qua tâm đều là trục đối xứng của đường tròn.

d) Sai.

Mọi đoạn thẳng AB đều có hai trục đối xứng là đường thẳng AB và đường trung trực của đoạn thẳng AB.

Bài 42 trang 89 SGK Toán 8 Tập 1: Đố.

a) Hãy tập cắt chữ D (h.62a) bằng cách gấp đôi tờ giấy. Kể tên một vài chữ cái khác (kiểu chữ in hoa) có trục đối xứng.

b) Vì sao ta có thể gấp tờ giấy làm tư để cắt chữ H (h.62b)?

Hình 62

Lời giải:

a) Cắt được chữ D:

Gấp đôi chữ D theo đường thẳng là trục đối xứng của chữ D như trên hình vẽ.

Một số chữ cái in hoa có trục đối xứng:

- Chỉ có một trục đối xứng dọc: A, M, T, U, V, Y

- Chỉ có một trục đối xứng ngang: B, C, D, E, K

- Có hai trục đối xứng dọc và ngang: H, I, O , X

b) Có thể gấp tờ giấy làm tư để cắt chữ H vì chữ H có hai trục đối xứng vuông góc.

Đối xứng trục toán lớp 8 bài 6 giải bài tập do đội ngũ giáo viên giỏi toán biên soạn, bám sát chương trình SGK mới toán học lớp 8. Được Soanbaitap.com biên tập và đăng trong chuyên mục giải toán 8 giúp các bạn học sinh học tốt môn toán đại 8. Nếu thấy hay hãy comment và chia sẻ để nhiều bạn khác cùng học tập.

#soanbaitap

#soanbaitap #giải bài tập #Bài 6. Đối xứng trục

0 notes

soanbaitap · 5 years ago

Link

Vẽ đoạn thẳng cho biết độ dài toán lớp 6 bài 9 giải bài tập được biên soạn từ đội ngũ giáo viên dạy giỏi môn toán trên toàn quốc giúp các em tổng hợp và ôn tập lại kiến thức trong bài vẽ đoạn thẳng cho biết độ dài và hướng dẫn giải bài tập sgk để các em hiểu rõ hơn.

Vẽ đoạn thẳng cho biết độ dài thuộc: Chương 1: Đoạn thẳng

I. Lý thuyết vẽ đoạn thẳng cho biết độ dài

1. Vẽ đoạn thẳng trên tia

Cách 1: Dùng thước đo có chia khoảng (tương tự như đo đoạn thẳng)

Cách 2: Dùng compa.

Nhận xét: Trên tia OxOx bao giờ cũng vẽ được một và chỉ một điểm MM sao cho OM=aOM=a (đơn vị độ dài)

2. Dấu hiệu nhận biết một điểm nằm giữa hai điểm khác

Trên tia OxOx nếu OM<ONOM<ON thì điểm MM nằm giữa hai điểm OO và N.N.

Trên tia OxOx nếu OA<OB<OCOA<OB<OC thì điểm BB nằm giữa hai điểm AA và C.C.

II. Hướng dẫn giải bài tập Vẽ đoạn thẳng cho biết độ dài toán lớp 6 bài 9

Bài 53 trang 124 SGK Toán 6 tập 1.

Đề bài: Trên tia (Ox), vẽ hai đoạn thẳng (OM) và (ON) sao cho (OM = 3cm, ON = 6cm). Tính (MN), so sánh (OM) và (MN).

Phương pháp giải - Xem chi tiết

+) Trên tia (Ox) có hai điểm (M) và (N,) (OM=a, ON=b.) Nếu (0<a<b) thì điểm (M) nằm giữa hai điểm (O) và (N.)

+) Nếu điểm (M) nằm giữa hai điểm (A) và (B) thì (AM + MB = AB)

+) Để so sánh hai đoạn thẳng ta so sánh độ dài của chúng.

Lời giải chi tiết

Trên tia (Ox) có (2) điểm (M,N) mà (OM < ON, ( 3cm<6cm)) nên điểm (M) nằm giữa hai điểm (O) và (N).

Do đó: (OM+MN=ON);

Suy ra (MN=ON-OM= 6-3=3(cm).)

Ta thấy (OM=3cm) và (MN=3cm)

Nên (OM=MN,(=3cm). )

Bài 53 trang 124 SGK Toán 6 tập 1.

Đề bài: Trên tia OxOx, vẽ hai đoạn thẳng OMOM và ONON sao cho OM=3cm,ON=6cmOM=3cm,ON=6cm. Tính MNMN, so sánh OMOM và MNMN.

Phương pháp giải - Xem chi tiết

+) Trên tia OxOx có hai điểm MM và N,N, OM=a,ON=b.OM=a,ON=b. Nếu 0<a<b0<a<b thì điểm MM nằm giữa hai điểm OO và N.N.

+) Nếu điểm MM nằm giữa hai điểm AA và BB thì AM+MB=ABAM+MB=AB

+) Để so sánh hai đoạn thẳng ta so sánh độ dài của chúng.

Lời giải chi tiết

Trên tia OxOx có 22 điểm M,NM,N mà OM<ON(3cm<6cm)OM<ON(3cm<6cm) nên điểm MM nằm giữa hai điểm OO và NN.

Do đó: OM+MN=ONOM+MN=ON;

Suy ra MN=ON−OM=6−3=3(cm).MN=ON−OM=6−3=3(cm).

Ta thấy OM=3cmOM=3cm và MN=3cmMN=3cm

Nên OM=MN(=3cm).

Bài 54 trang 124 SGK Toán 6 tập 1.

Đề bài: Trên tia OxOx, vẽ ba đoạn thẳng OA,OB,OCOA,OB,OC sao cho OA=2cm,OB=5cm,OC=8cmOA=2cm,OB=5cm,OC=8cm. So sánh BCBC và BABA.

Phương pháp giải - Xem chi tiết

Nhận xét: Trên tia Ox,OM=a,ON=b,Ox,OM=a,ON=b, nếu 0<a<b0<a<b thì điểm MM nằm giữa hai điểm OO và N.N.

Lời giải chi tiết

Ta có A,B,CA,B,C thuộc tia OxOx và OA=2cm,OB=5cm,OC=8cmOA=2cm,OB=5cm,OC=8cm.

Vì OA<OBOA<OB (2cm<5cm)(2cm<5cm) nên AA nằm giữa OO và BB do đó: OA+AB=OBOA+AB=OB suy ra BA=OB−OA=5−2=3cmBA=OB−OA=5−2=3cm

Vì OB<OCOB<OC (5cm<8cm)(5cm<8cm) nên BB nằm giữa OO và CC do đó: OB+BC=OCOB+BC=OC suy ra BC=OC−OB=8−5=3cmBC=OC−OB=8−5=3cm

Ta có: BA=3cmBA=3cm và BC=3cmBC=3cm

Suy ra BC=BA(=3cm).

Bài 55 trang 124 SGK Toán 6 tập 1.

Đề bài: Gọi A,BA,B là hai điểm trên tia OxOx. Biết OA=8cm,AB=2cmOA=8cm,AB=2cm. Tình OBOB. Bài toán có mấy đáp số.

Phương pháp giải - Xem chi tiết

Nhận xét: Nếu điểm M nằm giữa hai điểm A và B thì AM + MB = AB.

Lời giải chi tiết

Có hai trường hợp xảy ra:

- Trường hợp 1: AA nằm giữa OO và BB.

Ta có: OB=OA+AB=8+2=10cmOB=OA+AB=8+2=10cm.

- Trường hợp 2: BB nằm giữa OO và AA.

Ta có: OB+BA=OAOB+BA=OA

Suy ra OB=OA−BA⇒OB=8–2=6(cm)OB=OA−BA⇒OB=8–2=6(cm).

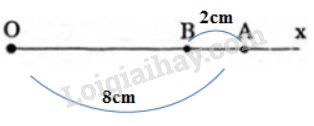
Vậy bài toán có hai đáp số là 10cm10cm và 6cm6cm.

Bài 56 trang 124 SGK Toán 6 tập 1.

Đề bài: Cho đoạn thẳng ABAB dài 4cm4cm. Trên tia ABAB lấy điểm CC sao cho AC=1cmAC=1cm.

a) Tính CBCB

b) Lấy điểm DD thuộc tia đối của tia BCBC sao cho BD=2cmBD=2cm. Tính CDCD.

Phương pháp giải - Xem chi tiết

+ Trên tia OxOx có OM=a;ON=bOM=a;ON=b. Nếu 0<a<b0<a<b thì điểm MM nằm giữa hai điểm OO và NN

+ Nếu điểm M nằm giữa hai điểm A và B thì AM+MB=AB.AM+MB=AB.

Lời giải chi tiết

Trên tia ABAB có hai điểm C,BC,B mà AC<AB(1cm<4cm)AC<AB(1cm<4cm) nên CC nằm giữa hai điểm AA và BB.

Do đó: AC+CB=ABAC+CB=AB suy ra CB=AB−AC=4−1=3(cm)CB=AB−AC=4−1=3(cm)

Điểm DD thuộc tia đối của tia BCBC nên điểm BB nằm giữa CC và DD.

Do đó: CD=CB+BD=3+2=5(cm)

Bài 57 trang 124 SGK Toán 6 tập 1.

Đề bài: Đoạn thẳng ACAC dài 5cm5cm. Điểm BB nằm giữa AA và CC sao cho BC=3cmBC=3cm.

a) Tính ABAB.

b) Trên tia đối của tia BABA lấy điểm DD sao cho BD=5cmBD=5cm. So sánh ABAB và CDCD.

Phương pháp giải - Xem chi tiết

+ Trên tia OxOx có OM=a;ON=bOM=a;ON=b. Nếu 0<a<b0<a<b thì điểm MM nằm giữa hai điểm OO và NN

+ Nếu điểm M nằm giữa hai điểm A và B thì AM+MB=AB.AM+MB=AB.

Lời giải chi tiết

a, Vì điểm BB nằm giữa AA và CC nên AB+BC=ACAB+BC=AC

Suy ra AB=AC–BC=5–3=2(cm)AB=AC–BC=5–3=2(cm).

b) Trên tia BCBC có hai điểm C,DC,D mà BC=3cm,BD=5cmBC=3cm,BD=5cm suy ra BC<BD(3cm<5cm)BC<BD(3cm<5cm)

Do đó CC nằm giữa BB và DD.

Suy ra BC+CD=BDBC+CD=BD

⇒CD=BD–BC=5−3=2(cm).⇒CD=BD–BC=5−3=2(cm).

Ta có: AB=2cmAB=2cm và CD=2cmCD=2cm

Nên AB=CD(=2cm)AB=CD(=2cm).

Bài 58 trang 124 SGK Toán 6 tập 1.

Đề bài: Vẽ đoạn thẳng ABAB dài 3.5cm3.5cm. Nói cách vẽ.

Phương pháp giải - Xem chi tiết

Sử dụng thước thẳng hoặc compa.

Lời giải chi tiết

Cách 1: Dùng thước kẻ

+ Vẽ tia Ax bất kì

+ Đặt cạnh thước (phần có vạch đo kích thước) nằm trên tia Ax sao cho vạch số 0 của thước trùng với gốc A của tia.

+ Vạch số 3,5cm của thước sẽ cho ta điểm B. Đoạn thẳng AB là đoạn thẳng cần vẽ.

Cách 2: Dùng thước kẻ và compa

+ Vẽ đường thẳng a bất kì.

+ Trên đường thẳng a lấy một điểm A bất kì. Dùng compa quay một vòng tròn tâm A, bán kính 3,5cm.

+ Đường tròn sẽ cắt đường thẳng a tại 2 điểm. Hai điểm này sẽ là điểm B cần tìm (bạn chọn lấy điểm nào cũng được).

Bài 59 trang 124 SGK Toán 6 tập 1.

Đề bài: Trên tia Ox, cho ba điểm M,N,P biết OM=2cm,ON=3cm,OP=3,5cm. Hỏi trong ba điểm M,N,P thì điểm nào nằm giữa hai điểm còn lại? vì sao?

Phương pháp giải - Xem chi tiết

Trên tia Ox,OM=a,ON=b, nếu 0<a<b thì điểm M nằm giữa hai điểm O và N.

Lời giải chi tiết

Vì cả 3 điểm M,N,P đều nằm trên tia Ox mà OM<ON<OP (do 2cm<3cm<3,5cm) nên điểm N nằm giữa hai điểm M và P.

Vẽ đoạn thẳng cho biết độ dài toán lớp 6 bài 9 giải bài tập được đăng ở chuyên mục Giải Toán 6 và biên soạn theo phần toán hình 6 thuộc SKG Toán lớp 6. Bài giải toán lớp 6 được biên soạn bởi các thầy cô giáo dạy giỏi toán tư vấn, nếu thấy hay hãy chia sẻ và comment để nhiều bạn khác cùng học tập.

#soanbaitap

#soanbaitap #giải bài tập #Bài 9. Vẽ đoạn thẳng cho biết độ dài

0 notes

soanbaitap · 5 years ago

Link

Ôn tập chương 2 hình học 7 câu hỏi và bài tập do đội ngũ giáo viên dạy tốt môn toán trên toàn quốc biên soạn. Đảm bảo dễ hiểu giúp các em hệ thống lại kiến thức và ôn tập chương 2 hình học lớp 7 trong bài đồng thời vận dụng vào giải các dạng bài tập liên quan để các em hiểu rõ hơn.

Ôn tập chương 2 hình học 7 thuộc: Chương 2: Tam giác

I. Lý thuyết

1. Tổng ba góc của một tam giác

Tổng ba góc của một tam giác bằng 180°

Với ΔABC ta có

2. Tam giác vuông

Định nghĩa: Tam giác vuông là tam giác có một góc vuông.

Định lý: Trong tam giác vuông, hai góc nhọn phụ nhau.

3. Hai tam giác bằng nhau

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

4. Các trường hợp bằng nhau của tam giác

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

ΔABC và ΔA'B'C' có:

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

5. Tam giác cân

Tam giác cân là tam giác có hai cạnh bằng nhau.

Tính chất

Trong tam giác cân, hai góc ở đáy bằng nhau.

- Dấu hiệu nhận biết:

+ Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.

+ Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

Định nghĩa tam giác vuông cân: Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.

Tính chất: Mỗi góc nhọn của tam giác vuông cân bằng 45°

Định nghĩa: Tam giác đều là tam giác có ba cạnh bằng nhau.

ΔABC đều ⇔ AB = AC = BC

Tính chất: Trong tam giác đều, mỗi góc bằng 60°

ΔABC đều ⇔ ∠A = ∠B = ∠C = 60°

- Dấu hiệu nhận biết:

+ Nếu tam giác có ba cạnh bằng nhau thì tam giác đó là tam giác đều.

+ Nếu tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.

+ Nếu một tam giác cân có một góc nhọn bằng 60° thì tam giác đó là tam giác đều.

6. Định lí Py – ta – go

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

ΔABC vuông tại A ⇒ BC2 = AB2 + AC2

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

ΔABC có BC2 = AB2 + AC2 ⇒ ∠BAC = 90°

II. Hướng dẫn giải bài tập vận dụng

Bài 1: Cho tam giác ABC có ∠A = 60°, ∠C = 50°. Tia phân giác góc B cắt AC tại D. Tính ∠ADB, ∠CDB

Hiển thị lời giải

Bài 2: Tìm số đo các góc của tam giác ABC có: 21∠A = 14∠B = 6∠C

Hiển thị lời giải

Trong tam giác ABC có: A^ + B^ + C^ = 180° (tổng ba góc trong tam giác)

Bài 3: Cho tam giác ABC có chu vi bằng 21cm. Độ dài ba cạnh của tam giác là ba số lẻ liên tiếp và AB < BC < AC. Tìm độ dài các cạnh của tam giác PQR biết tam giác ABC bằng tam giác PQR.

Hiển thị lời giải

Gọi độ dài cạnh AB là 2n - 1 thì độ dài cạnh BC là 2n + 1 và độ dài cạnh AC là 2n + 3Theo bài ra ta có: AB + BC + AC = 21 ⇒ (2n - 1) + (2n + 1) + (2n + 3) = 21⇒ 6n = 18 ⇔ n = 3Do đó, ta có: AB = 5cm, BC = 7cm, AC = 9cm

Theo giả thiết ta lại có: ΔABC = ΔPQR nên AB = PQ = 5cm, BC = QR = 7cm, AC = PR = 9cm

Vậy PQ = 5cm, QR = 7cm, PR = 9cm

Bài 4: Cho tam giác ABC có M thuộc cạnh BC sao cho ΔAMB = ΔAMC. Chứng minh rằng:

a) M là trung điểm của BC

b) AM là tia phân giác của góc A

c) AM ⊥ BC

Hiển thị lời giải

a) Vì ΔAMB = ΔAMC nên ta có: MB = MCMà M nằm giữa B và C⇒ M là trung điểm của cạnh BC

Ta lại có tia AM nằm giữa hai tia AB và AC nên tia AM là tia phân giác của góc ∠BAC

c) Vì ΔAMB = ΔAMC nên ta có: ∠AMB = ∠AMC

Mà M thuộc tia BC nên

Hay AM ⊥ BC (đpcm)

Bài 5: Cho tam giác ABC. Vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm C bán bính BA, chúng cắt nhau ở D (D và B nằm khác phía đối với bờ AC). Chứng minh rằng AD // BC

Hiển thị lời giải

Bài 6: Tam giác ABC có AB = AC, M là trung điểm của BC. Chứng minh rằng AM vuông góc với BC.

Hiển thị lời giải

Xét ΔAMB và ΔAMC có:AB = AC (gt)AM chungMB = MC (M là trung điểm của BC)

⇒ ΔAMB = ΔAMC (c-c-c)

Suy ra ∠BAM = ∠CAM; ∠AMB = ∠AMC (góc tương ứng bằng nhau)

Mà ∠AMB + ∠AMC = 180° (hai góc kề bù)

Nên ∠AMB = ∠AMC = 180°/2 = 90° hay AM ⊥ BC

Bài 7: Cho đoạn thẳng BC. Gọi A là một điểm nằm trên đường trung trực xy của đoạn thẳng BC và M là giao điểm của xy với BC. Chứng minh AB = AC

Hiển thị lời giải

Bài 8: Cho đường thẳng AB, trên hai nửa mặt phẳng đối nhau bờ là đoạn thẳng AB vẽ hai tia Ax ⊥ AB; By ⊥ BA. Trên Ax và By lần lượt lấy hai điểm C và D sao cho AC = BD. Gọi O là trung điểm của AB.

a) Chứng minh rằng: ΔAOC = ΔBOD

b) Chứng minh O là trung điểm của CD

Hiển thị lời giải

Bài 9: Cho ΔABC có ∠B = ∠C. Tia phân giác của góc B cắt AC tại D. Tia phân giác của góc C cắt AB tại E. So sánh độ dài đoạn thẳng BD và CE.

Hiển thị lời giải

Bài 10: Cho tam giác ABC (AB = AC) và I là trung điểm của đáy BC. Dựng tia Cx song song với tia BA sao cho hai tia BA và Cx nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng BC. Lấy một điểm D nào đó trên AB. Gọi E là một điểm nằm trên tia Cx sao cho BD = CE. Chứng minh rằng ba điểm D, I, E thẳng hàng.

Hiển thị lời giải

Xét hai tam giác BID và CIE ta có:BI = IC (I là trung điểm của BC)∠IBD = ∠ICE (Cx // AB, ∠IBD; ∠ICE là hai góc so le trong)BD = CE (gt)

⇒ ΔBID = ΔCIE (c-g-c)

Nên ∠BID = ∠CIE (hai góc tương ứng bằng nhau)

Hai góc này bằng nhau, chiếm vị trí đối đỉnh, có hai cạnh tương ứng BI và CI nằm trên một đường thẳng.

Vậy D, I, E thẳng hàng

Bài 11: Cho tam giác ABC cân tại A và có

, phân giác của góc B cắt AC tại D.

a) Tính các góc của tam giác ABC

b) Chứng minh DA = DB

Hiển thị lời giải

Bài 12: Cho tam giác ABC vuông tại A. Gọi M là trung điểm của AB, kẻ MH vuông góc với BC tại H. Chứng minh rằng CH2 - BH2 = AC2

Hiển thị lời giải

Bài 13: Cho tam giác ABC cân tại A có M là trung điểm của BC. Biết AB = 17 cm, BC = 16 cm. Tính AM.

Hiển thị lời giải

Bài 14: Cho góc xOy, trên Ox lấy 2 điểm A, B và trên Oy lấy hai điểm C, D sao cho OA = OC, OB = OD. Chứng minh rằng:

a) ΔABC = ΔCDA b) ΔABD = ΔCDB

Hiển thị lời giải

III. Hướng dẫn trả lời câu hỏi ôn tập chương 2 hình học 7

Câu hỏi ôn tập chương 2 Hình Học 7 trang 139 SGK Toán 7 tập 1:

1. Phát biểu định lí về tổng ba góc của một tam giác, tính chất góc ngoài của tam giác.

Lời giải

- Tổng ba góc của một tam giác bằng 180o

- Mỗi góc ngoài của một tam giác bằng tổng của hai góc trong không kề với nó.

Câu hỏi ôn tập chương 2 Hình Học (trang 139 SGK Toán 7 tập 1): 2. Phát biểu ba trường hợp bằng nhau của hai tam giác.

Lời giải

- Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

- Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

- Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Câu hỏi ôn tập chương 2 Hình Học 7 trang 139 SGK Toán 7 tập 1:

3. Phát biểu các trường hợp bằng nhau của hai tam giác vuông.

Lời giải

- Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

- Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

- Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Câu hỏi ôn tập chương 2 Hình Học 7 trang 139 SGK Toán 7 tập 1:

4. Phát biểu định nghĩa tam giác cân, tính chất về góc của tam giác cân. Nêu các cách chứng minh một tam giác là tam giác cân.

Lời giải

- Tam giác cân là tam giác có hai cạnh bằng nhau.

- Tính chất: Trong một tam giác cân, hai góc ở đáy bằng nhau

- Các cách chứng minh một tam giác là tam giác cân:

• Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

• Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.

Câu hỏi ôn tập chương 2 Hình Học 7 trang 139 SGK Toán 7 tập 1:

5. Phát biểu định nghĩa tam giác đều, tính chất về góc của tam giác đều. Nêu các cách chứng minh một tam giác là tam giác đều.

Lời giải

- Tam giác đều là tam giác có ba cạnh bằng nhau.

- Tính chất: Trong một tam giác đều, mỗi góc bằng 60o

- Các cách chứng minh một tam giác là tam giác đều:

• Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.

• Nếu một tam giác cân có một góc bằng 60o thì tam giác đó là tam giác đều.

Câu hỏi ôn tập chương 2 Hình Học 7 trang 139 SGK Toán 7 tập 1:

6. Phát biểu định lí Py – ta – go (thuận và đảo).

Lời giải

- Định lí Py – ta – go thuận:

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

- Định lí Py – ta – go đảo:

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

IV. Hướng dẫn giải bài tập ôn tập chương 2 hình học lớp 7

Bài 67 trang 140 SGK Toán 7 Tập 1:

Câu Đúng Sai 1. Trong một tam giác, góc nhỏ nhất là góc nhọn 2. Trong một tam giác có ít nhất là hai góc nhọn 3. Trong một tam giác góc lớn nhất là góc tù 4. Trong một tam giác vuông , hai góc nhọn bù nhau 5. Nếu góc A là góc ở đáy của một tam giác cân thì góc A < 90o 6. Nếu góc A là góc ở đỉnh của một tam giác cân thì góc A < 90o

Lời giải:

1. Đúng

2. Đúng

3. Sai. Tam giác nhọn có 3 góc đều nhọn.

4. Sai. Hai góc nhọn phụ nhau.

5. Đúng.

6. Sai. Ví dụ tam giác ABC có 3 góc lần lượt là 120º, 30º, 30º là tam giác cân có góc ở đỉnh bằng 120º.

Bài 68 trang 141 SGK Toán 7 Tập 1:

Các tính chất, sau đây được suy ra trực tiếp từ định lí nào ?

a) Góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.

b) Trong một tam giác vuông hai góc nhọn phụ nhau.

c) Trong một tam giác đều, các góc bằng nhau.

d) Nếu một tam giác có ba góc bằng nhau thì tam giác đo là tam giác đều.

Lời giải:

- Các tính chất ở các câu a, b được suy ra từ định lí "Tổng ba góc của một tam giác bằng 180o".

* Chứng minh:

a) ?4 bài 1 – trang 107.

b) Tam giác ABC vuông tại A

- Tính chất ở câu c được suy ra từ định lí "Trong một tam giác cân hai góc ở đáy bằng nhau".

* Chứng minh:

Giả sử có tam giác ABC đều ⇒ AB = AC =BC ⇒ ΔABC cân tại A và cân tại B

- Tính chất ở câu d được suy ra từ định lí: "Nếu một tam giác có hai góc bằng nhau thì tam giác đo là tam giác cân".

* Chứng minh:

⇒ AB = AC = BC ⇒ ΔABC là tam giác đều.

Bài 69 trang 141 SGK Toán 7 Tập 1:

Cho điểm A nằm ngoài đường thẳng a. Vẽ cung tròn tâm A cắt đường thẳng a ở B và C. Vẽ các cung tròn tâm B và tâm C có cùng bán kính sao cho chúng cắt nhau tại một điểm khác A, gọi điểm đó là D. Hãy giải thích vì sao AD vuông góc với đường thẳng a.

Lời giải:

Gọi bán kính cung tròn tâm A là r, bán kính cung tròn tâm B và C là r’.

Xét ΔABD và ΔACD có:

AB = AC (=r)

DB = DC (=r')

AD cạnh chung

Nên ΔABD = ΔACD (c.c.c)

- Gọi H là giao điểm của AD và a

ΔAHB và ΔAHC có

AB = AC (= r)

AH cạnh chung

⇒ ΔAHB = ΔAHC (c.g.c)

Bài 70 trang 141 SGK Toán 7 Tập 1:

Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M trên tia đối của tia CB lấy điểm N sao cho BM = CN.

a) Chứng minh rằng tam giác AMN là tam giác cân

b) Kẻ BH ⊥ AM, kẻ CK ⊥ AN. Chứng minh rằng BH = CK

c) Chứng minh rằng AH = AK

d) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì ? Vì sao

e) Khi góc BAC = 60o và BM = CN = BC hãy tính số đo các góc của tam giác AMN và xác định dạng của tam giác OBC

Lời giải:

a) ΔABC cân tại A suy ra

Ta lại có :

- ΔABM và ΔACN có

AB = AC (Do ΔABC cân tại A).

BM = CN(gt)

⇒ ΔABM = ΔACN (c.g.c)

⇒ AM = AN (hai cạnh tương ứng) ⇒ ΔAMN cân tại A.

b) Xét ΔBHM vuông tại H và ΔCKN vuông tại K có:

BM = CN (gt)

⇒ ΔBHM = ΔCKN (cạnh huyền – góc nhọn)

⇒ BH = CK (hai cạnh tương ứng)

c) Theo câu b ta có ΔBHM = ΔCKN ⇒ HM = KN (hai cạnh tương ứng)

Mà AM = AN ⇒ AM –MH = AK – KN hay AH = AK.

d) ΔBHM = ΔCKN

Vậy tam giác OBC là tam giác cân tại O.

e) Khi góc BAC = 60º và BM = CN = BC

Tam giác cân ABC có góc BAC = 60º nên là tam giác đều

⇒ AB = BC và góc B1 = 60º

Ta có: AB = CB, BC = BM (gt) ⇒ AB = BM ⇒ ΔABM cân ở B ⇒

Mà theo tính chất góc ngoài trong ΔBAM thì

Tương tự ta có

* Ta chứng minh tam giác OBC là tam giác đều.

Bài 71 trang 141 SGK Toán 7 Tập 1:

Tam giác ABC trên giấy kẻ ô vuông là tam giác gì.

Lời giải:

Gọi H, K, I lần lượt là các điểm như trên hình vẽ:

Gọi độ dài mỗi ô vuông là 1:

- Áp dụng định lý Pytago vào tam giác AHB vuông tại H ta có : AB2 = AH2 + HB2 = 32 + 22 = 13.

- Áp dụng định lý Pytago vào tam giác AKC vuông tại K ta có : AC2 = AK2 + KC2 =22 + 32 = 13.

- Áp dụng định lý Pytago vào tam giác BIC vuông tại I có: BC2 = BI2 + IC2 = 12 + 52 = 26.

Nhận thấy AB2 = AC2 ⟹ AB = AC nên ∆ABC cân tại A (1)

Áp dụng định lý Pytago đảo ta thấy AB2 + AC2 = 13 + 13 = 26 = BC2 nên ∆ABC vuông tại A (2)

Từ (1) và (2) suy ra ∆ABC vuông cân tại A.

Bài 72 trang 141 SGK Toán 7 Tập 1:

Đố vui: Dũng đố Cường dùng 12 que diêm bằng nhau để sắp xếp thành.

a) Một tam giác đều.

b) Một tam giác cân mà không đều.

c) Một tam giác vuông.

Em hãy giúp Cường trong trường hợp trên.

Lời giải:

a) Xếp tam giác đều: Xếp tam giác với mỗi cạnh là bốn que diêm.

b) Một tam giác cân mà không đều: 2 cạnh bên 5 que diêm, cạnh đáy 2 que.

c) Xếp tam giác vuông: Xếp tam giác có các cạnh lần lượt là ba, bốn và năm que diêm. (Cạnh huyền 5 que diêm, 2 cạnh bên lần lượt là 3, 4 que diêm vì 52 = 32 + 42).

Bài 73 trang 141 SGK Toán 7 Tập 1:

Đố. Trên hình 152, một cầu trượt có đường lên BA dài 5m, độ cao AH = 3m, độ dài BC = 10m, CD = 2m. Bạn Mai nói rằng đường trượt tổng cộng ACD gập hơn hai lần đường lên BA. Bạn Vân nói rằng điều đó không đúng ? Ai đúng ai sai.

Lời giải:

+ ΔAHB vuông tại H

Theo định lí Py–ta- go ta có

HB2 = AB2 – AH2 = 52 – 32 =25 - 9 =16

Suy ra HB = 4 (m)

Suy ra HC = BC – HB = 10 - 4 = 6(m)

+ ΔAHC vuông tại H

Theo định lí Py-ta-go ta có

AC2 = AH2 + HC2 = 32 + 62 = 9 + 36 = 45.

Suy ra AC = √45 ≈ 6,7(m)

Độ dài đường trượt ACD bằng: 6,7 + 2= 8,7 (m)

Và hai lần đường lên BA bằng 5.2 =10 (m)

Đo độ dài đường trượt ACD chưa bằng hai lần đườg lên BA

Vậy bạn Mai nói sai, bạn Vân nói đúng.

Ôn tập chương 2 hình học 7 câu hỏi và bài tập được biên soạn bám sát chương trình SGK mới môn toán lớp 7, được Soanbaitap.com tổng hợp và đăng trong chuyên mục giải toán 7 giúp các em tiện tham khảo đề học tốt môn toán 7. Nếu thấy hay hãy chia sẻ và comment để nhiều bạn khác cùng học tập.

#soanbaitap

#soanbaitap #giải bài tập #Ôn tập chương 2 (Câu hỏi – Bài tập)

0 notes

soanbaitap · 5 years ago

Link

Luyện tập trang 137 lớp 7 giải bài tập do đội ngũ giáo viên dạy tốt môn toán trên toàn quốc biên soạn. Đảm bảo chính xác, dễ hiểu giúp các em nắm được cách làm và các bước giải bài tập trong bài luyện tập trang 137 lớp 7.

Luyện tập trang 137 thuộc: Chương 2: Tam giác

I. Hướng dẫn giải bài tập luyện tập trang 137 SGK

Bài 65 trang 137 SGK Toán 7 Tập 1:

Cho ΔABC cân ở A (∠A < 90o). Vẽ BH ⊥ AC (H ∈ AC), CK ⊥ AB (K ∈ AB).

a) Chứng minh rằng AH = HK

b) Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là tia phân giác của góc A

Lời giải:

a) Xét ΔABH vuông tại H và ΔACK vuông tại K có:

AB = AC (Do ΔABC cân tại A)

góc A chung

Nên ΔABH = ΔACK (cạnh huyền – góc nhọn) ⇒ AH = AK (hai cạnh tương ứng).

b) Xét ΔAIK vuông tại K và ΔAIH vuông tại H có:

AH = AK (theo phần a)

AI chung

⇒ ΔAIK = ΔAIH (cạnh huyền – cạnh góc vuông).

⇒ góc IAK = góc IAH (hai góc tương ứng)

Vậy AI là tia phân giác của góc A.

Bài 66 trang 137 SGK Toán 7 Tập 1:

Tìm các tam giác bằng nhau trên hình 148.

Lời giải:

+ Hai tam giác vuông AMD và AME

có:

AM chung

⇒ ΔAMD = ΔAME ( cạnh huyền - góc nhọn)

⇒ MD = ME và AD = AE ( Hai cạnh tương ứng) (1)

+ Hai tam giác vuông MDB và MEC

có

MB = MC (GT)

MD = ME (chứng minh trên)

⇒ ΔMDB = ΔMEC ( cạnh huyền – cạnh góc vuông)

⇒ BD=CE ( hai cạnh tương ứng) (2)

Từ (1) và (2) ⇒ AD+BD=AE+CE ⇒ AB=AC.

+ Xét ΔAMB và ΔAMC có:

MB = MC (GT)

AB = AC (chứng minh trên)

AM chung

⇒ ΔAMB = ΔAMC (c.c.c)

Kiến thức áp dụng

+ Dựa vào trường hợp bằng nhau về cạnh huyền và góc nhọn:

Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác đó bằng nhau

+ Dựa vào trường hợp bằng nhau về cạnh huyền và cạnh góc vuông:

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

+ Dựa vào trường hợp bằng nhau thứ nhất của tam giác.

Luyện tập trang 137 lớp 7 giải bài tập được biên soạn bám sát chương trình SGK mới môn toán lớp 7, được Soanbaitap.com tổng hợp và đăng trong chuyên mục giải toán 7 giúp các em tiện tham khảo đề học tốt môn toán 7. Nếu thấy hay hãy chia sẻ và comment để nhiều bạn khác cùng học tập.

#soanbaitap

#soanbaitap #giải bài tập #Luyện tập trang 137

0 notes

soanbaitap · 5 years ago

Link

Các trường hợp bằng nhau của tam giác vuông toán lớp 7 bài 8 giải bài tập do đội ngũ giáo viên dạy tốt môn toán trên toàn quốc biên soạn. Đảm bảo dễ hiểu giúp các em hệ thống lại kiến thức trong bài các trường hợp bằng nhau của hai tam giác vuông đồng thời vận dụng vào giải các dạng bài tập liên quan để các em hiểu rõ hơn.

Bài 8. Các trường hợp bằng nhau của tam giác vuông thuộc: Chương 2: Tam giác

I. Lý thuyết về các trường hợp bằng nhau của tam giác vuông

1. Các trường hợp bằng nhau đã biết của tam giác vuông

• Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác đó bằng nhau (cạnh – góc – cạnh).

• Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

• Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác đó bằng nhau.

2. Trường hợp bằng nhau về cạnh huyền, cạnh góc vuông

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

II. Hướng dẫn giải bài tập vận dụng sgk

Bài 1: Cho tam giác ABC cân tại A, kẻ AD vuông góc với BC. Chứng minh rằng AD là tia phân giác của góc A?

Hướng dẫn giải:

Xét hai tam giác vuông ADB và ADC có

AD chung

AB = AC (gt)

Nên ΔADB = ΔADC (cạnh huyền – cạnh góc vuông)

Suy ra ∠BAD = ∠CAD (góc tương ứng bằng nhau)

Do đó AD là tia phân giác của góc A.

Vậy AD là tia phân giác của góc A.

Bài 2: Cho tam giác ABC cân tại A, kẻ BH ⊥ AC, CK ⊥ AB. Gọi I là giao điểm của BH và CK. Chứng minh AI là tia phân giác của góc A.

Hướng dẫn giải:

Xét hai tam giác AHB và AKC có:

AB = AC (gt)

Nên ΔAHB = ΔAKC (cạnh huyền - cạnh góc nhọn)

Suy ra AH = AK (cạnh tương ứng)

Xét hai tam giác vuông AHI và AKI ta có:

AI là cạnh chung

AH = AK

Nên ΔAHI = ΔAKI (cạnh huyền - cạnh góc vuông)

⇒ ∠A1 = ∠A2 (góc tương ứng bằng nhau)

Do đó AI là tia phân giác góc A

III. Hướng dẫn trả lời câu hỏi sgk bài 8 các trường hợp bằng nhau của tam giác vuông

Trả lời câu hỏi Toán 7 Tập 1 Bài 8 trang 135:

Trên mỗi hình 143, 144, 145 có các tam giác vuông nào bằng nhau ? Vì sao ?

Lời giải

- hình 143 :

Xét tam giác ABH vuông tại H và tam giác ACH vuông tại H có:

AH chung

BH = CH (gt)

⇒ ΔABH =ΔACH (hai cạnh góc vuông)

- hình 144 :

Xét tam giác DEK vuông tại K và tam giác DFK vuông tại K có:

DK chung

∠(KDE) = ∠(KDF) (GT)

⇒ ΔDEK =ΔDFK (cạnh góc vuông – góc nhọn kề)

- hình 144 :

Xét tam giác OMI vuông tại M và tam giác ONI vuông tại N có:

OI chung

∠(MOI) = ∠(NOI) (GT)

⇒ ΔOMI = ΔONI (cạnh huyền – góc nhọn)

Trả lời câu hỏi Toán 7 Tập 1 Bài 8 trang 136:

Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (hình 147). Chứng minh rằng ΔAHB =ΔAHC (giải bằng 2 cách)

Lời giải

- Cách 1: ΔABC cân tại A nên ∠B = ∠C và AB = AC

Xét hai tam giác vuông ΔAHB và ΔAHC đều vuông tại H có:

AB = AC (GT)

∠B = ∠C

⇒ ΔAHB =ΔAHC (cạnh huyền – góc nhọn)

- Cách 2:

Xét hai tam giác vuông ΔAHB và ΔAHC đều vuông tại H có:

AB = AC

AH chung

⇒ ΔAHB = ΔAHC (cạnh huyền – cạnh góc vuông)

IV. Hướng dẫn giải bài tập sgk bài 8 các trường hợp bằng nhau của tam giác vuông

Bài 63 trang 136 SGK Toán 7 Tập 1:

Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC. Chứng minh rằng

a) HB = HC

b) góc BAH = góc CAH

Lời giải:

a) Xét hai tam giác vuông ΔABH và ΔACH đều vuông tại H có:

AB = AC (gt)

AH cạnh chung

Nên ΔABH = ΔACH (cạnh huyền - cạnh góc vuông)

Suy ra HB = HC

b) Ta có ΔABH = ΔACH (cmt)

Suy ra góc BAH = góc CAH (hai góc tương ứng)

Kiến thức áp dụng

Nếu cạnh huyền và một cạnh góc vuông của tam giác này bằng cạnh huyền và cạnh góc vuông của tam giác kia thì hai tam giác vuông đó bằng nhau.

Bài 64 trang 136 SGK Toán 7 Tập 1:

Các tam giác vuông ABC và DEF có góc A = góc D = 90o, AC = DF. Hãy bổ sung thêm một điều kiện bằng nhau để ΔABC = ΔDEF.

Lời giải:

- Bổ sung AB =DE thì ΔABC = ΔDEF (c.g.c)

- Hoặc Bổ sung góc C = góc F (2 tam giác bằng nhau theo trường hợp g.c.g)

- Bổ sung BC = EF thì ΔABC = ΔDEF (cạnh huyền - cạnh góc vuông)

Bài 65 trang 137 SGK Toán 7 Tập 1:

Cho ΔABC cân ở A (∠A < 90o). Vẽ BH ⊥ AC (H ∈ AC), CK ⊥ AB (K ∈ AB).

a) Chứng minh rằng AH = HK

b) Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là tia phân giác của góc A

Lời giải:

a) Xét ΔABH vuông tại H và ΔACK vuông tại K có:

AB = AC (Do ΔABC cân tại A)

góc A chung

Nên ΔABH = ΔACK (cạnh huyền – góc nhọn) ⇒ AH = AK (hai cạnh tương ứng).

b) Xét ΔAIK vuông tại K và ΔAIH vuông tại H có:

AH = AK (theo phần a)

AI chung

⇒ ΔAIK = ΔAIH (cạnh huyền – cạnh góc vuông).

⇒ góc IAK = góc IAH (hai góc tương ứng)

Vậy AI là tia phân giác của góc A.

Bài 66 trang 137 SGK Toán 7 Tập 1:

Tìm các tam giác bằng nhau trên hình 148.

Lời giải:

+ Hai tam giác vuông AMD và AME

có:

AM chung

⇒ ΔAMD = ΔAME ( cạnh huyền - góc nhọn)

⇒ MD = ME và AD = AE ( Hai cạnh tương ứng) (1)

+ Hai tam giác vuông MDB và MEC

có

MB = MC (GT)

MD = ME (chứng minh trên)

⇒ ΔMDB = ΔMEC ( cạnh huyền – cạnh góc vuông)

⇒ BD=CE ( hai cạnh tương ứng) (2)

Từ (1) và (2) ⇒ AD+BD=AE+CE ⇒ AB=AC.

+ Xét ΔAMB và ΔAMC có:

MB = MC (GT)

AB = AC (chứng minh trên)

AM chung

⇒ ΔAMB = ΔAMC (c.c.c)

Kiến thức áp dụng

+ Dựa vào trường hợp bằng nhau về cạnh huyền và góc nhọn:

Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác đó bằng nhau

+ Dựa vào trường hợp bằng nhau về cạnh huyền và cạnh góc vuông:

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

+ Dựa vào trường hợp bằng nhau thứ nhất của tam giác

Các trường hợp bằng nhau của tam giác vuông toán lớp 7 bài 8 giải bài tập được biên soạn bám sát chương trình SGK mới môn toán lớp 7, được Soanbaitap.com tổng hợp và đăng trong chuyên mục giải toán 7 giúp các em tiện tham khảo đề học tốt môn toán 7. Nếu thấy hay hãy chia sẻ và comment để nhiều bạn khác cùng học tập.

#soanbaitap

#soanbaitap #giải bài tập #Bài 8. Các trường hợp bằng nhau của tam giác vuông

0 notes

soanbaitap · 5 years ago

Link

Định lý Pytago toán lớp 7 bài 7 giải bài tập do đội ngũ giáo viên dạy tốt môn toán trên toàn quốc biên soạn. Đảm bảo dễ hiểu giúp các em hệ thống lại kiến thức trong bài định lý pitago lớp 7, đồng thời vận dụng vào giải các dạng bài tập liên quan để các em hiểu rõ hơn.

Bài 7. Định lý Pytago thuộc: Chương 2: Tam giác

I. Lý thuyết về định lý Pytago

1. Định lý Pytago

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

ΔABC vuông tại A ⇒ BC2 = AB2 + AC2

2. Định lý Pytago đảo

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

ΔABC có BC2 = AB2 + AC2 ∠BAC = 90o

II. Hướng dẫn giải bài tập vận dụng sgk bài 7 Định lý Pytago

Bài 1: Cho tam giác ABC vuông tại A. Gọi M là trung điểm của AB, kẻ MH vuông góc với BC tại H. Chứng minh rằng CH2 - BH2 = AC2

Hướng dẫn giải:

Nối C với M ta được tam giác vuông CMH

Áp dụng định lí Py – ta – go ta có:

Do đó: CH2 - BH2 = (CM2 - MH2) - BH2

= CM2 - (MH2 + BH2) = CM2 - BM2

Mà MA = MB (gt)

Nên CH2 - BH2 = CH2 - MA2 = AC2

Vậy CH2 - BH2 = AC2

Bài 2: Tam giác ABC có ∠A = 120°, BC = a, AC = b, AB = c. Chứng minh: a2 = b2 + c2 + bc

Hướng dẫn giải:

III. Hướng dẫn trả lời câu hỏi bài tập sgk bài 7 Định lý Pytago

Trả lời câu hỏi Toán 7 Tập 1 Bài 7 trang 129:

Vẽ một tam giác vuông có các cạnh góc vuông bằng 3cm và 4cm. Đo độ dài cạnh huyền

Lời giải

Đo được cạnh huyền 5cm

Trả lời câu hỏi Toán 7 Tập 1 Bài 7 trang 129:

Lấy giấy trắng cắt tám tam giác vuông bằng nhau. Trong mỗi tam giác vuông đó, ta gọi độ dài các cạnh góc vuông là a và b, gọi độ dài cạnh huyền là c. Cắt hai tấm bìa hình vuông có cạnh bằng a+b

a)Đặt bốn tam giác vuông lên tấm bìa hình vuông như hình 121. Phần bìa không bị che lấp là một hình vuông có cạnh bằng c, tính diện tích phần bìa đó theo c

b) Đặt bốn tam giác vuông còn lại lên tấm bìa hình vuông thứ hai như hình 122. Phần bìa không bị che lấp gồm hai hình vuông có cạnh là a và b; tính diện tích phần bìa đó theo a và b

c) từ đó rút ra nhận xét gì về quan hệ giữa c2 và a2 + b2 ?

Lời giải

a) diện tích phần bìa hình vuông cạnh c là c2

b) diện tích hai phần bìa hình vuông lần lượt là a2 và b2

c) nhận xét c2 = a2 + b2

Trả lời câu hỏi Toán 7 Tập 1 Bài 7 trang 130: Tìm độ dài x trên các hình 124, 125

Lời giải

Áp dụng định lí Py – ta – go

Tam giác ABC vuông tại B

⇒ x2 + 82 = 102

⇒ x2 = 102 – 82 = 36

⇒ x = 6 (cm)

Tam giác DEF vuông tại D

⇒ 12 + 12 = x2

⇒ x2 = 1 + 1 = 2

⇒ x = √2 (cm)

Trả lời câu hỏi Toán 7 Tập 1 Bài 7 trang 130:

Vẽ tam giác ABC có AB = 3cm; AC = 4cm; BC = 5cm. Hãy dùng thước đo góc để xác định số đo của góc BAC

Lời giải

Số đo góc BAC là 90o

IV. Hướng dẫn giải bài tập sgk định lý Pytago

Bài 53 trang 131 SGK Toán 7 Tập 1:

Tìm độ dài x trên hình 127.

Lời giải:

- Hình a

Áp dụng định lí Pi-ta-go ta có:

x2 = 122 + 52 = 144 + 25 = 169 ⇒ x = 13

- Hình b

Ta có: x2 = 12 + 22 = 1 + 4 = 5

⇒ x = √5

- Hình c

Theo định lí Pi-ta-go 292 = 212 + x2

Nên x2 = 292 - 212 = 841 - 441 = 400

⇒ x = 20

- Hình d

Theo định lí Pi-ta-go ta có:

x2 = (√7)2 + 32 = 7 + 9 = 16

⇒ x = 4

Kiến thức áp dụng

Định lý Pytago: “ Trong tam giác vuông, tổng bình phương cạnh góc vuông bằng bình phương cạnh huyền”.

Bài 54 trang 131 SGK Toán 7 Tập 1:

Đoạn lên dốc từ C đến A dài 8,5m, độ dài CB bằng 7,5m. Tính chiều cao AB.

Lời giải:

Áp dụng định lí Py–ta–go vào tam giác vuông ABC vuông tại B ta có:

AB2 + BC2 = AC2

Nên AB2 = AC2 – BC2

= 8,52 – 7,52

= 72,25 – 56,25

=16

⇒ AB = 4 (m)

Kiến thức áp dụng

Định lý Pytago: “ Trong tam giác vuông, tổng bình phương cạnh góc vuông bằng bình phương cạnh huyền”.

Bài 55 trang 131 SGK Toán 7 Tập 1:

Tính chiều cao của bức tường, biết rằng chiều dài của thang là 4m và chân thang cách tường 1m.

Lời giải:

Kí hiệu như hình vẽ:

Vì mặt đất vuông góc với chân tường nên góc C = 90º.

Áp dụng định lí Pi-ta-go trong ΔABC ta có:

AC2 + BC2 = AB2

⇒ AC2 = AB2 - BC2 = 16 - 1 = 15

⇒ AC = √15 ≈ 3,87(m) hay chiều cao của bức tường là 3,87m.

Kiến thức áp dụng

Định lý Pytago: “ Trong tam giác vuông, tổng bình phương cạnh góc vuông bằng bình phương cạnh huyền”.

Bài 56 trang 131 SGK Toán 7 Tập 1:

Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau.

a) 9cm, 15cm, 12cm.

b) 5dm, 13dm, 12dm.

c) 7m, 7m, 10m.

Lời giải:

a) Ta có 92 = 81 ; 152 =225 ; 122 =144

Mà 225 = 144 + 81

Nên Theo định lí Py – ta – go đảo, tam giác có độ dài 3 cạnh 9cm ,12cm ,15cm là tam giác vuông.

b) Ta có 52 = 25 ; 132 =169 ; 122 =144

Mà 169 = 144 + 25

Nên Theo định lí Py – ta – go đảo tam giác có độ dài 3 cạnh 5dm ,13dm ,12dm là tam giác vuông.

c) Ta có 72 = 49 ; 102 =100

Mà 100 ≠ 49 + 49

Nên tam giác có độ dài 3 cạnh 7m, 7m, 10m không là tam giác vuông

Kiến thức áp dụng

Định lý Pytago đảo: “Nếu một tam giác có bình phương một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông”.

Bài 57 trang 131 SGK Toán 7 Tập 1:

Cho bài toán "ΔABC có AB = 8, AC = 17, BC = 15 có phải là tam giác vuông hay không ? Bạn Tâm đã giải thích bài toán đó như sau:

AB2 + AC2 = 82 + 172 = 64 + 289 = 353

BC2 = 152 = 225

Vì 353 ≠ 225 nên AB2 + AC2 ≠ BC2

Vậy ΔABC không phải là tam giác vuông."

Lời giải trên đúng hay sai ? Nếu sai hãy sửa lại cho đúng

Lời giải:

Lời giải của bạn Tâm sai. Sửa lại như sau:

AB2 + BC2 = 82 + 152 = 64+225 = 289

AC2 = 172 = 289.

⇒ AB2 + BC2 = AC2

Vậy tam giác ABC là tam giác vuông tại B (Theo định lí Py-ta-go đảo)

Kiến thức áp dụng

Định lý Pytago đảo: “Nếu một tam giác có bình phương một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông”.

Bài 58 trang 132 SGK Toán 7 Tập 1:

Đố. Trong lúc anh Nam dựng tủ cho đứng thẳng, tủ có bị vướng vào trần nhà không ?.

Lời giải:

Gọi d là đường chéo của tủ.

Ta có d2 = 202 + 42 = 400 + 16 = 416

⇒ d = √416 ≈ 20,4 dm

Suy ra d < 21dm (là chiều cao của căn phòng)

Như vậy khi anh Nam đẩy tủ cho đứng thẳng tủ không bị vướng vào trần nhà

Bài 59 trang 133 SGK Toán 7 Tập 1:

Bạn Tâm muốn đóng một nẹp chéo AC để chiếc khung hình chữ nhật ABCD được vững hơn. Tính độ dài AC, biết rằng AD = 48cm, CD = 36cm.

Lời giải:

Áp dụng định lí Py-ta-go trong ΔACD vuông tại D ta có:

AC2 = AD2 + CD2 = 482 + 362 = 2304 + 1296 = 3600

⇒ AC = 60(cm)

Bài 59 trang 133 SGK Toán 7 Tập 1:

Bạn Tâm muốn đóng một nẹp chéo AC để chiếc khung hình chữ nhật ABCD được vững hơn. Tính độ dài AC, biết rằng AD = 48cm, CD = 36cm.

Lời giải:

Áp dụng định lí Py-ta-go trong ΔACD vuông tại D ta có:

AC2 = AD2 + CD2 = 482 + 362 = 2304 + 1296 = 3600

⇒ AC = 60(cm)

Bài 61 trang 133 SGK Toán 7 Tập 1:

Trên giấy kẻ ô vuông (độ dài cạnh của ô vuông bằng 1) cho tam giác ABC như hình 135. Tính độ dài mỗi cạnh của tam giác.

Lời giải:

Áp dụng định lí Pi-ta-go trong ΔAMB vuông tại M ta có:

AB2 = AM2 + MB2 = 22 + 12 = 5

⇒ AB = √5

Áp dụng định lí Pi-ta-go trong ΔANC vuông tại N ta có:

AC2 = AN2 + NC2 = 32 + 42 = 25

⇒ AC = 5

Áp dụng định lí Pi-ta-go trong ΔBKC vuông tại K ta có:

BC2 = BK2 + KC2 = 32 + 52 = 34

⇒ BC = √34

Bài 62 trang 133 SGK Toán 7 Tập 1:

Đố. Người ta buộc con cún bằng sợi dây có một đầu dây buộc tại điểm O làm cho con Cún cách điểm O nhiều nhất 9m. Con Cún có thể tới các vị trí A, B, C, D để canh giữ mảnh vườn hình chữ nhật ABCD hay không ?

Lời giải:

Theo định lý Pytago ta có:

+) OA2 = 42 + 32 = 16 + 9 = 25

⇒ OA = 5m < 9m

+) OC2 = 62 + 82 = 36 + 64 = 100

⇒ OC = 10m > 9m

+) OB2 = 42 + 62 = 16 + 36 = 52

⇒ OB = √52m ≈ 7,21 (m) < 9m

+) OD2 = 32 + 82 = 9 + 64 = 73

⇒ OD = √73 ≈ 8,54(m) < 9m

Như vậy con Cún có thể tới các vị trí A, B, D nhưng không tới được vị trí C.

Định lý Pytago toán lớp 7 bài 7 giải bài tập được biên soạn bám sát chương trình SGK mới môn toán lớp 7, được Soanbaitap.com tổng hợp và đăng trong chuyên mục giải toán 7 giúp các em tiện tham khảo đề học tốt môn toán 7. Nếu thấy hay hãy chia sẻ và comment để nhiều bạn khác cùng học tập.

#soanbaitap

#soanbaitap #giải bài tập #Bài 7. Định lí Pi-ta-go

0 notes

soanbaitap · 5 years ago

Link

Tam giác cân toán lớp 7 bài 6 giải bài tập do đội ngũ giáo viên dạy tốt môn toán trên toàn quốc biên soạn. Đảm bảo dễ hiểu giúp các em hệ thống lại kiến thức trong bài tam giác cân lớp 7, đồng thời vận dụng vào giải các dạng bài tập liên quan để các em hiểu rõ hơn.

Bài 6. Tam giác cân thuộc: Chương 2: Tam giác

I. Lý thuyết về tam giác cân lớp 7

1. Định nghĩa tam giác cân

Tam giác cân là tam giác có hai cạnh bằng nhau.

Ví dụ: Ta có tam giác cân ABC cân tại A (AB = AC). Ta gọi AB và AC là các cạnh bên, BC là cạnh đáy, ∠B và ∠C là các góc ở đáy, ∠A là góc ở đỉnh.

2. Tính chất tam giác cân

Trong tam giác cân, hai góc ở đáy bằng nhau.

Dấu hiệu nhận biết:

• Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.

• Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

Định nghĩa tam giác vuông cân: Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.

Ví dụ: ΔABC vuông cân tại A

Tính chất: Mỗi góc nhọn của tam giác vuông cân bằng 45o

Ví dụ: ΔABC vuông cân tại A ⇒ ∠B = ∠C = 45o.

3. Tam giác đều

Định nghĩa: Tam giác đều là tam giác có ba cạnh bằng nhau: ΔABC đều ⇔ AB = BC = AC

Tính chất: Trong tam giác đều, mỗi góc bằng 60o: ΔABC đều ⇔ ∠A = ∠B = ∠C = 60o

Dấu hiệu nhận biết:

• Nếu tam giác có ba cạnh bằng nhau thì tam giác đó là tam giác đều.

• Nếu tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.

• Nếu một tam giác cân có một góc nhọn bằng 60o thì tam giác đó là tam giác đều.

II. Hướng dẫn giải bài tập vận dụng sgk

Bài 1: Cho tam giác ABC cân tại A có ∠A = 50°

a) Tính ∠B, ∠C

b) Lấy điểm D thuộc AB, điểm E thuộc AC sao cho AD = AE. Chứng minh DE // BC

Hướng dẫn giải:

Bài 2: Cho tam giác ABC cân tại A và có

, phân giác của góc B cắt AC tại D.

a) Tính các góc của tam giác ABC

b) Chứng minh DA = DB

Hướng dẫn giải:

III. Hướng dẫn trả lời câu hỏi bài tập bài 6 tam giác cân lớp 7

Trả lời câu hỏi Toán 7 Tập 1 Bài 6 trang 126:

Tìm các tam giác cân trên hình 112. Kể tên các cạnh bên, cạnh đáy, góc ở đáy, góc ở đỉnh của các tam giác cân đó.

Lời giải

Các tam giác cân trên hình 112:

-ΔADE cân tại A: có các cạnh bên là AD và AE; cạnh đáy: DE; góc D và góc E là hai góc ở đáy; góc A là góc ở đỉnh

-ΔABC cân tại A: có các cạnh bên là AB và AC; cạnh đáy: BC; góc B và góc C là hai góc ở đáy; góc A là góc ở đỉnh

-ΔAHC cân tại A: có các cạnh bên là AH và AC; cạnh đáy: HC; góc H và góc C là hai góc ở đáy; góc A là góc ở đỉnh

Trả lời câu hỏi Toán 7 Tập 1 Bài 6 trang 126:

Cho tam giác ABC cân tại A. Tia phân giác của góc A cắt BC ở D (hình 113). Hãy so sánh (ABD) ̂ = (ACD) ̂

Lời giải

-ΔABD và ΔACD có

AB = AC

∠(BAD) = ∠(CAD) (do AD là tia phân giác góc A)

AD chung

Nên ΔABD = ΔACD ( c.g.c)

⇒ ∠(ABD) = ∠(ACD) (hai góc tương ứng)

Trả lời câu hỏi Toán 7 Tập 1 Bài 6 trang 126:

Tính số đo mỗi góc nhọn của một tam giác vuông cân

Lời giải

Giả sử ΔABC vuông cân tại A

∠A + ∠B + ∠C = 180o

Và ∠A = 90o; ∠B = ∠C

⇒ 2. ∠B = 180o – 90o = 90o

⇒∠B = ∠C = 90o:2 = 45o

Trả lời câu hỏi Toán 7 Tập 1 Bài 6 trang 126:

Vẽ tam giác đều ABC (hình 115)

a) Vì sao ∠B = ∠C ; ∠C = ∠A ?

b) Tính số đo mỗi góc của tam giác ABC

Lời giải

a) ∠B = ∠C khi xét tam giác ABC cân tại A

∠C = ∠A khi xét tam giác ABC cân tại B

b) Tam giác ABC có 3 góc bằng nhau và bằng 180o/3 = 60o

IV. Hướng dẫn giải bài tập sgk bài 6 tam giác cân lớp 7

Bài 46 trang 127 SGK Toán 7 Tập 1:

a) Dùng thước có chia xentimet và compa vẽ tam giác ABC cân ở B có cạnh đáy bằng 3cm, cạnh bên bằng 4cm.

b) Dùng thước có chia xentimet và compa vẽ tam giác đều ABC có cạnh bằng 3cm.

Lời giải:

a) Vẽ đoạn thẳng AC = 3cm.

- Trên cùng một nửa mặt phẳng bờ AC vẽ cung tròn tâm A bán kính 4cm và cung tròn C bán kính 4cm.

- Hai cung tròn trên cắt nhau tại B.

- Vẽ các đoạn thẳng AB, BC ta được tam giác ABC.

b) Vẽ đoạn thẳng AC = 3cm

- Trên cùng một nửa mặt phẳng bờ AC vẽ cung tròn tâm A bán kính 3cm và cung tròn C bán kính 3cm

- Hai cung tròn trên cắt nhau tại B

- Vẽ các đoạn thẳng AB, BC ta được tam giác ABC.

Bài 47 trang 127 SGK Toán 7 Tập 1:

Trong các tam giác trên các hình 116, 117, 118 tam giác nào là tam giác cân tam giác nào là tam giác đều ? Vì sao?

Lời giải:

- Hình 116

Ta có ΔABD cân vì AB = AD

ΔACE cân vì AC = AE

Do AB = AD , BC = DE nên AB + BC = AD + DE hay AC = AE

⇒ ΔACE cân

- Hình 117

Ta tính được

- Hình 118

* ΔOMN là tam giác đều vì ba cạnh bằng nhau OM = MN = NO

* ΔOMK cân tại M vì OM = MK

* ΔONP là tam giác cân tại N vì ON = NP

Bài 48 trang 127 SGK Toán 7 Tập 1:

Cắt một tấm bìa hình tam giác cân. Hãy gấp tấm bìa đó sao cho hai cạnh bên trùng nhau để kiểm tra rằng góc ở hai đáy bằng nhau ?.

Lời giải:

Các bước tiến hành.

- Cắt tấm bìa hình tam giác cân.

- Gấp tấm bìa sao cho hai cạnh bên trùng nhau.

- Quan sát phần cạnh đáy sau khi gấp lại chúng trùng nhau.

Vậy hai góc ở đáy của tam giác cân bằng nhau.

Bài 49 trang 127 SGK Toán 7 Tập 1:

a) Tính các góc ở đáy của một tam giác cân biết góc ở đỉnh bằng 40o.

b) Tính góc ở đỉnh của một tam giác cân biết góc ở đáy bằng 40o.

Lời giải:

Bài 50 trang 127 SGK Toán 7 Tập 1:

Hai thanh AB và AC của vì kèo một mái nhà thường bằng nhau và thường tạo với nhau một góc bằng.

a) 145o nếu là mái tôn.

b) 100o nếu mái là ngói.

Tính góc ABC trong từng trường hợp.

Lời giải:

Bài 51 trang 128 SGK Toán 7 Tập 1:

Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc cạnh AB sao cho AD = AE

a) So sánh góc ABD và ACE

b) Gọi I là giao điểm của BD và CE. ΔIBC là tam giác gì ? Vì sao ?

Lời giải:

a) Xét ΔABD và ΔACE có:

AB = AC (gt)

Góc A chung

AD = AE (gt)

Nên ΔABD = ΔACE ( c.g.c)

Vậy ΔIBC cân tại I

Bài 52 trang 128 SGK Toán 7 Tập 1:

Cho góc xOy có số đo 120o điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc với Ox, kẻ AC vuông góc với Oy. Tam giác ABC là tam giác gì ? Vì sao?

Lời giải:

Hai tam giác vuông ABO (góc B = 90º) và ACO (góc C = 90º) có :

⇒ ΔABO = ΔACO (cạnh huyền – góc nhọn)

⇒ AB = AC (hai cạnh tương ứng) ⇒ ΔABC cân.

Tam giác cân ABC có góc A = 60º nên là tam giác đều.

Kiến thức áp dụng

+ Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông khác thì hai tam giác đó bằng nhau.

+ Tam giác cân có 1 góc bằng 60º là tam giác đều.

Tam giác cân toán lớp 7 bài 6 giải bài tập được biên soạn bám sát chương trình SGK mới môn toán lớp 7, được Soanbaitap.com tổng hợp và đăng trong chuyên mục giải toán 7 giúp các em tiện tham khảo đề học tốt môn toán 7. Nếu thấy hay hãy chia sẻ và comment để nhiều bạn khác cùng học tập.

#soanbaitap

#soanbaitap #giải bài tập #Bài 6. Tam giác cân

0 notes

soanbaitap · 5 years ago

Link

Trường hợp bằng nhau thứ ba của tam giác Góc Cạnh Góc toán lớp 7 bài 5 giải bài tập do đội ngũ giáo viên dạy tốt môn toán trên toàn quốc biên soạn. Đảm bảo dễ hiểu giúp các em hệ thống lại kiến thức trong bài trường hợp bằng nhau thứ ba của tam giác, đồng thời vận dụng vào giải các dạng bài tập toán liên quan để các em hiểu rõ hơn.

Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc(g.c.g) thuộc: Chương 2: Tam giác

I. Lý thuyết về trường hợp bằng nhau thứ ba của tam giác Góc Cạnh Góc

1. Tính chất

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

(∆ABC) và (∆ A'B'C ') có:

(left.begin{matrix} widehat{B}=widehat{B'}\ BC=B'C' \ widehat{C}=widehat{C'} end{matrix}right} Rightarrow Delta ABC=A'B'C ')

2. Hệ quả

- Hệ quả 1: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

- Hệ quả 2. Nếu cạnh huyền và góc nhọn của tam giác vuông nay bằng cạnh huyền, góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

II. Hướng dẫn trả lời câu hỏi bài tập sgk bài 5 trường hợp bằng nhau thứ ba của tam giác góc cạnh góc

Trả lời câu hỏi 1 Bài 5 trang 121 SGK Toán 7 Tập 1.

Đề bài: Vẽ thêm tam giác A′B′C′A′B′C′ có: B′C′=4cm;ˆB′=60o;B′C′=4cm;B′^=60o;ˆC′=40oC′^=40o. Hãy đo để kiểm nghiệm rằng AB=A′B′.AB=A′B′. Vì sao ta kết luận được ΔABC=ΔA′B′C′ΔABΔA′B′C′?

Phương pháp giải - Xem chi tiết

Vẽ tam giác ABCABC có AC=a;AC=a; ˆA=xo;A^=xo; ˆC=yoC^=yo.

Cách vẽ:

- Vẽ đoạn AC=aAC=a

- Trên cùng một nửa mặt phẳng bờ ACAC vẽ tia AxAx và CyCy sao cho ˆCAx=xoCAx^=xo; ˆACy=yoACy^=yo

Hai tia cắt nhau ở BB, ta được tam giác ABCABC cần vẽ.

Lời giải chi tiết

Đo kiểm tra thấy: AB=A′B′AB=A′B′

ΔABCΔABC và ΔA′B′C′ΔA′B′C′ có:

+) AB=A′B′AB=A′B′ (chứng minh trên)

+) ˆB=ˆB′=60oB^=B′^=60o

+) BC=B′C′=4cmBC=B′C′=4cm

Suy ra ΔABC=ΔA′B′C′ΔABC=ΔA′B′C′ (cạnh – góc – cạnh).

Trả lời câu hỏi 2 Bài 5 trang 122 SGK Toán 7 Tập 1.

Đề bài: Tìm các tam giác bằng nhau ở mỗi hình 94, 95, 96.

- Phương pháp giải - Xem chi tiết

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và góc kề của tam giác kìa thì hai tam giác đó bằng nhau.

Lời giải chi tiết

- Hình 94:

Xét ΔABDΔABD và ΔCDBΔCDB có:

+) ˆABD=ˆCDB(giảthiết)ABD^=CDB^(giảthiết)

+) BDBD cạnh chung

+) ˆADB=ˆCBD(giảthiết)ADB^=CBD^(giảthiết)

⇒ΔABD=ΔCDB⇒ΔABD=ΔCDB (g.c.g)

- Hình 95:

Áp dụng định lí tổng các góc của một tam giác vào ΔOEFΔOEF và ΔOHGΔOHG ta có:

ˆEOF+ˆOFE+ˆFEO=180oEOF^+OFE^+FEO^=180o (1)

ˆGOH+ˆOHG+ˆHGO=180oGOH^+OHG^+HGO^=180o (2)

ˆEOF=ˆGOHEOF^=GOH^ (đối đỉnh) (3)

ˆOFE=ˆOHGOFE^=OHG^ (giả thiết) (4)

Từ (1), (2), (3), (4) ta có: ˆFEO=ˆHGOFEO^=HGO^

Xét ΔEOFΔEOF và ΔGOHΔGOH có:

+) ˆOFE=ˆOHGOFE^=OHG^ (giả thiết)

+) EF=GHEF=GH (giả thiết)

+) ˆFEO=ˆHGOFEO^=HGO^ (chứng minh trên)

⇒ΔEOF=ΔGOH⇒ΔEOF=ΔGOH (g.c.g)

- Hình 96:

Xét ΔABCΔABC và ΔEDFΔEDF có:

+) ˆBAC=ˆDEF=90oBAC^=DEF^=90o

+) AC=EFAC=EF (giả thiết)

+) ˆACB=ˆEFDACB^=EFD^ (giả thiết)

⇒ΔABC=ΔEDF⇒ΔABC=ΔEDF (g.c.g)

III. Hướng dẫn giải bài tập trường hợp đồng dạng thứ ba của tam giác góc cạnh góc sgk

Bài 33 trang 123 SGK Toán 7 tập 1.

Đề bàiVẽ tam giác ABCABC biết AC=2cm;AC=2cm; ˆA=90o;A^=90o; ˆC=60oC^=60o.

Phương pháp giải - Xem chi tiết

Vẽ tam giác ABCABC có AC=a;AC=a; ˆA=xo;A^=xo; ˆC=yoC^=yo.

Cách vẽ:

- Vẽ đoạn AC=aAC=a

- Trên cùng một nửa mặt phẳng bờ ACAC vẽ tia AxAx và CyCy sao cho ˆCAx=xoCAx^=xo; ˆACy=yoACy^=yo

Hai tia cắt nhau ở BB, ta được tam giác ABCABC cần vẽ.

Lời giải chi tiết

Cách vẽ:

- Vẽ đoạn AC=2cmAC=2cm

- Trên cùng một nửa mặt phẳng bờ ACAC vẽ tia AxAx và CyCy sao cho ˆCAx=90oCAx^=90o; ˆACy=60oACy^=60o

Hai tia cắt nhau ở BB, ta được tam giác ABCABC cần vẽ.

Bài 34 trang 123 SGK Toán 7 tập 1.

Đề bài: Trên mỗi hình 98,99 có tam giác nào bằng nhau? Vì sao?

Phương pháp giải - Xem chi tiết

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Lời giải chi tiết

Xem hình 98)

Xét ΔABC∆ABC và ΔABD∆ABD có:

+) ˆCAB=ˆDABCAB^=DAB^ (giả thiết)

+) ABAB là cạnh chung.

+) ˆABC=ˆABDABC^=ABD^ (giả thiết)

⇒ΔABC=ΔABD⇒∆ABC=∆ABD (g.c.g)

Xem hình 99) (gọi tên như hình vẽ)

Ta có:

ˆB1+ˆB2=1800B1^+B2^=1800 (hai góc kề bù).

ˆC1+ˆC2=1800C1^+C2^=1800 (hai góc kề bù)

Mà ˆB2=ˆC2B2^=C2^ (giả thiết) nên ˆB1=ˆC1B1^=C1^

* Xét ΔABD∆ABD và ΔACE∆ACE có:

+) ˆB1=ˆC1B1^=C1^ (chứng minh trên)

+) BD=ECBD=EC (giả thiết)

+) ˆD=ˆED^=E^ (giả thiết)

⇒ΔABD=ΔACE⇒∆ABD=∆ACE (g.c.g)

Ta có:

DC=DB+BCDC=DB+BC

EB=EC+CBEB=EC+CB

Mà DB=ECDB=EC

Do đó: DC=EBDC=EB

* Xét ΔADC∆ADC và ΔAEB∆AEB có:

+) ˆD=ˆED^=E^ (giả thiết)

+) ˆC2=ˆB2C2^=B2^ (giả thiết)

+) DC=EBDC=EB (chứng minh trên)

⇒ΔADC=ΔAEB⇒∆ADC=∆AEB (g.c.g)

Bài 35 trang 123 SGK Toán 7 tập 1.

Đề bàiCho góc xOyxOy khác góc bẹt, OtOt là tia phân giác của góc đó. Qua HH thuộc tia OtOt , kẻ đường vuông góc với OtOt, nó cắt OxOx và OyOy theo thứ tự AA và BB.

a) Chứng minh rằng OA=OBOA=OB.

b ) Lấy điểm CC thuộc tia OtOt, chứng minh rằng CA=CBCA=CB và ˆOAC=ˆOBCOAC^=OBC^.

Phương pháp giải - Xem chi tiết

a) Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

b) Nếu hai cạnh và một góc xen giữa của tam giác này bằng hai cạnh và một góc xen giữa của tam giác vuông kia thì hai tam giác đó bằng nhau.

Lời giải chi tiết

a) Xét ΔAOH∆AOH và ΔBOH∆BOH có:

+) ˆAOH=ˆBOHAOH^=BOH^ (vì OtOt là phân giác của ˆxOyxOy^)

+) OHOH là cạnh chung

+) ˆAHO=ˆBHO(=900)AHO^=BHO^(=900)

⇒ΔAOH=ΔBOH⇒∆AOH=∆BOH ( g.c.g)

⇒OA=OB⇒OA=OB (hai cạnh tương ứng).

b) Xét ΔAOC∆AOC và ΔBOC∆BOC có:

+) OA=OBOA=OB (chứng minh trên)

+) ˆAOC=ˆBOCAOC^=BOC^ (vì OtOt là phân giác của ˆxOyxOy^)

+) OCOC cạnh chung.

⇒ΔAOC=ΔBOC⇒∆AOC=∆BOC (c.g.c)

⇒CA=CB⇒CA=CB ( hai cạnh tương ứng)

⇒ˆOAC=ˆOBC⇒OAC^=OBC^ (hai góc tương ứng).

Bài 36 trang 123 SGK Toán 7 tập 1.

Đề bài: Trên hình 100 ta có OA=OBOA=OB, ˆOAC=ˆOBDOAC^=OBD^.

Chứng minh rằng AC=BD.AC=BD.

Phương pháp giải - Xem chi tiết

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Lời giải chi tiết

Xét ΔOAC∆OAC và ΔOBD∆OBD có:

+ ˆOAC=ˆOBDOAC^=OBD^ (giả thiết)

+ OA=OBOA=OB (giả thiết)

+ ˆOO^ chung

⇒ΔOAC=ΔOBD⇒∆OAC=∆OBD (g.c.g)

⇒AC=BD⇒AC=BD (22 cạnh tương ứng).

Bài 37 trang 123 SGK Toán 7 tập 1.

Đề bàiTrên mỗi hình 101, 102, 103 có tam giác nào bằng nhau? Vì sao?

Phương pháp giải - Xem chi tiết

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Lời giải chi tiết

Tính các góc còn lại trên mỗi hình trên ta được:

Áp dụng định lí tổng ba góc của một tam giác ta có:

ˆA=1800−ˆB−ˆC=1800−800−400=600ˆH=1800−ˆG−ˆI=1800−300−800=700ˆE=1800−ˆD−ˆF=1800−800−600=400ˆL=1800−ˆK−ˆM=1800−800−300=700ˆQNR=1800−ˆNRQ−ˆRQN=1800−400−600=800ˆNRP=1800−ˆRPN−ˆPNR=1800−600−400=800A^=1800−B^−C^=1800−800−400=600H^=1800−G^−I^=1800−300−800=700E^=1800−D^−F^=1800−800−600=400L^=1800−K^−M^=1800−800−300=700QNR^=1800−NRQ^−RQN^=1800−400−600=800NRP^=1800−RPN^−PNR^=1800−600−400=800

- Xét ΔABC∆ABC và ΔFDE∆FDE (Hình 101)

+) ˆB=ˆD=80oB^=D^=80o

+) BC=DE=3BC=DE=3

+) ˆC=ˆE=40oC^=E^=40o

⇒ΔABC=ΔFDE⇒∆ABC=∆FDE (g.c.g)

- Xét ΔNQR∆NQR và ΔRPN∆RPN (Hình 103)

+) ˆQNR=ˆNRP=800QNR^=NRP^=800

+) NRNR là cạnh chung.

+) ˆNRQ=ˆRNP=400NRQ^=RNP^=400

Suy ra ΔNQR=ΔRPN∆NQR=∆RPN (g.c.g)

- Xét ΔHIGΔHIG và ΔLKMΔLKM (Hình 102)

+)GI=ML+)ˆG=ˆM+)ˆI=ˆK+)GI=ML+)G^=M^+)I^=K^

Ta có: ˆG,ˆIG^,I^ cùng kề với cạnh GIGI, còn ˆMM^ kề với cạnh MLML nhưng ˆKK^ không kề với cạnh MLML nên ΔHIGΔHIG không bằng ΔLKMΔLKM.

Bài 38 trang 124 SGK Toán 7 tập 1.

Đề bài: Trên hình 104104 ta có AB//CD,AC//BD.AB//CD,AC//BD. Hãy chứng minh rằng: AB=CD;AC=BD.AB=CD;AC=BD

Phương pháp giải - Xem chi tiết

Áp dụng:

- Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và góc kề của tam giác kia thì hai tam giác đó bằng nhau.

- Một đường thẳng cắt hai đường thẳng song song tạo ra cặp góc so le trong bằng nhau.

Lời giải chi tiết

Vẽ đoạn thẳng AD.AD.

Vì AB//CDAB//CD suy ra ˆA1=ˆD1A1^=D1^ (hai góc so le trong)

Vì AC//BDAC//BD suy ra ˆA2=ˆD2A2^=D2^ (hai góc so le trong)

Xét ΔADB∆ADB và ΔDAC∆DAC có:

+) ˆA1=ˆD1A1^=D1^ (chứng minh trên)

+) ADAD cạnh chung

+) ˆA2=ˆD2A2^=D2^ (chứng minh trên)

⇒ΔADB=ΔDAC⇒∆ADB=∆DAC (g.c .g)

⇒AB=CD,BD=AC⇒AB=CD,BD=AC (các cạnh tương ứng)

Bài 39 trang 124 SGK Toán 7 tập 1.

Đề bàiTrên mỗi hình 105, 106, 107, 108 các tam giác vuông nào bằng nhau? Vì sao?

Phương pháp giải - Xem chi tiết

- Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

- Nếu hai cạnh và một góc xen giữa của tam giác này bằng hai cạnh và một góc xen giữa của tam giác vuông kia thì hai tam giác đó bằng nhau.

- Hệ quả: Nếu cạnh huyền và góc nhọn của tam giác vuông nay bằng cạnh huyền, góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Lời giải chi tiết

Hình 105

Xét ΔABH và ΔACH có:

+) BH=CH (giả thiết)

+) ˆAHB=ˆAHC=90o

+) AH cạnh chung

⇒ΔABH=ΔACH (c.g.c)

Hình 106

Xét ΔDKE và ΔDKF có:

+) ˆEDK=ˆFDK (giả thiết)

+) DK cạnh chung

+) ˆDKE=ˆDKF=90o

⇒ΔDKE=ΔDKF (g.c.g)

Hình 107

Áp dụng định lí tổng ba góc của một tam giác vào ΔABD và ΔACD ta có:

ˆABD+ˆBDA+ˆDAB=1800(1)ˆACD+ˆCDA+ˆDAC=1800(2)

Mặt khác ta có:

ˆDAB=ˆDAC(giảthiết)(3)ˆABD=ˆACD=900(4)

Từ (1), (2), (3), (4) suy ra ˆBDA=ˆCDA

Xét ΔABD và ΔACD có:

+) ˆDAB=ˆDAC(giảthiết)

+) AD cạnh chung

+) ˆBDA=ˆCDA (chứng minh trên)

⇒ΔABD=ΔACD (g.c.g)

Cách khác:

Xét ΔABD vuông tại B và ΔACD vuông tại C, ta có:

+) ˆDAB=ˆDAC(giảthiết)

+) AD cạnh chung

⇒ΔABD=ΔACD (cạnh huyền-góc nhọn)

Hình 108

Áp dụng định lí tổng ba góc của một tam giác vào ΔABD và ΔACD ta có:

ˆABD+ˆBDA+ˆDAB=1800(5)ˆACD+ˆCDA+ˆDAC=1800(6)

Mặt khác ta có:

ˆDAB=ˆDAC(giảthiết)(7)ˆABD=ˆACD=900(8)

Từ (5), (6), (7), (8) suy ra ˆBDA=ˆCDA

Xét ΔABD và ΔACD có:

+) ˆDAB=ˆDAC(giảthiết)

+) AD cạnh chung

+) ˆBDA=ˆCDA (chứng minh trên)

⇒ΔABD=ΔACD (g.c.g)

⇒BD=CD (hai cạnh tương ứng )

⇒AB=AC (hai cạnh tương ứng )

(Hoặc ta có thể chứng minh ΔABD=ΔACD giống như cách khác của hình 107)

Xét ΔDBE và ΔDCH

+) ˆEBD=ˆHCD=900

+) BD=CD (chứng minh trên)

+) ˆBDE=ˆCDH (đối đỉnh)

⇒ΔDBE=ΔDCH (g.c.g)

⇒DE=DH (hai cạnh tương ứng)

Xét ΔABH và ΔACE

+) ˆA chung

+) AB=AC (chứng minh trên)

+) ˆABH=ˆACE=900

⇒ΔABH=ΔACE (g.c.g)

⇒AH=AE (hai cạnh tương ứng)

Xét ΔADE và ΔADH

+) Cạnh AD chung

+) AE=AH (chứng minh trên)

+) DE=DH (chứng minh trên)

⇒ΔADE=ΔADH (c.c.c)

Bài 41 trang 124 SGK Toán 7 tập 1.

Đề bài: Cho tam giác ABCABC, các tia phân giác của các góc BB và CC cắt nhau ở II. Vẽ IDID ⊥⊥ ABAB (D∈ABD∈AB), IEIE ⊥⊥ BCBC (E∈BCE∈BC ), IF⊥ACIF⊥AC (F∈ACF∈AC)

CMR: ID=IE=IFID=IE=IF.

Phương pháp giải - Xem chi tiết

Áp dụng hệ quả: Nếu cạnh huyền và góc nhọn của tam giác vuông nay bằng cạnh huyền, góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

- Lời giải chi tiết

Tam giác BIDBID vuông tại DD.

Tam giác BIEBIE vuông tại EE.

Xét hai tam giác vuông BIDBID và BIEBIE có:

+) BIBI là cạnh chung

+) ˆB1=ˆB2B1^=B2^ ( vì BIBI là phân giác góc BB)

⇒ΔBID=ΔBIE⇒∆BID=∆BIE (cạnh huyền - góc nhọn)

⇒ID=IE⇒ID=IE (hai cạnh tương ứng) (1)

Tam giác CIFCIF vuông tại FF.

Tam giác CIECIE vuông tại EE.

Xét hai tam giác vuông CIFCIF và CIECIE có:

+) CICI cạnh chung

+) ˆC1=ˆC2C1^=C2^ ( vì CICI là phân giác góc CC)

⇒ΔCIF=ΔCIE⇒∆CIF=∆CIE (cạnh huyền - góc nhọn).

⇒IE=IF⇒IE=IF (hai cạnh tương ứng) (2)

Từ (1) và (2) suy ra: ID=IE=IFID=IE=IF.

Bài 43 trang 125 SGK Toán 7 tập 1.

Đề bài: Cho góc xOyxOy khác góc bẹt. Lấy các điểm A,BA,B thuộc tia OxOx sao cho OA<OB.OA<OB.

Lấy các điểm C,DC,D thuộc tia OyOy sao cho OC=OA,OD=OB.OC=OA,OD=OB. Gọi EE là giao điểm của ADAD và BC.BC.

Chứng minh rằng:

a) AD=BCAD=BC;

b) ΔEAB=ΔECD∆EAB=∆ECD;

c ) OEOE là tia phân giác của góc xOy.xOy.

Phương pháp giải - Xem chi tiết

a) Nếu hai cạnh và một góc xen giữa của tam giác này bằng hai cạnh và một góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

b) Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

c) Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

Lời giải chi tiết

a) Xét ΔOAD∆OAD và ΔOCB∆OCB có:

+) OA=OCOA=OC (giả thiết)

+) ˆOO^ chung

+) OD=OBOD=OB (giả thiết)

⇒ΔOAD=ΔOCB⇒∆OAD=∆OCB (c.g.c)

⇒AD=BC⇒AD=BC (hai cạnh tương ứng).

b) ΔOAD=ΔOCB∆OAD=∆OCB (chứng minh câu a)

⇒ˆD1=ˆB1⇒D1^=B1^; ˆA2=ˆC2A2^=C2^ (các góc tương ứng)

Mặt khác:

ˆA1+ˆA2=1800A1^+A2^=1800 (Hai góc kề bù)

ˆC1+ˆC2=1800C1^+C2^=1800 (Hai góc kề bù)

Do đó ˆA1+ˆA2=ˆC1+ˆC2A1^+A2^=C1^+C2^

Mà ˆA2=ˆC2A2^=C2^ nên ˆA1=ˆC1A1^=C1^

AB=OB−OAAB=OB−OA (1)

CD=OD−OCCD=OD−OC (2)

OC=OA,OD=OBOC=OA,OD=OB (giả thiết) (3)

Từ (1), (2) và (3) suy ra AB=CD.AB=CD.

Xét ΔEAB∆EAB và ΔECD∆ECD có:

+) ˆA1=ˆC1A1^=C1^ (chứng minh trên)

+) AB=CDAB=CD (chứng minh trên)

+) ˆB1=ˆD1B1^=D1^ (chứng minh trên)

⇒ΔEAB=ΔECD⇒∆EAB=∆ECD (g.c.g)

c) ΔEAB=ΔECD∆EAB=∆ECD (chứng minh câu b)

⇒EA=EC⇒EA=EC (hai cạnh tương ứng).

Xét ΔOAE∆OAE và ΔOCE∆OCE có:

+) OA=OCOA=OC (giả thiết)

+) EA=ECEA=EC (chứng minh trên)

+) OEOE cạnh chung

⇒ΔOAE=ΔOCE⇒∆OAE=∆OCE (c .c.c)

⇒ˆAOE=ˆCOE⇒AOE^=COE^ (hai góc tương ứng)

Vậy OEOE là tia phân giác của góc xOy.

Bài 44 trang 125 SGK Toán 7 tập 1.

Đề bàiCho tam giác ABCABC có ˆB=ˆCB^=C^. Tia phân giác của góc AA cắt BCBC tại D.D.

Chứng minh rằng.

a) ΔADB=ΔADC.∆ADB=∆ADC.

b) AB=AC.AB=AC.

Phương pháp giải - Xem chi tiết

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Lời giải chi tiết

a) Áp dụng định lí tổng các góc của một tam giác vào ΔABDΔABD và ΔACDΔACD ta có:

ˆB+ˆA1+ˆD1=180o(1)ˆC+ˆA2+ˆD2=180o(2)B^+A1^+D1^=180o(1)C^+A2^+D2^=180o(2)

ˆB=ˆCB^=C^ (giả thiết) (3)

ˆA1=ˆA2A1^=A2^ (vì ADAD là tia phân giác góc AA) (4)

Từ (1), (2), (3), (4) suy ra ˆD1=ˆD2D1^=D2^

Xét ΔADB∆ADB và ΔADC∆ADC có:

+) ˆA1=ˆA2A1^=A2^ (chứng minh trên)

+) ADAD cạnh chung

+) ˆD1=ˆD2D1^=D2^ (chứng minh trên)

⇒ΔADB=ΔADC⇒∆ADB=∆ADC (g.c.g)

b) ΔADB=ΔADC∆ADB=∆ADC (chứng minh câu a)

⇒AB=AC⇒AB=AC (hai cạnh tương ứng).

Trường hợp bằng nhau thứ ba của tam giác Góc Cạnh Góc toán lớp 7 bài 5 giải bài tập được biên soạn bám sát chương trình SGK mới môn toán lớp 7, được Soanbaitap.com tổng hợp và đăng trong chuyên mục giải toán 7 giúp các em tiện tham khảo đề học tốt môn toán 7. Nếu thấy hay hãy chia sẻ và comment để nhiều bạn khác cùng học tập.

#soanbaitap

#soanbaitap #giải bài tập #Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc – cạnh – góc(g.c.g)

0 notes