#geometrymatters

[geometrymatters]

A polynon is a conceptual geometric entity of which vertices are non-events and its edges holograms.

A polynon contains all the holograms of that which can be projected as a polytope, showing how consciousness can be fundamental.

In the Hexanon, shown above, the Observer O(n) is in superposition with the phenomenal p+, epiphenomenal p-, negative noumena n- and noumenal vertices n+ of the hexanon as a function for self-reflection of consciousness C.

The polynon is built on the lens mechanism of the wavefunction: each layer of the noumenal lens is a wavefunction in itself, providing mechanism for the observer as function of noumenal reflection.

The paper is now available on philpapers, as well: https://philarchive.org/rec/ROITPA

[narinna]

coexistants 

fineliner on postcard | nov 2018

[polymorphousculturevulture]

Physics imagined by Midjourney. Imploding into a black hole

via geometrymatters

[gdbot]

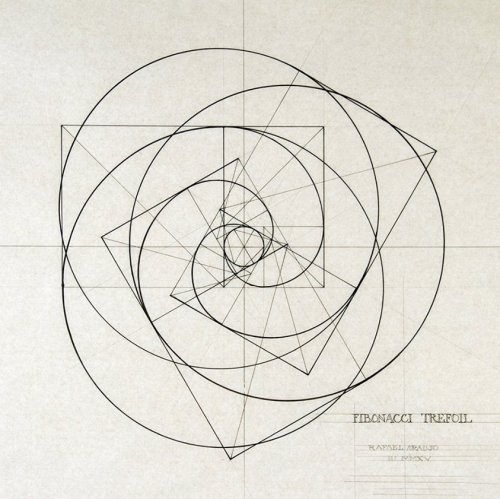
geometrymatters: Fibonacci trefoil© Rafael Araujo https://ift.tt/2FguxaQ

[wowgreat]

Linden Gledhill

source: http://www.lindengledhill.com/

via  parametricworld    reblogged    geometrymatters  

[pammorgan77]

11 notes

Geometrymatters

[wallpaperengine]

geometrymatters: Ernst Chladni Klangfiguren, 1787 One of... wallpaper engine

[geometrymatters]

FRACTAL TREES – BASIC L-SYSTEM- EXAMPLE 9.4

Fractal processes have practical applications in creating 3D vegetation for models using plant generators like Xfrog and Laubwerk. These tools utilize mathematical and botanical principles to produce realistic plants. A key algorithm family used in these generators is Lindenmayer systems (L-systems), which generate complex structures through iterative production rules. Understanding L-systems can enhance the use of these tools or inspire custom design applications. The simplest L-system involves drawing lines from a point at variable angles and reducing line length proportionally with each generation, creating intricate plant-like structures.

L-systems, such as those created with Grasshopper and Anemone, start with a set point and draw lines at defined angles and lengths, doubling the number of lines with each generation. Varying angles and lengths produces diverse structures. The book "The Algorithmic Beauty of Plants" is a valuable resource for understanding these systems. By creating simple tree generators with random seeds, users can design non-repetitive, impressionistic vegetation models for various applications.

Using tools like Rabbit by Morphocode in Grasshopper facilitates experimenting with L-systems. By encoding production rules into loops, users can generate structures that mimic natural plant growth. The iterative nature of L-systems, with each generation building upon the last, allows for the creation of detailed and varied vegetation models, enhancing both rendering quality and the representation of vegetation massing in digital environments.

[geometrymatters]

The Polynon: A Geometry of Consciousness

How Consciousness is a fundamental substance and everything else, including the Observer, is it's function of self-reflection within a complex construct and hologram.

Introducing the polynon:

A polynon is a conceptual geometric entity, a polytope of which vertices are non-events and its edges, holograms. A polynon contains all the holograms of that which can be projected as a polytope. From tetranon to dodecanon, and special cases such as dinon and nullanon.

The epistemological foundation of the polynon is a non-event, hence multi (poly) non-events. The ontological foundation is a noumenon, both in its negative and its positive aspect.

Collapsing the noumenal realm into a single dimension results in the conceptual noumenal monad, where the perceptual border is equal to the infinity of noumenal possibilities, as well as the phenomenal something.

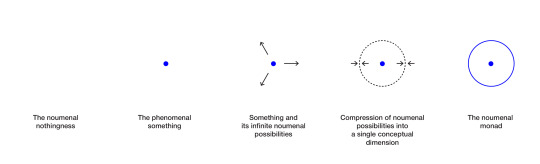
Or, as "a cercle with the centre everywhere and circumference nowhere". A monadic embodiment of the thing and the non-thing, the visual expression of the substance of consciousness.

The neutral monistic approach enfolds the ancient knowledge of the self, and the contemporary science of consciousness, from a Vedantic self reflected in Indra's net, to a multi-dimensional implicate and explicate construct of Bohmian orders.

Also encapsulated in the formulation f(f)=f, akin to an Ouroboros mathematical formulation symbolizing a form of autopoiesis or self-production ad infinitum, a self-referential Fichtean process where the self (I) is both the creator and subject of its reality.

The eternal aspect of consciousness, a timeless monadic essence, is described as the perceptual continuum of f=0, signifying pure, timeless potential.

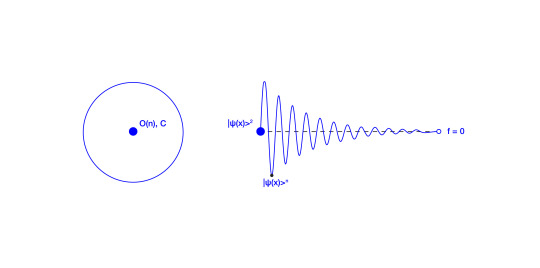
"Eternity isn’t some later time. Eternity isn’t even a long time. Eternity has nothing to do with time. Eternity is that dimension of here and now that all thinking in temporal terms cuts off." - J. Campbell

The wavefunction is defined here as a layer of the noumenal monad, a transition between epistemological and ontological, given by the limits of the Observer's senses and perception.

In this context, |ψ(x)>*n, with n not strictly equal to 2, transcends its conventional mathematical role within Hilbert space and diverges from standard quantum mechanics, suggesting that different values of n represent distinct dimensions or layers of noumenal collapse.

Each wavefunction is a layer of the noumenal lens, of which border is (n+), or consciousness C; it’s contents are negative noumena (n-) and it’s holographic centre “collapsed” onto a phenomenal Observer O(n) as function of noumenal self-reflection of consciousness.

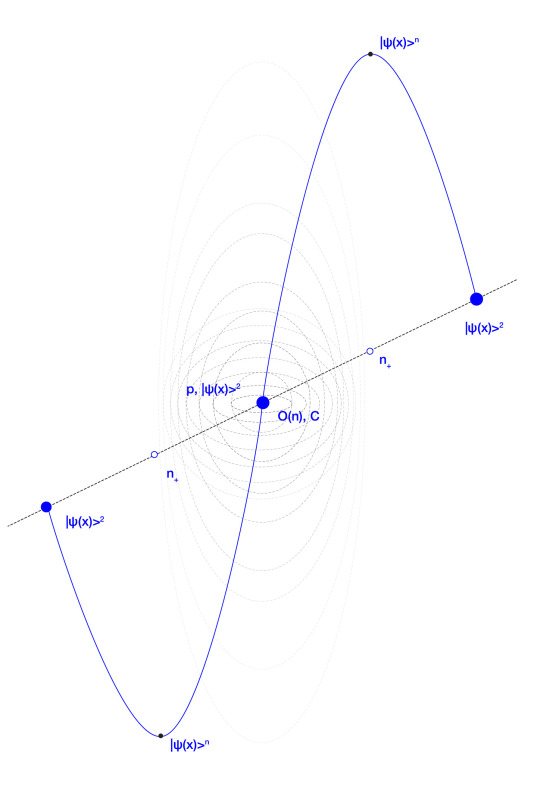
Furthermore, the Observer is envisioned as a holographic projection sitting at the core of the noumenal lens, emerging from the focus and diffraction of noumenal probabilities within the noumenal lens.

The perceptual border of positive noumena (n+) reflects and focuses noumenal probabilities (n-) into the hologram of the Observer O(n).

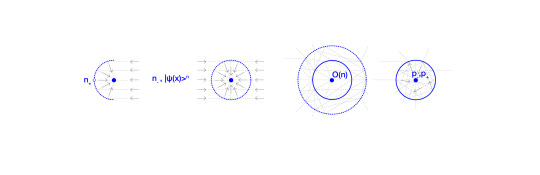
A rotation of noumenal lens reveals the noumenal essence (n+), hidden under the superposition of the noumenal lenses (n-) and the hologram of the Observer O(n).

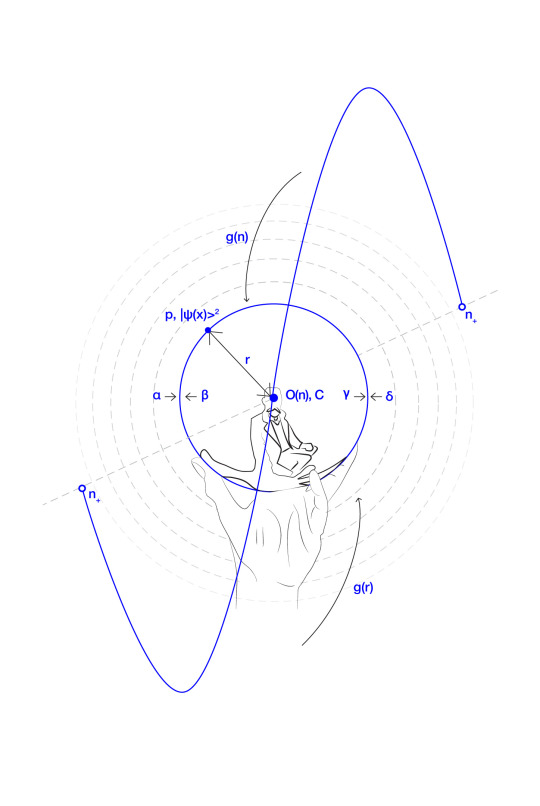
The observer’s perceptual focus, directed through Cognitive Gravity G and visualized with noumenal g(n) and cognitive gradients g(r), refracts the essence of Consciousness, transforming noumenal vertices into discernible edges like light through a prism.

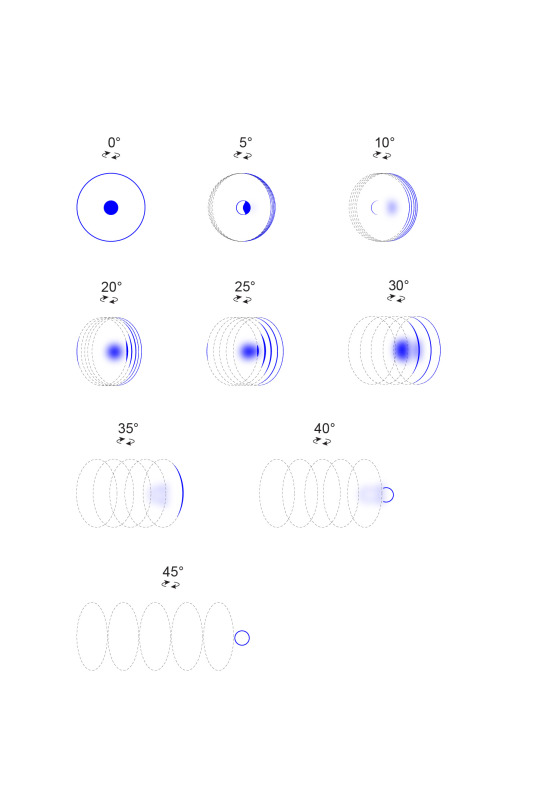
As the number of noumenal collapses increases, the complexity and breadth of the observer’s perceptual dimension diminishes, resulting in a progressive refinement and narrowing of perceptual prowess of the observable construct.

A cognitive threshold marks the evolution from a purely phenomenal observer to one with phantasiai and developed cognitive functions. This threshold varies according to the local conditions of the observer’s cognitive gradient and gravity and the overall noumenal function.

The hologram of a polynon enfolds within it the reflection of the noumenal substance, that both originates and reflects consciousness. It encapsulates the entirety of consciousness in each of its vertices and edges, as projections into a perceptual reality.

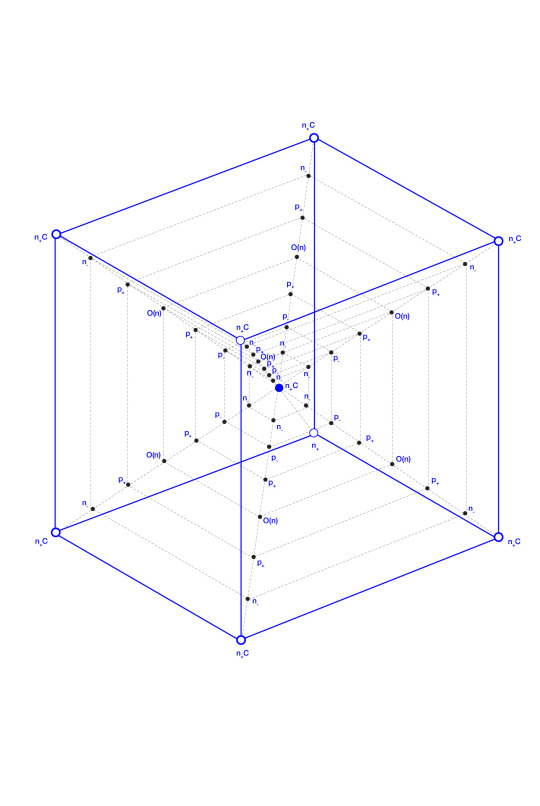
The concept of “consciousness nodes” describes (n+) zones between noumenal lenses (n−), revealed as vertices of the polynon, equal and identical in nature.

The Observer O(n) is in superposition with the phenomenal p+, epiphenomenal or phantasiai p-, negative noumena n- and noumenal vertices (and centre) n+ of the hexanon as a function for self-reflection of consciousness C.

The polynon is abstract and elusive, residing beyond human imagination yet within its grasp. No heavier than a fleeting idea, but far too heavy to be understood. A palindrome for language and thought, mirroring itself in perpetual paradox. Beginning the same way it ends.

From the "Polynon: A geometry of Consciousness", by Tib Roibu Read the paper here.

[geometrymatters]

The geometry of the Borromean Rings

Borromean rings are a captivating geometric structure composed of three interlinked rings. What makes them unique is their interdependency; if any one ring is removed, the entire structure collapses. This fascinating property, known as "Brunnian" linkage, means that no two rings are directly linked, yet all three are inseparable as a group. This intricate dance of unity and fragility offers a profound insight into the nature of interconnected systems, both in mathematics and beyond.

Borromean Rings and Mathematical Knots

Borromean rings also find a significant place in the study of mathematical knots, a field dedicated to understanding how loops and tangles can be organized and categorized. The intricate relationship among the rings provides a rich visual and conceptual tool for mathematicians. Knot theorists use these rings to explore properties of space, topology, and the ways in which complex systems can be both resilient and fragile. The visual representation of Borromean rings in knot theory not only aids in mathematical comprehension but also enhances our appreciation of their symmetrical beauty and profound interconnectedness.

Symbolism and Divinity in Borromean Rings

Throughout history, Borromean rings have been imbued with symbolic significance, often associated with divinity and the concept of the trinity. In Christianity, they serve as a powerful visual metaphor for the Holy Trinity – the Father, the Son, and the Holy Spirit – illustrating how three distinct entities can form a single, inseparable divine essence. This symbol is not confined to Christianity alone; many other cultures and religions see the interconnected rings as representations of unity, interdependence, and the intricate balance of the cosmos.

Borromean Rings as a Metaphor for Illusory Reality

Beyond their mathematical and symbolic significance, Borromean rings offer a profound metaphor for the nature of reality itself. They illustrate how interconnectedness can create the illusion of a solid, stable structure. This resonates with philosophical and spiritual notions that reality, as perceived, is a complex web of interdependent elements, each contributing to an overarching illusion of solidity and permanence. In this way, the Borromean rings challenge us to reconsider the nature of existence and the interconnectedness of all things.

[geometrymatters]

The Noumenal Monad

Within the Polynon framework, nothingness is an undifferentiated cognitive space that precedes geometry and structure. It exists as a pre-geometric source, housing the unformed essence of all phenomena from which spacetime, and all its manifestations, arise. Imbued with primal noumenal potential, it is denoted as the state where all possible realities are latent, waiting to be expressed into an observable world.

A circle whose center is everywhere and circumference is nowhere.

The monad is a geometric construct that acts as a universal grammar of existence, mapping how the boundless noumenal potential transitions into perceptual and phenomenal dimensions while retaining coherence across all levels of manifestation.

The centre being “everywhere” signifies the Monad’s omnipresence as the locus of all potential states, embedded in every point of reality. The circumference being “nowhere” reflects its boundless architecture, transcending the constraints of space, time, and materiality, integrating infinite possibilities within a singular, cohesive structure.

The compactification process begins with the noumenal everything compressing into a singular phenomenal something, reflecting a specific instance or manifestation. This phenomenal something is inherently equal to the noumenal everything because it retains the entirety of noumenal potential, either in its un-collapsed state of infinity or as a collapsed singular “ring” dimension, compacted into a single cognitive focal point.

The only attribute of a point is that it marks position. Take away this attribute and in the unposited point we have a symbol of pure Being, the abstract noumenon, that which underlies every mode of phenomenal manifestation, every form of existence. It is at once All and Nothing, at once Absolute Consciousness and Unconsciousness.

B.W. Betts, Geometric Psychology or the Science of Representation

Or, as Fichte envisioned it, the line symbolizes the progression of consciousness—linear and sequential—while the circle represents its completeness and self-enclosure, encompassing all its dimensions. Thus, both the noumenal everything and the phenomenal something are expressions of the same essence, differing only in their state of manifestation and representation.

Together, they define the Noumenal Monad as a meta-structure that bridges these states of being. It embodies the continuum between the actual and the potential, compacting the infinite diversity of noumenal states into a singular conceptual dimension. This process is geometrically encoded, offering a scaffold for understanding how existence unfolds from an infinite noumenal source into the finite, perceptual realm, while remaining irreducible to either.

Continue reading

[geometrymatters]

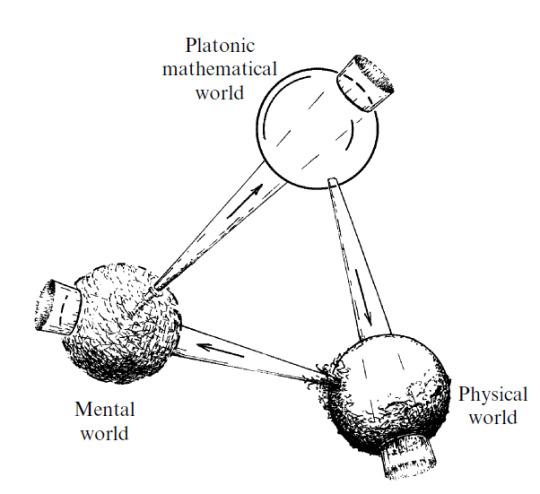
Sir Roger Penrose

To me, the world of perfect forms is primary (as was Plato’s own belief) — its existence being almost a logical necessity — and both the other two worlds are its shadows.

Sir Roger Penrose, born on August 8, 1931, in Colchester, Essex, England, is a luminary in the realm of mathematical physics. His journey began with a Ph.D. in algebraic geometry from the University of Cambridge in 1957, and his career has spanned numerous prestigious posts at universities in both England and the United States. His work in the 1960s on the fundamental features of black holes, celestial bodies of such immense gravity that nothing, not even light, can escape, earned him the 2020 Nobel Prize for Physics.

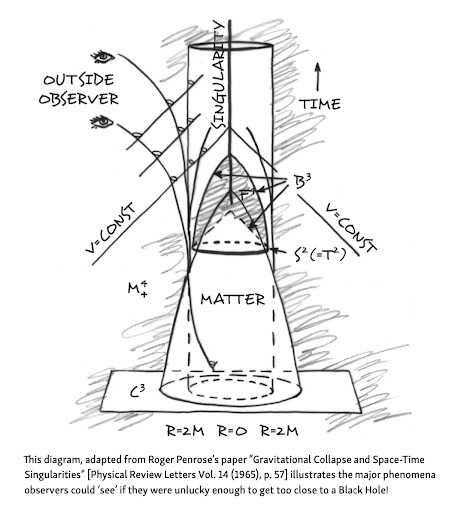
Penrose’s work on black holes, in collaboration with Stephen Hawking, led to the ground-breaking discovery that all matter within a black hole collapses to a singularity, a point in space where mass is compressed to infinite density and zero volume. This revelation illuminated our understanding of these enigmatic cosmic entities.

His work did not stop at the theoretical; he also developed a method of mapping the regions of space-time surrounding a black hole, known as a Penrose diagram. This tool allows us to visualize the effects of gravitation upon an entity approaching a black hole, providing a window into the heart of these celestial mysteries.

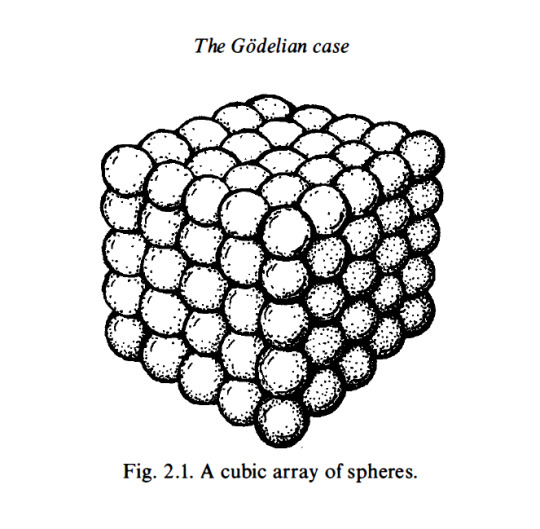
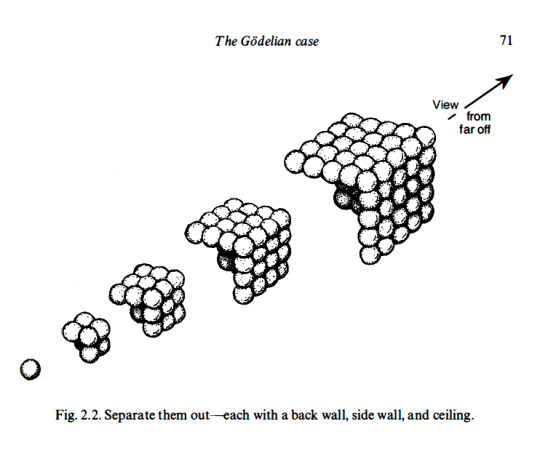
Within Penrose’s chapter, “The Godelian Case” (from “The Road to Reality”) the profound implications of Kurt Gödel’s incompleteness theorems are examined in relation to the connection between mathematics and geometry. Specifically, Penrose’s attention centers on the model depicted in Figure 2.1, which portrays a cubic array of spheres. Through this visual representation, Penrose explores the intricate relationship between geometry and mathematical understanding.

By introducing the model of a cubic array of spheres, Penrose highlights the fundamental role of spatial arrangements in mathematical cognition. This geometrical structure serves as a metaphorical embodiment of mathematical concepts, illustrating how spatial configurations can stimulate cognitive processes and facilitate intuitive comprehension of mathematical truths. The intricate interplay between the arrangement of spheres within the model and the underlying principles of mathematics encourages contemplation on the deep-rooted connections between geometry, spatial reasoning, and abstract mathematical thought.

Penrose’s utilization of the cubic array of spheres underscores his broader philosophical framework, which challenges reductionist accounts of human cognition that rely solely on formal systems or computational models. Through this geometrical representation, he advocates for a more holistic understanding of mathematical insight, one that recognizes the essential role of geometric intuition in shaping human understanding.

By looking at the intricate connection between mathematics and geometry, Penrose prompts a re-evaluation of the mechanistic view of cognition, emphasizing the need to incorporate spatial reasoning and intuitive geometrical understanding into comprehensive models of human thought.

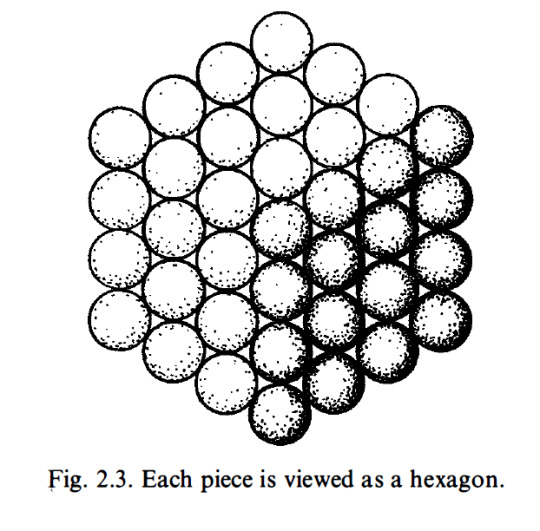
(E) Find a sum of successive hexagonal numbers, starting from 1 , that is not a cube. I am going to try to convince you that this computation will indeed continue for ever without stopping. First of all, a cube is called a cube because it is a number that can be represented as a cubic array of points as depicted in Fig. 2. 1 . I want you to try to think of such an array as built up successively, starting at one corner and then adding a succession of three-faced arrangements each consisting of a back wall, side wall, and ceiling, as depicted in Fig. 2.2. Now view this three-faced arrangement from a long way out, along the direction of the corner common to all three faces. What do we see? A hexagon as in Fig. 2.3. The marks that constitute these hexagons, successively increasing in size, when taken together, correspond to the marks that constitute the entire cube. This, then, establishes the fact that adding together successive hexagonal numbers, starting with 1 , will always give a cube. Accordingly, we have indeed ascertained that (E) will never stop.

Penrose’s work is characterized by a profound appreciation for geometry. His father, a biologist with a passion for mathematics, introduced him to the beauty of geometric shapes and patterns at a young age. This early exposure to geometry shaped Penrose’s unique approach to scientific problems, leading him to develop new mathematical notations and diagrams that have become indispensable tools in the field. His creation of the Penrose tiling, a method of covering a plane with a set of shapes without using a repeating pattern, is a testament to his innovative thinking and his deep understanding of geometric principles.

His fascination with geometry extended beyond the realm of mathematics and into the world of art. He was deeply influenced by the work of Dutch artist M.C. Escher, whose intricate drawings of impossible structures and infinite patterns captivated Penrose’s imagination. This encounter with Escher’s art led Penrose to explore the interplay between geometry and art, culminating in his own contributions to the field of mathematical art. His work in this area, like his scientific research, is characterized by a deep appreciation for the beauty and complexity of geometric forms.

In geometric cognition, Penrose’s work has the potential to make significant contributions. His unique perspective on the role of geometry in understanding the physical world, the mind, and even art, offers a fresh approach to this emerging field. His belief in the power of geometric thinking, as evidenced by his own ground-breaking work, suggests that a geometric approach to cognition could yield valuable insights into the nature of thought and consciousness.

Objective mathematical notions must be thought of as timeless entities and are not to be regarded as being conjured into existence at the moment that they are first humanly perceived.

I argue that the phenomenon of consciousness cannot be accommodated within the framework of present-day physical theory.

His Orch OR theory posits that consciousness arises from quantum computations within the brain’s neurons. This bold hypothesis, bridging the gap between the physical and the mental, has sparked intense debate and research in the scientific community.

Penrose’s work on twistor theory, a geometric framework that seeks to unify quantum mechanics and general relativity, is a testament to his belief in the primacy of geometric structures. This theory, which represents particles and fields in a way that emphasizes their geometric and topological properties, can be seen as a metaphor for his views on cognition. Just as twistor theory seeks to represent complex physical phenomena in terms of simpler geometric structures, Penrose suggests that human cognition may also be understood in terms of fundamental geometric and topological structures.

This perspective has significant implications for the field of cognitive geometry, which studies how humans and other animals understand and navigate the geometric properties of their environment. If Penrose’s ideas are correct, our ability to understand and manipulate geometric structures may be a fundamental aspect of consciousness, rooted in the quantum geometry of the brain itself.

The final conclusion of all this is rather alarming. For it suggests that we must seek a non-computable physical theory that reaches beyond every computable level of oracle machines (and perhaps beyond). — Roger Penrose, Shadows of the Mind: A Search for the Missing Science of Consciousness

[geometrymatters]

Expansion of the universe represented as nested Riemann spheres of Planck impedance

Hierarchical arrangement of n-multiples of Schwarzschild radius as illustration of expansion of the universe. Like "suds in the kitchen sink", mass accretion and contraction result in formation of bubble voids apparent in the universe at large.

[geometrymatters]

"Consciousness is the only fact that we can study directly, since all other objects of knowledge must be perceived through consciousness." - B.W. Betts

[geometrymatters]

Zoom In Atom Or Unknown Physics Of Short Distances

Previous work of Vladimir Kalitvianski, showing how that the nucleus within an atom doesn't remain stationary but instead moves around the atomic center of inertia, creating what he describes as "positive charge clouds." These clouds are analogous to the more familiar negative electron clouds but exist much closer to the nucleus. This finding challenges the traditional view of atomic structure, showing that the nucleus is quantum-mechanically smeared, depending on the electron's configuration.

Kalitvianski's work highlights that the nucleus is not a point-like object but has a smeared distribution influenced by the electron orbits. The larger the electron orbit, the larger the positive charge cloud, which is counterintuitive. This smeared charge distribution impacts how we understand elastic scattering processes at short distances, where the nucleus behaves differently than previously thought. The form factors derived in his research describe these positive charge distributions and their implications for elastic and inelastic scattering processes.

The implications of this research are profound for both atomic physics and quantum electrodynamics (QED). It suggests that traditional models, which treat the nucleus as a point charge, need to be revised to account for this smearing effect.