#hilbertposting

[s-lycopersicum]

Have you ever seen polygonal approximations of the Hilbert curve?

Now you have!

[mathsuggestions]

Reaxiomatize Euclidean geometry.

[heycerulean]

BIRD 359 be like: alexander hilBIRD elias selBIRD dimitri VULTUREdin anyway fanart goes crazy hilbert as a Himalayan Vulture @officer-achilles this was half inspired by your hilbertposting (/pos) so i'm tagging you :)

[s-lycopersicum]

Cursed to be the lone appreciator of the true beauty Hilbert curve, which is not in the rendered curves themselves, but on the intricate transformation of a number into a two-dimensional coordinate, and back again. The equilibrium in the numerical bases. The symmetry in the state transitions. Truly...

(↑ Lost in abstract delusions, please ignore.)

[s-lycopersicum]

I fixed up my script so I could generate these more easily, so here the same polygonal approximation of the Hilbert curve as before, with two extra steps to really hammer in the space-filling nature of it:

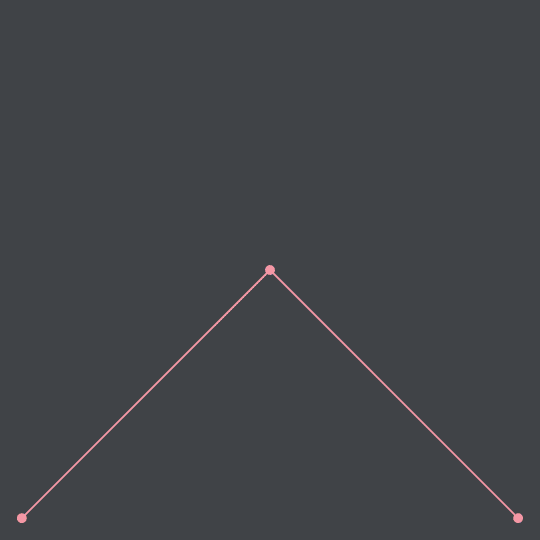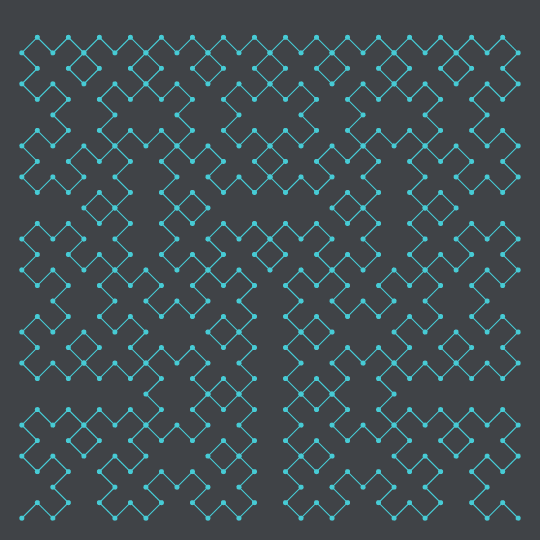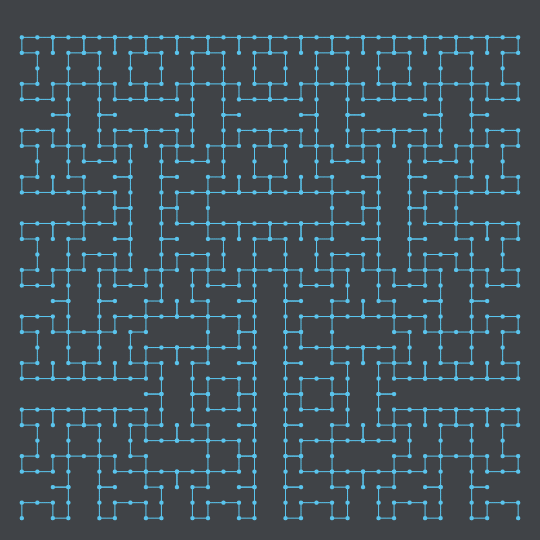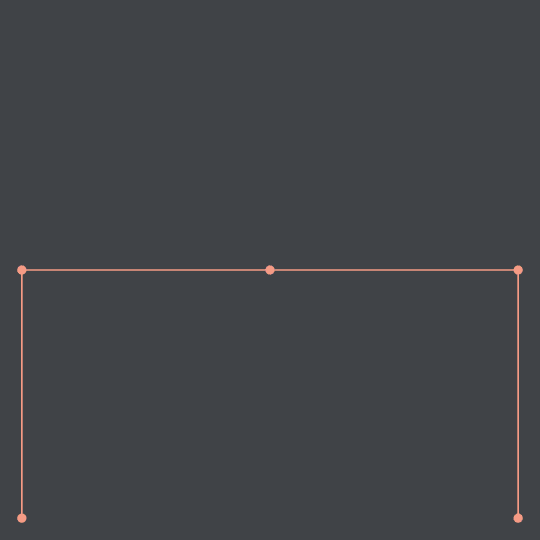
And this one here is the Moore variant of the Hilbert curve (also referred to as the Moore curve):

In the Moore variant, the curve starts and ends on the bottom-center point, providing a continuous path through the plane.

[s-lycopersicum]

Still in a bit of a hilbertposting mood, so I'm gonna ramble a bit on this!

So, the Hilbert curve! If you've heard about it, you have probably seen it depicted like this:

These are not the curve itself, but the steps to construct the curve. You divide a plane into quadrants and connect them in that order, them divide each of those into further quadrants, connecting them as well, and so on... into infinity. That leaves you with an 1D line that weaves through the entire 2D plane (see this video by 3Blue1Brown for a much better explanation).

In short, it is an useful construct to map line coordinates into plane coordinates, and back again. And even though these construction steps are not the Hilbert curve, they can still be used as discrete approximations, specially in computer science.

But! Those are not good visual approximations of the Hilbert curve, mainly because the points move. For example, let's say you have to draw a circle with a polygon, but you can only use a fixed number of vertices. It might end up looking like this:

The vertices are placed where the circle would be, evenly spaced from one another, and then connected with edges. And the more vertices you have, the more accurate the polygon looks. Crucially, the vertices are in the right place, it's the edges that are inaccurate.

If we apply the same principle to the Hilbert curve, this is what we end up with:

In some places, you may even see shapes like this incorrectly labeled as a variant of the Hilbert curve, when they are in fact THE curve itself. The vertices are in the right place, and the more of them you have, the more accurate the curve looks.

I guess the immediate difference being that, with a normal curve, as you add vertices to the approximation, the polygon appears to calm down as it settles to its place. But with the Hilbert curve (and all space-filling curves, I'd say), the approximation gets wilder, as it eventually has to fill the entire screen.

Have you ever seen polygonal approximations of the Hilbert curve?

Now you have!

[s-lycopersicum]

So, let's say you have a one-dimensional coordinate—which is just a number, really—between 0.0 and 1.0. Technically, this range should be exclusive, but 1.0 is just 0.9999... anyway, a number, right. Let's see... How about 0.786?

Now, we put that number (call it H) in base 4, Wolfram can help with that. It's likely we'll end up with a repeating decimal (as changing bases will often do) which isn't a problem, but I don't have all day, so let's say H = 0.3021₄. Note the base 4, alright? Alright.

Now here's our magic formula:

This is something like a state machine, but I used colors instead of arrows. The numbers inside are mapping between a base 4 number to a base 2 pair. That's how we'll get our two-dimensional coordinate. Notice how one base 4 will "split" into two base 2, isn't that beautiful?

To use it, we start in the red state, and "input" the first digit of H. The mapping then gives us the first digits of X and Y, and the next state to use. We then repeat until we're done! On keep going in towards infinity.

Here, see:

RED, H=0.3021₄ → X=0.1___₂, Y = 0.0___₂, PURPLE

The first digit of H is 3, and starting on red, that tells us that the first digit for X is 1, and for Y is 0. Then, we continue to purple. Easy, right? Now, the rest looks like this:

PURPLE, H=0.3021₄ → X=0.11__₂, Y = 0.01__₂, TEAL TEAL, H=0.3021₄ → X=0.110_₂, Y = 0.010_₂, TEAL TEAL, H=0.3021₄ → X=0.1101₂, Y = 0.0100₂, TEAL

And that's the gist of it! Now all we have to do is convert X and Y from base 2 to base 10 and we're done. Though a small caveat here is that four digits isn't nearly precise enough, y'know?

But that's it, real easy! A few extra points:

To map from two dimensions to one, you just run it backwards.

If you put it all in an actual state diagram, it looks really pretty, but a bit less readable.

The mappings in each state are derived from the curves above them. If you mirror those curves, you get a different set of states that can still be used the same way! Also, you need them for some other Hilbert curve variants.

Though I love the base 4/base 2 balance, the whole thing can be done in base 2, which means with a bit of work you can make a fixed-precision Hilbert curve mapping circuit!

Cursed to be the lone appreciator of the true beauty Hilbert curve, which is not in the rendered curves themselves, but on the intricate transformation of a number into a two-dimensional coordinate, and back again. The equilibrium in the numerical bases. The symmetry in the state transitions. Truly...

(↑ Lost in abstract delusions, please ignore.)