#quantumerrorcorrection

[govindhtech]

Quobly And Inria to Advance Silicon-Based Quantum Computing

Quobly, Inria

Quobly and Inria collaborate to scale and create a quantum sector.

The French national institute for digital science and technology, Inria, and quantum microelectronics leader Quobly have formed a strategic relationship. This alliance combines hardware engineering and software knowledge to develop a sovereign value chain and link silicon-based quantum technology with cutting-edge control software. Quobly is adding low-level software layers from embedded, industrial, and operating systems to its research and development to produce a fully integrated, fault-tolerant, and scalable quantum computing architecture. This collaboration was agreed upon at VivaTech 2025.

Large-scale quantum computing software development structure

Quobly and Inria are developing middleware, the low-level software layer that connects physical qubits and quantum algorithms.

Their combined experience aims to produce a logically structured quantum computing stack with software and hardware to handle scaling up.

The partnership will focus on co-designing silicon-based qubit-specific middleware and robust quantum error correction techniques.

This method aims to enable practical applications in chemistry, materials science, pharmaceutical innovation, optimisation, and complex systems models.

Promoting sovereign solutions

This alliance connects start-ups, government research labs, and industry participants behind national and European quantum innovation projects, strengthening the ecosystem.

They participate in CEA-Inria's national Q-Loop effort, funded by France 2030. The program began in September 2024.

France and Europe want to lead quantum computing, hence the Q-Loop initiative develops error correction methods on French hardware platforms.

White papers and coordinated initiatives indicate the alliance's commitment to Europe's strategic thinking.

Partnership with controlled industrialisation strategy

This project follows Quobly's industrial plan, which called for OVHcloud's June 2025 deployment of a “perfect” quantum emulator.

This emulator allows Quobly to test silicon qubit algorithms before scaling up its next quantum computer, a turning point in its software suite.

Due to this expansion, Quobly has expanded its software engineering teams to synchronise software development, hardware limits, and industrial goals.

This partnership with Inria is a crucial milestone in their objective to create integrated quantum computing platforms where hardware and software are co-designed for scalability', said Quobly co-founder and CEO Maud Vinet. She noted that middleware R&D strengthens Quobly's industrial strategy and ability to provide fault-tolerant quantum solutions for industrial and scientific applications.

Inria Chairman and CEO Bruno Sportisse said the collaboration is part of the company's quantum industry investment in France. He noted that they are developing a sovereign quantum value chain that covers hardware and software to speed the development of reliable, high-performance quantum systems and increase Europe's competitiveness in this crucial industry.

Conclusion

The article describes a strategic partnership between Inria, France's digital science and technology institute, and quantum microelectronics pioneer Quobly. This partnership aims to construct a scalable, fully integrated quantum computing system using silicon qubits. They'll use silicon-specific middleware and error correction protocols to bridge physical qubits with quantum algorithms. Quobly's industrial roadmap, which includes a quantum emulator, and France's Q-Loop program are supported by the collaboration. This alliance aims to develop a sovereign quantum value chain in France to make it a leader.

[govindhtech]

Quantum State Tomography (QST) Importance, Benefits & future

Quantum State Tomography

QST is a key quantum information science method for reconstructing unknown quantum states from experimental measurements. Study a complicated, unseen thing's interactions with its environment from multiple angles to understand it.For quantum states, QST works similarly. QST measures an ensemble of identical quantum systems to reconstruct the original state as measuring a quantum system constantly changes its state. This reconstructed state is usually shown as a density matrix with all the quantum system's probabilistic information.

Quantum State Tomography Importance

For various reasons, QST is essential for quantum technology development:

Characterisation and Verification: QST helps scientists precisely characterise quantum computing and communication resources like coherence and entanglement. It verifies quantum protocols and devices. Quantum State Tomography recreates the quantum state to identify quantum system errors and noise. Developing reliable quantum hardware and developing quantum processes requires this.

Quantum State Tomography is essential for validating quantum algorithms throughout development and implementation. It helps debug quantum software and assures its reliability by checking if the quantum state matches the expected output.

Quantum Device Benchmarking: QST standardises quantum components and processors. Determine a quantum gate or circuit's state to evaluate quantum hardware.

Fundamental Research: Beyond technology, QST is essential for understanding decoherence, quantum non-locality, and complicated quantum systems.

Benefits of QST

Comprehensive State Information: QST provides a density matrix of pure and mixed quantum states. This is more instructive than measuring a few observables.

Identification of Quantum Resources: It explicitly displays required quantum resources like entanglement for several quantum information activities.

QST works with photons, trapped ions, superconducting qubits, and more.

This diagnostic tool effectively helps understand and resolve quantum devices and experiments. Quantum State Tomography Drawbacks

Scalability issues (exponential growth) are the largest challenge. QST requires more measurements and processing resources as qubits (N) rise. Reconstructing the density matrix for an N-qubit system requires 4 N −1 linearly independent measurements. Thus, full QST is not possible for systems with more than 4-6 qubits.

QST involves precise quantum system control and calibration, making it challenging to do numerous experiments experimentally.

QST's exceptional sensitivity to noise and experimental defects may cause errors in the reconstructed state. Numerous denoising methods are needed.

Using Bayesian inference or Maximum Likelihood Estimation to rebuild the density matrix after post-processing measurement data is computationally intensive for bigger systems.

“No-Cloning Theorem” By quantum mechanics' no-cloning theorem, no unknown quantum state can be copied perfectly. Quantum State Tomography demands numerous identical state copies, which may be challenging to generate reliably.

Compressed Sensing QST: Quantum states' sparsity reduces measurement requirements. A sparse basis allows compressed sensing algorithms to reconstitute a quantum state with fewer measurements than standard methods.

Machine Learning: Neural networks and other machine learning methods are being developed to learn noise models, denoise experimental data, and reconstruct quantum states. The processing cost and number of experiments should decrease.

Classical Shadows: A promising method that estimates a wide range of quantum state properties from a small set of random measurements, making it more scalable than full QST.

Noise and Error Resistance: Developing increasingly complicated experimental methods and algorithms that can tolerate measurement errors and environmental noise.

Developing efficient measurement schemes: Creating experimental setups that speed up and improve measurement accuracy.

Computing Efficiency: Improving reconstruction algorithms' speed and resource efficiency for real-time experiment analysis.

Quantum State Tomography Future

Quantum information science and quantum computing are crucial to QST's future. QST will become more specialised, dependable, and efficient as quantum systems grow in size and complexity.

Advanced Machine Learning Integration: AI and machine learning integration is expected to improve state reconstruction accuracy and efficiency, decrease noise, and produce the best measurement plans. This will involve data-driven methodologies and increasingly complicated neural network topologies.

Scalable and Specialised Tomography: Partial tomography and classical shadows, which are superior for characterising large-scale quantum processors, will replace full QST. Quantum hardware architecture-specific tomography protocols and quantum feature confirmation techniques will also be in demand.

Real-time and In-situ Tomography: Developing real-time QST methods to provide immediate feedback during quantum operations to dynamically tune and control quantum systems. In-situ tomography inside the quantum device will gain importance.

Quantum-enhanced tomography studies how quantum resources can improve QST techniques.

Benchmarking and Certification of Quantum Technologies: As quantum computers become more powerful, QST will become increasingly crucial in verifying quantum gates, benchmarking their performance, and ensuring that quantum algorithms are viable.

QST is essential for understanding and validating quantum error correcting codes to build fault-tolerant quantum computers.

[govindhtech]

Hybrid Cat-Transmon Architecture Transforms QEC Scale

Cat-Transmon Hybrid Design

The California Institute of Technology and the AWS Centre for Quantum Computing have developed a new quantum computing architecture that will significantly reduce the hardware overhead required to build fault-tolerant quantum computers. This novel Hybrid Cat-Transmon Architecture concept uses “cat qubits” and “transmon qubits” to improve  quantum error correction  using existing, validated experimental methods.

Building reliable logical qubits from physically noisy components requires quantum error correction. QEC sometimes takes many physical qubits to produce a stable logical qubit, making it prohibitively expensive. The hybrid architecture, which reduces physical qubits, solves this problem immediately.

Utilising Biassed Noise for Efficiency

A key innovation of this design is its use of dissipative cat qubits as data qubits. The biassed noise of cat qubits makes them promising. Z-type errors are more likely than X-type errors (usually by a factor of 10³ to 10⁴) due to physical imperfections such photon loss and dephasing. One might purposely accelerate QEC by taking advantage of this large “noise bias”.

Using cat qubits to boost QEC efficiency was difficult, especially with “bias-preserving gates” (sometimes termed “cat-cat gates”) between cat qubits. These gates had “onerous experimental requirements” such strong planned dissipation and extremely good coherence. The hybrid approach successfully overcomes these obstacles by monitoring error syndromes with transmon qubits. It allows high-fidelity syndrome measurement and is more practical.

Innovative Gates for Complete Error Correction

The architecture controls suppressed X faults and dominating Z mistakes with two types of Hybrid Cat-Transmon Architecture entangling gates for complete scalability:

The cat qubit's transmon-controlled X operation, the CX Gate, fixes common Z errors. The qubits' natural free evolution under dispersive coupling makes its implementation easy. Operating the transmon with near "chi matching" in the |g⟩,|f⟩ manifold maintains a significant noise bias, while doing so in the |g⟩,|e⟩ manifold may reduce the cat's noise bias. Preventing single transmon decay faults from creating cat X mistakes makes it a “moderately noise biassed” gate.

CRX Gate: A new cat-controlled transmon X rotation that eliminates residual, suppressed X faults ensures the architecture's perfect scalability to arbitrarily low logical error. Unlike the exponentially noise-biased CX gate, the CRX gate's X-error suppression increases considerably with the cat's mean photon number. Composite pulse sequences of number-selective transmon pulses and storage mode drivers implement it.

This gate uses pulse shaping and dynamical decoupling to reduce coherence faults and dephasing. The CRX gate enables high-fidelity cat Z and controlled-Z (CZ) rotations and single-shot Z-basis cat readout with exponentially suppressed error.

CX and CRX gates are desirable because they leverage intrinsic dispersive coupling, require little planned dissipation, and don't require sophisticated Hamiltonian engineering.

Performance and Hardware Efficiency Potential

Numbers from the research predict significant performance gains. Cat-transmon gates have 99.9% fidelity and 200 ns speed. They maintain a considerable noise bias between 10³ and 10⁴. With realistic physical error rates of 10⁻³ and a storage mode loss rate to dispersive coupling (q) ratio between 10⁻⁵ and 10⁻⁴, current state-of-the-art coherence may attain this level of performance

Architecture uses thin rectangular surface codes to maximise biassed noise benefits. These algorithms reduce qubit overhead by protecting against Z mistakes more than X faults.

The cat-transmon approach reduces logical memory overhead far more than quantum architectures without biassed noise. Using current specifications, the cat-transmon architecture might achieve a logical memory error rate of less than 10⁻¹⁰ with merely 200 qubits (100 cat and 100 transmon). To match the overhead of the cat-transmon design, an unbiased-noise architecture needs over 1000 qubits or lowers physical error rates to less than 10⁻⁴.

Future View

The design is promising, but decoherence, notably of transmon qubits, limits its performance. Some devices have ultra-high intrinsic storage lifetimes (tens of milliseconds), but transmon lifespan must be improved to use them. More coherence enhancements are needed for 2D devices to reach deep sub-threshold.

Researchers are also studying fluxonium qubits, which may have higher anharmonicities and longer coherence durations, improving performance. CX and CRX gate adjustments are also being considered to improve the architecture. Cat-transmon benefits should last through the next steps, which include lattice surgery to evaluate fault-tolerant logical processes. Magic state distillation may benefit from intrinsic noise bias, cutting overheads further.

[govindhtech]

Bias-Tailored Quantum LDPC Codes Boost Quantum Computing

Quantum-LDPC codes

University of Southern California researchers made a major quantum error correction (QEC) breakthrough, which is essential to developing quantum computers. Their unique technology, outlined in “Bias-Tailored Quantum LDPC codes,” creates a new family of “bias-tailored” quantum codes to improve fault tolerance and speed up quantum computation by exploiting quantum hardware faults.

Environmental noise can produce qubit decoherence and errors, compromising computation integrity. Due to its fragility, quantum operations require robust error correction. Reduce computational resources for efficient error mitigation is a serious challenge for researchers.

Understanding and Using Noise Asymmetry

Our research is driven by the discovery that quantum technology often exhibits an imbalance between mistake types. These errors usually appear as:

Bit-flip errors: Qubit (0 or 1) reversals.

Phase-flip faults affect quantum superposition.

Inaccuracies are often more widespread in one type. In superconducting qubit systems, phase-noise can be five orders of magnitude stronger.

This imbalance is instantly rectified by “bias-tailoring”. These programs adjust to the most common error type rather than handling all errors identically. This boosts computing performance and reduces fault tolerance resources. As shown by the Hashing threshold, a lower bound on the physical error rate below which a quantum code can theoretically suppress mistakes, this strategy allows quantum codes to take advantage of higher noise bias's increased channel capacity. The threshold for depolarising noise is 18.9%, but infinite bias raises it to 50%, providing strong theoretical support for bias-tailoring.

Single-Shot Decoding for Fast Recovery

In addition to bias-tailoring, the researchers introduced “single-shot” decoding. This unique method recovers data from noisy measurements in a single processing cycle, avoiding repetitive decoding delays and speeding computation.

A New Code Hierarchy: Bias-Tailored Lifted Product

Shixin Wu, Todd A. Brun, and Daniel A. Lidar from the University of Southern California lead the study to create a hierarchy of new codes. These are based on the hypergraph product code, which can combine smaller quantum codes into larger, more durable ones. The researchers created two code versions with differing error repair and resource allocation advantages by deliberately removing “stabiliser blocks” operators that discover flaws without destroying quantum information.

Joschka Roffe et al. in Quantum additionally highlighted wider research on bias-tailored low-density parity-check (LDPC) codes and how they can exploit qubit noise asymmetry. Quantum LDPC codes may encode several qubits per logical block, enabling fault-tolerant processing, making them a potential replacement for surface codes, especially for long-range quantum structures.

The unique “bias-tailored lifted product” structure provides a flexible framework for bias-tailoring beyond 2D topological codes like the XZZX code. This framework extends the quantum code's effective distance in the limit of infinite bias by modifying the stabilisers of lifted product codes, allowing them to fully use biassed error channels.

Two novel code variants:

This version simplifies code to maximise resource optimisation. Stabiliser measurements and physical qubits are cut in half. The minimal distance that quadratically grows compared to typical designs allows this while maintaining excellent error correction capabilities.

Reduced Code: This version compromises but decreases hardware needs similarly. In exchange for single-shot protection against bit-flip or phase-flip noise, it preserves single-shot functioning under balanced noise or depolarising noise, which randomly modifies a qubit's state. Designers can adapt performance to quantum gear's specific properties.

Practice and Performance

To illustrate, USC researchers created a “3D XZZX” code by expanding the popular two-dimensional surface code to a cubic lattice. This reduced code family addition proves their theoretical framework. Surface codes are popular due to their high error thresholds and planar structural compatibility.

In asymmetric noise situations, bias-tailored lifting product codes can suppress errors by several orders of magnitude better than depolarising noise, according to numerical simulations using Belief Propagation plus Ordered Statistics Decoding. As X-bias rose, a bias-tailored lifted product code beat conventional codes and reduced word mistakes. The XZZX toric code, notable for its performance under biassed noise, may be readily derived as a special example of the bias-tailored lifted product, demonstrating its wide applicability.

Due to their lower qubit overheads than surface codes, quantum LDPC codes can encode more logical qubits at a comparable word error rate, enabling scalable quantum storage.

To Scalable and Reliable Quantum Computers

This research helps build practical and effective quantum computers. These innovative codes handle noisy quantum hardware and optimise resource efficiency through bias-tailoring and single-shot decoding to provide scalable and reliable quantum systems for real-world use. The versatility of these code design possibilities allows variable trade-offs between noise characteristics and hardware overhead, enabling future quantum machines to address difficult computing problems.

[govindhtech]

Quantinuum Universal Gate Set Quantum Computing

Universal gate set

Quantinuum pioneers scalable, universal, fault-tolerant quantum computers.

Quantinuum, the world's largest integrated quantum business, demonstrated the first fault-tolerant universal gate set with reproducible error correction. This achievement is considered a vital first step towards scalable, industrial-scale quantum computing and a ten-fold improvement over industry benchmarks.

This milestone allows Quantinuum to build Apollo, its universal, fault-tolerant quantum computer, by 2029. The company is the first to transition from “NISQ” (noisy intermediate-scale quantum) to utility-scale quantum computers, de-risking the sector. A fully fault-tolerant universal gate set with repeatable error correction is needed to use quantum computing to solve medical, energy, and financial problems.

Breakthrough Explained: Universal Fault-Tolerance Quantum computers process data via gates. A universal gate set needs Clifford gates, which are easy to replicate, and non-Clifford gates, which are harder to build but necessary for quantum computation. Quantum computers without non-Clifford gates are classically simulable and non-universal. A fault-tolerant quantum computer corrects its own errors to produce reliable outputs. All operations, including Clifford and non-Clifford gates, must be error-resilient and error-corrected to be fault-tolerant.

Quantinuum's success

Quantinuum worked in this area, according to two recent publications:

Magic State Production and Non-Clifford Gate Breakeven

The first paper describes how quantum scientists perfected magic state production using their System Model H1-1 to create a fault-tolerant universal gate set. They achieved a record magic state infidelity of 7×10^-5, outperforming prior published figures by a factor of 10. The group achieved a new record for two-qubit non-Clifford gate infidelity (2×10^-4), delivering the first break-even gate with a lower logical error rate than physical one. Combining this, they created the first fault-tolerant universal gate set circuit, a major industry milestone.

Code Swapping

Universal fault-tolerance uses “code switching,” which alternates error-correcting codes. Quantinuum demonstrated this technology in its second paper alongside UC Davis academics. This method set a new record for magic states in a distance-3 error correcting code with 28 qubits instead of hundreds, 10 times better than previous attempts. The components for a universal gate set with repeatable and real-time Quantum Error Correction (QEC) are complete. These advancements can speed up the deployment of powerful quantum applications by lowering qubit needs by an order of magnitude.

Advances in Quantum AI

Quixer Rises With the news that Quixer, its quantum-native transformer, now runs natively on quantum hardware, Quantinuum has advanced quantum AI. Quantum-native AI revolutionises the industry. Quixer, unlike other “copy-paste” approaches that transformed classical models to quantum circuits, is a quantum transformer built from the ground up utilising quantum algorithmic primitives. Quixer scales and saves resources as quantum computing fault tolerance improves. Quixer may study language modelling, picture categorisation, quantum chemistry, and new quantum-specific use cases. For genomic sequence analysis, it performed similarly to conventional approaches.

Logical qubit teleportation breaks record Quantum achieved a new record for logical teleportation fidelity, rising from 97.5% to 99.82%, solidifying its hardware superiority. Quantinuum's H2 technology is the industry standard for complex quantum processes since this logical qubit teleportation fidelity exceeds a break-even point. Teleportation is important for large-scale fault-tolerant quantum computers and a sign of system maturity due to its high performance requirements. It speeds quantum error correction and long-range communication during logical processing, improving computation. Quantinuum's QCCD architecture is flexible and powerful due to its all-to-all communication, real-time decoding, and high-fidelity conditional logic.

Looking Ahead

Helios, Sol, ISC High Performance 2025 The next-generation Quantinuum system, Helios, is expected to be the most powerful quantum computer until Sol arrives in 2027.

The company will also be a significant player at ISC High Performance 2025 in Hamburg, Germany, from June 10–13. Quantinuum will show how its quantum technologies tie with HPC and AI at Booth B40. Besides a live demonstration of NVIDIA's CUDA-Q platform on Quantinuum's H1 hardware, the team will address near-term hybrid use cases, hardware developments, and future roadmaps, enabling hybrid compute solutions in chemistry, AI, and optimisation. With a record Quantum Volume of 2^23 = 8,388,608, Quantinuum leads the industry in performance, hybrid integration, scientific innovation, worldwide collaboration, and accessibility.

Fully fault-tolerant universal gate set with repeatable error correction

Break down this idea to comprehend it:

Gate Set: Universal

Quantum computers process data with gates.

Clifford and non-Clifford gates are the main types.

Clifford gates are easy to imitate and install on standard computers.

Non-Clifford gates, which are harder to implement, are essential for quantum processing when combined with Clifford gates.

The “machinery to tackle the widest range of problems” is a system that can operate Clifford and non-Clifford gates. Without non-Clifford gates, quantum computers are limited to simpler tasks, non-universal, and always copied by conventional computers.

Fault-tolerant quantum computer

A fault-tolerant quantum computer recognises and fixes its own errors to produce reliable output. Quantinuum seeks “the lowest in the world” system error rates.

[govindhtech]

Krylov Quantum Diagonalization on 56-Qubit Quantum Processor

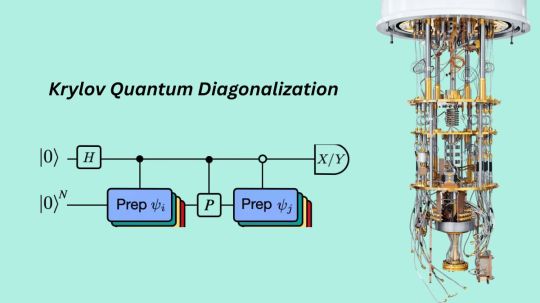
Researchers from IBM and the University of Tokyo achieved a significant quantum computing milestone by successfully demonstrating the Krylov Quantum Diagonalisation (KQD) method on an  IBM Heron quantum processor. One of the largest many-body systems ever simulated on a quantum processor was the Heisenberg model on a 2D heavy-hex lattice of up to 56 Qubit in this pioneering experiment. This Nature Communications article shows how KQD can bridge the gap between small-scale quantum demonstrations and fault-tolerant quantum computing.

The Krylov Quantum Diagonalisation Method

KQD is a hybrid quantum-classical algorithm that modifies common classical Krylov subspace techniques. Its major goal is to estimate ground-state energy of quantum many-body systems.

KQD offers a strong alternative to Variational Quantum Algorithms (VQAs), which feature unreliable convergence guarantees and prohibitive iterative optimisation for scaling to larger systems. KQD avoids the considerable quantum error correction that Quantum Phase Estimation (QPE) required for circuit depths needed for important concerns, despite its theoretical precision.

The core of KQD is two steps:

Quantum Subroutine: The quantum processor creates a many-body Hilbert space subspace. Trotterized unitary evolutions are used to create a Krylov basis by applying powers of the time evolution operator ($U \coloneqq e^{-iHdt}$) to an initial reference state ($|\psi_0\rangle$

After being computed on the quantum computer, these matrix elements projections of the Hamiltonian and overlap matrix within the subspace are classically diagonalised to solve a generalised eigenvalue problem and estimate the approximate low-lying energy eigenstates.

The exponential convergence of KQD to ground state energy is a big gain. With increasing Krylov dimension, the error from projecting into this unitary Krylov space decreases rapidly, even with substantial noise. KQD is ideal for pre-fault-tolerant quantum devices because of its convergence guarantee and ability to predict time evolutions utilising shallow circuits.

Experimental IBM Hardware Implementation

Trials were conducted on the IBM_montecarlo Heron R1 processor system. With fixed-frequency transmon qubits connected via tunable couplers, this 133-qubit device provides less crosstalk and faster two-qubit gates than previous generations.

The study focused on the spin-1/2 antiferromagnetic Heisenberg model on heavy-hexagonal lattices, a crucial condensed matter system. They streamlined quantum circuits and improved viability on noisy hardware by using the model's U(1) symmetry, which conserves Hamming weight (or particle number). regulated reference state initialisations instead of complicated regulated temporal evolutions reduced circuit depth.

The studies used particle-number sectors $k=1$, $k=3$, and $k=5$. Initial computational basis states have the right amount of particles.

The $k=1$ experiment used a 57-qubit CPU.

Subset of 45 qubits utilised in $k=3$ experiment.

The $k=5$ experiment used 43 qubits.

The 5-particle experiment's largest subspace dimension was 850,668, near to 20 qubits and larger than the Hilbert space's 19 qubits. KQD can reach huge effective Hilbert spaces even when calculations are limited to symmetry sectors. To finish all tests in the 24-hour device recalibration window, the Krylov space size was set at $D=10$ for all studies.

Simplifying the circuit was crucial. Due to its three-coloring of edges, the heavy-hexagonal lattice structure allowed regulated preparation and Trotterized temporal evolutions with three two-qubit gate layers. Therefore, fewer noise models were needed to mitigate errors. Two second-order Trotter steps were used for time evolutions for $k=3, 5$ (resulting in nine two-qubit layers) to balance accuracy and circuit depth.

Best Error Prevention Methods

Success in the noisy intermediate-scale quantum (NISQ) era requires error management. The group implemented complex error mitigation and suppression strategies:

Probabilistic Error Amplification (PEA): Learning the system's noise and amplifying it at different intensities extrapolates data to the ideal, zero-noise limit.

TREX reduces state preparation and measurement (SPAM) mistakes by converting noise into a quantifiable multiplicative factor utilising random Pauli bit flips before measurement.

Pauli Twirling: Converts noise channel into a simpler Pauli noise channel for mistake characterisation and mitigation.

Dynamic Decoupling: Pulse sequences during qubit idle reduce cross-talk and interactions.

At noise amplification settings of 1, 1.5, and 3, 300 spun instances with 500 shots each were used for the single-particle experiment. For multi-particle testing ($k=3, 5$) at factors of 1, 1.3, and 1.6, 100 twirled instances with 500 shots each were employed to limit runtime from increased circuit sizes.

Results and Implications

Although noisy, the practical results confirmed the expected exponential convergence of the ground state energy with increasing Krylov dimension. The projected energies for the 3- and 5-particle sectors matched noiseless classical simulations within experimental error limitations.

The $k=1$ experiment found a slightly different lowest energy. This shows that noise caused effective leakage out of the $k=1$ symmetry subspace, highlighting the risk of relying on symmetry conservation on noisy hardware. The authors believe superior device calibration may explain the consistency of the $k=3$ and $k=5$ experiments.

This study advances quantum simulation by more than two orders of magnitude in effective Hilbert space dimension and more than a factor of two in qubit count. It shows that significant convergence may be achieved despite hardware noise, providing important information for pre-fault tolerance methods. The heavy-hexagonal architecture fit KQD's circuit topology, highlighting algorithm-hardware co-design.

KQD provides a stable framework for quantum simulation, allowing quantum diagonalisation techniques to supplement computational quantum sciences and maybe allow meaningful quantum simulations before total fault tolerance is reached.

[govindhtech]

Nord Quantique Unveils Multimode Encoding for Efficient QEC

Multimode Encoding

A quantum computer that solves problems 200 times faster and uses 2,000 times less power than a supercomputer—“a first in applied physics”

Researchers at Canadian firm Nord Quantique discovered a small physical qubit with error correction. This technique could revolutionise quantum computing by reducing power consumption and speeding operation. Quantum computers, which can solve complicated problems 200 times faster and use 2,000 times less energy than supercomputers, could result from it.

The company plans to build a 1,000-logical-qubit computer by 2031. It is expected to be more energy-efficient than high-performance computing (HPC) systems and small enough to fit in a data centre.

Addressing Quantum Computing's Main Issue

When chilled to near absolute zero, quantum information is notoriously sensitive to heat, vibration, and electromagnetic interference. The integrity of this information has long been a challenge in quantum computing. These disadvantages are addressed by quantum error correction (QEC) in most quantum systems. QEC combines multiple physical qubits into a single “logical” unit to absorb and rectify errors, preventing a single failure from contaminating a calculation.

The old method requires dozens or hundreds of physical qubits to make a single logical qubit, which is a major drawback. Quantum computers get bigger, more complex, and need more power as qubits increase exponentially. Julien Camirand Lemyre, CEO of Nord Quantique, noted that the sector has traditionally struggled with the number of physical qubits used for quantum error correction.

Nord Quantiques' “First in Applied Physics” Solution

This hurdle is addressed by Nord Quantique's innovation. Their technique cleverly avoids massive clusters of physical qubits by using a single physical component as a logical qubit. A functioning prototype of their “bosonic qubit,” which includes quantum error correction directly into its hardware, was shown in 2024. This architecture is “a first in applied physics” and a step towards utility-grade, scalable quantum machines, according to Nord Quantique.

This system relies on a superconducting aluminium cavity cooled to practically absolute zero, called a bosonic resonator. Photons store quantum information in this cavity in several electromagnetic “modes.” This unique method, multimode encoding, encodes the same quantum state in parallel by distributing information throughout the physical structure. The qubit has internal fault tolerance because its intrinsic redundancy allows the other modes to fix the problem if one is interfered with. This allows a 1:1 ratio between logical and physical qubits, reducing the need for external error correction.

Multimode encoding, developed by Nord Quantique, allows integrated error correction and reduces the number of physical qubits needed for fault tolerance in quantum computers.

A full explanation of multimode encoding:

Mechanism and Structure

Nord Quantique's major component is a superconducting aluminium cavity cooled to almost zero degrees, its bosonic resonator.

The cavity stores quantum data with photons. Some electromagnetic patterns inside the resonator hold quantum information. These patterns are called “modes”.

The electromagnetic field resonance pattern in the cavity is unique for each “mode”.

Parallelised Encoding and Internal Fault Tolerance Multimode encoding encodes the same quantum state over many electromagnetic patterns, or “modes.”

Dividing information among multiple modes within the same physical structure gives the qubit the ability to detect and correct specific types of interference.

This indicates that the other modes provide enough context and redundancy to retrieve the quantum information if one mode is interfered with or errors.

In contrast to conventional quantum error correction, this approach gives every qubit inherent fault tolerance.

Effect on Qubit Ratio and Error Correction

External error correction is less intensive with multimode encoding.

It allows logical and physical qubits to be 1:1. A single logical qubit used to require dozens or hundreds of physical qubits. This conventional method increased quantum computer size, complexity, and energy cost.

We can develop quantum computers with outstanding error correction without actual qubits via multimode encoding. the business, said Nord Quantique CEO Julien Camirand Lemyre.

Dependability, Performance

Nord Quantique improves fault tolerance with multimode encoding and Tesseract code, a “bosonic code” This code reduces potential quantum defects such bit flips, phase flips, control errors, and qubit leakage. After filtering out a few runs, the qubit retained its state during 32 rounds of error correction without decay. This implies that multimode encoding can maintain quantum information in stable conditions.

Nord Quantique's “bosonic qubit” architecture relies on multimode encoding to build quantum error correction into the hardware. This “a first in applied physics” could lead to utility-grade, scalable quantum devices that are more compact and energy-efficient than previously thought.

[govindhtech]

Double Quantum Dot Spin-State Transitions By Coupling To ASQ

Double Quantum Dot

The quest to build scalable quantum computers requires fast and accurate qubit readings. Recently developed quantum dot readout procedures use robust latching, reinforced optical cavities, and electrically adjustable Andreev spins to overcome this important barrier. These advances enable more complex  quantum circuits and mid-circuit observations.

QuTech, Delft University of Technology, the University of Maryland, Cornell University, Michèle Jakob, Katharina Laubscher, Patrick Del Vecchio, Anasua Chatterjee, Valla Fatemi, and Stefano Bosco developed a protocol for fast and accurate spin qubit readout in germanium quantum dots. This technique uses Andreev spins, quasiparticle excitations at the superconductor-semiconductor interface, to its advantage. On June 25, 2025, Quantum News (a branch of Quantum Zeitgeist) published their article “Fast readout of quantum dot spin qubits via Andreev spins”.

Their goal is to precisely modify spin states in a double quantum dot (DQD) by attaching it to an asymmetric superconducting quantum dot (ASQ). The team's numerical simulations reveal that the ASQ can efficiently screen the spin on one of the DQD's dots, changing the ground state from doublet to singlet as the coupling strength increases. This mechanism's novel electron spin control may assist spintronics and quantum information processing.

The study also indicates that the superconducting phase difference greatly affects the coupled system's energy and spin states. Simulations reveal phase-dependent splitting of singlet and triplet states, indicating an effective exchange interaction from DQD-ASQ hybridisation. This interaction, modulated by the superconducting phase, affects energy level splitting in the DQD's (0,1) and (1,1) charge sectors. This provides a crucial approach to build quantum processor spin configurations.

The researchers recognise this idealisation and plan to loosen the models' zero-bandwidth approximation (ZBA), which assumes infinite impedance in superconducting leads to simplify computations. In addition to assessing practicality by integrating more realistic device features and geometries, further study will examine the coupled system's dynamic behaviour, including finite temperature and decoherence. Its compatibility with germanium-based devices makes heterogeneous quantum computing architectures possible.

A broader pattern of quantum dots is making tremendous progress, including Andreev spin coupling. readout

In an article published in Nature Communications on July 5, 2023, a team led by Nadia O. Antoniadis and Mark R. Hogg achieved a cavity-enhanced single-shot readout of an electron spin in a semiconductor quantum dot in under 3 nanoseconds, with a fidelity of 95.2% ± 0.7%.

Over two orders of magnitude faster than earlier optical investigations, which obtained 82% fidelity in 800 ns. Low photon collection rates and measurement back-action are overcome by boosting the optical signal with an open microcavity. Readout durations are far shorter than spin relaxation and dephasing times, enabling quantum technology. With 37% system efficiency, their microcavity device detects photons in 1.8 ns for 98% of traces at zero magnetic field. This allows real-time electron spin dynamics and quantum leap detection.Simulations suggest 99.5% fidelity in less than a nanosecond, and greater advances are expected.

On February 13, 2023, J. Corrigan et al. disclosed latched readout for the quantum dot hybrid qubit (QDHQ) in Applied Physics Letters. This method overcomes the rapid decrease of the excited charge state, which makes single-shot readout difficult in simpler arrangements. The qubit excited state was converted to a tunnel-rate-restricted metastable charge configuration for persistence up to 2.5 milliseconds. This boosts the integrated charge sensor's sensitivity and increases measuring time flexibility. The latching of a five-electron QDHQ in the (4,1)–(3,2) charge configuration is caused by an orbital splitting (200-500 µeV), which is more flexible than valley splittings that limit three-electron configurations.

On February 13, 2024, Kenta Takeda et al. demonstrated a fast (few microseconds) and exact (>99% fidelity) parity spin measurement in a silicon double quantum dot in npj Quantum Information. This paper addresses the need for quantum error correcting algorithms to measure faster than decoherence. A micromagnet enhances the Pauli spin blockage (PSB) process in their method. This technique provides a large Zeeman energy difference, relaxing unpolarized triplet states quickly for parity-mode PSB reading. They optimised charge sensing and pulse engineering to achieve measurement infidelities below 0.1% in 2 µs integration time. This is far faster than the average spin echo coherence times of 100 µs for silicon qubits.

Quantum technology applications require rapid and accurate qubit reading, as shown by these many breakthroughs. To overcome quantum computing's core challenges, researchers are improving silicon's optical and charge-based detection and using exotic Andreev spins in germanium. Fault-tolerance and complexity of quantum computers rise due to fast, accurate measurements needed to extract final processing outputs and enable quantum error correction feedback mechanisms.

[govindhtech]

Magic-State Distillation with Ideal Zero-Level Distillation

Magic-State Distillation

Zero-Level Magic-State Distillation Works

Researchers devised 'zero-level distillation', which might drastically minimise the resource overhead associated with building  fault-tolerant quantum computers (FTQCs), a vital first step in realising their transformative promise. The technique intends to improve Magic-State Distillation (MSD), a vital step towards universal quantum computers, by operating directly at the physical qubit level rather than using resource-intensive logical qubits.

Prime factorisation and quantum chemistry are two problems quantum computers may solve better than traditional machines. Current “noisy intermediate-scale quantum computers” (NISQ) cannot run complex algorithms due to noise and a restricted amount of qubits. The best solution is FTQCs, which protect quantum information with quantum error correction.

FTQCs struggle to implement non-Clifford gates like the T gate, which are necessary for universal computation but difficult to build fault-tolerantly. Magic-State Distillation creates high-fidelity magic states from noisy ones for gate teleportation. However, traditional MSD protocols require many logical qubits, which is a huge practical impediment.

Recently proposed “zero-level distillation” distils everything at the physical level to solve this problem. This method uses physical qubits and nearest-neighbor two-qubit gates on a square lattice instead of error-corrected Clifford operations on logical qubits. The fundamental idea is to use the Steane code, a ⟦7,1,3⟧ stabiliser code, to detect and distil errors, even with noisy Clifford gates.

Essentials of Zero-Level Distillation: Physical-Level Operation: Physical qubits first non-fault-tolerantly encode a noisy magic state into Steane code. A Hadamard test of the logical Hadamard operator uses a seven-qubit cat state as an ancilla for effective operation with constrained qubit connectivity. Odd measurement parity rejects the method. Surface Code Integration: After being encoded in the Steane code, the distilled magic state is translated directly or transported to a planar or rotating surface code, which is noise-resistant and 2D lattice-compatible and might be used in FTQCs. Teleportation requires lattice surgery to mix and separate Steane and surface codes. Superconducting qubit systems can use circuits designed for nearest-neighbor interactions on a square lattice. Qubit mobility reduces circuit depth with one-bit teleportation.

Positive Results and Implications: Zero-level distillation dramatically reduces magic state logical error rates in numerical simulations. The physical error rate is $10^{-4}$, whereas the logical error rate ($p_L$) is improved by two orders of magnitude to $10^{-6}$. At $10^{-4}$, $p_L$ shows a one-order-of-magnitude gain, even at $p = 10^{-3}$. The logical error rate is around $100�times p^2$. Distillation has a high success rate, with 70% at $p = 10^{-3}$ and 95% at $p = 10^{-4}$.

Teleportation requires just 25 physical circuit depth (or 42 for direct code conversion, which uses more qubits but has a deeper depth). This efficiency reduces time and area overhead for FTQCs.

Effect on Future Quantum Computing:

Early FTQCs: Zero-level distillation works effectively in early FTQCs due to limited physical qubit availability. Despite scaling to $100 \times p^2$, it is viable because to a spatial overhead of almost one logical qubit. This could enhance NISQ capabilities and enable $10^4$ continuous rotation gate operations using Clifford gates.

Full-Fledged FTQCs: Zero-level distillation reduces the amount of physical qubits needed for accuracy when combined with multilevel distillation. Using magic states from zero-level distillation, “(0+1)-level distillation” achieves error rates of $10^{-16}$ in typical level-1 distillation. An overall logical error rate scaling of $O(p^6)$ may minimise spatiotemporal overhead by around one-third. Another concept, “magic state cultivation,” inspired by zero-level distillation, can reduce spacetime overhead by two orders of magnitude and scale to $O(p^5)$.

This integrated strategy promotes research and technology advances and offers a low-cost path to quantum computing.

[govindhtech]

Microsoft’s Quantum 4D Codes Standard for Error Correction

Quantum 4D Codes

Microsoft Quantum 4D Codes Improve Fault-Tolerant Computing and Error Rates.

Microsoft announced a new family of quantum 4D geometric quantum error correction algorithms that will reduce qubit overhead and simplify fault-tolerant  quantum computing. Quantum computing has made significant progress. This discovery, revealed in a business blog post and an arXiv pre-print, could make scalable quantum computers possible by solving one of the field's biggest problems: quantum mistakes.

The unique “4D geometric codes” use four-dimensional mathematical frameworks to enable fault tolerance, a vital requirement for quantum computation. Unlike conventional error correction methods that need multiple measurement rounds, quantum 4D codes offer “single-shot error correction.” They can recover from faults with a single round of measurements, simplifying quantum system speed and design by reducing time and hardware. Microsoft Quantum highlights that these cutting-edge methods can be utilised with other qubits, advancing the research and making quantum computing more accessible to professionals and non-experts.

This invention rethinks topological quantum coding. Two-dimensional designs are typical of conventional technologies like surface codes. Microsoft researchers turned to a four-dimensional lattice, called a tesseract, its 4D equivalent of a cube. The algorithms use complicated geometric properties in this higher-dimensional mathematical space to boost efficiency. By rotating quantum 4D codes into perfect lattice structures, scientists reduced qubit count while maintaining fault tolerance.

This advanced geometric technique allows “4D geometric codes” that preserve the topological security of traditional toric codes, which “wrap” qubits around a donut-shaped grid. Quantum 4D codes have a faster encoding rate and better error correction. Their eight-bit Hadamard coding shows how to encode six logical qubits with 96 physical qubits. This unique specification allows the code to detect four errors and fix up to three, displaying extraordinary efficiency.

Microsoft also published impressive performance metrics. Despite a physical error rate of 10³, the Hadamard lattice code has reduced errors by 1,000-fold, resulting in a logical error rate of 10⁶ each correction round. This is far better than rival low-density parity-check (LDPC) quantum codes and rotational surface codes. In some decoding methods, the pseudo-threshold, the point at which logical error rates improve over unencoded processes, approaches 1%. Simulations have verified both single-shot and multi-round decoding methods, and quantum 4D geometric codes outperform several alternatives, especially when corrected for logical qubits.

These codes go beyond theory. Microsoft built them to work with upcoming quantum hardware architectures that allow all-to-all connection. This includes photonic systems, trapped ions, and neutral atom arrays. Surface codes require perfect geometric locality and are sometimes confined to two-dimensional hardware architectures, but quantum 4D geometric codes thrive on hardware that can execute operations over distant qubits. Syndrome extraction was simplified by creating a “compact” circuit for parallel hardware and a “starfish” circuit for qubit-limited systems that reuse ancilla qubits. Low code depth and resource efficiency are also due to these circuits.

In addition to stability and efficiency, the programs support universal quantum computing. Lattice surgery, space group symmetries, and fold-transversal gates can be used to build Clifford operations like Hadamard, CNOT, and phase gates, which are covered in the work. Logical Clifford completeness ensures all essential operations can be performed in the protected code space. Distillation and magic state injection have been employed to achieve universality and increase capabilities beyond the Clifford group.

They enable non-Clifford gates for generic quantum algorithms but increase overhead. The researchers developed diagonal unitary injections and improved multi-target CNOTs for multi-qubit operations to reduce spatial and temporal computing expenses for quantum chemistry and optimisation.

These advances affect hardware scaling and practicality. With current technology, a tiny quantum computer with 2,000 physical qubits and the Hadamard code can produce 54 logical qubits. To scale up to 96 logical qubits, the stronger Det45 algorithm would need 10,000 physical qubits. A utility-scale computer with 1,500 logical qubits might be built using ten modules with 100,000 physical qubits each. The clear path includes early tests to demonstrate entanglement, logical memory, and basic circuits. For practical quantum applications, deep logical circuits and magic state distillation must be proven.

Though hopeful, the study had gaps and unsolved questions. Low-depth local circuits may not be able to implement quantum 4D symmetries' topological gates, a hardware efficiency requirement. Showing whether these topological approaches may achieve Clifford completeness is another ongoing issue. The team assumes perfect lattices and estimates that geometric rotation may save cost by a factor of one as code distance increases. Finally, subsystem variations of these algorithms may have further benefits, but their performance and synthesis costs have not been adequately investigated.

Microsoft's quantum researchers' achievement increases quantum error correction and potentially speed up fault-tolerant quantum computing systems.

[govindhtech]

VarQEC With ML Improves Quantum Trust By Noise Qubits

Variational Quantum Error Correction (VarQEC) is a novel method for resource-efficient codes and quantum device performance that optimises encoding circuits for noise characteristics using  machine learning (ML) . Error mitigation approaches for near-term quantum computers are advanced by this approach.

Problems with Quantum Errors and QEC

Fragile quantum systems limit quantum computing, despite its revolutionary computational potential. Qubits—quantum information building blocks—are prone to decoherence, quantum noise, and gate defects. Without sufficient corrective mechanisms, quantum computations quickly become unreliable.

Quantum system mistakes can take many forms:

A qubit can switch between zero and one.

Phase-flip mistakes occur when a qubit's quantum state phase changes unexpectedly.

Gate errors are caused by quantum gates (devices used to manipulate qubits, including lasers or magnetic fields) malfunctioning.

To solve these issues, typical QEC methods like Shor's code and surface codes encode logical qubits across several physical qubits. These methods have large resource requirements (surface codes require thousands of physical qubits for a single logical qubit), complicated decoding techniques, and poor adaptation to real-world quantum noise. This high overhead hinders realistic quantum computation.

VarQEC: Machine Learning-Based Approach

Due of these limits, scientists are exploring more flexible and resource-efficient methods. VarQEC uses machine learning and AI to support quantum computing. The inverse AI supporting quantum computing is becoming important for real-world use, despite the focus on how quantum computing enhances AI. The article “Learning Encodings by Maximising State Distinguishability: Variational Quantum Error Correction” by Andreas Maier from Friedrich-Alexander-Universität Erlangen-Nürnberg and Nico Meyer, Christopher Mutschler, and Daniel Scherer from Fraunhofer IIS introduced VarQEC.

Key VarQEC Features:

VarQEC uses a new machine learning goal called the “distinguishability loss function.” This function is the training objective by testing the error correction code's ability to differentiate the target quantum state from noise-tainted states. VarQEC maximises this distinguishability, making encoding circuits more resilient to device-specific errors.

Encoding Circuit Optimisation: VarQEC optimises encoding circuits for device-specific errors and resource efficiency. Unlike static, pre-defined codes, error correction can be tailored to each quantum device. Flexibility is needed because quantum systems are dynamic and error rates and types vary owing to hardware and environmental changes.

Practical Application and Performance Gains: The study revealed how VarQEC can maintain quantum information on actual and simulated quantum hardware. Experiments learnt error correcting codes to adapt to IBM Quantum and IQM superconducting qubit systems' noise attributes. These efforts led to persistent performance gains over uncorrected quantum states in specific ‘patches’ of the error landscape. Successful hardware deployment proves machine learning-driven error prevention strategies.

Hardware-Specific Adaptability: The study stressed the importance of matching error correcting code design to hardware architecture and noise profiles. In connectivity experiments on IQM devices, star and square ansatz topologies performed similarly, suggesting that topology may not always affect efficacy. Still, the discovery of a faulty qubit on an IQM device showed how sensitive codes are to qubit performance and how important calibration is.

The Broader AI for QEC Landscape With VarQEC

VarQEC shows how AI, specifically machine learning, may improve QEC.

To decode lattice-based codes like surface codes, Convolutional Neural Networks (CNNs) can find error patterns faster and utilise less computing power. For surface code decoding, Google Quantum AI uses neural networks to rectify errors faster and more accurately.

Enhancing Robustness and Adaptability: Reinforcement Learning (RL) approaches can instantaneously adjust error correction plans to changing error types and rates. Supervisory machine learning models like recurrent neural networks can handle time-dependent error patterns like non-Markovian noise. IBM researchers found and fixed failure patterns using machine learning (ML).

Generative models like Variational Autoencoders (VAEs) and RNNs can capture complex error dynamics like non-Pauli errors and non-Markovian noise, improving prediction accuracy and proactive maintenance.

Even though QEC encodes information with many qubits and mathematically restores corrupted states to discover and rectify defects, QEC and QEM must be distinguished. QEM reduces mistakes and their effects by using statistical methods to get the best result from noisy data or improving hardware stability. As its name implies, VarQEC corrects undesirable results immediately.

VarQEC's Future and Challenges

Despite promising results, VarQEC and AI in QEC confront many challenges:

Future VarQEC work should focus on adding increasingly complicated, device-specific noise models into the training process to account for correlated noise and qubit-specific oscillations. The assumption of uniform noise levels will be exceeded.

Scalability: Testing VarQEC on larger qubit systems and more complex quantum circuits is the next step in determining its suitability for harder algorithms. This is consistent with the larger issue of improving machine learning models to handle more qubits without increasing processing load.

Alternative Designs: VarQEC may increase performance by testing other ansatz designs and optimisation methodologies.

AI in QEC has challenges such data scarcity and integration due to the absence of quantum error datasets for ML model training, which requires data augmentation. To smoothly integrate AI-driven QEC into quantum computing platforms, physicists, computer scientists, and engineers must study hardware-software co-design and interdisciplinary collaboration.

In conclusion

VarQEC is a promising machine learning-based quantum computing failure solution. Customising error correction codes to quantum hardware noise helps make fault-tolerant and useful quantum systems conceivable.

[govindhtech]

Neutral Atom Quantum Computing By Quantum Error Correction

Atom-Neutral Quantum Computing

Microsoft and Atom Computing say neutral atom processors are resilient due to atomic replacement and coherence.

Researchers have showed they can monitor, re-initialize, and replace neutral atoms in a quantum processor to decrease atom loss. This breakthrough allows the creation of a logically encoded Bell state and extended quantum circuits with 41 repetition code error correction rounds. These advances in atomic replenishment from a continuous beam and real-time conditional branching are a huge step towards realistic,  fault-tolerant quantum computation using logical qubits that surpass physical qubits.

Quantum Computing Background and Challenges:

Delicate qubits' quantum states are prone to loss and errors, making quantum computing difficult. Neutral atom quantum computer architectures experienced problems reducing atom loss despite their potential scalability and connectivity. Atoms lost from the optical tweezer array due to spontaneous emission or background gas collisions might create mistakes and quantum state disturbances.

Quantum error correction (QEC) is essential for achieving low error rates (e.g., 10⁶ for 100 qubits) for scientific or industrial applications, as present physical qubits lack reliability for large-scale operations. By encoding physical qubits into “logical” qubits, QEC handles noise using software.

Atom Loss Mitigation and Coherence Advances:

A huge team of Microsoft Quantum, Atom Computing, Inc., Stanford, and Colorado physics researchers addressed these difficulties. Ben W. Reichardt, Adam Paetznick, David Aasen, Juan A. Muniz, Daniel Crow, Hyosub Kim, and many more university participants wrote “Logical computation demonstrated with a neutral atom quantum processor,” a groundbreaking article. They found that missing atoms may be dynamically restored without impacting qubit coherence, which is necessary for superposition computations.

The method recovers lost atoms and replaces them from a continuous atomic beam, “healing” the quantum processor during processing. Long-term calculations and overcoming atom number constraints require this functionality. The neutral atom processor offers two-qubit physical gate fidelity and all-to-all atom movement with up to 256 Ytterbium atoms. Infidelity of two-qubit CZ gates with atom movement is 0.4(1)%, while single-qubit operations average 99.85(2)%. The platform also uses "erasure conversion" to identify and fix gate flaws by translating them into atom loss.

Important Experiments: The study highlights several achievements:

Extended Error Correction/Entanglement:

Researchers completed 41 rounds of symptom extraction using a repetition code, which is a considerable increase in complexity and duration for neutral atom systems. A logically encoded Bell state was also “heralded” and measured to be ready. Encoding 24 logical qubits with the distance-two ⟦4,2,2⟧ code yielded the largest cat state ever. This considerably reduced X and Z basis errors (26.6% vs. 42.0% unencoded).

Logical Qubits' Algorithmic Advantage:

Using up to 28 logical qubits (112 physical qubits) encoded in ⟦4,1,2⟧, the Bernstein-Vazirani algorithm achieved better-than-physical error rates. This showed how encoded algorithms can turn physical errors into heralded erasures, improving measures like anticipated Hamming distance despite reduced acceptance rates.

Repeated Loss/error Correction:

Researchers repeated fault-tolerant loss repair between computational steps. Using a ▦4,2,2⟧ coding block, encoded circuits outperformed unencoded ones over multiple rounds by interleaving logical CZ and dual CZ gates with error detection and qubit refresh. They performed random logical circuits with fault-tolerant gates to prove encoded operations were better.

Bacon-Shor Code Correction Beyond Loss:

Neutral atoms successfully corrected defects in the qubit subspace and atom loss using the distance-three ⟦9,1,3⟧ Bacon-Shor code for the first time. This renewing ancilla qubit technique can address both sorts of problems with logical error rates of 4.9% after one round and 8% after two rounds.

Potential for Quantum Computing

This work shows neutral atoms' unique potential for reliable, fault-tolerant quantum computing by combining scalability, high-fidelity operations, and all-to-all communication. In large-scale neutral atom quantum computers, loss-to-erasure conversion for logical circuits is useful. This discovery, along with superconducting and trapped-ion qubit breakthroughs, shifts quantum processing from physical to logical qubit results. Better two-qubit gate fidelities and scaling to 10,000 qubits will enable durable logical qubits and longer distance codes, enabling deep, logical computations and scientific quantum advantage.

[govindhtech]

Zuchongzhi 3.0 Quantum Computer Authority With 105 Qubits

Zuchongzhi 3.0 quantum computer

Chinese researchers introduced Zuchongzhi 3.0, a 105-qubit superconducting quantum gadget. A computing effort that would take the world's most powerful supercomputer 6.4 billion years to complete was completed in seconds by the team. This groundbreaking achievement, previously reported on arXiv and described in a Physical Review Letters study, strengthens China's growing influence in the quest for quantum computational advantage, a crucial turning point at which quantum computers can outperform classical machines in certain tasks.

Zuchongzhi 3.0 outperforms Google's Sycamore quantum computing  efforts by a million times. The work was led by Pan Jianwei, Zhu Xiaobo, and Peng Chengzhi of the University of Science and Technology of China (USTC).

Key Performance and Technical Advances:

Revolutionary Speed and Computational Advantage: Zuchongzhi 3.0 completed complex computational tasks in seconds. The Frontier supercomputer, the world's most powerful classical supercomputer, would take roughly 6.4 billion years to simulate the same procedure. This benchmark demonstrates a staggering 10^15-fold (quadrillion-times) speedup compared to typical supercomputers. In hundreds of seconds, the processor produced one million samples.

Outperforming Google: The processor outperformed Google's 67-qubit Sycamore experiment by six orders of magnitude. Additionally, it is around a million times quicker than Google's latest Willow processor findings, which have 105 qubits. Zuchongzhi 3.0 achieved a 10^15-fold speedup, restoring a healthy quantum lead, while Google's Willow chip achieved a 10^9-fold (billion-fold) speedup.

Upgraded Hardware and Architecture: Zuchongzhi 3.0's 105 transmon qubits in a 15-by-7 rectangular lattice outperform 2.0. The device uses 182 couplers to increase communication and enable flexible two-qubit interactions. The chip uses “flip-chip” integration and a sapphire substrate with improved materials like tantalum and aluminium connected by an indium bump technique to reduce noise and improve thermal stability.

Improved Fidelity and Coherence: The processor has 99.62% two-qubit and 99.90% single-qubit gate fidelity. With 72 microsecond relaxation time (T1) and 58 microsecond dephasing time (T2), qubit stability improved significantly. These advancements allow Zuchongzhi 3.0 to execute more complex quantum circuits within qubit coherence time.

Benchmarking Method

Random circuit sampling (RCS), a famous quantum advantage benchmark, was used in a 32-cycle experiment with 83 qubits. A sequence of randomly selected quantum operations must be performed to measure system output.

The exponential complexity of quantum states makes this procedure impossible for classical supercomputers to replicate. The USTC team carefully compared their findings to the most famous classical algorithms, including those modified by its researchers who had “overturned” Google's 2019 quantum dominance claim by improving classical simulations. This proves the quantum speedup is real given existing knowledge.

Zuchongzhi 3.0 faces competition from other leading processors due to substantial advances.

Google Willow (2024, Superconducting): Zuchongzhi 3.0 and Willow share 105 qubits and 2D grids. Although Google Willow had longer coherence (~98 µs T1) and slightly higher fidelities (e.g., 99.86% two-qubit fidelity vs. Zuchongzhi's 99.62%), its main focus was quantum error correction (QEC), demonstrating that logical qubits outperform physical qubits in fidelity. Willow focused on dependability and scalable machine building blocks, while Zuchongzhi 3.0 ran a larger circuit with physical qubits for raw computing power and speed.

IBM Heron R2 (2024, Superconducting): IBM's highest-performance CPU, this modular and scalable CPU contains 156 qubits. IBM emphasises “quantum utility” for real-world concerns like molecular simulations rather than speed testing.

Amazon Ocelot (2025, Superconducting Cat-Qubits): This small-scale prototype uses “cat qubits,” which suppress specific error types, to provide hardware-efficient error correction and reduce the number of qubits needed for fault tolerance. This experimental vehicle tests a quantum error control system instead of computing speed records.

Microsoft Majorana 1 (2025, Topological Qubits): This chip's novel method promises built-in error protection, stability, and scalability with eight topological qubits. Although it cannot currently match 100-qubit superconducting processors in processing power, its potential for large-scale, error-resistant quantum computation makes it important.

Limitations and Prospects

Despite its impressive findings, the report acknowledges issues. Despite its computing advantage, the random circuit sampling benchmark does not solve actual problems. Critics say this method favours quantum processors. Traditional supercomputing approaches are also threatening quantum advantage.

Multi-qubit operation mistakes remain a key issue, especially as circuit complexity increases. Like previous NISQ (Noisy Intermediate-Scale Quantum) devices, the present processor lacks quantum error correction (QEC), hence errors may accumulate during long calculations. Zuchongzhi 3.0's inability to perform time-consuming, complex calculations for real-world tasks like cracking cryptographic techniques does not influence current encryption methods.

Given the rapid development of quantum hardware, the next step may focus on fault tolerance and error correction, two crucial components of large-scale, practical quantum computing. USTC uses Zuchongzhi 3.0 to fix surface code problems. Experts expect economically important quantum advantages in materials science, finance, medicine, and logistics in the coming years if current rates of improvement continue.

With both countries investing substantially and making progress alternately, quantum computing has become a key frontier in the U.S.-China technology race.

[govindhtech]

What Is NISQ Era, It’s Characteristics And Applications

The Noisy Intermediate-Scale Quantum (NISQ) period, coined by physicist John Preskill in 2018 to describe quantum computers then and now, describes quantum computing. Although these devices may conduct quantum processes, noise and errors limit their capabilities.

Describe NISQ Era

NISQ devices typically have tens to several hundred qubits, although some have up to 1,000. Atom Computing's 1,180-qubit quantum processor reached 1,000 qubits in October 2023. IBM's Condor has over 1,000 qubits, although sub-1,000 CPUs are still common in 2024.

Characteristics

Key features of NISQ systems include:

Qubits' quantum states last for a short time.

Noisy Operations: Hardware and environmental noise can create quantum gate and measurement errors. Quantum decoherence and environmental sensing affect these computers.

Due to a paucity of quantum error correction resources, NISQ devices cannot continuously discover and repair errors during circuit execution.

Hybrid algorithms: NISQ methods often use classical computers to compute and compensate for quantum device constraints.

Situation and Challenges

Situation and Challenges Even though quantum computing has moved beyond labs, commercially available quantum computers have substantial error rates. Due to this intrinsic fallibility, some analysts expect a ‘quantum winter’ for the business, while others believe technological issues will constrain the sector for decades. Despite advances, NISQ machines are typically no better than traditional computers at broad problems.

NISQ technology has several drawbacks:

Error Accumulation: Rapid error accumulation limits quantum circuit depth and complexity.

Limited Algorithmic Applications: NISQ devices cannot provide fully error-corrected qubits, which many quantum algorithms require.

Scalability Issues: Increasing qubits without compromising quality is tough.

Costly and Complex: NISQ device construction and maintenance require cryogenic systems and other infrastructure.

It is unclear if NISQ computers can provide a demonstrable quantum advantage over the finest conventional algorithms in real-world applications. In general, quantum supremacy experiments like Google's 53-qubit Sycamore processor in 2019 have focused on problems difficult for conventional computers but without immediate practical applicability.

Developments

New innovations and exciting uses Despite challenges, progress is being made. Current research focusses on qubit performance, noise reduction, and error correction. Google proved Quantum Error Correction (QEC) is practical and theoretical. Microsoft researchers reported a dramatic decrease in error rates utilising four logical qubits in April 2024, suggesting large-scale quantum computing may be viable sooner than thought.

Chris Coleman, a Condensed Matter Physicist and Quantum Insider consultant, says dynamic compilation strategies that make quantum systems easier to use and innovations in supporting systems like cryogenics, optics, and control and readout drive advancements.

Applications

NISQ devices enable helpful research and application exploration in several fields:

Quantum Chemistry and Materials Science: Simulating chemical processes and molecular structures to improve catalysis and drug development. Quandela innovates NISQ-era quantum computing by employing photonics to reduce noise and scale quantum systems.

The Quantum Approximate Optimisation Algorithm (QAOA) and Variational Quantum Eigensolver (VQE), which use hybrid quantum-classical methods, are designed for NISQ devices to produce practical results despite noise. Optimisation Issues: Manage supply chain, logistics, and finance.

Quantum Machine Learning: Using quantum technologies to process huge datasets and improve predictive analytics.

Simulation of quantum systems for basic research.

Although they cannot crack public-key encryption, NISQ devices are used to study post-quantum cryptography and quantum key distribution for secure communication.

Cloud platforms are making many quantum systems accessible, increasing basic research and helping early users find rapid benefits.

To Fault-Tolerant Quantum Computing

The NISQ period may bridge noisy systems and fault-tolerant quantum computers. The goal is to create error-corrected quantum computers that can solve increasingly complex problems. This change requires:

Improved Qubit Coherence and Quality: Longer coherence periods and reduced quantum gate error rates for more stable qubits. Improved Quantum Error Correction: Effective and scalable QEC code creation. For fault-tolerant quantum computers, millions of physical qubits should encode fewer logical qubits.

Having far more qubits than NISQ devices' tens to hundreds.

New Qubit Technologies: Studying topological qubits, used in Microsoft's Majorana 1 device and designed to be more error-resistant.

As researchers develop fault-tolerant systems, observers expect the NISQ period to persist for years. Early fault-tolerant machines may exhibit scientific quantum advantage in the coming years, with comprehensive fault-tolerant quantum computing expected in the late 2020s to 2030s.

In conclusion, NISQ computing is a complicated industry with challenging difficulties to overcome, but it is also a rapidly evolving stage driven by a dedicated community of academics and commercial specialists. Advancements lay the groundwork for quantum technology's revolutionary potential and the future.

[govindhtech]

AMO Qubits: Scalable Decoding for Faster Quantum Computing

AMO Qubits Faster

Recent advances have made atomic, molecular, and optical (AMO) quantum computers possible. Despite its scalability and long coherence lengths (the time qubits can stay in their quantum state), syndrome extraction has always been slow, limiting AMO approaches. Syndrome extraction is a crucial measuring process in  quantum error correction that gives fault information without altering qubit quantum states. This slow technique hinders functional quantum computation with AMO qubits.

Riverlane experts and the University of Sheffield conducted the investigation to accelerate quantum error correction, particularly surface code decoding using AMO qubits. Surface codes are one of the best solutions to prevent quantum information mistakes. Decoding involves repairing errors without affecting quantum state.

Fast transversal logic, which speeds up quantum operations, disrupts structural properties that allow real-time decoding techniques like lattice surgery. Transversal logic may reduce syndrome extraction rounds, increasing the logical clock rate, or quantum computation speed. Its incompatibility with effective decoders was a problem.

The researchers created two novel windowed decoding methods to avoid this. These new protocols restore modularity and locality to overcome the decoding challenge. By restoring modularity and locality, decoding becomes easier.

In numerical simulations with the Stim quantum circuit simulator, performance improved significantly. Compared to lattice surgery, the revolutionary approaches accelerated transversal logic by an order of magnitude. This significant speedup increases computational cost slightly.

Additional simulations showed that “Ghost Decoding” worked. This approach suppressed errors exponentially as code distance, a measure of error correction code efficacy, increased. Importantly, the simulations showed that even at vast distances, “Ghost Decoding” did not require more decoding runs than the code distance, making it possible for general deployment.

The study also stressed the importance of properly adjusting parameters like decoding passes and “ghost singletons,” which are artificial mistake measures to improve accuracy. The quantum circuit structure determines the number of decoding passes, which increases as transversal CNOT gates approach closer. This flexibility is needed to support quantum algorithms and hardware limitations.

Our unique windowed decoding approaches overcome AMO qubits' slower syndrome extraction tempo, a major limitation. This work proves that large-scale algorithms can run on the promising AMO platform by increasing the logical clock rate by an order of magnitude with no overhead. Future research will analyse these protocols' shortcomings and develop better error correction methods to reach fault-tolerant quantum computation.

Publicly releasing simulated Stim circuits shows a commitment to reproducibility. The research “Scalable decoding protocols for fast transversal logic in the surface code,” by Mark L. Turner, Earl T. Campbell, Ophelia Crawford, Neil I. Gillespie, and Joan Camps, presents these methods and their results.

Understanding Transversal Logic Transversal logic is used in quantum computing, specifically for logical operations on encoded qubits. Quantum error correction codes like the surface code encode quantum information over numerous physical qubits to prevent errors. Quantum computation uses logical gates to process encoded data.

Transversal logic allows quantum operations on encoded qubits without physical modification. The alternative is “exploit higher connectivity.” Logical gates can be applied across encoded qubits in a simpler, often local fashion to transversal logic instead of lattice surgery's complex measurement sequences.

Sources say transversal logic's key benefit is increasing the logical clock rate. The logical clock rate is the speed at which error-corrected logical qubits can perform quantum calculations. Reducing syndrome extraction rounds speeds up calculations. As indicated, AMO syndrome extraction is slow. Transversal logic reduces these rounds, speeding computations.

Lattice surgery, an effective decoding method, struggles with rapid transversal logic. Transversal logic violates structural properties needed for real-time lattice surgery decoding, sources say. The localised nature of faults and error syndromes during typical operations may explain these structural traits, which help decoders analyse information. Transversal logic alters its structure, making real-time decoding harder.

Research in the news item addresses this conflict. Researchers have created new windowed decoding protocols that return modularity and locality to decoding to take advantage of transversal logic's performance advantages while preserving efficiency. This avoids the decoding bottleneck and enables transversal logic's order-of-magnitude speedup.

Transversal logic promises to speed up processing by reducing syndrome extraction overhead for quantum operations on encoded qubits. Due to improved protocols that eliminate this conflict, transversal logic, notably for AMO qubits, can now be decoded faster.

[govindhtech]

Tesseract Algorithm For Quantum Error Correction

Tesserat Algorithm

Nord Quantique's Tesseract code has revolutionised quantum error correction and advanced fault-tolerant, scalable quantum computing. This feat marks a turning point in quantum technology development, leading to new methods and possibilities.

Nord Quantique is creating cutting-edge quantum computers using bosonic codes, which take advantage of photon redundancy. In quantum modes, these boson particles directly introduce error resilience. Bosonic codes can do this, unlike qubit-based systems. Instead of using discrete two-level systems (qubits) to encode information, bosonic codes use quantum modes' continuous photon spectrum.

Nord Quantique developed the bosonic Tesseract code to secure quantum data from errors. Photon quantum states are organised using the Tesseract code, which resembles a four-dimensional cube. The code's structure makes errors easier to spot than other methods.

By using photon redundancy, Nord Quantique's architecture directly addresses a major quantum computing development obstacle. This helps the company develop scalable, fault-tolerant quantum technologies.

Nord Quantique considers bosonic codes a quantum error correction revolution. This technology is believed to make building quantum computers with logical qubits easy, avoiding usual system inefficiencies. Popular quantum platforms struggle to provide an error-resistant logical qubit without millions of physical qubits.

However, bosonic codes eliminate this enormous burden. Traditional systems sometimes require data center-scale hardware and have prohibitive running expenses due to scaling problems to achieve quantum computing performance levels.

Nord Quantique avoids these crucial hurdles using bosonic codes. This streamlined method simplifies fault-tolerant quantum system construction. Beyond reducing hardware, our strategy accelerates the transition from experimental prototypes to utility-scale quantum systems with real-world applications.

Multimode bosonic codes improve error correction, which is necessary for fault tolerance. Bosonic codes efficiently encode quantum information using photons in quantum modes. Due to photon redundancy, this can also correct for natural flaws.

Even though single-mode GKP codes have shown error robustness, their scaling concerns in actual applications highlight the need for better architectures. Multimode codes like the Tesseract code distribute logical information among interconnected bosonic modes to cover this gap. This distribution enhances quantum system stability and fault tolerance.

Nord Quantique embeds a logical qubit into two bosonic modes using the Tesseract technique, a milestone. This design improves error correction with higher-dimensional phase space. This approach enhances error detection and addresses photon loss, a major photonic system shortcoming. Tesseract code structure simplifies quantum state control and improves hardware stability. The Tesseract method is expected to outperform single-mode GKP qubits by an order of magnitude under optimum conditions.

Significant Tesseract Code Implementation Developments:

Nord Quantique demonstrated hardware-efficient scalability with autonomous quantum error correction using the Tesseract algorithm. Tesseract encodes logical qubits over many bosonic modes to increase error thresholds. Importantly, it does this with a minimal hardware footprint, unlike standard qubit architectures that require hundreds of physical qubits to provide equal robustness.

Real-time error insights: Tesseract's extra quantum modes provide custom error detection features. Tesseract code leakage problems can be prevented when the qubit's quantum state leaves the encoding space. This suppression is aided by real-time confidence scores from mid-circuit measurements during quantum computation.

Path to FTQC: The Tesseract code's intrinsic architecture shows how multimode bosonic codes can efficiently improve quantum error correction. This solution avoids incremental scaling inefficiencies in typical systems. Tesseract redefines and speeds up fault-tolerant quantum computer development by condensing QEC functionality into fewer physical components.

The deployment of the Tesseract code marked a turning point in Nord Quantique's development path. It lets you build logical qubits with error correction from the start. This eliminates the need to scale up many physical qubits to ensure error resilience. Higher-dimensional bosonic codes like the Tesseract code improve quantum error correction without increasing hardware complexity.

It embeds deeper error-detecting mechanisms in multidimensional phase space. A common trade-off between quantum system size and computing precision is avoided by this unique method. Fault tolerance is achieved with little physical resources.

The company welcomes anyone interested in this breakthrough to learn more. Technical papers and news releases are available for further investigation.