math-phi

[math-phi]

述語論理における妥当式とトートロジーその４（これ絶対そこまで大事じゃない…）

・その3

・その2

・その1

！本稿から、「ならば」の論理記号を「⇒」にしました！

今回で終わりです。（おそらく）

前回のまとめ

∀xFx∨¬∀xFx　これはトートロジー

∀xFx⊃∃xFx　これもトートロジー

∀xFx⊃Fa　これはトートロジーではない

結局、述語論理においてトートロジーなんていうものは考えられない。これが結論に��りそうです。そもそも、トートロジーは命題論理で出てきた概念であって、それを述語論理に移したとき、それに対応するものが存在することなど保証されていません。

しかし、『論理学』(野矢茂樹)には、

妥当式のすべてがトートロジーというわけでは、もちろんありません。(p.102)

とある。

つまり、述語論理においてもトートロジーと妥当式はしっかり分けられる。

その分け方について長々と、「その4」まできたわけだが、ついにわかった。

まず、トートロジー：原子命題においてどのような真理値を割り当てても、全体が必ず真（つまり1）になっている論理式、であるので、この定義をそのまま述語論理にも適用する。

※原子式＝原子命題を表す記号、原子命題＝否定詞も接続詞も含まない命題

述語論理での原子式はどうなるのか？

∀xFx∨¬∀xFx　この論理式における原子式は、Fxである。（つまり量化を無視する）

つまり、Fx∨¬Fxとしてトートロジーかどうかを判別すればよいのである。

（これって僕の考えていたことと似ているじゃん）

∀xFx⇒∃xFx　これの場合は、Fx⇒Fxと考えるので、

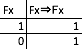
ということで、こいつらはトートロジーになる。

しかし待て。この考え方だと、∃xFx⇒∀xFxもトートロジーになりやしないか？

答えはyes。実はそうなる。明らかに誤っている（そもそも何を以って誤っていると言えるのだろうか？）のに、トートロジーになる。

つまり、述語論理において、妥当式とトートロジーの関係性は下のようになっている。

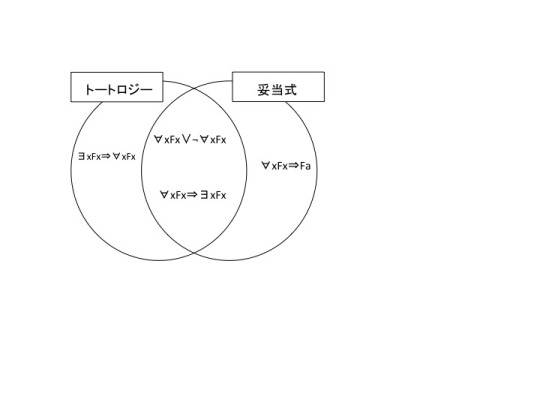
あまり納得いかないが、そういうことで。

これそこまで大事じゃないからここらで決着ということで。

end

[math-phi]

疑問点走り書き

・述語論理の妥当式、トートロジー（述語論理の基本定理ほか）

・ラッセルパラドクス、包括原理、縮約規則

・外延性公理

・ならば（⇒）、同値（⇔）の差異

・基本法則Vが悪いのかどうか

[math-phi]

『記号論理入門』メモ、第１章

『記号論理入門[新装版]』（前原昭二、日本評論社、2005）いいことばっか書いてある！

痒い所に手が届く感じ。特に、びっしりの注釈ゾーンは本当に論理学するためのポイントが詰まっている。（命題と命題関数の話とか、集合の話とか、変数の話とか、外延の話とか、etc...）

・命題は真（1=1）か偽（1=2）

では、a=1、a=bは？

変数を含む命題、x+3=xyを（この命題をF(x,y)とおく）考えてみると、F(1,4)は真だが、F(2,2)は偽

・∀x(f(x)=0)は恒等式、∃x(f(x)=0)は方程式

・F(x)のF( )を述語(predicate)と呼ぶ。そして、概念、条件、集合、こいつらは述語、性質と同じものだと考えることができる（やはり述語記号はF( )のことだったんだな）

命題関数F(x)を〈xはFである〉と読むとすれば、F(　)は〈・・・はFである〉という部分に相当します。その意味でF(　)のことを述語(predicate)とよびます。また、F(x)を〈xはFという性質をもつ〉と読みますならば、定数aに対して命題f(a)が正しい場合、このFはaのもつ1つの性質であると考えることもできるわけです。

ー『記号論理入門』p.5,line.1

概念とか条件とかいう言葉もあります。しかしそれらは、形式的に割りきって考えてしまえば、結局のところ、いずれも〈述語〉とか〈性質〉というものと区別する必要はないものです。

ー『記号論理入門』p.8,line.2

・ある性質Fをもつ具体的な個物があり、一方で、その性質のみを抽象的に考えたものを概念と呼ぶ。しかし、論理学では、性質Fをもつ個物たちと、概念そのものを同一視する。だが、ふつう、〈・・・は人間である〉という性質そのものと、〈人間〉という概念は、それぞれ別のイメージを我々に抱かせる。

しかしながら、われわれの記号論理学は、そのような人間心理の微妙な差異を区別し得る程には精巧なものではありません。そのように曖昧なものをそのまま受け入れるには、あまりにも明皙なものであり過ぎるのであります。

ー『記号論理入門』p.8,line.12

・概念には2つの側面がある。

ある〈性質〉：内包(intension)

その性質を持つもの全体からなる〈集合〉：外延(extension)

・外延性公理（これのこと→）　∀x(x∈F⇔x∈G)⇒F=G

FとGをともに性質と考える場合にも、また集合と考える場合にも、〈FとGは等しい〉とか〈FとGは同じである〉といいます。とくに集合と考える場合には、この命題は ∀x(x∈F⇔x∈G) と表され、これを簡単に F=G と書きます。

ー『記号論理入門』p.11,line.18

（ (※) ∀x(x∈F⇔x∈G)⇒F=G に対して）これは当りまえのことであります。しかし、場合によっては、集合に関する＝が、このこととは無関係に定義されていると考えることがあります。それはとくに、〈集合〉を〈もの〉と考える場合であります。[いまのわれわれは、〈集合〉と〈もの〉とを区別して考えているのですが……]。そうして、〈もの〉一般について、＝というものがあらかじめ定義されてしまっているようなときには、この(※)はもはやけっして自明ではなくなります。少なくとも、＝の定義から明らか、というわけにはいかぬ場合が起ります。とはいうものの、われわれの集合に対する直観は、この(※)がつねに成立することを要求しますので、そのような場合には、われわれは、この(※)を集合に対する1つの公理と考え、それを外延性の公理(axiom of extensionality)とよびます。

ー『記号論理入門』p.11,line.27

・[Q]この外延性の公理について、＝がもの一般について定義されていると自明でなくなる理由がわからないな。集合に関する＝が、このこととは無関係に定義されているときっていつだよ。（なにはともあれ僕には自明にしか見えない・・・）

・∀x(F(x)∧G(x))は命題で、F(x)∧G(x)は命題関数

・同値の定義

(A⇔B)⇔((A⇒B)∧(B⇒A))

・[Q]【FはGでない】の表現方法が4通りあるけれど、意味はすべて異なる。しかし僕には違いがわからない。

∀x(F(x)⇒¬G(x))

¬∀x(F(x)⇒G(x))

∀x(F(x)⇔¬G(x))

¬∀x(F(x)⇔G(x))

1と2、3と4の違い（部分否定なのか全部否定のか）はわかるが、1と3、2と4の違いがわからない。ベン図で考えればわかるやもしれん。⇔と⇒の差異がまだ曖昧なんだな。

・F(x)は1変数xの命題関数

・∀xF(x)、∃xF(x)は命題を表す（つまり真偽が定まる）

・∀xF(x,y)、∃xF(x,y)は1変数yの命題関数

・見かけ上の変数（例えば、∀xとか∃yという限定作用素の作用範囲における変数x,y）を束縛変数、それ以外の変数を自由変数

・∀x∀yF(x,y) 　これは命題で、x,yは束縛変数

・∃x(ax^2+bx+c=0)においては、xが束縛変数、a,b,cは自由変数（a,b,cの値により、この命題の真偽が定まる）

・∫f(x)dxにおいても、xが束縛変数と考えられる

疑問点いくつか残るので、解決したらまた書く。

束縛変数、自由変数についての理解がまだ甘い気がするなぁ。

[math-phi]

論理学の本

・『論理学』（野矢茂樹、東京大学出版）

命題論理、述語論理、メタ論理、直観主義論理、ゲーデルの不完全性定理と論理学の概観を一気につかむといったところ。現在、読み途中[2015-12-28]。この本、僕はわかりやすくて良いなと思ったけれど、厳密に学ぶものとしては相応しくないとの声を各方面からいただいてしまっている。ということで、本当に厳密に論理学するなら他の本に移行する必要があるのかもしれない。個人的には、わかりやすいし入りやすい良い本だとは思っている。内容も薄っぺらいわけではないし。ただ、ゲーデルの不完全性定理まで詰め込むとかはやり過ぎだと感じた。ゲーデル入れておくと売れるからだとかなんとか…。ひぇえ。

・『記号論理入門』（前原昭一、日本評論社）

記号論理学のかっちりした教科書、だと思う。新しい用語が出てくるときは、それをしっかり定義してあるので、迷子になっても前頁へ戻って、理解を確認することができる。『論理学』では扱わない推論図を用いて証明が進んでいくのも、よい。ただし扱う範囲は命題論理がメイン。ただ、補遺の充実度が満腹必至。

・

[math-phi]

包括原理

前回?の続き

参考文献

包括原理と自然数(矢田部俊介,2006)

https://proofwiki.org/wiki/Definition:Comprehension_Principle

http://sigswo.org/papers/SIG-SWO-A404/Property.pdf

『包括原理と自然数』には、包括原理の説明（たぶん定義ではない?）がこうある。

任意の ϕ にたいし {x : ϕ(x)} の形の集合の存在を保証する。

そしてこう続く。

包括原理は非常に強力な集合の存在保証原理であり、古典論理の上では矛盾 (Russell Paradox) を導く。

まずは前半から見ていこう。これはつまり、任意のΦ（これはたぶん概念のこと）があったとき、Φを満たすものから構成される“集合”がありますよ！ということだろう。

英語の定義？も調べてみると、こんな風に書いてあった。

The comprehension principle states:

Given any property, there is a set which consists of all objects having that property.

comprehension principle:包括原理

property:特性、固有性

set:集合

object:対象

(Property と言う用語には異なる複数の意味があるのでここで整理しておきたい． ・論理学用語 論理学では Property とは単項述語をさす．すなわち human(X)の human は red(X)の redと同様 Property と呼ばれる． Sort 論理では sortal と言う概念を導入することによって上の混乱を避けている．human は sortal であり，red は nonsortal であり，両者は区別される．しかし，真理値を持つ通常の述語と Sort 述語を区別するという目的はあるものの，あくまでも Property の分類をしていると言うことでは変わらない．

ーhttp://sigswo.org/papers/SIG-SWO-A404/Property.pdfより引用)

まあ和訳すれば、「ある性質を考えるとき、その性質を満たす対象からなる集合が存在する」といったところか。

こういうところに集合論や論理学を厳密に考える難しさがあると思っていて、というのも、普段の生活では何かが存在していることを敢えて明言したり気にかけたりしない。

何らかの性質がありそれを満たす対象があること、それらを集め一塊とみなしたものが“確かにある”こと、（それらを要素とする集合が存在すること）こんなことは言うまでもなく、認めることだと思っている。でもそうではない。そうではないのだ。

集合が存在することすら、許可がなければ考えられない・・・。

（…まじ?）

よし。とにかく、これで、包括原理についてはわかった。その問題点（包括原理は非常に強力な集合の存在保証原理であり、古典論理の上では矛盾 (Russell Paradox) を導く。）を見てみよう。

(包括原理と自然数を参照)

はい。わからぬ。

どこまでが古典論理の範囲内の話で、どこまでが包括原理の話なのか整理しよう。

Φ(x)=x∉x と考えれば、集合 R = {x : x ∉ x}が存在することは包括原理から保証される。つまり、最初の部分は包括原理に依っている。

となると、その後の部分（R∈Rの部分？）が古典論理に依っている部分ということか。

[疑問点]

R∈Rの部分が古典論理に依っているのかどうか。（古典論理の上で矛盾を導く、と言うとき、何を指して「古典論理の上で」とついているのか）

と思い、いろいろまた調べているとやはりytbさんのブログ（ラッセルのパラドックス：傾向と対策 (3.1.0) : 古典論理を制限するラッセル・パラドックスへの証明論的アプローチ（縮約規則！） - あいまいな本日の私（旧））に辿り着く。しかもこのブログ、今回書いてるネタそのものじゃないか！っていう。

それによると、

この縮約規則が、パラドックスにおける矛盾の導出に大きな役割を果たしていることはすぐにわかります。

1.ラッセル・パラドックスで実際に証明しているのは以下の二つ ・R∈R→( R∈R→⊥) ・(R∈R→⊥)→ ( (R∈R→⊥)→⊥) 2.ところが、縮約規則によって以下が（包括原理を持つ集合論の定理として）導出される ・R∈R→⊥ ・(R∈R→⊥)→⊥ 3.従って、2の上式と下式から、modus ponens より矛盾が導出される。 ということです。この証明のやり方で矛盾を導出するには、縮約規則は不可欠です。

とのことです。（このブログでは、→がならばで、⊥が矛盾を表している）

えーとつまりどういうことだ。

縮約規則がなかったら、R∈R→( R∈R→⊥) までしか言えないってことか。

ブログには、ラッセルのパラドクス導出の手順がこう書いてある。

R={x: ?(x∈x)} は包括原理のより存在を保証され、 任意のx について x∈R ⇔ ? (x∈x) を満たす。xにR自身を代入すれば R∈R ⇔ ? (R∈R) となる。 つまり R∈R ⇔ R∈R→⊥ である。

⇔の片側をとり、 R∈R→( R∈R→⊥) が導出される。

古典論理上の縮約規則 (the contraction rule) より、R∈R→⊥ が導出される。

この2番目がしっくり来てないのだな。

「⇔の片側をとる」ってなに？

つづく。

とりあえずまとめておくと、

ラッセルのパラドクスが生まれる原因は、包括原理と古典論理（縮約規則）の２つ。しかし僕は縮約規則の方がいまいちまだ理解に至っていない状態。

[math-phi]

述語論理における妥当式とトートロジーその3（そこまで重要かこれ？）

前回、前々回の続き

おさらい。述語論理のトートロジーと妥当式の具体例。(こいつらすべて妥当式)

∀xFx∨¬∀xFx　これはトートロジー

∀xFx⊃∃xFx　これもトートロジー

∀xFx⊃Fa　これはトートロジーではない

さて、改めて、述語論理におけるトートロジーってなに？ってことで。

図書館で論理学関連の著作を漁っていたら、見つけました。(※著作名を失念しました。調べておきます。)

さてさて、書いてあるじゃないですか。

述語論理のトートロジーは、命題論理のトートロジーの原子命題を述語論理の任意の文に書き換えたものである。

あれ？やっぱり僕の考え方は正しかったのでは？

僕は、∀xFx⊃∃xFxが妥当式(恒真)だけれどトートロジーでないと思っていました。なぜかと言うと、この論理式を命題論理に無理やり戻すと、A⊃Bになるからです。（A:∀xFx、B:∃xFx、∀xFxと∃xFxは別の命題なので、A、Bという別の命題で表現しなければいけません）すると、A⊃Bは、命題論理においてトートロジーではないので、ゆえに∀xFx⊃∃xFxはトートロジーでないと判断できる！と、考えたからです。

一方、∀xFx∨¬∀xFxは妥当式かつトートロジーの例になりえるのじゃないかと思いました。というのも、∀xFx∨¬∀xFxを命題論理に無理やり戻すと、A∨¬Aになります。これはAの真理値に依らず常に真です。つまりトートロジーなのです。

この説明を先生にしたところ、命題論理での考え方を勝手に述語論理に応用している?から不適当だと言われました。そして、∀xFx⊃∃xFxはトートロジーで、∀xFx∨¬∀xFxもまたトートロジーだと言われました。

いやでも、この本の定義に従うと、∀xFx⊃∃xFxはトートロジーじゃないと思うんだよなあ。わからん。

述語論理の基本定理:述語論理の恒真性＝トートロジー＋量化記号

とにかく“述語論理の基本定理”とやらを調べればわかりそう。しかしGoogleで検索しても出てこない。図書館で調べてまた書きます。

つづく。

続き！

[math-phi]

ラッセルのパラドクスの解決法（what is 包括原理?）

論理学界隈で有名？なytbさん(@ytb_at_twt)のaskに質問したところ、なんと返事がいただけたので。質問と答えについて少し。

https://ask.fm/ytb_at_twt/answers/132860309834#_=_

質問：ラッセルのパラドクスの3つの解決策とは、「タイプ理論」と「公理的集合論の分出公理」と、もう1つはあと何ですか？そもそも、前に挙げた2つの解決策は理解として正しいですか？

回答：ラッセルのパラドクスの3つの解決策とは ①言語を制限するが論理は保持する（型理論） ②言語と論理は保持するが包括原理は制限する ③言語と包括原理は保持するが論理は制限する（非古典論理上の素朴集合論） です。②に関し、もちろん分出公理は包括原理の制限されたフォームの一つですが、置換公理や無限公理なども同じく制限されたフォームであるため、分出公理だけ取り上げるのはフェアではないかもしれません。

ほうほう。僕はいくつか勘違いをしていたようです。

ラッセルのパラドクスに対する解決法は2つだと思っていたということ。→３つ

分出公理はパラドクス解決方法の代表。→分出公理は、あくまで解決方法の1つである「包括原理の制限」のうちのある特定の場合に過ぎない。

回答にある解決方法3つを見ていく。

①型理論

これはいわゆるタイプ理論。

気になるのは、これが、言語を制限するが論理は保持する場合の解決法であるということ。この「言語を制限する」とはつまり、“AはBである”みたいな文章がタイプ理論に従うと、BのタイプがAのタイプより1つ上でなくてはならない点で制限されている、という意味だろうか。

個人的にはタイプ理論は素晴らしいと思っていて、その理由は筋が通っているから。階層を考えて、パラドクスが生じないようにかっちり説明できるから。(＝論理は保持しているから?)

ちなみに、②と③を見てみると、②言語と論理は保持するが包括原理は制限する、③言語と包括原理は保持するが論理は制限する、とある。ホウ・・・。

ここで、“言語”、“論理”、“包括原理”が三竦みの関係だと考えると、タイプ理論は「論理と包括原理は保持するが言語は制限する」となる。

でも回答では、「言語を制限するが論理は保持する」となっている。・・・包括原理は？包括原理は保持しないの？そもそも包括原理ってなんや？

②言語と論理は保持するが包括原理は制限する（分出公理がいい例）

いや、②も③も包括原理を理解しないと始まらないので、包括原理について調べました。

包括原理ってなんですかね。（http://blog.livedoor.jp/s-koide/tag/%E5%8C%85%E6%8B%AC%E5%8E%9F%E7%90%86）ここから引用しました。

∃y∀x[(x∈y) ⇔ Φ(x)]   ただし y は Φ(x) 中で自由ではない.

これが包括原理ですね。

えーと、とりあえず長くなりそうなので、改めて包括原理について書きます。

つづく。

続きを書きました。(2015-12-28)

[math-phi]

述語論理における妥当式とトートロジーその２（ほぼ解決）

前回の続き

！※前回の記事の最後に書いた「・一階の述語論理でも、妥当式＝トートロジーである」は誤りでした。

この前まで、妥当式とトートロジーの違いがわかっておりませんでしたが、多分わかりました。

『論理学』p.100辺りをしっかり読みました。見えてきました。その全貌が。

まずそれぞれの語句の意味を押さえます。

妥当式：論理記号の意味のみによって真となる論理式

逆に、論理記号でないものとは、定項、述語記号、議論領域のことです。つまり、[定項、述語記号、議論領域の]解釈に依らず、常に真となる論理式が妥当式だというわけですね。（※論理記号は、x,yとかの変項、¬、∧、∨、⊃、⇔、∀、∃、あとは括弧とか?）

いやまだわからぬ。具体的に１つずつ確認する。

定項：変更の値となる固有名。（命題関数Fxにおいて、Faを考えるときのaのこと）ここでいう、定項の解釈とは、設定された議論領域D内において具体的な個物をいれていく作業のこと。

述語記号：これがいまいちわからない。おそらく、述語記号は、命題関数FxでいうところのFのことであろう。述語記号の解釈っていうのは、具体的にどういった命題にするかってことだろう。“Fxy”を“x���yを愛する”にするのか、“xはyを憎んでいる”にするのかどっちにするのか。

議論領域：これは簡単。設定された対象の範囲。議論領域の解釈は、範囲をどこに設定するのか。例えば議論領域を人間と解釈すると、変項には佐藤くんやら山田さんなどが入る。

さて、整理が終わった。妥当式は、以上見てきた「定項、述語記号、議論領域」の解釈によらず真、つまり、「定項、述語記号、議論領域」の解釈がどんなものであっても真。

「わかんねえよ！そろそろ具体例くれよ！」ってことで、具体例。

述語論理の妥当式たちはこういうやつだ

∀xFx∨¬∀xFx

∀xFx⊃∃xFx

∀xFx⊃Fa

はあ確かに、「aに何を入れても、どんなFでも、どんな議論領域でも」こいつらは成り立つな。

※「xに何を入れても、どんなFでも、どんな議論領域でも」じゃないよね？定項ってaのことだよね？xは変項だよね？

さて、疑問点のもう一つ。トートロジーってなんやねん問題にいきますか。

命題論理においては、「トートロジー＝妥当式」でしたが、述語論理においては違います。

妥当式のすべてがトートロジーとは限らないのが述語論理です。つまり、「トートロジー⊂妥当式」です。妥当式より嚴しい条件なのがトートロジーです。

ではさっきの具体例のうち、どいつがトートロジーで、どいつがトートロジーでない例なのかというと、

∀xFx∨¬∀xFx　これはトートロジー

∀xFx⊃∃xFx　これもトートロジー

∀xFx⊃Fa　これはトートロジーではない

なるほど。しかし、いまだトートロジーの定義がわかりません。そして調べてもよくわかりません。上の３つは先生に判定してもらっただけです。

ちなみに、『記号論理入門』(前原昭二)に、すべてのトートロジーは古典命題論理の範囲で証明可能（���(古典)命題論理の完全性）とありました。でもこれはあくまでも命題論理の話なんですよね。今、気になっているのは述語論理のトートロジーです。

ただ、具体例の一番下の∀xFx⊃Faがトートロジーでないってのはなんとなくわかります。これ、aが定項ですよね。だから、これが真になるのは、x=aのときなんですよ。ってこれなんか可笑しいな？

わっかんねー。てことで次回に続きます。（解決してない…）

次回に続きました！(2015-12-27)

◯疑問点

・述語記号とは何か？

・述語論理のトートロジー

参考文献

http://math.stackexchange.com/questions/629198/validity-vs-tautology-and-soundness

http://math.artet.net/?eid=1412322

https://www.sist.ac.jp/~suganuma/kougi/other_lecture/SE/math/logic/logic.htm

[math-phi]

フレーゲの基本法則Ⅴが持つ問題点（外延がダメなのではない）その２

前回の続き？

「外延という考え方に問題はない。問題は基本法則Vにある！」ということがイマイチ理解できていませんが、少し理解できた気がするので少し書いておく。

そもそも外延はほぼ集合と同じ。（厳密には異なるものの、いまやほとんど同じことになっている by先生）つまり、集合の考え方に問題はないなら、外延の考え方に問題はないことと同じ。そう思っていたのですが、この書き方は少しよくなかった。

集合論（外延）には問題が大ありなのです。その問題を放置したままにしておくと、俗にいうラッセルのパラドクスが生まれてしまうのです。

だから、ラッセルや論理学者たちは、その問題点を封じる方法を編み出してきたのです。

ラッセル：タイプ理論

論理学者たち：公理的集合論（分出公理）

そして、その問題点の出処がいわゆる、内包公理です。

（ラッセルの≒無制限な）内包公理：すべての命題Fに対してFxを満たすようなxの集合が存在する

∃G∀x(x∈G⇔Fx)

※この論理式が正しいのか不安。要調べる。

つまり内包公理は、ある概念があったとしたら、それを満たすような（その外延となる）要素の集合があるよね！ってこと。もしこのとき、ある概念として“自分自身を要素として持たない”をやってしまうと、ラッセル���パラドクスが生じる。こういう流れ。だから、そういったことが生じないように、以下の様な方法をとる。

ラッセルのタイプ理論：タイプで考えるのでパラドクスは回避

公理的集合論：分出公理にしてしまう（対象がないところに対象を作り出すことはできない。つまり、すでにある対象からしか対象をとってくるしかない。＝分出公理が言いたいこと）

フレーゲの第V法則：任意の概念F,Gについて、Fの外延とGの外延が同一であるのは、すべての対象aについてFaであるのはGaであるときに限る

これを論理式で書きたい。外延を集合と同一視?すれば下のようになる。（※外延を表現する論理記号を持たないので、集合を扱う論理記号を拝借する）

{x|F(x)}={x|G(x)}⇔∀x(F(x)⇔G(x))

左辺：Fの外延とGの外延が同一、右辺：すべての対象についてFa=Ga

さて、ラッセルの視点からこの第Ⅴ法則を評価してみると、第Ⅴ法則は外延（という本当は二階のもの）を一階の対象として扱っているので可笑しい、と指摘できる。

つまり、左辺は二階の話で、右辺は一階の話なのに、フレーゲはその階数を気にしていないので駄目だ、というわけである。（第Ⅴ法則において、左辺から右辺で階数が一つ下がっている、と考えたのがラッセルのアイデアなのだ）

という話を今日、先生と少ししてきたのだけど、わかったような、わからないような…まだまだ第Ⅴ法則ネタは続く。つづく…

このブログすげえ・・・公理的集合論の話とかいろいろ載っている。

反復的集合観と公理的集合論 - 再帰の反復

[math-phi]

実数の定義（論理主義の）と有理数の稠密性

『数学を哲学する』§論理主義の最後ら辺（p.159〜）で、ラッセルによる（デデキント切断の考え方を借りた）実数の定義が出てきました。

言い換えれば、断面とは、有理数からなる、最大メンバーをもたない連結で有界なクラスである。断面は、有理数における「デーデキント切断」と呼ばれているものに対応している。ラッセルは、実数を断面と同一視した。(p.160,line.1)

…僕も一応、理系の端くれではあるので、デデキントの切断ぐらい知っている。（知っている≠理解している、理解している＝使うことができる）だからこの文章の内容をつかむことはまだできる。

つまりラッセルによると、「実数：有理数からなる集合」ということである。もちろん、『数学を哲学する』にちゃんと具体例が挙げられている。

・実数2は、2（すなわち、2/1）より小さいすべての有理数（正も負も）からなる集合

・2の平方根は、実数√2より小さいすべての有理数（正も負も）からなる集合

ここで疑問が一つ。

これ、異なる実数が同一の定義になりやしないか…？

何故そう思ったか、というと

有理数と実数を比べると、数直線上に並べたときに有理数はスカスカな一方、実数はギッシリしている。（これは実数の連続性、だよな?）

そして数直線を考えてみる。

 -------0----0.1--0.5----1----√2-----1.5---√3----2--------10----->

例えばまあ、こんな風になっているとしよう。

さてその上で、数直線をズームしてみよう。（Qは有理数、Rは無理数(実数)を表す）

ズーム。数直線をズームしてみる。すると以下のようになっていることは有り得るんじゃないか？

-------Q1--R1---Q2--------R2-------R3------>

この場合、R2とR3の定義になっている有理数の集合を構成する要素はどうなっているか。

R2⇒「Q2、Q1、Q0、Q-1、・・・」

R3⇒「Q2、Q1、Q0、Q-1、・・・」

あれ?これ同じやん…?

実数のほうが有理数より数が全然多い（ぎっしりしている）のだから、あいだに有理数の存在しない実数の2つ並びが考えられちゃうじゃないか!?と、思ったわけです。

-------

しかしこれは私の数学的知識（解析学の知識）が足りなかったゆえの誤解でした。

R2とR3の定義は同じになりません！なぜなら有理数の稠密性があるからです!

有理数の稠密性とは

【任意の実数xと任意のε>0に対し,ある有理数qで|x-q|<εを満たすものが存在する】

※http://www.dokugaku-math.net/?p=134　

※http://www004.upp.so-net.ne.jp/s_honma/archimedes/archimedes.htm

を参考にしました。（かっちり理解するためには解析学の教科書を読む必要がある。）

有理数の稠密性を、今回の場合にそった形で言うならば、【実数の任意の開区間は、必ず有理数を含む】

つまり、どのような実数の2つ並びを考えても、そのあいだに有理数が存在する。ゆえに、ラッセルの定義（デデキント切断）に誤りはなかったのです。

有理数の稠密性の証明は機会があれば。

[math-phi]

述語論理における妥当式とトートロジー

『論理学』p.100〜105あたりのおはなし。

トートロジーは述語論理の中で妥当式として再解釈されることになりますが、妥当式のすべてがトートロジーというわけでは、もちろんありません。(p.102,line.13)

ほほう・・・

「じゃあトートロジーじゃないけど妥当式なものってなんやねん？」といった疑問が浮かぶのは至極当然のことでしょう。でもそれがわからない…

そもそもトートロジーってなんだっけ？

→命題論理では、トートロジー：真理値分析の結果、原子式の真理値に���を入れても常に1になっているような命題

→妥当式：論理記号の意味のみによって真とされる論理式

Q.じゃあ命題論理での妥当式ってなんだ？

Q.命題論理では妥当式＝トートロジーじゃないのか？

Q.トートロジーと妥当式の違いってなに？！わからん！

と、いろいろ疑問点が浮かんできます。そこでネットの海を漁ってみると、ウィキペディアにそれらしい記述が！（https://ja.wikipedia.org/wiki/%E4%B8%80%E9%9A%8E%E8%BF%B0%E8%AA%9E%E8%AB%96%E7%90%86）

命題論理においては、論理公理 (logical axiom) と呼ぶ論理式の集合と、ある論理式たちから新たな論理式を導出する規則（推論規則）を導入し、論理公理から推論規則の有限回の適用によって得られる論理式全体とトートロジー全体が一致するようにすることができる（命題論理の健全性と完全性）。一階述語論理においても、適切に論理公理と推論規則を導入することで、論理公理から推論規則を使って導出される論理式全体と恒真論理式全体が一致するようにできる。

これはつまり、こういう解釈でいいのかな…？

・命題論理では、妥当式＝トートロジーである

・一階の述語論理でも、妥当式＝トートロジーである

つづく（つづけ）

続きを書きました。(2015-12-20)

あと、さらに興味深いPDFを発見！（https://www.google.co.jp/url?sa=t&rct=j&q=&esrc=s&source=web&cd=5&cad=rja&uact=8&ved=0ahUKEwj4lunGk9TJAhWEJZQKHRM-A2oQFggzMAQ&url=http%3A%2F%2Fwww.geocities.jp%2Fminao_kukita%2Ffiles%2Flecture_notes%2FCT-chap3.pdf&usg=AFQjCNEvzFbEMJLJZx9XqDnmdgdSJtTLjw&sig2=XIAj2ZegxLpRcUCJMXYfSw）

ここにタブローの方法とやらが載っていて、このPDFによるとタブローを使えば述語論理の妥当性が判定できるとのこと。

このタブローですが、以前どこかの大学の講義目録「論理学」をちらっと見た時に、“タブローまでやって終わりにします”という文言があったので、名前と存在は知っていましたが、まさか妥当性を判定する方法だったとは。

タブローの方法、ぜひマスターしたいところである。

[math-phi]

フレーゲの基本法則Ⅴが持つ問題点（外延がダメなのではない）

数学の哲学をちまちまと、『数学を哲学する』を読んで進めています。

そこで���『数学を哲学する』“論理主義”(p.148辺り)の項での疑問点。「基本法則Vではなく外延が問題なのでは？」

つまりどういうことかと言うと、「ラッセルによって基本法則Vに問題ありと指摘されたが、僕には、基本法則Vではなくそもそもの“外延”という考え方に問題があるように思える。つまり問題箇所として指摘されるべきは“外延”であって基本法則Vではないんじゃ…!?」

しかしどの教科書を見ても基本法則Vに問題があると書かれている。これはいかに…という疑問が解決したのでまとめておこうかなと。

まず論理主義の流れとしては

フレーゲが論理学を用いた数学の構築を目指す→論理主義を完成させたフレーゲが著作を出版する→それを読んだラッセルが間違い指摘の手紙をフレーゲに送る→基本法則Vに問題がありますと書かれたその手紙をフレーゲが読む→フレーゲの構想が(一部)崩壊→ラッセルがその崩壊を回避する形で論理主義を完成させる→ラッセルがそのまとめとして『プリンキピア・マテマティカ(Principia Mathematica)』を出版する

ということになっていますが、今回の舞台はそのラッセルの手紙のところ。基本法則Vに問題点（ようは矛盾）がありますというそれ。（個人的には、フレーゲが『算術の基本法則』を出版してラッセルが矛盾の存在を指摘するというこの一連の流れが展開的に盛り上がっているようで非常に好き。）

さて本題。まずは外延、基本法則V、ラッセルの指摘をまとめると、

・外延：概念の外延とは、その概念があてはまる対象すべてからなるクラスである(『数学を哲学する』p.145,line.9)

つまり外延とはざっくり言うと集合（クラス）のことである。さらにわかりやすく言うと、外延とはつまり概念を引っ張ってくるときに、引っ張ってきたものを集合にしましょう、という考え方とも言える（言えるかな？不安）。

例えば…）ネコの概念を考えるとき、フレーゲでない人は“ネコの概念”という言い方で満足していたのだが、フレーゲはこれを“ネコの概念の外延”＝“すべてのネコが入った集合”としたのである。※ラッセルの言うところの“ネコの概念”＝フレーゲが言うところの“ネコの概念の外延”、といったところでしょうか。

・基本法則V：任意の概念F,Gについて、Fの外延とGの外延が同一であるのは、すべての対象aについて、FaであるのはGaであるとき、そのときにかぎる場合であり、その場合にかぎる(『数学を哲学する』p.148,line.10)

つまりFの外延＝Gの外延のときは、FとGが同じ対象について成り立っているのだということである。これはざっくり言うと（本当はざっくりじゃダメなんだよね。はっきり書くことができるようになったとき、また書く。）、外延（集合？）をモノのように扱うことを許すということ、になる。

・ラッセルの指摘：xがFの外延であり、かつFxが偽であるような概念Fが存在する

わからん…が、最初はチンプンカンプンだったものの今は少しわかる。つまり、ラッセル集合のようなものを外延として考えることができるということ。（たぶん、この書き方は正しくない気がする）

結局、僕が何を言いたくて何を書きたかったのか、そして今回何がわかったのかというと、「集合や外延といった考え方には、制限が必要！なのに、基本法則Ⅴは制限が甘い！ゆえにダメ！」ということ。

先人��ちが集合に対してどういった制限をかけてきたのか↓

・ラッセルのタイプ理論

・公理的集合論の分出公理　任意の集合 X と論理式 ψ(x) に対して、X の要素 x で ψ(x) をみたすような x 全体の集合が存在する.

一方、基本法則Vはこういった制限の体をなしていない…。

でも基本法則の何が具体的に駄目なのかきっちりわかっていない自分…

つづく

[math-phi]

政治哲学4（ロールズ以後）

講義の復習。教科書は『法哲学』p.169-176

世代間正義

Ⅰ.世代間正義の革新性

(1)古代〜ロールズ以前

世代間正義への無関心、正義の観点からの考察は皆無（※正義の時間的境界）

●発展史観：将来は、今よりより良くなっていくだろうという考え方（→将来世代を配慮する必要なし、という前提）

(2)ロールズ

正義にかなった貯蓄原理：近接世代間への配慮

・心理的前提（子孫への配慮）からの資本貯蓄[→原初状態における相互関心を少し緩める]、正義にかなった社会という目標

・よく秩序付けられた世界、秩序ある社会

Ⅱ,問題と概念

(1)現実問題

・年金、・国債、・環境問題（とくに温暖化、生物多様性）

(2)将来世代という概念

世代{・コホート(同時期出生集団)　・過去世代、現在世代、未来世代}

特徴

属性の不可知性（300年後の人がどのような価値観や嗜好を持っているのかわからない）

影響の方向性（我々が将来に対して、良い行いをしても賞賛されることはなく、また悪い行いをしても報復されることはない）

同一性の依存性（将来世代が何人から成るのかといったことが、我々の行動に依っている）＝“非同一性問題”

Ⅲ.主要な理論

(1)権利説

将来世代は、現在世代に配慮を要する権利をいまもっている

※批判1：不存在の者達が主体の権利があるのか？（死んだら権利ないのに、いないのに権利あるのか？）

※批判2：同一性の依存性

------2015--------------------2115-------->(t)

　　   Pc---------------------->Ic

          Pd---------------------->Id

このとき「Ic≠Id」になるので、Ic世代がPc世代に対して環境問題云々を解決させると、その影響を受けた結果（つまり環境問題解決��原因で）、Ic世代ではなくId世代が生まれてくることになる→権利主体の不存在を要求する権利になってしまう！

(2)拡張ロールズ説

格差原理または正義にかなった貯蓄原理を環境問題に応用してみる

→あらゆる世代の代表が集まった原初状態から始める

※批判1：同一性の依存性

正義原理の採択→原初状態の採択者の一部は実は不存在

※批判2：正義にかなった貯蓄原理の前提は、環境問題にそぐわない

※批判3：格差原理の応用は、数学的には奇妙な結果に

Ⅳ.残された課題

結局、世代間正義を上手く説明するような理論はいまのところはない→新たな理論の必要性あり

・共同体論（byアヴナー・ドゥ-シャリット）

----

Q.世代間正義に弱い一般原理のようなものは使えないのか？

[math-phi]

量化における否定の位置と意味

『論理学』(野矢茂樹)を進めている。

そこで、述語論理（p.98辺り）で疑問あり。量化もいれたとき、否定¬はどうなるのか…。（そもそも、否定についての理解が怪しいので確認してみる）

Fxy：xはyを愛する

1. ¬∀x∃yFxy

2. ∀x¬∃yFxy

3. ∀x∃y¬Fxy

4.¬(∀x∃yFxy)

この4通りがまず考えられる。が、この4つのうち2つは同じ意味↓

1. ¬∀x∃yFxy ＝ 4.¬(∀x∃yFxy)

括弧をつける���とにより意味の誤解を防ぐことができるが、括弧がついていなくても基本的に意味は一通りに定めることができるようになっている。1.に比べて4.は否定の適用範囲が明確なのは間違いない。

さて、意味を確認していく。

まず、否定なしのパターンが、∀x∃yFxy：誰にでも愛する人がいる（誰しも、愛する人を持っている）

そして各場合は…

1. ¬∀x∃yFxy ＝ 4.¬(∀x∃yFxy)：誰にでも愛する人がいるわけではない（愛する人がいない人もいる）

2. ∀x¬∃yFxy ＝ ∀x¬(∃yFxy)：誰も、誰も愛していない（誰かを愛している人は一人もいない）

3. ∀x∃y¬Fxy ＝ ∀x∃y¬(Fxy)：誰しも、愛してない人が一人はいる（誰にでも、愛していない人が少なくとも一人はいる）

たぶんこれで合っているはず。

ちなみに書き換え法則

¬∀xFx＝∃x¬Fx

∀x¬Fx＝¬∃xFx

¬∃xFx＝∀x¬Fx

∃x¬Fx＝¬∀xFx

あとで書き換え法則を使って、上の1.〜4.を書き換えてみるか。

[math-phi]

政治哲学3（ロールズ以後）

講義の復習。教科書は『法哲学』p.157-168

グローバルな正義

Ⅰ.正義の空間的境界(=国境)を越える

(1)プラトン、アリストテレス〜ロールズ以前：国境の内部だけで正義は打倒する（グローバルな正義は考えていない）

(2)ロールズ：『正義論』国内正義論（＋戦争の正義）、『諸人民の法』国際正義論

Ⅱ.貧困という現実

その背景

(1)世界銀行の絶対的貧困線（貧困線(poverty line,poverty threshold):統計上、生活に必要な物を購入できる最低限の収入を表す指標）

・1日1.25ドル未満：20世紀後半で20億人

・1日2ドル：2010年で8億人

(2)所得の南北格差

Ⅲ.貧困を前にした個人の倫理（P.シンガー、現代の選好功利主義者）

(1)2つの原理

・強い一般原理：悪しきことを、それに匹敵する犠牲なしに防止できる限り、防止するべきである

例)貧困対策NGOへの寄付→自分自身の生活が絶対的貧困に陥るほどしなくてよい

・弱い一般原理：悪しきことを道徳的に重要な犠牲なしに防止できる限り、防止するべきである

例)飲み会に行かずにNGOへ寄付

(2)弱い一般原理を発展させる

・浅い水たまりに溺れかかっている幼児→他に大勢の大人がいたら救わない理由に、ならない！→他の義務者の存在・人数は、義務を弱めず、消滅させない

・幼児が少し離れた所にいたら、救わない理由に、ならない！→悪しきことが生じている場所との距離は義務を弱めず、消滅させない

Ⅳ.貧困を前にした社会の責任

(1)リアリズムの克服（国際関係論のお話）

・リアリズム（現実主義）：ホッブズ的自然状態。つまり、みな（国家）好き勝手にしている

・リベラリズム（理想主義）：国際関係にも、規範・ルールが存在し、みな遵守できる

(2)ロールズ正義論の修正と活用

ロールズ「社会＝相互協力で、各社会は相互に影響しあわないと仮定」

※C.ベイツ「各社会は相互に影響しあわない仮定はおかしい。国際社会にも相互協力はある（国際的依存性）」

→原初状態に、各国の代表が集合して政治システムを決めていけばグローバルな正義が達成できる？（グローバルな格差原理：国際的不平等は、最も不利な国の最大の利益とならない限り是正すべき）

(3)ロールズの逆襲

・C.ベイツを批判→ロールズ「国内正義論は拡張すべきでない、分配的正義は国内でしか成り立たない」

・国際的な原初状態で伝統的国際法を証明する正義原理

-------

・P.シンガーの理論は、自身の嗜好等で消費する金銭を寄付せよというものだけれど、現実問題としてそれが成り立つことが非常に難しそう（というか成り立っていない）点で、改良の余地ありなのでは？

寄付がすべてだとして、消費を控えるようになると、今までの資本の回り方がずれ、結果的に望ましくないことに帰結��る可能性あるのでは？（これは功利主義っぽい発想）

[math-phi]

政治哲学2（ロールズ以後）

講義の復習。教科書は『法哲学』p.99-114

平等論

Ⅰ.3つの視点(1980s〜)

①何の平等か？平等の尺度、②平等と個人の責任、③平等か優先性か十分性か？

※1970〜、冷戦中、自由市場VS統制経済（平等）

Ⅱ.何の平等か？センの問題提起”Equality of what?”

・厚生の平等、ダメ

・資源の平等、だからロールズでいいじゃん？しかし問題あり

・潜在能力の平等、コレが良い！

Ⅲ.厚生の平等とその難点

厚生の平等：効用を最大化せずに、平等化する

(1)功利主義の伝統

効用：快楽、選好→効用の最大化

(2)厚生（≒効用）の平等化

(3)難点

適応的順応形成（J.エルスター）：貧弱な選択肢のみが利用可能だと、その選択肢に満足してしまう

例)絶対的貧困層の人々にとっての「御馳走」、DV被害者の「彼はいい人」

→●高価な嗜好（R.ドゥウォーキン）：高価な好みや生き方を自分で選択し、発展させてきた人に所得再分配をしてしまうことになるぞ

例)シャンパン好きと発泡酒好きがいたら、効用を平等にするためには、シャンパンと発泡酒を同じ量だけ与え？なければならない。しかし、シャンパンの方が高価なのは確か。どうする。

Ⅳ.資源の平等

(1)先駆者ロールズ

・功利主義批判

・基本財（モノで考える）

(2)ドゥウォーキン

●理想理論：現実社会の条件を考えない

オークションを行って分配する。

仮想例)無人島で島の私的財を平等に分配したいとき、皆平等な金額（貝殻？）を最初に持っていると仮定し、オークションを反復。→羨望テストをクリア＝平等の実現

つまり各人が、他のあらゆる人の財の束よりも自分の財の束を好ましいと思う状態に！（無羨望としての衡平）

●非理想理論：仮説的保険市場

現実社会：身体障害、能力の差などがある→稼得能力が低い場合に備えた架空の保険

だが現実にはそのような保険はない→強制保険としての累進課税＋社会保障

つまり、アメリカの税制はより平等的になる余地を残している

-------

講義中のQ

・平等を実現するのは誰か？

①市場なのか？②政府なのか？③市民（教会）なのか？

①：小さな政府、リバタリアニズム

②：大きな政府、福祉国家

※①、②、③が別個でなく、関連している。つまり、②の政策によって、①と③をコントロールできる。

個人的には、能力を平等の対象にしている点について、後天的な要素（≒努力など）を無視しているのが気になるが、それもまた能力だとすれば、説明としてはついている。うーむ。

[math-phi]

政治哲学1（ロールズ）

講義の復習。教科書は『法哲学』p.31-60

Ⅰ.ロールズの正義論が生まれるまでの背景は2つ。

1.社会的背景：1960s、人種差別、所得格差、価値観の対立

→属性、所得、価値観の異なる人々を含む正義にかなった社会とは一体？（これがスタート）

特に、1960年代のアメリカは黒人差別がひどかった。また、米軍によるベトナム戦争の介入は、国民にとって「これは正しい戦争なのか？」「正義なのか？」という疑問を突きつけた。

2.学問的背景

・功利主義：個人の別個性を無視、少数派の犠牲

・直観主義：首尾一貫した原理的思考がない

・社会契約説：現代的な再構築

この時代、功利主義（ピーター・シンガー）が主流派だったので、それを覆す？ロールズのインパクトは大きかった。

功利主義の問題点、嫌われた新興宗教のはなし。

Ⅱ.ロールズの正義論の基礎

(1)原初状態：

自由平等な個人、無知のヴェール（＝肌が見えない）、相互的無関心【決定バイアスを防ぐ】

(2)基本財（＝価値観の差異に関係なく、誰もがより多く所有していたいと考える財）

：自然的基本財（健康）、社会的基本財（表現の自由）

社会的基本財の分配の仕方こそが社会の基本構造に依っている。

Ⅲ.正義の2原理

(1)第1原理：平等な自由の原理

☓平等も自由も大事

◯基本的諸自由を平等に持つ

※日本国憲法の自由権にあたるもの（表現の自由とか）

(2)第2原理：格差原理

☓格差を小さく

◯最も不利な人々の利益を最大化するような不平等はよい

つまり累進課税のような不平等なら認めましょうということ

[α]A:100,B:30、[β]A:40,B:20

この場合、βのほうが格差は小さい（＝より平等）が、ロールズはB（弱者）の人の利益を最大化しようと考えるので、αを理想的とする。

・正義にかなった貯蓄原理（貯蓄率0はダメ、しかし貯蓄し過ぎもよくない）

・公正な機会の平等の原理≠機会の平等（公正にするために何者かを優位にしたり（あるいは制限したり）とかはオッケーということ。例えば、独禁法）

(3)原理間の関係

・第1原理���第2原理に優先する→自由の優先度

・公正な機会の平等は格差原理に優先

ある原理が充足されるまで、次の原理は考えない。つまり、全員の自由度が平等になっていないうちから、弱者の利益を確保んどは考えなくてよい。

※辞書的順序をはっきり→その場その場で優先順位を設定するような直観主義とは別物

(4)なぜ全員一致で採択？

マクシミン戦略：最大利得の最大化

ハーサン「平均効用の最大化がより合理的」→功利主義

Ⅳ.四段階（無知のヴェールが剥がれていく）

1.原初状態

2.立憲段階：第1原理の制度化

3.立法段階：第2原理の制度化

4.遵守段階

Ⅴ.『正義論』その後

(1)政治的リベラリズム

(2)国際的正義への応用

リベラルな社会（正義の2原理に基づく社会）以外にも尊重されるべき社会あり。

-------

そもそも社会の基本構造は、・政府のあり方、・市場のあり方、の二つで決まる。※ロールズは政府のあり方を重視している。

・マクシミン戦略をよりゲーム理論風に考えてみる

状態の差異を相手の戦略だとして、マクシミン戦略が支配戦略にならないパターンは…

・正義にかなった貯蓄原理に関連した世代間正義の疑問として、「現在世代は資本を消費する代わりに、次世代にその結果出来上がった新たな資本を残しているでは？」

→持続可能性を考慮すべき。

弱い持続可能性：社会（＝インフラ）と自然（＝石油など）の両方

強い持続可能性：自然のみ

・結局、ロールズの理想とする国家は、西側諸国のことになるんだよね。？