Don't wanna be here? Send us removal request.
Text
MATHEMATICS 6 SYNTHESIS
After days with late night reviews, periods of pure brain fogginess during lectures, and frustrating one mistake results on quizzes, we have finally made it. We have completed our final year of mathematics in PSHS-CARC.
I honestly did not think I was going to be able to make it this far. I thought math would be the death of my Pisay career on multiple occasions, especially during my earlier years. I entered this institution consistently representing my elementary school in MTAP competitions since 1st grade, but I went through this math curriculum feeling like I was the least intelligent scholar on campus. The thought that my application may have been mixed up by a way more deserving student than me definitely crossed my mind multiple times for the past six years of my stay here, partly because of my apparent struggles in science and mathematics subjects. Ironically, these are subjects that served as my passion during my elementary school years.
Mathematics 6, however, reinvigorated my passion for math and shaped me up to be more confident in my computational ability. It is definitely mind-boggling that the subject that was structured to be the culmination of past mathematics topics became the skeleton key for me to be sure of my place here in Pisay. Sure, there were still periods where I doubted I was going to pass a long test or became completely lost in a lecture. However, overall, Math 6 was an exciting and thrilling ride that had a relatively free-flowing level of difficulty, but was still enough to keep me on my toes.
In particular, the 4th quarter topics meant the most to me. To know that there were visualizations of worlds outside of the 2D Cartesian coordinate system was refreshing to me given that I have been using that same one for the past six years now. The introduction of both the polar and 3D coordinate systems gave me a much more challenging view on mathematics as a whole, especially with my unstable foundation on trigonometry and slight inability to view objects with depth perception involved.
Up until now, however, I don't exactly see a practical purpose for me to learn about integrals besides it being a precursor to most mathematics subjects in college. I know when to apply them and I know how to manipulate the equations in order to apply integration. However, I have not gotten any real life examples on its application yet. The closest we got to that was during the 3rd quarter with the centers of mass and the disks and the cylindrical shells, but that is mainly for physics and engineering concepts that are far away from the career I want to pursue. Nonetheless, they were still very fun to go through.
All in all, I am glad I was able to fully immerse myself in the 8AM classes I had for Mathematics 6. I would like to thank Sir Dex for his guidance and willingness to teach us despite us being lost multiple times along the way. I personally see him as the best teacher in Pisay due to his expert level skills in instruction and keeping the atmosphere in class highly conducive to learning with his half-spoonfeeding half-"letting us be independent" style of teaching. I would also like to thank my classmates for comforting me in my struggles and guiding me through lessons that I was completely lost on. I would have never made it to my final year in Pisay without you. Lastly, I give a pat on the back to myself. I guess I deserve it, somehow.
Mamba out. <333
0 notes
Text
The 3D Coordinate System
Moving out of the frigid landscapes of the polar coordinate system, we now have the mountains created by the 3D coordinate system, a topic not necessarily new to us with its applications in Physics 2, but still a stranger to me nonetheless. The amount of new concepts that were being thrown at us in this new topic was extremely overwhelming for me, especially since I was not gifted with natural depth perception to easily visualize 3D planes like my other friends in class. However, if Sir Dex masters the topic, and he admits to not having that level of depth perception either, then surely I can put in some time to answer practice problems related to the lesson.
Even in plotting points, I found it difficult to answer problems exploring all the concepts surrounding the 3D coordinate system, from distances to planes, to volumes of figures, to properties of spheres. However, most intimidating of them all are the graphs. For example, the graph of y = x^2 on the Cartesian plane would look entirely different on a 3D plane. This is not even incorporating equations where all three components (x, y, z) are present. Apparently, there was literally no tactics or tricks to graph the equations. It was simply visualization, which is extremely difficult for me to go through at the moment.
I am actually really worried about my results for the upcoming long tests. This was framed as the easiest lesson simply giving us bonus points for our grade, but now, I'm not so sure. Regardless, I'm not going to take my foot off the gas pedal now. I'm going to give it my all now to finalize my (hopefully) 1.00 final grade in math to end my year off.
Figure 3. Notes on the 3D Coordinate System (wow ayos ng notes ko dito haha)

0 notes
Text
Polar Equations and Graphs
Continuing our trek through the polar coordinate system, we discussed polar equations and graphs. From lines to circles to lemicons to roses, we encountered some visually appealing graphs based on patterns from the actual equations. We also learned how to convert polar equations to Cartesian ones, and vice versa. At first, it was a doozy. I was still on my "hangover" state in trying to grasp the lesson, where everything was still slightly cloudy for me. Thus, going from simple points to more intimidating graphs in a matter of one meeting was a giant leap for me to muster.
These beginner's struggles were most apparent during the conversion from polar to Cartesian equations and vice versa. I know it is simply just manipulation and substitution in order to get a desired a result. However, my brain is not that creative enough in mathematics to know what to do, when to do it, and at what certain moments when it comes to these types of conversions. This was already difficult for me during the integrals, which slightly became my entire mathematics life during the past three quarters.
Nonetheless, encountering the equations for the lemicons and the roses for the very first time, then plotting the points leading up to the graph was fun. I was genuinely giddy and hyped when I discovered the pattern of the petals when I plotted the points of the roses for the first time, and I had a good laugh with my other seatmates who graphed the lemicons. It was math highlighted best with some sort of childlike innocence looming in the air, and as we move on to the 3D coordinate system, I hope it stays that way.
Figure 2. Practice Problems on Polar Equations and Graphs

0 notes
Text
Polar Coordinates
To kick off my final year of math in Pisay, we were now transitioning away from the world of integrals and into a new realm of coordinate systems. For our first step, we discussed the polar coordinate system, a navigation tool usually implemented by aircrafts and seacrafts. Instead of the usual x and y coordinates, this system uses r and theta, with the former being its distance to the origin and the latter being the angle. It was a very intriguing lesson for me to go through, and for the first time this school year, it explained to me what that figure on the mini whiteboard at the front of the Room 305 class contained.
With that being said, I was not necessarily expecting my experience with the polar coordinate system to be a smooth ride since it is an entirely new topic even with its simplicity once you get the hang of it. Thankfully, the use of a scientific calculator was permitted during the long test, which allowed me to focus more on the actual polar coordinate concepts rather than the unit circle, which I mostly forgot after my review for the CETs. Besides that, however, the other concepts were fine. Plotting the points were easy to grasp, and converting from polar to Cartesian and vice versa was simply plug and play on the formulas given.
I'm really excited to see where this lesson takes us even if there are only two or three other meetings left to tackle the lesson. It is a shame that this is only a tiny part of our Math 6 curriculum, but I suppose it is a representation of how simple it is to understand given that it is only allotted for half of the 4th quarter. Hopefully, I can see some fun equations and graphs to work with for next lesson.
Figure 1. Notes on the Polar Coordinate System

0 notes
Text
3rd Quarter Synthesis
Going into the 3rd quarter, I was somewhere around my last battery cells of motivation. It has always been a recurring pattern for me to lose gas around this time of the school year, perhaps because there is no semestral break in between the 2nd and the 3rd quarter, or perhaps because most of my competitions usually take place during this period. Entering classes became a nuisance for me rather than an opportunity to learn, a betrayal of a promise I made for myself to live my last days in high school with high spirits and a passion to learn. I could feel the candle in my heart getting dimmer and dimmer as the days passed. I thought I was going to tank all of my subjects, including math.
However, Thursday and Fridays for me became a safe haven amidst the chaotic other days of the week. Besides these two days having fewer classes in general, it started off the day with a subject that was sure to grind some gears inside of me to work: Math. A lot of things change over time, but an academic constant for me is my determination to push through math despite being in either a motivational dry spell or in a burnout, mainly because I know I can't mess around with Math and get a solid grade like what I usually do to other subjects. You could say I am lucky because this quarter was easier in comparison to the past two, and you're probably right. If I had to choose when to be dead tired, I would choose this quarter for Math.
Nonetheless, I like finding practical meaning in what I am learning, and this quarter was literally all about that. The complicated intricacies I was going through during the previous quarters are now explained in the real world with the lessons in the 3rd quarter. From arc lengths to centroids, the crossover between Math and other subjects throughout my Pisay journey was starting to unravel, and in a series of surprising events, Math for me became a shield away from the heavy workload demands of the other subjects.
As the 3rd quarter comes to a close and graduation looms closer and closer, I hope everyone knows that this Math journey was unlike any other. From the hectic math problems being thrown around in the multi-purpose hall to the cozy atmosphere of the 4th floor while they answer the quizzes, Math has become one of the hallmarks of Pisay culture in a way. Furthermore, Sir Dex has also put himself in the hearts of his students, with some even considering him the best teacher they have ever had in Pisay despite only knowing our batch in a span of months. As for me, well, I want to take the next quarter focusing more on the relationships I have now rather than my academics. Of course, I'm not completely dropping my academic life, but some things are worth treasuring more than others.
0 notes
Text
Centroid of a Plane Region
To cap off what has been a 3rd quarter joyride in Mathematics 6, we have a lesson that confuses you enough to focus, but strips off this facade to reveal a relatively fun lesson. Solving for the centroids of plane regions was simply just an extended version of yesterday's topics, incorporating the same concepts of area discussed in the 1st quarter and adding a unique integral to it. I have to admit that I have never really wondered where specific coordinates a plane region would balance properly, but some unknown curiosity inside of me was satiated after this lesson.
I'm writing this down now because I know I'm going to get confused during the long test. I need to remember that x-bar means the moment about the Y-AXIS, while y-bar means the moment about the X-AXIS. I know for a fact that a problem will come out with those specific words used, and I need to realize whether or not to use x-values or y-values in dealing with the problem. Of course, there are other curveballs to worry about (equations using 2nd quarter concepts on integrals, remembering the right formulas, etc.), but this main one will screw me over if I am not careful.
LT 2 is shaping up to be somewhat of a breeze, but I'm still keeping my guard up because I don't want to eat my own words. Hopefully it doesn't become another version of the previous LT, because that was terrible.
Figure 5. Practice Problems on Solving the Centroid of a Plane Region

0 notes
Text
Center of Mass of a Rod
Calculating the center of mass of a rod would be my first ever experience with a lesson where I actually found integrals somewhat useful in my daily life. It was somewhat connected to concepts in Physics, which still remains somewhat of an interesting subject for me even if I did not completely pursue it as either a core or an elective. Specifically, the point mass systems were somewhat of a redemption lesson for me since it was a topic that was reduced to a learning guide during the Bridging Program at the height of the pandemic. It made me wish that I could go through the math and physics lessons through a face-to-face setup, because even if I know deep inside that I would struggle mightily, it would still remain somewhat meaningful in my heart.
The incorporation of the integral in the lesson was, in my opinion, slightly forced, as if you really did not need the integral to solve the problem. However, it is in the curriculum, so no complaints from me here. The only curveball the lesson really throws at you is if the linear density is not given at the start of the problem, and even if it requires some level of mathematical creativity that is completely absent within every bone in my body, it is still solvable in a way that doesn't squeeze out the brain matter in your head.
All in all, it is a nice lesson to start off the latter half of this quarter. I don't really know why I feel this way, but the lesson was cozy in a way. It didn't have the hectic, volatile, high-octane vibe that most math lessons usually have, and during the class discussions, it is as if Sir Dex was simply telling a story in front of his whole class. It was the pleasure of math at its very core, and hopefully those vibes carry over tomorrow for plane regions.
Figure 4. Practice Probems on Solving the Center of Mass of a Rod

0 notes
Text
Arc Length
I really have nothing to say about this lesson because it's the easiest one so far this quarter. I don't need to do mental gymnastics in my head like in washers and shells for the first time in weeks. Solving for the arc length of a function is the prime definition of plug and play. All I need is the formula and the job is pretty much done from there.
However, I know one huge pitfall that could cause me my downfall in the long test: forgetting to get the derivative of the function before solving the integral. I just have to keep in my mind this time that the equation calls for f'(x) and not f(x) like the past lessons. This isn't even mentioning that I have to square f'(x) once I get the derivative, but with enough practice problems, that should hopefully iron itself out.
The slate for LT 3.1 is now set, and while it's not exactly the gauntlet I was expecting, it still calls for at least a few hours dedicated to review. I personally dislike how washers and shells aren't optional choices in the long test. I just think it kills the part that makes math fun in some way: the creativity and free will to solve problems with your own knowledge tree. However, I do understand that the curriculum requires us to master both methods, so be it. Super excited for the long test! Hopefully I do well.
Figure 3. Practice Problems on Arc Length (although I only solved one problem in class)

0 notes
Text
Cylindrical Shells
I actually find cylindrical shells to be easier than applying disks and washers, and those sentiments are shared by Sir Dex. With this new lesson, I can essentially avoid washer-type questions with its pesky two integrals by applying the same format to cylindrical shells only requiring one integral. If the long test gave me an option to solve with either method (I highly doubt that's happening), I would simply choose cylindrical shells for every single problem.
With that being said, I can see how people can mix up the equations for both lessons now. For example, one could put pi in the equation for cylindrical shells then put 2pi in the equation for disks and washers. To give a more obvious example, one could get lost with when to get the square of f(x)/f(y), which only applies for the equation involving disks and washers. I have also had cases where I would forget the extra x/y in the equation for cylindrical shells. However, with enough practice problems, I can hopefully smooth things over.
So far, I'm definitely more confident in my mathematical ability now in comparison to past quarters, although that's probably because the lessons are easier now and Sir Dex is a god-tier teacher. It's just comforting to know that I don't need to scratch and claw my way to a solid math grade nowadays, and that I can walk into my math lessons with some level of confidence. Hopefully, I can sustain that throughout the quarter.
Figure 2. Practice Problems on Cylindrical Shells (grabe raming ex parang iilang nasa barkada namin)

0 notes
Text
Disks and Washers
We are starting off the 3rd quarter with a doozy. While I expected the applications of integrals to be somewhat similar to word problems in algebra, which required interpretation of the situation before setting up the equation, I was not ready for the extra curveballs it was going to throw at me before the integral was even formed. Disks and washers threw in entirely new concepts that required graphical interpretation that I just did not have going into the lesson.
The amount of moving parts that the lesson had, from the bounds of the integral to what axis should be displayed, then to what f(x)/f(y) should be was hard to juggle in my head, and that's not even throwing in past quarter lessons if f(x)/f(y) wasn't a simple integral you could find on the table. The quiz also had its own intricacies. The choices that were given for each item were already somewhat simplified, so I didn't realize until hours into my attempt that I got the right answers in my calculations, just not entirely the same as the ones in the quiz. I know practice makes perfect in math, but normally, I have a plan on what specific weakness I have to target per lesson. In this case, however, my limitations in every part of the computational process was exposed.
Amidst the chaos, however, what helped me a lot was the same trick that Sir Dex claims to have used when he was learning the lesson for the first time: drawing a rectangle. It's simply too difficult in my head to imagine a cylinder during graphical analysis, but with a rectangle, I can somewhat picture what the integral would look like, bounds and f(x) and all. It is honestly a lifesaver. I don't know how else anyone would understand the lesson without it.
All in all, it's actually a solid lesson. It has enough challenges that keep me on my toes, but I know for a fact that once I understand these lessons, it will be smooth-sailing from there. For now, however, I need lots of training.
Figure 1. Practice Problems Involving Disks and Washers (graphs were in another piece of paper which was lost amidst the notebook turned filecase)
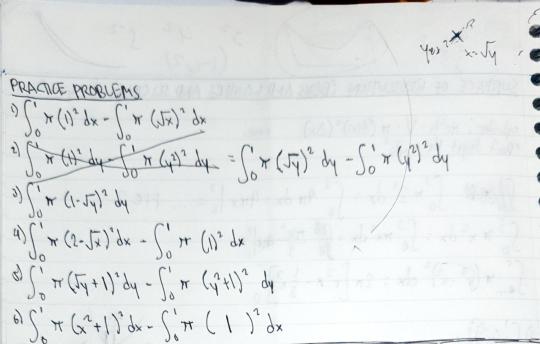
0 notes
Text
2nd Quarter Synthesis
2nd quarter brought back feelings that resurfaced for the first time since mathematics in the face-to-face setup: the feeling of dread knowing that a score less than 50% of the long test total is possible. For the first time in a long time, the threat of failure in a subject was actually scratching its nails on the wooden door, and as a result, I was pressured to keep myself on guard and catch up on the lessons as another one flew past me. It didn’t help either that the lessons work in conjunction with each other; the failure to understand IBS leads to a catastrophic mess of confusion for the rest of the five weeks of lessons.
However, this is no longer Grade 7/8/9 me writing this blog, This is a newfound me with wisdom on how to survive these kinds of situations. No longer did I simply accept my fate and go into the long tests with whatever stuck with me through the diffusion process during the lectures. For once, I was opening the KHub and finding practice problems on the lessons, even going so far as to searching the web in case I wasn’t confident in my computational abilities. I don’t exactly know what sparks me to do this. Perhaps I want to sustain my high scores on the past LTs. Perhaps I want to make it to the Top 20 of the batch. Perhaps I just have a natural impulse to do better than what is asked of me. No matter the reason, I’m happy.
The easiest lesson to learn was, hands down, the integrals yielding inverse trigonometric functions. It sounds weird to state that you can mentally solve integrals, but this lesson is an example of how you can solve equations in less than five seconds. I know it was simple, but it gave me a newfound confidence that I could at least get a passing score on the long test. Of course, I was aiming for higher than that, but to have it somewhat guaranteed was a huge relief.
Anything involving the theorems in solving trigonometric integrals, however, were scary. I confess that I don’t even master the lesson up until now. It requires so much creativity and background knowledge on integrals that lack of either one of those elements will leave you either demotivated or sluggish in solving the problem. It’s just too much mental gymnastics for me to handle, especially with other subjects also throwing in their own complications.
All in all, however, it was fun. What I like about math is that it destroys any preconception that SYP years are simply eight hours of relaxation in the school. The common stereotype in our batch is that we seem happier and calmer in comparison to the rest of the campus, but when the discussion revolves around math, we are equally as stressed as the rest of the students. However, it helps to have friends that you have bonded with for six years, witnessing their academic and emotional growth as the time passes. Remedial sessions were seen as a form of punishment before the pandemic, but now, my friends and I are completely willing to surrender our free time just to understand the lessons with no judgment from each other whatsoever. Sir Dex’ willingness to teach 24/7 also helps, especially in a field that raises mixed emotions among the student body. Lastly, I also want to recognize me, just for being me.
3rd quarter will revolve around the applications of what I learned, and I could not be more excited and scared at the same time. Hopefully I can still play my cards right for the remaining months of my high school life. But for now, a temporary rest.
0 notes
Text
Integration Using Partial Fractions
While I don’t find integration using partial fractions difficult, it is a lengthy process that requires laser-focus attention to detail. The integration part can actually be automatically solved, but mistakes in partial fraction decomposition revolves more around arithmetic, and the one gripe I have when it comes to arithmetic is the fact that margin of error is higher for being careless in comparison to algebra and calculus. It’s a lesson that has stuck by me for years now, and with that comes mental slip-ups as a result of being accustomed to mastering it.
However, where I might fail is determining the partial fraction form for the problem’s denominator. I’m actually surprised I didn’t get a perfect score on the quiz first try, and while reviewing the quiz, I have yet to know why what I chose was the incorrect answer. Clearly, I need to brush up on my factoring skills, because failing to get the correct partial fraction yields me a 1/5 in the short response portion.
Just as a sidenote, I got a 29/30 on the first long test! The one mistake I got was extremely frustrating, but I’m not going to take away my performances on the other parts of the long test, like the perfect extended response portion and the one item with the definite integral. Hopefully, I can replicate that performance in the 2nd long test. Perhaps, just perhaps, I could even top it with enough work.
Figure 6. Practice Problems on the Integration of Partial Fractions

0 notes
Text
Integration Yielding Inverse Trigonometric Functions
I recognize Integration Yielding Inverse Trigonometric Functions as the lesson that you can automatically get the final answer to. Of course, there’s the whole confusion in memorizing what form has 1/a in it, and there are also cases when u != x, which leads to another fractional constant being added to the left side of the integral. However, even these minor inconveniences can be made into a shortcut if you know what you are doing, and as a result, I am glad that I am able to do some of the problems mentally.
Nonetheless, I don’t want to fall into the trap of forcing an equation to follow this process. Even Sir Dex gave this cautionary warning at the end of his lesson. The problems yielding inverse trigonometric functions only has three forms, so no matter how you twist the original problem into your own convenience, some problems will still require IBS, some with trigonometric substitution, and some with partial fractions. Therefore, I still need to master the previous and next lesson after this, because this lesson is meant to be somewhat of an easy points generator that prevents you from getting a single digit score on the long test.
So far, I’m happy with my learning for the 2nd long test. Of course, I don’t want to get too overconfident, which is why I’m laying out at least one day of my three-day weekend to study math (I don’t have an exam on Monday). However, I also need to get into the long test with some sort of innate swagger, some sort of charisma to shake off the nerves. But before that, Hell Week...
Figure 5. Practice Problems on Integration Yielding Inverse Trigonometric Functions

0 notes
Text
Integration by Trigonometric Substitution
Integration by Trigonometric Substitution is easy in a sense that it only builds upon the lessons that were covered in the first long test. As long as you know the structure of the equation and you know when to use cos, sec, or tan, you are pretty much set. It was simply an extra appendage to a process that I have 80% mastered at this point.
The most fun part of the computational process, however, was when the triangle was involved. Most of my friends dreaded this part and simply preferred to use the inverse trigonometric identities in their final answers, but I simply saw it as an application of the only trigonometry I know. There was one specific moment in class when Sir Dex monitored my progress in displaying the final answer in terms of x using the triangle, and as I was surrounded by my clueless friends, I popped off. For the first time in my Pisay career, I felt like a math wizard, a Hogwarts student contributing points to House Gryffindor. However, I’m not even close to completely understanding the steps before that. Just like IBS and IBP, it still includes intricacies that you need to fix in order to get one of the three forms you want. What’s the point of the triangle method when my computed values are wrong, right?
It seems that the pattern for the next lessons is they are new limbs and complexities appearing out of the already fine-tuned process of solving IBS, and I’ll take it. January is usually when I get rusty at math, but hopefully I still remember how to do this come exam week.
Figure 4. Practice Problems on Integration by Trigonometric Substitution

0 notes
Text
Trigonometric Integrals
This was, by far, the most difficult lesson I have had during my Math 6 journey, and it is on pace to become the hardest lesson for this quarter. Even the grandest of math wizards were stumped by this topic, and that alone makes me worried about my own learning process. With so many identities to memorize and manipulations of the original problem to get a more desired form, this lesson requires expert levels in both natural mathematical ability and limitless creativity.
The problems revolving around sine and cosine were definitely the simplest, but it was not even close to being smooth-sailing. In particular, the case involving angle identities yielded the more complicated problems, since the formulas were hard to memorize and it required more creativity than usual to solve. However, no other sine-cosine problem could trump tangent-secant ones. Any problem involving tangent or secant would turn me off completely. The fact that you can only factor out either tan^2 x or sec x tan x made it complicated to solve, and this is not even mentioning the entire process of solving for the integral of sec raised to an odd number. All in all, it was a complete maze to go through, to the point that most of my close friends decided to schedule remedial classes.
With the coverage of the long test now set, it is shaping up to be the hardest one this quarter. I am going to need all the practice problems I can get from these lessons, and hopefully we can make it somewhere between the 25-30 point range. But for now, that tabular method is looking really attractive right now, because it might yield me some surefire points.
Figure 3. Practice Problems on Trigonometric Integrals

0 notes
Text
Integration by Parts (IBP)
I actually found IBP easier than IBS despite my opinion being in the minority. Oddly enough, my views on the topic are the same as what Sir Dex thinks as well, and this is coming from someone who was absent during the day the topic was introduced. While I wasn’t able to answer majority of the practice problems due to this, I’m actually shocked that I was able to catch up on the math lessons in a short timespan despite the two-day long absence, a contrast to when I had to stress myself out catching up on backlogs after being absent for one day in my earlier Pisay years. I guess that’s what Sir Dex’ willingness to schedule a remedial class, the lighter workload of the CRBL, and a new perspective on learning does to you.
Anytime the problem fits the structure for the tabular method, I am happy. These kinds of problems, if they appear in the LT, will save a lot of time, especially for a subject like math that requires both speed and accuracy in computation. It definitely helps as well that IBP has a form to be followed (udv = uv - Svdu; the S is the integral symbol), which allowed me to simply plug and play the values I ended up solving. However, the lesson was still far from easy. Just like IBS, it still had its own intricacies that prevented you from applying IBP immediately, all of it culminating in one problem that had a repeating answer towards the end of it: e^x cos x dx. That problem ended up being the climax of the lesson from what I have heard, but hopefully that doesn’t pop up in the LT. I cannot even put to words how to solve this problem.
Every quarter, I always had a lesson that I could bank on to get me a high score during the LT, and IBP might serve that role for me this quarter. Of course, I’m not simply going to let go of the other topics to master this one, but I will take great care in solving some problems surrounding IBP in hopes of reinforcing my already slightly extensive knowledge on the process. Trigonometry is coming up next, and I am willing to bet that IBS and IBP will be used for it. I just hope I survive...
Figure 2. Practice Problems on IBP

0 notes
Text
Integration by Substitution (IBS)
We are opening the 2nd quarter with an absolute mindbender of a lesson, and once again, I was left dumbfounded as Sir Dex continued to scribbled in his iPad what simply looked like scribbles of different colors in my eyes. As the class went on, I always found myself simply watching other people’s solutions and copying them on my notebook in hopes that I understand them later. However, the fact that Sir Dex implied the lesson’s importance in the upcoming concepts made me realize that this was the foundation for the 2nd quarter, playing a role similar to what antidifferentiation did for the 1st quarter. With this in mind, the struggle was not only frustrating, but painful as well.
I wouldn’t consider any part of this lesson as “easy.” The only example problem that I was able to solve on my own, albeit with mild confidence, was the very first one with the quantity raised to 1000. After that, it was completely downhill. Each problem brought with it a certain complication that was pulling you back from directly solving it using IBS, and the fact that it was the first step in completing the problem made it discouraging.
I will need to spend at least one hour of my free time to work on some practice problems on this topic. Otherwise, you’re looking at a possible quarter of scratching and clawing to get a grade of 2.00, and I don’t want to revert back to that lifestyle. Hopefully, I will be able to get the process surrounding IBS soon, and the rest of the topics become somewhat easier as a result.
Figure 1. Practice Problems on IBS

0 notes