qhd4

[qhd4]

Love killing stuff in maths. "Kill the kernel", "kill the second cohomology group", "kill the commutators", "kill the constant term", "kill the Lie bracket." Yes. Hell yeah even.

[qhd4]

tell me about the Knight's Tour

that is what I did every time I was bored when I was about 7

(for who don't know what this is check this)

I calculated how many patterns of this closed circuit could have (which I failed because I soon realised there are a LOT of patterns and brute force attack won't be really effective)

Upon further research, I found out:

There are actually over 26 trillion closed Knight’s Tours on the standard 8×8 board.

26,534,728,821,064 closed tours 13,267,364,410,532 unique ones (since each closed tour can be rotated or reflected)

The rule that is used to calculate this is Warnsdorff's rule.

You’re on a square. The knight has a few options. Warnsdorff says "Look ahead. Count how many valid moves each option has. Pick the one with the least future freedom."

Why?

Because if you don’t, you’ll trap yourself later. It’s basically the knight saying “Let me first visit the squares that are hardest to reach later.”

Does it always work?

Nope.

But on an 8×8 board, starting from most squares, Warnsdorff’s Rule tends to find a complete tour. With a good tie-breaker strategy, it works almost every time.

Why does it seem to work so well?

Because the knight’s mobility varies across the board:

Corners have only 2 possible moves

Edges have 3–4

Centre can have up to 8

Warnsdorff’s Rule pushes the knight away from the highly-connected centre and into the periphery early, clearing the hard-to-reach squares while it’s still possible to get out.

Is there a formal proof of its correctness? Nope.

Warnsdorff proposed the rule in 1823, but:

There’s no general proof that it always yields a knight’s tour

It’s a heuristic, not a theorem

It just works a lot, not always

Mathematicians have studied why it often works, but they’ve also shown counterexamples where it fails. And I was able to find one too.

Let’s consider the 8×8 board, starting at sq(0, 0), the top-left corner.

If you apply Warnsdorff’s Rule naively with no tie-breaking, it fails. It gets stuck before completing the tour. The knight ends up in a dead-end after only 60-ish moves, unable to legally finish the tour.

Why does it fail? Because when multiple candidate squares have equal minimal onward moves, the rule just picks one arbitrarily.

If your tie-breaking is dumb (say, you always pick the first one in the list), you might:

Burn the escape routes early

Leave an isolated square that’s now unreachable

So even though each step looks optimal locally, the knight unknowingly walks into a trap.

If this makes sense....?

[qhd4]

they should put a disclaimer at the beginning of elementary school math. “from 1st to 3rd grade we work in the semiring N.” y’know so kids don’t get confused by the lack of negative numbers

[qhd4]

ye, I wanted to ask the same thing, how does this construction go for singular/chech cohomology?

Relative de Rham Cohomology

One interesting thing from my dissertation was looking at relative de Rham cohomology and whether we get a long exact sequence like we do for singular (co)homology. The answer is we do and we'll go through the constuctions and results in this post!

This is covered briefly in Differential Forms in Algebraic Topology by Bott and Tu and in a bit more detail in Riemannian Geometry and Geometric Analysis (Second Edition) by Jost. However some details like the functoriality of the de Rham cohomology of a pair and the naturality of one of the homomorphisms in the long exact sequence aren't touched on. I filled in these details in my diss!

In what follows, I will be assuming you are comfortable with de Rham cohomology, the theory of smooth manifolds and a bit of homological algebra. I might make some posts in the future about these but in the meantime, I cannot recommend enough Introduction to Smooth Manifolds by Lee.

1. Pairs of Smooth Manifolds

In the more general setting of topological spaces, we say a pair of topological spaces (X,A) is a space X and a subset A⊆X equipped with the subspace topology. The key here is that the structure on A is inhereted from the structure on X. Since in general, subsets of a smooth manifolds are not smooth manifolds, we must be more careful about which subsets we choose. For what follows, we will consider a pair of smooth manifolds (M,S) to be a smooth manifold M and a smoothly embedded submanifold S⊆M. The notion of maps of pairs carries over with no issue since the restriction of a smooth map to a smoothly embedded submanifold is smooth. That is, a smooth map of pairs F:(M,S)->(N,T) is a smooth map F:M->N such that F(S)⊆T.

2. de Rham Cohomology of a Smooth Map

The motivation for relative (co)homology is to study how a subspace contributes to the (co)homology of the whole space. In a sense, it is the (co)homology of the space without the affect of the subspace. For singular homology, singular n-simplies of a subspace A⊆X are already also singular n-simplices of X and hence span a submodule of the nth singular chain module of X. So we may take the quotient Cₙ(X)/Cₙ(A) and produce a new chain complex. However, this approach doesn't quite work for de Rham cohomology since differential forms on an embedded submanifold S⊆M aren't automatically differential forms on M. If we wanted to take this approach, we would have to worry about methodically extending differential forms from a submanifold to the whole manifold. However that might get messy and perhaps might involve too much analysis. There is, however, a neat algebraic solution!

The idea is to somehow study differential forms on M whose restriction doesn't contribute to the cohomology on S. More specifically, we will construct the de Rham cohomology of a pair in such a way that cohomology classes are represented by closed forms on M whose restriction to S is exact. As in Bott-Tu, we can actually define a more general cochain complex given a smooth map F:N->M by noticing the restriction of a form to a submanifold is precisely the pullback of the pair by the inclusion. So more generally, we will define cohomology classes represented by differential forms on M whose pullback to N is exact.

Definition 2.1:

Proposition 2.2:

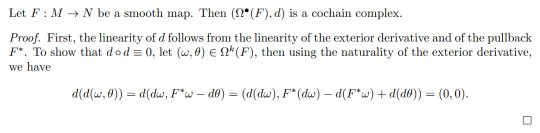
Definition 2.3:

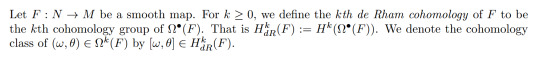
Remark 2.4:

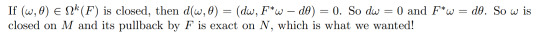
We now consider two obvious linear maps.

Proposition 2.5:

This means that β is a cochain map and hence induces a well-defined map in cohomology. Whilst α is not quite a cochain map, it's easy to check that it induces a well-defined map in cohomology given by α*[θ]:=α[(θ)]. Combining these with the pullback of F:N->M, we get a long exact sequence!

Lemma 2.6:

3. de Rham Cohomology of a Pair

Now that we have developed the more general case, we will bring our focus back to the de Rham cohomology of a pair of smooth manifolds. As alluded to in the previous section, we define the cohomology of a pair to be the cohomology of the inclusion map!

Definition 3.1:

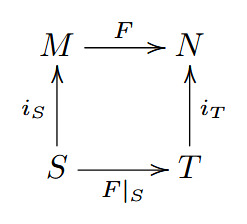
Just as smooth maps between smooth manifolds induce well-defined maps of their respective de Rham cohomology groups, smooth maps of pairs also induce well-defined maps of the respective relative de Rham cohomology groups! This results is the first of two that is completely my own. The key to the proof is the following commutative diagram:

Lemma 3.2:

We can now show that α* in Lemma 2.6 is a natural transformation, which is the second of my two results. This along with a quick argument to show that β* is induced by the inclusion M->(M,S) will actually show that de Rham cohomology satisfies the Exactness Axiom in the Eilenberg-Steenrod Axioms.

Proposition 3.3:

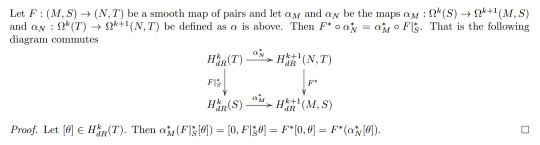
You might wonder now whether we also have excision for de Rham cohomology and we do! The proof can be found in Jost's book!

If you have any questions, I'd love to chat about this (or anything else about my dissertation)!

[qhd4]

why is topology.

actually good question, general topology is a fun little game, but not really something worth studying in itself, it gives you some unified language to talk about basic continuity, open sets etc.

but for my purposes i.e. manifolds, it's... still necessary lol, I'm just ad libbing the answer, I can't in good conscience say you don't need topology, it's not hard tho, and there are some fun exercises, to try and construct spaces with this or that property, plus once you get to algebraic topology, that is vitally important to anything and everything.

[qhd4]

imagine being a biologist, sleeping during math class and reinventing calculus

Imagine being so bored you invent calculus

[qhd4]

wait, algebraic geometry is done? then what the fuck am I doing with my life?:'(

Another weekend of studying algebraic geometry nearing its conclusion. If only I had more time to spend in this remarkable subject..... one day..... one day........

[qhd4]

this usually means that either we don't know the function exists, or the diagram is stating, that if the filled arrows exist, then so does the dashed one. see e.g. the universal property diagrams for your favorite construction

this is maybe a stupid question but why are some arrows in diagrams like this dashed and others arent??? i cannot figure it out...

[qhd4]

which apeirogon are we talkin?

Hot take but a regular apeirogon and a circle are not the same things

[qhd4]

Is there an everywhere smooth, nowhere analytic function?

It's clear that the points where a function is analytic is an open set, but this is not enough of course.

[qhd4]

Tw (pranking):

Keep reading

[qhd4]

ayy lmao

Interesting math fact of the day #156:

Either p is a square mod q and q is a square mod p or neither is true.

[qhd4]

If you only work over some nice fields/rings then I guess you can get away with less, but also embrace the axiom of choice and be free

the saddest thing about finally learning algebraic geometry is the realisation that everything there is infected by the axiom of choice. in undergrad it felt confined to fringe counterintuitive results about duplicating spheres but now i find myself using facts like "every non-unit of a ring is contained in some maximal ideal" all the time to prove very general things about schemes :(

[qhd4]

the poll is closed now, but even the suggestion is appalling, don't taint my beautiful complex geometry with orientation reversal please 🥺

If you say "it depends on your definition" you are missing the point of this post

[qhd4]

i mean up to R it is, look at axiom 3

Once again I find myself striving to invent weird objects in algebra. Expand below to see something somewhat like a group.

Define a somewhat group as a set G equipped with a binary operation m and a transitive and reflexive relation R such that the following properties are satisfied (quantifying over the elements of G) 1. R(x0, x1) and R(y0, y1) implies R(m(x0, y0), m(x1, y1)) 2. R(m(x, m(y, z)), m(m(x, y), z)) 3. There exists an element 0 such that for all x we have R(m(x, 0), x) and R(m(0, x), x) and further there exists some y such that R(m(x, y), 0) alongside some z such that R(m(z, x), 0).

I have produced the following example of a somewhat group which is not a group and for which R is not an equivalence relation.

[qhd4]

Funky stuff indeed, but it messes with my head that you use multiplication for the operation and 0 for the identity lol

Once again I find myself striving to invent weird objects in algebra. Expand below to see something somewhat like a group.

Define a somewhat group as a set G equipped with a binary operation m and a transitive and reflexive relation R such that the following properties are satisfied (quantifying over the elements of G) 1. R(x0, x1) and R(y0, y1) implies R(m(x0, y0), m(x1, y1)) 2. R(m(x, m(y, z)), m(m(x, y), z)) 3. There exists an element 0 such that for all x we have R(m(x, 0), x) and R(m(0, x), x) and further there exists some y such that R(m(x, y), 0) alongside some z such that R(m(z, x), 0).

I have produced the following example of a somewhat group which is not a group and for which R is not an equivalence relation.

[qhd4]