#‘cos^2(x)-sin^2(x)=1-2sin^2(x)’???

[hurdy-girly]

Me when I get rickrolled by my TRIGONOMETRY TEACHER

[dialalagirl]

Alr so remember this?

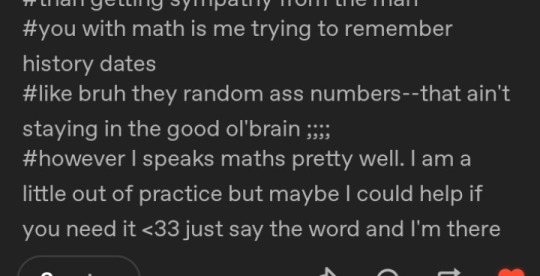
Yea um

I have one to ask, I'll translate it to my best ability,,

What is the tangent of the smallest angle that satisfies the following equation?

cos²x+cos(2x) = sin²x+sin2x

A) √5-1 / 2 B) 2+√5 C) 1 +√5

D) √5/2 E) √5+1 / 2

(It feels so embarrassing asking like this but i want to get more comfortable asking for help :">)

(And ik my academic vocabulary could probably be a 13th reason for a uni professor but we're just gonna ignore that–)

don't be embarrassed!!!! there's nothing wrong with needing help <333 I brushed up on my trig and I believe the answer is A) 'cause (it took me a while to figure out how to type it on a computer, so if I made a mistake, plz forgive me cx):

cos2(x)+(cos2(x)−sin2(x))=sin2(x)+2sin(x)cos(x)

2cos2(x)−sin2(x)=sin2(x)+2sin(x)cos(x)

2cos2(x)−sin2(x)−sin2(x)−2sin(x)cos(x)=0

2cos2(x)−2sin2(x)−2sin(x)cos(x)=0

2(cos2(x)−sin2(x)−sin(x)cos(x))=0

cos2(x)−sin2(x)−sin(x)cos(x)=0

tan(x)=√5-1 / 2

I tried not to write too many steps 'cause maybe it is easier to read that way? idk, communication always gets me :'>

hope this helps! and if you need further clarification, lemme know <33

[zoropookie]

hi, I'm attracted to my crush Heizou like the earth is attracted to the sun— with a large force inversely proportional to the distance squared. He's the sin(90) 4 me. If we we're to be convertices, i wanna be the second convertex. to assure you that at the end of the line, i'll be there waiting for him. these formulas describe how much x²-1, if the value of x is 12. sin (π/2 – A) = cos A & cos (π/2 – A) = sin A

sin (π/2 + A) = cos A & cos (π/2 + A) = – sin Asin (3π/2 – A) = – cos A & cos (3π/2 – A) = – sin A sin (3π/2 + A) = – cos A & cos (3π/2 + A) = sin A sin (π – A) = sin A & cos (π – A) = – cos A sin (π + A) = – sin A & cos (π + A) = – cos A sin (2π – A) = – sin A & cos (2π – A) = cos A sin (2π + A) = sin A & cos (2π + A) = cos A. before seeing him, my heart is a nul set, but when a vector of magnitude from his eyes at a deviation of theta radians made a tangent to my heart, it differentiated. whenever I see him, it was like, I was electrocuted with an amount of 200-1700 volts of electricity. my love for him is like the derivative of e^x, it remains constant and never change. my baby, 1+tan2A = sec2A sec2A – 1 = tan2A (1/cos2A) -1 = tan2A. putting the value of cos A = ⅘.

(5/4)2 – 1 = tan2 A tan2A = 9/16 tan A = 3/4 (sin30° + cos30°) – (sin 60° + cos60°)

= ½ + √3/2 – √3/2 – ½ = 0 If cos A = 4/5, then tan A = Cos A = ⅘. my love for him is a quadratic equation with real roots, which only he can solve by making good binary relation with me. the cosine of my love for you extends to infinity. Baby, simplify 4x³+3x²+3x-1 where x=3. and he'll know what my heart says. He is an essential to me as an element to a set. the geometry of my life revolves around his acute personality. sin(2x) = 2sin(x) • cos(x) = [2tan x/(1+tan2 x)]cos(2x) = cos2(x)–sin2(x) = [(1-tan2 x)/(1+tan2 x)] cos(2x) = 2cos2(x)−1 = 1–2sin2(x)

tan(2x) = [2tan(x)]/ [1−tan2(x)] sec (2x) = sec2 x/(2-sec2 x) csc (2x) = (sec x. csc x)/2. my baby, when he solves this equation for "i" .

hiiii pookie how are you? i hope you're doing well!!!! kiss kiss/p

i'm not sure if this is a copypasta or not, but if it's not, that's extremely impressive and you're super smart hahahahahaha!!!

i'm doing as good as i can lol hopefully you slept well, i'm answering this after ur regular hours

[wisdomrays]

TAFAKKUR: Part 242

MUSLIM CONTRIBUTIONS TO MATHEMATICS: Part 2

Abu Kamil (about 850–930), an Egyptian mathematician, wrote the Book on Algebra which consists of three parts:

(1) Solutions of quadratic equations,

(2) Application of algebra to geometry,

(3) Diophantine equations.

He improved the work of Khwarizmi and applied algebraic methods to geometry. His research was on quadratic equations, multiplication and division of algebraic quantities. His work also includes addition and subtraction of radicals. He found the following formulas:

ax.bx=abx2; a(bx)=(ab)x; (10–x)(10–x)=100+x2–20x

Abu Kamil also wrote the Book On Surveying and Geometry, which was intended for government land surveyors. There, he stated the nontrivial rules for calculating areas, volumes, perimeters, and diagonals of different objects in geometry

Ibrahim ibn Sinan (908–946), a grandson of Thabit bin Qurra, was both an astronomer and a mathematician. Fuat Sezgin writes, "He was one of the most important mathematicians in the medieval Islamic world." He studied geometry, and his work on calculation of the area under the graph of a parabola is especially appreciated. Going further than Archimedes, he introduced a more general method of integration.

Abu Bakr ibn Muhammad ibn al-Husayn al-Karaji (953–1029), also known as al-Karkhi, is regarded as the first person to have developed algebraic operations without using geometry. One of his major works was Al-Fakhri fi'l-jabr wa'l-muqabala (Glorious on algebra). Historian Woepcke recognizes Al-Fakhri as the beginning of the theory of algebraic calculus. Here, al-Karkhi introduced the monomials x, x2, x3, ... and 1/x, 1/x2, 1/x3, ... and explained product rules among them. Moreover, he was the first to find the solutions of the equations ax2n+bxn=c. Al-Karkhi proved the sum formula for integral cubes by using the method of proof by induction, and hence became the first to use this method.

Abu'l Hasan ibn Ali al-Qalasadi (1412–1486) was an Andalusian Muslim mathematician. His main contribution was to introduce algebraic symbolism, and he used short Arabic words for his symbols. For example, he used the symbol for the sound "sh" from the Arabic word meaning "thing" to represent what we call x, the unknown.

TRIGONOMETRY

Khwarizmi also contributed to trigonometry. He established accurate trigonometric tables for sine and cosine, and he was the first to introduce tangent tables. [16] In 1126, these works were translated into Latin by Adelard of Bath.

Al-Battani or Albetagnius (about 850–929) was a Muslim astronomer and mathematician. In his research on astronomy he used trigonometric methods which were a lot more advanced than the geometric methods used by Ptolemy. He introduced trigonometric ratios. For example, for a right triangle with adjacent sides a and b, he gives the formula b sin(A) = a sin(900 – A), which is equivalent to tan A = a/b. He was the first to introduce the cotangent function.

Muhammad Abu'l Wafa (940–998), born at Buzjan in Khorasan, introduced the use of secant, cosecant and tangent functions. He gave a new method of constructing sine tables. He calculated sin(30^0) with an accuracy of up to eight decimal digits. He improved spherical trigonometry and proved the law of sines for general spherical triangles. In particular, he developed the half/double angle formulas:

2 sin2 (x/2)=1–cos x; sin 2x=2sin x cos x

He was the first to introduce the notion of secant and cosecant, and hence completed the list of all six trigonometric functions.

Abu Abd Allah Muhammad ibn Muadh Al-Jayyani (989–1079) was an Arab mathematician from Andalus. He was the author of The Book of Unknown Arcs of a Sphere which was "the first treatise on spherical trigonometry." Here he mentioned formulas for right handed triangles and law of sines. He also stated the formula for the solution of a spherical triangle in terms of the polar triangle. He had a strong influence on the West.

Another outstanding mathematician Nasir al-Din al-Tusi (1201–1274) wrote Treatise On The Quadrilateral, considered the best book on trigonometry written in medieval times, later translated into French by Alexandre Carathéodory Pasha in 1891. In his book al-Tusi made enormous advances in plane and spherical trigonometry. The Dictionary of Scientific Biography states, "This work is really the first in history on trigonometry as an independent branch of pure mathematics and the first in which all six cases for a right-angled spherical triangle are set forth." The well-known sine law is also stated in this work: a/sin A = b/sin B = c/sin C.

Ghiyath al-Din al-Kashi (1393–1449) produces sine tables of up to eight decimal places. In 1424, he computed 2&#960; to an accuracy of sixteen decimal digits. He wrote a very impressive book on mathematics: Miftah al-Hussab (Key to Arithmetic). His main purpose in this book is to provide sufficient knowledge of mathematics for those who are working on astronomy,surveying, architecture, accounting and trading. He also describes how to find the fifth root of any number.

Unfortunately, the contributions of Muslims often go unrecognized. Muslim scholars contributed to science in many aspects such as mathematics, astronomy, geography, philosophy, medicine, art, architecture and so on. However, today few realize that in that era Islam played an important role in all aspects of life. Europe faced losing the works of major scholars, but as a result of their translations into Arabic most of this scholarship not only survived, but was further developed. Inspired by the Qur'an and hadiths, Muslims sought knowledge for the benefit of humankind. As the Qur'an says, "Are those who know equal to those who know not?"(Zumar 39:9). We should appreciate the scholars of all eras for their contributions to science.

[sstonki]

Exponential graph equation maker

Note that the first function is sin(a*x). You can also enter an exact value into the box at the top of the slider, followed by the GRAPH button or the Enter key.įor example, in the chart above, press 'reset'. When you enter your equations, you can refer to up to four variables that are controlled by sliders.Īnd you can adjust the value of each variable by moving the slider up or down. However, if you change the axis limits, this may no longer be true. The initial range of values on the x and y axes are in the same ratio, so a graph of y = x will be at 45°,Īnd circles would be round, not squashed into ellipses. The aspect ratio (ratio of width to height) of the graph window is exactly 4:3. GFE will check to ensure that the lower value is at the bottom of the y axis or the left of the x-axis. To change them, simply edit them in place and press GRAPH or the Enter key again. If you enter a value that is off the graph, the cursor will not show,īut the values of the functions for that x value will be displayed correctly.Īt each end of the x and y axis is a box containing the end values. You can enter the x value for the cursor manually into the text box in the upper left.Īfter entering a value press "Graph" or the enter key. It shows the values of each function where the cursor intersects that function. If you click on "show cursor", a thin vertical line appears. If left unchecked, each function is shaded in a different color. This allows you to more easily see where complex functions overlap, since the more overlap there is, the darker the shading. If this is checked, the shaded areas for all three functions are all the same light gray. When plotting inequalities, the "monochrome shading" checkbox can be used. The area of the graph where y is greater than the function value is shaded. The function will be plotted as a line as usual. GFE can be used to plot inequalities by changing the relational operator in the pull-down menu to the left of the function. It is best to always enter the correct expression yourself. It will add two extra closing parentheses so they balance and evaluate it as 2+(sin(x)) Note: This may not always produce the desired result. When you press GRAPH or enter, it will automatically add enough closing parentheses to balance them. You may have meant it as one over 2sin(x). Since there are no parentheses, it is executed from left to right so it sees it as one half of sin(x). For example if you enter 1/2sin(x) GFE inserts a multiply between the 2 and the sin. It will not work if the function is preceded by a variable name. For exampleģcos(2.1) will be automatically treated as if you entered 3*cos(2.1): three times the cosine of 2.1. If a function (such as sin() ) is preceded by a number, GFE assumes you want to multiply them. See PI definition for more.įor example you could enter sin(pi) or e^2.1 There are two constants you can refer to. Returns the smallest integer greater than or equal to x Returns the highest integer less than or equal to x Returns x rounded off to the nearest whole number Returns the absolute value of x (always positive or zero) The power to which you must raise e to get x.Į (approx 2.718) raised to the power of x. The power to which you must raise the 10 to get x. The trigonometry cotangent function, x in radians. The trigonometry cosecant function, x in radians. The trigonometry secant function, x in radians. The trigonometry tangent function, x in radians. The trigonometry cosine function, x in radians. The trigonometry sine function, x in radians. The function names are not case sensitive.Īll trigonometric functions operate in radians. GFE has the following built-in functions.

[drquanzae]

∫√1+2cotx(cscx+cots) dx

∫√1+2cosx/sinx(1/sinx+cosx/sinx) dx,

∫√sin²(x)2cos(x)+2cos²(x)/sin(x) dx

∫√cos²(x)+2cos(x)+1/sin(y) dx

∫cos(x)+1/sinx dx

∫2cos²(x/2)/2sin(x/2)cos(x/2) dx

∫cos(x/2)/sin(x/2) dx

=2ln(sinx/3)+constant

[toanthangthayloi]

Cách tìm tất cả các nguyên hàm của hàm số bậc nhất 1 ẩn

nguyên hàm hàm số mũ

nguyên hàm hàm số lượng giác

nguyên hàm hàm số chẵn lẻ

nguyên hàm hàm số hữu tỉ

nguyên hàm hàm số vô tỉ chứa căn

nguyên hàm hàm số mũ logarit

nguyên hàm hàm số vô tỷ chứa căn

nguyên hàm hàm số vô tỉ

nguyên hàm của hàm số   2 f x x  sin là

nguyên hàm của hàm số 2 mũ x

nguyên hàm của hàm số 2/4x-3

nguyên hàm của hàm số (1-2x)^5

họ nguyên hàm của hàm số là a. b. c. d

nguyên hàm hàm số hợp

nguyên hàm của hàm số 1/5x-2

nguyên hàm của hàm số 1/(sinx+cosx)^2

nguyên hàm của hàm số 1/2 x+3

nguyên hàm hàm ẩn

nguyên hàm của hàm số bậc 2

nguyên hàm hàm số nhất biến

nguyên hàm của hàm số fx bằng sin 2x

nguyên hàm của hàm số fx bằng căn 2x trừ 1

tìm nguyên hàm của hàm số bằng máy tính

nguyên hàm của hàm số fx bằng x mũ 4 + x là

nguyên hàm của hàm số tan bình x

nguyên hàm của hàm số fx bằng 2x cộng 1

bài tập nguyên hàm hàm hợp

bảng giá trị nguyên hàm

nguyên hàm của hàm số có căn

nguyên hàm của hàm số

nguyên hàm của hàm số mũ

nguyên hàm của hàm số lượng giác

nguyên hàm của hàm số f(x)=x^3+x

nguyên hàm của hàm số hữu tỉ

các dạng nguyên hàm nâng cao

nguyên hàm của 2 trên x

nguyên hàm fx

nguyên hàm f(u)

nguyên hàm của hàm số đa thức

nguyên hàm các hàm số đơn giản

nguyên hàm của hàm số chứa trị tuyệt đối

tìm nguyên hàm của hàm số thỏa điều kiện cho trước

nguyên hàm hàm số y=1 x trên tập xác định là

nguyên hàm đổi biến số hàm lượng giác

nguyên hàm của hàm số e^2x

nguyên hàm của hàm số e mũ x bình

nguyên hàm của hàm số e mũ x

nguyên hàm của hàm số y=e^x

họ nguyên hàm của hàm số e^x + x

e^2x là nguyên hàm của hàm số nào

e^x^2 là nguyên hàm của hàm số nào

e^x^3 là nguyên hàm của hàm số nào

nguyên hàm của hàm số x.e^x

nguyên hàm của hàm số 3 mũ x

nguyên hàm của hàm số 3^2x

e^ax+b nguyên hàm

e mũ u nguyên hàm

nguyên hàm của hàm số là gì

nguyên hàm của hàm số lượng giác nâng cao

nguyên hàm của các hàm số lượng giác

công thức nguyên hàm hàm số lượng giác

họ nguyên hàm của hàm số là gì

bảng nguyên hàm các hàm số thường gặp

nguyên hàm của hàm số hợp

bài tập nguyên hàm hàm số hữu tỉ

nguyên hàm h của hàm số f(x)=sinx cosx+2 bằng

họ nguyên hàm của hàm số

họ nguyên hàm của hàm số f(x)=4x(1+lnx)

họ nguyên hàm của hàm số f(x)=3x^2+1

tìm nguyên hàm h của hàm số f(x)=x21+x3

tìm nguyên hàm ln của hàm số f(x)=x−−√lnx

nguyên hàm của hàm số img1 là

họ nguyên hàm của hàm số img1 là

tìm nguyên hàm của hàm số img1

một nguyên hàm của hàm số img1 là

tìm họ nguyên hàm của hàm số img1

tìm nguyên hàm img1 của hàm số img2 biết img3

cho img1 là nguyên hàm của hàm số img2. tính img3

nguyên hàm của hàm số trên khoảng

tìm nguyên hàm của hàm số trên khoảng

hàm số có nguyên hàm khi nào

hàm số không là nguyên hàm của sin2x

hàm số không phải nguyên hàm của sin2x

hàm số có nguyên hàm trên k nếu

nguyên hàm của hàm số y=ax a 0 a khác 1 là

nguyên hàm hàm số lẻ

nguyên hàm của hàm số lnx/x

nguyên hàm của hàm số lũy thừa

nguyên hàm của hàm số là

nguyên hàm của hàm số ln

nguyên hàm của hàm số ln^3x/x

nguyên hàm của hàm số e mũ 2x

nguyên hàm của hàm số e mũ x mũ 3

nguyên hàm của hàm số fx = 7 mũ x

nguyên hàm của hàm số x nhân e mũ x

nguyên hàm của hàm số x nhân e mũ 2x

1/x là nguyên hàm của hàm số nào

nguyên hàm của hàm số y = cos bình x nhân sin x

hàm số 25cm là một nguyên hàm của hàm số nào sau đây

tìm nguyên hàm của hàm số online

nguyên hàm của 2 trên x bình

nguyên hàm của 2 phần x

nguyên hàm của hàm ẩn

nguyên hàm thương

nguyên hàm số phức

tìm nguyên hàm của hàm số fx = cos3x + pi trên 6

nguyên hàm hàm hợp

tìm một nguyên hàm của hàm số biết rằng

nguyên hàm của hàm số f(x)=x^3 trên r là

nguyên hàm của hàm số sin2x

nguyên hàm của hàm số sinx cosx

nguyên hàm của hàm số sin3x

nguyên hàm của hàm số sơ cấp

nguyên hàm của hàm số sin bình x

nguyên hàm của hàm số sinx

nguyên hàm của hàm số tan^2x

nguyên hàm của hàm số tan^3x

nguyên hàm của hàm số y=u′(x)u(x) là

u nguyên hàm

f(u) nguyên hàm

1/u nguyên hàm

nguyên hàm u^a

nguyên hàm của hàm số mũ và logarit

cách tính nguyên hàm của hàm số vô tỉ

biết là một nguyên hàm của hàm số và . tính

u/v nguyên hàm

nguyên hàm của hàm số cosx

nguyên hàm của hàm số x

nguyên hàm của hàm số f(x)=cos3x

nguyên hàm của hàm số f(x)=sin2x

nguyên hàm của hàm số f(x)=2x^3-9

f(x) là nguyên hàm của hàm số

nguyên hàm f(x) của hàm số thỏa mãn là

nguyên hàm của hàm số f(x)=cosx là

nguyên hàm của hàm số y=cos^2x.sinx

nguyên hàm của hàm số y=sin^3x.cosx

nguyên hàm của hàm số y=xe^x

nguyên hàm của hàm số y=sin^2x.cos^3x

nguyên hàm của hàm số y=x^2-3x+1/x

nguyên hàm của hàm số y=10^2x

nguyên hàm của hàm số y=cos5x.cosx

nguyên hàm số 0

nguyên hàm của hàm số y = 10 mũ 2x

nguyên hàm của hàm số 1/2 x+1

nguyên hàm của 1 hàm số

nguyên hàm của 1 số hàm cơ bản

một nguyên hàm của hàm số f(x)=2x+1

nguyên hàm của hàm số   22 5   x f x    là

nguyên hàm của hàm số 2sin3xcos2x

nguyên hàm của hàm số 2sinx

nguyên hàm của hàm số (2x+1)e^x

nguyên hàm của hàm số fx = 2sin 3 x cos2x

họ nguyên hàm của hàm số 2^2x

nguyên hàm của hàm số 3sin^2xcosx

họ nguyên hàm của hàm số 3x-1/(x-1)^2

nguyên hàm của hàm số cos 3x

họ nguyên hàm của hàm số (3x+1)^2019

nguyên hàm của hàm số x^3/x-1

nguyên hàm của hàm số căn 3x+2

nguyên hàm của hàm số x^3+x

nguyên hàm của hàm số căn 3 x + 2

nguyên hàm của hàm số 2x^3-9

họ nguyên hàm của hàm số 4x(1+ln)

nguyên hàm của hàm số 2x^4+x/3^2

nguyên hàm của hàm số f(x)=4x^3+x-1

nguyên hàm của hàm số f(x)=x^4+x^2

nguyên hàm của hàm số f(x)=x^4+x

tìm nguyên hàm của hàm số 1/4-x^2

tìm nguyên hàm của hàm số   2 4 3 f x  

nguyên hàm của hàm số y=5xx2+4y=5xx2+4 là

nguyên hàm của hàm số y=12x^5

nguyên hàm của hàm số y=x^5

nguyên hàm của hàm số f(x)= cos(5x-2)

họ nguyên hàm của hàm số fx = 5 mũ 2x

họ nguyên hàm của hàm số f(x)=cos+6x

nguyên hàm của hàm số 7^x

tìm nguyên hàm của hàm số 7 mũ x

nguyên hàm của hàm số y=7x là

tìm nguyên hàm của hàm số f(x)=7x

[pius2017]

Solve 2Cos^2(x)+2cos(x)+1=0 for all solutions 0<x <2pi x=

Solve 2Cos^2(x)+2cos(x)+1=0 for all solutions 0

Solve for t, 0 < t <2pi 20sin(t)cos(t)=-8sin(t) t= ? Solve Csc(2x)-2=0 for the four smallest positive solutions x= Solve 2Cos^2(x)+2cos(x)+1=0 for all solutions 0<x <2pi x= Solve 2sin^2(x)-5sin(x)+2=0 for all solutions 0 <x <2pi x=? Solve sin^2(w)=-5cos(w) for all solutions 0 < w < 2pi w= ? if you could go over the steps of at lease one that would really help me understand and pull apart what I…

[matheory]

LIMITS OF TRIGONOMETRIC FUNCTIONS CONTINUITY OF A FUNCTION AT A NUMBER Learning guides 3.8 and 4.1

Hello! Welcome back to the blog. For this entry, we will be discussing the limits of trigonometric functions and continuity of a function. Sit tight for this one since we need to recall trigonometric functions which were discussed in grade 10! To enhance our skills regarding these topics, we will be answering some exercises involving them. 

Learning guide 3.8.1 (Limits of Trigonometric Functions) In this learning guide, limits of trigonometric functions are introduced. There are two theorems discussed in this module. First, if c is an element of the domain of f(x) which is a trigonometric function, the limit of f(x) as x approaches c, would be f(c). The other theorem involves composition of trigonometric functions. These theorems would be helpful in solving the limits of trigonometric functions.

For this example, we are looking for the limit of the trigonometric function sin^2 x/1 - cos x as x approaches 0. Since sin^2 x can also be written as 1 - cos^2 x (pythagorean identities). Expanding 1-cos^2 x will give us (1 - cos x) (1 + cos x), and since 1 - cos x is also in the denominator, it will be cancelled out, leaving us with (1 + cos x). Since cos 0 is 1, the limit of the function would be 2. 

In this exercise, we will be using the concept of one-sided limits again. In the function, we can write cos 2x as (1-2sin^2 x). We can factor out 1/2 from sin x/2sin^2 x. From there we will get sin x / sin^2 x which will give us 1/sin x. This term would infinity since the denominator would be 0. The steps are basically the same with both 0+ and 0-, except we will get +∞ and -∞ respectively. Since the limits from both sides are not the same, the limit of the trigonometric function does not exist. 

Learning guide 3.8.2 (Limits of Trigonometric Functions) In this learning guide, new theorems on the limits of trigonometric functions are discussed. These theorems will help us in solving the limits of trigonometric functions when substitution will give us indeterminate forms. 

In this example, first, we multiplied the conjugate of the numerator to both numerator and denominator to get 1-cos^2 x, which is also equal to sin^2 x. Factoring out the terms will give us sin^2 x/ x^2 and 1/1+cos x. We can expand sin^2 x/x^2 to (sinx/x)(sinx/x) which are both equal to 1 by Theorem 1. This will leave us with 1/1+cos x. Substituting 0 to cos x, will give us cos 0 which is equal to 1. Thus, the limit of the function as x approaches 0 is 1/2. 

Learning guide 4.1 (Continuity of a function at a number) In this learning guide,  we are introduced to the concept of continuity. We know that a graph or a function is continuous when there are no breaks in the graph. We can check if a function is continuous at a certain point if it satisfies the given three conditions in the learning guide. Let’s check if the item below is continuous or not at the given number. 

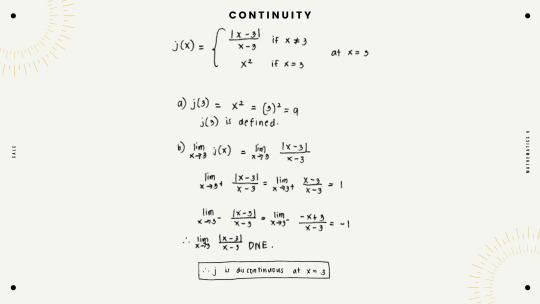
To check if the function is continuous at x=3, we need to evaluate if it satisfies the conditions. First, if j(3) is defined. Since the function has a value when 3 is substituted to x, we can say that it is defined. Let’s check if it also satisfies the next condition which is the limit of the function as x approaches 3 exists. To evaluate the limit, we will be using the function with the absolute value. We will be using the concept of one-sided limits for this. Since the individual limits are not equal, the limit of the whole function as x approaches 3, does not exist. Since it does not satisfy all three conditions, we can conclude that the function is discontinuous at x = 3. 

Reflection (Week 4 and 5)

For this week, I can say that I am more productive unlike last week. I focused on studying these learning guides since the long test is fast approaching. Working on the exercises in the learning guides really helped me understood the topic better. Even though some parts are hard, I had fun learning the topic. It has also challenged me in some ways since I had to recall topics which were discussed in previous grade levels. I will maintain my good habits this week so that I would also be productive in the weeks to come. 

-m.y. 

[gayyyyyce]

Sin(2x) = 2sin(x) cos(x)

Sin^2 (x) + cos^2 (x) = 1

Sin(x) = cos(x) tan(x)

Sin(x) = (1 - cos(2x))/2

[Sin(x)]’ = cos(x)

Sin(x) = [-cos(x)]’

Some basic trig identities (the last two involve calculus and derivatives, no need to worry much about those yet!)

But now, how would one “fuck” trig? Namely, sin(x)?

Let’s start with just the variable “fuck” for our angle and set up a right triangle!

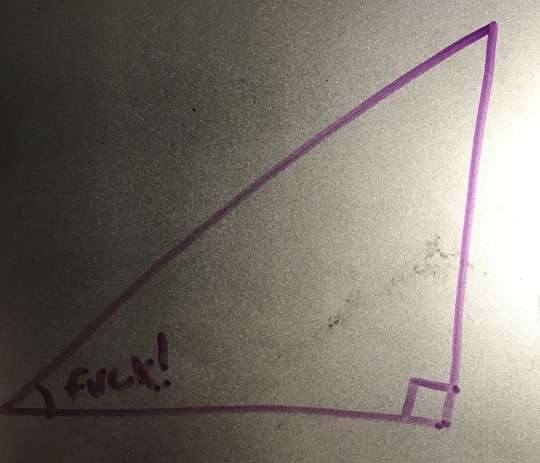
Like so.

Now, if you really want to find out how to fuck trig, you’ve gotta get more specific with your parameters! Naturally, I chose 69 for the hypotenuse. What unit this is (ie. inches, centimeters, furlongs, cubits, astronomical units, etc) is up to you. Whatever you require! This depends on how realistic you’re being about the width of the “object” you’re penetrating the triangle with is (take note penis-having folk: astronomical units are probably not appropriate for measuring your dick with) or how long/wide you want the triangle to be when penetrating you. Now, you’re going to want to consider what value you want “fuck” to have. I only made it into a right triangle because this is our first foray into “fucking trigonometry” and it’s easier this way. If you’re wanting to penetrate the triangle instead of vice versa, an equilateral triangle is probably the way to go, and I could help you with those calculations for your triangle if you really wish. However, I will stop helping you if you insist that astronomical units is appropriate for measuring the triangle or... you. Unless you’re an eldritch entity. In which case I would probably like to join you (dm me, plz).

Remember that the value of the angle “fuck” determines how long and wide your triangle is.

Now, here is a basic right triangle and some basic calculations. My suggested unit for the hypotenuse is millimeters, but go ahead with furlongs if you’re prepared to suffer the consequences!

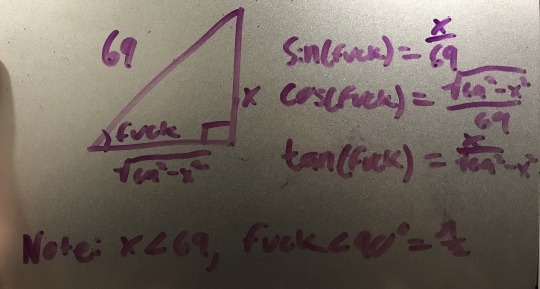
Have fun y’all and stay safe!

If cats knew what sin was they wouldn’t even care

[vaish19-blog]

Ad maths - Trignometric identities Aug 31st

1. tan 2x = 2tan x/[1 - (tan x)^2] We know that tan (x + y) = (tan x + tan y)/(1 - tan x tan y) Replacing y by x , we get  tan 2x =(tan x + tan x)/(1 - tan x tan x) tan 2x = 2 tan x/ [1 - (tan x)^2] 2. sin 3x = 3 sin x – 4 (sin x)^3 We have, sin 3x = sin (2x + x) sin (x + y) = sin x cos y + cos x sin y sin (2x + x) = sin 2x cos x + cos 2x sin x wkt sin 2x = 2 sin x cos x cos 2x = 1 - 2(sin x)^2 = 2 sin x cos x cos x + (1 – 2sin2 x) sin x (cos x)^2 = 1 - (sin x)^2 = 2 sin x (1 – sin2 x) + sin x – 2 (sin x)^3 = 2 sin x – 2 (sin x)^3 + sin x – 2 (sin x)^3 = 3 sin x – 4 (sin x)^3 18. cos 3x = 4 (cos x)^3 – 3 cos x We have, cos 3x = cos (2x +x) wkt cos (x + y) = cos x cos y - sin x sin y cos 2x = 2(cos x)^2 - 1 (cos x)^2 + (sin x)^2 = 1 cos (2x + x) = cos 2x cos x – sin 2x sin x = (2(cos x)^2 – 1) cos x – 2sin x cos x sin x = (2(cos x)^2 – 1) cos x – 2cos x (1 – (cos x)^2 ) = 2 (cos x)^3 – cos x – 2cos x + 2 (cos x)^3 = 4 (cos x)^3 – 3cos x. 19. tan 3x = [3 tan x - (tan x)^3]/[1 - 3(tan x)^2] We have tan 3x = tan (2x + x) wkt tan (x + y) = tan x + tan y/1 - tan x tan y tan (2x + x) = tan 2x + tan x/1 - tan 2x tan x wkt tan 2x = 2tan x/[1 - (tan x)^2] tan (2x + x) = [{ 2tan x/{1 - (tan x)^2} } + tan x]/[1 - { 2tan x/1 - (tan x)^2} tan x ] tan 3x = [2 tan x + tan x - (tan x)^3]/[1 - (tan x)^2 - 2 (tan x)^2 ] tan 3x = 3tan x - (tan x)^3/1 - 3(tan x)^2 20. (i) cos x + cos y = 2 cos {(x + y)/2} cos {(x - y)/2} (ii) cos x – cos y = –2 sin {(x + y)/2} sin {(x - y)/2} (iii) sin x + sin y = 2 sin {(x + y)/2} cos {(x - y)/2} (iv) sin x – sin y = -2 cos {(x + y)/2} sin {(x - y)/2} We know that cos (x + y) = cos x cos y – sin x sin y ... (1) and cos (x – y) = cos x cos y + sin x sin y ... (2) Adding and subtracting (1) and (2), we get cos (x + y) + cos(x – y) = 2 cos x cos y ... (3) and cos (x + y) – cos (x – y) = – 2 sin x sin y ... (4) Further sin (x + y) = sin x cos y + cos x sin y ... (5) and sin (x – y) = sin x cos y – cos x sin y ... (6) Adding and subtracting (5) and (6), we get sin (x + y) + sin (x – y) = 2 sin x cos y ... (7) sin (x + y) – sin (x – y) = 2cos x sin y ... (8) Let x + y = θ and x – y = φ. Therefore x= (θ + φ)/2 and y= (θ - φ)/2 Substituting the values of x and y in (3), (4), (7) and (8), we get cos θ + cos φ = 2 cos[(θ + φ )/2]cos[(θ + φ )/2] cos θ - cos φ = -2 sin[(θ + φ )/2]sin[(θ + φ )/2] sin θ + sin φ = 2 sin[(θ + φ )/2]cos[(θ + φ )/2] sin θ – sin φ = cos θ + cos φ = 2 cos[(θ + φ )/2]cos[(θ + φ )/2] Since θ and φ can take any real values, we can replace θ by x and φ by y. Thus, we get above equations Remark As a part of identities given in 20, we can prove the following results: 21. (i) 2 cos x cos y = cos (x + y) + cos (x – y) (ii) –2 sin x sin y = cos (x + y) – cos (x – y) (iii) 2 sin x cos y = sin (x + y) + sin (x – y) (iv) 2 cos x sin y = sin (x + y) – sin (x – y).

[rowanstree-blog]

Day #172

          Today I started with a Math class on graphing sinusoidal functions. I started off with a test on deriving the period from the graph of a sinusoidal function. After that, I watched a video on transforming sinusoidal graphs by adding a vertical stretch and a horizontal reflection to the base equation      y=sin (x). In this function, the visual graph ranged form -2pi to 2pi. Before I graphed the function, i wrote down all of the coordinates. I used the x values between 2pi and -2pi and then graphed it on a cartesian plane. I then graphed the function y=2sin(x). Because the 2 was added to the equation, the function experienced a vertical stretch as the amplitude stretched by a factor of two. After that, I graphed the function y=sin(-x). This caused the function to experience a horizontal reflection as it moves, approaching positive infinity on the x axis. Then, I graphed the whole function, y=2sin(-x). Relating to the original y=sin(x) function, the function as a whole experiences a vertical stretch and a horizontal reflection as I add coefficients and negative signs to the equation. Next, I watched a video on transforming cyclical graphs with vertical and horizontal stretches. I started with the equation y=cos(x), which starts at one and continues from there. I then changed the function to y=cos1/3x. By using KCF, the period increases by a factor of 3, this causes the function to experience a horizontal stretch because the period expands. I then altered the function even more by changing it to y=-2.5cos1/3x. because it is a negative 2.5, the function is flipped and instead starts at -1. The amplitude then increases by a factor of 2.5 concluding that there is a significant difference between the original cyclical function. I then watched another video on graphing sinusoidal functions and how to find the phase shift and vertical shirt of a sinusoidal function. All you have to do to find the P.S., you must take -c/d and simplify if needed. In order to find the V.S., all you have to do is take d in the equation. After that, I did a French lesson on Duolingo followed by a Chemistry class on Buffers. Buffers help to maintain and restore the pH balance where it it necessary. Buffer solutions consists of weak bases and acids to react with strong acids and bases when introduced to a reaction. This is beneficial to all mammalian systems. For example, human blood pH must range from 7.35-7.45. When there is an influx of hydronium into the blood, using Le Châtelier’s principle, the reaction will compensate for that influx, they are generally incorporated in a buffer solution. The same can happen when there is an influx of bases, the reaction will simply move to the right and restore proper pH or else the blood may become too alkaline or acidic. I then took a space science class on a history of Earth’s climate. When Earth first came to be, there was an abundance of ammonia and methane which caused it to be very hot. Once Oxygen-Production Cyanobacteria was introduced, the Earth cooled and life was capable of sustainability by Oxygen. Once these new elements were introduced, the Earth became practically a big snowball. These polar opposite states of the Earth are called the Greenhouse climate and the Icehouse climate and have become less extreme over the years. Our huge contribution to global warming is creating our current Icehouse state to move to the Greenhouse state early on which can have severe environmental impacts. Earth has sustained itself through many hard times and can most likely recover from our impact but the question is, can we recover from our impacts? After that, I took an environmental science class on how livestock agriculture contributes to air and water pollution. Manure and Urine are high in Nitrogen and Phosphate which can end up in ground water and surface water systems which can lead to eutroficaiton and contaminated water. Also, chemicals, hormones and antibiotics are being applied to the animals but their microbial resistance has strengthened and therefore has little to no effect on them but certainly the environment. Animal waste and metabolism exerts gases that contribute to global warming such as Methane. Feedlots can minimize environmental impacts, if properly managed but it is very hard to do so. I then did a quick exercise followed by an hour long lunch. After that, I took a women’s history class on Martha Graham who contributed a lot to modern, twentieth century dance through her expression of emotion. Her movements conveyed emotion that had not been articulated in ballet before, abdominal contractions articulated inner tension that was foreign but intriguing to audiences. After that, I took an economics class on perfect completion and why it matters Perfect competition is when there are many sellers with the same product, there is easy entry and exit in and out of the market and the sellers cannot raise prices or else they won’t get any sales. Perfect competition matters so that the perfectly competitive markets can thrive and provide a very limited amount of freedom to the sellers which is beneficial to the consumers. After that, I took a grammar class on the Oxford comma which is used as punctuation in long lists to steer clear of confusion. I then read “The Beauty Myth” on how many women live to look a certain way and remove certain aspects of themselves to please the Patriarchy.

[digitalnomadic]

Try using Euler's formula or something maybe for 89. Try covering sin^2 to 1/2[1-cos(pi/n)]. Or just plug them into wolframalpha or mathematica if you have that 😂. Wolfram could give you a different end result tho. I noticed this from doing the integral of x^2sin^2(n*pi*x/L) from 0 to L and negative infinity to infinity. So you could try doing uv sub also to simplify. I'm real tired from work rn and can't think of the best way, but I hope this helps! Edit: I interpreted this wrong. I thought you wanted a solution. Go to wolfram and plug in values of 1, 2, and so on for each and see how the value changes with the growing n! That should give you the right idea. Actually, idk if I'm doing this right. I'm too tired to think right now.

does anyone know how to find if these are convergent or divergent? *sad puppy eyes*