#automata theory

[felixcloud6288]

I need to rant for a moment and maybe some of you nerds on Tumblr will listen to me when I warn you about the dangers of invoking the empty language in a proof cause clearly, none of the students I TA for did.

In automata theory, a language refers to the set of input sequences that a machine accepts. This is equivalent to the user inputs that cause a program to close without error.

The empty language is a particular language that contains nothing in it. In other words, if a machine's language is empty, then every input you could try giving it will either generate an error or fail to shut the machine down.

And because the empty language is empty, there are many things about it that are vacuously true about it, and many contradicting statements can be simultaneously true about the empty language.

For example, the empty language is part of the set of languages that contain only palindromes and odd-length inputs (because there are no non-palindromes or even-length inputs in it). And the empty language is also part of the set of languages that contain only non-palindromes and even-length inputs (because there are no palindromes or odd-length inputs in it).

So whenever you do a proof about determining the characteristics of a language, you need to be very cautious about using the empty language in your proof because it may unexpectedly pass the vibe check.

Unless you 100% understand what will happen with the empty set, avoid using it in your proofs.

Anyway, this is just a long-winded way of saying I've had to take points off one particular exam question for most of the students I grade for something I've warned them constantly to avoid or be wary of.

[ssjkamui-digitalphoenixug]

Konrad Zuse und der Z3: Vor 80 Jahren erfand ein Deutscher den ersten Computer

Auf den Tag genau vor 80 Jahren stellte Konrad Zuse der Welt den ersten Computer vor. Was viele nicht wissen: Der Berliner Ingenieur veröffentlichte auch philosophische Schriften, die auf technisch-naturwissenschaftlicher Basis eine Weltsicht vermitteln, die sich später in Filmen wie Matrix wiederfand. Dieser Beitrag erschien zuerst in COMPACT 08/2020. Die großen Meilensteine unserer Geschichte beleuchtet unsere Sonderausgabe Schicksalstage der Deutschen: Von Karl dem Großen bis zum Fall der Mauer. Hier mehr erfahren.

Man sieht einen weiten, grenzenlosen Raum, in dem Farben und Linien zu verschwimmen scheinen. Überall sind gleichmäßig Knotenpunkte eines Rasters verteilt, dazwischen zucken rote Informationsblitze. Sie transportieren Daten kreuz und quer durch die unendlich wirkenden Weiten, unaufhörlich, ruhelos. Der Blick geht von oben herab in die Tiefe, auch dort leuchtet alles hell, ist alles in Bewegung. Das System, das man hier vor Augen hat, produziert eine endlose Rechnung, es hält die Welt am Laufen. Die Realität, derer wir gewahr werden, ist letztendlich eine virtuelle.

Was nach einer Szene aus dem Science-Fiction-Film Tron oder einem Video von Kraftwerk klingt, ist in Wirklichkeit ein Ölgemälde mit dem vielsagenden Titel Rechnender Raum. Dessen Schöpfer ist heute allerdings nicht unbedingt als Künstler bekannt, sondern vor allem als Vater des Computers. Den ersten funktionsfähigen digitalen Rechner dieser Art, den Z3, stellte er vor genau 80 Jahren, am 12. Mai 1941, in Berlin vor. Sein Bild Rechnender Raum entstand 1967 – und illustrierte seine philosophische Idee von der Wirklichkeit.

Genialer Tüftler

Zuse arbeitete anfangs nicht im Bereich der Elektronik, sondern in der Luftfahrt. Die Malerei war eine seiner frühen Leidenschaften – inspiriert wurde er dabei hauptsächlich vom italienischen Futurismus. Außerdem war er zeitweise als Reklamezeichner tätig. Seine Bilder verkaufte er, um sein Studium zu finanzieren, das er 1935 in Berlin mit Diplom abschloss. Danach kam er als Statiker bei den Henschel-Flugzeugwerken in Schönefeld unter. Nach Dienstschluss tüftelte er daheim in seiner Erfinderwerkstatt.

An seinem Broterwerb störte ihm vor allem eines: Er musste immer und immer wieder ein und dieselben Rechnungen durchführen. Konnte dies nicht auch eine Maschine erledigen?

Wie der britische Mathematiker Charles Babbage (1791–1871), der Erfinder der sogenannten Analytical Engine, dachte Zuse dabei zunächst an ein mechanisches Gerät, doch das erwies sich schon bald als unpraktikabel. Der Z1, den er 1938 fertigstellen konnte, las die Programme von gelochten Kinofilmstreifen ab, arbeitete aber unzuverlässig und hakte oft. Erst die Verbindung von Elektronik und Mechanik führte zum Erfolg: 1941 realisierte er, inzwischen selbständig, mit dem Z3 seine bekannteste Erfindung.

Im Gegensatz zu heutigen Computern stellte der Z3 fundamentale Logikfunktionen nicht mithilfe von Widerständen dar, sondern per elektrisch steuerbaren Schaltern. Durch diese Art der Konstruktion war er zwar langsamer als der 1942 im Auftrag des US-Militärs entwickelte ENIAC, aber weitaus leichter zu bedienen.

Zuses Rechner erfüllte als Erster das Merkmal der Turing-Vollständigkeit. Dieser liegt das hypothetische Modell einer sogenannten Turingmaschine (benannt nach dem britischen Logiker Alan Turing) zugrunde: Eine fiktive Apparatur, die ein Band nach links und rechts bewegen, die aktuelle Stelle auslesen und in Abhängigkeit vom Inhalt Programmcodes ausführen und das Band neu beschreiben kann. Somit war der Z3 in der Lage, jede mathematische Funktion zu berechnen.

Während der ENIAC zum Neuprogrammieren jedes Mal auseinander- und wieder zusammengebaut werden musste, besaß Zuses Rechner – wie heutige Computer – einen Befehls- und Datenspeicher sowie ein Rechenwerk. Mit Plankalkül hatte sein Erfinder dazu eigens eine Programmiersprache entwickelt. Der Z3 nahm damit vieles vorweg, was erst mit dem 1946 fertiggestellten EDVAC, dem Nachfolger des ENIAC, Standard werden sollte.

Im letzten Kriegsmonat 1945 verschlug es Zuse zunächst ins Allgäu. Im beschaulichen Hopferau entwickelte er den Z3 zum Z4 weiter. 1948 konnte er seinen neuen Rechner erstmals in Betrieb nehmen und damit die Milchgeldrechnungen der örtlichen Sennerei Lehern erstellen. Deren Inhaber wollte zunächst nicht glauben, dass der Ingenieur aus Berlin mit seiner Apparatur die Milchpreise schneller berechnen könne als seine eigenen Fachleute.

Ein Jahr später gründete der Erfinder in Neukirchen bei Fulda die Zuse KG und vertrieb seine Computer in Zusammenarbeit mit Heinz Nixdorf. Das Unternehmen wurde 1964 von der Schweizer Firma Brown Boveri & Cie. übernommen, 1971 sicherte sich Siemens 70 Prozent der Anteile. Zuse hatte sich inzwischen aus der Firma zurückgezogen, widmete sich wieder der Malerei – und entwickelte überaus bemerkenswerte philosophische Ideen auf naturwissenschaftlicher Basis, die die Welt, wie sie uns als Gewissheit erscheint, radikal infrage stellt.

Universale Turingmaschine

Im Jahr 1970 veröffentlichte er ein Buch, das den gleichen Namen trägt wie sein eingangs erwähntes Gemälde: Rechnender Raum. «Es geschah bei dem Gedanken der Kausalität, dass mir plötzlich der Gedanke auftauchte, den Kosmos als eine gigantische Rechenmaschine aufzufassen», so Zuse.

Seine These: Die materielle Welt, wie sie sich uns offenbart, ist nicht real, sondern eine Simulation, die mit einer gigantischen Rechenmaschine erzeugt wird. Wir leben also buchstäblich in einer Matrix, wie sie viele Jahre später von Hollywood in der gleichnamigen Filmtrilogie dargestellt wurde.

Grundlage für Zuses Annahme ist seine Beobachtung, dass die Expansion von elektromagnetischen Feldern, Gravitationsvektoren und Gasen erstaunlich gut mit der sogenannten Automatentheorie erklärt werden kann. Einer der simpelsten Automaten ist ein Lichtschalter, der durch Tastendruck vom Zustand «Licht aus» in den Zustand «Licht an» übergeht.

Die ausgefeiltesten, allerdings speicherbegrenzten Automaten sind jene, die sozusagen Turing-vollständig sind, also unsere heutigen Computer, Smartphones oder Tablets – und der perfekteste Automat wäre demnach jener, der einer universalen Turingmaschine mit unendlichem Speicher entspräche. Wenn nun ein Automat einen anderen simulieren könnte (und umgekehrt), gälten beide als Äquivalent.

Zuses These setzt genau hier an: Da sehr viele Teile der theoretischen Physik mithilfe von Computern simulierbar sind, könne man anhand der Automatentheorie daraus ableiten, dass die vermeintlich wirkliche Welt eine Computersimulation sei. Je besser diese Simulation funktioniere, desto wahrscheinlicher sei es, dass es sich bei der Wirklichkeit auch nur um eine Fülle von Rechenvorgängen auf einem Computer handle.

Damit befindet sich Zuse in Übereinstimmung mit wesentlich älteren philosophischen Theorien, die davon ausgehen, dass die materielle Welt nur Abbild von Informationen sei – und diese Informationen die eigentliche Wahrheit wären. Man findet diese Vorstellung schon bei Platon und Pythagoras, aber auch in der Kabbala, im christlichen Gnostizismus und im Buddhismus. Und in der hermetischen Alchemie ist das, was mit dem Begriff Azoth (auf Deutsch in etwa mit «Weltgeist» zu übersetzen) beschrieben wird, nichts anderes als ein Informations-Urstoff, der die Grundlage alles Bestehenden bildet. Zuses Rechnender Raum untermauert solche Konzepte wissenschaftlich.

«Es geschah …, dass mir plötzlich der Gedanke auftauchte, den Kosmos als eine gigantische Rechenmaschine aufzufassen.» Konrad Zuse

Zuses philosophische Ideen wurden unter anderem von Stephen Wolfram weiterentwickelt. In seinem 2002 erschienenen Buch A New Kind of Science (Eine neue Form der Wissenschaft) beschrieb der britische Physiker und Informatiker das Universum als ein digitales Wesen, das auf «simple programs» (einfachen Programmen) basiert.

Andere Autoren hingegen meinten, das Universum entspräche weniger einem zellulären Automaten als eher einem riesigen artifiziellen neuronalen Netz. Damit wäre es eine gigantische Künstliche Intelligenz, die sich sogar auf das Verhalten der Menschen einstellen könnte. Eine Vorstellung, die bei dem einen oder anderen für gewisse Paranoia sorgen dürfte.

In der Populärkultur tauchen Zuses Ideen zum Beispiel bei dem US-amerikanischen Science-Fiction-Autor Philip K. Dick (The Man in the High Castle) auf. Dieser wies darauf hin, dass so gut wie jede Religion davon ausgehe, dass sich der Mensch in einer Scheinwelt befände und die Ursünde des Menschen darin bestehe, vergessen zu haben, dass das irdische Leben nur eine Art Simulation sei. Und natürlich spielen Filme wie Tron, Matrix oder auch das Anime Digimon mit solchen Vorstellungen.

Abschied vom Materialismus

Man kann Zuses Ansatz als typische Ausprägung des aufgeklärten Westens kritisieren, der die Welt als ein perfektes Uhrwerk (oder eben als Computer) betrachtet. Unter dieser Prämisse kann der Mensch an Macht gewinnen, wenn er die Regeln des Systems (oder den Code) erlernt und für sich nutzt.

Man kann durch den Rechnenden Raum aber auch zu einem anderen Schluss gelangen: Wenn materieller Erfolg und das Streben nach materiellen Gütern sinnlos ist, weil sich alles nur in einer großen Computersimulation abspielt, ist das Anhäufen von Reichtümern ungefähr genauso relevant wie das Sammeln von Goldmünzen bei Super Mario.

Zuerst veröffentlicht auf

[chloe-of-astora]

When I say I'm doing girl math this is what I mean btw

[i-hear-a-sound]

like to charge reblog to cast. accord come home

[splatoonusna]

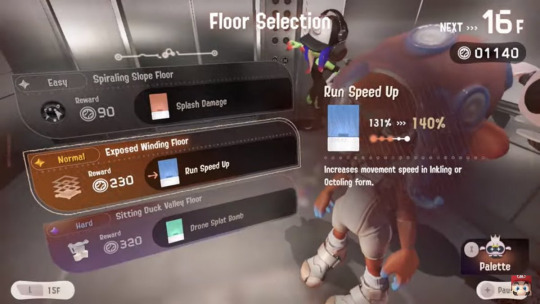
Someone on Twitter pointed out the Run Speed Up says "inkling or octoling form" I wonder if we're going to be able to pick our character OR I wonder if a certain Agent will make a return and we will be able to play as both in different scenarios?

Since Marina is nowhere to be found in the trailer my two theories are, Marina is somehow the antagonist or, with this inkling/octoling ability Marina is going to be supporting Agent 4 while Pearl supports 8?

[jonahmagnus]

Para natural chapter 8 is literally peak and yes it is that serious to me.... If you dont understand it perhaps you need to reread the comic because this is when Zack gets to connect a billion red strings and take their baby gloves off and start fucking balling at full speeds. Chapter 8 is basically when Zack is like "hey you know this story youve been reading for 500+ pages? Well" *nier automata opening credits*

[bioswear]

got this video of Yoko Taro’s funny little bow at the LA NieR Orchestra Concert

[futurehauntedghost]

Before the new episode of the anime drops, let me drop this theory that I’ve been having for a year now and why I think it might come true in the next episode.

My theory is that I think 9S is going to die in the stead of 2B. Let me explain.

So far the anime has had some, on first glance big differences compared to the game. Like Lily living instead of Anemone, and Eve dying before Adam. And it seems like these things would be a major change, but in hindsight, it changes overall nothing. The most we get from it is a character study from those characters when they are put in these new scenarios. This isn’t a bad thing.

I believe that the anime is telltaleing the viewers, making us think these are major changes that might change how the story goes and maybe even change the the ending but in reality, no matter how it gets there, Ending A and B still happen the same way. This also isn’t bad thing

Where this theory falls in is this thought I had, “Would Ending C & D change that much if 9S died instead of 2B” what I think is no.

Let me put you in this hypothetical: Your 2B, YoRHA is destroyed and you just escaped with 9S, and while this is very much a bad thing, seeing that most of YoRHA units got the virus and are now killing zombies, in the back of your head. This is perfect.

With the death of the commander and the whole space facility destroyed, you have no reason to kill 9S anymore. There’s nothing he can find out. And even if he did there was no reason to. Yeah there’s still the machines that are responsible for this, but after all of that is settled, you're done, forever!

You can just live your life with 9S on earth. Never having to worry if this will be the day you have to kill him ever again. And in a way with the facility destroyed there’s no way to come from being killed. So they can live their lives like humans! Finally living lives without care! Finally getting those T-shirts.

First you have to find 9S. Stop the machines so they can get to the good life fast. And as you ask your pod to give you his location to find him. And as you get close, you run across this bridge, and when you're halfway there you see him! You yell out to him but then you notice something.

…He’s been impaled by a sword.

By A2 no less…

As he falls lifeless on the ground. Your mind begins to scramble. He’s dead. He’s dead, forever. He’s not coming back again. And you’ll never see his face, his smile, his voice, ever again. He’s been taken from you just when you're finally free.

And it’s all of A2’s fault

A2 killed him before she could even say goodbye. Before she could say anything! She killed him! Something only she was supposed to do! She gets to decide when to kill him, not her!

So she’ll kill her! She’ll take her away from this earth with her own bare hands if she has to!

So yeah, I don’t think this would change anything with C & D. 2B would have the exact same bloodlust towards A2 in this scenario. And that rage would have been manipulated by the red girls the exact same way, because I’m mostly sure, that 2B didn’t even know why she was killing 9S, all that he found out too much information, information about what? She doesn’t know. And the truth would absolutely drive her insane.

Also it is a bit suspicious that the first OP of the second half isn’t on YouTube officially but the ED is. Which said ED just happened to be about 2B. And Almost as if the OP is going to change.

And it’s also weird that the 2nd Cour trailers, even the most recent episode, only consist of scenes and voice lines from the first episode. And yet the 2nd OP pretty much spoils what happens in C & D, but the first OP didn’t. Pretty suspicious. Just me though

[lowpawly]

so like this is absolutely a result of it not being something worth the time of the developers to change But in nier automata if you're connected to the internet you can find the bodies of other players that died while playing (you can either take their items or resurrect their body to fight with you) and the thing about that is no matter whether you're playing as 2B or 9S the body you leave behind has visible breast forms. so like if you so desire you can interpret that as 9S just binding all the time

exhibit a

[otogariado]

[glitched-eyes]

Just a thought, but has anyone else wondered if the chasm next to the mall in Nier Automata the same as the chasm of the Aerie in Nier?

We find Kaine's home underneath the shopping mall, so they're geographically in a similar place.

[felixcloud6288]

In case anyone's interested in understanding that math thing I posted yesterday, what I posted was something called the Pumping Lemma for Regular Languages.

A lemma is a minor theorem which has no real use outside its ability to be used for other proofs.

If you have a Regular Language, the Pumping Lemma is true by definition, and it cannot be used to prove a language is Regular. BUT, if you prove the Pumping Lemma cannot apply to a Language, you can use that to prove the Language is NOT Regular.

Read more for the journey about all this

Automata

Don't worry. This is not as complex as it sounds. An automata has a number of states that it operates in and a set of rules revolving around how it transitions between states.

Consider a calculator. You press certain buttons on it and it will display an output depending on the sequence you pressed. If you press '0 1 =', the calculator prints '1'. If you press '1 7 + 4 =', the calculator prints '21'. But if you press '1 / 0 =', the calculator throws an error. And if you press '1 + =', that also throws an error.

On the underside of the calculator, there's a set of logic responsible for processing your input. It contains a finite number of states that represent what inputs the calculator has read, a set of rules about how to transition between states, and maybe some other components depending on the machine. But not every sequence of input is recognized by the calculator.

In general, the set of all input sequences a machine recognizes is called its Language. And the set of all inputs it can process is called its Alphabet.

Regular Languages

Regular Languages are a particular type of Language. They are Languages that can be recognized by a specific automata called a Deterministic Finite Automata (DFA).

DFAs have five components to them:

A FINITE number of states

The Alphabet of the automata

The transition rules of the automata

The Start State

The Final States

The transition rules work as follows: If there is a rule that says something like (A, x) -> B, that means if we are currently on State A and read input x, we now transition to state B.

The Start State is one specific state in the DFA which we always start at. The Final States are a subset of the DFA's states where if any of them are the active state after reading the final input, the DFA accepts the input as part of the language.

So the way the DFA runs is you initially start in the Start State. Then for each input, you jump to another state based on the transition rules. You keep doing this until all the inputs are read. If the last state you're in is one of the Final States, then the input is accepted as part of the Language. Otherwise, it is rejected.

Here's a DFA which recognizes any sequence of 0's and 1's where the last two characters are '01'.

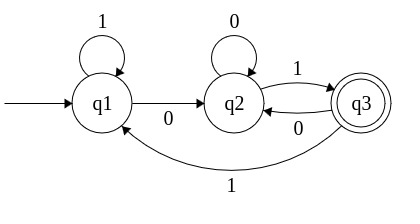
Each circle is a state in the machine.

q1 has a singular unlabeled arrow pointing to q1 indicating that is the start state. q3 is the Final State, indicated by the double circle.

Each labeled arrow represents a transition rule. For example, if we are in q1 and read a '0', we go to q2.

Some sequences that will be accepted are '101', '01', and '001101'. Some inputs sequences that will not be accepted are '1', '010', and '011'.

Pumping Lemma for Regular Languages

Consider the sequence '001101' for the earlier Language. Notice how there are more characters in the sequence than there are States in the DFA. That is because the DFA has a loop in it. You can go from q1 to q2 to q3 and back to q1. You can repeat a looping sequence as many times as you want and you'll still have a sequence in the language.

Here's the more technical definition for Pumping Lemma:

If you have a regular language L, there's a certain value P, called the Pumping length. If there is a string s which is in L whose length is greater than or equal to P, then you can apply the Pumping Lemma to it.

In that case, s can be broken down into three strings xyz. x is whatever comes before the part that loops, y is the first iteration of the looping part. z is everything after the loop.

The total length of xy is less than or equal to P. Meanwhile, the length of y is greater than 0.

After defining x, y, and z; you can then insert or remove y as many times as you want from your string, and you still have something that is accepted by the DFA.

So as an example, lets go back to '001101'. Let's say P=2 (because '01' is the smallest string we can create with the above DFA). 001101 is 6 characters long so we can pump it. And we can define x='0', y='0', z='1101'. This fits the requirement of xy's length being less than or equal to P, and y's length being greater than 0.

xz = '01101' which will be accepted.

xyyz = '0001101' which will be accepted

xyyyz = '00001101' which will be accepted

Using the Pumping Lemma

The Pumping Lemma cannot prove a language is regular because it's a characteristic of a Regular Language. BUT, you can prove a language is NOT regular by showing the Pumping Lemma doesn't work.

Let's consider a Language L that accepts any sequence of 0's and 1's where the number of 0's is the same as the number of 1's. So '01', '0110', and '001101001011' are in the language.

This language is not regular. We can prove it's not regular by showing a scenario where the Pumping Lemma will never work.

If the Pumping Lemma were true, we could choose P, then choose an xyz for any pumpable string in L.

Since we're trying to disprove the Pumping Lemma, things are inverted. We instead choose a string that will always be pumpable regardless of P. And we choose how many times we pump y which will generate a string that is NOT in the language.

So now let's show that the above language is not regular. We cannot choose our pumping length. But we can choose a string in L. We'll choose s = '0^P1^P'. This string is P '0''s followed by P '1''s. So if P=1, s = '01'; if P=2, s='0011' etc.

We cannot define how we split s into x, y, and z. But we can define roughly what they could be by the definitions in the Pumping Lemma. The length of xy is less than or equal to P, so that means xy is at most the P '0''s in s. And the length of y is greater than 0. Combining both rules means y is at least one of the '0''s in the first half and y is NOT ever going to be any of the '1''s. To simplify some things, we'll say y = '0^n' where n is any number from 1 to P.

Now consider if we pump y twice to make xyyz. xyyz = '0^(P+n)1^P'. xyyz is NOT in our language because we have a string which has more 0's than 1's. But if L was regular, xyyz should be in L. Since that's not the case, this means L cannot be a regular language.

Conclusion

So hopefully, you have a rough idea of how this worked. One of the utilities of this concept is determining the minimal amount of complexity needed to perform a certain task.

Regular Languages and their accompanying DFAs are amongst the simplest Languages and automata. They have no memory, cannot recall anything they've processed previously, and have no idea about what will happen in the future.

They only know exactly where they are in the moment and what they can do immediately from there. When a DFA is in a particular state, it does not know how it got there. It knows what states it can immediately go to, but it has no idea where it can go after.

So if you're trying to build a particular automata and you think it's simple enough to build with a DFA, you need to run it by this proof. If the Pumping Lemma can break, then your automata needs a more complex structure.

[ssjkamui-digitalphoenixug]

Digitalplatonismus: Informationstheorie und Philosophie

Zuerst veröffentlicht auf https://www.geopolitika.ru/de/article/digitalplatonismus-informationstheorie-und-philosophie

16.01.2022

Michael Kumpmann

Konrad Zuse war nicht nur ein Ingenieur, der den ersten Turing vollständigen Computer baute und deshalb ein Gerät erfand, was theoretisch jedes lösbare mathematische Rätsel lösen kann. Zuse wandte sich in seinem Buch “Der Rechnende Raum” von 1969 auch philosophischen Fragen zu. Seine Hauptthese dort ist, dass sich die Physik in einer Sackgasse befindet und viele Fragen nicht lösen kann, weil man einer grundlegenden Fehlinterpretation der Welt unterliegt: Man sieht die Welt materialistisch. Dabei zeigen viele Phänomene der Physik, dass Materialismus wahrscheinlich ein Irrweg ist, und alle Materie bloß Illusion ist. Die wirklich “Reale” Realität ist laut Zuse stattdessen Information.

Damit kam Zuse durch Informatik zum selben Schluss wie Platon, Hegel, und die meisten Religionen. Der Science Fiction Autor Philip Kindred Dick kam in seinem philosophischen Hauptwerk “Tractates Cryptica Scriptura” auf eine ähnliche Idee der idealistischen Verbindung aus Religion und Mathematik, nur war seine Herleitung nicht Mathematik und Physik, sondern die vergleichende Analyse religiöser Schriften. Spätere Autoren wie Rizwan Virk entwickelten diese Thesen weiter und beschrieben, dass man dank des Konzepts Neuronaler Netze das Universum als Produkt eines riesigen, hegelschen “Weltgeistes” sehen müsste.

Abseits abstrakter Fragen zur Kosmologie stellt sich nun die Frage, ob man diese Ideen und Denkweisen auch auf andere Bereiche der Philosophie anwenden kann. Und das kann. Dies geht. Und mit interessanten Ergebnissen.

Der erste interessante Punkt ist eine Frage der Berechenbarkeit. Berechenbarkeit beschreibt grob, welche Fragen ein bestimmtes System “lösen” kann. Meist geht es um konkrete Maschinen. Sprachen fallen aber auch drunter. Die schon eingangs erwähnte Turing Vollständigkeit ist hier von besonderer Relevanz. Eine Turing Maschine ist ein hypothetisches Gerät was aus einem Programm, einem Speicherband und einer beweglichen “Schreib-/Lese Einheit” besteht, was alle berechenbaren Probleme berechnen kann. In der Mathematik gilt eine Frage als beantwortbar, wenn man sie so formulieren kann, dass dieses fiktive Gerät damit umgehen kann. Dann gibt es noch die Church Turing These, die besagt, aus Sicht der Berechenbarkeit sind 2 Systeme Äquivalent zueinander, wenn sie ihre Funktionsweise gegenseitig simulieren können. (Um es sehr vereinfacht zu verdeutlichen. Jeder hier kann sich die 80er Jahre Version von Donkey Kong ziehen und auf seinem normalen Notebook zum Laufen bringen, weil der Spielhallenautomat, auf dem Donkey Kong damals lief, und das heutige Notebook, fundamental beides Computer sind.)

Und jetzt der “Spannende Punkt”. Die Simulationshypothesen sagen aus, weil Computer unsere Welt immer besser simulieren können, wird es wahrscheinlicher, dass die reale Welt auch eine berechnete Simulation ist. Es gibt aber bei diesen Überlegungen noch einen übersehenen Punkt. Wir Menschen haben diese Turing Maschine erst erdacht. Ergo fällt unser Geist auch unter diese Gesetzmäßigkeiten. Wir sind auch Turing Vollständig oder sogar mächtiger. Und wir verstehen das Universum immer besser und können immer bessere Vorraussagen und Vorherberechnungen treffen. Es gibt also einen Grundzug einer Äquivalenz zwischen dem schöpferischen Weltgeist und dem menschlichen Verstand. Der Weltgeist erschuf den Menschen nach seinem Ebenbild.

Es ist aber offensichtlich, dass ein einzelner menschlicher Verstand und ein Computer nicht alle Fragen dieser Welt lösen können. Da kommt jetzt nämlich ein anderes Element ins Spiel. Es gibt zwei Varianten von Turing Maschinen. Universelle, die alles berechnen können, weil sie ein unendliches Speicherband haben, und beschränkte Turing Maschinen, die endlich begrenzt sind. Und dies ist der Hauptunterschied zum “Schöpfer”. Der Mensch ist Endlich (Begrenzt) und kann nicht alle Information aufnehmen.

Eine gute Frage ist nun, was Technik für den Menschen bedeutet. Technik ist auch oft ein Speichermedium, was Information externalisiert und vom Geist entkoppelt. Was sich der Mensch nicht ewig merken kann, schreibt er auf, damit er es für später nachlesen kann. Damit dient Technik auch vor Allem dazu, die Speicherkapazitäten des Menschen zu erweitern, und den Unterschied zwischen begrenzter Turingmaschine und universeller Turingmaschine zu verkleinern. Man könnte hier Spenglers Metapher des “faustischen Menschen” verwenden und sagen, der Mensch versucht sich mit Hilfe der Technologie selbst zum Gott zu machen, indem er die “Frucht vom Baum der Erkenntnis” nimmt.

Ein sehr ähnliches Konzept ist die Idee der Informationsentropie und das damit verbundene Konzept des Maxwellschen Dämons. Informationsentropie ist grob gesagt der Wert, der aussagt, in wie weit es möglich ist, aus vorhandenen Informationen die fehlenden Infos zu rekonstruieren. Und wie viel fehlen darf, damit etwas noch “Lesbar” bleibt. Beispielsweise kann man erkennen, dass bei “Da ein” ein S fehlt. Da ist die Entropie gering. Aber bei “D n” ist die Entropie so groß, dass es schwer wird, zu erraten, was gemeint ist. Entropie ist somit auch der Grad des Unvermögens, aus bestehendem Wissen schlussfolgern zu können, was als Nächstes kommt. Thermodynamische Entropie gilt als Folge der Informationsentropie. In einem heißen Gas fliegen alle Bestandteile chaotisch umher. Deshalb kann man aus einem Abbild, wo alle Bestandteile des Gases or 10 Minuten waren, nicht wirklich ableiten, wo sie jetzt sind. Bei einem Kristall ist dies aber gut möglich, da dort alles starr, unbeweglich und geordnet ist. Man könnte hier auch grob sagen, Entropie ist ein Wert des Chaos.

Nach der Informationsentropie gilt auch, dass in jedem System die Entropie unweigerlich zu nimmt, die existierende Information weniger wird, und somit jede Ordnung gezwungen ist, in sich zusammen zu fallen. Gleichzeitig steigt damit aber auch das Potenzial, welche Art Information existieren könnte. [1][2] Dieser Punkt ist interessant, da er auf genau den Punkt hinaus läuft, den Dugin in seinem Text “Die Metaphysik des Chaos ansprach: Die Ordnung basiert auf der Extinktion oder Exklusion des Chaos. Das Chaos ermöglicht es aber, dass in ihm verschiedene Ordnungen entstehen können.[3]

Mit der Entropie wiederum hängt die Theorie des Maxwellschen Dämons zusammen. Der Maxwellsche Dämon ist eine hypothetische Maschine, welche über ein chaotisches System (ein Gas) gestülpt wird, und die Bestandteile dessen ordnen und sortieren soll. Es ist erwiesen, dass so ein System nicht auf Dauer funktionieren kann. Und zwar, weil u.A. Dieses Problem der potenziellen Information dazu führt, dass diese Maschine an ihre Speichergrenzen stoßen würde. Das Chaos könnte nur dauerhaft kontrolliert werden, wenn die Maschine einen unendlichen Speicher hätte (siehe die Überlegungen weiter oben, hierzu). Da die Maschine so etwas nicht hat, wird das Chaos irgendwann so groß, dass es in einer paradoxen Situation mündet, wo die Maschine selbst Chaos stiften und sich selbst langsam zerstören muss, um sich selbst erhalten zu können.

Dieser Maxwellsche Dämon lässt sich nun wiederum erstaunlich gut nutzen, um die Moderne und das “Gestell” zu analysieren.

Jeder moderne Staat ist nämlich de Facto ein Maxwellscher Dämon, der die Entropie beenden und die perfekte Ordnung erzwingen will. Angefangen von kommunistischen Planwirtschaften, die den Bedarf der Menschen von Oben herab planen wollten. (Der Gipfel dieser Entwicklung war Salvador Allendes Cybersyn, wo man die Kontrolle über einen großen Teil von Staat und Wirtschaft an einen Zentralcomputer abgeben wollte.)

Das Verhalten der dritten politischen Theorie und insbesondere Nazi Deutschlands mit Eugenik, Ahnenpässen, Vernichtungslagern etc. kann man sehr stark als eine große Operation zur Beseitigung von Chaos, Unreinheiten und Entropie beschreiben, auf Kosten von Freiheit, Menschlichkeit und Menschenleben.

Poppers Anhänger werden jetzt behaupten, liberale Gesellschaften seien der Schutz vor solchen Entwicklungen, aber diese Propaganda ist ein riesiger Trugschluss. Siehe Patriot Act, den Greueltaten, Unterdrückung, Vertreibung und Umerziehung indigener Völker im Namen von Kolonialismus und “White Mans Burden”, den Neocon Kriegen im Namen der Demokratie, dem übergriffigen "therapeutischen Staat", der die Leute zur Gesundheit erziehen will und den Bürger schon von Kindesbeinen an immer wieder auf gesundheitliche Störungen hin kontrollieren will, Cancel Culture, Political Correctness und anderer Formen von progressiver, antifaschistischer Gedankenpolizei und Netzzensur, EU Überregulierung, sowie vielen anderen Beispielen. In gewisser Weise führen liberale Staaten auch Eugenik dank Planned Parenthood und Anderem auch in privatisierter Form fort. Und in der Coronakrise gibt es auch im freiheitlichen Westen jetzt verpflichtende Zertifikate über biologische Reinheit, und das Thema "Lager für biologisch unreine" kommt in dieser neuen Form immer wieder auf. Siehe Australien. (Der Hauptunterschied zwischen dem Dämon im Liberalismus (2.0) und anderen Systemen ist, dass hier der Dämon errichtet wird, als ein System, dass alle Einschließt und dem sich keiner verweigern oder entkommen soll, während andere Systeme eher auf Verdrängung oder Vernichtung chaotischer Elemente ausgelegt waren.)

Egal in welcher Form. Jede politische Theorie der Moderne und jeder moderne Staat ist ein maxwellscher Dämon, der immer mehr das Chaos bekämpfen soll, auf Kosten der eigenen Bürger. In gewisser Weise ist der maxwellsche Dämon auch der Kern der Moderne, der von fast allen antimodernen Theorien erfasst wurde. Egal ob man es nun wie Heidegger "Gestell", wie Adorno "Instrumentale Vernunft", wie Herbert Marcuse “Eindimensionale Gesellschaft”, wie René Guénon "Herrschaft der Quantität", wie John C. Lilly "Feststoffintelligenz" oder sonst wie nennt. Alles von Ted Kaczinsky über Terence McKenna bis zu Rudolf Steiner läuft darauf hinaus, dass die Moderne ein Prozess der Errichtung einer Totalmaschine zur Ausmerzung des Chaos ist, welcher dabei gleich die Menschlichkeit mit auszumerzen droht. Und mit Methoden von Künstlichen Neuronennetzen, Genmanipulation, Transhumanismus usw. und Entwicklungen wie dem Great Reset wird das nahezu perfektioniert.

Nur, wie schon beschrieben, da kein unendlicher Speicher existiert, kann kein maxwellscher Dämon auf lange Sicht funktionieren. Alle Ordnung bleibt, um es buddhistisch zu sagen "Annica", also nicht dauerhaft, und vom ständigen Einsturz bedroht. Entropie und Chaos werden nicht ausgemerzt, sondern auf Dauer nur untern Teppich gekehrt. Und hinter den Mauern der geordneten Welt der Moderne und in deren Untergrund türmt sich das Chaos so lange auf, bis es die Staudämme einreisst. Bestes Beispiel hierfür ist die Tatsache, dass 2021 ein Schiff im Suez Kanal einen Unfall baute und damit beinahe eine Weltwirtschaftskrise auslöste.

Nur führt jeder Eingriff moderner Staaten, um das Chaos zu beheben, nach dem maxwellschen Dämon automatisch nur zu mehr Chaos und zur Notwendigkeit weiterer Eingriffe. (Man könnte es mit Ludwig von Mises als “Interventionsspirale” bezeichnen.)

Wie entkommt man diesem Dämon? Wahrscheinlich durch Blick in den Osten und auf Lehren wie Buddhismus und Taoismus, sowie die Kyoto Schule. Diese Lehren zeigen sehr gut auf, dass alles irgendwann zerfällt und das Endziel allen Seins irgendwann Chaos, Zerfall und das absolute Nichts bedeutet. Aber auch, dass wir Menschen nicht wirklich gegen die Entropie kämpfen können, und oft ein solcher Versuch die Entropie nur schlimmer macht. Stattdessen hilft nur, Abstand om Materiellen zu nehmen und sich stattdessen ewig gültigen, unveränderlichen göttlichen Prinzipien zuzuwenden. Da das Ewige sich nicht ändern kann, bleibt die Entropie bei Null und kann sich nicht vervielfachen, denn das Zweifache on Null wäre z.B. immer noch Null.

[1] Siehe https://www.uni-ulm.de/fileadmin/website_uni_ulm/archiv/haegele//Vorlesung/Grundlagen_II/_information.pdf Seite 6

[2] Ein Effekt der Entropie ist auch die Auflösung von streng getrennten Kategorien und das Ineinanderfließen, hin zu einem Mittelwert. Dies trifft auf die Postmoderne zu.

[3] Siehe dazu auch folgendes Zitat aus “Die Metaphysik des Chaos”:

“Um diese Schwierigkeit zu lösen, sollten wir uns dem Chaos nicht aus der Position des Logos, sondern aus der des Chaos selbst nähern. Es kann mit der weiblichen Vision verglichen werden, dem weiblichen Verständnis des Anderen, das nicht ausgeschlossen, sondern im Gegenteil in die Gleichheit eingeschlossen ist.

Logos betrachtet sich selbst als das, was ist und als das, was ihm gleich ist. Es kann die Unterschiede in sich akzeptieren, weil es das Andere, das außerhalb liegt, ausschließt. Der Wille zur Macht funktioniert also, das Gesetz der Souveränität. Hinter Logos, behauptet Logos, liegt nichts, nicht etwas. Logos, die alles andere als sich selbst ausschließen, schließen also Chaos aus. Chaos verwendet eine andere Strategie. Es schließt in sich alles ein, was es ist, aber zugleich auch alles, was es nicht ist. Allumfassendes Chaos beinhaltet also auch das, was nicht inklusive ist, nämlich das, was Chaos ausschließt. Das Chaos nimmt Logos also nicht als das Andere wahr, sondern als sich selbst oder als etwas Nicht-Existentes. Der Logos als erstes Prinzip des Ausschlusses ist in das Chaos eingeschlossen, darin präsent, von ihm eingehüllt und hat darin einen Platz gewährt, wie die Mutter, die das Baby trägt, in sich trägt, was ein Teil von ihr ist und was nicht von ihr gleichzeitig. Der Mann begreift die Frau als ein äußeres Wesen und versucht, in sie einzudringen. Die Frau betrachtet den Mann als etwas Inneres und versucht, ihn zu gebären und ihn zu gebären.

Chaos ist die ewige Entstehung des Anderen, das heißt des Logos.

Zusammenfassend lässt sich sagen, dass chaotische Philosophie möglich ist, weil das Chaos selbst Logos als eine innere Möglichkeit beinhaltet. Es kann es frei identifizieren, es schätzen und seine Exklusivität erkennen, die in seinem ewigen Leben enthalten ist. So kommen wir zur Figur des ganz besonderen, chaotischen Logos, das heißt eines völlig und absolut frischen Logos, das ewig von den Wassern des Chaos belebt wird. Dieses chaotische Logo ist gleichzeitig exklusiv (deshalb sind es eigentlich Logos) und inklusiv (chaotisch). Es geht anders mit Gleichheit und Andersartigkeit um.“

[arbieroo-art]

A show-reel exemplifying the kinds of algorithmic art I am currently pursuing. Visit me on YouTube for more.

[i-hear-a-sound]

yeah

[in-sightjournal]

Ask A Genius 1303: Cellular Automata, Discrete vs. Continuous Models, and Algorithmic Information Theory

Scott Douglas Jacobsen: Did you want to do any science stuff? Cellular automata is a discrete, rather than continuous, computational model dealing with grids of cells. In this case, these four-dimensional cells evolve based on rules. This is based on Stephen Wolfram’s book A New Kind of Science. He argues that simple rules can generate complex systems and suggests that this could model the…