#mathematical structure
Explore tagged Tumblr posts
Text


(CNN) — The dappled starlight and swirling clouds of Vincent van Gogh’s “The Starry Night” are thought to reflect the artist’s tumultuous state of mind when he painted the work in 1889.
Now, a new analysis by physicists based in China and France suggests the artist had a deep, intuitive understanding of the mathematical structure of turbulent flow.
As a common natural phenomenon observed in fluids — moving water, ocean currents, blood flow, billowing storm clouds and plumes of smoke — turbulent flow is chaotic, as larger swirls or eddies, form and break down into smaller ones.
It may appear random to the casual observer, but turbulence nonetheless follows a cascading pattern that can be studied and, at least partially, explained using mathematical equations.
“Imagine you are standing on a bridge, and you watch the river flow. You will see swirls on the surface, and these swirls are not random.
They arrange themselves in specific patterns, and these kinds of patterns can be predicted by physical laws,” said Yongxiang Huang, lead author of the study that published Tuesday in the scientific journal Physics of Fluids.
Huang is a researcher at State Key Laboratory of Marine Environmental Science & College of Ocean and Earth Sciences at Xiamen University in southeastern China.
“The Starry Night” is an oil-on-canvas painting that, the study noted, depicts a view just before sunrise from the east-facing window of the artist’s asylum room at Saint-Rémy-de-Provence in southern France.
Van Gogh had admitted himself to an asylum there after mutilating his left ear.
Using a digital image of the painting, Huang and his colleagues examined the scale of its 14 main whirling shapes to understand whether they aligned with physical theories that describe the transfer of energy from large- to small-scale eddies as they collide and interact with one another.

‘The Starry Night’ and turbulence theories
The atmospheric motion of the painted sky cannot be directly measured, so Huang and his colleagues precisely measured the brushstrokes and compared the size of the brushstrokes to the mathematical scales expected from turbulence theories.
To gauge physical movement, they used the relative brightness or luminance of the varying paint colors.
They discovered that the sizes of the 14 whirls or eddies in “The Starry Night,” and their relative distance and intensity, follow a physical law that governs fluid dynamics known as Kolmogorov’s Theory of Turbulence.
In the 1940s, Soviet mathematician Andrey Kolmogorov (1903–1987) described a mathematical relationship between the fluctuations in a flow’s speed and the rate at which its energy dissipates.

Huang and the team also found that the paint, at the smallest scale, mixes around with some background swirls and whirls in a fashion predicted by turbulence theory, following a statistical pattern known as Batchelor’s scaling.
Batchelor’s scaling mathematically represents how small particles, such as drifting algae in the ocean or pieces of dust in the wind, are passively mixed around by turbulent flow.
“This is cool. Indeed this is the type of statistics you would expect from algae blooms being swept around by ocean currents, or dust and particulates in the air,” said James Beattie, a postdoctoral researcher in the Department of Astrophysical Sciences at Princeton University in New Jersey, in an email.
Beattie wasn’t involved in this study but has conducted similar research on the artwork.
“In my paper, I only ever really looked at the large (swirls in the painting), so I didn’t see this second relation,” he said, referring to the Batchelor’s scaling.
‘An amazing coincidence’

Of course, Huang said, van Gogh would not have been aware of such equations but likely he spent a lot of time observing turbulence in nature.
“I think this physical relationship must be embedded in his mind so that’s why when he made this famous ‘Starry Night’ painting, it mimics the real flow,” Huang said.
Beattie agreed: “It’s an amazing coincidence that Van Gogh’s beautiful painting shares many of the same statistics as turbulence,” he said.
“This makes some sense — the models have been constructed to try to capture the statistics of eddies and swirls on multiple scales, each swirl communicating with other swirls through the turbulent cascade.
In some sense, Van Gogh painted something that represents this phenomenon, so why shouldn’t there be some convergence between the theoretical models and the statistics of Van Gogh’s swirls?”
The study team performed the same analysis and detected the same phenomenon in two other images:
— a painting, “Chain Pier, Brighton,” created by British artist John Constable in 1826-7;
— a photograph of Jupiter’s Great Red Spot, taken by NASA’s Voyager 1 spacecraft on 5 March 1979.
“Unlike ‘The Starry Night,’ this painting lacks well-defined swirling patterns, but the clouds are rich of structures with different scales, resembling those frequently seen in the sky,” the study noted of Constable’s artwork.

On display at the Museum of Modern Art in New York, “The Starry Night” is an enormously popular work of art that has been recreated in Lego bricks, drones and dominoes.
Huang said that scientists had long struggled to describe turbulent flow in fluid dynamics in a way that would allow them to predict the phenomenon and that a complete explanation remains a prevailing mystery of physics.
A thorough understanding would help with weather forecasting, flight turbulence and many other processes, he said.
“Even after more than 100 years (of) study, we even don’t know how to define this complex phenomenon,” Huang said.
“It’s extremely important, but it’s extremely difficult.”
"The fact that “The Starry Night” matched statistical models of turbulence even though the artwork doesn’t actually move could suggest that the statistical methods and tools are less precise than scientists may have thought," Beattie said.
"The painting can’t be precisely measured because it’s “actually not turbulence. … (I)t has no kinetic energy,” he said.
However, Beattie said that he was a huge fan of the work of art and that it reflected universality and the beauty of turbulence.
“I deeply love the fact that I can take my understanding of the turbulence in the plasma between galaxies and apply it to the turbulence between stars, between Earth and the Sun or in our own lakes, oceans and atmosphere,” he said.
“What I take away from studies like this is that (van Gogh) captured some of this universality in the beautiful (‘Starry Night’),” Beattie added.
“And I think people know this. They know that something wonderful has been embedded in this painting and we are drawn to it.”
#Vincent van Gogh#The Starry Night#painting#artwork#mathematical structure#turbulent flow#turbulence#mathematical equations#Yongxiang Huang#Physics of Fluids#State Key Laboratory of Marine Environmental Science & College of Ocean and Earth Sciences#Xiamen University#Saint-Rémy-de-Provence#asylum#whirling shapes#brushstrokes#whirls#eddies#Andrey Kolmogorov#Theory of Turbulence#Batchelor’s scaling#Museum of Modern Art#scientific theory
4 notes
·
View notes
Text
Mezzanine house | geometrical structure
0 notes
Text
i think john egbert should have a playing card themed sylladex where he has exactly 52 captchalogue cards and can only take things out at random after shuffling the deck. and every time he does it he has to say “is this your card?”
#i know its not a data structure but. cards are kinda mathematical and. i think it would be funny#homestuck#john egbert#chrono
134 notes
·
View notes
Text
Okay so to get the additive group of integers we just take the free (abelian) group on one generator. Perfectly natural. But given this group, how do we get the multiplication operation that makes it into the ring of integers, without just defining it to be what we already know the answer should be? Actually, we can leverage the fact that the underlying group is free on one generator.
So if you have two abelian groups A,B, then the set of group homorphisms A -> B can be equipped with the structure of an abelian group. If the values of homorphisms f and g at a group element a are f(a) and g(a), then the value of f + g at a is f(a) + g(a). Note that for this sum function to be a homomorphism in general, you do need B to be abelian. This abelian group structure is natural in the sense that Hom(A ⊗ B,C) is isomorphic in a natural way to Hom(A,Hom(B,C)) for all abelian groups A,B,C, where ⊗ denotes the tensor product of abelian groups. In jargon, this says that these constructions make the category of abelian groups into a monoidal closed category.
In particular, the set End(A) = Hom(A,A) of endomorphisms of A is itself an abelian group. What's more, we get an entirely new operation on End(A) for free: function composition! For f,g: A -> A, define f ∘ g to map a onto f(g(a)). Because the elements of End(A) are group homorphisms, we can derive a few identities that relate its addition to composition. If f,g,h are endomorphisms, then for all a in A we have [f ∘ (g + h)](a) = f(g(a) + h(a)) = f(g(a)) + f(h(a)) = [(f ∘ g) + (f ∘ h)](a), so f ∘ (g + h) = (f ∘ g) + (f ∘ h). In other words, composition distributes over addition on the left. We can similarly show that it distributes on the right. Because composition is associative and the identity function A -> A is always a homomorphism, we find that we have equipped End(A) with the structure of a unital ring.
Here's the punchline: because ℤ is the free group on one generator, a group homomorphism out of ℤ is completely determined by where it maps the generator 1, and every choice of image of 1 gives you a homomorphism. This means that we can identify the elements of ℤ with those of End(ℤ) bijectively; a non-negative number n corresponds to the endomorphism [n]: ℤ -> ℤ that maps k onto k added to itself n times, and a negative number n gives the endomorphism [n] that maps k onto -k added together -n times. Going from endomorphisms to integers is even simpler: evaluate the endomorphism at 1. Note that because (f + g)(1) = f(1) + g(1), this bijection is actually an isomorphism of abelian groups
This means that we can transfer the multiplication (i.e. composition) on End(ℤ) to ℤ. What's this ring structure on ℤ? Well if you have the endomorphism that maps 1 onto 2, and you then compose it with the one that maps 1 onto 3, then the resulting endomorphism maps 1 onto 2 added together 3 times, which among other names is known as 6. The multiplication is exactly the standard multiplication on ℤ!
A lot of things had to line up for this to work. For instance, the pointwise sum of endomorphisms needs to be itself an endomorphism. This is why we can't play the same game again; the free commutative ring on one generator is the integer polynomial ring ℤ[X], and indeed the set of ring endomorphisms ℤ[X] -> ℤ[X] correspond naturally to elements of ℤ[X], but because the pointwise product of ring endomorphisms does not generally respect addition, the pointwise operations do not equip End(ℤ[X]) with a ring structure (and in fact, no ring structure on Hom(R,S) can make the category of commutative rings monoidal closed for the tensor product of rings (this is because the monoidal unit is initial)). We can relax the rules slightly, though.
Who says we need the multiplication (or addition, for that matter) on End(ℤ[X])? We still have the bijection ℤ[X] ↔ End(ℤ[X]), so we can just give ℤ[X] the composition operation by transfering along the correspondence anyway. If p and q are polynomials in ℤ[X], then p ∘ q is the polynomial you get by substituting q for every instance of X in p. By construction, this satisfies (p + q) ∘ r = (p ∘ r) + (q ∘ r) and (p × q) ∘ r = (p ∘ r) × (q ∘ r), but we no longer have left-distributivity. Furthermore, composition is associative and the monomial X serves as its unit element. The resulting structure is an example of a composition ring!
The composition rings, like the commutative unital rings, and the abelian groups, form an equational class of algebraic structures, so they too have free objects. For sanity's sake, let's restrict ourselves to composition rings whose multiplication is commutative and unital, and whose composition is unital as well. Let C be the free composition ring with these restrictions on one generator. The elements of this ring will look like polynomials with integers coefficients, but with expressions in terms of X and a new indeterminate g (thought of as an 'unexpandable' polynomial), with various possible arrangements of multiplication, summation, and composition. It's a weird complicated object!
But again, the set of composition ring endomorphisms C -> C (that is, ring endomorphisms which respect composition) will have a bijective correspondence with elements of C, and we can transfer the composition operation to C. This gets us a fourth operation on C, which is associative with unit element g, and which distributes on the right over addition, multiplication, and composition.
This continues: every time you have a new equational class of algebraic structures with two extra operations (one binary operation for the new composition and one constant, i.e. a nullary operation, for the new unit element), and a new distributivity identity for every previous operation, as well as a unit identity and an associativity identity. We thus have an increasing countably infinite tower of algebraic structures.
Actually, taking the union of all of these equational classes still gives you an equational class, with countably infinitely many operations. This too has a free object on one generator, which has an endomorphism algebra, which is an object of a larger equational class of algebras, and so on. In this way, starting from any equational class, we construct a transfinite tower of algebraic structures indexed by the ordinal numbers with a truly senseless amount of associative unital operations, each of which distributes on the right over every previous operation.
#math#the ongoing effort of valiantly constructing complicated mathematical structures with 0 applications#i know i owe you guys that paraconsistency effortpost still#it's coming! just hard to articulate so far#so if you start with the equational class with empty signature your algebras are just sets#the first iteration of the construction gets you the class of monoids#but after that it's what i guess you could call 'near-semirings'?
48 notes
·
View notes
Text
Students complaining about basic algebra: “Whose idea was it to put the alphabet in math??”
Everyone in discrete mathematics:

#there are no numbers. it’s only letters.#and the letters represent sentences.#whose idea was it to take the numbers out of math 😭#discrete mathematics#discrete math#discrete structures#computer science#comp sci#comp sci major#i don’t actually hate it. it’s just a lot to be learning all at once.
13 notes
·
View notes
Text
Coming up with solutions to maths problems over text whilst half sleepy is a vibe honestly
#came up with the sketch of a near proof for why isolated subsets of R are countable#it's for my analysis homework and I'll do the fiddly details in the morning but the basic structure of the argument is there#maths posting#mathblr#maths#mathematics#lipshits posts
120 notes
·
View notes
Text
Surprising absolutely noone except undergraduate math students, it turns out math actually is only about numbers in the end!
#math#mathblr#mathematics#oh so you thought abstract algebra stopped being about numbers to get to more complex structures#and you thought fundamental logic is so abstract exactly because it is more general than just numbers#well guess what#gödel wants to have a word with you#my friend every statement that can possibly be made by humans ever can be made isomorphic to some structure of the natural numbers#even if that structure is a function space of the power set of the power set of the natural numbers#it is possible to write any finite set of axioms as an isomorphism to axioms about the natural numbers#however since the axiomatic definition of the naturals gives you some axioms already it is important to note that for some really fucked up#axiomatic systems you have to explicitly include axioms that prevent you from using thise axioms in sone ways#as in you can't use the set theorethic definition to choose elements of a set for example#you have to choose elements from a set with choice functions constructible from axioms provided#now for making set theory equivalent to the naturals the choice functions you can derive are equivalent to just choosing a natural#but it could be not the case
12 notes
·
View notes
Text

relevant to the concept of mathematical "morality"
4 notes
·
View notes
Note
sorry in advance if this is a weird question but do you think you will still be active in hockey fandom/blog etc after sid retires? i think about this all the time and it feels like a looming end date :(
I too tend to pre-grieve things, like, as a personality trait, but I don't particularly enjoy or encourage that part of myself! I think borrowing sadness from the future doesn't enable me to enjoy the now as much as I should, so I try to avoid doing it. I too Worry for the ~after~, but I try to steer my thoughts away from it!
That being said, I have a general rule of not guessing where I'm going to be in 5, 10, however many years, because my life has been kind of wild and wonky and unpredictable in so many ways, haha. I don't know who I'll be in 5 years, honestly! I've been here for 7 years and it's changed me and my life in so many cool and unexpected ways, and I think it's hubris to attempt to guess where I'll be in the distant (to me) future.
That being said, the Yzerman girlies [gender neutral] are still blogging about him, so Through Hockey Fandom Anything Is Possible:)
#also I think the fact that I have so many friendship structures built through hockey means there's real lasting power#consider the fact that there are supernatural fandom ppl on here even though the show has been over for years#a ''source material'' doesn't spell doom for a fandom honestly and I think that's really lovely :')#also this has been--mathematically--my longest fandom by MAGNITUDES#7 years... before this my longest fandom participation lasted 3 years [barely]#so it feels like a longterm investment slash personality trait:)#try not to borrow grief and worry from the future! trust future!you to deal with that when/if it comes
23 notes
·
View notes
Text
The Philosophy of Algebra
The philosophy of algebra explores the foundational, conceptual, and metaphysical aspects of algebraic systems and their relationship to reality, logic, and mathematics as a whole. Algebra, dealing with symbols and the rules for manipulating these symbols, has profound philosophical implications concerning abstraction, structure, and the nature of mathematical truth.
Key Concepts:
Abstract Symbols and Formalism:
Abstraction: Algebra involves abstracting mathematical concepts into symbols and variables, allowing general patterns to be manipulated without referring to specific numbers or quantities. Philosophers question whether these symbols represent real objects, mental constructs, or purely formal elements that exist only within the algebraic system.
Formalism: In formalism, algebra is viewed as a system governed by rules and manipulations of symbols, independent of any reference to an external reality. In this view, algebra is a logical game of symbol manipulation, with its own internal consistency, rather than something that necessarily describes real-world phenomena.
Algebra as a Structural Framework:
Structuralism: Algebra can be seen as providing a structural framework for understanding relationships between elements, often more abstractly than arithmetic or geometry. Structuralism in mathematics argues that algebraic objects, like groups, rings, or fields, should be understood in terms of the relationships they define within a system rather than as standalone entities.
Relationality: Algebra emphasizes relationships between objects rather than the specific nature of the objects themselves. For example, an equation expresses a relationship between variables, and group theory explores the relationships between elements in a set based on certain operations.
Algebraic Truth and Ontology:
Platonism vs. Nominalism: Algebraic Platonism suggests that algebraic objects (e.g., variables, equations) exist in a timeless, abstract realm, much like numbers or geometric forms. In contrast, nominalism denies the existence of abstract entities, viewing algebra as a language that refers to concrete, particular things or as a useful fiction.
Existence of Algebraic Structures: Are the objects and operations in algebra real in some metaphysical sense, or are they simply human constructs to facilitate problem-solving? Philosophers debate whether algebraic structures have an independent existence or are purely tools invented by humans to describe patterns.
The Nature of Equations:
Equality and Identity: Algebraic equations express equality between two expressions, raising philosophical questions about the nature of equality and identity. When two sides of an equation are equal, are they identical, or do they just behave the same under certain conditions? The concept of solving an equation also reflects deeper philosophical issues about finding correspondences or truths between different systems or forms.
Solvability and the Limits of Algebra: Throughout history, philosophers have explored the solvability of equations and the boundaries of algebra. The insolubility of quintic equations and the advent of Galois theory in the 19th century led to deep questions about what can and cannot be achieved within algebraic systems.
Algebra and Logic:
Boolean Algebra: The development of Boolean algebra, a branch of algebra dealing with logical operations and set theory, highlights the overlap between algebra and logic. Philosophers examine how algebraic operations can be used to model logical propositions and the nature of truth-values in formal systems.
Algebraic Logic: Algebra provides a framework for modeling logical systems and reasoning processes. The interplay between algebra and logic has led to questions about whether logic itself can be understood algebraically and whether the principles of reasoning can be reduced to algebraic manipulation.
Algebra and Geometry:
Algebraic Geometry: The relationship between algebra and geometry, particularly in the form of algebraic geometry, involves the study of geometric objects through algebraic equations. This intersection raises philosophical questions about how algebraic representations relate to spatial, geometric reality, and whether algebra can fully capture the nature of geometric forms.
Symbolic Representation of Space: In algebraic geometry, geometric shapes like curves and surfaces are described by polynomial equations. Philosophers explore whether these symbolic representations reveal something fundamental about the nature of space or if they are merely convenient ways to describe it.
Historical Perspectives:
Ancient Algebra: The origins of algebra can be traced to ancient civilizations like Babylon and Egypt, where early forms of symbolic manipulation were developed for solving practical problems. The philosophical importance of algebra evolved as these symbolic methods were formalized.
Modern Algebra: The development of abstract algebra in the 19th and 20th centuries, particularly group theory and ring theory, transformed algebra into a study of abstract structures, leading to new philosophical questions about the role of abstraction in mathematics.
Algebra and Computation:
Algorithmic Nature of Algebra: Algebra is inherently algorithmic, involving step-by-step procedures for solving equations or simplifying expressions. This algorithmic nature connects algebra to modern computational methods, raising questions about the role of computation in mathematical reasoning and whether algebraic methods reflect the underlying nature of computation itself.
Automated Proof Systems: The advent of computer-assisted proof systems, which rely heavily on algebraic methods, has led to philosophical debates about the role of human intuition in mathematics versus mechanical, algorithmic processes.
Historical and Philosophical Insights:
Descartes and Symbolic Representation:
René Descartes is often credited with the development of Cartesian coordinates, which provided a way to represent geometric problems algebraically. Descartes' work symbolizes the deep connection between algebra and geometry and raises philosophical questions about the nature of representation in mathematics.
Leibniz and Universal Algebra:
Gottfried Wilhelm Leibniz envisioned a universal algebra, or "characteristica universalis," that could serve as a universal language for all logical and mathematical reasoning. His philosophical insights anticipated the development of symbolic logic and formal systems that use algebraic methods.
Galois and the Limits of Algebra:
Évariste Galois' work in group theory and the solvability of polynomial equations led to new philosophical discussions about the limitations of algebra and the nature of symmetry. Galois theory provided insights into why certain equations could not be solved using standard algebraic methods, challenging assumptions about the completeness of algebraic systems.
Applications and Contemporary Relevance:
Algebra in Cryptography:
Modern cryptography relies heavily on algebraic structures like groups, rings, and fields. Philosophers examine the role of algebra in securing information and the philosophical implications of using abstract mathematical structures to solve real-world problems related to privacy and security.
Algebra and Quantum Mechanics:
Algebraic methods are crucial in formulating the laws of quantum mechanics, particularly in the use of operators and Hilbert spaces. Philosophers explore how algebra provides a framework for understanding quantum phenomena and the extent to which algebraic methods reflect physical reality.
Algebra and Artificial Intelligence:
In AI and machine learning, algebra plays a central role in developing algorithms and models. Philosophical discussions arise about the nature of intelligence and reasoning, and whether algebraic methods in AI reflect human-like thinking or merely computational processes.
The philosophy of algebra investigates the abstract nature of algebraic symbols and structures, the relationships they describe, and the metaphysical and epistemological status of algebraic truths. From ancient practical uses to modern abstract algebra and its applications in cryptography, computation, and quantum mechanics, the philosophy of algebra addresses deep questions about abstraction, formalism, and the role of symbols in understanding reality.
#philosophy#epistemology#knowledge#learning#chatgpt#education#ontology#metaphysics#Algebra#Philosophy of Mathematics#Abstract Structures#Formalism#Equations#Platonism vs. Nominalism#Boolean Algebra#Algebraic Logic#Galois Theory#Algebraic Geometry#Computation
3 notes
·
View notes
Text

So physicists can just omit cruical context clues from the structures of their mathematical equations and have no problems understanding how to understand it but then when someone omits an oxford comma…
#bgoriginal.mel#bgthoughts.mel#bgcrappost.mel#mathematics#math#science#physics#physicists#linguistics#grammar#english#sentence structure#oxford comma#albert einstein#general relativity#geometry
2 notes
·
View notes
Text
I think a great piece of advice for people who want to learn, but don’t know what to learn, is to take advantage of Wikipedia.
However, the second half of this advice is use that specific feature where some words are highlighted, and fall into rabbit holes. The best part about this is you don’t have to have anything super specific to search.
Say, for example, I was in the mood for some ELA type stuff, but I don’t know what kinds of stuff there is. I simply go on Wikipedia and search English. Admittedly, that doesn’t bring up much, but there IS a blue link to a page about the English language.
From there, I can click on things like “Indo-European language family” and “early Medieval England” and “British Empire” if I’m in the mood for more history things. Or, if I really want to learn about words, I can click the vocabulary section, or the phonology section, or the orthography section, or even the grammar section.
There’s so much to be learned in this one broad category, and it’s the same for every other subject you learn in school, which is a great place to start.
Math (mathematics)? Empirical sciences, number theory, and set theory are just in the opening paragraph. Not to mention the sections titled “relationship with astrology and esotericism” and “symbolical notation.”
History? Well, from history we can get to History of Earth, and it’s not hard to guess how much is there. There’s also anything that could be the History of; History of Mankind, History of Dinosaurs, History of Philosophy, literally pretty much anything you could want to learn about is on Wikipedia.
The point is, Wikipedia is an amazing tool and source of knowledge. This strategy is a great way to actually access that knowledge. Have fun!
#also non fiction yet well written books are a game changer for me#wikipedia#Wikipedia supremacy#school#history#study tips#sentence structure#writing#advice#mathematics#English#knowledge is SO cool#knowledge#knowledge is power
2 notes
·
View notes
Text
The Art of Origami: A Journey Through History, Use, and Mastery
In this series, we have been looking at various types of art as art forms. We have visited collage, multi-media art, Mexican Folk Art, ATC’s, Japanese Kintsugi, Street Art and Murals, pottery, Chinese Kites, and now Origami. Wow! That’s a lot of art. I hope you have been following and have enjoyed learning about these different types of art around the world. Origami, the traditional Japanese…

View On WordPress
#artistic expression#Creative Origami#Foldable Structures#Japanese art#Learning Origami#Origami#Origami and Mathematics#Origami Designs#Origami for Beginners#Origami History#Origami in Education#Origami in Engineering#Origami Manual#Origami Symbolism#Origami Techniques#Origami Therapy#Origami Tutorials#Paper Folding#Senbazuru Orikata#Traditional Origami
3 notes
·
View notes
Text
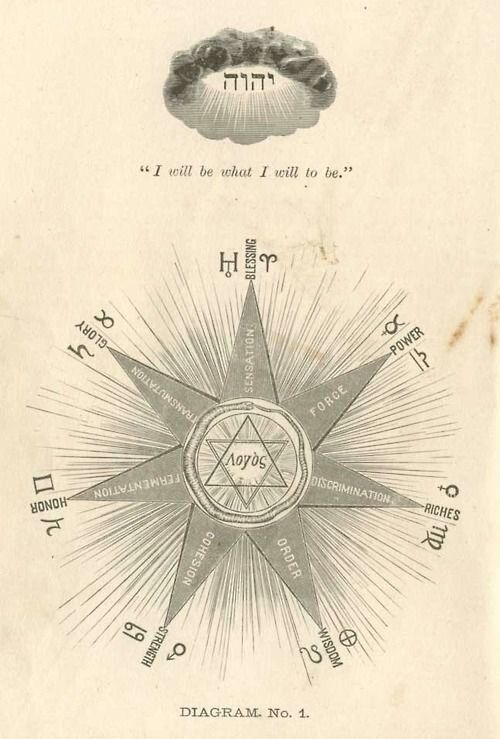
I will be what I will to be
#artists on tumblr#cosmology#symbolism#symbols#I will be what I will to be#diagram#universe#cosmos#structure of the universe#God#world#wisdom#order#alphabet#esoterism#geometry#mathematical calculation#astrology#astronomy
6 notes
·
View notes
Text
UPSC NDA II Syllabus 2025#nda #ndasyllabus #ndacoaching
UPSC NDA II Syllabus 2025 is officially released, and if you're planning to crack the NDA exam in 2025, this is the video you can’t afford to miss! Manasa Defence Academy, the best NDA coaching centre in Andhra Pradesh, breaks down the entire syllabus in an easy-to-understand way. From Mathematics to General Ability, current affairs to science, we cover everything with expert strategy and tips. Our academy trains students with physical coaching, English speaking, written tests, and SSB interview techniques – all under the guidance of retired defence officers.
Call:7799799221
Website:www.manasadefenceacademy.com
#UPSCNDAIISyllabus2025#ManasaDefenceAcademy#NDACoachingIndia#BestNDACoaching2025#NDASyllabus2025#NDAExamPreparation#NDA2025#SSBInterviewTips#DefenceJobsIndia#NDATrainingAcademy#trending#viral
#UPSC NDA II syllabus 2025#NDA 2025 syllabus#NDA 2025 preparation tips#NDA syllabus latest update#NDA exam 2025#NDA preparation strategy 2025#NDA syllabus explained#NDA subject wise syllabus#NDA full syllabus 2025#NDA coaching with hostel#Manasa Defence Academy NDA#best NDA coaching Andhra Pradesh#NDA coaching in Visakhapatnam#NDA 2025 exam pattern#NDA 2025 paper structure#NDA written exam topics#NDA GAT syllabus 2025#NDA mathematics syllabus 2025#NDA current affairs syllabus#NDA coaching after 10th#NDA coaching after 12th#NDA physical training#NDA English coaching#NDA with SSB preparation#NDA success strategy 2025#NDA toppers tips#NDA paper analysis 2025#NDA previous year questions#NDA online coaching#NDA offline coaching
0 notes
Text


0 notes