#max and eva
Explore tagged Tumblr posts
Text


Ayanami Rei ; Neon Genesis Evangelion ☆ Hobby Max
#ayanami rei#rei ayanami#nge#nge figure#nge rei#evangelion#evangelion figure#evangelion rei#rei#neon genesis evangelion#radio eva#hobby max#anime#anime figure#figure#figure collecting#anime figurine#figurine#anime collecting#scale figure#myfigurecollection#manga
448 notes
·
View notes
Text

i’ll never get over this photo oh my god
#loscar 4 eva#loscar#logan sargeant#oscar piastri#f1#formula one#lando norris#mclaren#charles leclerc#max verstappen#formula 1#piastri#lando#carlos sainz
431 notes
·
View notes
Note
Hi caro 🌹, following what you said in your previous post , you mentioned that Tom hardy is a soft type which I agree on and I get a feeling that he might be a soft natural too cause suits look like they're floating and they don't sit right on his body like what u said for Aaron taylor-johnson is . Emily browning is another case , I strongly believe she's a romantic or at the very least soft gamine . I like seeing them stand next to eachother in this movie ( the softness in their features and them being rahuvians in astrology make them complement eachother pretty well ! ) ( I want to add them to your list of couples so bad lol) thanks and have a swell day ☀️




emily browning is so yin! apple cheeks, full lips, rounded eyes, wavy wispy hair, soft jawline... naturals really do seem to come cast/coupled/teamed/shipped with romantic types frequently.
in a modern plot, the Natural is often painted as the active, Romantic as the passive part, until the roles switch; N is the facilitator for R to live their life how they please. "everything everything" in a nutshell: amandla stenberg = pure R, nick robinson = SN.
youtube
"love, simon" had picture-perfect N type clothing for nick, as if the costume department knew his kibbe ID. i think that's one of the reasons it blew up. jeans fabric, fleece, regular shirts, slightly longer but less sleek hair, casual > overstyling.

very subtly done, with soft lighting. which suits R, C, and N very well (DC is the exception, they are film noir). harsh lighting benefits sharp yang types on the other hand, so the G and D categories (SG as the exception, they are too yin), think eva green in sin city, the shadows of the blinds mimic her angular bones, creating harmony. she's been typed as D, SD, and TR, but in any case, she has yang bones. what do y'all think her type is? she is 5´7.

FN -TR with swapped expectations seems to be THE popular couple trope, btw. TR the strong, dominant, loveless, and hardened one, and FN the naively helpless romantic who's clumsy, shy, and often the sexualized part, even if we suspected it would be the TR! and they still have a hilarious height and size difference. FN is tall and burly, TR narrow and curvy. so, disney's hercules.

the D - G pairing axis tends to be a little edgier. especially as D is frequently a villain, contrarian, or antihero role, and G is the toiling protagonist on the hero's journey or the comedic relief. as soon as the "N with R, D with G" formula is broken, as "N with G, D with R", the couple is bittersweet, like katniss and peeta.
bonus: tom hardy has the typical "sharp shoulder sitting on top of nothing" menswear syndrome there: angled suits are for angled, pointy bones. naturals are too blunt-edged. that's why all of his well-known roles have character designs that sew the shoulders rounded, no pads, no classic construction.



#tom hardy#kibbe body types#nick robinson#kibbe#emily browning#kibbe types#mad max#batman#venom#hercules#megara#amandla stenberg#everything everything#love simon#simon#eva green#sin city#cub mail 🐅#ask
73 notes
·
View notes
Text
Okay listen, listen. Eden's Garden CH1 was great and I loved it and I'll make a more detailed analysis post about it at some point. And Eva in particular is fantastic and my favorite character. There's just- There's just a little, little issue I have with her FTEs, and if I don't talk about it I'm gonna explode.
Spoilers for P:EG CH1 and Eva's FTEs.
CW: I am about to be a Massive Fucking Nerd on main.
This post was originally going to be about how Eva's papers, the way she describes them, sound like they kinda suck. But then I realized that the way she describes the Riemann zeta function… is just wrong???? Like, it doesn't converge to- EVA WHAT THE FUCK ARE YOU SAYING?!?!?!?!
Like, look, I don't think "Eva sucks at writing papers actually” is the conclusion I'm meant to reach after doing her FTEs. I'm also pretty sure the mistakes she makes when describing the Riemann zeta function (henceforth "zeta function” for brevity) are just mistakes on the writers’ part, which is fine because that thing is very confusing.
And to be clear, Eva being bad at writing papers doesn't mean she's actually bad at science. I mean, she apparently solved the goddamn Riemann Hypothesis, and doesn't even think it's that big a deal!
Eva, sad [3rd FTE]: They'll put it on my gravestone: here lies the girl who could barely solve Riemann's stupid hypothesis.
(Thank you Ani from youtube for uploading these things it makes citation so much easier <3)
Girliepop if I solved a problem that's stumped mathematicians for over a hundred years (which carries a million dollar prize btw), you bet your fucking ass I want that on my gravestone! And look, I know that this is not necessarily due to her doing more impressive stuff in mathematics. That it's more so because she's internalized what other people think about her skills, and since a lot of people erroneously believe math is uncool she doesn't think this is as big a deal as it is. But the fact that she managed to solve this thing at all, not to mention at eighteen years old, already puts her in contention for best mathematician of the damn century. And that's incredible, because math is badass.
In short, Eva's cool and a great mathematician. But the way she talks about her other work, the papers she wishes got more recognition, makes me really doubt her actual skill as a writer of these papers. Let me explain.
There are three papers Eva mentions writing, or thinking about writing, across her FTEs. One about literature, another about lightspeed travel, and one about the Riemann zeta function.
Eva [1st FTE]: Earlier this year, I wrote a whole paper on an obscure subgenre of Western speculative fiction… I spent weeks on it, expecting it to receive a lot of attention from literary critics…
Eva [1st FTE]: I could write a research paper on the theoretical possibility of lightspeed travel, but no one would care, because…
Eva [4th FTE]: …I wrote a paper about how you can use tabletop gaming to understand [the Riemann zeta function].
Now, I can't say anything about the literature paper, because she gives no details on it. I also don't know enough about literature to know how long it usually takes to write papers on it, so I'll take her word for it that working for weeks on it is notable.
For the hypothetical paper about the "theoretical possibility of lightspeed travel", I have my doubts, but she also doesn't give enough details about what that paper would entail for me to definitively say anything about it. We'll get back to this one, though.
Meanwhile, the paper she gives the most details on is the Riemann zeta function one, and… yeah that one's trash.
There’s two reasons I say that. One is the technical issue with the description she gives, which basically boils down to “there’s severe inaccuracies in her explanation and also she just straight up gets some things wrong,” and is extremely nerdy and math heavy to explain; and the other is a much more fundamental problem with the very thesis of the paper, which doesn’t require math to explain, but I’ll leave for later.
I’ll start with the technical side and the things she gets wrong about the zeta function. I’ll try to make this accessible for non-math nerds, but fair warning, this is pretty difficult math so I can only do so much. That includes keeping to the tabletop analogy Eva used in the spirit of the thing.
By the way, take everything I'm about to say with a grain of salt. I'm a third year Physics major, so while I know way more math than the average person, I am by no means an expert. I am liable to get things wrong. In fact, I actually didn't know anything about the zeta function or the Riemann hypothesis before seeing these FTEs, I just researched them because I got curious about the Riemann hypothesis after seeing it show up in not one, but two fangans I've seen (it has a cameo in DR Despair Time if you're curious). However, even though I'm not an expert, I think I know enough to definitively say Eva's very wrong about a few things.
Lots of math incoming, TL;DR after the next red title
As a refresher, this is a paraphrased version of what she explains.
Eva (Paraphrased) [4th FTE]: Take 1, ½, ⅓, ¼, and so on for infinity, and pretend they are characters in a tabletop game (TTG). An enemy casts a status effect on your denominators so that they are all raised to the power of p, where the value of p is decided by dice roll. Now your characters are 1, 1/2ˆp, 1/3ˆp, etc. For your turn, you add all of your characters together, and that’s the zeta function ζ(p) = 1 + 1/2ˆp + 1/3ˆp + ... What is the value of ζ(p)?
This is good, that sum is indeed the first way to define the zeta function (more on that later), so it's correct. However, she then makes two statements.
Statement 1: If p is higher than 1, then you get a whole number; a number without decimals. ( ζ(p) = a whole number). Statement 2: If p is lower than 1, then you get 0, “an infinite amount of zeroes.” ( ζ(p) = 0).
(You’ll notice I put that last thing in quotes. I’ll get back to it)
Now, I’m going to ignore a few minor inaccuracies which Eva likely makes to simplify the concepts, because they’re not too important. For example; you can’t “add” infinite numbers, that’s not a thing. An infinite series can converge, which is slightly different from arithmetic addition. However, the two things are close enough that, for most people, the distinction doesn’t really matter. In other words, I’m fine with her saying she’s adding infinite numbers together, and similar claims.
There's one inaccuracy I can’t gloss over, though; Eva never tells Damon which dice is rolled to determine the value of p. In math terms, she never tells him the domain of the function (the domain of a function, btw, is the set of values for which the function is defined). Are the values p can take real or complex? Can it be any real/complex, or are there restrictions?
For the unaware, since this is gonna come up, I’ll define a complex number using the TTG analogy. A complex number is a special character born by adding together a real number "r" (one of the numbers you’re all familiar with), and another real number "b" equipped with (math: multiplied by) the Epic Tier item known as the imaginary unit “i”. This Epic item has the property that iˆ2 = -1. So basically a complex number "z" is one where
z = r + bi
where r,b are real and i is the imaginary unit. "r" is known as the real component, and "b" is the imaginary component.
(Note: All real numbers are complex numbers where b=0, but not all complex numbers are real)
In case you’re curious, these things are used in several fields, such as the study of electrical circuits with alternating current, and they appear in relation to the Schrödinger equation- I’m getting off track.
So, what dice does Eva want the opponent to roll to define p? Well, she never says it, but we can infer. She says that p can be “higher than 1,” and that clues us in that she’s probably rolling the dice of real numbers. After all, there’s no universally agreed upon definition of what it means for a complex number to be “higher than” another complex number. Meanwhile, she doesn’t mention any restrictions on what value p can take, so it’s safe to say she’s implying that p can be any real number higher than or lower than 1, aka any real number except maybe 1. Now, the zeta function doesn’t actually have that domain, but we’ll get to that.
For now, let’s analyze her statements assuming p is any real number other than 1. Let’s take a look at the first one.
Statement 1: If p is higher than 1, then ζ(p) is a whole number; a number without decimals.
This is wrong. Just so we’re clear, I could probably prove, with my somewhat limited math knowledge, that this statement can only work if the domain is more restrictive than “all real numbers other than 1” as described previously. It'd have to be defined only in whole numbers, for example.
However, I don’t need to. One of the first lines in the Wikipedia page of the zeta function says that ζ(3) (which is the value you get after “adding all your characters” when p = 3) is an irrational number. That is, among other properties, a number with infinite decimals. Eva could not be more wrong if she tried.
(Btw, yes I'm using Wikipedia as my only source. Not particularly rigorous research on my part, but this is a silly Tumblr post about funny killing game, there's a limit to my insanity)
I don’t even know how this happened, btw. It’s pretty clear this is a goof on the devs’ side (perfectly understandable btw, it took me several reads of the Wikipedia pages for both the zeta function and the Riemann hypothesis to even get them enough to write this post, and as stated I study a lot of math for my career), but I genuinely don’t know where they got the idea from. There’s nothing I could find about whole numbers in relation to the zeta function. There’s connections to prime numbers, which are all whole, but the series doesn't converge to them, the connection is a bit weirder than that. There's also some stuff Euler found about it converging to rational numbers for negative integers, but again, not whole numbers, and not even for real values above 1. So, yeah, no clue.
Anyways, what about the other statement?
Statement 2: If p is lower than 1, then you get 0, “an infinite amount of zeroes.”
This is also obviously wrong. In fact, reader! Can you think of a counterexample which is immediately obvious if you think about it for two seconds? A real number p lower than 1 such that ζ(p) isn't 0?
If you said “zero, because zero always breaks everything in very obvious ways,” you have good intuition! You could have also picked any other real number lower than 1, but those are less obvious.
For 0, the reason it’s so apparent is that any number raised to the power of zero is just 1, so 1 + 1/2ˆ0 + 1/3ˆ0 + … just turns into 1 + 1 + 1 + … and so on for infinity. Very obviously, the series diverges, it “goes to infinity.” This is very different from converging to 0.
And just so we’re clear, the series also diverges for any real value of p lower than 1, though I’ll leave proving that one as an exercise to the reader, with the help that I’ll tell you the infinite series 1 + ½ + ⅓ + ¼ + … also goes to infinity. Again, Eva could not be more wrong if she tried.
So, what went wrong here? Turns out, the way Eva defined the zeta function as an infinite series (a "sum of infinite numbers”) only works when p is a complex number with a real component higher than 1. That’s why it was important for her to say what dice we were rolling to determine p, what the domain of the function defined by the series is. For other numbers, you need to define zeta in different ways.
And what happened to the whole “infinite zeroes” thing? Well, you see, I have a theory. I think the devs must have read that the zeta function had “an infinite amount of zeroes for values of p with a real component lower than 1” (which is true, but doesn’t mean what they think it means), and misinterpreted from there. Fair mistake. I kinda wanna correct it using the TTG analogy, but I’ll leave that for the end of the post because it’s gonna derail the entire thing.
(I got carried away and explained everything I understood about the Riemann zeta function oops)
What you need to know for now; you can do some math tricks to define the zeta function outside of the infinite series Eva described, though a lot of those tricks are way above my pay grade. That way, you can evaluate the function for any complex value of p other than 1. In other words, you can roll different die for p, but it requires redefining what you're doing with that p.
Turns out, in doing that, some funky shit happens, and any time p equals -2n for any n which is a natural number (that is, p = -2 or -4 or -6 or -8, etc.), the zeta function will go to zero. Those values of p are known as the “trivial zeroes” of the function, and are obviously infinite in number. However, note that these trivial zeroes are exclusively negative even integers; there are plenty of real values of p lower than 1 for which the zeta function is not zero, so Eva still isn’t correct at all.
Though, to be clear, there are also zeroes of the function other than the trivial ones. This is actually where the Riemann hypothesis comes in. The hypothesis is that any non-trivial zero of the zeta function has a real component of exactly ½, with the only difference between them being the imaginary component (if you didn't follow, again, more detailed explanation at the bottom of the post). This (in our world) has not been definitively proven to work for every non-trivial zero, though it does work for the first several trillion.
Absurdly nerdy math rant over
So TL;DR, Eva made some pretty big mistakes when talking about the convergence of the zeta function, mainly stemming from not properly defining its domain, but also just straight up getting the convergence wrong. It doesn’t converge exclusively to whole numbers for real numbers above 1, and has to be defined in a different way for real values below 1, not to mention that she never brings up the full function is actually defined for complex numbers other than 1.
Obviously, this all likely stems from the creators not actually understanding the zeta function themselves, which is pretty funny.
But you wanna know what the bigger issue is? That even if Eva had properly explained the zeta function, her paper would still suck ass. Because there’s a much bigger, more fundamental issue with the very thesis it upholds.
I want you to take a step back. Really look past the complex math and weird terms and the contrast between the very serious sounding Riemann zeta function and the somewhat silly concept of a TTG…
And realize that the thesis of the paper Eva describes is “analogies exist.”
She can frame it however she likes, but ultimately, that’s what the point of the paper was. Eva, where the hell did you even get this published? In fact, I think it’s silly for you to say that it’d have been better received if your talent was different, because without it, I don’t see a world where this shit could even be submitted to any journal with even a modicum of self respect!
And look, she’s not wrong. I get her point, that mathematicians often don’t put in enough effort to communicate their work to the layman, and would benefit from explaining things in more creative ways. That’s cool. But that’s the kind of thing you would write for, like, an article or something.
But a paper is specifically meant for research. Calling this thing a paper almost feels insulting to mathematicians. Like the concept of using analogies to explain math is an unprecedented discovery that required actual research to figure out. Unless this paper was also the one where Eva solved the Riemann hypothesis (which God I hope that was a different paper), there's no new information being presented here. It's at best a personal opinion piece, which is not what scientific papers are for.
Am I silly for getting hung up on the wording of this being described as a paper instead of an article or opinion piece or whatever? Well, this entire post is silly, but I don't think it's because of that, because words mean things. And a scientific paper carries certain connotations that do not align with what Eva describes.
And this little issue casts doubt in her general skill as a paper writer. That's why I'm a bit skeptical about the paper she mentions about the "theoretical possibility of lightspeed travel.” Because, quite frankly, that paper topic sounds… meaningless? Like a bunch of technobabble?
Like, what exactly are you discussing about lightspeed travel? In fact, what are you actually referring to when you say "lightspeed travel"? Matter approaching lightspeed, or reaching or even exceeding lightspeed? The latter two are impossible according to current scientific consensus, btw. Or is she discussing a particular trick to get something from point A to point B in less time than it would take for light to cover that distance? There are papers discussing stuff like that, even if all the mechanisms are also thought to be impossible by consensus. And regardless of what she means by "lightspeed travel", what does she mean "theoretical possibility” of it? Like, genuinely, I have no clue. Is she speculating on whether or not it's possible? Is she speculating on the properties such travel would have? Is she proposing a theoretical method to do it? Is she doing something else entirely? The premise of the paper is too vague, is my point.
This worries me because… well, to put it bluntly, experts in related fields (such as mathematics) attempting to make cool sounding physics theories (such as a paper on the "theoretical possibility of lightspeed travel", whatever that means) which are completely wrong and nonsensical is a real, observable phenomenon in our world. Check out Angela Collier's "physics crackpots: a 'theory’” to find out more. And also check out the rest of her youtube channel it's great.
What Eva is doing with that paper honestly sounds remarkably close to what Angela describes there. In fact, let's check out whether or not Eva's hypothetical paper fits any of the four points Angela brings up to spot a crackpot theory.
1. “Addresses THE BIGGEST PROBLEMS in physics.”
By this, Angela means that the theory addresses a problem or topic that anyone with a passing interest in physics knows is a big deal. Things like dark matter, gravity, black holes, and yes, "lightspeed travel.” You're not going to see anyone with a crackpot theory on the equation of state of real gases or Eddy currents, because by the point you know what those things are in enough depth to be interested in them, you probably also know enough to determine what a good physics theory is and what isn't. Eva's paper fits this point, but that doesn't necessarily mean Eva is a crackpot physicist, right?
2 and 4. “Lacking mathematical rigor, experimental data, etc.” and “They are not physics theories”
I grouped these two because it's impossible for me to know whether Eva's paper would actually fit these points or not. She doesn't give enough details for me to say. I can tell you for sure it's not gonna have experimental data, but since it's theoretical physics, that's fine. So, we can maybe give her the benefit of the doubt? As long as she doesn't fit the last point too well maybe-
3. “Respond with anger, claim physics establishment has blacklisted them, cite Galileo/Einstein/etc."
Oh no.
Eva [1st FTE]: I could write a research paper on the theoretical possibility of lightspeed travel, but no one would care…
Oh no chat. She might actually be a crackpot physicist.
It doesn't help that her mentality in general is actually very in line with the mentality described in the Angela video mentioned above. That because she's a smart person (which she is; again, solved the damn Riemann hypothesis), she should be able to easily become recognized and respectable in any field she takes interest in. But that isn't how the world works. There's a reason people spend years of their life studying literature, physics, or mathematics, just to truly get a grasp of each discipline individually.
Ok, but, like, what's my point? Am I going to include her misunderstanding of the zeta function and the possibility of her being a "crackpot physicist” in any character analysis? No, of course not. You're very clearly meant to think Eva is genuinely skilled in every field she approaches, because this is a fangan and Ultimates can bend the limits of humanity to fit a narrative. I'm perfectly willing to accept that Eva solved the Riemann hypothesis, as you've seen throughout this post, even though I'd be highly skeptical of anyone making that same claim in the real world, "Ultimate” or not. The same way I'd accept that a fictional character of any kind could manage to accelerate a particle to exactly lightspeed, even though I'd immediately call bullshit if someone claimed to do it in real life. The standard for believability is different for fictional characters than real people, basically.
Really, when you boil it down, I only take issue with the things Eva says because I'm genuinely passionate about the topics she mentions, and because she gives enough details about her work for me to see the cracks in the writers’ knowledge of them. I'm assuming this is a common issue with any fangan that tries to really explain what being an "Ultimate” in a particular field entails, because no one is actually well versed enough in sixteen different talents to actually say that for sure. That's why Eva off-handedly mentioning that she solved the Riemann hypothesis is much more effective as a way to establish her skill than trying and failing to get her to actually explain the zeta function.
All in all, this is just a purely self-indulgent post for me to vent about issues I have with the way the writers tried to convey Eva's expertise. Feel free to completely ignore this for character analysis, because I sure will. I just needed to talk about it because I would explode if I didn't. Anyways, hope you enjoyed! If you made it this far, you deserve a function named specifically after you! See y-!
Oh right I almost forgot.
My Own Explanation of the Riemann Zeta Function Using the TTG Analogy
(Explained by someone with little more than Wikipedia access, take all this with a grain of salt)
Think of finding the zeroes of a function as a boss fight. You go up to them, and you cast a spell, generally in the form of a number, such that the function becomes zero when you cast it. For example, the Easy Function
f(x) = 2x - 6
can be defeated by casting “3”, since 2x3 - 6 = 0.
Every function also has a “domain”, which is a set of spells you can actually cast against it. For example, since 1/0 is undefined, the Medium Function g(x) = 1/x has a domain of all complex numbers except 0. Casting 0 against g has no effect. You need a special spell, “limit when x tends to infinity” (or negative infinity) to defeat it.
The zeta function is a Legendary Boss, defined by the infinite series ζ(s) = 1 + 1/2^s +1/3^s + …
(I changed p to s for a reason trust the process)
Many mathematicians had tried to defeat it before, but it seemed futile*. Its domain was thought to be all real numbers higher than 1 (they originally didn't think to use complex numbers against it), but no matter what number was picked, that first term was too powerful. Even casting “limit when s tends to infinity” only got zeta down to 1. Nothing in its domain seemed to work.
Until Riemann arrived.
The zeta function chuckled, thinking this one to be like all the many others before him. But the legendary mage Riemann had many a trick the zeta function hadn't seen before. Tricks to make make the domain of the function larger, so that new Number Spells could be cast against it. Where everyone else had only ever attempted to cast real numbers against this boss, he wouldn't be satisfied with that. Without warning, he cast the first of many powerful spells needed to do what needed to be done.
"Domain Expansion; Proof of Complexity"
Since you already knew this part, I'll skip the proof, but basically, Reimann quickly showed that the infinite series which defined the zeta function for real numbers higher than one actually worked for any complex number with a real component higher than one.
The zeta function was impressed, but unconcerned. It knew damn well there was still no spell in this new domain which could possibly defeat it. "Nice try, but I'm not scared of some imaginary unit” it claimed.
“I'm aware,” claimed Reimann. He raised his hands again, his mana swelling, and the zeta function frowned. “But you're mistaken if you think this is the end.”
Reimann looked at the Legendary Boss in front of him, and cast the following, powerful incantation, with the help of the runes described below.
"Domain Expansion; Analytic Continuation"

To truly defeat the zeta function, one must understand the concept of an analytic continuation. This is where I falter, for I myself don’t understand what the fuck that is. However, what I've been able to gather is that the function
𝜂(s) / (1 - 2/2ˆs) where 𝜂(s) = 1/1ˆs - 1/2ˆs + 1/3ˆs - …
is equal to the zeta function in the zeta function's domain, but is also defined outside of it. In particular, it's defined for any complex number with a positive real component, except for the points where
1 - 2/2ˆs = 0
(can't be dividing by zero after all!). That last thing excludes 1, for example.
Basically, think of the spell "Domain Expansion; Analytical Continuation” as a shapeshifting spell that transforms the zeta function from the previous definition:
ζ(s) = 1 + 1/2ˆs + 1/3ˆs + … for s complex numbers with a real component higher than 1.
to now being defined as:
ζ(s) = 𝜂(s) / (1 - 2/2ˆs) for the previously described new domain.
That way, its domain is expanded to include complex numbers with a real component between 0 and 1, aside from those where 2/2ˆs = 1.
But of course, Reimann wouldn't be satisfied with that. The next spell was simpler, but worthwhile nonetheless.
"Domain Expansion; Limiting Singularity Removal"
See, turns out, all the points "z” where the analytic continuation was undefined, other than 1, where removable singularities (I think? I don't actually know much about complex functions :v), which means the spell "limit when s tends to z” returns a finite number l. That way, you can define ζ(z) = l for all of these removable singularities, expanding the domain of the zeta function to all complex numbers with a positive real component, other than 1.
Don't worry if you don’t know what a limit is or you didn't follow this part, it's not too important for this. After all, that last spell didn't worry the zeta function. What had truly taken it aback was the analytic continuation, which suddenly exposed a few weak spots of the zeta function to the world. Now, Reimann could defeat it once and for all, as long as he found the right spell in the new domain.
However, the zeta function was a Legendary Boss for a reason. "Fancy tricks, but it won't be easy to find something to actually defeat me, you know,” it bluffed, hoping intimidation would work. Foolish hope.
"Oh, certainly,” Reimann agreed readily, smiling. The zeta function was confused for a moment, until it realized something horrifying.
Reimann's mana was swelling again. He wasn't done. And for the first time since it's run-in with Euler all those years back, the zeta function felt true fear.
“It won't just be easy,” Reimann smirked. “It will be trivial.”
"Domain Expansion; Functional Equation"

This is another point where the math is beyond me, but I'll try to explain. Basically, Reimann proved that that equality up there holds true as long as s is a complex number with a real component strictly higher than 0 and strictly lower than 1.
However, you'll notice that if you take s as a complex number with a real component equal to or lower than 0 (other than 0 itself), then the right side of the equation is actually well defined, because 1 - s is a complex number with a positive real component (and not equal to 1 unless s is exactly 0), meaning ζ(1 - s) is well defined. You also don't run into issues with any of the other factors of that equation, including the Gamma function (𝚪). What that means is that this equation can be used to extend the zeta function's domain to all complex numbers other than 0 and 1.
Think of this domain expansion as a shapeshifting curse. If you cast a complex number with a real component strictly higher than 0 (other than 1), then the zeta function defends by turning into either the analytic continuation from before:
ζ(s) = 𝜂(s) / (1 - 2/2ˆs)
or the limit for any values where 1 - 2/2ˆs.
Meanwhile, if you cast a number s with a real component equal to or lower than 0 (other than 0 itself), then the zeta function shapeshifts to be:
ζ(s) = 2ˆs 𝜋ˆ(s-1) sin(s𝜋/2) 𝚪(1-s) ζ(1-s)
The final step is yet another Domain Expansion; Limiting Singularity Removal on 0, where ζ(0) = -½. Again not really important for us.
In any case, Riemann had done it. Five consecutive domain expansions, so that the zeta function's domain now included all complex numbers except 1. The zeta function was on its last legs, all that was needed was the final touch. For the inexperienced, you might think finding a zero would still be difficult, but the truly expert mages among you might have already noticed the weak spot in the functional equation.
The sine function. A Common Enemy which goes to 0 whenever it's attacked by a whole number equipped with the Legendary Tier item 𝜋. And when a complex number with a negative real component is cast against the zeta function, sin(s𝜋/2) becomes one of the factors.
"You know what this means, don't you, zeta?” Riemann asked. And the zeta function couldn't muster a response before the legendary mage cast his final spell. "You lose.”
"Simple Spell; Negative Even Integer"
-2, -4, -8, etc. Any even integer s causes s/2 to be a whole number, so sin(s𝜋/2) goes to zero. And since it's multiplying everything else, the entire zeta function goes to zero. These negative even integers are known as the zeta function's "trivial zeroes", and because there are infinite negative even integers, it can be said that the zeta function has an infinite amount of zeroes.
However, just because the Riemann zeta function had been defeated, doesn't mean Reimann was satisfied. See, Riemann noticed that there were other values which could defeat the zeta function, and weren't negative even integers. These are the zeta function's non-trivial zeroes. And he noticed that all of these zeroes followed a pattern, so he tried to cast a Prophecy Spell.
A Prophecy Spell (or a theorem, in real math terms) is one that makes it so that, when certain conditions are met, something happens without fail. To cast a Prophecy Spell, you must prove it, which means using other prophecy spells, runes and unbreakable laws (axioms) to certify that it's a valid prophecy.
I'll give you an example in case you're not used to the concept of mathematical proof, and cast the Prophecy Spell “if b is a real number, then b0 = 0". To prove it, I'll use two axioms (these are the building blocks of mathematics, and don't need to be proven because they just Are).
1) 0 + c = c (0 is neutral to addition).
2) b(c + d) = bc + bd (Distributive Property)
Now, observe the following:
1) b(c + 0) = b(c + 0) [Trivially true.]
2) bc = bc + b0 [0's neutrality used on the left, distributive on the right]
3) 0 = b0 [Because bc = bc, you can nullify the terms]
I chose this because it happens to be the reason you can't divide by 0. Division is formally defined as multiplication with the reciprocal, so to divide by 0 you must first define its reciprocal 1/0. 1/0 would be defined as a number such that 0 x 1/0 = 1. But we just proved there's no real (or complex) number for which that can be true, so 1/0 isn't a number, thus is undefined.
In any case, now you know what's needed to cast a Prophecy Spell. However, Riemann couldn't finish the Prophecy spell about the non-trivial zeroes. He couldn't find proof or a counterexample to refute it. And so, his unfinished Prophecy Spell went down in history… as the Riemann Hypothesis.
“All non-trivial zeroes of the Riemann zeta function have a real component of exactly ½.”
Although it's been proven to hold true for trillions of non-trivial zeroes, it has never been properly proven or refuted, so the Riemann Hypothesis remains… unsolved.
God that was nerdy and cringy as hell. It was also super fun to write so I don't care :D
*Look, for the purpose of the post, I'm saying Riemann did all this shit and is the first one to find a value for which the zeta function becomes zero. This is likely not historically accurate. I'm just doing it so the explanation flows better. This should only be taken as an explanation of the function itself, and not the history behind it.
#p:eg#project: eden's garden#eva tsunaka#this post got way outta hand btw#it was supposed to be a silly little thing. like 1k words max#but then i blacked out and there were 5.7k words how did this happen#so very sorry to my mathphobic followers but i saw math in a fangan and got over excited#and then eva stabbed me in the back by getting Everything Wrong#i love her but oh my god this bothered me more than it should have#cw math#(?)
116 notes
·
View notes
Text

trans! the whole family!

bi! the whole family!

help! this whole trans family!


nevermind! HELP! this whole queer family!
#the villains of valley view#henry danger#the thundermans#lab rats#vic madden#eva madden#amy madden#jake madden#colby madden#kris hart#jake hart#piper hart#henry hart#hank thunderman#barb thunderman#phoebe thunderman#max thunderman#max design pro 😂😂😂. sorru#billy thunderman#nora thunderman#donald davenport#douglas davenport#tasha davenport#tasha dooley#adam davenport#bree davenport#chase davenport#leo dooley#marcus davenport#daniel davenport
257 notes
·
View notes
Text




Eva Green.
attends the "Furiosa: A Mad Max Saga" (Furiosa: Une Saga Mad Max) Red Carpet at the 77th annual Cannes Film Festival.
#eva green#evagreenedit#egreenedit#usercarrie#userquel#femalestunning#celebritessource#flawlessbeautyqueens#thequeensofbeauty#femaledaily#wonderfulwomendaily#userladiesofcinema#celebedit#celebsource#dailycelebs#cannes film festival#a mad max saga#photoset
253 notes
·
View notes
Text
Let's talk R-LDS
R-LDS or Resurrection-Linked Degenerative Sickness was alluded to in X-Men #4 and the Infinity Comics before being named in X-Men #7. We're told that Magneto has it and it's directly caused by Krakoan resurrection/The Five, kinda.

Here's Beast doing some alluding.
In the panels above, we learn that Hank McCoy is the only one working on the problem - the problem being Magneto's loss of his powers and his body breaking down rapidly - his very chromosomes unraveling. He seems quite sure that it could happen to 'any of us' though the lack of quarantine suggests it's not contagious.

The next bit of information we receive is from Magneto and Scott in conversation, reflecting on The Iron Night. They took down a wild sentinel that was attacking the town and Mags lost control over his powers immediately after, requiring Scott to knock him out for safety's sake. Scott is no scientist, and while Magneto is a genius polymath autodidact (with plenty of experience in genetics) it's not a character trait that's seen focus lately. Thus, I'm assuming they're discussing it as amateurs and as patient zero in Magneto's case.
Magneto confidently names the condition for the first time as well as using an acronym for it, suggesting it's confirmed to exist, he's had a positive diagnosis, and they're using the term enough to require shorthand. He even spells out the subtext for us - it was a hidden flaw in Krakoan resurrection. I'll come back to that notion. Scott says 'we don't know that for sure,' implying that R-LDS is just a theory or speculation, which Mags doesn't directly refute. Instead he lays out the worst case scenario. They can't both be right here, so what's the deal? Magneto's symptoms are obviously confirmed, but how did they get from there to here?
If Magneto is the first and only person affected by his condition, why are he and Beast so sure about its providence and everyone being in danger? How could they possibly link it to Krakoan resurrection? I'm no scientist but I do know that there's only so much you can conclude from a single data point. Magneto was indeed only resurrected by the Five once, but he died again after that on Arakko (X-Men Red #7). The body he's in came out of a portal from Overspace in Adam Brashear's underwater base (Resurrection of Magneto #3.) His body suffering a condition borne of something that happened to a different body doesn't make sense. Considering he's the only person to return to life that way AND the only one allegedly with R-LDS, that would be the place to start for Beast's sciencing.

There he is, good as new.
Word of God

In a recent AIPT interview, Tom Brevoort removed any ambiguity and just straight up confirmed it. With the caveat that his recent X-history knowledge seems pretty poor, he is the de jure ultimate authority on the matter. I don't agree with that, and not just because I don't respect him as a creator. This habit of on-panel ambiguity and editorialising in interviews is vexing.

It's especially vexing when he contradicts himself. He counterpoints his own information with some of what I just pointed out, but the fact that they've made a list of who was and wasn't resurrected suggests R-LDS is a plot point they're committed to. I have to wonder why he bothered giving a detailed answer to this question if it's 'yes,' then 'maybe', then 'it will definitely be a thing you'll see as we progress.' Saying all of that and then ending with 'we know very little so far' really makes me wonder what he's thinking. Tom Brevoort could have given his usual cagey answer about not wanting to spoil anything, but he didn't here. I'm saving most of my Brevoort-specific criticism for a separate piece, but this glib and irreverent tone is typical of his commentary - even managing a light jab at Jordan D White.
Frankly, I think it's a graceless and cynical development. There are so many character beats, mistakes, and conflicts to use from the First Krakoan Age that choosing to create R-LDS feels like a shot at the core of hopefulness and creativity that blew our socks off in 2019.
HoxPoX
House of X/Powers of X was hopeful and magical. After a decade plus of endless misery and genocides, dull stories and bizarre characterisation, for once mutants got a W. The ability to use mutants working together to right the horrendous wrongs they'd suffered was central to that - the power of community and cooperation. What they built wasn't perfect but The Five was something they got right.
What would possess someone to take the cornerstone of the greatest X-Men story of all time (don't @ me) and try to tear it down? Remember, when the dust settled we ended up in Moira X life 10E. In 10A, the original Krakoan experiment, the mutants won! They thrived and protected what was theirs against Dominions. It took a literal apex AI God existing outside of space and time directly opposing them to fail. Enigma, on the back foot, sent Omega Sentinel through time to start ORCHIS years early and ensure Krakoa's collapse. Am I to believe 'no, sorry. That was a dead end?'
Haven't we been here before?
We've had mutants suffer from the Legacy Virus and M-Pox already, and I might even be missing other examples of nebulous diseases that threatened to wipe out all mutants. Obviously it's the prerogative of the X-Office to use whatever plot points they want, but do we really have to do this again? There are plenty of ways to sideline Magneto as a combatant that don't require repackaging old storylines. We've even had Hank McCoy decades behind the curve desperately trying to catch up before - in All-New All-Different X-Men.
Small World
Defenders-era Hank McCoy might be the worst possible 616 scientist to tackle this problem. He's literally decades behind the science curve and doesn't have the experience in dealing with anything like this. He's not the same guy that worked on M-Pox or the Legacy Virus. He never set foot on Krakoa and has never met any of the Five. We don't know how much data was recorded or kept from The Five but Beast may not have access to it.
Why isn't he talking to Cecilia Reyes, Forge, Jean Grey, Reed Richards, Doctor Strange, Adam Brashear, Healer, Doctor Nemesis? Even doctor dickhead that extorted Storm has the ability to instantly diagnose anyone. It makes the world feel tiny, and when you're following an era of interconnectedness that's just so disappointing. Portraying him as supremely concerned about 'all of us being ticking time bombs' rings hollow if he's working on it solo. Hank McCoy has always had a sense of arrogance where his scientific ability is concerned but not to this degree. Look at the guy! He's hating the stress he's under.
Sins of Sinister and the White Hot Room
I have to wonder if the implications of linking Magneto's illness to The Five's resurrection have been fully considered. The Sins of Sinister timeline ran for a millennium with the Five resurrecting on an industrial scale. Rasputin IV would have noticed, or the Quiet Council. The mutants left behind in the White Hot Room in RotPox spent 15 years bringing back ALL the dead mutants. That's 16 million, minimum. 15 years is less than a thousand but it's still longer than the First Krakoan Age, several times over. Nobody noticed anything? Elixir, member of the Five and Omega biokinetic, with his unlimited mastery of DNA didn't notice anything? Destiny didn't see mutants falling apart? Sounds dubious as hell to me.
Towards the end of the era many humans were resurrected too. 5% of the Five's work was set aside for bringing back poor children etc through the Phoenix Foundation. Steve Rogers was resurrected into his current body on Judgement Day. I am extremely skeptical that this has been considered, and in Steve's case whether the X-Office can even use him.
Conclusion

Magneto's physical degradation has been swift. Here he is in Uncanny X-Men #700, implied to be at most 6 months before X-Men #1. I think I've demonstrated that the concept is nonsensical and to reiterate, I think it's a terrible narrative choice. If I'm being generous, it'll be interesting to see if they can explain R-LDS in a way that makes sense - if they can do something new and interesting with a tired concept. There's only been one issue since it was introduced, so perhaps I'm jumping the gun on breaking it down. Let's check back in 6 months.
What do you think of R-LDS? Do you think my reasoning is sound? As always, I'd love to hear what other fans think.
#x comics#magneto#R-LDS#the five#cyclops#krakoa#comics#x men#marvel#hope summers#proteus#goldballs#elixir#tempus#kevin mactaggert#josh foley#eva bell#max eisenhardt#resurrection of Magneto#from the ashes#tom brevoort#hank mccoy
114 notes
·
View notes
Text

Anya Taylor-Joy in Dior Haute Couture at the “Furiosa“ screening 77th annual Cannes Film Festival
#anya taylor joy#dior#cannes film festival#couture#editoral#red carpet#haute couture#cannes#furiosa#mad max#vintage style#vintage fashion#1950s#1950s style#50s aesthetic#princess gown#princess#evita#eva peron#fashion photography#black and white#christian dior#tiffany#tiffany and co#tiffany & co#diamonds#princess aesthetic#cinderella#1950s dior#✨
351 notes
·
View notes
Text






“How can I cheer you up a bit? Should we play pinball? Should I freestyle a rap in Italian for you?”
“What?”
“Listen to this: 'Eva, you shine like the stars in the sky; for you I would walk de Sahara like a camel, no lie. You're so fine-'”
“Enough, enough!”
PETAK, 21:15
#Skam#Skam Croatia#SRAM#Eva Šilović#Eva x Nikola#Eva x Nix#Evix#SRAM S1#SRAM 1x06#SRAM trying to force me to keep a lighting yellow x me resisting it#the lights reminded me of Tiffy & Max's first kiss in SkFr#except they changed color there if I'm not mistaken it was a different thing but I THOUGHT OF THEIR KISS OKAY#I'm always making parallels when it comes to Skam Remakes always it's annoying even for myself#but HEYYYY Mohnstad/Chriseva crowd here we go again!#my fave cheaters are back#and I like Nix! love it when it happens in remakes#anyway would Jakov offer to freestyle a rap in Italian to cheer Eva up?#IDTS!#P.S: did you know reblogging doesn't hurt?#it's like people on tumblr are allergic to it nowadays#creators wish you'd find our creations good enough to display them on your blogs...#My Creations
127 notes
·
View notes
Text



☆ Shikinami Asuka Langley // Rebuild of Evangelion "Ver.RADIO EVA Part.3" ☆ 1/7 / HOBBY MAX JAPAN ☆ October 2025 ¥20,350 ☆ Sculpt Shader Paint Sawada Kobo Cooperation kiking / Satou Yasuhiro
96 notes
·
View notes
Text

#demian 1919#emil sinclair#max demian#frau eva#franz kromer#alfons beck#knauer#pistorius#hermann hesse#doobles
155 notes
·
View notes
Text


Asuka Langley Souryuu ; Neon Genesis Evangelion ☆ Hobby Max
#asuka langley soryu#asuka langley#asuka#asuka figure#nge asuka#evangelion asuka#nge#nge figure#evangelion#evangelion figure#neon genesis evangelion#hobby max#radio eva#anime#anime figure#figure#figure collecting#anime figurine#figurine#anime collecting#scale figure#myfigurecollection#manga
375 notes
·
View notes
Text

Max Beckmann Adam and Eve 1917
81 notes
·
View notes
Text
This is a Demianworld...





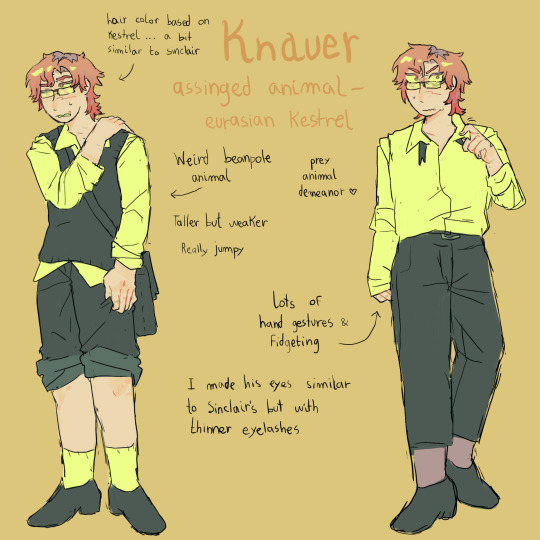

#my designsssss#demian (1919)#Emil sinclair#frau eva#max demian#pistorius#knauer#alfons beck#franz kromer#beatrice#herman hesse#my art
69 notes
·
View notes
Text
I'm doing a 911 rewrite because I am Icarus and love flying too close to the sun and the timeline is literally driving me nuts
#Like when do Hen and Eva breakup? 2008? 2009?#Which means that Hen and Karen had like max 1.5 years to get together and buy a house before Denny was born#In LA???#911#911 abc#911 show#hen wilson#karen wilson#evan buckley#evan buck buckely#maddie buckley#chimney han#bobby nash
21 notes
·
View notes
Text




Asuka Langley Sohryu : Radio Eva Part 3 Original Color ver [Neon Genesis Evangelion] 1/7 scale from Hobby Max coming August 2025.
#Asuka Langley Sohryu#Radio Eva#Part 3#Original Color#Neon Genesis Evangelion#1/7 scale#Hobby Max#Shin Seiki Evangelion#NGE#Evangelion#New Century Evangelion#Evangelion series#Asuka Langley Soryu#Souryuu Asuka Langley#Shikinami Asuka Langley#Asuka Langley#Anime Figures
23 notes
·
View notes