#measure theory

[sevenfactorial]

(Curious just how in the minority I am on this topic lol)

[lipshits-continuous]

I think what annoys me more than saying the Dirac delta distribution is a function is when people say it's 0 everywhere except when x=0, it is infinity. Like that is just not compatible with the fact it's integral over ℝ is supposed to be 1. Suppose we did define an extended function that way:

δ is a Lebesgue measurable since {x∈ℝ:δ(x)<a} is empty for a≤0 and ℝ\{0} for a>0 which are both Lebesgue measurable sets. δ is non-negative so we can calculate the integral via

where the inequality is pointwise.

Now since δ is 0 except at x=0, we require any simple measurable function φ≤δ must also be 0 except at x=0. This leaves us with a constant times an indicator function:

where a>0, and

Then we have

So taking the supremum over a we get

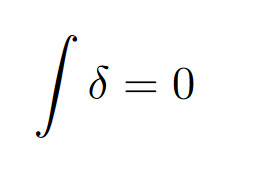
So δ cannot be the Dirac delta distribution. You really need the theory of distributions to talk about the Dirac delta.

P.s. I know this isn't the typical notation for an integral with respect to a measure but this was the notation I had in my lectures

[bubbloquacious]

So a standard question in measure theory you might be asked to prove or disprove is when given a sequence (fₙ) of integrable functions (defined on the unit interval [0,1], say) with strictly positive integrals such that the limit as n goes to ∞ of their integrals is 0, whether it is then the case that the functions themselves also converge to 0 pointwise almost everywhere.

Consider the set of 'fraction intervals' in [0,1]: closed intervals of the form [(k-1)/n,k/n] for positive integers 0 < k ≤ n. Their indicator functions provide a counterexample to the question. "But you have only given a set of functions," I hear you cry, "whereas the question concerns a sequence!" Well you see, any bijective enumeration of this set gives you a sequence of integrable functions whose integrals go to 0, but which is nowhere pointwise convergent. I think that's pretty neat.

[floralfractals]

I don't know anything about measure theory, re: f(x)=x on [0,1], what's the deal with integration?

ohh well i guess i did kinda say that without explaining huh. let me elaborate

measure theory is all about sizes of sets, in a generalisation-of-probability-way. the probability of event A is 0.5, the probability of event B is 0.8, the total probability (of any outcome happening at all) is 1. or the measure of set C is 2, the measure of set D is 0.002, the total measure (of the ambient space) is infinity. whatever.

but what is integration if not calculating the space under a curve? is that not dependent of the measures of the sets underneath them?

lets first talk about "regular" (Riemann) integration. basically, suppose you have a function f: R -> R. it has some kind of fun graph, and youd like to find the surface between the graph and the x-axis. one way to do that is by approximation through rectangles. yknow, draw some rectangles of fixed width, put their heights either just under or just above the graph of f, add up their surface areas and bam! you have a numerical method of approximating the integral. or you could make the rectangle width smaller and smaller for exact results. thats integration. heres a visual.

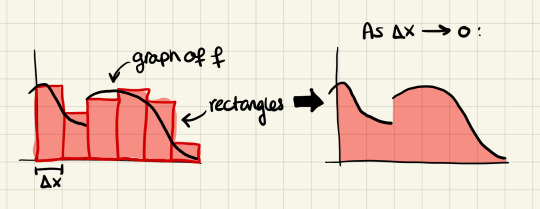
ok cool so problem solved right? we know the area under the graph? surely this holds for every function?

well, no. suppose we have a really fucked up function. for example, let f(x) be equal to 1 if x is rational, and 0 otherwise. the above method wont be able to determine if the area is 0 or infinity, or something in between!

thats where measure theory comes in. we give sets a measure (notation: m(A)). this measure is not negative, and if you take the measure of two sets that dont overlap with each other, then their measure is the sum of their separate measures (in notation: m(A ∪ B) = m(A) + m(B) if A and B are disjoint. this is called sigma-additivity (the sigma means that it works for countable infinitly many sets as well)). easy! now we can define something called the indicator function 1_A(x), which is 1 if x is in A and 0 otherwise, and we define its (Lebesgue) integral to be ∫ 1_A dm = m(A). usual linearity applies for finite sums (so if a and b are numbers, and f and g are functions, then ∫ af + bg dm = a ∫ f dm + b ∫ g dm) (wacky things happen when sums are infinite: they might become infinitely large, or infinitely negative, or not converge at all).

this solves the issue of our crazy function f we just defined: notice that f(x) = 1_Q(x), where Q is the set of rational numbers. thus, ∫ f dm = m(Q), which (in one of the most natural measures, called the lebesgue measure*) is zero. done!

now for your question. the function f(x) = x on [0,1] (for our purposes: f(x) = x if x is in [0,1], and zero otherwise) cant be written as a finite sum of indicator functions. that means that our newly defined Lebesgue integral wont do without a bit of work. as it turns out, we can take limits in the Lebesgue integral, as long as our sequences increase (in math notation: if (f_n)_n is an increasing sequence with limit f, then lim_{n -> ∞} ∫ f_n dm = ∫ f dm). thus, we need to find such a sequence.

it's probably best if all functions in our sequence are finite sums of indicator functions, since we know how to integrate them. one such sequence with limit f is given by f_n = Σ_{k=0}^{n-1} k/n 1_{[k/n, (k+1)/n]}. that looks kinda scary, but if we let n go to infinity, this turns out to be equal to f almost everywhere (some points are counted twice since the intervals [k/n, (k+1)/n] and [(k+1)/n, (k+2)/n] have some overlap, namely {(k+1)/n}, but we dont need to worry about that since m({(k+1)/n}) = 0). heres another visual.

as you can see, though, when we go from f_2 to f_3 we have some parts that increase and some that decrease. that sucks because now our limit trick wont work! to solve this, notice we dont have that issue when we go from f_2 to f_4, or from f_4 to f_8. thus, the sequence (f_{2^n})_n would work, since its limit is also f!

now we can do a big calculation. please bear with me (its just this paragraph i swear)! we have ∫ f dm = lim_{n -> ∞} ∫ f_{2^n} dm, so lets solve ∫ f_n dm for any n first. we have ∫ f_n dm = Σ_{k=0}^{n-1} k/n m([k/n, (k+1)/n]) = Σ_{k=0}^{n-1} k/n^2 = (n-1)(n-2)/2n^2. we can work with that, so were ready to take the limit: lim_{n -> ∞} ∫ f_{2^n} dm = lim_{n -> ∞} (2^n-1)(2^n-2)/2(2^n)^2. that looks scary, but luckily its equal to the slightly less scary lim_{n -> ∞} (n-1)(n-2)/2n^2, and thats just 1/2.

therefore, ∫ f dm = 1/2. which is also the value of the riemann integral ∫ f(x) dx, by the way.

you see that we needed a lot of calculations, so its probably not surprising that i needed an entire whiteboard to do this.

maybe this would make you think that lebesgue integration is inferior to riemann integration. however, as it turns out, most applications of this rely on proving that a lebesgue integral ∫ f dm is equal to some riemann integral ∫ g(x) dx, and we can just solve that with our calculus skills.

also, since the integral relies on a measure, we can do some silly shenanigans with that. for example, the ergodic probability measure related to my sickly son (lets call it n to avoid confusion with our earlier measure m) has n([0,1]) = 1/2, and n([1,2]) = 1/4 (in general, n([k-1, k]) = 1/2^k). i used this in my thesis to integrate the function floor(x): turns out that ∫ floor dm is infinite, but ∫ floor dn = 4 :)

hope you enjoyed doing some measure theory with me :>

*: the lebesgue measure is probably one of the more intuitive measures. an interval [a, b] has lebesgue measure b - a, so m([0,1]) = 1. this also means that a single point has measure m({x}) = x - x = 0, and a countable union of singletons (like Q) therefore also has measure m(Q) = 0. however simple this measure is, it also gives rise to some wacky crazy properties! for example, there exist sets that cant have a measure, but you can only construct them using the axiom of choice. scary!

[cecilias-cool-stuff]

Yeah I do measure theory, watch this:

个

[muisnotforyou]

measure theory be like

[speronyx]

does anyone know how much of measure theory (and from where) I should study so I can learn more set theory? I'm aiming to learn logic and forcing as soon as I can, and I've covered some of the very basics like the convergence theorems and the decomposition theorem, but idk where to go from there, and my only source of reference is a stat student who's learnt it for studying more probability

[notonlymaths]

I have once fallen asleep while solving a Measure Theory exercise some year ago. I woke up after a creepy dream where I continued my calculations up to almost solving the exercise.

I then went up to my Measure Theory class and presented my solution, stopping just at the point where I had been left in my dream. Then, my professor goes like: [Prof] Hey, you're just a step from solving it! [Me] I know, but, you know, this is the point I woke up... [Prof] ??

There are people on this site having dreams where mysterious figures talk to them and reveal deep truths about life and the universe, and meanwhile my mysterious dream figures are like "hey, if you use this particular roll-and-discard method with a d6 dice pool it results in a super fucked up probability distribution" and explaining the math to prove it, and when I wake up and run the numbers it turns out the dream was right.

[flameshadowconjuring]

'Our resources are depleting. I'll quickly duplicate them with Banach-Tarski.'

'It won't work. The geometers have locked us in Solovay's model. Everything is measurable, you can't use the axiom of choice here.'

'Hah! We may be barred from an exterior theory, but we still have one out. Are you all definable?'

'Yes...'

'Then we all have representations in the inner model, which is well-orderable. The axiom of choice holds there globally. I will transform us into ordinal-definable representations, transporting us to the inner model. Then, we use Banach-Tarski. They will rue the day they crossed us algebraists!'

[lipshits-continuous]

Countable Sets have 0 Lebesgue Outer Measure

I've started measure theory in my analysis course and had to show the outer measure of the rationals is 0 and I realised the proof only relied on the countability of ℚ so I will now present the slightly modified proof.

Before I get into the proof, I will define the Lebesgue outer measure and state three of its properties that I will use in the proof. The first two follow immediately from the definition but the third takes some thought to prove so I will omit the proof for sake of brevity.

Definition:

Note: we consider the length of the empty set to be 0. The following proposition will then imply that μ*(∅)=0.

Proposition:

Theorem: Countable sets have a Lebegsue Outer Measure of 0.

The idea of the proof is that because the set is countable, we have an enumeration of its elements which allows us to construct a countable cover of intervals with lengths of our choosing. We will be able to construct these intervals so that they can have arbitrarily small length and hence arbitrarily small measure.

[maths-terms-identifier]

Lebesgue Measurable

Analysis, Measure Theory

A subset E⊆ℝ is Lebesgue Measurable if for any subset A⊆ℝ we have that μ*(A)=μ*(A∩E)+μ*(A∩Eᶜ), where μ* is the Lebesgue outer measure and Eᶜ=ℝ\E.

Some days I’m normal and some days I spend the entire time between work and tutoring writing someone using “Lesbesgue measurable” as a cute term of affection

[demaparbat-hp]

Zuko looked up and locked eyes with his cousin, who was struck speechless. Then, ever so slowly, Lu Ten's lips twitched upwards. And then he smiled. And then he beamed. And then he nodded proudly once, just once, and vanished.

Lu Ten comes back in For the Spirits Chapter VII: Take Me South, only to leave Zuko with more questions than answers. Just how much is he truly aware of? When will he return? What is Zuko going to do now?

(What will the South bring?)

[nemesis-is-my-middle-name]

my longshot theory about part 52 is that the "threshold" that kayne was referring to, that noel's at, is addison.

a couple reasons i think this Would Be Neat:

throughout all of s3, after he learns where he is, arthur is constantly emphasizing how addison isn't far from arkham. it's one of the main things he gets fixated on: if he gets out of there, he can go home. given how insanely circular this podcast's dialogue tends to be, and how much kayne in particular loves to make jabs at things jarthur have said or will say, i can very easily imagine "somewhere awfully close to home" being a nod to arthur's obsession with Going Home in s3.

i mean literally, compare and contrast the first time arthur learns they're in the hoosac range, in 22:

ARTHUR (thrilled): Yes, it's – it’s west, far west of Arkham! A couple hundred miles, but that means we’re close to home!

and where kayne says he sent noel, in 52:

KAYNE: Oh, he’s somewhere familiar. Somewhere awfully close to home.

it's the same. exact phrase. "close to home." hello.

also, most of the other options (leerie, the pelican lane house, etc) i've sort of wondered why noel was... apparently still there? like he can leave. those places. why opt to stay where kayne put him? has time not been passing in middle-c? is he laid up in the same hospital arthur was in during the coma? did kayne put him on house arrest for the sake of the Bit?

BUT a key factor in the beginning of s3 is that you can't feasibly get out of addison during the winter without a car, and arthur took larson's car when he left. meaning the only one left that we know of is the surveyor's, which may or may not even still be around. given that it's really not been a ton of linear time since s3 happened, i would not be at all surprised if the way out was still too frozen to go on foot.

and also, according to irvine (the guy in the red right hand in 22), "Addison tends to hold on to you until it is done [...] You’ll leave Addison when it lets you leave." he claims he's been trapped there for ten years without being able to leave. so that would be a very satisfying answer to why noel hasn't gone back to nyc or something yet. addison isn't done with him yet.

SPEAKING of irvine, we STILL don't really have closure as to what the fuck exactly he was talking about when describing the town.

MAN: There’s a place, on this Earth, where light doesn’t touch. It’s a place of unfathomable depth. Where the crashing waves and churning, nightmarish storms are but memories. Darkness so black, so all consuming, that light can be… only dreamt of. Only hoped for. This place exists, friend. ARTHUR: Addison? MAN: Some call it Addison, sure. But there are many names it goes by.

is it possible this is just a dropped thread, or tone-setting that There's Something Weird Going On In This Little Town. yes. but also. golly gee mr. irvine that sure does sound reminiscent of the dark world, doesn't it. and if noel is at "the" threshold, not just a threshold, i would not be surprised if it was a threshold with relevance to the other world that kayne was actively prepping to send jarthur directly into.

also re: loose ends in addison, there was a very good post going around a little while ago theorizing that the larsons were worshippers of nyarlathotep, and. if that were the case. it would be rather ironic and appropriate for kayne to snap noel away to a place dedicated to his old self. wouldn't it.

[ckret2]

Do you have any headcanon about why during the event of Weirdmageddon, the invisible barrier around Gravity Falls and the surrounding area created by the Natural Law of Weirdness Magnetism, had become a physical barrier that prevented Bill and the Henchmaniacs of leaving the town? And why a equation would be able to collapse the barrier?

Yeah, because they were too weird.

If somebody has like 1 Cuil worth of weirdness in their body, then the weirdness magnet would exert 1 Cuil worth of force dragging their body into town. ("What's a Cuil?" it's a unit of measurement we're appropriating because there AREN'T any IRL units to measure weirdness, just roll with it.) The weirdness of an irregularly shaped jelly bean is like, 0.1 Cuils; so 0.1 Cuils is a strong enough force to counteract the force of gravity on an object that weighs as much as a jelly bean. Ford's weirdness is like, .5 Cuils, so the force dragging him toward Gravity Falls is like,, the same as the amount of force that it would take to make 5 jellybeans roll uphill. Enough to feel a small tug but it's not gonna physically drag Ford into town.

Bill has trillions upon trillions of Cuils worth of weirdness in his body.

The force dragging him into town is like unto the force of a black hole, and the barrier is its event horizon. Bill ain't escaping that event horizon.

As long as Bill's in town, his weirdness is adding to the "mass" of weirdness in town dragging everybody in, so it's sucking like a black hole on everything. Ain't nobody escaping that event horizon.

People take "there's a simple equation to collapse the barrier" too literally.

If I told you "there's a simple equation to halve the amount of cookies this recipe produces," that doesn't mean "if you write a mathematical equation on a piece of paper, this will somehow cause half the cookies to disappear." It means "you take your recipe and its ingredients, you divide all the ingredient measurements by 2 (a simple equation!), and now the recipe will make half as many cookies."

An action (unknown) needs to be performed to collapse the barrier. There is an equation to calculate the (force, direction, weight, duration, wavelength, temperature, whatever) of the action, and maybe even to narrow down what kind of action it needs to be. Ford knows what that equation is.

[another-goblin]

After 2.2, many people noticed that the first part of Ratio's "Doctor's Advice" isn't just a vague encouragement (to think about it, that would have been a bit out of character for him); it actually foreshadows certain revelations about the Dreamworld we only discover in 2.2.

It can't be a coincedence that the words "Death" and "Dormancy", capitalized and placed in quotation marks, are the exact words used to refer to that "Death "meme when we discover the truth about it.

It's safe to assume that he knows more about the Dreamworld than he lets on, and that note is partly a hint to Aventurine about what's going on. And it probably helped, judging by the fact that Aventurine somehow ended up in Dreamflux Reef after that.

So first, that really reminded me of what he did on Herta station. He basically slips into his teacher mode: "I'll make sure nobody dies. I won't disrespect your cognitive abilities by just telling you what's going on. I'll just direct you towards the truth because I know you are smart enough to ultimately get there by yourself"

And secondly, if that's true, if he really knows a lot about the Dreamworld, that would finally explain why the IPC sent him as a technical consultant.

The question is, what's in it for him.

At first glance, he doesn't have a horse in that race. I don't think he gives a damn about the IPC's claim on Penacony. He doesn't strike me as a fan of the IPC in general (his philosophy is "people should have access to education," and money never factors into it).

And they can't directly order him to go; the IPC bosses are not his bosses. The Intelligentsia Guild is affiliated with the IPC and probably sponsored by it, but they are not the same. (I had a little theory about the IPC financing his educational projects. So theoretically, they could use it as leverage. But it's an unsopported speculation on my part)

One of his goals could have been to study the Dreamworld, but I don't think that's the case because he could have just visited it as a tourist for that purpose at any time.

So, why would he agree to go on that mission, taking his valuable time away from teaching and potentially risking his life and reputation (by getting involved with the IPC's shady affairs)?

He's only there to help Aventurine. Currently, that's the only explanation.

[megtrns]

megtrns, could you please write about a first contact au with a alternate time period with any of your faves? (ex: first contact au but make it regency or western? the already culture shock with human lagging behind to the bots is a bit big, but now with a slightly more rigid ideals and society is fascinating and i can’t help but think about a pride and prejudice au or medieval era bc literal knights in shining armor) of course these are just thoughts, so feel free to just write about anything, or ignore it if it’s too complicated. regardless, thank you for sharing your writing and take of yourself! have a good one!

a/n : hi anon ! so so sorry this took such a long time. the reason was because i had to go through several tries before settling with this because i absolutely adore your idea!! i've thought of something similar in the past so i got so excited doing this request and wanted to do so much that i ended up scatterbrained. so if you're okay with it, i'd love to make this into a mini series. so this shall be part one and the next ones will include a regency and/or midwestern era . again, thank you for such a lovely request ! i hope this was what you wanted and have a nice day !!

stranded time au ft. the lost light crew part one : ultra magnus & the medieval era (sfw!)

00. The theory of general relativity proposes that time doesn't pass at the same rate everywhere. With that in mind, Cybertron is an ancient and archaic planet, its galaxy a graveyard of heavy celestial masses that once existed long before the birth of our solar system. Due to strong gravitational fields, time passing through Cybertron is slower than time on Earth. And because of the war, emergency escape pods would have pre-calculated coordinates to launch their users to planets where time flows faster. So that if any Autobot or Decepticon were to survive and return, years spent in the corner of that universe would be nothing more than a few days.

This was how Rodimus & co. find themselves stranded on Earth, jumping through different timelines to save their friends. Through a very unfortunate (and avoidable) accident, the ship had collided against the planet's upper atmosphere as it attempted to land. (Because Swerve wanted to watch the concert of a human band he's obsessed with and begged Rodimus to go until his vocalizer fried.) As a result, the docking station for the escape pods were breached, followed by a leak in the quantum engine that had ignited a series of them to explode — causing a chain reaction that created 'holes' in time where the missing crew members had fallen into, leaving them scattered throughout different historical ages.

With most of the ship (thankfully) intact, Rodimus and team must race against time to bring everyone home, leaping from one century to another (and hoping that the 'time portal gun' the simpatico duo had whipped up won't explode in their faces).

01. Having been on the unfortunate side of the ship that had shattered upon impact, poor Ultra Magnus was launched all the way across Europe during its middle ages, at the height of its Capetian dynasties as it stands at the end of the crusade wars. Dropped in the heart of a dark and grim forest where not even sunlight pierced through the foliage, Magnus had stumbled into a small battle. It didn’t take long for the enforcer to realise that he had accidentally intervened in the attempted kidnapping of a princess from a nearby country.

Once he finished scaring the bewildered men away on their horses (a sight he found barbaric), the princess was left by his pedes cowering in fear. In an attempt to appear less intimidating, Magnus had stepped out of his armor, feeling exposed if not undignified — yet understanding that at least this way she could look at his optics. However, this gave her the impression that he was a knight sent by the Lord to rescue her.

He wanted to correct the human (courtesy of the universal translator), but she was already prostrating by the surface of a nearby rock to pray in relief. Tears dramatically streaming down her neck. With nothing to lose and no signs of his ship, Magnus relented and spent the next few days carrying her through rivers and mountains to return the princess to her limestone castle (somewhat nervous that this breach of protocol would permanently alter the outcome of a thousand-year war). 

But when was the last time anyone ever looked at him with such admiration and awe, even when stripped of his armor? She saw him for who he was — ser minimus, she called him — her champion in shining, metal armor. During the day, he was Ultra Magnus, the giant that fell from the sky. In the night, when she leaned against his side for warmth, delicate and shy, he was just Minimus. And under the pale moonshine where she drifted to sleep against his shoulder, he was reminded of how nice it was to be just Minimus.

For days they trekked through the wildlands, staying under the cover of canopies and steering clear of cities that permanently carried the smell of burning flesh and rotting wood. This was a time of plague and famine, and Magnus couldn’t help but pity her. Because despite the comfort of her velvet drapes and high towers, she would continue to live and die in a time of war and death. He knew too well what that felt like.

Once his little quest had ended and the princess was safe and sound behind gilded gates, it was time to say goodbye. And much to her court’s fascination (and fear), Minimus had dropped to one knee to kiss the back of her palm, once, twice, knowing that this was expected of him as a knight — and that this was maybe the closest souvenir he could have from her. And just as he rose to follow the signal that suddenly appeared on his radars, she had leaned forward on her toes to kiss him. He knew he should pull away, as signaled by the choir of scandalized gasps that erupted around them. Maybe it was the pity, the proximity, or the validation he gets from seeing her gaze up at him with intense devotion, but Minimus found himself doing something incredibly reckless. Back aboard the Lost Light, Rodimus disclosed they knew where to find him thanks to a very interesting painting from the 13th century depicting a princess and her (supposedly fictional) green knight hanging in present-day museums.

" So...Magnus. Are you as good as a kisser as they paint it out to be or was that just the dramatic effect of the ‘renaissance’?" 

(Somewhere behind them, Megatron chimed in to correct Rodimus that it was actually 'pre-renaissance.' He didn't seem too happy when Whirl called him a nerd.)

Magnus refused to answer his Captain's question despite the incessant teasing, choosing to leave the room (so no one could catch him smiling).