#pascals 4-simplex

[art-of-mathematics]

I started to craft a visualization model for a Pascal"s 4-simplex.

Now I need to insert the 12 triangle disks. (I need to puzzle them into each other like a kind of interwebbing. )

I will describe this model and the math of it once I have finished it.

[szhmidty]

Ok I revisited this. I didn’t end up using energy levels, its still a geometric argument. Lets start with the 3dN case:

The “front” of our simplex is growing in 3 directions we’ll call i, j, and k. Eventually, the front will pass the edge of our cube of possible dice rolls. At this point the simplex volume no longer represents the probability of a given roll. However, can just subtract off the volumes of the sections of the simplex outside the cube, which themselves are simplex volumes. These 3 new simplexes each have 3 fronts of their own, however only 2 of them matter: 2 of them grow along the face of the cube, while the last one grows away from the cube and no longer matters. Simplex at N*i starts 2 new fronts along j and k; the simplex at N*j starts 2 new fronts along i and k, etc. For now, we find the volume we’ve occupied within the cube with

S(3, roll + 1 - 3) - 3*S(3, roll + 1 - 3 - N)

This pattern continues until the new fronts hit another edge of the cube. We had six fronts that mattered, however some of the fronts intersect at this point. The simplex growing from N*i has a front growing along j, and the simplex growing from N*j has a front growing along i: these fronts meet at N(i + j). So while we might have expected 6 new simplexes, we only have 3. Moreover, these new simplexes represent the intersection of the 3 simplexes from the last round, so we actually need to add their volume back because otherwise they get double counted in the subtraction. We find the volume occupied in the cube via

S(3, roll + 1 - 3) - 3*S(3, roll + 1 - 3 - N)  + 3*S(3, roll + 1 - 3 - 2*N)

(I really wish I could show a diagram but 3d diagrams are much harder to whip up quickly)

Now notice the coefficients: 1,3,3: these are the NchooseK numbers for a set of 3 objects. Initially, we don’t have to choose anything. Then, we have to subtract off the volume of the simplexes poking out in each direction. But those simplexes meet at some multiple of (i,j), (i,k), and (j,k), so we need to add those volumes back.

This pattern generalizes for higher dimensions.

For 4 dimensions (using I, J, K, L for cardinal directions), you start off with

S(4,roll + 1 - 4)

then the simplex pokes outside the cube, creating 4 sections of volume we need to cut off:

S(4, roll + 1 - 4) - 4*S(4, roll + 1 - 4 - N)

then those 4 sections eventually meet at cube vertices (I,J), (I,K), (I,L), (J,K), (J,L), (K,L), so you need to add 6 new simplex volumes back because each one is now being double counted:

  S(4, roll + 1 - 4) - 4S(4, roll + 1 - 4 - N)  + 6S(4, roll + 1 - 4 - 2N)

and finally eventually those 6 new simplexes meet at another set of cube vertices, (I, J, K), (I, J, L), (I, K, L) and (J,K,L): the volume of these simplexes have been added once by the original simplex, subtracted by round 2, added again by round 3, and so need to be subtracted off again:

S(4, roll + 1 - 4) - 4S(4, roll + 1 - 4 - N)  + 6S(4, roll + 1 - 4 - 2N)  - 4S(4, roll + 1 - 4 - 3N)

now notably the NchooseK numbers are also simplical numbers: both the nchoosek numbers appear in pascals triangle, where NchooseK is a given row, and the simplical numbers for a given dimension follow some diagonal. Which means we can express the above purely in terms of simplical numbers. We’ll additionally define S(n, X) = 0 for X<=0, the volume of the n-d cube of size N occupied by the simplex:

S(n, 1)*S(n, roll + 1 - n) - S(n-1,2)*S(n, roll + 1 - n - N) + S(n-2,3)*S(n, roll + 1 - n - 2N) ...

then you just divide out the volume of the cube to get the actual probability.

I have some matlab code that works (I tested it against anydice dot com, it works for all values as far as I can tell) but in the interest of FOSS I should probably write it in python.

Stats people who follow me: blanking on how to do something pretty basic.

My goal here is that given a set of n die rolls, I want to create a percentile for how lucky the given set is compared to the distribution of all sets of n die rolls. (You rolled a 20! This is luckier than 95% of outcomes when someone rolls 1 time!)

My basic thought - take the average of the set, compare it to the expected average, and then using the number of die rolls, do some variance calculation that tells me how surprising it is that the average is x above/below the expected average.

But I think I need some measure re: the range of values I can get - if you roll a 4 sided die with 9, 10, 11, 12 vs a d20, you'd be a lot more surprised if you average a 12 on the 4 sider.

@raginrayguns you seem like you know stats stuff?

[mathandnumberystuff]

This is a follow-up to my previous post about higher-dimensional analogs of Pascal’s triangle. Here I will discuss more properties of this extension.

Connection to the binomial theorem

It is well known that the n-th row of Pascal’s triangle gives the coefficients for (x + y)^n. In fact, the term A(r, n - r) is the coefficient for the term x^r*y^(n - r).

This works because each term in the expansion of (x + y)^n is computed by taking the product of the members an ordered list of n x’s and y’s formed by selecting one term (either x or y) from each factor (x + y). This leads the creation of all 2^n possible lists of n x’s and y’s, leading to 2^n terms in total. However, many of these terms are the same due to multiplication being commutative. More specifically, two lists will have the same product if and only if they have the same number of x’s and y’s in them. For example, in the expansion of (x + y)^7, three of the 128 terms encountered will be x*x*x*x*y*y*y, x*y*x*y*x*y*x, and y*y*y*x*x*x*x. These all have the same value of x^4*y^3.

When expanding (x + y)^n, each term will be of the form x^r*y^(n - r) for some nonnegative integer r, r ≤ n. The number of copies of this term encountered, in terms of r, is equal to A(r, n - r) due to each copy coming from a list of r x’s and (n - r) y’s. This explains why the coefficient of each term (which is equal to the number of copies of that term in the expansion) is A(r, n - r) AKA the r-th member of the n-th row of Pascal’s triangle.

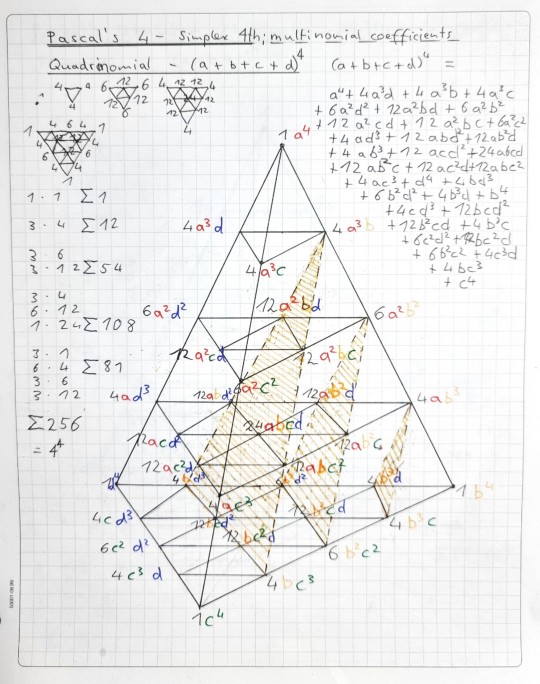
From this, it is easy to extend the idea to trinomials; expressions of the form (x + y + z)^n. In the expansion of this expression, each term is of the form x^r*y^s*z^(n - r - s) for some nonnegative integers r and s, r + s ≤ n. Before addition of alike terms, there is one term for each list of n x’s, y’s, and z’s, which get multiplied together. So, similar to the binomial theorem, the coefficient of x^r*y^s*z^(n - r - s) is the number of lists of r x’s, s y’s, and n - r - s z’s, equal to A(r, s, n - r - s). This number is the r-th number from the beginning, and the s-th number from the end, on the (n - r - s)-th row of the n-th layer of Pascal’s tetrahedron. Notice that r, s, and (n - r - s) are both the coordinates of the number and the exponents x, y, and z in the term. Also notice that the values r, s, and (n - r - s) can be permuted in any way and the value will be the same; this follows from the commutativity of the A function, but also can be easily derived by the fact that the expression (x + y + z)^n has symmetry between x, y, and z so permuting the exponents keeps the coefficient the same.

Of course, this also works in higher dimensions. In the expansion of (x0 + x1 + x2 ... + xd)^n, the coefficient x0^r0*x1^r1*x2^r2*...*xd^rd = A(r0, r1, r2 ... rd). The values r0 + r1 + r2 ... + rd need to add to n, of course, meaning that this value occurs on the nth layer of Pascal’s simplex.

In summary, the coefficients of the nth power of a polynomial with d terms are the numbers from the nth layer of Pascal’s d-dimensional simplex!

Factors of factorials or how many distinct numbers can be on each layer?

You might have noticed that a formula for A(r, s, t...) is (r + s + t...)!/(r!*s!*t!...). That is, it is the factorial of the sum of the coordinates divided by the factorial of each of the coordinates themselves. What if we set the sum to a constant value? It is clear that on the nth layer, every number will be a factor of n!. This means that as we progress up the dimensions, from triangle to tetrahedron to pentachoron, etc., the values on the nth layer will never be higher than n! no matter what the dimension is. (More on this later.)

Which are the possible terms on the nth layer, for various values of n?

For n = 0 it’s trivial::

0! = 1

For n = 1 it’s still trivial:

1!/(1!) = 1

For n = 2 we have:

2!/(1!*1!) = 2 2!/(2!) = 1

For n = 3 there is:

3!/(1!*1!*1!) = 6 3!/(2!*1!) = 3 3!/(3!) = 1

For n = 4:

4!/(1!*1!*1!*1!) = 24 4!/(2!*1!*1!) = 12 4!/(2!*2!) = 6 4!/(3!*1!) = 4 4!/(4!) = 1

For n = 5:

5/(1!*1!*1!*1!*1!) = 120 5!/(2!*1!*1!*1!) = 60 5!/(3!*1!*1!) = 20 5!/(2!*2!*1!) = 30 5!/(4!*1!) = 5 5!/(3!*2!) = 10 5!/(5!) = 1

In general, these numbers can be found by dividing n! by the product of factorials of numbers that add up to n. This sequence is A036038 in the OEIS, and its name, “triangle of multinomial coefficients”, emphasizes the property we just found. For each n, there is one distinct term for each set of positive integers that adds up to n. This term is located at all the places whose coordinates are permutation of this set of numbers, plus an optional number of zeroes. For example, 2 + 3 + 5 = 10, and so the partition of 10 into 2, 3, and 5 produces the terms A(2, 3, 5), A(2, 5, 3), A(5, 3, 2), A(0, 3, 5, 2), A(0, 0, 5, 0, 2, 3, 0) and more, all on the tenth layer of various dimensional simplexes. In fact, all take places in the layer that are equivalent under symmetry. The number of nonzero numbers in this partition is the smallest dimension of simplex in which the term occurs. The total number of distinct terms that can appear on the nth layer is the nth partition number.

Since a limit exists to the number of distinct terms that appear on a single layer, regardless of dimension, there must be some dimension at which new terms just stop appearing. For example, the 5th layer of Pascal’s triangle contains 1, 5, and 10. Pascal’s tetrahedron adds 20 and 30. Pascal’s pentachoron (4-dimensional simplex) adds 60 to the list, and Pascal’s hexateron (5-dimensional simplex) adds 120. But after that, each new dimension adds no new terms to the 5th layer. In fact, as different copies of the same term are equivalent under symmetry, the only terms added to the 5th layer after 5 dimensions (4 dimensions for the layer itself) are symmetric transformations of the terms on one facet!

To see how this works, think about how the shape of each layer gets built when dimensions are added. The 5th layer of Pascal’s tetrahedron is a triangle, and each side of the triangle is just the 5th row of Pascal’s triangle. The 5th layer of Pascal’s pentachoron is a tetrahedron, and each of its four triangular faces is the 5th layer of Pascal’s tetrahedron. In general, in n dimensions, each layer is an (n - 1)D cross section of the figure itself. The shape of the layer is an (n - 1)-dimensional simplex, and it has n copies of the same layer one dimension lower as its (n - 2)-dimensional facets. Each term from one of these facets is only symmetric to terms on other facets, not on the simplex’s interior. But after n = 5 dimensions, all of the terms on its 5th layer are equivalent, meaning symmetric, to the terms on one of its facets. So they all appear on facets, which means that past 5 dimensions, every term on the 5th layer of Pascal’s simplex occurs on the outside. This property is independent of the numbers in the simplex and is still interesting when considering the geometry alone.

And this happens sooner or later for every layer. Which means that if you start  with a long line of objects, build it into a triangle with the original line as the base, make that into the base of a pyramid, make that pyramid into the base of a 4D pyramid, make that pyramid into the base of a 5D pyramid... past some dimension, all of the objects added to pyramid will appear on the outside, on the pyramid’s facets.

In fact, it’s pretty easy to tell when this will happen. Remember, the number of nonzero coordinates is the minimum dimension of the simplex the term appears in. For layer n, the maximum minimum dimension for a term--in other words, the largest dimension containing a term not in previous dimensions--occurs when n is partitioned into the most parts. This happens when n is partitioned into n copies of 1. The coordinates for the term are A(1, 1, ...1, 1), with n 1s. This means that it occurs when Pascal’s simplex is n-dimensional. Also, since all the coordinates are identical, it is equidistant from each of its layer’s facets, meaning it is in the center of the nth layer. (It can also be proven to be in the center by the fact that it has no symmetric equivalents in the same dimension, again because the coordinates are identical.) This term is equal to n!.

New theorem: Going up the dimensions, the nth layer of Pascal’s triangle stops getting new distinct terms after n dimensions, and every term in the layer thereafter is on the hypersurface. The final distinct term occurs in n dimensions (layers are (n - 1)-dimensional). It is in the center of the layer and equals n!.

Now you might be thinking, “Wait, are the values of all these terms actually different? You’ve been referring to them as ‘distinct terms’ when their coordinates come from different partitions of the layer number, but what’s to say no two distinct terms on the same layer have the same value?” This actually does happen. In fact, it happens every time n!/(r0!*s0!...z0!) = n!/(r1!*s1!...z1!); that is, when a number can be written in two different ways as a product of factorials of numbers that sum to the same value. In fact, even if they don’t sum to the same value, one of the them can be padded with 1′s until they do. So any two products of factorials with the same value will suffice.

The smallest such identity is 3!*5! = 1!*1!*6!, which leads to A(3, 5) = A(1, 1, 6) = 56. Thus, on the 8th layer of Pascal’s Tetrahedron, the number 56 appears on coordinates that are permutations of both (1, 1, 6) and (0, 3, 5). From this identity, both sides can be multiplied by any factorial product, leading to the following equivalences:

A(1, 3, 5) = A(1, 1, 1, 6) = 504 A(2, 3, 5) = A(1, 1, 2, 6) = 2520 A(1, 1, 3, 5) = A(1, 1, 1, 1, 6) = 5040 A(3, 3, 5) = A(1, 1, 3, 6) = 9240 A(1, 1, 1, 3, 5) = A(1, 1, 1, 1, 1, 6) = 55440 ...

The number of distinct terms on each layer in n or more dimensions (or equivalently, on all dimensions taken together) is given by OEIS sequence A070289.

--

There are several other remarkable properties. Remember how I said that for each term A(r, s, t, ... z), the terms given by permutations of (r, s, t, ... z) are located at symmetrical positions under the layer’s simplectic symmetry? The number of these terms, since the layer has the shape and symmetries of a simplex, is just the number of ways to reflect or rotate a point to make distinct points using the symmetries of that simplex. But wait! This number is just the number of permutations of the coordinate--and what is a function that finds the number of permutations of a list of numbers? We have spent this entire blog post playing with one!

All that is needed to do is to express the number of occurrences of each distinct coordinate in the coordinate list. Let’s say that the first coordinate occurs a times in total, the second distinct coordinate occurs b times, the third occurs c times, etc. Then the total number of permutations is A(a, b, c, ... k), where the list has k distinct terms. Since the original coordinate list had d terms, the number of permutations is a term on the dth layer of a new Pascal’s simplex.

This doesn’t just work for integer coordinates either. In fact, it works for any list of d coordinates that can be mapped to a point in (d - 1)-dimensional space. Remember, the space is made of all the points in the d-dimensional space whose coordinates add to n, making a cross section through the d-dimensional space.

Each way to permute a list of coordinates in this space, when applied to the points, produces one of the transformations that make the symmetry group of the (d - 1)-dimensional simplex. The possible values of A(a, b, ... k) (the number of coordinate permutations) are the number of distinct points a single point can be mapped to under these transformations. Remember this, because it will be important.

Higher-dimensional kaleidoscopes

What really is a “line of symmetry”? Think about it. A symmetry is a set of transformations under which a set of points is invariant. For example, when an object has bilateral symmetry, it means that the position of each point can be reversed and it will match up to another point. If this reversal transformation is done to every point in 2D space, there will be a set of points that map to themselves. These points lie along a line, They are called the fixed points of the transformation, and the line they lie along is commonly called the “line” of symmetry of the aforementioned object.

Now let’s go back to our (d - 1)-dimensional space. Each point has d coordinates, leading to d! different permutations of coordinates and therefore d! different transformations of the points. It is easy to see that these transformations are one-to-one and onto, and therefore invertible. Furthermore, the fixed points under any transformation (besides the identity one) must all have some repeating numbers in their list of coordinates, as this is the only way that a non-trivial permutation of a list can output the same list. Conversely, each point with repeating numbers in its coordinates is a fixed point under some non-trivial transform.

Loosely speaking, the simplest-looking type of transform other than the identity transform is one that exchanges two coordinates while leaving the others the same. There are d*(d - 1)/2 of these. Each one can be described by starting with the d-by-d identity matrix and swapping two rows. This matrix acts as a linear transformation on R^d, and since it is a permutation matrix whose determinant is -1, it acts to reverse R^d; the fixed points make a subspace of dimension d - 1. The nth cross-section of R^d also gets reversed; the fixed points are the (d - 2)-dimensional intersection of the cross section and the subspace.

When d > 3, this intersection cannot be called a “line” of symmetry, as it is more than one dimension. Instead, let’s call it a hyperplane of symmetry. The d*(d - 1)/2 hyperplanes of symmetry together act like mirrors in space of d - 1 dimensions, and these transformations form a basis for the entire symmetric group. That is, any of the d! transformation of a single point can be formed by reflecting it through a combination of hyperplanar mirrors, like a kind of higher-dimensional kaleidoscope. Together, these mirrors cut the space into d! regions of points, these points together making up the set of all points not lying on any mirror.

Now, you might want to avoid the next part if you aren’t an expert on higher-dimensional geometry, as it contains a lot of advanced polytope terminology.

Each A(d - 1) polytope is a convex uniform polytope formed by a Wythoffian operation on a (d - 1)-dimensional simplex. As it is uniform, it must be vertex-transitive, which means that any two vertices can be mapped onto each other using symmetric transforms. We have already seen what the transforms making up (d - 1)-simplectic symmetry are. The number of possible vertices of such a polytope must be a number of distinct vertices that are produced by a single vertex after each transformation. Thus, the number of possible vertices of any Ad - 1; polytope must be of the form A(p, q, ... z) where p, q, ... add to d. For example, the tetrahedron (o3o3x in Coxeter diagram) has A(3, 1) = 4 vertices, the truncated pentachoron (o3o3x3x) has A(3, 1, 1) = 20 vertices, and the biexipetirhombated dodecadakon (now there’s a shape you don’t think about every day) (o3o3x3o3x3o3o3o3x3x3o) has A(3, 2, 4, 1, 2) = 69300 vertices.

A sequence that appears everywhere

I want to finish this article as soon as possible, but there is one last property of the A function and the multidimensional Pascal’s “corner” that I just have to mention. As I mentioned in the previous post, the nth layer of the d-dimensional structure has terms that sum to d^n. But what if we sum just the terms on the inside of the nth layer; that is, every term whose coordinates are all positive?

What does this mean in terms of the A function? Remember, the A function gives the number of ways to order a sequence made of copies of distinct numbers, each number of copies corresponding to one of its arguments. If there are d terms--call them p, q, r, ... z--, none of which are 0, the value of the function describes the number of runs of a sequence of p 0s, q 1s, r 2s ... z (n - 1)’s. Summing these values up for all possible positive integer values of p, q, r, ... z (that sum to n of course), we find the total number of n-digit strings that use every digit from 0 to d - 1, and only digits in that range.

If you remember one of my previous posts, you should be getting an epiphany right about now. If not, here is a quote straight from my “Starter constants and mysteries” post:

The A-th starter constant of the B-th powers is really the number of A-digit strings (I’m not calling them numbers, because the first digit can be 0 and it is still considered to have A digits), that use every digit from 0 to B - 1.

Yup, that’s right! It’s the starter constants! The sum of all A(p, q, r, ... z) for each set of d nonzero terms p...z that sum to n, is equal to SC(n, d)!