#spherical polar coordinates
Explore tagged Tumblr posts
Text
A new version of my book is now published. The free PDF and the leanpub versions are available now. The paperback and hardcover versions should be available on Amazon within the week. What has changed: V0.3.2 (Dec 8, 2023) Add to helpful formulas: Determinant form of triple wedge. Add figure showing the spherical polar conventions picked. Add a problem showing that \( (e^x)’ = x’ e^x \) only…
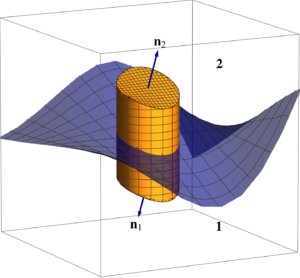
View On WordPress
#bivector commutation#derivative#exponential derivatives#Geometric Algebra for Electrical Engineers#multivector potential#repeated wedge product#spherical polar coordinates
1 note
·
View note
Text

Today we're heading into the eternal ice of Antarctica and keeping a special lady company. The beautiful Endurance is waiting for us in door no. 7

More about her here:
The three-masted schooner barque designed by Ole Aanderud Larsen (1884-1964) was built by the Framnæs shipyard in Sandefjord, Norway. When she was launched on 17 December 1912, she was named Polaris. She was 43.8 m long, 7.62 m wide and weighed 350 tonnes. In addition to square sails on the foremast and gaff sails on the main and mizzen masts, she had a 260 kW steam engine, which allowed a maximum speed of 10 knots (19 km/h). The ship was designed for polar conditions and constructed to minimise the pressure of the ice masses. With a thickness of 28 cm, the frames were made of greenheart wood, a particularly stable type of tropical wood, and were twice as thick as on conventional sailing ships of this size. The hull of the Endurance was designed to be relatively straight-sided, as it was only intended to sail in loose pack ice. She was therefore calmer in the sea than ships with a spherical hull, such as the Fram; however, this came at the cost of not being lifted significantly out of the pressure line in ice pressures and was therefore unsuitable for encasements in pack ice.
The ship was commissioned by the Belgian polar explorer Adrien de Gerlache and the Norwegian whaling magnate Lars Christensen, who actually wanted to use it for polar cruises of a more touristic nature. However, due to financial problems, Christensen was happy to sell his ship to Shackleton for 11,600 pounds sterling (approx. 934,000 euros, as of 2010) - an amount that was less than the original construction costs. Shackleton renamed her Endurance after his family's motto ‘Fortitudine vincimus’ (‘Through endurance we shall conquer’).
The Endurance left the port of Plymouth on 8 August 1914, around a week after Great Britain's entry into the First World War, and completed the journey to Antarctica with a stopover in Buenos Aires without any problems.
Before the crew of the Endurance could cross to the Antarctic mainland to cross the Antarctic as planned, the ship was trapped by the pack ice of the Weddell Sea in January 1915 like ‘an almond in a piece of chocolate’ - as the much-used comparison goes. After resisting the force of the pack ice for 281 days, the Endurance was crushed by the ice on 21 November 1915. The expedition team had previously saved themselves on a safe ice floe. Thanks to a masterly feat of seamanship and navigation, Shackleton and his crew managed to get out of this desolate situation without any losses with the help of three lifeboats that were salvaged from the Endurance.
Initially continuing with the pack ice and later on ice floes, the castaways drifted northwards in their camps along the Antarctic Peninsula until the floes broke into small pieces. They finally reached Elephant Island in their lifeboats. There, one of the boats was converted and set off for South Georgia with 6 men to fetch help, which was successful. Months later, the remaining men who were still stuck on Elephant Island were rescued by a Chilean navy guard boat.
In 2019, a private expedition attempted to locate the wreck of the Endurance, but was unsuccessful.
In January 2022, the Endurance 22 expedition began the search. The S. A. Agulhas II brought the expedition, in which marine physicist Stefanie Arndt from the Alfred Wegener Institute took part,[3] to the last coordinates of the Endurance mentioned. From the historical records, the expedition members knew that the ship must have sunk at ♁68° 39′ 30″ S, 52° 26′ 30″ W. According to the rules of the Antarctic Treaty, the wreck is a protected historical site that may not be touched.
On 5 March 2022, the expedition found the ship with a diving robot at a depth of 3008 m, 7.7 km from the recorded position. Photographs showed the wreck standing upright in excellent condition.
#naval history#tall ship#endurance#ernest shackleton#early 20th century#antarctica#advent calendar#day 7
158 notes
·
View notes
Text
Topics to study for Quantum Physics
Calculus
Taylor Series
Sequences of Functions
Transcendental Equations
Differential Equations
Linear Algebra
Separation of Variables
Scalars
Vectors
Matrixes
Operators
Basis
Vector Operators
Inner Products
Identity Matrix
Unitary Matrix
Unitary Operators
Evolution Operator
Transformation
Rotational Matrix
Eigen Values
Coefficients
Linear Combinations
Matrix Elements
Delta Sequences
Vectors
Basics
Derivatives
Cartesian
Polar Coordinates
Cylindrical
Spherical
LaPlacian
Generalized Coordinate Systems
Waves
Components of Equations
Versions of the equation
Amplitudes
Time Dependent
Time Independent
Position Dependent
Complex Waves
Standing Waves
Nodes
AntiNodes
Traveling Waves
Plane Waves
Incident
Transmission
Reflection
Boundary Conditions
Probability
Probability
Probability Densities
Statistical Interpretation
Discrete Variables
Continuous Variables
Normalization
Probability Distribution
Conservation of Probability
Continuum Limit
Classical Mechanics
Position
Momentum
Center of Mass
Reduce Mass
Action Principle
Elastic and Inelastic Collisions
Physical State
Waves vs Particles
Probability Waves
Quantum Physics
Schroedinger Equation
Uncertainty Principle
Complex Conjugates
Continuity Equation
Quantization Rules
Heisenburg's Uncertianty Principle
Schroedinger Equation
TISE
Seperation from Time
Stationary States
Infinite Square Well
Harmonic Oscillator
Free Particle
Kronecker Delta Functions
Delta Function Potentials
Bound States
Finite Square Well
Scattering States
Incident Particles
Reflected Particles
Transmitted Particles
Motion
Quantum States
Group Velocity
Phase Velocity
Probabilities from Inner Products
Born Interpretation
Hilbert Space
Observables
Operators
Hermitian Operators
Determinate States
Degenerate States
Non-Degenerate States
n-Fold Degenerate States
Symetric States
State Function
State of the System
Eigen States
Eigen States of Position
Eigen States of Momentum
Eigen States of Zero Uncertainty
Eigen Energies
Eigen Energy Values
Eigen Energy States
Eigen Functions
Required properties
Eigen Energy States
Quantification
Negative Energy
Eigen Value Equations
Energy Gaps
Band Gaps
Atomic Spectra
Discrete Spectra
Continuous Spectra
Generalized Statistical Interpretation
Atomic Energy States
Sommerfels Model
The correspondence Principle
Wave Packet
Minimum Uncertainty
Energy Time Uncertainty
Bases of Hilbert Space
Fermi Dirac Notation
Changing Bases
Coordinate Systems
Cartesian
Cylindrical
Spherical - radii, azmithal, angle
Angular Equation
Radial Equation
Hydrogen Atom
Radial Wave Equation
Spectrum of Hydrogen
Angular Momentum
Total Angular Momentum
Orbital Angular Momentum
Angular Momentum Cones
Spin
Spin 1/2
Spin Orbital Interaction Energy
Electron in a Magnetic Field
ElectroMagnetic Interactions
Minimal Coupling
Orbital magnetic dipole moments
Two particle systems
Bosons
Fermions
Exchange Forces
Symmetry
Atoms
Helium
Periodic Table
Solids
Free Electron Gas
Band Structure
Transformations
Transformation in Space
Translation Operator
Translational Symmetry
Conservation Laws
Conservation of Probability
Parity
Parity In 1D
Parity In 2D
Parity In 3D
Even Parity
Odd Parity
Parity selection rules
Rotational Symmetry
Rotations about the z-axis
Rotations in 3D
Degeneracy
Selection rules for Scalars
Translations in time
Time Dependent Equations
Time Translation Invariance
Reflection Symmetry
Periodicity
Stern Gerlach experiment
Dynamic Variables
Kets, Bras and Operators
Multiplication
Measurements
Simultaneous measurements
Compatible Observable
Incompatible Observable
Transformation Matrix
Unitary Equivalent Observable
Position and Momentum Measurements
Wave Functions in Position and Momentum Space
Position space wave functions
momentum operator in position basis
Momentum Space wave functions
Wave Packets
Localized Wave Packets
Gaussian Wave Packets
Motion of Wave Packets
Potentials
Zero Potential
Potential Wells
Potentials in 1D
Potentials in 2D
Potentials in 3D
Linear Potential
Rectangular Potentials
Step Potentials
Central Potential
Bound States
UnBound States
Scattering States
Tunneling
Double Well
Square Barrier
Infinite Square Well Potential
Simple Harmonic Oscillator Potential
Binding Potentials
Non Binding Potentials
Forbidden domains
Forbidden regions
Quantum corral
Classically Allowed Regions
Classically Forbidden Regions
Regions
Landau Levels
Quantum Hall Effect
Molecular Binding
Quantum Numbers
Magnetic
Withal
Principle
Transformations
Gauge Transformations
Commutators
Commuting Operators
Non-Commuting Operators
Commutator Relations of Angular Momentum
Pauli Exclusion Principle
Orbitals
Multiplets
Excited States
Ground State
Spherical Bessel equations
Spherical Bessel Functions
Orthonormal
Orthogonal
Orthogonality
Polarized and UnPolarized Beams
Ladder Operators
Raising and Lowering Operators
Spherical harmonics
Isotropic Harmonic Oscillator
Coulomb Potential
Identical particles
Distinguishable particles
Expectation Values
Ehrenfests Theorem
Simple Harmonic Oscillator
Euler Lagrange Equations
Principle of Least Time
Principle of Least Action
Hamilton's Equation
Hamiltonian Equation
Classical Mechanics
Transition States
Selection Rules
Coherent State
Hydrogen Atom
Electron orbital velocity
principal quantum number
Spectroscopic Notation
=====
Common Equations
Energy (E) .. KE + V
Kinetic Energy (KE) .. KE = 1/2 m v^2
Potential Energy (V)
Momentum (p) is mass times velocity
Force equals mass times acceleration (f = m a)
Newtons' Law of Motion
Wave Length (λ) .. λ = h / p
Wave number (k) ..
k = 2 PI / λ
= p / h-bar
Frequency (f) .. f = 1 / period
Period (T) .. T = 1 / frequency
Density (λ) .. mass / volume
Reduced Mass (m) .. m = (m1 m2) / (m1 + m2)
Angular momentum (L)
Waves (w) ..
w = A sin (kx - wt + o)
w = A exp (i (kx - wt) ) + B exp (-i (kx - wt) )
Angular Frequency (w) ..
w = 2 PI f
= E / h-bar
Schroedinger's Equation
-p^2 [d/dx]^2 w (x, t) + V (x) w (x, t) = i h-bar [d/dt] w(x, t)
-p^2 [d/dx]^2 w (x) T (t) + V (x) w (x) T (t) = i h-bar [d/dt] w(x) T (t)
Time Dependent Schroedinger Equation
[ -p^2 [d/dx]^2 w (x) + V (x) w (x) ] / w (x) = i h-bar [d/dt] T (t) / T (t)
E w (x) = -p^2 [d/dx]^2 w (x) + V (x) w (x)
E i h-bar T (t) = [d/dt] T (t)
TISE - Time Independent
H w = E w
H w = -p^2 [d/dx]^2 w (x) + V (x) w (x)
H = -p^2 [d/dx]^2 + V (x)
-p^2 [d/dx]^2 w (x) + V (x) w (x) = E w (x)
Conversions
Energy / wave length ..
E = h f
E [n] = n h f
= (h-bar k[n])^2 / 2m
= (h-bar n PI)^2 / 2m
= sqr (p^2 c^2 + m^2 c^4)
Kinetic Energy (KE)
KE = 1/2 m v^2
= p^2 / 2m
Momentum (p)
p = h / λ
= sqr (2 m K)
= E / c
= h f / c
Angular momentum ..
p = n h / r, n = [1 .. oo] integers
Wave Length ..
λ = h / p
= h r / n (h / 2 PI)
= 2 PI r / n
= h / sqr (2 m K)
Constants
Planks constant (h)
Rydberg's constant (R)
Avogadro's number (Na)
Planks reduced constant (h-bar) .. h-bar = h / 2 PI
Speed of light (c)
electron mass (me)
proton mass (mp)
Boltzmann's constant (K)
Coulomb's constant
Bohr radius
Electron Volts to Jules
Meter Scale
Gravitational Constant is 6.7e-11 m^3 / kg s^2
History of Experiments
Light
Interference
Diffraction
Diffraction Gratings
Black body radiation
Planks formula
Compton Effect
Photo Electric Effect
Heisenberg's Microscope
Rutherford Planetary Model
Bohr Atom
de Broglie Waves
Double slit experiment
Light
Electrons
Casmir Effect
Pair Production
Superposition
Schroedinger's Cat
EPR Paradox
Examples
Tossing a ball into the air
Stability of the Atom
2 Beads on a wire
Plane Pendulum
Wave Like Behavior of Electrons
Constrained movement between two concentric impermeable spheres
Rigid Rod
Rigid Rotator
Spring Oscillator
Balls rolling down Hill
Balls Tossed in Air
Multiple Pullys and Weights
Particle in a Box
Particle in a Circle
Experiments
Particle in a Tube
Particle in a 2D Box
Particle in a 3D Box
Simple Harmonic Oscillator
Scattering Experiments
Diffraction Experiments
Stern Gerlach Experiment
Rayleigh Scattering
Ramsauer Effect
Davisson–Germer experiment
Theorems
Cauchy Schwarz inequality
Fourier Transformation
Inverse Fourier Transformation
Integration by Parts
Terminology
Levi Civita symbol
Laplace Runge Lenz vector
6 notes
·
View notes
Text
riemann spheres as a fundamental type, pt.1 basics
ive been thinking on and off about riemann spheres for a while now, a couple weeks really, and so far i think there's some utility to them as a building block of a type system of some kind for a joke/toy computer language
background: riemann spheres are a neat tool in complex analysis where we imagine a sphere whose equator intersects the complex plane, and every number on the complex plane is representable by a point on the sphere such that a line is projected from the north pole and through that point onto the complex plane. naturally, this means that the north pole is P(∞) and the south pole is P(0). see below how that would look like with other unit points of the complex numbers
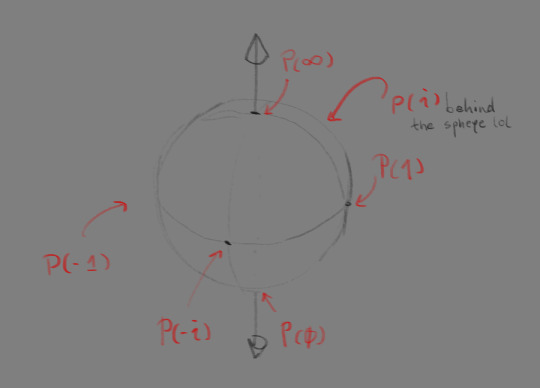
a neat thing the riemann sphere allows us is to define meaningful division by zero so now z/0 = ∞ clean and simple! and also its inverse, z/∞ = 0 is well behaved as well. this simplifies doing complex analysis but stereographic projection is an absolute bitch to work with turns out, and doing arithmetic on points on the sphere is a mess because it's not a linear mapping (it's continuous though so that's fine)
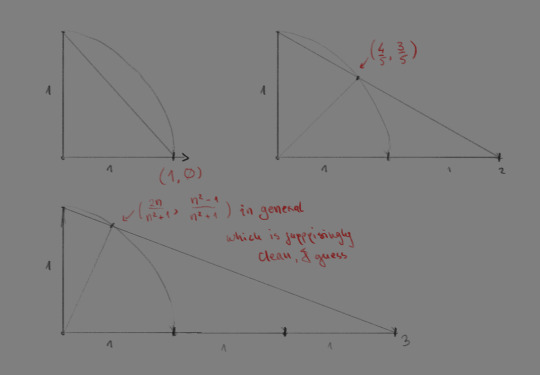
if we're dealing with ONLY real numbers in relation to a circular slice of the riemann sphere, it already starts looking like a mess; for any number n∈R its projective cognate on the circle is located at (2n/n²+1, n²-1/n²+1). on the real riemann sphere though? zoo wee mamma
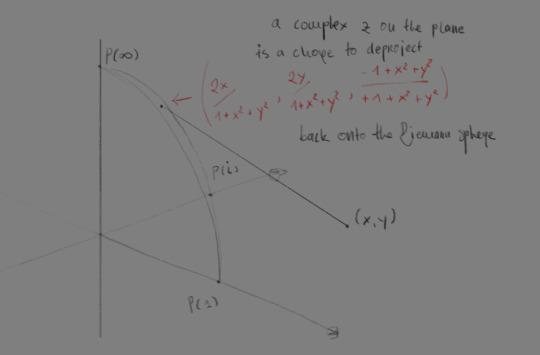
an arbitrary z∈C, represented as a point (x,y) on the complex plane, has to walk through a rather ugly mapping (related to the previous one) to find its point on the sphere; more accurately, given the coordinates (x,y) of the point on the plane, the point on the sphere is located at (2x/1+x²+y², 2y/1+x²+y², -1+x²+y²/1+x²+y²), which is godawful in spherical-to-polar coordinate terms, this is much simpler; for a polar pair (r,θ) the point on the unit sphere representing it is (φ,ξ) = (2*arctg 1/r, θ); and conversely projecting from the riemann sphere is also dead simple, given the zenith-azimuth pair (φ,ξ), (r,θ) = (ctg φ/2, ξ). of course, translating from polar to real coordinates is ALSO dead simple; x = r * cos θ, y = r * sin θ. if a computer system were to store complex numbers (or any coordinate on a 2d plane really), it makes sense to store them in terms of spherical coordinates of a riemann sphere, since this makes infinity well-behaved as a unit (zenith = 0, azimuth = literally who gives a fuck) and is surprisingly efficient. knowing that the zenith is ∈[0,π] and azimuth ∈[0, 2π] can allow for some formidably dumb optimisations that can save on space and ensure granularity. compared to storing them as 2d cartesian or polar coordinates, this provides the benefit of having neither number be larger than like 6.3, so an underlying/backing type that can offer great precision in this small range would be more efficient numerically than, say, floating points which have insane baggage and gaps
or iunno i'll look into that one a bit later, i'm just kind of furious right now that i rederived stereographic projection on my own when the formulas were right fucking there if id only just googled for them
#rambling#math#maths#mathematics#riemann sphere#stereographic projection#complex analysis#trigonometry#complex plane#complex numbers
5 notes
·
View notes
Text
Loxodromes, Part 1
Loxodromes (also known as rhumb lines) are a family of curves on the sphere . The family includes meridians (lines of constant longitude) and parallels (lines of constant latitude). The general loxodrome is a spherical spiral which intersects every meridian at the same angle. These curves are useful for navigation, because they describe the idealised course followed by a ship that maintains a constant compass bearing.
The navigator and scientist Thomas Harriot was an early investigator of the loxodrome; he was the first to rectify it (find a mathematical expression for its length) and among the first to rectify any curve. I'm planning to make another post about his method (based on a description in Robin Arianrhod's biography of him). First, though, I'm going to try to give an account of the loxodrome using modern calculus. (I'm leaning on a pretty good treatment on the atractor.pt website.)
The task of deriving the formula for the loxodrome is made much easier by having the right mathematical tools. In this case, the tools are the notion of a parameterised space curve, a vector-valued function, spherical polar coordinates, Cartesian coordinates, and basic differential and integral calculus.
A space curve, parameterised by the variable \(t\), is a function \(\gamma:\,I\rightarrow\mathbb{R}^{3}\), where \(I\subseteq\mathbb{R}\) is an interval, that associates a point \(\gamma\left(t\right)\in\mathbb{R}^{3}\) to each value of a parameter \(t\in I\).
As a first example, consider a meridian as a space curve. We'll use spherical polar coordinates with radius \(r\), longitude \(\theta\) and colatitude \(\varphi\). (Colatitude is latitude \(- \frac{\pi}{2}\): latitude measured from the North Pole.)
The equation of a meridian at longitude \(\theta_p\), as a function of \(\varphi\), is
\[m(\varphi) = (r\cos(\theta_p)\sin(\varphi),r\sin(\theta_p)\sin(\varphi),r\cos(\varphi))\]
The range of \(\varphi\) is \(]0,\pi[\).
Consider a loxodrome \(\ell_\alpha\) that intersects the meridians at angle \(\alpha\).
A fixed point \(P\) on \(\ell_\alpha\) has coordinates \((r, \theta_p, \varphi_p)\).
The fine article on atractor.pt starts with the case of \(\alpha = \frac{\pi}{2} + n+n\pi\), for some \(n\in\mathbb{Z}\). This example covers the loxodromes that coincide with parallels of latitude, and it's a fine warm-up, but not very revealing. Such loxodromes are most straightfordwardly thought of as being parameterized by longitude, \(\theta\).
The general loxodrome, with a spherical spiral form, corresponds to the case \(\alpha \neq \frac{\pi}{2} + n\pi, n\in\mathbb{Z}\).
In this case, the parameterisation of \(\ell_{\alpha}\) is given as a function of colatitude. Because of the nature of the spherical spiral, there is a just one point of the curve at each (co)latitude. Longitude would not work as a parameterisation for a spherical spiral, or at least longitude conventionally limited to the range \(-\pi\) to \(\pi\) would not.
We define a function
\[\begin{array}{ccll} \ell_{\alpha}: & ]0\,,\pi[ & \longrightarrow & \mathbb{S}^{2} \\\\ & \varphi & \mapsto & \left(r\cos\left(\theta_\alpha\left(\varphi\right)\right) \sin\varphi, r\sin\left(\theta_\alpha\left(\varphi\right)\right), r\cos\varphi\right),\end{array}\]
The next step is to find the formulas of the tangents to both the loxodrome \(\ell_\alpha\(\varphi)\) and the meridian \(m(\varphi)\). This is achieved by componentwise differentiation.
\[\begin{array}{rccl}\ell_{\alpha}^{\prime}(\varphi_{P}) & = & & r\,\theta'_\alpha\left(\varphi_{P}\right)\left(-\sin\left(\theta_{P}\right)\sin\left(\varphi_{P}\right)\,,\,\cos\left(\theta_{P}\right)\sin\left(\varphi_{P}\right),0\right)\\\\ & & + & r\left(\cos\left(\varphi_{P}\right)\cos\left(\theta_{P}\right)\,,\,\cos\left(\varphi_{P}\right)\,\sin\left(\theta_{P}\right)\,,\,-\sin\left(\varphi_{P}\right)\right)\end{array}\] and \[m'(\varphi_{P})=r\left(\cos\left(\varphi_{P}\right)\cos\left(\theta_{P}\right)\,,\,\cos\left(\varphi_{P}\right)\,\sin\left(\theta_{P}\right)\,,\,-\sin\left(\varphi_{P}\right)\right)\,.\]
These angle between these two tangents is \(\alpha\). Thus
\[\cos\alpha=\frac{\ell_{\alpha}^{\prime}\left(\varphi_{P}\right)\,|\,m'\left(\varphi_{P}\right)}{\Vert\ell_{\alpha}^{\prime}\left(\varphi_{P}\right)\Vert\times\Vert m'\left(\varphi_{P}\right)\Vert}\,.\]
After some calculating, we get
\[\cos\alpha=\frac{1}{\sqrt{1+[\theta_{\alpha}^{\prime}(\varphi_{P})]^2sin^2(\varphi_{P})}}\]
Isolating \(\theta_{\alpha}^\prime(\varphi_{P})\), we have
\[\theta'_\alpha(\varphi_{P}) = \pm\frac{\tan\alpha}{\sin\left(\varphi_{P}\right)}\]
(This solution is only possible because \(\cos\alpha\) is not \(0\) and \(\varphi\in\ ]0, \pi[\).)
It is now possible to integrate this expression with respect to \(\varphi\) to get a formula for \(\theta_\alpha(\varphi)\): choosing to integrate \(-\frac{\tan\alpha}{\sin\left(\varphi_{P}\right)}\), the formula is \(\theta_\alpha(\varphi)=\tan\alpha\ln\left(\cot\frac{\varphi}{2}\right)+k\), for some constant \(k\in\mathbb{R}\). Since \(\theta_\alpha(\varphi_{P})=\theta_{P}\), we get \(k=\theta_{P}-\tan\alpha\ln\left(\cot\frac{\varphi_{P}}{2}\right)\).
Therefore, if \(\alpha\neq\frac{\pi}{2}+n\pi\), with \(n\in\mathbb{Z}\), then a parametrisation of \(\ell_{\alpha}\) is given by:
\[\begin{array}{ccll}\ell_{\alpha}: & ]0\,,\pi[ & \longrightarrow & \mathbb{S}^{2}\\\\ & \varphi & \mapsto & \left(r\cos\left(\theta_\alpha\left(\varphi\right)\right)\sin\varphi\,,\,r\sin\left(\theta_\alpha\left(\varphi\right)\right)\sin\varphi\,,\, r\cos\varphi\right)\end{array}\,,\] with \(\theta_\alpha(\varphi)=\theta_{P}+\tan\alpha\left[\ln\left(\cot\frac{\varphi}{2}\right)-\ln\left(\cot\frac{\varphi_{P}}{2}\right)\right]\).
This result is less advanced than the formula for the loxodrome that Wikipedia gives. The calculation is "elementary" in the sense that it avoids hyperbolic trig functions and the Gudermannian function (whatever that is). Elementary doesn't mean simple.
0 notes
Text
APROPOS KERR METRIC AND INTERIOR SOLUTION
APROPOS THE VACUUM KERR METRIC AND INTERIOR KERR SOLUTION
Stuart Boehmer
According to a formula of Tolman (“Relativity, Thermodynamics and Cosmology,” Clarendon Press, 1934), with which apparently most authors are unfamiliar, and which can easily be reproduced with a little careful thought, the relationship between the spatial metric, gmn, and the space-time metric, Gmn, is not gmn = Gmn, but gmn = Gmn – G0mG0n/G00.
Therefore, a singularity coincident with the ergosphere is found to occur in the g33 component of the spatial metric (where u3 is the longitude), thereby rendering the standard vacuum Kerr metric theoretically useless as a practical model of a rotating black hole (see my prior missive, “Theory of Black Holes,” apropos my thought on singularities occurring in nature—the mathematical trick I used there to render impotent the singularity in g11 at the Schwarzschild radius doesn’t seem to work here).
Thus, in order to find a practical working model, there seems to be no shortcut except to do the hard work of solving the full, interior problem, including the consequent vacuum solution for the region of space exterior to the rotating dead star. This remains an open problem, but with the assistance of machine computation it is conceptually trivial, as we shall describe presently.
Define the problem in this way for specificity: use spherical polar coordinates where r is the radial distance from the center along a path of constant co-latitude and longitude (therefore g11 := 1). I see no reason to complicate matters by using the hyperbolic elliptic coordinate system chosen by Kerr. The black hole or dead star is assumed to be spherical (density a nonzero constant inside a sphere of radius r = R) and rotating with constant angular velocity w := du3/dt. Because, as we are about to describe, the solution is in terms of Taylor series, there is no a priori reason we cannot use general functions d(r,u2) and w(r,u2) expanded as Taylor series with known coefficients).
At this point, allow me to parenthetically describe the process of “Involution” (W. Seiler, Springer, 2009) for solving any differential equation or system of differential equations in terms of Taylor series and justify it as being just as good (and, for purposes of practical calculation in no way inferior to) finding a solution in terms of “elementary” functions—the obsession for which no doubt contributes to the fact that this conceptually trivial problem has remained open so long. Indeed, this method could be used to solve any problem in any theory of physics and no “open problems” should remain anywhere in the entire discipline of physics, conceptually.
The method is this: expand all known and unknown functions in terms of Taylor series; the known functions have known coefficients, and the unknown functions have unknown coefficients which can be derived recursively by equating the coefficients of like powers of the coordinates, by the standard procedure. See what I mean by “trivial?”
Now some old-fashioned people may object that any sound theory must be construed in terms of “elementary” functions, which are in some sense “known.” Of course, the only elementary functions except for polynomials are the trigonometric, hyperbolic trigonometric and exponential functions—all of which can be reduced to the exponential function, which in turn can be accurately calculated in terms of—guess what?—Taylor series or some equivalent infinite recursive process.
These days, we might regard elliptic integrals as elementary functions and there is an elaborate algebraic theory reducing the evaluation of an arbitrary elliptic function to those of the first, second and third kinds, but no one is interested in this theory any longer—it is simpler to just evaluate in terms of Taylor series by machine computation (the “NI” in UNIAC and ENIAC stand for “Numerical Integrator”—that is why computers were invented!).
Conclusion: computation by machine is just as respectable as any reduction to elementary functions—and there is no escaping the use of machine computation when calculating numerical values of “elementary” functions anyway!
The method of involution is often described as reducing calculus to algebra, because, of course, machine computation must terminate in a finite number of steps and the Taylor series just turns out to be polynomials of high degree. Polynomials are, ultimately, the only functions whose numerical values can be computed in a finite number of steps.
1 note
·
View note
Text
APROPOS KERR METRIC AND INTERIOR SOLUTION
APROPOS THE VACUUM KERR METRIC AND INTERIOR KERR SOLUTION
Stuart Boehmer
According to a formula of Tolman (“Relativity, Thermodynamics and Cosmology,” Clarendon Press, 1934), with which apparently most authors are unfamiliar, and which can easily be reproduced with a little careful thought, the relationship between the spatial metric, gmn, and the space-time metric, Gmn, is not gmn = Gmn, but gmn = Gmn – G0mG0n/G00.
Therefore, a singularity coincident with the ergosphere is found to occur in the g33 component of the spatial metric (where u3 is the longitude), thereby rendering the standard vacuum Kerr metric theoretically useless as a practical model of a rotating black hole (see my prior missive, “Theory of Black Holes,” apropos my thought on singularities occurring in nature—the mathematical trick I used there to render impotent the singularity in g11 at the Schwarzschild radius doesn’t seem to work here).
Thus, in order to find a practical working model, there seems to be no shortcut except to do the hard work of solving the full, interior problem, including the consequent vacuum solution for the region of space exterior to the rotating dead star. This remains an open problem, but with the assistance of machine computation it is conceptually trivial, as we shall describe presently.
Define the problem in this way for specificity: use spherical polar coordinates where r is the radial distance from the center along a path of constant co-latitude and longitude (therefore g11 := 1). I see no reason to complicate matters by using the hyperbolic elliptic coordinate system chosen by Kerr. The black hole or dead star is assumed to be spherical (density a nonzero constant inside a sphere of radius r = R) and rotating with constant angular velocity w := du3/dt. Because, as we are about to describe, the solution is in terms of Taylor series, there is no a priori reason we cannot use general functions d(r,u2) and w(r,u2) expanded as Taylor series with known coefficients).
At this point, allow me to parenthetically describe the process of “Involution” (W. Seiler, Springer, 2009) for solving any differential equation or system of differential equations in terms of Taylor series and justify it as being just as good (and, for purposes of practical calculation in no way inferior to) finding a solution in terms of “elementary” functions—the obsession for which no doubt contributes to the fact that this conceptually trivial problem has remained open so long. Indeed, this method could be used to solve any problem in any theory of physics and no “open problems” should remain anywhere in the entire discipline of physics, conceptually.
The method is this: expand all known and unknown functions in terms of Taylor series; the known functions have known coefficients, and the unknown functions have unknown coefficients which can be derived recursively by equating the coefficients of like powers of the coordinates, by the standard procedure. See what I mean by “trivial?”
Now some old-fashioned people may object that any sound theory must be construed in terms of “elementary” functions, which are in some sense “known.” Of course, the only elementary functions except for polynomials are the trigonometric, hyperbolic trigonometric and exponential functions—all of which can be reduced to the exponential function, which in turn can be accurately calculated in terms of—guess what?—Taylor series or some equivalent infinite recursive process.
These days, we might regard elliptic integrals as elementary functions and there is an elaborate algebraic theory reducing the evaluation of an arbitrary elliptic function to those of the first, second and third kinds, but no one is interested in this theory any longer—it is simpler to just evaluate in terms of Taylor series by machine computation (the “NI” in UNIAC and ENIAC stand for “Numerical Integrator”—that is why computers were invented!).
Conclusion: computation by machine is just as respectable as any reduction to elementary functions—and there is no escaping the use of machine computation when calculating numerical values of “elementary” functions anyway!
The method of involution is often described as reducing calculus to algebra, because, of course, machine computation must terminate in a finite number of steps and the Taylor series just turns out to be polynomials of high degree. Polynomials are, ultimately, the only functions whose numerical values can be computed in a finite number of steps.
0 notes
Text
[SOLUTION] Physics 396 Homework Set 7
1. In spherical-polar coordinates, the line element on the surface of the two-sphere takes the form dS2 = a2 (d✓2 + sin2 ✓d2 ), (1) where a is the constant radius of the sphere. The Christo↵el symbols can be computed from the metric and derivatives of the metric through the expression g↵ = 1 2 ✓@g↵ @x + @g↵ @x @g @x↵ ◆ , (2) where a repeated index implies a sum over that index. For diagonal line…
0 notes
Text
#o.#math#poll#this is almost all just stuff related to rotation lol#I didn't really have a good intuitive sense of it in high school / early college bc my high school physics teacher sucked#and rotation is harder to think about than linear#taylor series were only somewhat a hate but I didnt understand them. now I can do them in my sleep after taking that numerical analysis clas#s#I'm still bad at matrix multiplication (I have to look it up everytime) so I didn't put that on there but one day. one day.#plus my dad always has to ask me how to do it whenever he needs to do a change of basis at his job so I think I'm justified in it
1 note
·
View note
Text
Physics 396 Homework Set 7 solved
1. In spherical-polar coordinates, the line element on the surface of the two-sphere takes the form dS2 = a2 (d✓2 + sin2 ✓d2 ), (1) where a is the constant radius of the sphere. The Christo↵el symbols can be computed from the metric and derivatives of the metric through the expression g↵ = 1 2 ✓@g↵ @x + @g↵ @x @g @x↵ ◆ , (2) where a repeated index implies a sum over that index. For diagonal line…
0 notes
Text
Physics 396 Homework Set 7 solved
1. In spherical-polar coordinates, the line element on the surface of the two-sphere takes the form dS2 = a2 (d✓2 + sin2 ✓d2 ), (1) where a is the constant radius of the sphere. The Christo↵el symbols can be computed from the metric and derivatives of the metric through the expression g↵ = 1 2 ✓@g↵ @x + @g↵ @x @g @x↵ ◆ , (2) where a repeated index implies a sum over that index. For diagonal line…
0 notes
Text
Derivatives of spherical polar vector representation.
[Click here for a PDF version of this post] On discord, on the bivector server, ‘not a good username’ asked a question that I really liked. It’s a question that nagged me before too, but I hadn’t taken the time to puzzle through it properly. The main character in this question is the spherical polar form of a radial vector, which has the…
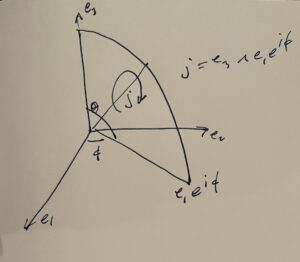
View On WordPress
#bivector#derivatives#Geometric Algebra#partial derivatives#power series#spherical polar coordinates
1 note
·
View note
Text
WhatsApp [email protected] STEREOTACTIC SYSTEM . EASY TO INSTALLON THE OPERATING BED.INDEPENDENT PACKAGING DESIGN, COMPLETEACCESSORIES,EASY TO CARRY. PROFESSIONAL FOCUS ON PROVIDING SKULL SURGERY FRAMECLEAR SCALE LINESALSO EQUIPPED WITH SOFTWARE SYSTEM.The cranial cavity is a limited space. There is a relationship between the position of any structure in the brain and the space of the brain, which can be determined by using the principle of analytic geometric coordinate system. The Cartesian coordinate system is based on the Cartesian principle. Three mutually perpendicular planes are set in the cranial cavity. The x y and z axes of the horizontal, coronal, and sagittal planes intersect at one point. The coordinates of the y and z axes are established; the polar coordinate system is also called the spherical coordinate system, which takes the center of the orientation instrument as the center of the sphere, and any point on the surface of the sphere can be determined by the radius of the sphere and the two angles between the vertical plane and the horizontal plane.
0 notes
Text
even when they talk about the same thing it can be different
genuine warning to anyone taking both physics and math classes:
both mathematicians and physicists use the variables (r, theta, phi) for spherical coordinates. but physicists usually use (r, theta, phi) = (radial, polar, azimuthal) and mathematicians usually use (r, theta, phi) = (radial, azimuthal, polar). the definitions of theta and phi are swapped.
Me in high school: yeah physics and math have a crazy amount of overlap and, you know, in a lot of ways, they talk about the same thing.
Me now, a physics major asking a math major something: I'm sorry what the actual fuck did you just say? What are those words? Why are you speaking like this? Can't you just explain it with numbers?
#if you only encounter spherical in one discipline you'll be fine#but I (physics major/math minor) got turned around quite often when I was studying#i still always make sure to double check which variable is which#physicists mathematicians and engineers can argue all day over acceptable approximations of pi. and i will enjoy that debate#but i wish we could agree on this
808 notes
·
View notes
Text
AHA
MY PROFESSOR SAID IT
MY PROFESSOR SAID ROTATION ISNT INTUITIVE
I AM VALIDATED
#I DONT THINK ANYONE UNDERSTANDS HOW MUCH I HATE ROTATING OBJECTS AND POLAR COORDINATES#SPHERICAL IS SOMEHOW BETTER#BUT WHEN THINGS ROTATE#IT IS DEATH#SO GOING TO OFFICE HOURS AND ASKING ABOUT THAT AND BEING TOLD THAT IS REALLY GOOD#IF IT ROTATES I WANT NOTHING TO DO WITH IT THOUGH
6 notes
·
View notes
Text
Whoever invented Spherical Coordinates had no reason to go that hard.
#who else loves Spherical coordinates?#cartesian and polar lovers don't @ me#math#calculus#i also stan the celestial coordinate system
4 notes
·
View notes