asshole75754 - Tumblr blog

asshole75754 · 3 years

Text

Introduction

Higher-Dimensional Space

The world around us exists in 3-dimensional (3D) space. There are 3 pairs of cardinal directions: left and right, forward and backward, and up and down. All other directions are simply combinations of these fundamental directions. Mathematically, these pairs of directions correspond with three coordinate axes, which are conventionally labelled X, Y, and Z, respectively.

The arrows in the diagram indicate which directions are considered numerically positive and which are negative. By convention, right is positive X, left is negative X, forward is positive Y, backward is negative Y, and up is positive Z, and down is negative Z. We shall refer to these directions as +X, -X, +Y, -Y, +Z, and -Z, respectively. The point where the coordinate axes intersect is called the origin.

As far as we know, the space we inhabit consists of these 3 dimensions, and no more. We may think that space has to be 3-dimensional, that it can’t possibly be anything else. Physically, this may be true, but mathematically, there is nothing special about the number 3 that makes it the only possible number of dimensions space can have. It is possible to have dimensions lower than 3: for example, 1D space consists of a single straight line stretching off to infinity at either end; and 2D space consists of a flat plane, extending in length and width indefinitely. However, nothing about geometry restricts us to 3 dimensions or less. It is quite possible—and mathematically straightforward—to deal with geometry in more than 3 spatial dimensions. In particular, we can have a 4th spatial dimension that lies perpendicular to all 3 of the familiar cardinal directions in our world. The space described by these 4 dimensions is called 4-dimensional space, or 4D space for short.

In a 4D world, there is another directional axis which is perpendicular to the X, Y, and Z axes. We shall label this axis W, and call the direction along this axis the fourth direction. This new axis also has positive and negative directions, which we shall refer to as +W and -W.

It is important to understand that the W-axis as depicted here is perpendicular to all of the other coordinate axes. We may be tempted to try to point in the direction of W, but this is impossible because we are confined to 3-dimensional space.

Why Bother?

Why bother trying to visualize a higher-dimensional space that we can neither experience nor access directly? Besides pure curiosity, 4D visualization has a wide variety of useful applications.

Mathematicians have long wondered how to visualize 4D space. In calculus, a very useful method of understanding functions is to graph them. We can plot a real-valued function of one variable on a piece of graph paper, which is 2D. We can also plot a real-valued function of two variables using a 3D graph. However, we run into trouble with even the simplest complex-valued function of 1 complex argument: every complex number has two parts, the real part and the imaginary part, and requires 2 dimensions to be fully depicted. This means that we need 4 dimensions to plot the graph of the complex function. But to see the resulting graph, one must be able to visualize 4D.

Einstein’s theory of Special Relativity postulates that space and time are interrelated, forming a space-time continuum of 3 spatial dimensions and 1 temporal dimension. While it is possible to visualize space-time simply by treating time as time and examining “snapshots” of space-time objects at various points in time, it is also useful to treat space-time geometrically. For example, the distance between two events is the distance between two 4D points. The light-cone also has a particular shape that can only be adequately visualized as a 4D object.

Furthermore, Einstein’s theory of General Relativity describes curvature in space-time. While it may not actually be a curvature into a physical spatial dimension, it is helpful to visualize it as such, so that we can see how space curves in 4D as a 3-manifold. If space in the universe had positive curvature, for example, it would be in the shape of a 4D hypersphere—but what exactly does that look like?

Many other interesting mathematical objects also require 4D visualization to be appreciated fully. Among them are 4D polytopes (4D equivalents of polyhedra), topological objects such as the 3-torus and the Real Projective Plane which can only be embedded without self-intersection in 4D or higher, and the quaternions, which are useful for representing 3D rotations. It is difficult to fully appreciate these objects without being able to see them in their native space.

Is it possible to visualize 4D?

Some believe that it is impossible for us to visualize 4D, since we are confined to 3D and therefore cannot directly experience it. However, it is possible to develop a good idea of what 4D objects look like: the key lies in the fact that to see N dimensions, one only needs an (N-1)-dimensional retina.

Even though we are 3D beings who live in a 3D world, our eyes actually only see in 2D. Our retina has only a 2D surface area with which it can detect light coming into our eye. What our eye sees is in fact not 3D, but a 2D projection of the 3D world we are looking at.

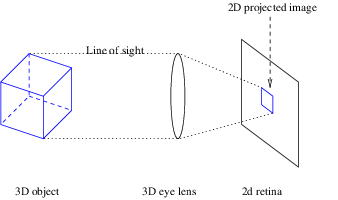
In spite of this, we are quite able to grasp the concept of 3D. Our mind is quite facile at reconstructing a 3D model of the world around us from the 2D images seen by our retina. It does this by using indirect information in the 2D images such as light and shade, parallax, and previous experience. Even though our retina doesn’t actually see 3D depth, we instinctively infer it. We have a very good intuitive grasp of what 3D is, to the point that we are normally quite unconscious of the fact we’re only seeing in 2D.

Similarly, a hypothetical 4D being would have a 3D retina, and would see the 4D world as 3D projections.

It would not directly see the 4th dimension, but would infer it using indirect information such as light and shade, parallax, and previous experience.

The key here is that what the 4D being sees in its retina is 3-dimensional, not 4-dimensional. The 4th dimension is inferred. But since we have a good intuitive grasp of 3D, it is not that difficult to understand what a 4D being sees in its retina. From there, we just need to learn how to infer 4D depth.

The rest of this document will describe in detail the basic principles of 4D visualization, as well as provide a number of examples of 4D objects. We shall take a purely geometrical approach and treat all 4 dimensions as spatial dimensions.

Dimensional Analogy

A very useful tool in exploring 4D, or higher dimensions in general, is dimensional analogy. Dimensional analogy is the process of examining how a particular geometric feature in a lower dimension relates to an equivalent geometric feature in our dimension, and then applying the same principle to relate our dimension to a higher one.

Let’s examine a few examples to see how this works.

Boundaries of Objects

Let’s begin with the very basics. Let’s start in a 1D world. The 1D world is like a piece of string. There is only one axis along which one may move along this string, the X-axis. The only dimension any object can have is length, because there aren’t any other dimensions to accomodate width or height. So the only possible objects in 1D are points, which are 0D, and lines, which are 1D.

In order to completely specify a line segment, it is enough to specify its starting point and its ending point. In other words, the boundary of an object in 1D consists of points, which are 0D.

Now, let’s move to the next higher dimension. The 2D world is a plane, like the surface of a piece of paper, but extending indefinitely in width and length. The 2D world is much more interesting than the 1D world, because a much larger variety of objects are possible. For example, we can have polygons and circles, in addition to points and lines:

What is the boundary of a polygon? A polygon is bounded by line segments, which are 1D. A circle also has a 1D boundary: even though it is a curved boundary, it is fully specified by a single parameter: angle. So 2D objects are bounded by 1D lines and curves.

Now let’s move on to the 3D world. Objects in the 3D world are bounded not by lines or curves, but by 2D surfaces. For example, a cube is bounded by 6 squares, and a ball is bounded by a spherical surface. The spherical surface is 2D, because any point on the sphere is fully specified by only two parameters: longitude and latitude.

We can see a pattern emerge here. Objects in 1D are bounded by 0D points; objects in 2D are bounded by 1D lines (or curves); and objects in 3D are bounded by 2D surfaces. In other words, points in 1D are analogous to lines and curves in 2D: they form the boundaries of objects in the respective dimensions. Similarly, bounding lines and curves in 2D are analogous to surfaces in 3D. So, by applying dimensional analogy, we see that in N dimensions, objects are bounded by (N-1)-dimensional boundaries.

This leads us to conclude that in 4D, objects are bounded not by points, lines, nor even surfaces, but volumes. It would be rather difficult to realize this without applying dimensional analogy. For example, as we shall see later, a 4D cube is bounded by 8 cubes. We call these bounding volumes the cells of the 4D cube.

Vision

Another application of dimensional analogy that has been mentioned before is the dimension of the retina in the eye of an N-dimensional creature. We are 3D beings, yet our eyes only see in 2D because our retina is only a 2D array of light-sensitive cells.

Why are our retinas only 2D? Surely it would be much better for us to have a 3D retina, so that we can see every part of our 3D world simultaneously?

The reason is that in order for us to see something, light must have an unobstructed path from that thing to the cells in our retina. A 2D retina works, because there is a 3rd dimension in which the light can travel unobstructed from the object onto the retina. However, if our retina were 3D, we would not see anything more, because light must pass the cells on the outer surface in order to reach the inner cells, so that what the inner cells see has already been seen by the outer cells. Since we are confined to 3D, there is no additional dimension in which light may travel to reach these inner cells by an independent path, which might have given us additional visual information.

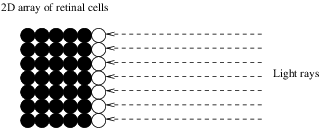
This fact leads us to conclude, by dimensional analogy, that a 2D creature must only have a 1D retina. As the diagram above shows, when a creature is confined to 2D, there is no unobstructed path for light to travel from a 2D object to an inner cell in a 2D retina. Any light that reaches an inner cell has already passed an outer cell, so having a 2D retina would not help the creature to see more.

We can also conclude by dimensional analogy that in 4D, it is possible to have a 3D retina, because there is now an extra dimension in which light can travel unobstructed from the object being seen to any point on the retina.

We shall make much use of dimensional analogy to understand 4D in the subsequent discussions.

On the Nature of Vision

Since we’re interested in visualizing 4D, let’s take a more careful look at vision itself.

A Deficient Vision

As mentioned in the previous chapter, we 3D beings have a 2D retina, whereas a hypothetical 2D being only has a 1D retina. We are able to see the entirety of a 2D image, whereas a 2D being can only see a 1D projection of it at a time. For example, when we look at a square, we see this:

Since a square is a 2D object, and 2D beings are obviously familiar with 2D objects, we may think that this is how a 2D being would see a square, too.

However, when a 2D being looks at the same square, it actually sees only this:

This thin line is actually the square viewed edge-on. This is the only view the 2D being can have of the square, because it is unable to leave the 2D plane and observe the square from a 3D point of view.

When we 3D beings look at the square from our 3D vantage point, we can see all 4 edges of the square and all 4 corners at the same time. But the 2D being can see at most only two of the square’s edges. It would need to walk around the square and look at it from different angles before it can see all 4 edges and all 4 corners.

Furthermore, it may not be able to tell from a single glance whether something is a square or something else, say a pentagon. It may be able to infer the 2D slope of the edges from the way light falling on the edge illuminates it, and, by doing so for each of the edges, infer that they are meeting at right angles, and thus deduce that the object is likely to be a square. However, it would need to walk around the object and look at it thoroughly before it could be sure that it’s a square and not some other shape.

Why is this important?

The Appearance of Diagrams

This seemingly trivial point has far-reaching consequences when learning to visualize higher dimensions. To see why this is so, consider how we 3D beings may try to explain what a cube is to a 2D being. We may try to draw a diagram of a cube, thus:

Since this diagram can be entirely contained in a 2D surface, we may imagine that the 2D being would see it as we do: a hexagon with three lines within, meeting at the center. However, this is what the 2D being actually sees:

If you look at this line very carefully, you will notice subtle variations in shading, based on which the 2D being can tell the edges apart. At most two or three of the outer edges of the diagram can be seen at a time. Even after walking around the diagram and looking at it from every angle, the most the 2D being can discern is that the diagram is a hexagon: it cannot see the three edges inside the diagram at all!

To help our 2D being see the entire diagram, we would need to erase parts of the edges so that it can walk into the hexagon and explore the 3 quadrilateral “rooms” within it, thus forming a kind of mental “floor plan” of our diagram. Alternatively, we would have to construct the outer edges of the hexagon with some semi-transparent material, so that the 2D being can see through it and discern the 3 inner edges.

In other words, what is to us an obvious diagram of a cube is far from obvious from the 2D being’s point of view. We see the diagram of the cube from our “overhead” 3D point of view, and can see every part of it simultaneously. The 2D being has no such luxury; it has to painstakingly explore each part of the diagram separately, and concessions such as holes in edges through which it can pass, or transparency in some of its edges, must be made in order to ease this process.

Floor Plans

Why should we care about a hypothetical 2D being’s deficient vision, since we 3D beings do not suffer from such crippling limitations? This is because a similar situation applies to us when we attempt to visualize higher dimensions.

As we begin to explore the methods of visualizing 4D, we will be making much use of 3D diagrams and images that depict higher-dimensional objects—much like our diagram of the cube above is a 2D depiction of the cube, not the 3D cube itself. However, we can’t draw 3D diagrams on a 2D computer screen, and even if we could, our eyes can only see a 2D representation of them at a time. So we are in a similar situation to the 2D being looking at a 2D diagram: we can only see a 2D representation of the 3D diagram, not the 3D diagram itself.

This point is vitally important to keep in mind as we begin to explore 4D visualization. The 2D images we will see may depict some 3D construct; it is crucial not to conflate the 2D images with the 3D construct that they are intended to convey. The 2D being looking at our diagram of a cube sees only a single line, which is of no help in understanding what a cube is. Similarly, a mere 2D image for us is of no help in understanding higher-dimensional objects either.

What is needed, in the case of the 2D being, is to explore the diagram thoroughly, and form a mental picture of the “floor plan” of the diagram, so to speak. It is this mental floor plan—a hexagon with three edges inside it, or rather, a hexagon made of three adjoining quadrilaterals—that gives the 2D being a glimpse into the nature of the cube.

Similarly, when we look at 2D representations of 3D diagrams, we need to understand that the 2D images themselves are not an adequate depiction of the higher-dimensional object. What is needed in our case is to form, in our mind, a “3D floor plan” of the 3D diagram being conveyed by the 2D images. It is this 3D mental model, not the 2D images themselves, that gives us a glimpse into the nature of the higher-dimensional object. Merely staring at the 2D images, as compelling as they may be, will not magically cause us to see 4D.

Keeping this in mind, let us now begin to look at some of the tools by which we may study the 4D world.

Cross-sections

Using Cross-sections

Since we are creatures confined to 3D, we have no way of directly exploring higher-dimensional objects. We can, however, employ various indirect means to study and understand them. One method is to intersect a higher-dimensional object with our world to see what its various cross-sections look like.

To illustrate this, let’s apply dimensional analogy again. Suppose we are only 2D beings, living in a 2D world, and unable to see into the 3rd dimension. Suppose we’re trying to understand what a cylinder is. We know what circles and squares are, because these objects exist in our 2D world and we can directly handle and see them. But we haven’t the slightest idea what a cylinder might be. We have no way of directly seeing such an object, because our retina is only 1D, and a 2D retina is needed to adequately perceive a 3D object. What we can do, is to examine what happens when a cylinder passes through our 2D world:

As the cylinder does this, we can observe its cross-sections with our planar world. For example, if the cylinder descends through our world vertically, we would see a series of circular cross-sections, all of a constant size.

Now, as we have mentioned in the previous chapter, 2D beings cannot actually see the above image directly; they can only see the circular cross-sections from the side. The cross-sections will appear as line segments that show curvature from the way they interact with nearby light sources. Nevertheless, it is reasonable to assume that, as diligent 2D beings trying to understand 3D, we will, through careful study of these cross-sections from various angles, eventually form a mental model of these cross-sections that more-or-less corresponds with what is depicted above. For the sake of conciseness, we will continue to present these 2D images as they would appear from 3D; however, it is to be understood in each case that 2D beings can only imagine such diagrams in their mind after careful study.

In any case, from these circular cross-sections, we may conclude that the cylinder must be something circular.

We can also observe the cylinder passing through our world in a different orientation:

This time, the cylinder passes through round-side first. What we see is a series of rectangular cross-sections that seem to grow and shrink in length but remain constant in width. From this, we conclude that the cylinder must have something rectangular about it.

Thus far, we learned that a 3D cylinder is something that is both circular and rectangular. This is obviously correct. Examining cross-sections has yielded valuable information about the shape of a cylinder.

A Fundamental Weakness

Now, still supposing we are only 2D creatures, we have a hard time understanding how something can be both circular and rectangular at the same time, as we’ve just learned. As 2D creatures, we only have experience with 2D shapes, and none of them are simultaneously a circle and a rectangle. We may try to investigate this further by observing the cylinder pass through our 2D world at a 45-degree angle:

The cross-sections are now rather puzzling:

They consist not of regular circles or rectangles but of ellipses in various states of truncation. Unless we knew beforehand, we would probably not be able to deduce the shape of a cylinder from these cross-sections. We may even think that these are cross-sections of a different object altogether.

This illustrates a fundamental weakness of the cross-sections method: although it does yield some useful information, it is difficult to synthesize this information into a coherent model of the actual object. For example, if we only knew the above sequence of cross-sections of the cylinder, it would be rather hard for us to deduce that a cylinder has two circular lids and a curved side.

The following sequence of cross-sections further illustrate this weakness:

Can you guess what 3D object would produce this sequence of cross-sections?

Probably not, unless you knew it beforehand.

These are, in fact, cross-sections of the 3D cube, which are produced when the cube passes through the 2D world corner-first. It is rather difficult to know this just by examining these cross-sections alone; information about the object such as the number of vertices (corners) and the number and shape of its faces are not readily apparent. Most people probably don’t even know that a cube can make a hexagonal cross-section with a plane!

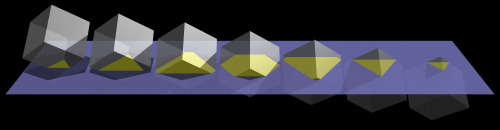
Now, as 3D beings, we at least have some knowledge of 3D geometry to be able to imagine the cross-sections stacked on top of each other, and perhaps deduce a vaguely cube-like shape from them. But consider the following sequence of cross-sections of a 4D object with 3D space:

Can you figure out what the 4D object is?

Likely not, unless you knew it beforehand, since you would have a hard time understanding just how these cross-sections could fit together. Without an intuitive grasp of 4D, it is very hard to reconstruct the original object from them.

The fundamental problem with cross-sections is that we are examining the object piecemeal. Important features such as the number and shape of facets, the number of vertices (corners), and the overall shape of the object, are only implied, not explicit.

A better approach is to use projections, as we will discuss in the next chapter.

137 notes · View notes