coconut2877-blog

[coconut2877-blog]

12/16/2019 a closed loop :)

In preparation of the break, Vincent and I finalized the framework of our data-driven experiments. We were able to link the two initially separate experiments and form a beautiful closed loop. 

Components/rational of the work:

Exp 1. retrieve sounds from neighbors

Goal: Interpolate the sound of hitting at one particular point on a drum from sounds of its neighboring points.

Methodology:

- 4-point interpolation

- Use scattering transform as a bridge to interpolate raw audios from neighboring raw audios. number of scales J is a hyperparameter here to see what is a good scale that has a good leverage between frequency and time resolution that recovers both timbre and the temporal envelope of sounds.

- Create Laplacian heat map for all the points on the drum surface. This should be done for spaces formed by both Scattering transform and Fourier transform for comparison purposes.

- Retrieve raw audio from scattering space by regression and gradient descent. A few gradient descent schemes and choices of cost function (Mean square error vs. cross-entropy ) can be explored here. One optimal scheme would be chosen in the end to proceed with the rest of the experiments.

- To evaluate how good the sound retrieval is: 1. compare with the ground truth sound synthesized at the point, by listening. 2. use exp. 2′s wave2shape model, see if it can retrieve the correct physical parameters. 

Rationals:

- Scattering transform transforms quantities from nonlinear (raw audio) spaces to linear spaces (scattering). 

- Direct interpolation in nonlinear spaces is a much harder problem, as common distance metrics do not always work. e.g. Averaging two audio waveforms doesn’t mean anything - if you want some audio that’s right in the “middle” of a sine wave and a cosine wave, interpolation by averaging gives you zero!

- As a result, to interpolate quantities in the nonlinear space (raw audio space), an equivalent interpolation in scattering can be made with simple linear interpolation, and then be transformed back to raw audio. 

- Linear interpolation can only be done in spaces that follows a euclidean distance metrics. Theorem proves that scattering transform possesses this property, whereas some other transformation don’t, for example Fourier transform.

- A Laplacian close to zero at the interpolation point is an extra precaution to ensure credibility of the linear interpolation approach. It quantifies how “curved” the space is, and decides if the linear interpolation between four neighboring points would overlap with the point of interest.

Contribution:

- This experiment is a way of verifying Scattering transform’s ability of preserving the topology in nonlinear raw audio space. 

Exp 2. retrieve shapes from sounds

Goal: Learn the underlying physical parameters of sounds synthesized with my physical modeling tool.

Methodology:

- Dataset of synthesized percussive sounds sampled by varying Theta (length 5 vector of physical parameters) and excitation places. A few variations of training sets can be made here to expose the model to different sounds

       -  train on sounds from exciting only one spot of the drum, test on other spots

       -  train on sounds from a variety of shapes (while leaving a few shapes out), and test on the shapes that’s left out

       - train on everything

Model: Fully Convolutional Neural Network

- number of layers ~ log(n), where n is number of scattering coefficients

- choice of kernel size

- follow the common practice of 1 convolutional layer + RELU + pooling

The loop

Over the break:

1. Heat map

2. Make dataset

3. Build the CNN model

4. Start training if possible.

[coconut2877-blog]

12/2/2019 Q&A on scattering transform

The week of thanksgiving, I submitted my abstract to FA2020 and sat down with Vincent for a session of Q&A on scattering transform, the key question being - why Morlet wavelets are able to capture higher-resolution information of transient sounds while normal spectrograms cannot. 

Combining Vincent’s explanations and looking at the textbook  “A Wavelet Tour of Signal Processing” by Stéphane Mallat, I summarized the following:

To extract the key information in these notes:

1. normal Fourier transform results in uniform/regular time-frequency bins in the spectrogram, while scattering transform results in a T-F bin layout that is stretched out in time at lower frequencies, but highly condensed in time at high frequencies. (refer to top of the second image)

2. When extracting information from audio signals using spectrograms as a medium, we want as much high resolution info as possible. A way of thinking about spectrograms is to view them as pixelated summary of info. The more pixels in one area the more fine-grained it is. We want our sounds, when being represented in this form, to fall into as many “pixels” as possible. 

3. Transient sounds are usually of high frequency, and short in time. To capture the characteristic of this “chirp”, fitting it into a T-F layout that is too coarse for its total time length can result in a “smearing out” of information. We don’t want a short sound to fall into only one T-F bin, the end representation would be an average in time/frequency, an averaged timbre. 

4. Thus, we propose to use wavelets as basis and perform scattering transform, where basis are being referred to as scales. They create a T-F layout whose resolution can be “adaptively chosen”, and thus provide a better framework to represent transient audio signals.

[coconut2877-blog]

12/9/2019 interpolating sound of a drum

This week consists of an inspiring talk and some progress on my first data-driven experiment - interpolating sound of a drum.

MARL talk by Stephon Alexander

Stephon Alexander is a theoretical physicist and jazz musician, he came to NYU last week for a MARL talk on the topic of Physics and Sound. Bearing in mind the difficulty to present a rather abstract topic to the general audience (even though in his case the audience are already people in the musical research field), I particularly marveled at his storytelling techniques. He started off with the notion of symmetry in physics/general science - equations, electromagnetic theories, electron spins, time-space reversal symmetry, DNA/RNA pairing sequences. He touched on symmetry between studies of physics and musical tones - physicists like Kepler discovered laws of planetary movements based on musical tones. He was able to define abstract concepts using graphic metaphors. The transformation invariant in math can be shown through folding and rotating a piece of paper while keeping it looking exactly the same. His own work - spiral arrays, a geometric representation of musical scales, is introduced through something every music people is familiar with - circle of fifth. He then used this familiar image, expanded it into 3rd dimension, 4th dimension, to show that the music scale relations still persist. 

His talk was abstract from the start to end, but still interesting enough to keep us focused. I thought about my own research and the symmetric philosophy within it, how I can convince people that a mutual translation between shapes and sounds is a beautiful thing to pursue, how a inverse problem is worth investigating even if no instant real-world applications can be said.

Progress on interpolating sounds of a drum

Through guidance of Vincent, I started experimenting with the Kymatio library - a scattering transform computation library. We were able to perform a preliminary proof-of-concept experiment that recovers percussive sounds from the interpolated scalograms. More research on optimization problems when recovering sounds from scalograms is planned. Meanwhile, it’s important to note some of the assumptions we made in this experiment and realize their limitations. 

Nuances:

- In scattering transform, a few analogies can be made with a standard short time fourier transform (STFT), in order to get more intuition on the time-frequency duality. In STFT there are the notions of window size, time resolution and frequency resolution. In scattering transform, there's the notion of J = number of scales in the scalogram, indicating number of coefficients to represent each time bin, and determine the window size w = 2^J. As a result, bigger J gives more frequency resolution, whereas smaller J gives more time resolution. In the preliminary experiment of recovering sounds from scalograms, using a smaller J recovers the time-dependent decaying envelope pretty well but struggles to capture the timbre, while using a big J results in an averaged out “timbre cloud” in time without any particular shape. Ideally we want a J in the middle that can recover both the sound and texture. 

- Recovering sounds from scalogram has no direct functions implemented like inverse Fourer Transform, instead the process is done iteratively by initializing a random time-domain vector and perform gradient descent on the error between its scalogram and the real scalogram you want to recover. Our preliminary experiment is done with the simplest formulation possible - cost function as mean square error and a standard gradient descent algorithm. The next step would be to try other cost function, add momentum, bold driver, and other deep learning optimizer algorithms to improve the process. 

- Complications on topology: our “interpolating sound of a drum” experiment is based on an implicit assumption - laplacian of scattering transform on a particular point on the drum being close to zero. In other words, only if topology in SC domain is flat would interpolating from adjacent points be valid. If the SC space is curved and we are interpolating mid point from its 4 adjacent points, the average of 4 adjacent points might not coincide with the mid point. Thus the more curved, the more inaccurate this interpolation would be. 

[coconut2877-blog]

11/25/2019 organizing thoughts and connecting dots

Scalograms

This week I was guided to take a more in-depth look at scattering transform (wavelets), an alternative data representation of transient sounds. What are the mathematical forms of the basis we will be using - Morlet wavelets, how to go from audio in time-domain to “scalograms” spanned by these wavelets. 

From my interpretation, our goal is to interpolate phase, amplitude, and modal information of a given audio signal. However, percussive sounds are often short, with decaying amplitudes, and localized in time. Instead of using fourier transform, where the basis is sinusoids, we propose to use scattering transform, where we use alternative basis “wavelets” that are localized in time and are more sensitive to temporal changes. There are multiple ways of defining the wavelets, depending on how the mathematical norm is defined. We proceed by taking fourier transform of the audio signal, pass through filter bank of Morlet wavelets, and get scalograms (coefficients of wavelets that represents the audio). Similarly, audio signals can be reconstructed from the spectrogram reconstructed by scalogram. 

Experiment 1 - interpolate sound of a drum is postponed to the following week because of this much needed crash course on scattering transform.

Feedback from Katherine

I talked to my teacher from creative coding Katherine Bennett, about the conceptual and visual aspects (in the sound synthesizer) of my thesis. She reminds me of the conceptual complexity in my plugin tool, and the demanding expectation thrown at users to grasp it instantly through a digital interface. She encouraged me to expand the tool into an experience, that people can feel or touch, and influence the making in more straightforward ways. 

I realized the tool’s complexity when I was designing the 3-step instruction, and that it’s still cumbersome for a plugin to have multi-step instruction. I have decided to disregard that for now, build the technical functionalities first, incorporate as much flexibility (in excitation and materiality) as possible, and worry about building experience next semester.

Connecting the dots

This week I’m also preparing to talk about what I do in accessible terms. I realized the importance of visual hints and analogies, both from ITP student’s thesis presentation and my classmates’ feedback. I put together a slide to go over with Kat next week. Meanwhile, I took sometime to organize what I did so far, to think about how to make sense of it all.

Here is how I connected the dots/outline of my slides:

Theme: Translation between physical objects and sounds they make

physical objects  -> what sound

1. what is physical modeling

2. how does the FTM work

3. How does my tool work

sound -> what physical object

4. [regarding data driven approach] what is data-driven approach

- motivation: not because the machine can learn/solve everything, but because viewing things as data gives rich representations, new problems to look at, new ways of evaluating sounds

- Finding representation that captures essence of the audio is important to training any machine learning model

5. preliminary experiment 1 - interpolating sound of a drum

be aware that the same thing can have multiple representations

same with data in mathematical world. The interesting thing about these different representations is that - there’s topology within it. different things in the same representation can be close and far. 

this experiment looks at sounds in different representations, see if closeness in one topological space implicates closeness in another. If this work, then knowing something in one space will lead to knowing the same thing’s representation in another space.

(I think) this is in a way an evaluation of the physical modeling algorithm as well - does it capture positional excitation as well as one expects. how sensitive is this formulation to varying excitations

6. experiment 2 - hearing shape of a drum machine

- input: sounds 

- output: modal information

- this model itself fits sound into a modal formulation of percussive sounds

- implicitly reflect shapes of the drum

[coconut2877-blog]

11/18/2019 experiments on transforming to and from abstract representations

Continuing last week’s experiments on sampling a dataset that has even coverage on 5 of the physical parameter spaces in my algorithm - tau, omega, p, dispersion, alpha, my mentor Vincent and I came up with a rough plan for the following experiments throughout the year. We have decided to submit our abstract for the FA2020 (Forum Acousticum) workshop in Lyon, deadline on Dec.1. 

In this blog I’ll first document a visual representation of dataset I collected, and then present the continuing plans. 

Below are visual representations of my validation set - 

Each dot represents one sample projected onto the corresponding 2D parameter space. x and y axis are all bounded to the range I've selected for each parameter. As shown in the diagram, validation set is carved from the middle of the total parameter space, training and test set would be falling into rest of the space surrounding it. It’s common in machine learning to design the dataset in such a topology, as the model needs to learn from the “peripheral” of a dataset, and eventually use what it already learned to “fill up” the center. 

Following experiments with data:

The overall picture is that we have a working physical modeling (using Functional Transformation method) sound synthesizer, and two experiments to carry out  -

1. fix shape of the drum, probe sounds synthesized at different excitation points on the drum, and investigate if we are able to interpolate sound of the drum from neighboring locations, using scattering transform. 

2. vary drum shapes, train a neural network to learn the wave to shape mapping, via a scattering transform as shallower layers.

Both would be evaluated by sonification and or shape comparisons.

For the past week I implemented a python script for the first experiment, in which it takes a position of excitation, and outputs the sound synthesized at this point. For our next meeting on Wednesday, Vincent and I would experiment with Kymatio - a scattering transform python library with convenient visualization and investigate if plan 1 work as we expected. 

[coconut2877-blog]

11/11/2019 algorithms

This week I did some calculations and implemented in python both the difference equation (version A) and impulse response (version B) synthesis algorithms. Since both need pre-calculations of the modal/decay rate information, computation time is very similar. In python version A even takes more time than B. Unsure if it’s still the case in a real-time audio stream, I’m going to implement it in C++ the following week and test it out. At the same time, version A and B with same parameters yields the same timbral info, however pitch and decay rate is a little bit off. I’ll investigate this problem between the two algorithms meanwhile. 

version A with delta function excitation worked out on paper

version A with fancy excitation

waveform of version A vs. B : a little bit off in decay rates and pitch, but following roughly the same timbral envelope.

At the same time, I started fabricating my dataset for machine learning model. Details can be seen in the following jupyter notebook screenshot.

[coconut2877-blog]

11/3/2019 GUI refinement and from sound to shapes

This week I implemented my initial GUI idea, and got insightful feedback from my music tech friend Ray, who is also an experienced music producer. With his suggestions I discovered an unusual direction to push towards with this plugin.

I also had my first official meeting with Vincent and he guided me through figuring out a plan for my inverse problem, using machine learning.

GUI refinement and feedback:

Above is the new GUI I implemented. On the left side are parameters corresponding to sound qualities; on the right are visualizable parameters, which simultaneously control the lower graphics. Center of the graphics is a “string” with length and thickness represented as width and height, density as how dense the checkerboard fillings are, and tension as how red the string is (blue being a looser string). 

The user would change parameters on the left to achieve sounds they like, choose the dimensionality of the object, base length of the object, and two out of three among “density”, “thickness”, and “tension” (Not implemented in the GUI yet.) And then see how the remaining one visual parameter change (both through graphics and the slider) when tweaking the sounds. 

Though I wish i have a more impressive/straightforward tool that spits out a compelling visual difference whenever making a different sound, under real world scenarios “one cannot hear the shape of a drum”. Instead, at least with my physical model (and verified by Prof. Selesnick), you hear the leverage between spatial dimensions and materiality of the object. Not as visually satisfying as a one-on-one mapping from sounds to shapes, but the sound-> shape relationship is still non-trivial. It is left for me to design a GUI that explains the philosophy in an efficient way.

Feedback from Ray:

I told Ray about my plugin and the visualization component. He pointed out that because of the relationship between sounds and the lower graphics, the graphics would be a nice distribution codec. 

“It’s so hard to describe sounds, especially timbral qualities. As producers there are great needs to send friends sounds you fabricated and liked, and more importantly give them instructions on how to replicate that sound. Something like your lower part graphics would be a fun and easy alternative audio codec to distribute, as long as you can recover the sound by drag and dropping this visual codec onto your plugin.”  

This functionality is definitely an interesting one to explore, I would look into visual codecs and the possibility of deciphering them once I come to later stages of prototyping.

From sounds to shapes

Following would be my workflow of solving the inverse problem from sounds to shapes.

1. Define the inverse problem as having an input vector theta (sound parameters) times an unknown matrix A, yielding the output vector y (sound signal). The inverse problem would be solving for A inverse times y. Alternatively it can be conceptualized as knowing the decoder (theta -> y), trying to find the encoder (y -> theta)

2. Create dataset: Randomly sample theta to fabricate ~100k sound samples, using my FTM sound synthesis tool. Need to make sure a clear division between training and validation sets. 

3.  Use “scattering transform” (wavelet scalogram) to remove invariance and extract features of the sound signals.

4. Feed features into some neural network, choose cost function (most likely mean square error of the predicted theta and ground truth theta plus some regularization terms), back propagate and update parameters of the neural net through minimizing the cost. 

5. Obtain model that transforms sound signals to sound parameters theta.

Nuances:

Sound signals y are usually the convolution of excitation(player) and impulse response of the object (instrument), varying excitation with the same object may yield drastically different results. It’s important to disentangle variability accounted by players from that of instruments, when dealing with more complex models. But for now, assuming excitation to be of the same type might suffice, to gain insight on the inverse model. It would definitely be a future research direction.

Next week I’ll focus on debugging difference-equation implementation of FTM on python, to allow for both less glitchy plugin implementation and quicker way to fabricate my 100K dataset.

[coconut2877-blog]

10/27/2019 the week of revelations

It’s been a week full of interesting conversations and exciting opportunities. I attended DCASE 2019 as a volunteer and got wonderful feedback from people in the world of musical information retrieval/sound events detection, most importantly found myself a mentor in MIR. I also refined my visualization design goal, which I would explain in detail in the following paragraphs.

Progress in designing visualization:

Before I was formulating the question as - recover parameters that i can visualize, and then make a GUI that let users tweak those visual parameters to get different sounds. However, i found this process a bit straightforward, and does not quite qualify as a thought experiment. I spent long hours trying to get the re-parametrization sound right (and realized that my original model assumed a lot of physical properties while synthesizing the sound, which makes sense since the stress is on timbral rather than physical qualities). Especially after a great conversation with my peer Jessica, I realized that some of the steps I include in this researching/prototyping process is “for the sake of completion”, or for the sake of being rigorous while not conveying much interesting aspects. For a sound generating tool, visual aspects are often times secondary. Asking users to spend time changing shapes in hope of getting a sound they want is not as rewarding as making the sound available first, and then prompt them into thinking about what it might look like.

So then I reformulated my visualization design goal - the sound parameters would remain the same, but while tweaking the sound parameters, users may see the changes in visualization. I reexamined the parametrization, hoping to find a relationship between sound qualities and shapes. Not to my surprise, this relationship is not a one-on-one mapping. In other words, one sound may correspond to millions of possible shapes/materials. The visualization is an under-determined inverse problem!

After some messy calculations shown above, I found that:

In order to fully determine the visualization of a given sound, length of the string and two of three parameters - density of material, cross sectional area, and tension in the string, needs to be defined. And I leave these choices to the users.

To summarize my design decisions, users may first pick a sound (from tweaking sound parameters), then choose a shape (length), and finally choose to fix two of three physical parameters(density+cross-sectional area, density + tension in string, or cross-sectional area + tension). The remaining one visualizable parameter would be changed (visually) accordingly.

By design, this GUI is meant to not only enable flexible/natural sound synthesis, but also inform users on how to interpret them in relations to their shapes.  Some takeaways may include :

-  Knowing the fact that to fabricate one desired sound, there would be infinite physical possibilities. 

- In order to fully determine the solution/“sounding object” of this underdetermined inverse problem, how many variables we would have to know in advance.

etc.

My baby String model is now completed on the sound part, I would implement the GUI according to one of the hand-written notes attached above.

Inverse Problem:

This is related to the second part of my thesis - Recover physical parameters of the sounding object from the sounds it makes. My initial thought was to use a machine learning approach. I talked to post doc in MARL lab Vincent Lostanlen about this, and he agreed to start an independent study with me on this topic!

Here are some of my afterthoughts after meeting him and a few other people at the conference (peer in music tech Sri, MARL Phd student Tom, Professor Mark Plumbley from Queens Mary University):

- There would be two parts of investigating this inverse problem: one is data-driven and the other is timbral-driven. 

- Data driven: given a sound, train a supervised machine learning model to recover parameters in my physical modeling formulation. Dataset (sound and its parameters) needs to be constructed using my sound synthesis tool. Vincent also suggested the addition of noise and reverberation on my sound samples in this approach. (This would also be my final project for MIR class.)

- Timbral driven:  analyze and visualize the “topology” of sounds made with my physical model. By topology, I roughly interpreted as orderly placing (order determined by keeping all other variables fixed and changing only one)all the sounds I’m able to generate using this tool, visualize the “distance” between adjacent sounds, and find its relationships between the “distance” in the physical space. Writing this down I have to say it’s sort of making sense but not quite. As mentioned in the last post I did want to evaluate the ability/complexity of this physical model as a sound synthesis tool. I did not expect to enter the realm of abstract mathematical spaces. However whatever legitimate approach is out there I am willing to explore under mentorship of great people in this field, just a few floors above me.

- The above timbral driven approach often times involves using something I’ve never done before - unsupervised machine learning (finding implicit patterns/invariance in data without labels). or Manifold learning, as Vincent mentioned.

- Vincent introduced me to Mark and a similar study he conducted in 2013 - “Hearing the shape of a room”, where Mark is solving the inverse problem of room impulse response, rather than in my case, impulse response of an object. Mark gave us a very abstract lecture on defining the “space” we’re searching for when recovering the sound->shapes mapping. He told us “you want to search on a bigger subspace as the smaller ones have discontinuity at the boundaries!” Then he picked up a DCASE flyer, folded it to a quarter of its size and showed us that sounds triggered at any point on the surface may be mapped to within this one quarter surface, through rotating and flipping this space. He also animated the different ways of “transforming” this flyer space so that “discontinuity may be avoided”. I felt very lost but inspired. I don’t know what to say so I attach here the notes Vincent drew, under the light of two men’s intelligence. 

[coconut2877-blog]

10/19/2019 inspirations and visualization continued

A few highlights of the week

- Attended 147th AES conference and met Dr. Tamara Smyth, advisor of Jennifer Hsu’s PHD dissertation I just read about last week. Sat through her paper presentation (also very relevant to my research) and got to introduce myself to her. Discovered a paper in the poster session, on machine learning approach to modal synthesis, coadvised by Julius O Smith. This also ties into the MIR portion of my thesis. 

- Derived a rough formulation of the second-order recursive filter (rather than an impulse representation) for my FTM string model, have to verify with Prof. Selesnick next week. If this is correct, this filter can be implemented in JUCE and or even P5.js and would largely improve the computational efficiency.

- Carefully refined parameters based on paper “Digital Sound Synthesis of String Vibrations with Physical and Psychoacoustic Models by Rabenstein and Müller”, where they outlined the detailed formulation and discrete-time realization through impulse-invariant transformation.

- Started programming a baby string model on JUCE, still in the process of putting in new parameters and exploring GUI options.

More on AES:

References: “On the Similarity between Feedback/Loopback Amplitude and Frequency Modulation by Tamara Smyth”, “Modal Representations for Audio Deep Learning by Skare et al”

- Dr. Smyth’s presentation clarified/consolidated some of my interpretations towards her work. I feel lucky to have listened through her research process in person and think about how she was able to start from a rather physical standpoint, and arrive at a more abstract and general approach to fabricating sounds. Her abstraction (in terms of physical implications) yet accuracy (in terms of mathematical formulations) is what I want to get out of my research. And this sheds light to one of the possible paths. Her slides started from a simple model of coupled oscillators and a general(parametric) formulation of this model. (I’m still unsure how coupled oscillators in physics relates to classical FM and AM synthesis, maybe the feedback aspect is what inspired by physics?) But her paper topic is about proving equivalence between a loopback frequency modulation model and a feedback amplitude modulation model. Both are one of many mathematical representations of specific types of sound synthesis methods. Her goal, if I haven’t interpreted wrong, was to alter the original(simpler) representation, and derive a closed-form solution of these sound synthesis algorithms, so that properties of the sound fabricated can be parametrized (represented by some coefficients). I found this similar to Prof. Selesnick’s attempt of turning original physical parameters into ones that convey qualities of the sounds. I wonder if I can utilize this physics-inspired sound synthesis tool I already have, and focus on exploring how much tonal complexity can be achieved by this formulation. Would it ever be as complex as naturally-occurring sounds? what about comparing with sounds made with feedback FM mentioned above?

-  Another “nice surprise” paper I found in AES is titled “Modal Representations for Audio Deep Learning by Skare et al”. This paper is on, given a generalized modal representation of sounds (summation of sinusoids of different frequencies with different decay rates/amplitude gains) and assuming that the sounds of interest can be formulated this way, want to train a machine learning model that learns the coefficients tailored to the given sound.  These coefficients may therefore be thrown into the modal formulation and would theoretically recover the sound. I’ve not read the entire paper yet, but I believe there is a generative ml model aspect as well, which i’m not very familiar with. However, the thought of learning modal representations of sounds with machine learning has come to my mind before. This should especially be straightforward if my FTM formulation is assumed here. In any case, I need to talk to my MIR professor more about this idea before writing more. 

[coconut2877-blog]

10/13/2019 visualization and digressions

This week I pinned down my research goals in two directions, one focusing on sound synthesis based on physical models, the other on user control/visualization.

Visualization

I have decided to start from visualizing the string model.

Before when I was building the plugin, parameters available to control by users are simplified to be as few as possible because 1. the more physical parameters included the more confusing for the users to adjust 2. parameters are deliberately picked and transformed to convey quality of sounds rather than the “look” of the model, because again it’s more intuitive for sound-oriented users.

However, since I’m visualizing the model, including more “visualizable” parameters seems to become the goal here.  I began by categorizing parameters based on its ability to be visualized

Complete list of parameters:

E  - Young’s modulus (measures resistance of a material to elastic deformation under load)

I - moment of inertia (determine the torque needed for a desired angular acceleration about a rotational axis)

Ts - Tension

rho - density

A - cross-section area

d1 - frequency independent damping

d3 - frequency dependent damping (d3<0)

l  - string length

Previous simplified list of parameters:

c - derived from Ts, rho, A, describing propagation speed of the wave traveling in the system

p - derived from d1 and d3, describing damping of the system

S - derived from E, I, rho, A, also correlated with d3, d1, c

tau - derived from d1 and d3, implying duration of the sound generated

omega - derived from S, c, d3, d1, implying pitch of the sound

Dispersion - derived from S, d3, d1, c, implying inharmonicity of the sound

l - length of string is simplified to be of unit length.

Visualization of parameters:

I wanted to recover the lost visual aspects of the model - to do that I need to recover the visualizable parameters : l, rho, A, Ts/S (might be able to color code tension and stiffness in the string), x (where on the string that I’m exciting). There are still some parameters not ready to be visualized: d1 and d3.

d1 and d3 are frequency independent and dependent damping coefficients, in my PDE formulation they are simply numbers in front of the corresponding derivative terms, but where do they come from physically?

Through research I found:

References: “Computational Physics by Nicholas J. Giordano and Hisao Nakanishi”, “The Physics of Vibrating Strings by Nicholas J. Giordano” , “Physically-informed Percussion Synthesis with Nonlinearities for Real-time Applications by Jennifer Hsu”

- Air drag and bridge coupling are what accounts for damping in a string model. The former being nonlinear and the latter being mostly linear. Longitudinal waves traveling through the string is another factor in non-harmonic sound generation. However this factor is often times omitted in a transverse displacement formulation.

- Longitudinal force signal has large contribution to the high frequencies (several kilohertz), because the speed of longitudinal waves are much bigger than transversal waves.  

- presence of stiffness contributes to the dispersive effect of sound (the inharmonicity)

- The fundamental difference in a linearly and nonlinearly formulated system is that - when exciting a linear system at a larger force the resulting sound would just be of higher value; while in a nonlinear system, larger force results in complete spectral change, for example the “twang” sound when plucking a guitar string hard enough.

Conclusion

I recovered the original parameters and implemented a preliminary string model in Matlab. I’ve been playing around with tweaking several parameters to synthesize different sounds. I’d like to figure out a range for each of the parameters, and their physical equivalences before implementing them with JUCE. Next I’ll focus on sketching what i want visually and prototype my sketch in JUCE graphics.

Sound Synthesis

efficiency-wise:

Since in FTM approach a transfer function can be written down. Rather than deriving the underlying impulse response and synthesizing sound based on the impulse, I wonder if it’s possible to derive a difference equation and design a recursive system that would largely simplify the computation. I’ll work on it this following week.

reference-wise:

References: “Max Matthews interview”, “Physically-informed Percussion Synthesis with Nonlinearities for Real-time Applications by Jennifer Hsu”, “Digital Sound Synthesis of String Vibrations with Physical and Psychoacoustic Models by Rabenstein and Müller”

Reading these inspires me to diverge from trying to be as physically accurate as possible, and moving onto exploring the sound I synthesized in a spectral sense.  Max Matthews brought up his research interest at the time - study of inharmonic timbres, specifically how stretching he ratio between overtones affected sense of key changes and cadences. Dr. Hsu who just graduated from UCSD focused on studying algorithms of inharmonic percussive sounds synthesis. She brought up a lot of interesting points on achieving inharmonicity, and her dissertation’s background section largely coincided with what I have been researching for the past weeks. Rabenstein and Müller’s paper combined their FTM sound synthesis approach with the famous critical bands study, which “degraded” the resolution of synthesized sounds without compromising the human perception towards them.

[coconut2877-blog]

10/6/2019 more research and questioning

This week I read a few more recent publications of Dr. Rabenstein and his students, started an online course on physical modeling as an extra resource, and had an interesting conversation with my peer. I came up with a rough execution plan/agenda to at least get me started. And of course there are always more questions.

From research papers:

References: “Spatial Sound Synthesis for Circular Membranes”, “A Physical String Model with Adjustable Boundary Conditions”, “Tubular Bells: A Physical and Algorithmic Model”

I looked at three research papers on sound synthesis, all in some ways building upon the FTM method. One of them investigates in building spatial sound synthesis/reproduction(in wave field synthesis) for circular membrane, one proposed a flexible way of adjusting boundary conditions for string model, and the last one was interested in tubular bell sound synthesis. Following are some bullet points I summarized:

This might be overlooked often, but another free gift FTM approach gives us is in its spatial aspect - sounds can be chose to be synthesized corresponding to any point on the vibrating structure. Thus this approach informs about the sound radiation into the free field as well!

A lot of things can be done utilizing the spatial aspect of this model, for example accurate reproduction of sound using ambisonics/wave field synthesis/VBAP technologies

(Right now for 2D/3D models I only have rectangular surface and box models) If I want to fabricate circular membrane/spheres/cylinders sounds, the most straightforward way would be to use the corresponding coordinate system! I was using cartesian, and these new shapes can be accessible with polar coordinates and cylindrical coordinates.

The second paper introduces a state space method for modeling a general boundary condition, which allows more flexible boundaries modeling without recalculating the eigenfunctions every time.

The third paper reveals equations for modeling tubular bells! It also comes with an implemented VST plugin. So more shapes can be employed.

Feedback from peer: 

CY has a somewhat similar idea - a sound design tool that conveys emotional quality of the objects. e.g. size, mood, temperature etc. My idea is not as user-centered and design-oriented, but entails the same subjects - objects and their sounds.

We talked about our different approaches and then he suggested something interesting. “Instead of building things ground up, sometimes it’s more effective to do top down.” Make the end results evident/appealing, and then reconstruct the bottom. I found this proposition ties into my other idea, a tool that infers back the physical properties from sound. 

 Thoughts: 

The overall thesis doesn’t have to use FTM all the time. It can be a series of projects - all conveying relationship between physical properties and sounds. maybe one or two using FTM.

FTM’s best use is that it can convey shapes, and tweak shapes - so visualization is a must.

A friend of mine told me how natural/comprehensive the physical modeling tool AAS made (mentioned in last post) are, which reminds me of further distinguishing my project outcomes from theirs. These “perfect” plugins by AAS have tons of parameters to tweak as well, however my guess is that the parameters directly implicate properties of the delay lines/filters used to model the physical shapes, rather than the shapes themselves. While sound design users don’t normally care about what the sound actually looks like, it would be important on my end to contribute the “first” visualization, and visual-oriented controls. 

Design a series of experiment/thought experiment: 

For this part I attempt to brainstorm and list a spectrum of tools/installations/projects I want to make with this concept. I would pick one to start from next week.

Assumption: we can form a translation between physical properties and sound

Thought experiment series:

With two different objects(e.g. vessels) in hand, how much effort does it take to make one sound exactly like the other. (possible method: inverse filtering)

A physical modeling sound synthesis tool with visualization and unusual interface. (possible method: FTM + JUCE plugin + jitter(computer vision)/leap motion/MIDI keyboard/customized touch board)

A tool that has input as sounds, output as physical parameters of these sounds assuming they come from a model that is a string or a surface or a box. (possible method: Musical information retrieval with dataset constructed by my physical model sound synthesis tool.)

A pendulum that confuses virtual world with reality (collab w Wenjing)

A speaker array that accurately duplicates physical dimensions of the sounding object (for example a string), and then let the sound shuffles, see if anything significantly changes. A visualization can also be accompanied with this - shuffle a visual puzzle piece simultaneously with the sounds, and gradually put the pieces back together.

… 

Others on waitlist:

more resonance-related experiments, have to look into helmholtz resonators and speaker designs

visualize waves?? place two speakers towards each other and let the sound wave interfere, let sound move object

Questions: 

- How is exciting an object on the surface different from exciting the air within it, can we physically describe it?

- What makes something sound life-like? if every animal that makes sounds have vocal cords, does it relate to the materiality of their vocal cords?

- Other terms encountered during research and need further investigations: 

measuring resonance of objects/vessels

acoustic repulsion

acoustic holograms

[coconut2877-blog]

9/28/19 ground already shaking

This week I weighed more carefully my propositions and my stance in the study. There are certainly frustrating parts but these assessments as a whole helped me realize what is really possible.

My contradiction:

This week I talked to my ECE professor Dr. Selesnick about my initial idea of deriving customized algorithms from what is already there, more specifically combining DWG and FTM. We talked about limitations of FTM, and the difference between traditional approach and my approach(effects of eliminating the SLT step). It turns out that my approach is a subset of FTM, where the PDE formulations are simple enough to conclude that the eigenfunctions of SLT transform are sinusoidal functions of different frequencies. On one hand he proposed that for solving more complex shapes I would have to look into SLT literature, on the other hand he said depending on my purposes I don’t have to feel obliged to stick onto FTM method. He also thought instead of thinking about advancing the algorithm, maybe I should use what I already know and build non-existing tools around it. For example turning the conventional mouse-dragged slider interface I built into something more unusual/intuitive to use, maybe a visualization of shapes it can morph into. 

This meeting, as well as pre-thesis’ class activity - telling your partner what motivates you in this theme, made me reexamine my goals. Below I list things I want and not want from this project

I want to:

Build a physical modeling tool that is flexible enough, in terms of the shapes it can take on, and the way that it is morphed. 

This tool has to differ from the physical modeling tools existing in market (commercial plugins made by Applied Acoustics Systems)

This tool has to remind users of where the sound comes from. This does not limit to defining the exciters/resonators/sizes like what AAS did. They’ve done it pretty well and it makes no sense to repeat their paths. Some more intriguing ways of presenting the tool might include - infer back physical parameters from analyzing its sound, combine analog and digital domain (real exciter + virtual resonator, virtual exciter + real resonator), design creative interfaces etc.

I don’t want to:

This tool’s main focus would not, and would probably exceed my time/math capability to be as physically accurate as possible. Converting what other ECE Phds spent years (the theories/algorithms) deriving into something more accessible should be the focus.

This tool would not become a UX design. I do want to collaborate with artists and makers and make work utilizing the tool. However the process is more prone to a speculative design one than a user-centered one. 

Some remaining questions/things to think about:

If the project has become a collection of artwork/tools triggered by some fundamental theories of physical modeling, what kind of research process should it take on? Would it just be a brainstorm of ideas or something I can follow rigorously. 

There is probably a lot of disciplines to follow when it comes to speculative design, where should I start?

I still have a lot of papers to read, in order to get a sense of what current researchers in physical modeling are doing. My reference is from early 2000s and the author of the book is still advising students, publishing papers, producing results. 

What tools are already built:

I checked out AAS(Applied Acoustics System)’s plugins. This company build physical modeling products mainly in the form of plugins. I didn’t look into their algorithms yet from the way their plugin is designed - sections of exciters, resonators and parameters for changing mass/sizes, I speculated that it is using the DWG method developed by researchers like Julius Smith. The plugin sounds convincing, with pretty comprehensive functionalities already. In the example of Ableton Live + AAS collab plugins, they implemented percussive(Collision), strings(Tension), electronic circuits (Electric) sounds separately. 

Looking into their website/CTO tech talk I found the below quotes inspiring:

“

But the real interest of physical modeling is not so much how realistic it can be but how natural and expressive it is. As we explained previously, physical modeling generates sound in response to input signals. Its output is not deterministic and always varies depending on the nature of the control signals and what is being played. In other words, it is dynamic and this is how real life instruments behave!

For example, hit a note on a piano regularly. The note played will always be the same but if you listen carefully , the sound is always different. Why? Because when you hit the note the first time, the hammer hits a note at rest which sets it into vibration. When the hammer hits the string again, it is already vibrating and will now interact differently with the hammer. Hit it once more and the hammer will hit the string when it is in another point in its oscillation and again will produce a different sound. This is what makes acoustic sounds so rich and lively, they are never quite the same. Now this is something physical modeling reproduces naturally which is not the case with other methods such as sampling.

Another department in which physical modeling is very strong is in the reproduction of transients. This is the part of a sound during which the signal varies very rapidly, such as in attacks as opposed to the sustained part of a note where the waveform is very stable. Perceptually, transients are crucial and they give the tonal signature of an instrument. There is a very interesting psycho-acoustic experiment where one removes the attacks from recorded notes played on different instruments. In other words, one then only listens to the sustained phase of the notes. Well, in these conditions, it becomes very difficult to recognize the instrument.

”

More theories:

From the FTM+DWG chapter in my reference book by Trautman and Rabenstein, I summarized:

Three filters from the DWG need to be inferred from FTM - loss filter, dispersion filter and fractional delay filter. Each has equations that connects filter coefficients with FTM physical parameters, done in Bank, 2000.

The spectral synthesized is only accurate in the lowest partials.

Computational saving is approximately 70% compared to direct FTM simulation. but it depends on number of partials need to be calculated, and parameter update rate of the physical model.

This combination is not any more useful for vibrating bars or high parameter update rates. Moreover it might cause audible transients in the DWG since the filter coefficients are not varied as smoothly as in the FTM.

From Julius Smith's lecture recorded at CIRMMT in Mcgill University in 2010, I summarized:

DWG is a method largely based on D’Alembert’s traveling wave formulation of string vibrations. How to equate this traveling wave(describing string vibrations as waves traveling to the left + waves traveling to the right) and the standing wave description(describing string vibrations as superpositions of sinusoidal modes) derived by Bernoulli had been a conundrum, and was resolved at a later time. This equivalence relates to me in that it also explains why time-based approach(FDM, DWG) and frequency-based approach(FTM, MS) coexist in physical modeling.

DWG starts from the traveling waves model, adds filters of various kinds to simulate different mechanisms in and out of the instruments. For example pianos need filters to mock the felt hammers striking on strings, clarinets need delay lines and nonlinear filters to circulate and reflect air off the reed within the instrument, guitars need filters for modeling stiffness, damping, pickup position/direction of the string etc. These mechanical components are linked together in blocks, can commute(doesn’t change the output when changing sequence of the filters), and are what constitutes the entire model. 

At the time of this lecture, lots of research are going into performance/gestural synthesis, 

Documentation of a newly started collaboration:

Last week I started a collaboration with ITP student Wenjing Liu. We have conceptualized an installation/idea on blurring the boundary between virtual and real sounding objects. 

Our initial idea is an elastic ball as a pendulum, swinging and banging into two “walls” on the side one is a real wall and one is a virtual wall - one producing real wall-ball collision sound and the other a synthesized one. Slowly the virtual wall will morph into something completely different until the audience can pick up the difference.

We prototyped a max msp + arduino + distance sensor project and here are some photo documentations. 

[coconut2877-blog]

FOR PRE-THESIS 9/23 CLASS

15 THINGS THAT INSPIRE ME:

Pina Bausch/Louise Bourgeois

Greta Thunberg

Bjork

ARUP 

Cycling 74 and their recent conference

Simone Giertz

Miranda Cuckson/Du Yun

Twin Peaks

Natasha Barrett

Andrei Tarkovsky

SFMOMA sound exhibition in summer 2017/The MET Breuer’s vessel exhibition’s idea but not their final presentation

IRCAM

Forensic Architecture

Dylon Thomas/Edgar Allen Poe

Susan Sontag

WHY

Pina Bausch/Louise Bourgeois:

Both women, artists, one for movements and another for shapes and textures,

Watching their works remind me of how important it is to still have a heart, to allow strength and vulnerability at the same time, to be detached yet passionate.

They motivate me to feel more, see more, hear more, to live more intensely.

Interests: - ability to express explicitly in another medium - self-expression - combination of strength and vulnerability

Greta Thunberg and her movement:

She came across as a person with a lot of courage and determination. I care about environmental issues and support her with my whole heart.

Interests: - Humanistic goal - environmental issues - Clarity

Bjork:

I admire her energy, inimitable visions for sounds and visuals, on-going explorations of everything new (especially new media technologies), and her love for this world.

Things she care about and present are always on large scales, appear in overwhelming intensity and sometimes bring unease, which I also learnt to appreciate.

Interests: - Humanistic vision - new media technology+music - work that brings unease

ARUP:

An engineering/architecture firm that always seeks for creative solutions. Projects range from Bjork’s reverberation chamber on stage to National Sawdust’s conversion from warehouse into a concert venue. I like the range and unusualness of the projects/issues they are trying to solve, and would love to be a part of it.

Interests: - Sustainablility  - turning artistic vision into engineering problem

Cycling 74:

I was at MASS MOCA for their most recent conference, and was amazed by their international team and what MAX MSP as a tool is capable of doing.

The empty space they cultivated and a few max objects derived from that inspire me to build tools that are similarly open-ended.

Interests: - versatile platform - Creative solutions

Simone Giertz:

She’s a maker with out-of-this world/ridiculous ideas and incredible executing power, more importantly a strange sense of humor.

She inspires me to act immediately without feeling insecure about the outcome.

Interests: -being absurd - Creative solutions

Miranda Cuckson/Du Yun:

Their dedication to what they do motivates me everyday.

Interests: - Building tools for these artists I admire - Articulation/Crafts - Contemporary music 

Twin Peaks:

The characters and metaphors originated from this TV series follow me everywhere. 

Interests: - Visual aesthetics - Storytelling aesthetics - Building of characters

Natasha Barrett:

Her ability to apply rigorous research methods onto the creation of interesting arrangements of sound amazes me.

Interests: - Rigorous logic - Articulation/Crafts - Art+science combination 

Andrei Tarkovsky/Eric Rochmer:

Their visual and storytelling aesthetics are something that make me pause. 

Interests: - Visual aesthetics - Storytelling aesthetics - Ambiguity

SFMOMA sound exhibition in summer 2017/The MET Breuer’s vessel exhibition:

The former marks the beginning of my journey, first time being exposed to the range and capacity of contemporary sound art works.

The latter shared and refined a similar idea of what I had, capturing the resonance of each unique object and ascribing them sonic profiles. Although the outcome is not exactly what I pictured.

Interests: - Sonic arts - Materiality and their sonic profiles - Convey research goal in an artistic way

IRCAM:

This is also the beginning of my journey, and still where I eventually want to end up in. 

I love collaboration of art and science, pursuing artistic goals with scientific methods.

Interests: - collaboration of art+science - Rigorous research methods - Convey research goal in an artistic way

Forensic Architecture:

I came across this organization only recently at the Whitney Biennial and comments from my friend. Their research methods, humanistic vision and artistic expression fits my goals.

Interests: - Humanistic vision -Rigorous research methods - Convey research goal in an artistic way

Dylon Thomas/Edgar Allen Poe:

These writers I view as being the most original. With their wild words and imaginations even the most flamboyant moving images in our present digital world fades.

Interests: - Poetry and use of words - the art of absurd

Susan Sontag:

She writes with incredible concision, intensity, and clarity without being scholarly boring. Her views/analysis on ordinary matters inspire me to think harder over things I encounter, to keep on the life-long project of self-transformation.

Interests: - Rigorous logic -Clarity

Five Questions:

SFMOMA sound exhibition in summer 2017/The MET Breuer’s vessel exhibition:

How can I really capture the resonance of an object without imposing any artifacts?(this means without applying any additive component/subtractive filters to artificially “shape” the sonic properties of the object in question)

Cycling 74: 

How can I build a tool that provides the most freedom for people from any background/of any purpose to use?

Forensic Architecture:

How can I embody my technical difficulties/deeply-mathematical research findings in a form that people might grasp rather easily? How to present the potential of my scientific findings in a creative way?

Simone Giertz:

Would absurdity be a good language to have when illustrating my tool?

Andrei Tarkovsky/Eric Rochmer:

How to use words, visuals, storytelling to convey the intrinsic ambiguity of my research interest. A lot of problems cannot be solved, do not need to be solved, do not necessarily possess clear market value. However, how to still make meaning out of these ambiguous pursuits.

Reflections on reading

Some of the words I found helpful - 

“Find what interests other researchers. Look online for recurring issues and debates in the archives of professional discussion lists relevant to your interests. Search online and in journals like the Chronicle of Higher Education for conference announcements, conference programs, calls for papers, anything that reflects what others find interesting.”

“Those nouns are derived from verbs expressing actions or relationships: to conflict , to describe , to contribute , and to develop . Lacking such “action” words, your topic is a static thing.”

“So the best way to begin working on your focused topic is not to find all the information you can on it, but to formulate questions that direct you to just that information you need to answer them.”

“You can also find research problems in your sources. Where in them do you see contradictions, inconsistencies, incomplete explanations?”

At the beginning, I found myself clueless facing pools of research topics, even in a rather specific realm like mine. Asking/formulating questions and starting by answering these first have been very helpful. 

Reading through different approaches to physical modeling for the past week, I carefully followed the analysis and comparisons of each method. My reference book mentioned a promising solution of combining two of the four approaches and its potentiality. It sheds lights on the possibility of modifying/advancing existing methods and motivates my contribution to the broader research field. However the book was written in early 21th century, and I can imagine that a lot has changed since then. More time needs to be spent on researching the more recent findings.

[coconut2877-blog]

9/18/19 standing ground

This week I focus on the historical context of physical modeling. 

What has been done? 

What are the similarities and differences among the three commonly used approaches? 

To what extent are people modeling shapes and materials?

How are people simulating resonating bodies?

Am I sure about my own PDE (partial differential equations) formulations?

How to do sanity checks for the sounds I fabricated ?

My reference would be “Digital Sound Synthesis by Physical Modeling Using the Functional Transformation Method” by Lutz Trautman and Rudolf Rabenstein, and Dr. Julius O Smith’s online book “Physical Audio Signal Processing”. The former outlines theoretical proofs and applications of FTM, and the latter focuses on another method developed in CCRMA called DWG (Digital WaveGuide Networks).

How they used to do it

Classically physical modeling is done in roughly 4 ways - FDM (Finite difference method), DWG (Digital waveguide method), MS (model synthesis), and the relatively newer method FTM (functional transformation method), aka my approach(although not exactly as I discovered and would explain later). FDM and DWG are time-based synthesis while MS and FTM are frequency-based approaches. Both FDM and FTM relies on formal physical formulation, while MS and DWG start from analyzing existing recorded sounds. I will briefly describe all the approaches and then point out their limitations and possible combinations.

FDM

FDM starts from solving one or a set of partial differential equations with initial-boundary conditions that describe the given structure’s vibrational mechanism. Then it discretizes any existing temporal and spatial derivatives by Taylor expansion. This approach is straightforward, general, and works with most complex shapes, however tends to neglect higher-order terms. It is possible to improve its accuracy by using smaller discretization, although at the same time it would introduce heavy computations. It is often an offline method, not suitable to be implemented in real-time synthesis. The solution contains time-evolution of all the points on the object in question.

FTM 

FTM shares the same formulation as FDM but solves the equations differently. It eliminates the temporal and spatial derivatives by carrying out two transformations consecutively - Laplace transformation and SLT (Sturm-Liouville transformation). Both transformations turn the entire equation to be expressed in terms of another domain parallel to time-space, from (t,x) to (s,mu). In the alternate domain, derivatives on t and x are transformed to simple-to-solve algebraic equations in terms of s and mu. Afterwards, the solution maybe written in the form of a transfer function multiplying the activation function (derived from whatever force is exerted on the object). This transfer function may be inverted back to time-space domain and a solution would be obtained. The transfer function has its poles and zeros, from which we derive analytical solutions for each frequency partials and their decay rates. This approach is frequency-based in that the final solution is a summation of sinusoidal waves of different modes, with their own decay exponential terms. It accurately simulates the partials resulting from the sounding object however reaches its limitation when it comes to larger modes. It is more computational-friendly than FDM, however limits itself into simpler geometries - most of the time rectangular and circular shapes.

DWG

DWG analyzes a recorded sound and simulate the exact sound with bidirectional delay lines(for simulating traveling waves in both directions), digital filters, and some nonlinear elements. The method is based on Karplus-Strong algorithm and the filter coefficients+impedence of traveling waves are interpolated from the sound. This method is the most efficient but cannot describe a parametrized model. All changes in physical parameters need to be recorded again and be re-interpolated.

MS

MS considers objects as coupled systems of substructures and characterizes each substructure with their own mode/damping coefficient data. It then synthesizes sounds by summing all weighted modes. The modal data is usually obtained by measurements of the object itself rather than deriving from an analytical solution like FTM, and thus MS cannot react to parameter change in the physical model. Furthermore since no analytical solution is derived, MS requires measurements on discretized spatial points and the accuracy here is compromised.

So what do we wanna use

Based on the summary from Trautmann and Rabenstein’s book I extracted:

“

frequency-based method are generally better than time-based methods due to the frequency-based mechanisms in the human auditory system

for more complicated systems simulations of spatial parameter variations is much easier in the FDM than FTM since eigenvalues can only be calculated numerically in FTM.

FDM is the most general and the most complex synthesizing method. It can handle arbitrary shapes.

FTM is limited to simple spatial shapes like rectangular or circular membranes

DWG is even more limited than FTM or MS. It can only simulate systems accurately having low dispersion due to the use of low-order dispersions.

human ear seems to be more sensitive to the number of simulated partials than to inaccuracies in the partial frequencies and decay times

“

How my approach is slightly different from FTM

My approach is technically a FTM approach however with slight modifications. FTM first formulates the physical model, perform Laplace and SLT transform, get transfer function, and then derive the impulse response by inverting the transfer function back to time-space domain. My approach follows the same formulation, however only perform the Laplace transform. At this point I would assume the solution to be of sinusoidal form and calculate explicitly what the spatial derivatives are. Due to properties of sinusoidal form, even high order derivatives wouldn’t escape their original forms. After that, I derive the transfer function and would only perform inverse-laplace transform to obtain the impulse response, instead of performing inverse-laplace transform and inverse-SLT transform.

Whether this approach yields utterly different results, why would people go through the trouble of performing SLT spatial transformation, and whether it’s safe to assume the solution be of sinusoidal form is still under investigation. 

What can be done 

FTM+DWG

From FTM we can derive accurate modes and their decay rate coefficients, however it costs computational power to synthesize the actual sound (summation of multitudes of mode, calculation of exponentials, sine operations etc) 

On the other hand from DWG we design filters based on pre-recorded sounds (not flexible to morph between different physical parameters), however very computationally-efficient to synthesize the sounds. 

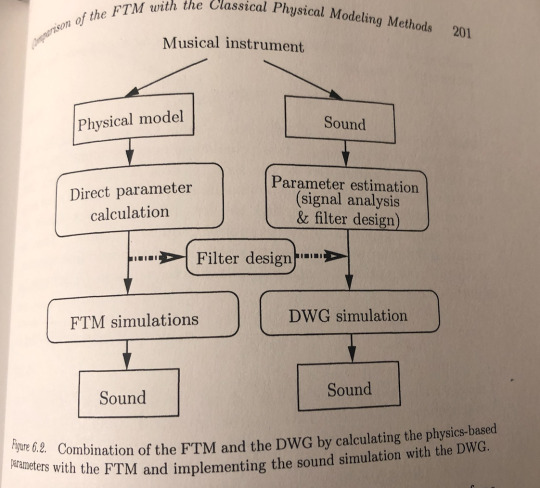
The book mentions a promising solution of combining the two methods - use accurate modes/decay rate information obtained from FTM to design filters and leave the sound synthesis business to DWG. Next week I will explore further on the combination of these two approaches.

[coconut2877-blog]

9/10/19 the very start

I’m interested in the translation between physical properties and sounds. This translation is bidirectional, ambiguous yet carefully derived, and potentially creates transformative experience. 

Drama that leads to this 

This past summer marks the burst of my frustration towards music and sounds, which, along with the people involved in it, used to be what saves me from misery and gives me strength.  Experimental music and electronics sounds exhaust me. I miss string noise, hammers stroke on soft woods, and resonating bodies.

In my journal I wrote 

“

maybe deep down i still repel the idea of electronics, those blatant spectrums without any physical carrier. objects are what give me attachments.

i want sound to be coming from vibration of surfaces, strings, wooden enclosures, vocal cords, stomaches and skins.

”

Serious Stories that lead to this

Last fall Prof. Selesnick and his DSP lab got me started on physical modeling, the idea of physically simulating how a sounding object vibrates is intimidating yet fascinating somehow - to have the freedom to adjust certain properties (parameters) of an inorganic or organic entity, and synthesize its corresponding sound, to extend appearances beyond rationality and inspect on the sounds it’s capable of making.  

My initial project was using a method called functional transformation method, which wisely avoided the heavy computations incurred in common numerical methods (i.e. finite element methods) while faithfully solving the original partial differential equations, to synthesize sound generated by vibrations of 1D string and 2D surfaces. By the end of the semester I created a plugin for DAW with a GUI that allows users to adjust physical parameters of simple 1D string and 2D rectangular surface models, and accordingly synthesize the sounds in real-time. The end product was convincing yet incomplete, due to its raw-looking GUI and glitch in sounds from computational inefficiency. The rest of the school year I extended it into the third dimension, which already implies a “virtual sounding object” since the box model is technically vibrating (the displacement of the box) in the fourth dimension. Fourth dimension in a spatial sense rather than the time axis that people usually assume. 

Thoughts/Progress over the summer

As of now I realized the shortcoming of a real-time synthesizer. After reading certain chapters in “Digital Sound Synthesis by Physical Modeling Using the Functional Transformation Method”, I realized that my solution needs to be evaluated to see if it falls under the “real-time friendly domain”, if advancing/solving for one time step in the solution takes longer then the actual sampling rate of the plugin. I also thought about the “accessibility” of the form of this project, since plugin still assumes users having DAWs on their laptops, and knowing how to download and install new plugins. As essentially, a tool, this project would need more straightforward, and intuitive if not fun interfaces, and even evoke thinking about sounds in different ways.

I’m trying to synthesize sound as accurately as possible, however that is not the only goal, as it would become a known known problem. Tons of researchers have yielded satisfying theoretical approaches, just that no one I know(I haven’t really searched either) of have built it into a comprehensive and accessible tool yet. I feel that the project I completed above is a good start for making a more flexible physical modeling tool, however that would only mark the start of something bigger/more abstract. 

Looking into the “big blue sky”

I drew a map on my notebook, noting where I go from here. Completing a rather comprehensive tool that implements the physical process is one of my goals, but I also want to move back from where it might end - reverse-engineering the sound back to its physics. A friend brought up a paper Fisher wrote years ago, “on hearing the shape of a drum”, which turns the problem into a complete set theory question centered around mapping from one space to another. I’m not prone to this approach...

What does a sound implies about its shape, dimensionality, and materials? Is it possible to excite an object in a particular way so that it creates a sound alien to its shape? How are speakers designed to remove its intrinsic resonance? What kind of questions are worth asking? What approaches can be legit of investigating this reverse-engineering process? Machine learning or listening tests? 

I have a lot more to do - read about historical context of physical modeling and where my method stands in it, figure out different approaches to model the resonant bodies and experiment with my own transducer + resonator + signal combination, see if MIR (musical information retrieval) is a convincing reverse-engineering approach. 

With that i end with a photo of my notebook.