Text
Koordinat Polar
dalam matematika adalah suatu sistem koordinat 2-dimensi di mana setiap titik pada bidang ditentukan dengan jarak dari suatu titik yang telah ditetapkan dan suatu sudut dari suatu arah yang telah ditetapkan.

Koordinat radial sering dilambangkan dengan r, dan koordinat angular dilambangkan dengan φ, θ, atau t.
Koordinat polar r dan φ dapat dikonversi ke dalam sistem koordinat Kartesius x dan y menggunakan fungsi trigonometri sinus dan kosinus:



0 notes
Text
Integral Volume Benda

Volume Benda Putar Mengelilingi Sumbu x
Kasus volume benda putar yang diputar mengelilingi sumbu x dibagi menjadi dua permasalaha. Permasalahan pertama, volume benda putar yang dibatasi sebuah kurva. Kasus yang kedua adalah volume benda putar yang dibatasi dua buah kurva.
Volume benda putar pada interval yang diputar mengelilingi sumbu x

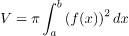
2. Volume benda putar pada interval yang diputar mengelilingi sumbu x dan dibatasi kurva f(x) dan g(x).
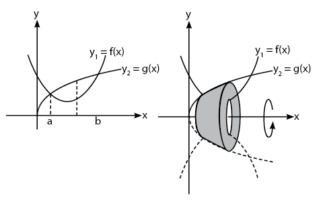

Volume benda putar yang mengelilingi sumbu y
Seperti halnya volume benda putar yang diputar mengelilingi sumbu x, volume benda putar yang diputar mengelilingi sumbu y juga dibedakan menjadi dua jenis kasus. Pertama, volume benda putar yang dibatasi sebuah kurva dan diputar mengelilingi sumbu y. Kedua, volume benda putar yang dibatasi dua buah kurva dan diputar mengelilingi sumbu y.
Volume benda putar pada interval yang diputar mengelilingi sumbu y

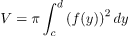
2. Volume benda putar pada interval yang diputar mengelilingi sumbu y dan dibatasi kurva f(y) dan g(y)


0 notes
Text
Integral Parsial
Integral parsial didasarkan pada rumus turunan dari perkalian dua fungsi.
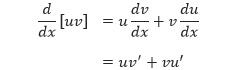
di mana u dan v adalah fungsi-fungsi yang terdiferensialkan dalam x. Jika u’ dan v’ kontinu, kita dapat mengintegralkan kedua ruas dari persamaan di atas dan memperoleh:
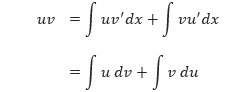
Dengan menulis kembali persamaan di atas, diperoleh teorema berikut.
Teorema 1: Integral Parsial Jika u dan v adalah fungsi-fungsi dalam x yang kontinu dan terdiferensialkan, maka
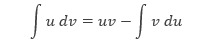
Rumus integral parsial ini menyatakan integral aslinya ke dalam bentuk integral yang lain. Berdasarkan pemilihan u dan dv, akan lebih mudah menyelesaikan bentuk integral yang kedua daripada bentuk aslinya. Karena pemilihan u dan dv sangatlah krusial dalam proses integral parsial, berikut ini panduan dalam memilih u dan dv.

Panduan dalam Proses Integral Parsial
Cobalah untuk memisalkan dv sebagai bagian yang sangat rumit dari integran yang sesuai dengan aturan dasar integral. Sehingga u merupakan faktor lainnya dari integran.
Cobalah untuk memisalkan u sebagai bagian dari integran yang turunannya lebih sederhana dari u. Selanjutnya dv merupakan faktor integral lainnya.
Perhatikan bahwa dv selalu memuat dx dari integran aslinya.
0 notes
Text
Luas Daerah Integral
Integral banyak sekali penggunaanya, seperti dalam menghitung luas daerah dibidang datar menggunakan integral,menghitung panjang busur, menghitung luas selimut benda putar, menghitung volume benda putar Untuk menghitung luas ini kita harus memahami apakah daerah yang dimaksud berada di atas kurva, di bawah kurva, di atas sumbu x ataupun di bawah sumbu x. Untuk itulah maka kita perlu memahami gambar kurva.
Untuk lebih jelasnya perhatikan kasus-kasus berikut

Jika kurva berada di bawah sumbu x maka metodenya adalah

Jika di antara dua kurva maka caranya sebagai berikut

Contoh soal
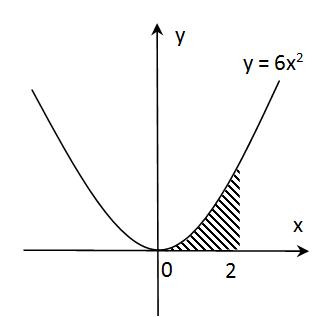

0 notes
Text
Integral Tak Wajar
Dalam kalkulus, integral tak wajar adalah limit dari integral tentu dengan batas pengintegralan mendekati bilangan riil tertentu, atau ∞ −∞ atau, pada beberapa kasus, keduanya.
Dengan kata lain, integral tak wajar adalah limit dalam bentuk

atau dalam bentuk

Contoh Soal

Menurut teorema integral tak tentu, definisi integral tak wajar, dan konsep limit tak hingga, berlaku
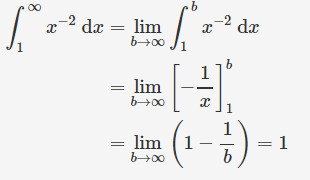
Jadi, integral tersebut konvergen ke 1
0 notes
Text
Integral Subtitusi Trigonom
Selain dengan cara subtitusi dan parsial, perhitungan integral juga bisa dilakukan dengan metode substitusi trigonometri yakni, mengubah/memisalkan variabel pada fungsi yang ingin diintegralkan dengan trigonometri.
Metode substitusi trigonometri digunakan jika pada fungsi yang akan diintegralkan berbentuk atau mengandung unsur:

Untuk integral fungsi yang berbentuk √a² + x², berlaku:

Untuk integral fungsi yang berbentuk √a² – x², berlaku:

Untuk integral fungsi yang berbentuk √x² – a², berlaku:

1. Memahami Identitas trigonometri dan Trigonometri sudut rangkap

2. Memahami Turunan Dasar Trigonometri.

3. Memahami Integral Dasar Trigonometri.

4. Memahami Invers Dasar Trigonometri.

0 notes
Text
Integral Reduksi Trigonom
Dalam mempelajari integral, kita sering menemui bentuk integral trigonometri yang tidak biasa, dan terlihat menyusahkan. Seperti dalam mencari bentuk integral trigonometri dalam bentuk perpangkatan, apalagi jika pangkat yang ditanyakan lebih dari dua. Untuk memudahkan kita dalam menyelesaikan tantangan tersebut, kita dapat menggunakan rumus reduksi untuk integral trigonometri, sehingga pemecahan masalah bisa menjadi lebih sederhana. Dan berikut ini adalah penurunan rumus reduksi trigonometri untuk integral {sin (x)}^n dx, integral {cos (x)}^n dx, dan integral {tan (x)}^n dx.
1. Penurunan Rumus Reduksi Integral {sin (x)}^n dx
Kita tahu bahwa

Bagaimana dengan

Kita tahu bahwa

Maka


2. Penurunan Rumus Reduksi Integral {cos (x)}^n dx

Berakibat

3. Penurunan Rumus Reduksi Integral {tan (x)}^n dx


Jadi

0 notes
Text
Integral Fungsi Rasional

Jika pangkat P(x) pangkat Q(x) atau n m, maka penyelesaian integral tersebut bergantung pada faktor-faktor dariQ(x). Setiap suku banyak dengan koefisien real dapat dinyatakan sebagai perkalian dari faktor –faktor linear dan kuadrat sedemikian sehingga tiap-tiap faktor mempunyai koefisien real.
Ada 4 kasus dari pemfaktoran penyebut ( Q(x) ) yaitu :
Faktor linear dan tidak berulang.
Faktor linear dan berulang.
Faktor kuadratik dan tidak berulang.
Faktor kuadratik dan berulang
KASUS 1 : Penyebut terdiri dari faktor -faktor Linier tidak Berulang

dengan A1, A2 , … , An konstanta yang akan dicari.
KASUS 2 : Penyebut terdiri dari faktor-faktor linier Berulang
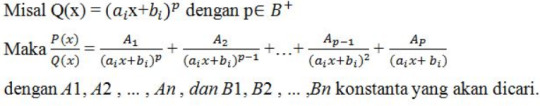
KASUS 3 : Penyebut terdiri dari faktor-faktor kuadrat tidak Berulang
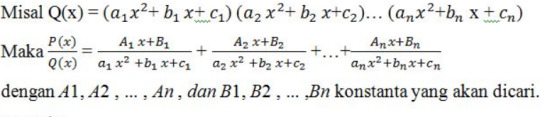
KASUS 4 : Penyebut terdiri dari factor-faktor kuadrat berulang

0 notes
Text
Integral Tertentu
a. Pengertian
Integral tertentu adalah integral yang memiliki nilai batas atas dan batas bawah. Batas-batas yang diberikan umumnya adalah suatu nilai konstanta. Namun dapat juga batas-batas tersebut berupa variabel.
b. Rumus Dasar
Untuk mencari nilai integral tertentu dari suatu fungsi, pertama kita substitusikan batas atas ke dalam fungsi hasil integral, kemudian dikurangi hasil substitusi batas bawah pada fungsi hasil integral. Secara matematis dapat ditulis sebagai berikut :

c. Sifat-Sifat

0 notes
Text
INTEGRAL TAK TENTU
a. Pengertian
Integral tak tentu dalam bahasa Inggris di kenal dengan nama Indefinite Integral atau kadang juga di sebut dengan Antiderivatif yang merupakan suatu bentuk operasi pengintegralan suatu fungsi yang menghasilkan suatu fungsi baru. Fungsi ini belum memiliki nilai pasti (berupa variabel) sehingga cara pengintegralan yang menghasilkan fungsi tak tentu ini disebut “integral tak tentu”.
Jika f merupakan integral tak tentu dari suatu fungsi F maka F’= f. Proses untuk memecahkan antiderivatif adalah antidiferensiasi Antiderivatif yang terkait dengan pasti integral melalui “Teorema dasar kalkulus”, dan memberikan cara mudah untuk menghitung integral dari berbagai fungsi.
b. Cara Baca
Silahkan Lihat Integral Berikut

Teman-teman ada yang bisa membacanya.?
Rumus di atas di Baca dengan “Integral Tak Tentu Dari Fungsi f(x) Terhadap Variabel X”
c. Rumus Integral Tak Tentu
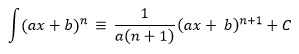
0 notes
Text
Fungsi (Function)
Wow! It’s been so long since I’ve posted, perdón. I admit my time management has been poorly organized these days, and you know, the one thing that keeps everyone from doing what they’re supposed to do: KEMAGERAN! :(
But, anyway I’m back posting the 3rd week topic, which is Function. Seperti biasanya, I’m gonna explain the definition first then go straight to the material.
Seperti yang dilansir dari web Wikipedia, Fungsi dalam istilah matematika merupakan pemetaan setiap anggota sebuah himpunan (domain) kepada anggota himpunan lain (kodomain). Anggota himpunan yang dipetakan bisa berupa apa saja (orang, objek, dll), namun pada umumnya (terutama yang akan dibahas di sini) anggotanya merupakan bilangan.
Adapun gambaran sederhana mengenai fungsi yang saya dapatkan dari laman web mathisfun.com, bahwa ada 3 bagian utama yang terdapat dari sebuah fungsi, yaitu:
1. The Input (nilai masukan, domain) 2. The Relationship (hubungan antara input dan output) 3. The Output (nilai keluaran/hasil, kodomain)
Contoh Fungsi f(x)=2x+1, di mana 2x+1 merupakan relasi atau hubungan dari fungsi tersebut. Jika kita mengganti nilai x menjadi 1, maka 1 merupakan nilai inputnya, dan hasil dari proses aritmatik nya merupakan outputnya: Maka f(1) = 2(1)+2 = 2+2 = 4 (output)
Pemberian nama pada fungsi tidak selamanya dengan huruf ‘f’, bisa juga diganti dengan huruf lain ataupun dengan sebuah kata. Nama fungsi dengan f adalah bentuk yang paling umum.

Namun, ada juga fungsi yang tidak memiliki nama, di mana hanya terdiri dari variabel output, variabel input dan relasinya.

Huruf ‘x’ pada fungsi, pun, hanyalah sebuah variabel. Di mana variabel tersebut mewakili nilai-nilai yang akan dimasukkan pada fungsi itu nantinya. Variabel tersebut bisa diganti dengan huruf lainnya.
Contoh soal:

I guess that’s it for this topic. Any questions you may ask me via the ask box on my blog. Thank you and see you on the next post!
0 notes
Text
Harga/Nilai Mutlak (Absolute Value)
Hola! I am back with another post. Thank God, this one is posted right on time, no more late-late situation just like the one before this.
This week’s material is all about absolute value. Atau di dalam bahasa Indonesia-nya berarti Harga / Mutlak. Materi ini sudah ada sejak SMK, I did study about it, but then, I forgot (kebiasaan pelajar di Indonesia hehehe). Seperti biasanya, I will describe the definition of absolute value first.
Apakah nilai mutlak itu?
Secara sederhana, yang dahulu saya biasa pahami, nilai mutlak adalah nilai yang mutlak bersifat positif. Namun, after I’ve done some research here and there, ternyata nilai mutlak adalah how far a number is from zero (seberapa jauh sebuah angka dari titik 0). Kudos to mathisfun.com for serving such an easy way to understand it! Tapi, juga dijelaskan di laman mathisfun.com, nilai absolut selalu bersifat positif. No negatives! Karena yang ditanyakan pada nilai mutlak adalah “Seberapa jauh kah?” bukan “Ke arah mana kah?” Jadi, pemahaman saya selama ini tidak salah. Nilai mutlak mempunyai simbol tersendiri yaitu: | x | atau juga biasanya ditulis sebagai abs(x).
Misalnya, nilai mutlak dari 5 adalah 5, perhatikan gambar di bawah ini

pic credit goes to: www.broexcel.com
Jarak dari 5 ke 0 adalah 5 unit (4, 3, 2, 1, 0).
Begitu pula dengan nilai mutlak dari -5 adalah 5 agar lebih mudah dipahami maka perhatikan ilustrasi di bawah ini

pic credit goes to: www.broexcel.com
Kita bisa melihat bahwa, jarak titik -5 ke 0 adalah 5 unit (-4, -3, -2, -1, 0). Maka 5 unit tersebut adalah nilai absolut dari -5.
Jadi, bisa disimpulkan, nilai mutlak tidak mempedulikan bahwa suatu nilai bersifat positif ataupun negatif, nilai mutlak akan selalu bernilai positif.
Selanjutnya, kita akan membahas mengenai ketidaksamaan pada nilai absolut dengan memberikan langsung contoh soalnya:

Sooo, I think that’s all for this post. The video is coming as soon as possible. I promise you won’t be waiting years, kok! Adios!
0 notes
Text
Ketidaksamaan (Inequalities)
Hola! I am back with another post. First thing’s first, I am so sorry, I didn’t get to post the 2nd meeting material last week due to the heavy schedule and all that. Tapi, jangan khawatir, di post ini, I will explain about Inequalites atau yang biasa disebut Ketidaksamaan.
Beforehand, I want to describe the definition of the inequalities itself. Apakah ketidaksamaan itu?
Menurut laman mathisfun.com dan mathplanet.com, simply,
Inequalities (ketidaksamaan) ialah suatu kalimat matematis yang menyatakan hubungan antara 2 buah nilainya yang tidak setara atau sama.
Misalnya: a ≠ b, di mana nilai a tidak sama dengan nilai b. Selain yang sudah dijelaskan, ada beberapa simbol/tanda lain yang menyatakan ketidaksamaan 2 buah nilai, seperti:

Selanjutnya, I will show you an example on how to find the solution to an inequalities:

I guess that is it for this post. The video will be uploaded soon, I promise. Adios!
0 notes
Text
Types of Numbers
Hola! Back again with another post. But, you may notice something different. Yep, I moved my blog to Tumblr now. I did want to use Tumblr as my blog platform pas mata kuliah ALIN, but I couldn’t because Tumblr was blocked back then. Now it’s back on board, I can happily use Tumblr.
As you can read on the title, I am about to explain about numbers di dunia matematika. Some people may only know just two types of numbers, which are positive or negative. This post may help them broaden their knowledge about numbers in math world.
First thing’s first, what are numbers actually? Menurut laman Wikipedia, Bilangan merupakan suatu konsep matematika yang digunakan untuk pencacahan dan pengukuran. Sedangkan menurut my POV, numbers are symbols consists of 0,1,2,3,4,5,6,7,8,9, ... that are used to represent/label the value of something measurable. (Bilangan adalah simbol yang digunakan untuk mewakili/melabeli nilai sesuatu yang bisa diukur).
Selanjutnya, I will describe types of numbers one by one including its examples.
Bilangan Asli (Natural/Counting Numbers) Bilangan ini hanya tediri dari bilangan positif saja, dan di mulai dari angka 1 ke atas. Kelompok bilangan ini merupakan bilangan yang sering kita gunakan pada kehidupan sehari-hari untuk menghitung (counting) hal - hal sederhana. Contoh: 1, 2, 3, 4, 5, 6, ...
Bilangan Cacah (Whole Numbers) Bilangan yang terdiri dari bilangan positif dimulai dari angka 0. Dengan kata lain, kelompok bilangan cacah adalah kelompok bilangan asli yang ditambah dengan angka 0. Contoh: 0, 1, 2, 3, 4, 5, ...
Bilangan Bulat (Integers) Bilangan yang terdiri dari seluruh bilangan baik itu negatif maupun positif. Contoh: -3, -2, -1, 0, 1, 2, 3, ...
Bilangan Prima (Prime Numbers) Bilangan yang tediri dari bilangan asli yang lebih besar dari 1 dan hanya bisa habis dibagi oleh dirinya sendiri dan angka 1. Sedikit trivia, bahwa 2 merupakan satu-satunya angka prima yang merupakan prima bersifat genap. Contoh: 2, 3, 5, 7, 11, 13, 17, ...
Bilangan Rasional (Rational Numbers) Bilangan yang dapat dinyatakan sebagai pecahan (a/b) di mana keduanya, pembilang dan penyebut merupakan anggota dari bilangan integer. Contoh: ½, ⅛, ²²/₇, ⁻³/₂ ...
Bilangan Irasional (Irrational Numbers) Bilangan yang tidak bisa dinyatakan dalam bentuk pecahan. Contoh: √7, √3, √5, ....
Bilangan Riil (Real Numbers) Bilangan yang terdiri dari bilangan cacah, termasuk bilangan rasional dan bilangan irasional. Contoh: 0, 1, ¼, ⅔, √2, √5, ...
Bilangan Kompleks (Complex Numbers) Bilangan yang bisa dinyatakan dalam bentuk a + bi, di mana a dan b adalah bilangan riil, dan i adalah penyelesaian dari suatu persamaan. a merupakan bagian riil dan b adalah bagian imajiner. Contoh: 3 + 2i
Bilangan Imajiner (Imaginary Numbers) Bilangan kompleks yang bisa dituliskan sebagai bilanagn riil dikalikan dengan satuan imajiner i. Sebuah bilangan imajiner bisa ditambahkan dengan sebuah bilangan riil yang membentuk suatu bilangan kompleks. Contoh: i−2 = −1, i2 = −1
1 note
·
View note