edreitega-blog

[edreitega-blog]

¿Por qué la vida se ha empeñado en esa tarea extraña de definir una cosa por otras que no son de su orden, por desquiciar de alguna manera el orden y conexión inmediata de las cosas.-orden y conexión inmediatas que la ciencia clásica pretendió descubrir y grabar en principios eternos?

La finalidad de esta extraña tarea de la vida, desde Descartes, consiste sencillamente en que por este procedimiento se puede conseguir vivir los objetos como Mundo, mientras que, en el plan inverso, la vida vive desviviéndose en ellos, vive en un Universo. 

Y cunbdo la vida se pone en plan de vivirse desviviéndose por los objetos y en los objetos, aparecen implicados e implícitos los aspectos que pudieran producir el efecto inverso: el de interiorizar los objetos, dando la supremacía a la vida interior. Y los aspectos que pudieran libertar.- y que de hecho históricamente han libertado a la vida del imperio de los objetos y del universo que forman son: definir una cosa por otra,-lo geométrico por lo algebraico, lo algebraico por lo lógico. 

Posee, pues, sentido perfecto decir que, en contra de ciertas apariencias sectariamente deformadas, nunca ha sido la vida espiritual tan independiente de las cosas, tan espiritual, como desde Descartes y en nuestros días; y es en su ser mismo más espiritual que en la Edad Media,- o en otra de las que pasan apologéticamente por modelos en cosas espirituales. 

E índices exactos de la creciente espiritualización de la vida mental son la fundamentación algebraica de la geometría, la geometría analítica, y la fundamentación lógica de las matemáticas. Y esta creciente espiritualización, conseguida por la ciencia, es la que asegura en su ser mismo un creciente y entitativo derecho a la inmortalidad. 

-Introducción filosófica a Los Elementos de Euclides, Juan David García Bacca 

[edreitega-blog]

´´Con Descartes la vida se revela a sí misma e inventa para sí el modo de vivirse como creadora de esencias, cual poder que transforma las cosas geométricas en esencias geométricas de estilo analítico, de modo que, en adelante, la geometría no sólo poseerá conexión de tipo científico (dada por la lógica formal) sino contextura científica nueva: la del análisis o álgebra en general. 

Con ello la vida inventó creadoramente, sin apoyo en lo real inmediatamente dado, esencias para las cosas geométricas, mostrando en este hecho trascendental que fundar la filosofía en el ¨Yo pienso¨, es decir en la espontaneidad creadora mental, traía consigo la creación de esencias  para las cosas. Que exista, por tanto, un ¨Yo pensante¨ no es vulgar e insignificante hecho para todo el universo -cual lo es el que haya piedra más o piedra menos, gato más o menos o fotón más o menos-. sino que es un hecho trascendental  que trasciende y se eleva por sobre todos los demás hechos y cosas que de hecho haya en el mundo; y esta presencia soberana de un Yo pensante en el mundo de las cosas trae como consecuencia el que ellas se puedan en adelante aparecer como ¨objetos¨ y en nuestro caso como ¨objetos algebraicos¨.

Por la presencia de un Yo pensante que se ponga a pensar geometría, el universo de las cosas geométricas adquiere esencia analítica. La creación de la geometría analítica es a la inversa, la que certifica y da testimonio de que el universo de los seres hay un Yo pensante con espontaneidad creadora o inventiva de esencias. De modo que la filosofía cartesiana no es un invento inofensivo; él es el que ha hecho posible una ciencia geométrica potenciada, científica en segunda potencia: lógica y analítica. 

Hasta Descartes, para citar el modelo clásico, la mente humana ha estado en este universo casi como una cosa entre las demás cosas, casi como decimos con una frase castellana, de ¨cuerpo presente¨, dada a las cosas, en pian de ajustar lo más exacta y adecuadamente posible verdad ontológica (verdad del entendimiento) con verdad óntica y ser. Sólo los estoicos se liberaron en un punto de esta sujeción de la mente a los objetos: poniendo entre las cosas geométricas un tipo de conexión que ellas de por sí no tienen, a saber el lógico formal. 

Desde Descartes la mente impondrá a las cosas geométricas conexión lógica y esencias analíticas.

Con el correr de tiempo histórico se irán introduciendo en la ciencia geométrica otros tipos de formulación analítica de las cosas geométricas; y llegaremos, por ejemplo con Riemann y Gauss, a una geometría diferencial. Pero en el fondo estamos aún dentro de la invención cartesiana”. 

-Introducción filosófica a los Elementos de Euclides, Juan David Garcia Bacca. 

[edreitega-blog]

Dark matter, Dario Salamone

[edreitega-blog]

Why haven’t we found a cure for cancer?

Why is it so difficult to cure cancer? We’ve harnessed electricity, sequenced the human genome, and eradicated small pox. But after billions of dollars in research, we haven’t found a solution for a disease that affects more than 14 million people and their families at any given time.

Cancer arises as normal cells accumulate mutations. Most of the time, cells can detect mutations or DNA damage and either fix them or self destruct. However, some mutations allow cancerous cells to grow unchecked and invade nearby tissues, or even metastasize to distant organs. Cancers become almost incurable once they metastasize. And cancer is incredibly complex. It’s not just one disease. There are more than 100 different types and we don’t have a magic bullet that can cure all of them.

For most cancers, treatments usually include a combination of surgery to remove tumors and radiation and chemotherapy to kill any cancerous cells left behind. Hormone therapies, immunotherapy, and targeted treatments tailored for a specific type of cancer are sometimes used, too. In many cases, these treatments are effective and the patient becomes cancer-free. But they’re very far from 100% effective 100% of the time. So what would we have to do to find cures for all the different forms of cancer? We’re beginning to understand a few of the problems scientists would have to solve.

First of all, we need new, better ways of studying cancer. Most cancer treatments are developed using cell lines grown in labs from cultures of human tumors. These cultured cells have given us critical insights about cancer genetics and biology, but they lack much of the complexity of a tumor in an actual living organism. It’s frequently the case that new drugs, which work on these lab-grown cells, will fail in clinical trials with real patients.

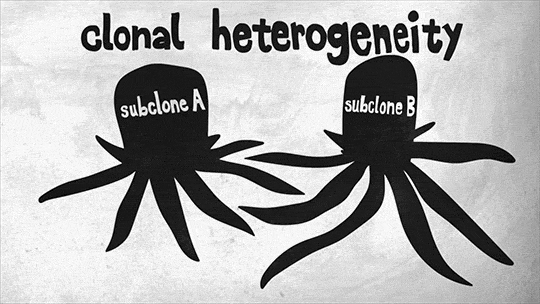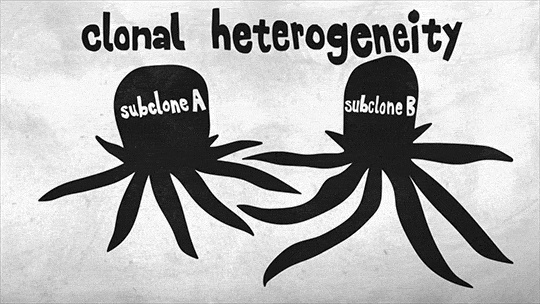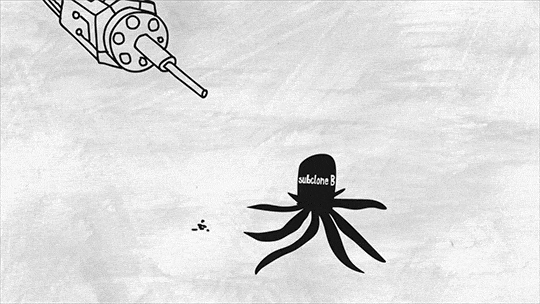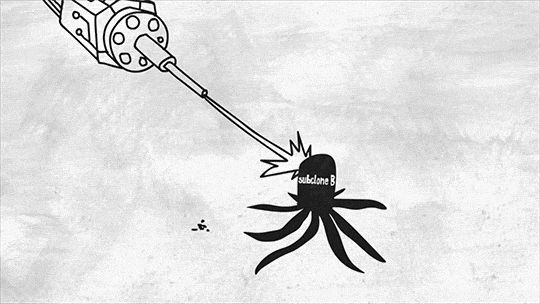
One of the complexities of aggressive tumors is that they can have multiple populations of slightly different cancerous cells. Over time, distinct genetic mutations accumulate in cells in different parts of the tumor, giving rise to unique subclones.

For example, aggressive brain tumors called glioblastomas can have as many as six different subclones in a single patient. This is called clonal heterogeneity, and it makes treatment difficult because a drug that works on one subclone may have no effect on another.

Here’s another challenge. A tumor is a dynamic interconnected ecosystem where cancer cells constantly communicate with each other and with healthy cells nearby. They can induce normal cells to form blood vessels that feed the tumor and remove waste products. They can also interact with the immune system to actually suppress its function, keeping it from recognizing or destroying the cancer. If we could learn how to shut down these lines of communication, we’d have a better shot at vanquishing a tumor permanently.

Additionally, mounting evidence suggests we’ll need to figure out how to eradicate cancer stem cells. These are rare but seem to have special properties that make them resistant to chemotherapy and radiation. In theory, even if the rest of the tumor shrinks beyond detection during treatment, a single residual cancer stem cell could seed the growth of a new tumor. Figuring out how to target these stubborn cells might help prevent cancers from coming back.

Even if we solved those problems, we might face new ones. Cancer cells are masters of adaptation, adjusting their molecular and cellular characteristics to survive under stress. When they’re bombarded by radiation or chemotherapy, some cancer cells can effectively switch on protective shields against whatever’s attacking them by changing their gene expression. Malignant cancers are complex systems that constantly evolve and adapt. To defeat them, we need to find experimental systems that match their complexity, and monitoring and treatment options that can adjust as the cancer changes.

But the good news is we’re making progress. Even with all we don’t know, the average mortality rate for most kinds of cancer has dropped significantly since the 1970s and is still falling. We’re learning more every day, and each new piece of information gives us one more tool to add to our arsenal.

From the TED-Ed Lesson Why is it so hard to cure cancer? - Kyuson Yun

Animation by Artrake Studio

[edreitega-blog]

Girl With Blue Veil Gustav Klimt  circa 1902-1903

[edreitega-blog]

If Satan is supposed to be evil then why would he punish evil people for eternity? Wouldnt that make him a good guy? If he was truly evil then he’d reward evil people and hell would be heaven for the evil. In that case then everyone wins.

[edreitega-blog]

Hay que tener presente que la realidad acaba siempre por desbordar los marcos construidos por nuestra razón. Por ello, tenemos que estar siempre atentos a las divergencias que se susciten entre la realidad objetiva y nuestra concepción racional. Tales divergencias son ineludibles, debido al hecho de que la realidad es infinitamente compleja, se matiza indefinidamente y se encuentra en continua transformación; mientras que nuestra razón construye conceptos más o menos rígidos, más o menos esquemáticos y siempre incompletos. Porque la realidad es demasiado fluida y de una riqueza tan inagotable, como para que jamás se pueda encerrar en el marco rígido y abstracto de nuestras representaciones categoriales y de los sistemas funcionales edificados con las categorías

Elí de Gortari, Dialéctica de la Física.

[edreitega-blog]

Pulley Logic Gates

By  Alex Gorischek

To demonstrate how computers work, he has made a physical example of how binary logic gates work using pulleys and weights. For anyone who doesn’t know much about logic gates (Wikipedia), it’s a great lesson in one of the fundamentals of circuitry. Using an old chessboard, eyelets, rings, weights, and string, Alex has designed a system that can show off all of the logic gates. This includes: NOT, BUFFER, NAND, AND, OR, NOR, XOR, XNOR. 

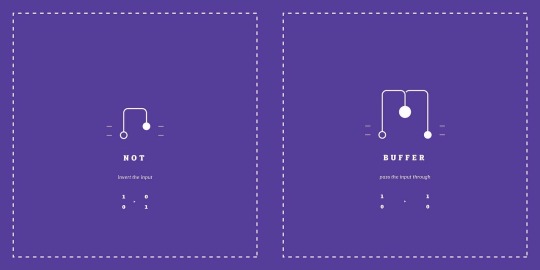
Not

0 in, 1 out; 1 in, 0 out.  Whatever you put in, you don't get out.

( GIFs: via Imgur - From: https://vimeo.com/93042377 by Alex Gorischek  )

Buffer

If you take the not of not, you get what you put in - 0 in, 0 out, 1 in, 1 out.

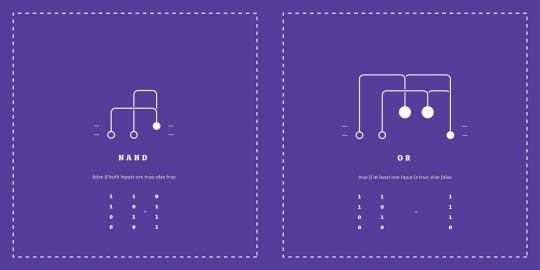
Nand

Both inputs must be brought up to 1 to lower the output to 0.

And

If you negate the result of Nand, you get And.  Both inputs must be brought up to 1 to raise the output up to 1.

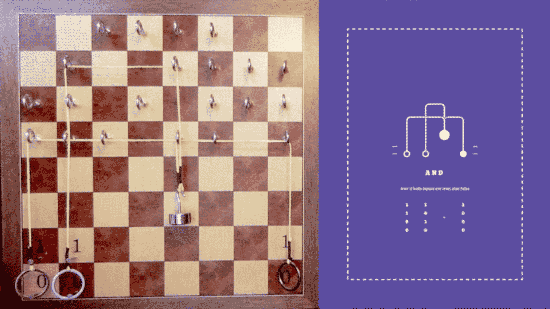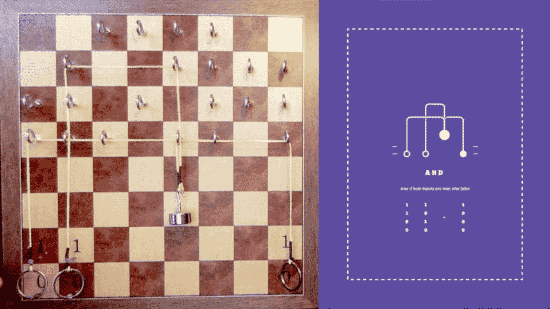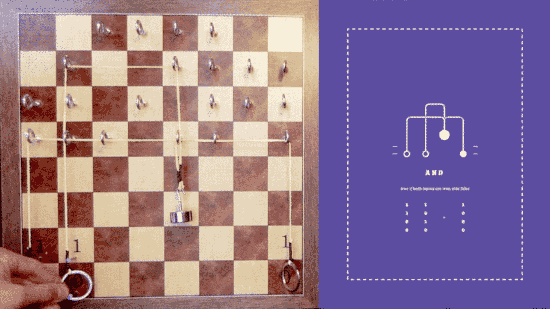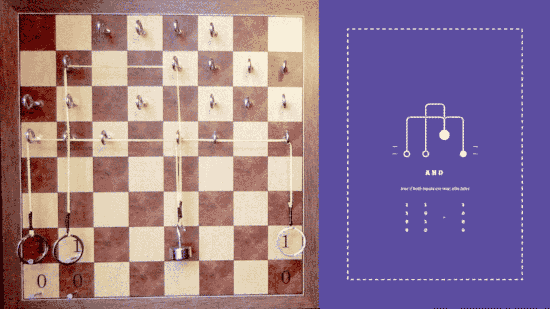
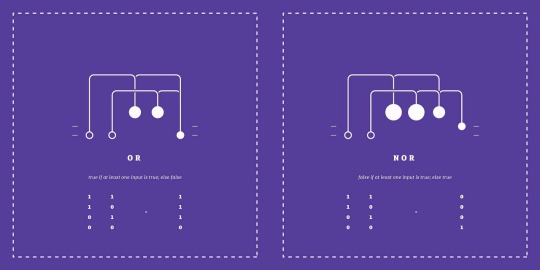
Or

If you not both inputs, and then Nand them together, you get Or.  If either input is raised to 1, the output raises to 1.

Nor

Negate both inputs, nand them together, and negate the output.

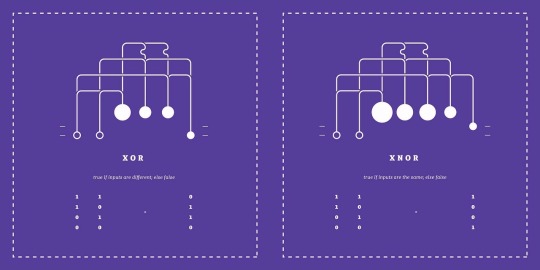
Xor

Xor is complicated - The large weight ands the inputs together.  The medium weights negate the inputs, but are pulled up by the large one when both are 1.  When you nor those together, you get Xor.

Xnor

This is comparatively simple - just negate the output of Xor, and you&

#039;re there! Source:

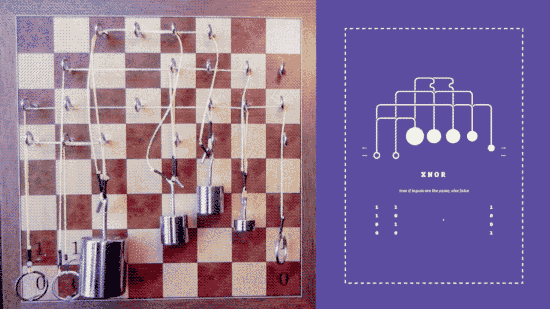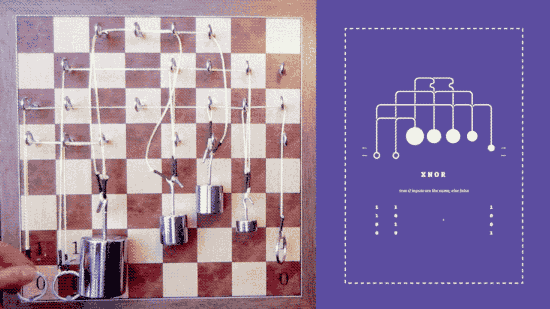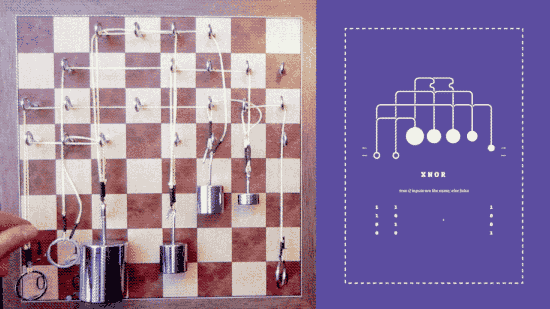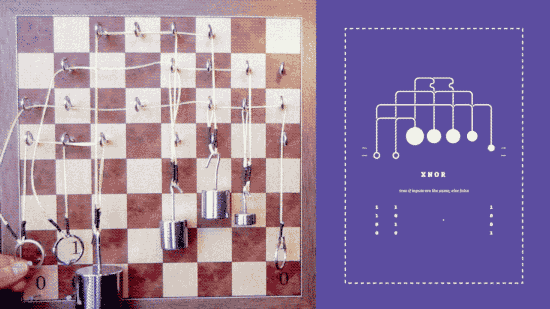
The principles of logic can be realized in so many systems that it makes you understand how they really are universal. All you need is something that takes an input and produces the opposite output - a NOT gate; something that take two inputs and produces an output when any one of the inputs is active - an OR gate; and something that takes two inputs and produces an output only when both inputs are active - an AND gate. Once you have AND, OR and NOT you can build any other logic gate you need. They form a universal basis for logic. You can even do better - a single NAND, i.e. a NOT AND gate, is universal. Yes, you can make any other logic gate by simply combining NAND gates.

This sounds powerful but you also need to keep in mind that you can use logic gates to build a fully functioning computer. All you need to build a computer is lots of NAND gate. Pulley Logic Gates demonstrates how a set of ropes and pulleys can be used to implement the basic gates. To understand what is going on notice that binary values correspond to zero or one as written on the board - i.e. up is 1 and down is 0. For example, you immediately get a NOT gate with a single piece of rope. When one end is up the other is down and vice versa - it is an inverter.

[edreitega-blog]

Quantum Questions Inspire New Math

 Quantum Questions Inspire New Math by Robbert Dijkgraaf.

Picture: by James O’Brien 

Picture: by James O’Brien for Quantum Magazine.

Picture: by James O’Brien .

[edreitega-blog]

Gymnopédie No.1

[edreitega-blog]

[edreitega-blog]

Annunakis, claramente. 

The Ancient Babylonians knew about a form of trigonometry more advanced than the modern-day version – about 1,000 years before its supposed invention by the Ancient Greeks, academics in Australia say.

The astonishing claim is based on a 3,700-year-old clay tablet inscribed with a table of numbers.

Known as Plimpton 322, it is already known to contain evidence that the Babylonians knew Pythagoras’ famous equation for right-angled triangles, long before the Greek philosopher gave his name to it.

And researchers at the University of New South Wales (UNSW) have claimed it also shows the Babylonians developed a highly sophisticated form of trigonometry – the system of maths used to describe angles that has tortured generations of school pupils with sine, cosine and tangent.

Continue Reading.

[edreitega-blog]

Setenta y seis días.

Un año atrás decidí comenzar la gran travesía de remediar las deficiencias que tuve durante mi preparatoria y que me llevaron a pasar dos meses de mi vida académica en FES Zaragoza, en Biología. Fue un largo año, sucedieron infinidad de cosas, tomé infinidad de decisiones, de pasos, de lecturas y afortunadamente llegué a nuevos juicios, los cuales estoy contento de haber alcanzado. Por alguna razón, me conduje por mí mismo al camino que ahora estoy por tomar, claro, siempre me han gustado las matemáticas pero... ¿ser un matemático? De verdad que fue absolutamente fortuito el haber decidido esto tan rápido y sencillamente llegar hasta aquí, a un día de comenzar mi camino como matemático. Suena bien, ¿no? Me encanta, siempre supe que lo que fuera que fuera a estudiar tendría un nombre complejo o rimbombante; y heme aquí teniendo sueños tan grandes como encontrar el cero no trivial de la función Zeta de Riemann, lógica matemática, mecánica cuántica y con un hambre inmensa de nuevo conocimiento. 

Ya conté los días efectivos de clase que tendrá este semestre, setenta y seis días para atascarme de nuevo conocimiento como si no pudiera volver a hacerlo en mi vida. Vamos, solo setenta y seis días inmerso en un mundo diferente, inmenso, complejo y completamente digno de atención. Voy a empeñarme, a hacer un compromiso con estas letras y yo mismo, a lograrlo, a tener las mismas ansias de conocer al mundo que tengo hoy y que tenía hace un año, mas bien más, porque en serio me maravilla la complejidad de todo mi universo visible. Yo vine aquí a conocer, para poder crear alguna vez, no, no me voy a detener hasta haber alcanzado a esa persona que siempre he tenido en mente. No te olvides, sí a mí mismo me digo, NO te olvides de las inmensas expectativas que te tienes a ti mismo, conocimiento integral, Edrei, no lo olvides. 

6/08/2017

Entonces comenzamos, 76 días dedicados al conocimiento del mundo a través del lenguaje matemático, mañana literalmente comienza mi nueva vida como universitario. Así que, Edrei, de verdad esfuérzate, hazlo, rompe al mundo, conócelo y crea algo que no haya sido creado antes. Ve hacia la frontera del conocimiento con esfuerzo y enfoque, no te distraigas con banalidades y hábitos humanos comunes, puedes lograr cosas muy grandes si diriges tu potencial. 

24 de Noviembre, ese día tendrás que evaluar todo el conocimiento alcanzado y los nuevos juicios formulados, sé que serás muy diferente para entonces, que tendrás en la cabeza aún más cosas. Confío en ti, Edrei, el conocimiento es creación, y lo sabes muy bien. Setenta y seis días, y comenzamos. 

[edreitega-blog]

Hey guys! I’ve compiled a list of resources that are helpful when studying science in general, & also when studying specific branches of science. I hope you find it useful!

General:

Crash Course [Youtube]

Khan Academy [videos, practice worksheets, etc]

Bozeman Science [Youtube]

Veritasium [Youtube]

Kurzgesagt – In a Nutshell  [Youtube]

Memrise [practice, app & web]

Thought Co. [articles]

iTunes U [app]

Sparknotes [notes on specific topics]

Wikiversity [articles]

Brightstorm [videos]

Cliffsnotes [study guides]

CK-12 [free online textbook]

Brilliant [problem-solving]

Alison [online courses]

Coursera [online courses]

Cosmo Learning [resources]

Biology

Amoeba Sisters [Youtube]

The Biology Corner

Learning Centre [animations]

Schmoop [study guides]

Beverly Biology [Youtube]

Chemistry

Periodic Videos [Youtube]

Tyler DeWitt [Youtube]

Chem Collective

Learn Chemistry

Chemistry Study Skills

Physics

Physics Central

Step-by-Step Science [Youtube]

Physics.org [revision & exam help]

Physics Galaxy [Video Lectures]

Open Yale Courses

the Physics Classroom

Earth Sciences

Geology.com 

NASA

National Geographic [study resources]

Sporcle [study guide]

Instagram || Other Posts || Resources || About || Ask

[edreitega-blog]

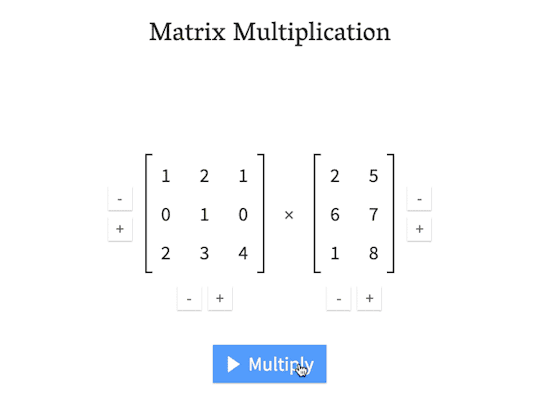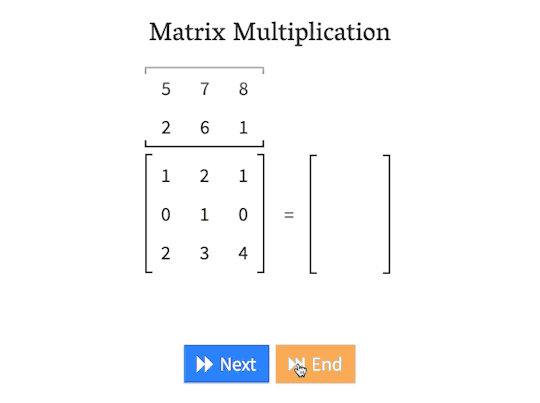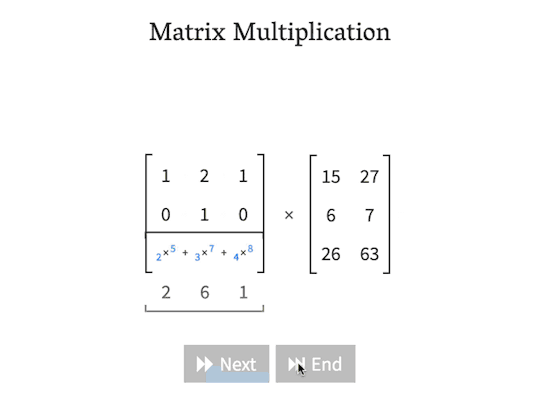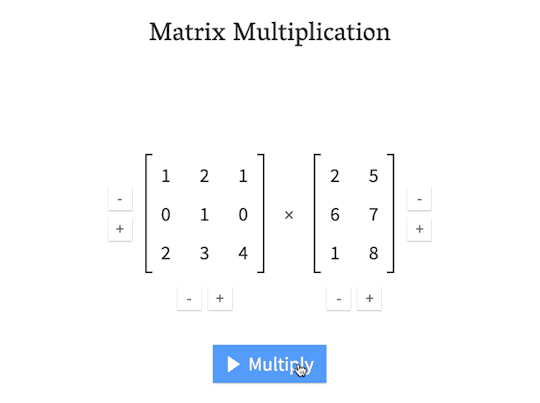
An interactive matrix multiplication calculator for educational purposes

matrixmultiplication.xyz

“One day it just snapped in my mind how the number of rows of the first matrix has to match the number of columns in the second matrix, which means they must perfectly align when the second matrix is rotated by 90°. From there, the second matrix trickles down, “combing” the values in the first matrix. The values are multiplied and added together. In my head, I called this the “waterfall method”, and used it to perform my calculations in the university courses. It worked.”

[edreitega-blog]

Infinite Growth