fichamentos01

[fichamentos01]

Trabalho Final (Estatística Aplicada à Comunicação) | Por Émerson Rodrigues, Luis Augusto Melo e Pedro Silva

Quase 80% dos alunos do Curso de Jornalismo da UFC utilizam transporte público para chegar à Universidade

Pesquisa foi realizada com discentes matriculados a partir de 2015

A maioria dos alunos matriculados no Curso de Jornalismo da Universidade Federal do Ceará (UFC) utilizam o transporte público para chegarem até a instituição. Os dados são de pesquisa realizada por três discentes do curso, com o objetivo de compreender o deslocamento dos estudantes de suas casas até a sede do curso.

Segundo o estudo, 78,6% dos alunos matriculados no Jornalismo utilizam o transporte coletivo, como ônibus e topiques, para chegar até a UFC. Outros 10% dos discentes utilizam carro ou moto próprios para se deslocarem até a universidade. Estudantes que vêm a pé representam 5,7% do total, enquanto aqueles que utilizam transporte da prefeitura de seu município ou de associação estudantil são 4,3%. 1,4% dos discentes ainda chegam ao Centro de Humanidades por meio de carro ou moto de terceiros (Uber, táxi, moto táxi etc).

Realizada entre os dias 10 e 11 de junho, a pesquisa ouviu 70 estudantes do Curso de Jornalismo da UFC regularmente matriculados a partir do ano de 2015. A margem de erro é de 10 pontos percentuais para mais ou para menos, com intervalo de confiança de 95%. Isso quer dizer que há uma probabilidade de 95% dos resultados retratarem a realidade, considerando a margem de erro. Ao todo, o Curso de Jornalismo da UFC conta com 242 estudantes matriculados de 2015 até o primeiro semestre de 2019.

Implicações do deslocamento

O estudo também produziu dados relacionados aos locais onde os estudantes residem e como isso influencia no deslocamento. De acordo com a sondagem, 78,6% dos alunos que cursam Jornalismo moram em Fortaleza, enquanto 21,4% vivem na Região Metropolitana da cidade.

Na capital cearense, a Regional 3, que engloba bairros como Parquelândia, Parque Araxá, Pici e Antônio Bezerra, concentra a maior quantidade de estudantes matriculados no curso - 23,6% do total. No outro lado da cidade, a Regional 6, de bairros como Messejana, Edson Queiroz e Jangurussu, aparece na segunda posição com 20%, seguido de perto pela Regional 4, onde o Curso de Jornalismo se situa, com 18,2%.

No aspecto financeiro, 47% dos discentes do curso gastam entre R$ 51,00 e R$ 100,00 mensais para fazerem o trajeto até o Centro de Humanidades. 23% gastam até R$ 150,00 para chegarem à sede do curso. Em seguida, 17,2% dos alunos desembolsam até R$ 50,00. Aqueles que despendem de R$ 151,00 a R$ 200,00 são 7,1%, e acima deste valor são 5,7% dos discentes.

O valor gasto com o deslocamento também se relaciona com a quantidade de ônibus/topiques que os estudantes pegam. Dentre os entrevistados que utilizam o transporte público para se deslocar até a universidade, 41,5% afirmaram pegar duas conduções para fazer o trajeto e 29,3% disseram que pegam somente um. Já 15,5% afirmaram pegar 3 ônibus e 10,3%, 4 ou mais. Outros 3,4% dos entrevistados que afirmaram utilizar o transporte público para chegar ao Curso de Jornalismo não responderam a esta questão.

Entre os alunos que responderam o questionário, 52,9% afirmaram que vem de casa diretamente para o Curso de Jornalismo, enquanto 45,7% disseram que vão para outros lugares primeiro. 1,4% dos entrevistados não responderam a esta questão.

No que diz respeito ao tempo de locomoção dos discentes, o levantamento aponta que 35,7% dos estudantes chegam ao Centro de Humanidades em, no máximo, 30 minutos. Outros 32,9% precisam de pelo menos uma hora para cumprirem o trajeto. A sondagem segue com 22,8% alunos levando até uma hora e meia para chegarem à UFC e 8,6% que chegam a passar até duas horas em deslocamento para chegar à sede do curso.

O que dizem os números

A maioria dos estudantes entrevistados moram na Regional 3. Isso se relaciona com a quantidade de pessoas que se deslocam a pé ou de carro/moto próprios. Além disso, por morarem perto, eles costumam gastar entre R$ 51 e R$ 100 com o transporte e, geralmente, pegam apenas um ônibus.

A segunda regional com a maior quantidade de estudantes é a 6, que compreende bairros como a Messejana, e se caracteriza por ser muito distante da sede do curso. Devido a presença maior de estudantes vindos da periferia, o crescimento de estudantes dessas localidades se tornou uma realidade.

Além disso, assim como a Regional 6 é a segunda com mais estudantes, a segunda quantidade de valores gastos apontados pela pesquisa está entre R$ 101 e R$ 150. Isso pode significar o deslocamento grande e que a quantidade de ônibus utilizadas para chegar ao curso é alta. Exemplo disso é que não existem ônibus que vêm diretamente da Messejana para o Benfica.

A terceira Regional com mais estudantes é a 4, onde a sede do Curso de Jornalismo se localiza. Ao contrário da Regional 6, os estudantes aqui moram muito próximos ao Centro de Humanidades. Isso pode se correlacionar com quantidade de estudantes que se deslocam a pé para o curso e com o valor gasto com o deslocamento que varia entre R$ 0 e R$ 50.

O tempo de deslocamento mais apontado pelos participantes da pesquisa está entre 1 e 30 minutos. Esse valor pode estar relacionado aos estudantes que moram na Regional 3 (1º) e na Regional 4 (3º). Como moram mais próximos, eles não levam muito tempo para se deslocar de suas residências para a sede do Curso de Jornalismo.

O segundo tempo de deslocamento mais apontado é entre 31 minutos e 1 hora. Esse valor deve ter sido apontado devido ao engarrafamento das vias que levam ao bairro Benfica. Possivelmente, esse não seja o tempo levado por estudantes da Regional 6 para chegar ao local de destino.

O terceiro tempo de deslocamento mais apontado está entre 1 hora e 1 hora e 30 minutos. Provavelmente, esse é o tempo de deslocamento de quem utiliza transporte público e vem de locais como a Regional 6. A distância, no nosso entendimento, inclusive, tem forte relação com o número de ônibus que os estudantes utilizam.

Chama atenção também o fato de 25,8% dos discentes terem respondido que pegam 3 ou mais ônibus diariamente, fato que também se relaciona com os 45,7% alunos que disseram que não vem diretamente para a universidade, em virtude de terem outros compromissos, como estágios e outras atividades.

MAIS INFORMAÇÕES SOBRE A PESQUISA

Acesse o questionário completo utilizado pelos pesquisadores: https://drive.google.com/open?id=1v_B9KXEphh9my09rplyE-ulJB6BhBe8RlE5oi18MYn4

Acesse o infográfico e os gráficos gerados pelos pesquisadores: https://drive.google.com/open?id=1Q4P5nlvr2h8Wt6vkjj4Vrle3Quvmhkr1

Acesse os dados completos gerados pela pesquisa: https://drive.google.com/open?id=1Tfqm2V7kLSK38OKNf5UQd9hw0hweQYjSvDlpw-xJZHs

[fichamentos01]

5º Exercício (Limpeza de dados) | Por Émerson Rodrigues

Pouco mais de 8% das vereadoras que disputaram eleições 2016 no CE se elegeram, apontam dados do TRE

Das 4.239 vereadoras que disputaram as eleições 2016 no Estado, apenas 352 foram eleitas. Os dados são do Tribunal Regional Eleitoral do Ceará (TRE-CE). O número representa 8,30% do total de candidatas postulantes às Casas Legislativas municipais. À título de comparação, entre os 9.011 candidatos do sexo masculino, 1.824 foram eleitos - 20,24% do total de postulantes, quase três vezes mais se comparado as candidatas mulheres.

Ao todo, 13.250 pessoas se candidataram ao cargo de vereador no Ceará, sendo 68% homens e 32% mulheres. Desse total, 2.176 foram escolhidos pelos cearenses para um mandato de quatro anos. Entre os eleitos, a disparidade entre os sexos também chama atenção, já que os homens ocupam 83,82% das cadeiras, enquanto as mulheres apenas 16,18%.

[fichamentos01]

4º Exercício | Por Émerson Rodrigues

Link: http://blogdoeliomar.com.br/2019/05/10/pesquisa-xp-investimentos-avaliacao-de-membros-do-governo-caiu-mas-a-de-mourao-fica-estavel/

A matéria que eu gostaria de comentar foi publicada pelo jornalista Eliomar de Lima em seu blog no Jornal O Povo. A notícia afirma em seu título que uma pesquisa da XP Investimentos mostrou que a avaliação de membros do governo caiu, mas a do vice-presidente Hamilton Mourão se manteve estável.

O primeiro aspecto a se destacar é o fato do título mostrar que a avaliação de membros do governo caiu. No entanto, caiu em relação ao que? Outra pesquisa da XP Investimentos? Outra pesquisa de outro instituto de pesquisa? E outra coisa: quem seriam esses membros? Não seria melhor nomear um ou outro? Ou até destacar a avaliação de Jair Bolsonaro e de algum ministro seu com maior destaque na mídia, como o juiz Sergio Moro?

Durante o texto, outros erros se seguem. Em nenhum momento, a notícia traz a margem de erro da pesquisa e a amostragem de pessoas entrevistadas, algo essencial para uma sondagem de opinião como essa. Há também uma má hierarquização das informações, na minha visão, visto que o título traz como destaque a avaliação de membros do governo e não a avaliação da gestão Bolsonaro, que aparece antes do que é destacado no título.

As informações, na minha opinião, também aparecem incompletas. No segundo parágrafo, por exemplo, Eliomar mostra que a avaliação da gestão do presidente como boa ou ótima ficou estável (35%), mas o índice dos que a classificam como ruim ou péssima oscilou cinco pontos, de 26% para 31% de abril para cá. Assim, falta algumas informações importantes (quem considera o governo regular, quantas pessoas foram ouvidas pela XP Investimentos, etc).

Da mesma forma, no parágrafo seguinte, é mostrado que a nota dos integrantes do governo caiu, porém, apenas as avaliações do juiz Sergio Moro e do presidente Jair Bolsonaro são mostradas. E a avaliação dos outros? Quem são esses outros? Qual deles oscilou mais?

Dito isso, acredito que a notícia não deveria ser publicada da forma que está, para não confundir o leitor, nem deixá-lo exposto a informações claramente incompletas.

[fichamentos01]

3º Exercício | Por Émerson Rodrigues

Para o presente exercício, nos utilizamos do manual de redação do Jornal Folha de São Paulo. A seguir, voc�� pode conferir o que está explicitado nas páginas 37 e 38 do documento, obtido a partir da plataforma passeidireto.com. Para acessar o manual de redação, contudo, você precisa se cadastrar gratuitamente no site acima.

“numerais — A Folha adota duas regras gerais para padronizar a grafia de numerais em seus textos:

a) Só escreva por extenso números inteiros de zero a dez além de cem e mil, sejam cardinais ou ordinais: Andou dez quilômetros; Acabou o percurso em sétimo lugar; Havia 50 pessoas no auditório e apenas 11 ficaram até o final; Ele foi o 23º da turma; Ele tirou nota zero em português e matemática;

b) Em números maiores ou iguais a 10 mil, escreva o algarismo seguido da palavra que designa a ordem de grandeza: A China já tem mais de 1 bilhão de habitantes; Um ano-luz equivale a 9,5 trilhões de quilômetros; O equipamento custou US$ 20 milhões ou 20 milhões de dólares. Atenção: seguindo essa regra, escreva Havia 2.500 pessoas na manifestação e não Havia 2,5 mil pessoas na manifestação; 2.000 e não 2 mil ou dois mil.

Além dessas duas regras gerais, observe a seguinte padronização:

a) A Folha não faz uso de algarismos romanos, exceto ao se referir a texto de lei e para respeitar a grafia original de um substantivo próprio: papa João 23, dom Pedro 2º mas artigo 23, inciso I e XV de Piracicaba;

b) Use algarismos nos seguintes casos, mesmo contrariando regras anteriores:

1) Números seguidos de símbolos - 2%, 8h, 22h45, 10s, 5 kg, 20 m, 4ºC, 100 km, 360º, 1min23s476. Mas atenção: acima de 9.999, evite o uso de símbolos como km. Escreva Uma unidade astronômica equivale à distância média entre o Sol e a Terra, cerca de 150 milhões de quilômetros em vez de 150.000.000 km ou de 150 milhões de km;

2) Idade - Maria de Campos, 4;

3) Tabelas e gráficos;

4) Dimensão, medida, peso, proporção ou comparação - Quando forem formados por dois ou mais elementos: Um terreno de 10 metros por 40 metros; A proposta foi recusada por 45 votos a 2; 5 partes de gim e 1 de vermute; O presidente do Haiti governou 15 anos, o do Brasil, 5, o da França, 7;

5) Resultado de jogos esportivos - A seleção brasileira venceu por 1 a 0;

6) Dias do mês - 1º de abril, 10 de outubro (só o primeiro dia do mês deve ser em ordinal);

7) Ano - 1992; 2030 (sempre sem o ponto que indica milhar);

8) Século - Jesus Cristo nasceu no século 1º a.C.; O século 20 acaba em 31 de dezembro do ano 2000;

9) Números com decimais - A mesa tinha 2,1 metros de comprimento;

c) Não use algarismo no início de frase. Modifique a oração para tirar o algarismo do começo ou, em último caso, escreva o número por extenso;

d) Cuidado com o problema dos pontos e das vírgulas. Em português, usa-se o ponto para marcar os milhares (2.000) e a vírgula para os decimais (1,2). Como na notação norte-americana ocorre o inverso, os erros são comuns;

e) Muito cuidado ao traduzir numerais de outras línguas para o português. Quem traduzir un billion de francs por um bilhão de francos estará perdendo 999 bilhões de francos. Em francês moderno, billion designa trilhão (1012) e não bilhão (109). Algo semelhante ocorre em alemão, italiano, espanhol e até em português, dependendo do país. No inglês, a situação é ainda mais confusa. Quem traduzir billion de texto norte-americano para bilhão acertará. Se o texto for britânico, é preciso verificar se billion não tem no caso o sentido de trilhão, como no inglês mais clássico. Consulte quadro com as grandezas e seus nomes em várias línguas no anexo As Grandezas, País por País;

f) Na numeração de artigos de leis, decretos e portarias, usa-se o ordinal até nove e o cardinal de dez em diante: artigo 1º, artigo 9º, artigo 10. Papas, soberanos, séculos, capítulos de obras etc. recebem o ordinal até dez e o cardinal de 11 em diante: Paulo 6º, século 10º, Leão 13, século 20. Quando o numeral antecede o substantivo, usa-se sempre o ordinal: 20º capítulo. Veja arredondar”.

O manual da Folha de São Paulo mostra a forma correta de usar os números nos textos publicados no jornal. Porém, em nenhuma parte do documento são dadas aos jornalistas orientações a respeito de como fazer uma apuração mais elaborada em reportagens e matérias que se utilizarão de dados. Tais informações seriam importantes para que os jornalistas, principalmente os iniciais no jornal, pudessem ter um boa base de parâmetros de apuração.

No mais, me surpreendeu o fato de que a Folha não faz uso de algarismos romanos, exceto ao se referir a texto de lei e para respeitar a grafia original de um substantivo próprio. Confesso que nunca havia reparado em tal aspecto, que, de fato, está devidamente presente nas matérias que pesquisei sobre o papa João Paulo II, ou João Paulo 2º, como a Folha prefere.

Cabe ressaltar também que os exemplos explicitados no manual de redação são didáticos e ilustram bem como o jornal prefere que as informações numéricas estejam presentes no texto. No tópico tabela e gráficos, no entanto, não foi dado NENHUM EXEMPLO de como trabalhar com tais elementos, essenciais no que diz respeito a matérias que envolvam números. Em suma, na minha opinião, o material traz informações relevantes, mas falta alguns aspectos para que se torne também um bom manual de redação para jornalistas que utilizam números.

[fichamentos01]

1º Exercício | Por Émerson Rodrigues

Notas dos alunos em exercício da disciplina de ESTATÍSTICA APLICADA À COMUNICAÇÃO

Para visualizar em PDF, clique aqui:

[fichamentos01]

2º Exercício | Por Émerson Rodrigues

2018 registra pior taxa de desemprego dos últimos 19 anos no Brasil

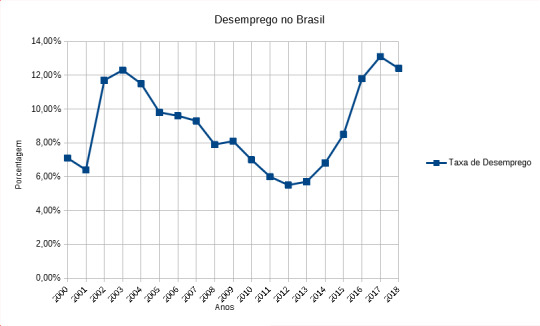
Dados da Pesquisa Nacional por Amostra de Domicílio Contínua (Pnad Contínua) do Instituto Brasileiro de Geografia e Estatística - Taxa de desemprego no Brasil desde os anos 2000 

2000 - 7,1%

2001 - 6,4%

2002 - 11,7%

2003 - 12,3%

2004 - 11,5%

2005 - 9,8%

2006 - 9,6%

2007 - 9,3%

2008 - 7,9%

2009 - 8,1%

2010 - 7,0%

2011 - 6,0% 

2012 - 5,5% 

2013 - 5,7%

2014 - 6,8%

2015 - 8,5%

2016 - 11,8%

2017 - 13,1%

2018 - 12,4%

[fichamentos01]

Fichamento 05 | Por Émerson Rodrigues

Visualize Isto - Nathan Yau

Capítulo 1 - Contando histórias com dados

O autor inicia o capítulo nos fazendo pensar em algum trabalho que já vimos que envolve visualização de dados. Ele explica que qualquer trabalho, neste estilo, que nós possamos lembrar está relacionado com uma história. A visualização desses dados, assim, ajuda a contar uma história.

Mais do que números

Dados são uma representação da vida real. Uma excelente frase de Yau que resume seu pensamento sobre o que são e qual a importância da visualização de dados. Para o pesquisador, dados podem ser tediosos se não soubermos o que procurar neles, porém, podem nos ajudar a enxergar muito além, quando entendemos que eles não são apenas um amontoado de números.

Em suma, os dados, enquanto objetivos, geralmente têm uma dimensão humana contida. Yau cita o exemplo do desemprego para mostrar que isso, de fato, acontece, já que cada pessoa desempregada não é um simples dado estatístico. “Os dados representam indivíduos, então você deveria abordar os dados desta forma”.

Jornalismo

Yau cita um fato pessoal de aconteceu com ele, na época em que era estagiário no jornal The New York Times. Lá, ele aprendeu a relatar dados como notícias, o que estava muito relacionado com o design, organização, confirmação dos dados, investigação e pesquisa. Para Yau, quando você olhar para um gráfico, por exemplo, você tem a chance de entender os dados. Um gráfico, juntamente com o seu design, não servem apenas para fazer uma visualização de dados, mas também para explicar o que a visualização mostra.

Artes

Neste tópico, mais uma vez, Yau cita o The New York Times, explicando que o jornal apresenta os dados e nos dá os fatos. Por outro lado, no entanto, a visualização é menos voltada para a análise e mais para tocar sua emoção.

Aqui, Yau também ressalta que dados e visualização de dados nem sempre precisam ser fatos frios e concretos. Para o pesquisador, o leitor não está procurando um resultado analítico todas as vezes. Às vezes, ele só quer refletir sobre o que os dados mostram. Yau usa de uma analogia para explicar essa parte melhor: nem todo filme é um documentário, assim, nem toda visualização de dados tem que ser em forma de gráficos ou mapas tradicionais.

No vídeo abaixo, Nathan Yau, autor de Visualize Isto, resume bem o que é visualizar dados na sua visão:

Entretenimento

Yau lembra também que a visualização de dados também ganhou espaço no entretenimento. Ele cita, por exemplo, o Facebook, que utilizou da atualização de status para calcular o dia mais feliz do ano. Assim, os dados, na medida em que nos “conhecem” melhor, revelam um pouco sobre nós mesmos e a sociedade.

Compelindo

Yau diz, entretanto, que as histórias nem sempre têm o objetivo de informar ou entreter. Às vezes, elas são feitas para promover urgência ou obrigar as pessoas a agir. A visualização de dados, para Yau, não fica atrás, na medida em que ela também ajuda a contar uma história. O pesquisador é enfático, porém, ao dizer que a influência dos dados sobre seus leitores dependem de como eles são apresentados. Em resumo, depende da forma como se conta a história mostrada por esses dados.

A citação a seguir explica bem o que Yau defende como apresentação correta dos dados: “Pense no desenvolvimento da personagem. Cada dado específico tem uma história por trás, assim como qualquer personagem de um livro tem um passado, presente e futuro” (p.7).

O que procurar

Antes de se contar uma história, é preciso aprender a construir sentenças. Logo, para apresentarmos dados, é preciso primeiro procurar padrões e relações entre informações presentes nestes dados.

Padrões

Você cresce com a idade. Chega um momento em que para de crescer fisicamente (talvez aí o crescimento passe a ser na base das experiências e histórias pessoais). Você envelhece. Seus cabelos ficam grisalhos a medida em que o tempo passa. Essas mudanças, para Yau, acontecem tão devagar que você sequer percebe. “A mudança em si pode ser tão interessante quanto o processo de mudança” (p.8). Em suma, há padrões nos exemplos citados acima. “Tente abordar seus dados de uma forma mais exploratória e você provavelmente terá respostas mais interessantes” (p.9).

Neste outro vídeo, David McCandeless dá uma palestra interessante sobre “a beleza da visualização de dados”. Vale a pena conferir:

[fichamentos01]

Fichamento 04 | Por Émerson Rodrigues

 Estatística para Ciências Humanas - Jack Levin

Capítulo 4 - Medidas de Tendência Central

No início do capítulo 4, Jack Levin inicia a discussão lembrando que é comum vermos o termo “média” em nosso cotidiano, graças a utilidade que o termo pode representar como parâmetro de uma pesquisa/levantamento. Em pesquisas, Levin explica que esse termo “médio” é conhecido como medida de tendência central, e não inclui somente média aritmética, mas também a moda e a mediana.

Moda

É o termo que mais se repete. Segundo Levin, pode ser encontrada com muito mais facilidade por exame do que por cálculo. O pesquisador lembra que a moda pode ser tanto unimodal, quando há apenas um ponto de frequência máximo, quanto ter dois mais pontos de frequência.

Mediana

Medida de tendência central que corta a distribuição em duas partes iguais, quando os dados são dispostos por ordem de tamanho. Vale lembrar que, se uma distribuição tiver um número de elementos ímpares, a mediana será o dado que cai exatamente no meio da distribuição. Se a distribuição for par, no entanto, ela contará com dois valores considerados “centrais”, ou seja, a mediana será uma média aritmética simples desses dois valores.

Média Aritmética

Medida de tendência central mais costumeiramente vista, a média aritmética nada mais é do que o cálculo que consiste em somar um conjunto de escores e dividir o total pelo número de parcelas, ou seja, somar os elementos presentes em uma distribuição e dividir o valor obtido pelo total de elementos.

Diferentemente da moda, o valor obtido na média nem sempre é o que ocorre com mais frequência, assim como pode não ser necessariamente o ponto central de uma distribuição, caso da mediana. Levin então explica que a média aritmética pode ser tomada como “centro de gravidade”, isto é, um ponto de qualquer distribuição em torno do qual se equilibram as discrepâncias positivas e negativas, onde podemos conceituar discrepância como sendo a distância da média a qualquer escore bruto.

Assim, para calcularmos uma determinada discrepância, basta subtrair a média aritmética de qualquer escore bruto obtido. Vale lembrar que, quanto maior a discrepância, maior a distância entre o valor total dos elementos somados da distribuição e a média da mesma.

Forma de distribuição

A forma de uma distribuição pode influenciar o pesquisador na escolha de uma medida de tendência central, segundo Levin. Ele cita o exemplo de que, em uma distribuição unimodal, perfeitamente simétrica, a moda, a mediana e a média serão idênticas, visto que o ponto de frequência máximo é também o valor “mais central” e o “centro de gravidade” dos dados. Isso quer dizer que as medidas de tendência central coincidirão no ponto central, exatamente em um “pico” da distribuição.

Levin então explica um aspecto muito importante quando o pesquisador trabalha com uma distribuição assimétrica: ele deve escolher qual medida de tendência central será a que melhor representa aquela distribuição, visto que média, mediana e moda não vão coincidir em um mesmo ponto.

Aqui ele também traz uma informação muito debatida por nós em sala de aula: a média é muito influenciada pelos valores extremos, enquanto que a mediana sofre pouca ou até mesmo nenhuma influência por eles. Portanto, numa distribuição em que a média, a moda e a mediana não coincidem, a mediana estará sempre entre a média e a moda, por isso é a medida de tendência central mais apropriada para ser usada em casos como esse.

Objetivo de pesquisa

Qual a medida de tendência ideal? Se o pesquisador estiver com pressa ou trabalhando com uma distribuição bimodal, ele geralmente vai utilizar a moda. Essa medida, contudo, pede uma análise cuidadosa dos dados, por isso, caso o pesquisador queira uma medida que seja exata, a decisão fica geralmente entre a mediana e a média.

Em uma distribuição assimétrica, o pesquisador, de acordo com Levin, deveria optar pela mediana, visto que ela nos dar um quadro balanceado dos escores extremos, além de ser usada como ponto de distribuição. No entanto, a média tem preferência sobre a mediana, já que pode ser facilmente usada em análises estatísticas mais avançadas. Além disso, a média é mais estável que a mediana, ou seja, se for realizada uma amostragem de uma população, a média variará menos do que as medianas.

Confira no vídeo abaixo uma vídeo aula rápida sobre média aritmética, moda e mediana com o professor Ítalo Benfica!

Capítulo 5 - Medidas de Variabilidade

Levin começa esse capítulo esclarecendo que, embora a média, a moda e a mediana sejam ótimas para descobrir, a partir de um único número, o que é “médio” e “típico” numa distribuição, elas fornecem apenas uma visão incompleta de um conjunto de dados, o que pode causar confusões ou distorções. Diante disso, o capítulo 5 vai discutir sobre as medidas de variabilidade mais conhecidas - amplitude total, desvio médio e desvio padrão - que ajudam a acabar com essas confusões e/ou distorções.

Amplitude total

Diferença entre o maior e o menor número de uma distribuição. Segundo Jack Levin, calcular a amplitude total é algo simples, mas possui uma enorme desvantagem: é inteiramente dependente de apenas dois elementos de uma distribuição. Isso quer dizer que uma simples troca do menor e do maior número pode fazer com que amplitude total varie bastante, o que torna essa medida de variabilidade pouco exata no que diz respeito justamente a variabilidade de um determinado objeto estudado.

Desvio Médio

Distância entre qualquer elemento da média aritmética da distribuição. Para termos acesso ao valor absoluto do desvio médio de uma sequência de dados, precisamos saber primeiro qual o valor de discrepância de cada elemento da distribuição em relação a média. O segundo passo é somar esses valores e dividi-los pelo número de elementos do conjunto de dados. O valor obtido após esse cálculo indica que, em média, os elementos desse conjunto de dados oscilam 2,67 unidades em torno da média.

Desvio Padrão

Neste tópico, descobrimos que o desvio médio foi “deixado de lado” pelos pesquisadores para dar lugar ao desvio padrão, que nada mais é do que a raiz quadrada da média das discrepâncias ao quadrado e que é indicado pela letra grega sigma.

Significado do Desvio Padrão

Segundo Levin, o desvio padrão, assim como o desvio médio, representa a variabilidade média de discrepâncias com relação a média aritmética. Outro ponto importante é que quanto maior a variabilidade em torno da média de uma distribuição, maior o desvio padrão.

Comparação entre amplitude total, desvio médio e desvio padrão

A amplitude total pode ser considerada um mero índice preliminar da variabilidade de uma distribuição, segundo Levin, já que sua obtenção é simples e fácil, mas ela não é muito confiável. Todavia, a amplitude total pode nos ajudar a mensurar o desvio padrão, que é cerca de ⅙ do tamanho da amplitude total. O autor ressalta também que, enquanto o amplitude total é calculada a partir de dois elementos de um conjunto de dados (o maior e o menor), o desvio padrão e o desvio médio levam em conta todos os escravos da distribuição. Apesar de confiável, o desvio padrão, no entanto, também apresenta algumas desvantagens, incluindo o fato do cálculo ser difícil e demorado.

Por fim, confira no vídeo abaixo, uma importante aula sobre medidas de dispersão. O Canal é o Professor Guru!

[fichamentos01]

Fichamento 03 | Por Émerson Rodrigues

Estatística para Ciências Humanas - Jack Levin

Capítulo 7 - Amostras e populações

Logo no início do capítulo 7, Jack Levin inicia a discussão com os conceitos de População e Amostra, utilizando-se de exemplos comuns como a quantidade de estudantes de uma universidade ou membros de um sindicato X. Ele define então população - ou universo - como sendo um conjunto de indivíduos que possuem, pelo menos, uma característica em comum.

Em virtude de o pesquisador não ter nem tempo nem recursos econômicos suficientes para fazer pesquisas com 100% dos indivíduos de um determinado grupo, ele pôs-se a estudar apenas uma amostra desse grupo, que seria um número menor de sujeitos tirados dessa população. Assim, a partir da amostra, o pesquisador busca tirar conclusões do grupo em que esta amostra foi extraída.

Dito isso, Levin destaca que o processo de amostragem está presente no nosso cotidiano. Aqui, a primeira ideia que vem a minha cabeça são as pesquisas eleitorais, encomendadas, em sua maioria, por jornais e institutos ligados ao mercado de ações. No dia do primeiro e segundo turnos das eleições, tais sondagens podem até não ser tão exatas, no entanto, não restam dúvidas de que elas trazem um importante parâmetro para os eleitores situarem seus candidatos dentro da corrida eleitoral, algo que tem tanto aspectos positivos quanto negativos.

Assista ao vídeo abaixo e entenda um pouco mais sobre os conceitos de população e amostra:

Métodos de Amostragem

Neste tópico, Jack Levin ressalta que o pesquisador que trabalha com amostras utiliza técnicas mais elaboradas e sistemáticas de amostragem do que as comumente usadas no dia a dia, sempre com a preocupação de saber se sua amostra é bem representativa da população estudada. Assim, se todos os componentes de uma população tiverem igual oportunidade de participar da amostra, diz-se que o método usado é o da amostragem casual. Se não for o caso, fala-se então em amostragem não-casual.  

Amostras Não-casuais

Também conhecida como amostragem acidental, esta amostra se baseia com exclusividade no que convém ao pesquisador. Em outras palavras, o pesquisador simplesmente inclui os sujeitos convenientes na amostragem e exclui os inconvenientes.

Um tipo muito comum de amostragem não-casual é a de quotas, segundo Levin, em que diversas características de um população, como idade, sexo e classe social são amostradas nas mesmas proporções em que figuram na população. É esse, inclusive, o tipo de amostra utilizado nas pesquisas de intenções de voto. Assim, se a população brasileira é composta majoritariamente por mulheres, então, na amostra, deve-se ter, obrigatoriamente, mais mulheres do que homens.

Amostras casuais

Já a amostragem casual dá a cada membro da população igual oportunidade de fazer parte da amostra. Para essa amostra dê certo, Levin lembra que todos os sujeitos de uma população devem ser identificados antes da extração da amostra. Um exemplo de uma amostra casual simples é citado pelo autor de Estatística para Ciências Humanas. Quem nunca vendou os olhos para tirar um papel de amigo secreto de um recipiente que atire a primeira pedra.

Esse é o exemplo mais explicativo possível, visto que, ao vendar os olhos, nós temos a possibilidade de selecionar qualquer pessoa participante da brincadeira aleatoriamente. O pesquisador, entretanto, não retira nomes de um chapéu, mas utiliza de uma tábua de números aleatórios para conseguir êxito com sua amostragem.

Confira no vídeo abaixo os tipos de amostragem utilizadas em pesquisas científicas:

Erro amostral

O objetivo de um pesquisador é tentar obter uma amostra que represente uma população na qual ele tem interesse. Dito isso, Jack Levin ressalta que amostras casuais simples dão mais representatividade as características populacionais do que as amostras não-casuais, visto que aquelas dão a todos os membros da população a mesma oportunidade de seleção.

No entanto, é de se esperar sempre alguma diferença entre uma amostra, aleatória ou não, da população da qual ela foi extraída. Esse fator, conhecido como erro amostral, aparece tanto se a pesquisa for bem executada ou não, apesar das boas intenções do pesquisador.

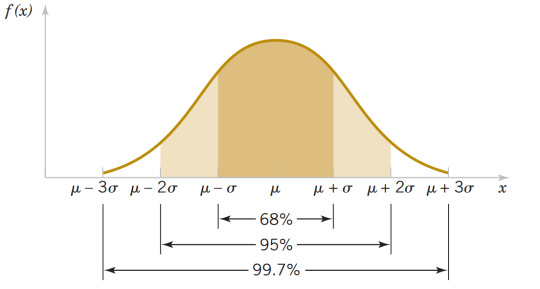
Distribuição Amostral de Médias

Levin inicia esse outro tópico com uma pergunta que muitos alunos devem tê-lo feito ao se deparar com um erro amostral: como é possível generalizar de uma amostra para uma população? Antes de seguir para essas discussões, o autor, porém, afirma que é necessário examinar algumas características de uma distribuição amostral de médias.

São elas: a distribuição amostral de médias aproxima-se da curva normal; a média de uma distribuição de médias amostrais é igual à verdadeira média populacional, ou seja, se calcularmos a média das médias amostrais teremos média igual ao valor da verdadeira média populacional; e o desvio padrão de uma distribuição de médias amostrais é menor do que o desvio padrão da população.

A Distribuição de Médias Amostrais Vista como uma Curva Normal

Diante das explicações, a curva normal então pode ser considerada uma distribuição de probabilidades, indo da probabilidade mais “baixa” até a mais “alta”. Diante disso, podemos dizer que as probabilidades decrescem à medida em que nos distanciamos da média das médias, isto é, da verdadeira média populacional.

Erro padrão da média

Na prática, segundo Levin, o pesquisador raramente faz coleta de dados de mais do que uma ou duas amostras, a partir das quais ele ainda deseja generalizar para a população toda, afinal, “extrair uma distribuição de médias amostrais requer o mesmo esforço que o de estudar individualmente cada membro da população”.

Diante disso, ele não teria como estimar qual o desvio padrão e a média das médias de sua distribuição amostral. Levin destaca, contudo, que o estudioso possui um bom método para estimar o desvio padrão a partir dos dados que lhe fornecem uma única amostra. Tal estimativa é conhecida como erro padrão da média.

“Com a ajuda do erro padrão da média, podemos encontrar o intervalo de valores dentro do qual a verdadeira média populacional pode cair. Podemos, também, estimar a probabilidade com que a nossa média populacional realmente cairá dentro desse mesmo intervalo (de valores de médias). Este é o conceito de intervalo de confiança”.

Intervalos de confiança

Na tomada de decisões estatísticas nunca há possibilidade de ter certeza absoluta. O uso do intervalo de 95%, por exemplo, quer dizer que há 95 possibilidades em 100 de estar-se correto. No entanto, devemos sempre ter em mente que a média amostral do pesquisador poderia ser uma daquelas 5 possibilidades em 100 que caíram fora do intervalo estabelecido.

Uma coisa importante de se dizer é que, quando aumentamos o intervalo de confiança de uma amostra, mais é difícil estimar a verdadeira média populacional. Por isso, o estudioso deve escolher entre estar correto com maior precisão ou estar correto com maior confiança.

Estimativa de proporções

Não raro o pesquisador procura obter uma estimativa duma proporção populacional a partir de outra proporção resultante do estudo de uma amostra casual. O maior exemplo disso são as pesquisas de intenções de voto, feitas antes das eleições. Quando um pesquisador anuncia que 45% dos brasileiros votarão em Fernando Haddad (PT), no entanto, ele reitera com convicção de que não está 100% correto. Em geral, as pesquisas de intenções de voto no Brasil, por exemplo, tem de 95% de intervalo de confiança.

Referências

LEVIN, Jack. Estatística para Ciências Humanas. 2004.

[fichamentos01]

Fichamento 02 | Por Émerson Rodrigues

Como Mentir com Estatística - Huff Darrel

Capítulo 3 - Os numerozinhos que não estão lá

No capítulo 3 do seu livro Como Mentir com Estatística, Huff Darrel inicia a discussão citando o exemplo da pasta Doake’s, que, segundo a própria Doake’s, leva as pessoas que a usam a ter 23% menos cáries do que pessoas que utilizam outras marcas. Uma informação em letras minúsculas, no entanto, diz que apenas 12 pessoas participaram da pesquisa, o que expõe que os numerozinhos que não estão lá, ou pelo menos os que não estão na “cara do público consumidor”, podem ser muito importantes para o contexto.

Darrel explica que, no caso da Doake’s, os testes poderiam levar a três situações: as cáries das pessoas envolvidas nos testes diminuírem, aumentarem ou aparecerem na mesma proporção. Nos dois últimos casos, a pesquisa é arquivada, enquanto que no primeiro, mais cedo ou mais tarde, um grupo pode mostrar uma redução no número de cáries digna de manchetes.

O pesquisador explica que um teste envolvendo um pequeno número de pessoas, como o das pastas Doake’s, pode levar a resultados imprevisíveis, algo menos provável quando a amostragem é expandida. Para justificar isso, Darrel cita o caso do cara-ou-coroa. Segundo testes científicos, a probabilidade de a face da moeda voltada para cima ser cara ou coroa é de 50%, desde que esse experimento seja repetido em um número próximo a 1.000 jogadas.

Agora, se sua paciência durá 10 jogadas, por exemplo, existe grande chances de seus resultados não chegarem a 50%. “Apenas quando há um número grande de tentativas é que a lei das médias fornece uma descrição ou predição realmente útil”, explica o pesquisador. No caso do cara-ou-coroa, um número de tentativas próximo a 1.000 faz com que os resultados fiquem próximos de 50%. Huff Darrel explica, entretanto, que o número da amostra, às vezes, não é o que parece.

Para comprovar isso, ele cita o exemplo de um teste da vacina de poliomielite feito com pouco mais de 1.000 crianças de uma comunidade. Enquanto algumas tomaram a vacina, outras não receberam a medicação para servir de controle. Resultado: a comunidade foi atingida por uma epidemia, mas nenhuma das crianças, tanto as vacinadas quanto as não vacinadas, contraíram a doença.

Darrel lembra que isso aconteceu porque, na taxa normal, apenas dois casos de pólio seriam esperados de um grupo de tal tamanho (pouco mais de 1.000 crianças), ou seja, apenas em um grupo 15 a 20 vezes maior do que esse que seria possível se obter “uma resposta significativa de alguma coisa”.

Darrel finaliza essa primeira parte de argumentação do capítulo destacando, porém, que nem tudo é culpa da classe médica, já que a pressão pública e o jornalismo apressado acabam lançando um tratamento não comprovado.

Confira no vídeo abaixo um exemplo de como a manipulação de estatísticas ainda continuam a acontecer nos dias atuais:

Como evitar sermos enganados?

Darrel então se faz uma pergunta: “como evitar sermos enganados por resultados inconclusivos?”. Para ele, existe uma maneira simples de fazer com que isso não ocorra conosco, leitores leigos: entender o numerozinho que não está lá. Uma fonte importante de orientação é o nível de significância das pesquisas, que são geralmente uma probabilidade estatística daquela pesquisa ser precisa.

Quanto menor o nível de significância, mais poderemos acreditar que os números que vemos são, de fato, representações próximas do real. Ou seja, se o nível de significância for de 1%, então haverá 99 chances em 100 de que uma aparente diferença (ou seja lá o que for) seja verdadeira.

Outro numerozinho que pode nos ajudar a não sermos enganados é o que nos informa a faixa de variação, ou o desvio da média que é dada. Darrel alerta, no entanto, que algumas médias podem ser mais piores do que úteis. Afinal, “nada conhecer sobre um assunto é, frequentemente, mais sadio do que saber o que não é verdade”.

Nesse ponto, Darrel usa o exemplo a respeito da habitação americana. Nos EUA, segundo a pesquisa, são, em média, formadas por 3,6 pessoas, o que significa, de acordo com o levantamento, que a maioria das famílias tem de 3 a 4 pessoas. Assim sendo, a maioria dos construtores constroem casas com dois dormitórios.

Essa estatística, atesta o pesquisador, é enganosa, visto que apenas 45% do total das famílias americanas se constituem de três ou quatro pessoas, enquanto que 35% são de uma ou duas pessoas e 20% são de mais de quatro pessoas. Ou seja, a média não mostra qual é a maior proporção das famílias americanas, algo que trouxe consequências extremamente caras para os construtores. “O número fracionário fez-nos esquecer o óbvio, que todos conhecemos, da simples observação: muitas famílias são pequenas, e algumas são grandes”, resume Darrel.

E por que então o numerozinho que não está lá continua sem estar lá? Pelo simples fato de sua ausência geralmente passar despercebida justamente por aqueles que mais deveriam comprovar a veracidade das informações: os jornalistas. E pior: às vezes, os próprios jornalistas acabam por repassar conteúdos com informações matemáticas equivocadas.

Um exemplo claro trazido por Huff Darrel diz respeito a um anúncio que o pesquisador encontrou no Time. No anúncio diz: “hoje, a energia elétrica acha-se disponível para mais de três quartos das fazendas americanas”. Darrel explica logo depois que o “truque” do anúncio está na palavra disponível. Isso quer dizer que três quartos das fazendas americanas têm eletricidade à disposição, mas não significa que três quartos das fazendas possuem energia elétrica.

Referências:

DARREL, H. Como mentir com estatística. 1954

[fichamentos01]

Fichamento 01 | Por Émerson Rodrigues

A numeracia e a formação dos jornalistas - Susana Pereira, José Azevedo, António Machiavelo

Introdução

Os autores iniciam a discussão destacando a dificuldade dos profissionais da comunicação em utilizar a matemática na produção de notícias. Eles lembram ainda que o uso da matemática é fundamental tanto em contextos cotidianos quanto profissionais, destacando que a numeracia é uma das dez competências essenciais no exercício da profissão de jornalista.

Pereira, Azevedo e Machiavelo pontuam que o uso da matemática nas matérias jornalísticas é essencial para dar credibilidade ao que se está sendo discutido, o que dar mais confiança aos leitores que estão lendo aquela notícia. Os erros matemáticos cometidos pelos profissionais da imprensa em suas respectivas notícias e reportagens, no entanto, são um problema grave da falta de contato de nossa profissão com os números - algo que, em parte, ocorre desde o período de faculdade. Os erros também podem ser associados ao curto espaço de tempo para elaboração da matéria e à pirâmide invertida.

Antes de prosseguir, confira no vídeo abaixo alguns conceitos importantes sobre Jornalismo de Dados!

Metodologia e desenho de investigação

Para discutir o tema, os autores do artigo aqui fichado fizeram um estudo com 53 pessoas, no ano letivo 2012/2013. Ao todo, 26 alunos da turma do 3º ano da vertente de jornalismo e 27 alunos de uma das turmas do 1º ano.

Para aplicação no estudo desenvolveu-se o inquérito por questionário “A Matemática nas notícias de jornais portugueses” utilizando excertos de notícias de jornal. Depois de validado, o questionário foi utilizado para recolher dados quantitativos sobre a capacidade de adaptar as competências de identificação e correção de erros matemáticos ao contexto de notícias. Desenvolveram-se oito questões, seis das quais com erros matemáticos e duas sem erros.

Resultados

Os resultados da análise da numeracia dos alunos participantes apresentam-se em três partes. Primeiro faz-se uma caracterização dos alunos incluindo informação sociodemográfica e opções acadêmicas. Em um segundo momento, apresentam-se os dados referentes ao desempenho dos alunos com base em três níveis diferentes de conhecimento matemático — identificação da existência de erro, descrição do erro e sugestão de correção. Por fim, foram expostos os dados referentes ao desempenho dos alunos no teste.

Quando analisado as respostas dos estudantes quanto a existência de erros, identificação de erros e correção dos mesmos, os pesquisadores descobriram que a proporção de respostas corretas, no que se refere a existência ou não de erros varia muito de acordo com a pergunta.

Por exemplo, apenas 5,7% dos indivíduos concluíram, corretamente, que existe um erro na pergunta 6 e, por sua vez, 58,5% referiram não existir erro na número 4 que, de fato, não apresentava erros. Para os pesquisadores isso pode ser resultado do fato da maioria dos inquiridos ter respondido “Não” ou “Não sei” a todas as questões nas quais se solicitava para verificar se existia algum erro, o que pode ajudar a justificar a elevada proporção de respostas corretas quanto à existência de erro na pergunta 4.

Os dados da primeira tabela permitem ainda observar que existiu uma clara dificuldade dos indivíduos na identificação correta dos erros que efetivamente existem nas perguntas, já que em qualquer uma delas, são menos de 25% os alunos que identificam corretamente de que erro se trata.

Há ainda uma grande diferença entre a percentagem de alunos que afirmou existir erro numa determinada questão (naqueles que tinham algum erro) e a proporção de indivíduos que foram capazes de identificar corretamente de que erro se tratava. A pesquisa apontou, porém, que aqueles que conseguiram identificar os erros, em sua maioria, conseguiu corrigir as porcentagens, o que sugere que eles tinham competências matemáticas adequadas para retificar os erros, indicando também que possuem um conhecimento aprofundado do conceito ou processo envolvido.

Dos 53 indivíduos que participaram da pesquisa, 22 corrigiram algum erro nas questões. Destes alunos, dois corrigiram erros em três das oito questões e seis corrigiram os erros em duas delas. Os 14 participantes restantes apenas corrigiram o erro em um dos oito questionamentos.  

Embora não seja estatisticamente significativa a diferença entre alunos de estudaram Matemáticas e suas Tecnologias e Artes Visuais © de uma forma mais aprofundada no Ensino Médio e alunos que estudaram com maior aprofundamento as Ciências Humanas (H), aqui em consideração uma diferença era expectável na medida em que os alunos que frequentaram formação na área C têm uma maior componente curricular de matemática do que os outros, onde ela é residual.

No entanto, deve salientar-se que as competências necessárias para responder corretamente às questões colocadas não requerem conhecimentos mais complexos do que os que são abordados no ensino básico. Este aspecto sugere que as diferenças de desempenho entre os alunos que optaram por uma área ou por outra no ensino secundário se podem dever à regularidade com que utilizam os conhecimentos matemáticos adquiridos no ensino básico — enquanto os alunos da área de Ciências e Tecnologias ou Ciências Socioeconômicas reforçam aprendizagens previamente assimiladas no ensino básico, isso não ocorre de forma tão consistente com os alunos de Línguas e Humanidades ou Artes Visuais.

Além disso, os dados permitem ainda verificar que as aprendizagens ao longo do curso não contribuíram para uma melhoria do nível de numeracia dos adultos.

Discussões e conclusões

Por fim, após analisar os dados da pesquisa, os autores concluem que o nível de conhecimentos matemáticos por parte dos participantes da pesquisa é inferior às necessidades da profissão de jornalista. Pereira, Azevedo e Machiavelo se mostram ainda preocupados com a não melhora dos níveis de competências matemáticas dos estudantes ao longo do ano, indicando que a faculdade de comunicação não educa neste sentido. Assim, os pesquisadores concordam que existe uma falta de investimento na formação em matemática nos cursos de jornalismo.

Para os autores da pesquisa, o fato mais relevante para a diferenciação entre sujeitos que participaram da pesquisa parece ser a sua formação do ensino secundário, uma vez que que o desempenho global dos questionados no teste foi superior entre aqueles que optaram pela formação em Ciências e Tecnologias ou Ciências Socioeconômicas no ensino secundário (ensino médio e fundamental), isto é. que possuíam uma maior formação na área da matemática. O resultado, assim, destaca a importância da formação geral na área das competências quantitativas.

Referências:

AZEVEDO, J.; MACHIAVELO, A.; PEREIRA, S. A numeracia e a formação de jornalistas. Prisma.com

[fichamentos01]

Trabalho Final - Jornalismo de Dados | Por Émerson Rodrigues, Carlos Vinícius e Tainã Maciel

Mês de março registra maior número de atendimentos por picada de escorpião em Fortaleza

Quantidade de casos pode estar associado a precipitações, revela pesquisa

Março foi o mês com maior número de atendimentos por picadas de escorpião no Centro de Assistência Toxicológica (Ceatox) do Instituto Doutor José Frota (IJF), em Fortaleza, durante o primeiro semestre de 2018. Segundo dados do Ceatox, 310 pessoas foram atendidas no Centro em decorrência de picadas de escorpião em março. De acordo com uma pesquisa de estudantes da disciplina de Jornalismo de Dados, da Universidade Federal do Ceará (UFC), a quantidade de casos pode estar associada, mesmo que indiretamente, ao índice de precipitações.

Março, com 310 atendimentos, lidera a lista dos meses com mais pessoas picadas, seguido de junho (296), maio (292), abril (285), fevereiro (242) e janeiro (216). Ao todo, 1.922 pessoas foram atendidas pelo Ceatox nos primeiros seis meses deste ano. Confira os dados na tabela abaixo:

Estudantes da disciplina de Jornalismo de Dados, ministrada pelo professor Riverson Rios, na Universidade Federal do Ceará (UFC), descobriram, no entanto, que o número de atendimentos mensais pode estar associado a quantidade de chuvas em Fortaleza.

Segundo dados da Fundação Cearense de Meteorologia e Recursos Hídricos (Funceme), fevereiro foi o mês em que mais choveu na capital cearense, com 263 milímetros, seguido de maio (248 mm), março (228 mm), abril (220 mm), janeiro (162 mm) e junho (41 mm). Confira os dados na tabela abaixo:

Os alunos do professor Riverson descobriram, comparando os dados, que os meses que sucederam meses chuvosos são os que mais apresentaram aumento no número de pessoas atendidas por picadas de escorpião no Ceatox do IJF.

Por exemplo, fevereiro, mês mais chuvoso da primeira parte do ano em Fortaleza, com 263 milímetros, é sucedido por março, mês em que o Centro de Assistência Toxicológica do IJF mais atendeu pacientes picados por escorpião.

E a relação continua. Maio foi o segundo mês em que mais choveu no primeiro semestre na capital cearense, com 248 mm. Por sua vez, junho foi o segundo mês em que mais pessoas foram atendidas no Ceatox: 296 no total.  

Março e abril, contudo, não seguem a mesma linha, já que, enquanto março ficou em terceiro lugar entre os meses mais chuvosos, abril figura na quarta posição quando o assunto é o número de atendimento por picadas de escorpião. Vale destacar, entretanto, que os meses tiveram um índice de precipitação muito parecido (em março choveu 228 mm e em abril, 220 mm), o que ajuda a explicar o motivo da relação não ter sido seguida “à risca”.

Ataques de escorpião aumentam com chuvas, diz especialista

A farmacêutica Karla Magalhães, que compõe a equipe do Núcleo de Assistência Toxicológica do IJF, ressalta que é comum que o número de ataques de escorpião aumente durante períodos com maior incidência de chuvas:

— Em relação aos escorpiões, e acidentes com animais peçonhentos de forma geral, as estatísticas, os dados epidemiológicos, revelam que realmente o aumento de chuva acarreta o aumento da incidência por vários fatores. Em relação aos escorpiões é porque eles ficam muito nos esgotos, nas tubulações de esgotos, então quando há inundação, além de serem arrastados junto com o lixo, eles tendem a procurar locais mais seguros, até porque os escorpiões respiram pela pele, eles não querem ficar afogados, então tem tendência a procurar lugares secos, para sua própria sobrevivência e reprodução —  explica Karla.

A dona de casa Ana Geane Rodrigues, 41, foi picada por um escorpião no dedo da mão direita enquanto levava o lixo para fora de casa, em 7 de abril. Ela conta que sentiu uma dor muito forte no momento da picada e que, logo depois, o local começou a inchar, ficar dormente e arder.

Como as dores só aumentavam, dona Geane teve que procurar atendimento no Ceatox do IJF, onde tomou uma medicação e foi liberada. Hoje, passados sete meses após o susto, ela revela “que se protege como pode” na hora de jogar o lixo fora.

E se eu for picado?

- Primeiramente, fique calmo. Evite fazer exercício, porque isso faz com que a velocidade de circulação do veneno na corrente sanguínea aumente;

- Procure se manter sentado e eleve o membro que foi picado;

- Ingira bastante líquido;

- Evite tomar leite e bebidas alcoólicas;

- Não morda ou tente sugar o veneno do local da picada;

- Procure orientação de algum serviço de saúde, caso, por exemplo, do Centro de Informação e Assistência Toxicológica do IJF, cujo número é (85) 3255 5050. O Centro pode orientar a pessoa a procurar um médico a depender da gravidade dos sintomas.

O animal

Os escorpiões são seres invertebrados e de ampla distribuição pelo mundo. Considerados os aracnídeos mais antigos do mundo, seus fósseis indicam que habitam a Terra há mais de 400 milhões de anos. Eles são também conhecidos pelos seus ferrões localizados no fim da cauda, conhecidos como telson, e as glândulas de veneno. A substância liberada contém neurotoxinas, histaminas e enzimas - apesar de todas as espécies produzirem toxinas, menos de trinta espécies podem causar morte em humanos.

Segundo o boletim entomológico divulgado pela Secretaria de Saúde do Estado do Ceará (SESA) no mês de agosto, os principais relatos de acidentes envolvendo escorpiões estão relacionados às espécies do gênero Tityus, tais como Tityus bahiensis, Tityus obscurus, Tityus stigmurus e Tityus serrulatus, sendo esta última responsável pelos casos mais severos.

No Brasil, especialmente no Nordeste, as notificações de acidentes por escorpiões têm crescido mais de 100% nos últimos 10 anos, ultrapassando o número de acidentes ofídicos. No estado do Ceará, este agravo correspondeu a 72% dos acidentes por animais peçonhentos nos últimos dois anos (2016-2017) segundo o Sistema de Informação de Agravos de Notificação (Sinan), que notificou 11.446 casos, sendo que 8.188 foram ocasionados por escorpiões.

O Núcleo de Vetores (NUVET), obedecendo o fluxo de encaminhamento das amostras zoológicas estabelecido pelo Ministério da Saúde (MS), recebeu 258 escorpiões coletados pelas Regionais de Saúde. O levantamento das espécies coletadas, além das duas de importância médica Tityus serrulatus e Tityus stigmurus, as espécies Tityus martinpaechi, Tityus pussilus, Bothriurus asper, Bothriurus rochai, Rhopalurus rochai, Rhopalurus agamemmon e Physoctonus debilis foram capturadas nos municípios cearenses que realizaram trabalho de controle de escorpiões.

A espécie Tityus stigmurus possui a maior distribuição geográfica encontrada em 40 municípios cearenses; já os Rhopalurus rochai vem no segundo lugar aparecendo em 39 municípios do Ceará.

O “Boletim Epidemiológico ESCORPIÕES | Agosto 2018” pode ser consultado na íntegra acessando o link:

https://www.saude.ce.gov.br/download/boletins/

SERVIÇO

Centro de Assistência Toxicológica (Ceatox) do Instituto Doutor José Frota

Endereço: Rua Barão do Rio Branco, nº 1816, Centro - Fortaleza

Contato: (85) 3255 5050

[fichamentos01]

9º Exercício (MarkDown) | Por Émerson Rodrigues e Tainã Maciel

Nesse exercício analisamos um pouco do perfil dos eleitores que ajudaram a eleger Renato Roseno (PSOL) para mais um mandato na Assembleia Legislativa.

Confira no link abaixo:

http://rpubs.com/ebr/renatorosenovotacao

[fichamentos01]

Exercício 08 (Gerando um mapa) | Por Émerson Rodrigues

ELEIÇÕES 2018 - Partidos eleitos por Estado*

LINK INTERATIVO:  http://127.0.0.1:14497/custom/googleVis/GeoChartID191062a1de2.html

LEGENDA:

Preto: 2º turno

Azul: PSDB

Lilás: PP 

Marrom: MDB

Verde: PSB

Cinza: PSD

Rosa: DEM 

Vermelho: PT

Amarelo: PHS

CÓDIGO:

# fazendo um mapa dados <- read.csv("estados.csv")

est<data.frame(estado=c("Acre","Alagoas","Amapa","Amazonas","Bahia","Ceara","Distrito Federal","Espirito Santo","Goias","Maranhao","Mato Grosso","Mato Grosso do Sul","Minas Gerais","Para","Paraiba","Parana","Pernambuco","Piaui","Rio de Janeiro","Rio Grande do Norte","Rio Grande do Sul","Rondonia","Roraima","Santa Catarina","Sao Paulo","Sergipe","Tocantins"),partido=c("PP","MDB","2ºturno","PT","PSB","DEM","PCdoB","PSD,,"PHS"))

geo<gvisGeoChart(est,"estado","partido",options=list(region="BR",displayMode="region",resolution="provinces",colors['black','blue','brown','green','grey','pink','purple','red','yellow']"))

plot(geo)

*dados aleatórios

[fichamentos01]

Exercício de Limpeza de Dados | Por Émerson Rodrigues

PDT se torna partido com mais prefeitos e vereadores do Estado

O Partido Democrata Trabalhista (PDT) elegeu 51 prefeitos nas eleições municipais de 2016, segundo dados do Tribunal Regional Eleitoral do Ceará (TRE-CE), e se tornou a sigla com mais representantes nas prefeituras cearenses. O PDT, que também foi o partido com mais candidatos disputando o pleito de 2016 - 1442 postulantes a uma vaga nas prefeituras ou nas casas legislativas municipais -, ainda elegeu 223 vereadores, distribuídos entre as 184 cidades cearenses.

PT, com 204 políticos eleitos, PSD, com 192, MDB, com 187, e PR, com 151, completaram o top 5 de legendas com mais candidatos eleitos no pleito de outubro de 2016. Já os cinco partidos com mais postulantes a cargos eletivos nas eleições de 2016 foram o PDT, como já dito, com 1442 candidatos, o MDB, com 1049, o PSD, com 930, o PT, com 905 e o PR, com 751 postulantes.

Naumi Amorim e Roberto Cláudio são eleitos no 2º turno

Pela primeira vez na história do Estado, a cidade de Caucaia teve uma disputa de segundo turno na disputa municipal. O Caucaia, segundo a Constituição de 1988, é a única cidade, além de Fortaleza, a ter disputa de 2ª turno no Estado, por possuir um colégio eleitoral com mais de 200 mil eleitores.

Na disputa pela Prefeitura da cidade, quem levou a melhor foi Naumi Amorim (PMB), que venceu Eduardo Pessoa (PSDB) no segundo turno - Naumi recebeu 80.756 votos (54.23% dos votos válidos, excluindo-se brancos e nulos), enquanto que Pessoa recebeu 68.149 votos (45,77%).

Já em Fortaleza, Roberto Cláudio (PDT) foi reeleito para um mandato de mais quatro votos à frente da capital cearense. O pedetista recebeu 678.847 votos, o que corresponde a 53,57% dos votos válidos. O segundo lugar ficou com o candidato do PR, Capitão Wagner. Wagner recebeu 46,43% dos votos válidos, totalizando 588.451 votos.

As demais cidades cearenses elegeram seus prefeitos no primeiro turno. Disputaram as prefeituras, 504 candidatos, sendo eleitos 184, mesmo número de cidades do Estado. Outros 320 não foram eleitos.

Os cinco prefeitos mais votados

Roberto Cláudio e Naumi Amorim integram a lista dos cinco prefeitos eleitos que receberam mais votos nas eleições de 2016, segundo dados do TRE-CE. Roberto Cláudio (PDT) foi o mais votado, com 678.847 votos.

Na sequência, aparecem Firmo Camurça (PR), reeleito para a Prefeitura de Maracanaú, com 81.315 votos; Naumi Amorim (PMB), com 80.756 votos, eleito prefeito de Caucaia; Ivo Gomes (PDT), com 57.908 votos, eleito prefeito de Sobral; Arnon Bezerra, eleito prefeito de Juazeiro do Norte, completa a lista, com 55.378 votos.

Célio Studart é vereador mais votado do Estado

Na disputa por uma vaga nas câmaras municipais, os cinco candidatos mais votados no pleito de 2016 disputaram uma vaga na Câmara Municipal de Fortaleza (CMFor). Célio Studart (SD) foi eleito com o maior número de votos, 38.278 no total.

Na sequência aparecem, Adail Junior (PDT), com 15.912 votos, Salmito Filho (PDT), com 15.551 votos, e Antônio Henrique (PDT), com 13.401 votos. Aílton Lopes (PSOL) ficou em quinto lugar, com 12.483 votos, mas não conseguiu se eleger por conta do quociente eleitoral, que exigia da coligação PSOL/PCB ao menos 29.200 votos. A coligação, porém, só conseguiu 28.795, o que impediu Ailton de ser eleito por exatos 405 votos.

Ao todo, 13.250 candidatos a vereador disputaram a eleição. No total, 316 foram eleitos por média, 1860 foram eleitos pelo quociente eleitoral e 9.362 herdaram uma vaga de suplente. Outros 1712 não foram eleitos.

Com informações do Tribunal Regional Eleitoral do Ceará (TRE-CE)

[fichamentos01]

Fichamento 05 | Por Émerson Rodrigues

Visualize Isto - Nathan Yau

Capítulo 1 - Contando histórias com dados

O autor inicia o capítulo nos fazendo pensar em algum trabalho que já vimos que envolve visualização de dados. Ele explica que qualquer trabalho, neste estilo, que nós possamos lembrar está relacionado com uma história. A visualização desses dados, assim, ajuda a contar uma história.

Mais do que números

Dados são uma representação da vida real. Uma excelente frase de Yau que resume seu pensamento sobre o que são e qual a importância da visualização de dados. Para o pesquisador, dados podem ser tediosos se não soubermos o que procurar neles, porém, podem nos ajudar a enxergar muito além, quando entendemos que eles não são apenas um amontoado de números.

Em suma, os dados, enquanto objetivos, geralmente têm uma dimensão humana contida. Yau cita o exemplo do desemprego para mostrar que isso, de fato, acontece, já que cada pessoa desempregada não é um simples dado estatístico. “Os dados representam indivíduos, então você deveria abordar os dados desta forma”.

Jornalismo

Yau cita um fato pessoal de aconteceu com ele, na época em que era estagiário no jornal The New York Times. Lá, ele aprendeu a relatar dados como notícias, o que estava muito relacionado com o design, organização, confirmação dos dados, investigação e pesquisa. Para Yau, quando você olhar para um gráfico, por exemplo, você tem a chance de entender os dados. Um gráfico, juntamente com o seu design, não servem apenas para fazer uma visualização de dados, mas também para explicar o que a visualização mostra.

Artes

Neste tópico, mais uma vez, Yau cita o The New York Times, explicando que o jornal apresenta os dados e nos dá os fatos. Por outro lado, no entanto, a visualização é menos voltada para a análise e mais para tocar sua emoção.

Aqui, Yau também ressalta que dados e visualização de dados nem sempre precisam ser fatos frios e concretos. Para o pesquisador, o leitor não está procurando um resultado analítico todas as vezes. Às vezes, ele só quer refletir sobre o que os dados mostram. Yau usa de uma analogia para explicar essa parte melhor: nem todo filme é um documentário, assim, nem toda visualização de dados tem que ser em forma de gráficos ou mapas tradicionais.

No vídeo abaixo, Nathan Yau, autor de Visualize Isto, resume bem o que é visualizar dados na sua visão:

Entretenimento

Yau lembra também que a visualização de dados também ganhou espaço no entretenimento. Ele cita, por exemplo, o Facebook, que utilizou da atualização de status para calcular o dia mais feliz do ano. Assim, os dados, na medida em que nos “conhecem” melhor, revelam um pouco sobre nós mesmos e a sociedade.

Compelindo

Yau diz, entretanto, que as histórias nem sempre têm o objetivo de informar ou entreter. Às vezes, elas são feitas para promover urgência ou obrigar as pessoas a agir. A visualização de dados, para Yau, não fica atrás, na medida em que ela também ajuda a contar uma história. O pesquisador é enfático, porém, ao dizer que a influência dos dados sobre seus leitores dependem de como eles são apresentados. Em resumo, depende da forma como se conta a história mostrada por esses dados.

A citação a seguir explica bem o que Yau defende como apresentação correta dos dados: “Pense no desenvolvimento da personagem. Cada dado específico tem uma história por trás, assim como qualquer personagem de um livro tem um passado, presente e futuro” (p.7).

O que procurar

Antes de se contar uma história, é preciso aprender a construir sentenças. Logo, para apresentarmos dados, é preciso primeiro procurar padrões e relações entre informações presentes nestes dados.

Padrões

Você cresce com a idade. Chega um momento em que para de crescer fisicamente (talvez aí o crescimento passe a ser na base das experiências e histórias pessoais). Você envelhece. Seus cabelos ficam grisalhos a medida em que o tempo passa. Essas mudanças, para Yau, acontecem tão devagar que você sequer percebe. “A mudança em si pode ser tão interessante quanto o processo de mudança” (p.8). Em suma, há padrões nos exemplos citados acima. “Tente abordar seus dados de uma forma mais exploratória e você provavelmente terá respostas mais interessantes” (p.9).

Neste outro vídeo, David McCandeless dá uma palestra interessante sobre “a beleza da visualização de dados”. Vale a pena conferir:

[fichamentos01]

2º Exercício | Por Émerson Rodrigues

# Émerson Rodrigues e Tainã Maciel

# Índice pluviométrico do Bairro José Walter em Fortaleza, 2017

# Desenvolvido por Émerson Rodrigues e Tainã Maciel

j <- c(140, 135, 156, 120, 100, 30, 27, 10, 25, 20, 35, 60) plot (j, type="h",      col= "yellow",      main= "Índice pluviométrico do Bairro José Walter",      xlab= "Meses do ano",      ylab= "Precipitações",      lwd= 5,      xaxt= "n",      ylim= c(0,160)) axis (1, at= 1:12, labels= c("jan","fev","mar","abr","mai","jun","jul","ago",                             "set","out",'nov',"dez"))