jmarsreb-blog

[jmarsreb-blog]

The Quotient Topology

Earlier (in Topology (pt. 1)) we discussed what a topology is. Here, we describe how to create new topologies from old.

Recall that an equivalence relation on a set $X$ is a subset $R \subset X \times X$ which satisfies three requirements;

(1) For all $x \in X$, $(x,x) \in R$.

(2) If $(x,y) \in R$, then $(y,x) \in R$.

(3) If $(x,y) \in R$ and $(y,z) \in R$, then $(x,z) \in R$.

As discussed earlier, an equivalence relation is a way of generalizing the notion of equality. We sometimes then denote that two elements are equivalent, that is, $x \sim y$ if $(x,y) \in R$. In this case, we say that $\sim$ denotes our equivalence relation.

If $x \in X$, we denote by $[x]$ the equivalence class of x. That is to say if $\sim$ is our equivalence relation, then

$$[x] = \{y \in X \ : \ x \sim y\}$$.

Remark: If $x, y \in X$, then we have that $[x] \cap [y] = \emptyset$ or $[x]$. To see this, let $z \in [x] \cap [y]$. Then we have $z \sim x$ and $z \sim y$. If $x$ and $y$ are not equivalent, then have that there is no such $z \in X$ which satisfies this relation, and so $[x] \cap [y] = \emptyset$. If there is such a $z$, then we get that for all $y \in [x]$, $y \sim z$, since transitivity gives us $x \sim y$ and $x \sim z$ implies $y \sim z$.

This can also be summarized as the following way: $[x]$ and $[y]$ are either disjoint or the same.

Take $\mathbb{R}$ to be the collection of real numbers; that is, the set $\mathbb{Q}$ unioned with all of the irrational numbers (numbers which cannot be expressed as $p/q$, where $p$ and $q$ are integers). We can define an equivalence relation on $\mathbb{R}$ as follows; if $x, y \in \mathbb{R}$, we say that $x \sim y$ if $x-y \in \mathbb{Z}$. That is, they differ only by an integer. We then need to check the requirements.

(1) We have $x -x  = 0 \in \mathbb{Z}$, so $x \sim x$ for all $x \in \mathbb{R}$.

(2) If $x - y \in \mathbb{Z}$, then $y - z = -(x-y) \in \mathbb{Z}$.

(3) If $x - y \in \mathbb{Z}$, $y - z \in \mathbb{Z}$, then we have $x - z = (x - y) + (y - z) \in \mathbb{Z}$ (here, add and subtract $y$).

So this is indeed an equivalence relation.

Now, let’s define a quotient. If $X$ is a set, and $\sim$ an equivalence relation, we define the quotient of X by $\sim$ to be

$$X/\sim = \{[x] \ : \ x \in X\}.$$

That is, this is the set of all equivalence classes of $X$.

Going back to our prior example, let’s try to see what $\mathbb{R}/\sim$ is. Taking $x \in \mathbb{R}$, we get

$$ [x] = \{\ldots, x-1, x, x+1, \ldots\}.$$

So let’s examine the half-open unit interval, $I = [0,1)$. For all $x \in \mathbb{R}$, we claim that there is a $y \in I$ such that $x \in [y]$. To see this, simply note that we can write our number in base 10 as an integer followed by some decimal expansion; hence, when we subtract the integer off, we get just the decimal expansion, which is in $[0,1)$. For example, we have $34.92$, we just subtract $34.92$ by $34$ to get $0.92$. So we have that $\mathbb{R}/\sim = I$ as sets.

The question is then can we extend this study to topologies; that is, is there some natural choice of a topology on $X/\sim$ if $X$ is a topological space?

Remark: One thing we will be using throughout is that there is a natural map $\pi : X \rightarrow X/\sim$, which is the map that sends a point $x$ to it’s equivalence class $[x]$. It’s clear that such a map is well-defined, since $x = y$ implies that $x \sim y$. Furthermore, we see that this is surjective; if $[x] \in X/\sim$, we simply take the point $x \in X$ and we see that $\pi(x) = [x]$. The map is not necessarily injective, since $[x]$ does not consist of just one point.

Remember that we said that topology was all about continuous maps, and so since we have this natural map $\pi : X \rightarrow X/\sim$, we might want to take the topology on the quotient space to be the one which makes this map continuous. This is, in fact, the correct notion, and is called the quotient topology. More formally, the quotient topology is the topology on $X/\sim$ such that $U \subseteq X/\sim$ is open if $\pi^{-1}(U)$ is open.

Remark: One thing that wasn’t mentioned in the set theory section was how functions behave with unions and intersections. Let $f : X \rightarrow Y$ be a well-defined function. Then $$f^{-1}\left( \bigcup U_\alpha \right) = \bigcup f^{-1}(U_\alpha),$$ and there is an analogous result for intersections. To see this, let $x$ be in the left hand side of the above. Then we have that it is in the pre-image of a union; so there is some $y \in \bigcup U_\alpha$ so that $f(x) = y$. But $y \in \bigcup U_\alpha$ implies $y \in U_\alpha$ for some $\alpha$. Hence, $x \in f^{-1}(U_\alpha)$, or the in the union. Likewise, if $x$ is in the right hand side, then $x \in f^{-1}(U_\alpha)$ for some $\alpha$, which means there is a $y \in U_\alpha$ such that $f(x) = y$. But this implies that $y \in \bigcup_\alpha U_\alpha$, and so $x$ is in the left hand side. So they are equal.

Remark: One should question whether this really defines a topology. Recall that we need to satisfy three axioms: (1) $X/\sim$ and $\emptyset$ need to be in this topology, (2) this is closed under arbitrary unions, and (3) this is closed under countable intersections.

(1) We see that $\pi^{-1}(X/\sim) = X$ which is open, and so this is in the topology. Likewise, $\pi^{-1}(\emptyset) = \emptyset$ which is open, and so this is in the topology.

(2) Let $\{U_\alpha\}$ be a collection of open sets, then we have that $$\pi^{-1}\left(\bigcup U_\alpha \right) = \bigcup \pi^{-1}(U_\alpha),$$ and so this is open.

(3) The argument is analogous to that of (2).

So indeed the quotient topology is a topology on the quotient space.

It turns out that the quotient topology is special, in the sense that it satisfies a universal property. That is, if we have a map $f : X \rightarrow Y$ which is continuous, and $f(x) = f(x’)$ whenever $x \sim x’$, then there is a unique continuous function, denoted by $\bar{f} : X/\sim \rightarrow Y$ where $f = \bar{f} \circ \pi$. In other words, the maps factor through.

Why exactly is this the case? First, let’s establish that $\bar{f}$ exists. Let $[x] \in X/\sim$, for all representatives $x’ \in [x]$ let $\bar{f}(x’) = f(x)$. Then this function is well-defined, since $[x] = [y] \rightarrow \bar{f}(x’) = \bar{f}(y’)$ for all $x’ \in [x], y’ \in [y]$. To see that this function is continuous, take $U \subseteq Y$ open. Then $V = \bar{f}^{-1}(U) = \{ [x] \in X/\sim \ : \ f(x’) \in U \text{ for all } x’ \in U\}.$ We then have $\pi^{-1}(V) = \{x \in X  \ : \ [x] \in V\} = f^{-1}(U)$. Since $f$ is continuous, this implies $\pi^{-1}(V)$ is open, which tells us that $V$ is open in the quotient topology. $\bar{f}$ is also continuous.

To see that $\bar{f}$ is unique, say we had another function $\bar{g}$ which satisfies the condition that $f$ factors through it. Then we have that $f(x) = \bar{g} \circ \pi(x) = \bar{g}([x]) = \bar{f}([x])$. Since this holds for all $x \in X$, we get that $\bar{f} = \bar{g}$, and so they were the same maps all along. Hence, $\bar{f}$ is unique.

Remark: Going off of the language of Munkres, our projection map $\pi : X \rightarrow X/\sim$ is sometimes referred to as a quotient map; in general, a map $\rho : X \rightarrow Y$ is said to be a quotient map if it satisfies the property that $U \subseteq Y$ open if and only if $\rho^{-1}(U)$ is open in $X$. Quotient maps induce quotient topologies on the spaces they map to.

Remark: Another important concept with these maps is the idea of saturated. A subset $C \subseteq X$ is said to be saturated (with respect to the surjective map $\pi :X \rightarrow Y$) if $C$ contains every set $\pi^{-1}(\{y\})$ that it intersects. That is, if $C \cap \pi^{-1}(\{y\}) \neq \emptyset$, then $\pi^{-1}(\{y\}) \subseteq C$. So $C$ is saturated if it equals the complete inverse image of a subset of $Y$. A quotient map then maps saturated open sets of $X$ to open sets of $Y$.

Remark: In the universal property claim, we can replace continuity with quotient and get the same result.

Claim [Munkres, Corollary 22.3]: Let $g : X \rightarrow Z$ be a surjective continuous map. There is an induced equivalence relation on $X$ via $x \sim y$ if and only if $x, y \in g^{-1}(z)$ for some $z \in Z$. Thus, we have the quotient space $X/\sim$. The map $g$ induces a bijective continuous map $f: X/\sim \rightarrow Z$, which is a homeomorphism if and only if $g$ is a quotient map.

Proof: The property given in the above statement shows us that there is indeed a map $f : X/\sim \rightarrow Z$ which is continuous since $g$ is continuous. Furthermore, we get that $f$ is a bijection; it is surjective, since for all $z$ we have that there is an $x \in g^{-1}(\{z\})$, so $f([x]) = z$, and it is injective since $f([x]) = f([y])$ implies that $x, y \in g^{-1}(z)$ for some $z \in Z$, so $[x] = [y]$. Hence, $f$ is a bijective continuous function from $X/\sim$ to $Z$.

We have an if and only if statement, so let’s start with the implication. Let $f$ be a homeomorphism, and let $U \subseteq Z$. We need to show that $U$ is open if and only if $g^{-1}(U)$ is open.The implication is clear, so we assume that $g^{-1}(U)$ is open. Then this implies that $g^{-1}(U) = \pi^{-1}(f^{-1}(U))$ is open, but since $\pi$ is the projection map we have that $f^{-1}(U)$ is open, and since $f$ is a homeomorphism we get that $U$ is open. So we get that $U$ is open if and only if $g^{-1}(U)$ is open, so $g$ is a quotient map.

Now assume that $g$ is a quotient map. Then we need to show that $f$ is a homeomorphism; we know that it is bijective and continuous, and furthermore a remark from prior tells us that it is a quotient map. So we see that if $U \subseteq X/\sim$ open, then $U = f^{-1}(f(U))$, since $f$ is bijective, and so $f(U)$ is an open map. Hence, $f^{-1}$ is a continuous map which is also bijective, so $f$ is a homeomorphism. QED

This claim is important in the following example.

Example: Let $\mathbb{R}/\mathbb{Z}$ be the quotient space from prior; that is, $x, y \in \mathbb{R}$ are equivalent if $x -y \in \mathbb{Z}$. Let $S^1$ be the unit circle equipped with the subspace topology given by $\mathbb{R}^2$; that is, $S^1 = \{(x,y) \in \mathbb{R}^2 \ : \ x^2 + y^2 = 1\}$. Then we would like to show that $\mathbb{R}/\mathbb{Z} \cong S^1$; that is, these spaces are homeomorphic. The intuition is that $\mathbb{R}/\mathbb{Z}$ as a set is $[0,1)$, and what the topology is doing is gluing $1$ to $0$ so that we have the circle.

To formally see this, let $g : \mathbb{R} \rightarrow S^1$ be the map which sends $g(x) = (\cos(2\pi x), \sin(2\pi x))$. First, notice that $g$ is clearly continuous, since it is continuous in each component. Next, we see that $g$ is surjective, and furthermore if $x - x’ \in \mathbb{Z}$, then $g(x) - g(x’) = (-2\sin(\pi x - \pi x’) \sin(\pi x + \pi x’), 2\sin(\pi x - \pi x’)\cos(\pi x + \pi x’)) = (0,0)$, or in other words $g(x) = g(x’)$. So elements which are in the same equivalence class in $\mathbb{R}/\mathbb{Z}$ get mapped to the same point in $S^1$. Furthermore, we see that this is the only case in which this can happen (to see this, for the second coordinate to be zero we need that $x$ and $x’$ differ by an integer or $x + x’ = \pi n - \pi/2$, where $n$ is an integer. If this is the case, we get that $\sin(\pi(x + x’)) \neq 0$). So we have $\mathbb{R}/\mathbb{Z} = \{g^{-1}(z) \ : \ z \in S^1\}$. So $g$ is a surjective continuous map, and so we have a bijective continuous map $f : \mathbb{R}/\mathbb{Z} \rightarrow S^1$ which is induced by this map. If we see that $g$ is a quotient map, then we win.

To see that $g$ is a quotient map, we just need to check that $U \subseteq S^1$ is open if and only if $g^{-1}(U)$ is open. It’s clear that $g$ is a continuous map, and so the implication follows.

To show the next part, it suffices to show that $g$ is an open map; that is, a map which sends open sets to open sets. A lemma from Analysis tells us that open sets in $\mathbb{R}$ are countable union of disjoint open intervals. So it suffices to show that open intervals are mapped to open sets. Let $(a,b)$, where $-\infty < a < b < \infty$, and we want to see whether $g((a,b))$ is open. But we see that if $a < 0$ and $b > 1$, $a \geq 0$, $b > 1$, $a < 0$, $b \leq 1$, then this is the whole circle and so it is open. If $0 < a < b < 1$, then we get that this is an open arc in the circle, which is indeed an open set in $S^1$, and so $g((a,b))$ is open.

Since $g$ is an open map, we have that $g^{-1}(U)$ is open implies that $g(g^{-1}(U)) = U$ is open, so $g$ is a quotient map. Hence, the prior claim tells us that $f : \mathbb{R}/\mathbb{Z} \rightarrow S^1$ is a homeomorphism, and so these spaces are homeomorphic.

Before moving on, we quickly remark on another way to produce new topological spaces. If $X$ and $Y$ are two topological spaces, we can equip the product $X \times Y$ with something called the product topology, which is the topology generated by $\{U \times V \ : \ U \text{ is open in } X, V \text{ is open in } Y\}$.

Example: Let $I = [0,1]$, and take $I^2/\sim$, where $(x,0) \sim (x,1)$ for all $x \in I$, $(0,y) \sim (1,y)$ for all $y \in I$. Equip this space with the quotient topology. Then we would like to show that this is homeomorphic to $S^1 \times S^1$ equipped with the product topology. Here, let’s regard $S^1 = \{ z \in \mathbb{C} \ : \ |z| = 1\}$ equipped with the subspace topology of $\mathbb{C}$. Then $f : I^2 \rightarrow S^1 \times S^1$ can be given by $(x,y) \mapsto (e^{2\pi i x}, e^{2\pi i y})$, where $e^{ix} = \cos(x) + i \sin(x)$. This is again clearly surjective and continuous, since the exponential here is continuous. We remark that the induced equivalence relation given by the pullback of this map matches the equivalence relation we just gave (you’ll have to break it up into cases to really see this). So showing that this is a quotient map gives us the desired homeomorphism. Again, it suffices to show that $f$ is an open map, but this is clear since it maps open arcs to open arcs, so we have that $I^2/\sim \cong S^1 \times S^1$. Furthermore, $\mathbb{R}^2/\mathbb{Z}^2 \cong S^1 \times S^1$ by a similar argument, and transitivity gives $\mathbb{R}^2/\mathbb{Z}^2 \cong I^2/\sim$. So, these spaces are all homeomorphic.

Notice that we were doing in the last problem was taking the square and gluing together sides; that is, we have the following picture, where we glue the blue side along the blue side, the red side along the red side, and the orange points are all glued together.

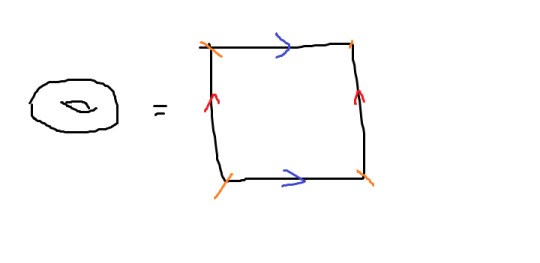
We see that this gives us the two Torus, which is viewed as a donut.

[jmarsreb-blog]

Topology (pt. 1)

Let $X$ be a set. We call the a subset of the powerset $T_X \subseteq \mathcal{P}(X)$ a topology if it satisfies three axioms;

(1) $X, \emptyset \in T_X$,

(2) $T_X$ is closed under arbitrary unions; that is, if $\{E_\alpha\}$ is a collection of sets such that $E_\alpha \in T_X$ for all $\alpha$, and $\alpha$ could be an uncountable collection, then $\bigcup_\alpha E_\alpha \in T_X$,

(3) $T_X$ is closed under countable intersections; that is, if $\{E_\alpha\}$ is a collection of at most countably many sets where the $E_\alpha \in T_X$, then $\bigcap_\alpha E_\alpha \in T_X$.

The sets which are in $T_X$ are called open sets. If $E \subset T_X$ such that $E^C \in T_X$, we call $E$ a closed set.

Remark: Open and closed are not mutually exclusive terms. We can have sets which are both open and closed; for example $X$ is open, since $X \in T_X$, while $X$ is closed since $X^C = \emptyset \in T_X$.

Remark: To be precise, we should write $(X, T_X)$ as a tuple which denotes a set $X$ and it’s topology. However, in general, the topology is understood from context, so we drop it when talking about $X$.

What topologies do is they classify continuous functions. That is, if $X$ and $Y$ are topological spaces (spaces equipped with topolgies denoted $T_X$ and $T_Y$ respectively), then a function $f : X \rightarrow Y$ is continuous if, for all $E \in T_Y$, we have $f^{-1}(E) \in T_X$. This matches our definition of continuous in the $\mathbb{R}$ sense (that is, the epsilon-delta sense) while also generalizing it to abstract spaces.A function $f : X \rightarrow Y$ is called a homeomorphism if $f$ is bijective, continuous, and $f^{-1}$ is also continuous. If there exists a homeomorphism between two topological spaces, we call those spaces homeomorphic.

Remark: Much like a bijection between sets means that the sets are essentially the same and an isomorphism between groups means that they are the same, a homeomorphism acts as a way of saying two topological spaces are essentially the same.

Example: One example of a topology is $\mathcal{P}(X)$ itself; this is called the discrete topology.

Example: Another example of a topology is the trivial topology, which consists of just $X$ and $\emptyset$.Example: Let $B_r(X) = \{y \in \mathbb{R} \ : \ |x-y| < r\}$. This is sometimes referred to as the ball of radius r centered at x. We say that a set $U$ is open in $\mathbb{R}$ if, for all $x \in U$, we have that there is an $\epsilon > 0$ so that $B_\epsilon(x) \subseteq U$. Notice that $B_r(X)$ itself is an open set; it is also sometimes referred to as the open ball of radius r centered at x for this reason.

In the example, we had that these balls somehow generated the topological space. We expand on this now; we say that a collection of sets $\{B_\alpha\}$ form a base for a topological space $X$ with topology $T_X$ if, for all $U \in T_X$ we have $U = \bigcup_\alpha B_\alpha$. That is, we can write every open set as a union of the basis elements. Here, the basis elements are the open balls, since denoting the necessary $\epsilon >0$ for each $x$ by $\epsilon_x$, we have $U = \bigcup_{x \in U} B_{\epsilon_x}(x)$.

Let $X$ be a topological space, and $x \in X$ a point. We call a subset $V \subseteq X$ a neighborhood of x if there is an open set $U$ such that $x \in U \subseteq V$. If $S$ is a collection of points, we have that $V$ is a neighborhood of S if, for all $x \in S$, we have that there is an open set $U$ so that $x \in U \subseteq V$. That is, $V$ is a neighborhood of all the points $x \in S$.

We call a topological space Hausdorff if it satisfies the following: for all $x, y \in X$, $x \neq y$, there are neighborhood $V_x, V_y$ of $x$ and $y$ respectively so that $V_x \cap V_y = \emptyset$. In a sense, this is saying that we can find neighborhoods which are separate from each point.

Remark: If there are neighborhoods which satisfy this, then in particular there are open neighborhoods which satisfy this.

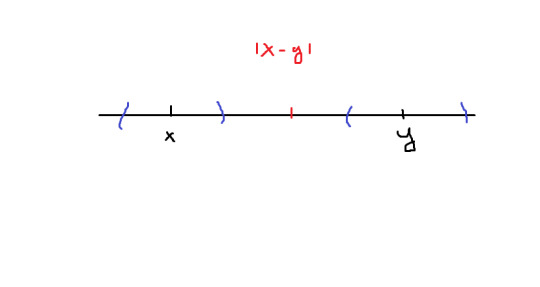
Example: One example of a Hausdorff space is $\mathbb{R}$; take $x \neq y \in \mathbb{R}$. Let $r = |x-y|/4$. Then we have $x \in B_{r}(x)$, $y \in B_{r}(y)$. Let $z \in B_r(x) \cap B_r(y)$. Then we have $|x-z| < |x-y|/4$ and $|y-z| < |x-y|/4$. By the triangle inequality, we get $|x-y| < |x-z| + |y-z| < |x-y|/2$; but this is a contradiction if $|x-y| \neq 0$. Hence, $B_r(x) \cap B_r(y) = \emptyset$. We can visually see this contradiction below;

Non-Example: Let $X$ be an uncountable set; for example, $\mathbb{R}$. Let $T_X$ be the cofinite topology; that is, the collection of sets $U \subseteq X$ such that $X^C$ is at most countable, and throw in $\emptyset$. Then we can quickly see that $T_X$ is a topology;

(1) $X \in T_X$, since $X^C = \emptyset$, and $\emptyset \in T_X$ since we threw it in.

(2) Take an arbitrary collection of sets in $T_X$, denoted by $\{E_\alpha\}$. Then DeMorgan’s laws say that (after throwing at all the null-sets, which aren’t contributing anything) $\left(\bigcup_\alpha E_\alpha\right)^C = \bigcap_\alpha E_\alpha^C \subseteq E_{\alpha_0}^C$ for some $\alpha_0$ in the indices, which is countable and so this is countable. Hence, the arbitrary union is in $T_X$.

(3) If $\{E_\alpha\}$ is an at most countable collection of sets in $T_X$, none of which are the null-set since that makes this trivial, then DeMorgans tells us $\left( \bigcap_\alpha E_\alpha\right)^C = \bigcup_\alpha E_\alpha^C$ is a countable union of countable things, and so countable.So this is indeed a topology. However, take $x \neq y \in X$, and take any neighborhoods $V_x, V_y$. We have there are open sets $x \in U_x \subseteq V_x$, $y \in U_y \subseteq V_y$, and we must have $U_x \cap U_y \neq \emptyset$. Assuming otherwise, then we have that DeMorgan’s tells us $U_x^C \cup U_y^C = X$, which is impossible since $X$ is uncountable and these are countable sets. Therefore, $V_x \cap V_y \neq \emptyset$.

We can also think about general sets in $X$ and their relation to open and closed subsets. The interior of a subset is the largest open subset contained in it, while the closure of a subset is the smallest closed set containing it. Going back to neighborhoods, then, $V_x$ is a neighborhood of $x$ if $x$ is in the interior of $V_x$, denoted by $\text{Int}(V_x)$.

Another important concept when studying topological spaces is the concept of compacity. A cover of a topological space $X$ is a collection of sets $\{E_\alpha\}$ such that $X \subseteq \bigcup_\alpha E_\alpha$. An open cover is a cover in which all of the sets are open. A refinement of a cover is a subcollection $\{E_{\alpha_i}\}$ such that $X \subseteq \bigcup_i E_{\alpha_i}$. A topological space is then said to be compact if every open cover admits a finite refinement. A subset $\emptyset \neq Y \subseteq X$, where $X$ is a topological space, admits something called the subspace topology, which is the induced topology $T_Y = \{U \cap Y \ : \ U \in T_X\}$. That is, take all of the open sets in $X$ and intersect them with $Y$.

A subset $Y \subseteq X$ is said to be compact in terms of it’s subspace topology.

Remark: This is equivalent to just saying that if there is an open cover of the subset, it admits a finite refinement. That is, we don’t necessarily have to jump down to the subspace topology.

Remark: Let $X$ be a topological space, $U \subseteq X$. To show that $U$ is open, it suffices to show that for every $x \in U$, there is an open subset $U_x \subseteq U$. This is because $\bigcup_{x \in U} U_x = U$, and an arbitrary union of open sets is still open.

Remark: In a Hausdorff space, a compact set is closed. To see this, let $H \subseteq X$ be compact. For $H$ to be closed, $H^C = X - H$ has to be open. We use the trick above. Fix $y \in X-H$. For all $x \in H$, we have that there are $U_x, V_x$ so that $x \in U_x$, $y \in V_x$, $U_x \cap V_x = \emptyset$. Let these $U_x, V_x$ be open. Then we have that $\bigcup_{x \in H} U_x$ is an open cover of $H$, and so by compactness we get that there is a finite refinement $\bigcup_{i=1}^k U_{x_i}$. Examine $\bigcap_{i=1}^k V_{x_i} \subseteq X-H$, since none of these meet any of the $U_{x_i}$ which contain $H$. Then since we have a finite intersection of open sets, it’s still open, and furthermore $y \in V_{x_i}$ for all $i$. Hence, $X-H$ is open by the prior remark, so $H$ is closed.

[jmarsreb-blog]

Sets (pt. 2)

Now that we have some idea about sets, let’s start talking about how we can relate sets to one another. The idea behind this is in functions and relations. We’ll start with discussing relations.

A relation between two sets, $A$ and $B$, is simply a subset $R \subseteq A \times B$. This is a very general thing; without any sort of restrictions, this doesn’t say much about our two sets.

We now ask a more spiritual question, which is what does it mean for elements to be equal to each other? Well, in our initial approach, elements are equal if they are the same. But examine, say, $1/2$ and $2/4$ in $\mathbb{Q}$, the rational numbers. These numbers are the same, as we all know, but they aren’t represented by the same thing. So it’s maybe not always sufficient to just say that things are equal if they are the same, since if we do this we would have some issue with what was just stated.

So let’s think of equivalence as a relation, and try to figure out what restrictions we need to put on this relation in order for it to match up with our preconceived notions of equality. For one, our equivalence relation should only be on elements within the same set; we wouldn’t want to get too crazy. So let’s set $R \subseteq A \times A$ to be a relation.

Next, we need an element to be equal to itself, since this is how we originally wanted to do things. So let’s say $(a,a) \in R$ for all $a \in A$.

Now, we want things to be symmetric; we wouldn’t want $a = b$ but $b \neq a$, this would be silly. So let’s say if $(a,b) \in R$ then we want $(b,a) \in R$ as well.

Finally, we want transitivity. If $a = b$, and $b = c$, we want to be able to deduce that $a = c$. Since they are both the same as $b$, they should be the same. So, if $(a,b) \in R$, $(b, c) \in R$, then we demand that $(a,c) \in R$ as well.

These conditions are what we need for a relation to be an equivalence relation. If $(a,b) \in R$, $R$ an equivalence relation, we generally denote this as $a \sim b$ or $a = b$ or $a \equiv b$ (or you get the point, there’s a lot of ways to do this).

Now, this is one reason relations are interesting. Another is that they help us construct functions in a rigorous manner. A function $f : A \rightarrow B$ is a special kind of relation which says that $(a,b) = (a,b’)$ implies that $b = b’$. We write $b$ as $f(a)$. We generally think of functions as way of relating elements from one set $A$ to another set $B$.

Functions are great, and presumably you’ve seen many throughout your life. A maybe trivial example is $f : \{1,2\} \rightarrow \{1,2,3\}$ such that $f(1) = 2$ and $f(2) = 1$. The image of $f$ in this case is the set $\{1,2\}$. In general, the image of a function is the collection of elements which it maps to.

One thing we want to do is be able to classify sets; one way to do this was through size. It turns out functions are a good way of measuring the sizes of things, but first we’ll need a few things.

A function $f$ is said to be injective if $f(a) = f(b)$ implies $a = b$. This means that every element maps uniquely to some element in the codomain (which is the space that is being mapped to). Our function above was injective, since we did not have two elements mapping to the same element. A nonexample of an injection is the function $f: \{1,2\} \rightarrow \{1,2,3\}$ where $f(1) = f(2) = 1$. Then $f(1) = f(2)$ but $1 \neq 2$.

A function $f$ is said to be surjective if, for all $b \in B$, we have an $a \in A$ so that $f(a) = b$. In other words, every element in the codomain is hit by some element in the domain. Our functions so far have not been surjective, but an example would be $f : \{1,2,3\} \rightarrow \{1,2\}$ where $f(1) = 1$, $f(2) = 2$, and $f(3) = 2$. This is also an example of a function which is not injective.

So we’ve seen that functions can be injective, surjective, and neither injective nor surjective. In general, the best case scenario for a function is to be injective and surjective -- this means that every element maps uniquely to a point in the codomain, and every element in the codomain is hit. A function which satisfies this is called bijective. For example, $f : \{a,b,c\} \rightarrow \{1,2,3\}$ where $f(a) = 1$, $f(b) = 2$, and $f(c) = 3$ is a bijective function.

Going back to our concept of size, what does injective say about the sizes of the sets? If I have $f : A \rightarrow B$ injective, we see that every element $A$ is uniquely mapped to an element in $B$, but there may be more elements which are not hit at all since the function is not necessarily surjective. So we see that the existence of an injection implies that $|A| \leq |B|$.

Likewise, if $f : A \rightarrow B$ is surjective, then we see that every element in $B$ is hit by some element in $A$, but it may not be unique; that is, there may be more than one element which hits the same element, since the function is not necessarily injective. Therefore, we see that $|B| \leq |A|$.

So, a bijection tells us that $|A| \leq |B|$ and $|B| \leq |A|$. The only case where this happens is when $|A| = |B|$, so in fact the existence of a bijection implies that our sets are the same size! At least, this makes sense in the finite case. So we’ll also use this as our notion of size moving into the infinite sets.

Before getting too far along, we also need to define some operations on functions. If $f : A \rightarrow B$, $g : B \rightarrow C$ are functions, then we have the composition of these functions is $g \circ f = g(f) : A \rightarrow C$; that is, it’s a function from $A$ to $C$.

Let’s now think about what this composition tells us about our functions. For example, if our composition is injective, what do we know about $f$ and $g$? Well, we know that $g(f(a)) = g(f(b))$ implies $f(a) = f(b)$. If our function $f$ was also injective, we then get that $f(a) = f(b)$ implies $a = b$, and so our function $g$ is injective! However, outside of this, we may not get that $g$ is injective. It’s a good exercise to explore the same concepts with surjectivity (and also the composition of injective and surjective functions remains injective/surjective).

Using the above, we then get that the composition of bijective functions is bijective, which is good if we’re going to use this to compare sizes. This, in some way, gives us transitivity on the cardinality of sets; if $|A| = |B|$, $|B| = |C|$, then $|A| = |C|$, since there exists a bijection from $A$ to $B$, a bijection from $B$ to $C$, and we can compose these to get a bijection from $|A|$ to $|C|$.

We discussed briefly the image, but there will also be something called the inverse image or pullback of a function. Denoted by $f^{-1}(y)$, this is all of the elements which map to $y$.

Question: What does injection/surjection say about the inverse image/image?

Let’s remark here that we have a natural injection $f: X \rightarrow \mathcal{P}(X)$ via $f(x) = \{x\}$, so we know that $|X| \leq |\mathcal{P}(X)|$. Is it possible that $\mathcal{P}(X)$ has the same size as $X$? The answer is no, for obvious reasons. So we have $|X| < |\mathcal{P}(X)|$.

For a slight aside, let’s explore the implication of defining the sizes of sets as we just have. We have that $\mathbb{N} = \{1,2,\ldots\}$, i.e. the collection of all whole numbers greater than or equal to $1$, is an infinite set. Likewise, we have that $\mathbb{Z} = \{\ldots,-1,0,1,\ldots\}$ is also a negative set. We have that $\mathbb{N} \subseteq \mathbb{Z}$, so clearly we should also have $|\mathbb{N}| < |\mathbb{Z}|$, right?

If you bought the last argument, don’t feel bad. It’s a very unintuitive thing, but it turns out these sets actually share the same size. The reason is as follows: let $f : \mathbb{N} \rightarrow \mathbb{Z}$ be a function which sends $1$ to $0$, $2$ to $-1$, $3$ to $1$, and so on and so forth. If you believe the sizes are different, then it should be the case that this is not a bijection. So let’s explore this.

Injectivity: Well, if $f(a) = f(b)$, then this implies that they map to the same integer. But we don’t have repeats in the assignment given above, so the only way this happens is if $a = b$. So it is injective, which tells us that $|\mathbb{N}| \leq |\mathbb{Z}|$, as we would expect.

Surjectivity: So now there should be a number $x \in \mathbb{Z}$ which I do not hit. What would that number be, though? I can keep going on in $\mathbb{N}$ with this alternating assignment until it hits $x$ for any $x$ you give me, which should tell us that the sets are the same size...

And this is where some intuition falls apart. It turns out that this is a bijection between these sets, and so they are of the same “size.” If a set shares a bijection to $\mathbb{N}$ ,we say that it is countable. If it shares a bijection to $X_n = \{1, \ldots, n\}$, we say it is finite. One may then wonder where the madness stops; we can see that $\mathbb{Q}$ is also countable, although the argument is not pretty, but with Cantor’s diagonalization argument we get that $\mathbb{R}$ is not the same “size” as $\mathbb{N}$. So $\mathbb{R}$ is not countable. We call these kinds of sets uncountable.

If someone has ever told you that there are different “sizes” of infinity, then you can now feel satisfied at knowing what that person was trying to say.

[jmarsreb-blog]

Sets (pt. 1)

Sets are the building blocks for mathematics, and so it seems fit to start there. We think of a set as a collection of (distinct) objects.

The classic examples of sets are just $X = \{1,2\},$ the natural numbers $\mathbb{N}$ which consists of all numbers greater than 0, and the integers $\mathbb{Z}$ which consist of all whole numbers. A natural example is also $\emptyset$, which is known as the empty set, or the set which contains no elements.

Sets are natural objects, but the definition I gave isn’t quite a good one. We’ll leave the ambiguity there for now, but we may come back to more rigorous set theory later. (One may wonder; is the set of all sets which do not contain themselves a set?)

There are some natural operations we want to do with sets. For example, if I want to combine sets, I can take the union of them. That is, if $A$ and $B$ are sets, the union of the sets $A \cup B$ is the collection of elements which is either in $A$ or $B$. We’ll generally write this as

$$ A \cup B = \{x \ : \ x \in A \text{ or } x \in B\}.$$

Translating this, this says that $A \cup B$ is the collection of elements $x$ such that $x$ is in $A$ or $x$ is in $B$. We read the colon as “such that” and what follows are the conditions for the elements in the set. This is sometimes referred to as set builder notation.

Pictorially, we can think of a union as the blue shaded region in the following picture:

Another thing we may want to do is look at the elements which are contained in two given sets, $A$ and $B$. This is referred to as the intersection, and we formally write this as

$$ A \cap B = \{ x \ : \ x \in A \text{ and } x \in B\}.$$

Pictorially, we have the intersection is the blue shaded region in the following:

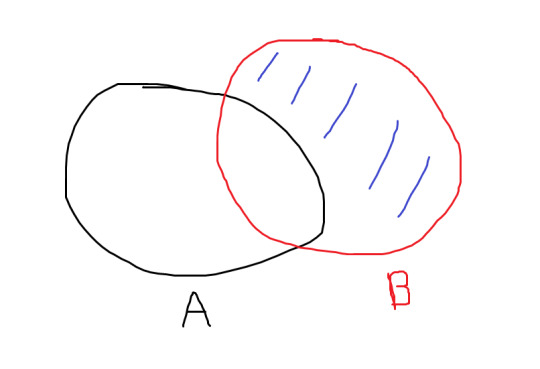
Sometimes we wish to look at elements which are in one set but not the other. This is referred to as set minus. That is, if $A$ and $B$ are sets, the set minus of them is

$$ B - A = \{x \ : \ x \in B \text{ but } x \notin A\}.$$

Again, we can think of this pictorially, where the elements in $B-A$ are the blue shaded region:

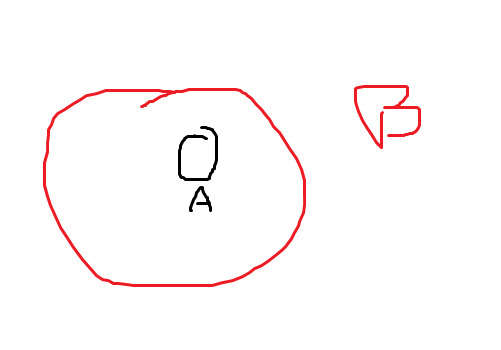
We say that $A$ is a subset of $B$ if we have that, for all $x \in A$, $x \in B$. That is, all of the elements which belong to $A$ also belong to $B$. One should have the following picture in their head:

We say that two sets are equal if $A \subseteq B$ and $B \subseteq A$, and we write it as $A = B$. You can think of this as saying that they share all of the same elements.

If we have some universal set $X$, we often write the complement as $A^C$, which is understood to be the set of elements which are not in $A$. We can also think of this as $X - A$.

Remark: If $A, B \subseteq X$, then we can think of $B - A$ as $B \cap A^C$.

A nice exercise is to verify when associativity (that is, parentheses don’t matter), commutativity (order doesn’t matter), and distributivity apply when using parentheses and intersections/unions. For example, we have that

$$ A \cup (B \cup C) = A \cup B \cup C,$$

which gives us associativity for unions, and we have

$$ A \cup (B \cap C) = (A \cup B) \cap (A \cup C) $$

which gives distributivity between unions and intersections.

One special relation we have is called deMorgan’s laws. These state the following; let $\{E_i\}$ be a countable (we’ll come back to this later, for now just think finite) collection of sets, then we have

$$ \left( \bigcup_i E_i \right)^C = \bigcap_i E_i^c$$

and

$$ \left( \bigcap_i E_i \right)^C = \bigcup_i E_i^c.$$

Proof: To prove this in the finite case, it suffices to do it for two sets. So lets say we have $E_1, E_2$ are sets. Taking $x \in (E_1 \cup E_2)^C$, we see that this says that $x \notin E_1 \cup E_2$. In other words, $x$ is not in $E_1$ or $E_2$. But this is the same as saying that $x$ is not in $E_1$ and it is not in $E_2$, or $x \in E_1^c \cap E_2^c$. Hence, $(E_1 \cup E_2)^C \subseteq E_1^C \cap E_2^C$.

Now, take $x \in E_1^C \cap E_2^C$. Then in the same way we’ve done above, we have that $x$ is not in $E_1$ and it is not in $E_2$, but this is the same as saying $x$ is not in $E_1$ nor $E_2$, which comes out to $x \notin (E_1 \cup E_2)^C$. So $E_1^C \cap E_2^C \subseteq (E_1 \cup E_2)^C$, and we have equality. The argument when we flip intersection and union is the same.

Why was doing it for two sets sufficient? Say we have sets $E_1, \ldots, E_n$, and we want to figure out

$$ \left( \bigcup_{i=1}^n E_i \right)^C.$$

We can rewrite the inside as

$$ \left( \bigcup_{i=1}^{n-1} E_i \cup E_n \right)^C.$$

Now, using what we’ve just shown, we know it holds for two sets, so we get that this is equal to

$$ \left( \bigcup_{i=1}^{n-1} E_i \right)^C \cap E_n^C.$$

We can then continue this way until we get the desired result. This is the essence of induction, which I won’t go into yet.

Another important trick is to “disjointify” sets. We say that two sets $A$ and $B$ are disjoint if $A \cap B = \emptyset$; that is, they do not share any elements. A disjoint union is a union of sets which are disjoint. The reason this is important is for notions of size; for now, staying in the realm of finite sets, we say that the size or cardinality of a set is simply the number of elements in that set. So if $X = \{1,2\}$, then the size, denoted by $|X|$, of $X$ is simply 2. When we have a disjoint union, we get to add up the sizes of the sets to get the size of our union; when we do not have a disjoint union, this is not the case.

For example, let $X = \{1,2\}$, $Y = \{2,3\}$ and $Z = \{3,4\}$. Then $X \cap Y = \{2\}$, which is not the empty set, and so these are not disjoint. We have $X \cup Y = \{1,2,3\}$, which has three elements. So $|X \cup Y| \neq |X| + |Y|$ in this context. On the flip side, we have $X \cap Z = \emptyset$; these sets are disjoint. So taking their union, we have $X \cup Z = \{1,2,3,4\}$, which has size 4, and so we do have $|X \cup Z| = |X| + |Z|$. In some sense, it is easier to calculate the size of the union provided our sets are disjoint.

To transform a union into a disjoint union, we can rewrite it as $A \cup B = A \cup (B-A)$. If $A \cap B = \emptyset$, we see that $B - A = B$, so $A \cup B$ remains the same. Generally, we see that $A \cap (B-A) = \emptyset$, so these are indeed disjoint sets. As such, we now get that we can calculate $|A \cup B| = |A| + |B-A|$. To verify this, taking our prior example, we have $|X| = 2$, $Y-X = \{3\}$, and so $|Y-X| = 1$. Hence, $|X| + |Y-X| = |Y \cup X|$.

Finally, one last operation we can do to sets is the Cartesian product. If $A$ and $B$ are two sets, we define the Cartesian product to be the set of all ordered pairs $(a,b)$ so that $a \in A$, $b \in B$. That is,

$$ A \times B = \{(a,b) \ :  \ a \in A, b \in B \}.$$

For finite sets, one may ask again what the size of this set is. Here, we see that size acts multiplicatively; $|A \times B| = |A| \cdot |B|$. To see this in a small setting, take $X$ and $Y$ from prior. Then

$$X \times Y = \{(1,2),(1,3),(2,2),(2,3)\}.$$

So we see that $|X \times Y| = 4 = |X| \cdot |Y|$.

To finish, let’s examine the powerset of a set. The powerset of a set, let’s say $X$, denoted by $\mathcal{P}(X)$, is the collection of all subsets of $X$. For example, if $X = \{1,2\}$, then

$$\mathcal{P}(X) = \{\emptyset, \{1\}, \{2\}, \{1,2\}\}.$$

If we again think about size, we can note that there is a nice combinatoric way of figuring out the size of the powerset of a finite set. Say we have $n$ elements in our set; then each subset of $n$ either contains that element or it doesn’t. So we have two options for each element, and as a result we see that $|\mathcal{P}(X)| = 2^{n}$.