kaygun - Tumblr blog

kaygun · 2 years ago

Text

A Collatz-like Conjecture for the Projective Line

Description of the problem

Consider the following self-map of the projective line over integers $\mathbb{P}(\mathbb{Z})$: $$ T(a:b) = \left(\frac{a}{ord_2(a)}:\frac{3b+a}{ord_2(3b+a)}\right) $$ where $ord_2(a)$ is the largest power of $2$ that divides $a$. The question is the following:

If we define $x_{n+1} = T(x_n)$ for an initial point $x_0 = (a_0:b_0)$ do we always get a cycle. That is, for every inital point $(a_0:b_0)$ is there a $k>0$ and $N>0$ such that $x_{N+k} = x_N$?

Implementation

Let us start with the order function. Rather, let me implement a function that returns a number divided by the $p$-part of that number

(defun reduction (n p) (if (zerop (mod n p)) (reduction (/ n p) p) n))

REDUCTION

and let us test

(mapcar (lambda (m) (list m (reduction m 2))) (loop repeat 30 collect (1+ (random 1000))))

((352 11) (17 17) (744 93) (741 741) (858 429) (763 763) (162 81) (274 137) (180 45) (312 39) (171 171) (595 595) (25 25) (602 301) (605 605) (828 207) (477 477) (398 199) (50 25) (379 379) (175 175) (8 1) (362 181) (174 87) (940 235) (393 393) (845 845) (187 187) (656 41) (897 897))

Next, I need a projective reduction:

(defun projective (xs) (let* ((a (car xs)) (b (cadr xs)) (r (gcd a b))) (list (/ a r) (/ b r))))

PROJECTIVE

and we test

(loop repeat 20 collect (let ((xs (list (+ 2 (random 20)) (+ 2 (random 20))))) (list xs (projective xs))))

(((7 14) (1 2)) ((15 8) (15 8)) ((8 4) (2 1)) ((15 16) (15 16)) ((16 20) (4 5)) ((13 20) (13 20)) ((9 4) (9 4)) ((18 18) (1 1)) ((4 6) (2 3)) ((6 11) (6 11)) ((11 3) (11 3)) ((9 21) (3 7)) ((16 3) (16 3)) ((10 10) (1 1)) ((8 5) (8 5)) ((13 14) (13 14)) ((20 11) (20 11)) ((16 10) (8 5)) ((13 12) (13 12)) ((21 9) (7 3)))

Let us implement the iteration function

(defun iterate (fn init &optional result) (if (member init result :test #'equal) (nreverse result) (iterate fn (funcall fn init) (cons init result))))

ITERATE

Let us test

(iterate (lambda (n) (mod (incf n) 10)) 0)

(0 1 2 3 4 5 6 7 8 9)

And finally the function that I would like to test:

(defun my-func (xs) (let* ((a (car xs)) (b (cadr xs))) (projective (list (reduction a 2) (reduction (+ a (* 3 b)) 2)))))

MY-FUNC

and let us test

(loop repeat 10 collect (let ((a (1+ (random 100))) (b (1+ (random 100)))) (iterate #'my-func (list a b))))

(((90 18) (5 1)) ((43 55) (43 13) (43 41) (43 83) (43 73) (43 131) (43 109) (43 185) (43 299) (43 235) (43 187) (43 151) (43 31) (43 17) (43 47) (43 23) (43 7) (43 1)) ((40 17) (5 91) (5 139) (5 211) (5 319) (5 481) (5 181) (5 137) (5 13) (5 11) (5 19) (5 31) (5 49)) ((70 52) (35 113) (35 187) (35 149) (35 241) (35 379) (35 293) (35 457) (35 703) (35 67) (35 59) (35 53) (35 97) (35 163) (35 131) (35 107) (35 89) (35 151) (35 61) (35 109) (35 181) (35 289) (35 451) (35 347) (35 269) (35 421) (35 649) (35 991) (35 47) (35 11) (35 17) (35 43) (35 41) (35 79)) ((81 87) (9 19) (3 11) (1 3) (1 5) (1 1)) ((34 85) (1 17) (1 13) (1 5) (1 1)) ((9 68) (3 71) (1 9) (1 7) (1 11) (1 17) (1 13) (1 5) (1 1)) ((83 63) (83 17) (83 67) (83 71) (83 37) (83 97) (83 187) (83 161) (83 283) (83 233) (83 391) (83 157) (83 277) (83 457) (83 727)) ((100 70) (5 31) (5 49) (5 19)) ((36 36) (1 1)))

But we must check if the sequence terminates for all initial choice of points. Since we can't do that, we are going to check if this is true for random initial points

(loop repeat 2000 collect (let ((a (1+ (random 10000))) (b (1+ (random 10000)))) (length (iterate #'my-func (list a b)))))

(81 79 128 58 77 13 332 158 51 202 233 103 84 648 20 376 334 39 292 48 13 72 51 106 75 46 37 131 60 284 209 442 223 27 91 33 32 52 78 47 487 194 75 24 123 91 29 346 13 184 125 117 206 59 168 84 45 57 143 16 177 114 45 4 313 51 368 188 401 489 153 395 772 48 77 178 92 277 379 183 101 50 20 192 159 26 52 29 103 37 94 12 47 147 138 92 27 94 8 5 39 40 53 49 106 62 424 167 36 234 182 23 195 13 61 207 110 7 57 240 162 339 132 19 22 226 139 29 37 268 176 37 150 148 101 553 64 29 111 194 256 8 52 188 61 51 258 89 50 42 59 81 29 294 102 125 21 8 65 210 340 183 180 129 135 187 43 168 56 29 43 106 110 36 82 50 72 62 413 70 177 187 8 294 203 93 35 498 183 85 277 36 72 20 321 283 36 214 26 36 57 141 230 18 143 6 48 118 113 35 135 11 34 147 236 209 244 150 83 32 193 179 187 132 125 452 25 79 14 43 231 143 421 61 32 230 33 121 69 84 254 41 87 229 523 185 42 102 330 69 221 77 55 57 238 19 249 72 34 36 82 96 149 590 141 55 106 42 33 423 324 411 114 398 56 101 5 30 86 10 177 55 159 319 32 142 372 271 53 61 48 117 27 193 170 37 144 80 87 114 95 60 143 317 49 142 299 159 160 50 20 238 70 155 221 61 75 33 230 82 17 72 25 260 91 85 48 32 28 133 350 233 233 375 117 42 78 17 82 86 68 65 89 39 588 27 69 78 141 50 72 325 10 41 85 16 49 40 478 281 91 472 95 24 28 6 244 22 59 39 70 55 51 44 139 59 66 87 125 16 287 595 35 815 415 182 273 50 16 293 54 30 167 377 172 167 240 95 226 19 195 101 72 186 136 315 57 54 73 766 18 45 7 28 291 290 377 56 116 90 14 145 261 165 41 92 145 31 152 13 93 141 90 220 36 35 88 271 301 89 142 84 49 525 43 139 17 85 280 125 254 71 414 211 94 161 194 508 40 140 98 190 91 171 276 15 119 136 10 29 177 699 38 281 172 37 69 93 267 9 146 135 4 32 473 34 250 4 450 97 106 73 80 438 66 77 245 153 28 39 114 30 84 49 64 101 71 110 23 16 21 35 413 235 600 278 58 51 85 373 55 76 11 64 71 59 164 165 273 85 19 37 124 216 22 365 73 471 15 57 53 42 291 272 36 61 386 116 630 320 12 14 65 184 118 26 26 319 170 50 63 330 161 105 159 65 23 113 374 10 219 356 182 312 92 80 69 79 172 38 221 188 92 44 96 196 211 44 207 70 179 20 60 55 82 213 27 304 45 164 117 58 627 120 66 100 23 139 62 31 87 331 197 24 131 39 20 108 221 76 52 287 306 471 57 59 326 56 62 213 176 270 136 171 19 104 84 43 23 369 300 265 574 50 28 355 196 314 32 193 27 241 39 82 31 23 161 265 15 90 346 263 197 71 213 265 369 242 384 112 6 38 127 16 179 46 172 24 252 231 60 55 202 81 221 41 106 55 187 211 94 71 155 108 97 39 221 16 135 276 58 289 61 598 150 230 151 139 43 35 38 63 25 341 24 26 200 79 139 69 68 51 509 78 24 55 76 182 90 156 135 65 51 121 300 461 9 57 178 23 79 105 15 970 43 506 16 97 15 915 63 54 72 204 187 109 291 49 51 357 87 234 34 312 56 104 79 139 100 75 396 79 19 195 294 32 65 301 121 101 190 186 204 2 49 146 284 74 25 47 34 219 98 48 151 435 196 175 144 59 177 210 97 58 48 104 150 257 31 46 30 32 32 107 41 26 87 146 73 70 199 25 22 38 88 128 19 24 173 93 51 63 50 246 41 157 65 16 132 288 70 109 221 86 68 176 40 211 270 17 14 287 83 101 27 575 83 28 60 351 11 85 84 45 13 31 246 42 390 109 51 45 103 309 83 4 134 14 97 74 89 136 21 71 169 91 224 264 135 147 19 59 16 108 33 172 140 28 215 190 420 137 33 26 209 12 30 292 219 59 9 101 384 214 216 162 105 166 91 356 186 233 244 133 106 110 54 41 32 291 92 34 84 618 16 43 98 125 217 427 30 278 57 54 47 64 17 141 29 176 25 49 262 52 398 138 176 270 78 218 230 160 135 25 161 47 10 58 420 236 142 21 408 23 285 603 86 47 20 97 53 156 184 237 6 245 247 49 343 69 201 144 151 119 102 64 119 75 45 392 139 33 117 18 11 138 511 110 70 122 52 106 186 124 24 95 248 425 601 59 75 50 207 59 60 201 83 117 140 187 25 33 126 87 84 675 29 146 66 17 126 73 11 262 515 181 89 52 136 31 140 48 41 300 76 584 105 219 191 143 99 539 197 252 313 126 60 35 28 300 232 255 192 29 122 268 80 218 28 6 72 106 54 116 33 66 216 136 19 98 21 80 273 48 156 93 73 242 152 42 140 13 106 20 154 109 94 129 266 56 482 53 135 514 106 34 224 38 204 82 55 120 207 203 47 137 143 88 98 38 70 62 413 241 44 91 29 11 209 205 117 434 260 25 159 12 140 356 749 34 149 45 60 65 46 43 160 151 31 167 18 14 140 123 65 24 88 91 21 368 63 145 140 201 59 94 379 47 120 114 208 360 180 98 64 56 108 41 146 46 151 445 49 82 227 261 66 201 282 121 176 51 20 41 41 100 455 26 6 40 37 34 324 369 55 43 185 84 15 118 44 85 83 6 298 211 202 39 143 30 146 192 128 59 72 88 30 80 104 495 183 27 164 648 302 107 138 22 21 221 244 68 18 229 780 177 20 63 9 49 320 53 33 184 395 118 153 163 191 88 77 151 191 136 288 111 13 80 157 89 184 129 306 8 116 508 238 256 31 388 39 214 138 69 256 35 83 18 6 139 269 33 217 177 292 151 37 9 122 34 36 165 123 31 156 23 55 98 45 41 1108 198 233 169 85 81 110 27 343 77 121 213 232 344 87 354 16 247 41 36 21 41 173 25 361 93 114 97 10 65 29 87 168 141 89 136 82 10 120 88 9 88 35 199 223 67 185 445 274 126 22 19 20 167 39 76 50 157 218 108 45 109 200 56 335 18 89 177 59 332 147 136 36 38 81 150 94 28 109 61 108 32 89 55 106 86 228 46 205 33 53 91 359 67 36 232 89 21 173 234 62 93 47 8 192 22 226 96 113 74 189 83 140 38 200 1009 104 74 95 134 17 345 240 121 8 25 81 243 33 23 47 168 55 48 72 12 51 112 81 54 143 334 19 54 214 513 444 64 48 289 132 211 56 344 11 201 54 24 115 514 48 14 97 9 371 29 23 448 101 43 25 130 36 221 125 413 59 42 439 19 105 387 98 228 63 194 21 302 116 228 146 180 237 29 343 161 8 227 72 66 52 69 200 87 312 393 105 56 61 132 88 17 312 186 38 84 222 29 443 148 112 176 8 11 111 142 112 211 283 337 194 26 107 355 53 91 34 196 23 182 168 138 35 41 233 55 138 75 45 480 86 97 294 61 35 337 222 386 143 57 30 24 180 13 92 15 414 10 40 66 13 428 60 529 373 123 107 31 58 116 225 99 182 130 61 67 53 154 404 215 46 272 10 257 309 23 232 153 27 118 357 218 128 64 61 63 417 264 62 161 36 33 109 338 76 53 315 57 15 219 41 28 20 113 134 17 9 725 67 64 300 214 33 13 139 388 274 230 16 137 49 74 21 232 39 150 164 121 616 108 102 112 24 174 84 289 109 305 268 99 95 279 351 16 6 25 283 82 81 532 171 337 57 49 387 188 70 64 50 166 50 47 73 101 259 24 221 117 38 143 149 75 138 101 332 26 158 115 70 162 314 366 81 18 120 257 252 20 241 184 45 195 123 134 76 335 73 181 216 174 103 222 74 36 99 338 106 39 327 157 279 345 123 8 31 176 120 63 298 259 31 190 398 88 37 104 141 169 335 20 138 178 87 26 54 43 96 66 108 157 284 84 132 185 15 364 342 42 6 198 116 33 33 35 65 133 99 31 66 67 36 58 79 147 418 27 40 34 72 29 644 266 164 16 10 397 157 90 63 74 537 29 167 23 388 60 98 9 399 154 759 120 154 70 11 45 51 38 65 79 32 105 287 47 262 138 162 157 6 84 192 363 34 120 171 32 149 217 11 65 196 176 31 217 80 103 153 202 92 99 61 453 64 22 81 41 22 371 10 174 271 291 172 62 256 33 11 112 122 116 169 114 23 70 58 296 149 39 196 48 114 23 270 101 18 100 142 8 82 155 76 11 211 50 45 386 105 77 79 192 237 77 358 213 127 242 56 46 57 347 849 188 401 28 82 328 279 150 30 77 60 308 4 193 16 41 28 150 34 21 272 98 151 51 164 43 112 489 73 47 22 33 10 90 7 41 54 492 124 50 71 371 393 150 592 109 602 75 89 160 162 95 68 637 10 371 184 145 527 82 402 31 38 169 82 256 252 318 207 180)

0 notes

kaygun · 2 years ago

Text

Twin Primes, Cousin Primes, Sexy Primes, and Prime Triplets

Description of the problems

Today, I am going to write about primes. Specifically, certain progression of primes. Let us fix our notation: I am going to use $p_n$ for the $n$-th prime number.

A pair of consecutive primes $(p_n,p_{n+1})$ are called

twin primes if $p_{n+1} - p_n = 2$,

cousin primes if $p_{n+1} - p_n = 4$,

sexy primes if $p_{n+1} - p_n = 6$.

Three consecutive primes $(p_n, p_{n+1}, p_{n+2})$ are called a triplet if $p_{n+2} - p_n = 6$.

Today, I am going to write a clojure program that will give us these prime pairs and triples for the first few prime numbers.

An implementation in clojure

I am going to implement a lazy sequence of prime numbers and then we are going to filter it. First, I am going to need a function that returns the smallest prime number that comes after a given number.

(defn next-prime [n] (if (= n 2) 3 (let [m (+ n 2) t (-> n Math/sqrt int (+ 2))] (if (some #(zero? (mod m %)) (range 2 t)) (next-prime m) m))))

#'prep/next-prime

Let us test:

(into [] (map next-prime [2 3 5 119]))

[3 5 7 127]

Next, the lazy sequence of primes

(def primes (lazy-seq (iterate next-prime 2)))

#'prep/primes

Let us test:

(into [] (take 20 primes))

[2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71]

Next, the main engine:

(defn find-primes [n window-size gap] (->> primes (take n) (partition window-size 1) (filter (fn [xs] (= gap (- (last xs) (first xs)))))))

#'prep/find-primes

The code takes a window size. This is because I am going to use the same function to filter pairs as well as triples. I am also giving the gap size since we are going to check several gap sizes.

Let us start with twin primes:

(into [] (find-primes 200 2 2))

[(3 5) (5 7) (11 13) (17 19) (29 31) (41 43) (59 61) (71 73) (101 103) (107 109) (137 139) (149 151) (179 181) (191 193) (197 199) (227 229) (239 241) (269 271) (281 283) (311 313) (347 349) (419 421) (431 433) (461 463) (521 523) (569 571) (599 601) (617 619) (641 643) (659 661) (809 811) (821 823) (827 829) (857 859) (881 883) (1019 1021) (1031 1033) (1049 1051) (1061 1063) (1091 1093) (1151 1153)]

Next, cousin primes

(into [] (find-primes 200 2 4))

[(7 11) (13 17) (19 23) (37 41) (43 47) (67 71) (79 83) (97 101) (103 107) (109 113) (127 131) (163 167) (193 197) (223 227) (229 233) (277 281) (307 311) (313 317) (349 353) (379 383) (397 401) (439 443) (457 461) (463 467) (487 491) (499 503) (613 617) (643 647) (673 677) (739 743) (757 761) (769 773) (823 827) (853 857) (859 863) (877 881) (883 887) (907 911) (937 941) (967 971) (1009 1013) (1087 1091) (1093 1097) (1213 1217)]

Then sexy primes

(into [] (find-primes 200 2 6))

[(23 29) (31 37) (47 53) (53 59) (61 67) (73 79) (83 89) (131 137) (151 157) (157 163) (167 173) (173 179) (233 239) (251 257) (257 263) (263 269) (271 277) (331 337) (353 359) (367 373) (373 379) (383 389) (433 439) (443 449) (503 509) (541 547) (557 563) (563 569) (571 577) (587 593) (593 599) (601 607) (607 613) (647 653) (653 659) (677 683) (727 733) (733 739) (751 757) (941 947) (947 953) (971 977) (977 983) (991 997) (1013 1019) (1033 1039) (1063 1069) (1097 1103) (1103 1109) (1117 1123) (1123 1129) (1181 1187) (1187 1193) (1217 1223)]

And finally triplets

(into [] (find-primes 200 3 6))

[(5 7 11) (7 11 13) (11 13 17) (13 17 19) (17 19 23) (37 41 43) (41 43 47) (67 71 73) (97 101 103) (101 103 107) (103 107 109) (107 109 113) (191 193 197) (193 197 199) (223 227 229) (227 229 233) (277 281 283) (307 311 313) (311 313 317) (347 349 353) (457 461 463) (461 463 467) (613 617 619) (641 643 647) (821 823 827) (823 827 829) (853 857 859) (857 859 863) (877 881 883) (881 883 887) (1087 1091 1093) (1091 1093 1097)]

0 notes

kaygun · 2 years ago

Text

Set of All Partitions of a Finite Set

Description of the problem

Assume $A$ is a finite set. Today, I would like to write a lisp function that returns the set of all partitions of $A$.

An algorithm

For an element $x\in A$, assume we constructed the set of all partitions of $A\setminus \{x\}$. Then for any partition $p$ of $A\setminus\{x\}$, the set $p\cup \{\{x\}\}$ is a partition of $A$. Moreover, if $p = \{ a_1,\ldots,a_k \}$ is a partition of $A\setminus \{x\}$ then each $p_i$ obtained from $p$ by replacing $a_i$ with $a_i\cup \{x\}$ is another partition of $A$.

Algorithm Partitions Input: A finite set A Output: Set of all partitions of A Initialize: Result <- {} Begin If A is empty or A contains a single element Return { A } Else Pick an element x from A P <- Partitions( A \\ {x} ) For each V in P: Add { V, {x} } to Result For each v in V Let W be a copy of V Add x to the copy of v in W Add W to Result End End End Return Result End

An implementation in common lisp

Here is an implementation of the algorithm above in Common Lisp:

(defun partitions (xs) (labels ((insert (ys) (let ((x (car xs)) (res nil)) (cons (cons (list x) ys) (dotimes (i (length ys) res) (let ((zs (copy-list ys))) (push x (elt zs i)) (push zs res))))))) (if (= 1 (length xs)) (list (list xs)) (mapcan #'insert (partitions (cdr xs))))))

PARTITIONS

Let us test:

(format nil "~{~a~%~}" (partitions '(0 1 2 3 4 5)))

((0) (1) (2) (3) (4) (5)) ((1) (2) (3) (4) (0 5)) ((1) (2) (3) (0 4) (5)) ((1) (2) (0 3) (4) (5)) ((1) (0 2) (3) (4) (5)) ((0 1) (2) (3) (4) (5)) ((0) (2) (3) (4) (1 5)) ((2) (3) (4) (0 1 5)) ((2) (3) (0 4) (1 5)) ((2) (0 3) (4) (1 5)) ((0 2) (3) (4) (1 5)) ((0) (2) (3) (1 4) (5)) ((2) (3) (1 4) (0 5)) ((2) (3) (0 1 4) (5)) ((2) (0 3) (1 4) (5)) ((0 2) (3) (1 4) (5)) ((0) (2) (1 3) (4) (5)) ((2) (1 3) (4) (0 5)) ((2) (1 3) (0 4) (5)) ((2) (0 1 3) (4) (5)) ((0 2) (1 3) (4) (5)) ((0) (1 2) (3) (4) (5)) ((1 2) (3) (4) (0 5)) ((1 2) (3) (0 4) (5)) ((1 2) (0 3) (4) (5)) ((0 1 2) (3) (4) (5)) ((0) (1) (3) (4) (2 5)) ((1) (3) (4) (0 2 5)) ((1) (3) (0 4) (2 5)) ((1) (0 3) (4) (2 5)) ((0 1) (3) (4) (2 5)) ((0) (3) (4) (1 2 5)) ((3) (4) (0 1 2 5)) ((3) (0 4) (1 2 5)) ((0 3) (4) (1 2 5)) ((0) (3) (1 4) (2 5)) ((3) (1 4) (0 2 5)) ((3) (0 1 4) (2 5)) ((0 3) (1 4) (2 5)) ((0) (1 3) (4) (2 5)) ((1 3) (4) (0 2 5)) ((1 3) (0 4) (2 5)) ((0 1 3) (4) (2 5)) ((0) (1) (3) (2 4) (5)) ((1) (3) (2 4) (0 5)) ((1) (3) (0 2 4) (5)) ((1) (0 3) (2 4) (5)) ((0 1) (3) (2 4) (5)) ((0) (3) (2 4) (1 5)) ((3) (2 4) (0 1 5)) ((3) (0 2 4) (1 5)) ((0 3) (2 4) (1 5)) ((0) (3) (1 2 4) (5)) ((3) (1 2 4) (0 5)) ((3) (0 1 2 4) (5)) ((0 3) (1 2 4) (5)) ((0) (1 3) (2 4) (5)) ((1 3) (2 4) (0 5)) ((1 3) (0 2 4) (5)) ((0 1 3) (2 4) (5)) ((0) (1) (2 3) (4) (5)) ((1) (2 3) (4) (0 5)) ((1) (2 3) (0 4) (5)) ((1) (0 2 3) (4) (5)) ((0 1) (2 3) (4) (5)) ((0) (2 3) (4) (1 5)) ((2 3) (4) (0 1 5)) ((2 3) (0 4) (1 5)) ((0 2 3) (4) (1 5)) ((0) (2 3) (1 4) (5)) ((2 3) (1 4) (0 5)) ((2 3) (0 1 4) (5)) ((0 2 3) (1 4) (5)) ((0) (1 2 3) (4) (5)) ((1 2 3) (4) (0 5)) ((1 2 3) (0 4) (5)) ((0 1 2 3) (4) (5)) ((0) (1) (2) (4) (3 5)) ((1) (2) (4) (0 3 5)) ((1) (2) (0 4) (3 5)) ((1) (0 2) (4) (3 5)) ((0 1) (2) (4) (3 5)) ((0) (2) (4) (1 3 5)) ((2) (4) (0 1 3 5)) ((2) (0 4) (1 3 5)) ((0 2) (4) (1 3 5)) ((0) (2) (1 4) (3 5)) ((2) (1 4) (0 3 5)) ((2) (0 1 4) (3 5)) ((0 2) (1 4) (3 5)) ((0) (1 2) (4) (3 5)) ((1 2) (4) (0 3 5)) ((1 2) (0 4) (3 5)) ((0 1 2) (4) (3 5)) ((0) (1) (4) (2 3 5)) ((1) (4) (0 2 3 5)) ((1) (0 4) (2 3 5)) ((0 1) (4) (2 3 5)) ((0) (4) (1 2 3 5)) ((4) (0 1 2 3 5)) ((0 4) (1 2 3 5)) ((0) (1 4) (2 3 5)) ((1 4) (0 2 3 5)) ((0 1 4) (2 3 5)) ((0) (1) (2 4) (3 5)) ((1) (2 4) (0 3 5)) ((1) (0 2 4) (3 5)) ((0 1) (2 4) (3 5)) ((0) (2 4) (1 3 5)) ((2 4) (0 1 3 5)) ((0 2 4) (1 3 5)) ((0) (1 2 4) (3 5)) ((1 2 4) (0 3 5)) ((0 1 2 4) (3 5)) ((0) (1) (2) (3 4) (5)) ((1) (2) (3 4) (0 5)) ((1) (2) (0 3 4) (5)) ((1) (0 2) (3 4) (5)) ((0 1) (2) (3 4) (5)) ((0) (2) (3 4) (1 5)) ((2) (3 4) (0 1 5)) ((2) (0 3 4) (1 5)) ((0 2) (3 4) (1 5)) ((0) (2) (1 3 4) (5)) ((2) (1 3 4) (0 5)) ((2) (0 1 3 4) (5)) ((0 2) (1 3 4) (5)) ((0) (1 2) (3 4) (5)) ((1 2) (3 4) (0 5)) ((1 2) (0 3 4) (5)) ((0 1 2) (3 4) (5)) ((0) (1) (3 4) (2 5)) ((1) (3 4) (0 2 5)) ((1) (0 3 4) (2 5)) ((0 1) (3 4) (2 5)) ((0) (3 4) (1 2 5)) ((3 4) (0 1 2 5)) ((0 3 4) (1 2 5)) ((0) (1 3 4) (2 5)) ((1 3 4) (0 2 5)) ((0 1 3 4) (2 5)) ((0) (1) (2 3 4) (5)) ((1) (2 3 4) (0 5)) ((1) (0 2 3 4) (5)) ((0 1) (2 3 4) (5)) ((0) (2 3 4) (1 5)) ((2 3 4) (0 1 5)) ((0 2 3 4) (1 5)) ((0) (1 2 3 4) (5)) ((1 2 3 4) (0 5)) ((0 1 2 3 4) (5)) ((0) (1) (2) (3) (4 5)) ((1) (2) (3) (0 4 5)) ((1) (2) (0 3) (4 5)) ((1) (0 2) (3) (4 5)) ((0 1) (2) (3) (4 5)) ((0) (2) (3) (1 4 5)) ((2) (3) (0 1 4 5)) ((2) (0 3) (1 4 5)) ((0 2) (3) (1 4 5)) ((0) (2) (1 3) (4 5)) ((2) (1 3) (0 4 5)) ((2) (0 1 3) (4 5)) ((0 2) (1 3) (4 5)) ((0) (1 2) (3) (4 5)) ((1 2) (3) (0 4 5)) ((1 2) (0 3) (4 5)) ((0 1 2) (3) (4 5)) ((0) (1) (3) (2 4 5)) ((1) (3) (0 2 4 5)) ((1) (0 3) (2 4 5)) ((0 1) (3) (2 4 5)) ((0) (3) (1 2 4 5)) ((3) (0 1 2 4 5)) ((0 3) (1 2 4 5)) ((0) (1 3) (2 4 5)) ((1 3) (0 2 4 5)) ((0 1 3) (2 4 5)) ((0) (1) (2 3) (4 5)) ((1) (2 3) (0 4 5)) ((1) (0 2 3) (4 5)) ((0 1) (2 3) (4 5)) ((0) (2 3) (1 4 5)) ((2 3) (0 1 4 5)) ((0 2 3) (1 4 5)) ((0) (1 2 3) (4 5)) ((1 2 3) (0 4 5)) ((0 1 2 3) (4 5)) ((0) (1) (2) (3 4 5)) ((1) (2) (0 3 4 5)) ((1) (0 2) (3 4 5)) ((0 1) (2) (3 4 5)) ((0) (2) (1 3 4 5)) ((2) (0 1 3 4 5)) ((0 2) (1 3 4 5)) ((0) (1 2) (3 4 5)) ((1 2) (0 3 4 5)) ((0 1 2) (3 4 5)) ((0) (1) (2 3 4 5)) ((1) (0 2 3 4 5)) ((0 1) (2 3 4 5)) ((0) (1 2 3 4 5)) ((0 1 2 3 4 5))

An implementation in clojure

Here is an implementation in clojure:

(defn partitions [xs] (letfn [(insert [ys] (let [x (first xs)] (cons (conj ys [x]) (for [i (range (count ys))] (let [zs (vec ys)] (update zs i conj x))))))] (if (= 1 (count xs)) [[ xs ]] (mapcat insert (partitions (rest xs))))))

0 notes

kaygun · 2 years ago

Text

Non-crossing Partitions and Dyck Words

Description of the problem

Working with Dyck words and non-crossing linear chords, I realized that one can also generate all non-crossing partitions of a finite set using Dyck words. I just need a new conversion function.

Non-crossing partitions

Consider the finite set $[n] = {0,1,\ldots,n}$ and a partition $\mathcal{P}$ of $n$. We call such a partition as non-crossing if the corresponding chord diagram has no crossings.

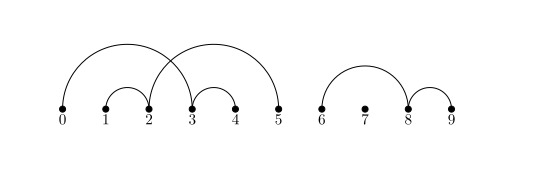
Implementation

Let me start with a slightly improved version of the generation of all Dyck words of a specific length:

(defun dyck-words (n &optional (a 0) (acc '(()))) (labels ((insert (xxs ys) (mapcar (lambda (xs) (append xs ys)) xxs))) (if (= a n) (insert acc (loop repeat n collect 1)) (append (dyck-words n (1+ a) (insert acc '(0))) (if (> a 0) (dyck-words (1- n) (1- a) (insert acc '(1))))))))

Next, a new function that converts a Dyck word into a non-crossing partition:

(defun unwind (xs stack &optional res) (if (or (null xs) (= 0 (car xs))) (values xs stack res) (unwind (cdr xs) (cdr stack) (cons (car stack) res)))) (defun convert (xs &optional (pos 0) stack res) (cond ((null xs) res) ((= 0 (car xs)) (convert (cdr xs) (1+ pos) (cons pos stack) res)) (t (multiple-value-bind (ys st re) (unwind xs stack) (convert ys pos st (cons re res))))))

(mapcar #'convert (dyck-words 6))

(((0 1 2 3 4 5)) ((0 1 2 3 5) (4)) ((0 1 2 5) (3 4)) ((0 1 5) (2 3 4)) ((0 5) (1 2 3 4)) ((5) (0 1 2 3 4)) ((0 1 2 4 5) (3)) ((0 1 2 5) (4) (3)) ((0 1 5) (2 4) (3)) ((0 5) (1 2 4) (3)) ((5) (0 1 2 4) (3)) ((0 1 4 5) (2 3)) ((0 1 5) (4) (2 3)) ((0 5) (1 4) (2 3)) ((5) (0 1 4) (2 3)) ((0 4 5) (1 2 3)) ((0 5) (4) (1 2 3)) ((5) (0 4) (1 2 3)) ((4 5) (0 1 2 3)) ((5) (4) (0 1 2 3)) ((0 1 3 4 5) (2)) ((0 1 3 5) (4) (2)) ((0 1 5) (3 4) (2)) ((0 5) (1 3 4) (2)) ((5) (0 1 3 4) (2)) ((0 1 4 5) (3) (2)) ((0 1 5) (4) (3) (2)) ((0 5) (1 4) (3) (2)) ((5) (0 1 4) (3) (2)) ((0 4 5) (1 3) (2)) ((0 5) (4) (1 3) (2)) ((5) (0 4) (1 3) (2)) ((4 5) (0 1 3) (2)) ((5) (4) (0 1 3) (2)) ((0 3 4 5) (1 2)) ((0 3 5) (4) (1 2)) ((0 5) (3 4) (1 2)) ((5) (0 3 4) (1 2)) ((0 4 5) (3) (1 2)) ((0 5) (4) (3) (1 2)) ((5) (0 4) (3) (1 2)) ((4 5) (0 3) (1 2)) ((5) (4) (0 3) (1 2)) ((3 4 5) (0 1 2)) ((3 5) (4) (0 1 2)) ((5) (3 4) (0 1 2)) ((4 5) (3) (0 1 2)) ((5) (4) (3) (0 1 2)) ((0 2 3 4 5) (1)) ((0 2 3 5) (4) (1)) ((0 2 5) (3 4) (1)) ((0 5) (2 3 4) (1)) ((5) (0 2 3 4) (1)) ((0 2 4 5) (3) (1)) ((0 2 5) (4) (3) (1)) ((0 5) (2 4) (3) (1)) ((5) (0 2 4) (3) (1)) ((0 4 5) (2 3) (1)) ((0 5) (4) (2 3) (1)) ((5) (0 4) (2 3) (1)) ((4 5) (0 2 3) (1)) ((5) (4) (0 2 3) (1)) ((0 3 4 5) (2) (1)) ((0 3 5) (4) (2) (1)) ((0 5) (3 4) (2) (1)) ((5) (0 3 4) (2) (1)) ((0 4 5) (3) (2) (1)) ((0 5) (4) (3) (2) (1)) ((5) (0 4) (3) (2) (1)) ((4 5) (0 3) (2) (1)) ((5) (4) (0 3) (2) (1)) ((3 4 5) (0 2) (1)) ((3 5) (4) (0 2) (1)) ((5) (3 4) (0 2) (1)) ((4 5) (3) (0 2) (1)) ((5) (4) (3) (0 2) (1)) ((2 3 4 5) (0 1)) ((2 3 5) (4) (0 1)) ((2 5) (3 4) (0 1)) ((5) (2 3 4) (0 1)) ((2 4 5) (3) (0 1)) ((2 5) (4) (3) (0 1)) ((5) (2 4) (3) (0 1)) ((4 5) (2 3) (0 1)) ((5) (4) (2 3) (0 1)) ((3 4 5) (2) (0 1)) ((3 5) (4) (2) (0 1)) ((5) (3 4) (2) (0 1)) ((4 5) (3) (2) (0 1)) ((5) (4) (3) (2) (0 1)) ((1 2 3 4 5) (0)) ((1 2 3 5) (4) (0)) ((1 2 5) (3 4) (0)) ((1 5) (2 3 4) (0)) ((5) (1 2 3 4) (0)) ((1 2 4 5) (3) (0)) ((1 2 5) (4) (3) (0)) ((1 5) (2 4) (3) (0)) ((5) (1 2 4) (3) (0)) ((1 4 5) (2 3) (0)) ((1 5) (4) (2 3) (0)) ((5) (1 4) (2 3) (0)) ((4 5) (1 2 3) (0)) ((5) (4) (1 2 3) (0)) ((1 3 4 5) (2) (0)) ((1 3 5) (4) (2) (0)) ((1 5) (3 4) (2) (0)) ((5) (1 3 4) (2) (0)) ((1 4 5) (3) (2) (0)) ((1 5) (4) (3) (2) (0)) ((5) (1 4) (3) (2) (0)) ((4 5) (1 3) (2) (0)) ((5) (4) (1 3) (2) (0)) ((3 4 5) (1 2) (0)) ((3 5) (4) (1 2) (0)) ((5) (3 4) (1 2) (0)) ((4 5) (3) (1 2) (0)) ((5) (4) (3) (1 2) (0)) ((2 3 4 5) (1) (0)) ((2 3 5) (4) (1) (0)) ((2 5) (3 4) (1) (0)) ((5) (2 3 4) (1) (0)) ((2 4 5) (3) (1) (0)) ((2 5) (4) (3) (1) (0)) ((5) (2 4) (3) (1) (0)) ((4 5) (2 3) (1) (0)) ((5) (4) (2 3) (1) (0)) ((3 4 5) (2) (1) (0)) ((3 5) (4) (2) (1) (0)) ((5) (3 4) (2) (1) (0)) ((4 5) (3) (2) (1) (0)) ((5) (4) (3) (2) (1) (0)))

0 notes

kaygun · 2 years ago

Text

Non-crossing Linear Chords

If you haven't heard: Southeast of Turkey is hit (twice in a day) earthquakes of magnitude 7.4 and 7.8 this week. The government response has been inept, slow, and inadequate in most places. The reasons for this are long-coming. There is a huge relief effort by volunteers, national and international relief organizations. I urge you to donate to an international organization of your choosing, or a national (AHBAP, AFAD, AKUT) relief organization.

Description of the problem

I needed something that would occupy my mind and prevent me from reading news 24/7. So, I chose this.

For a natural number $n\geq 1$, consider the set $[2n]={0,1,\ldots,2n}$. A partition $\mathcal{P}$ of $[2n]$ is called a linear chord of length $n$ if for every $X\in \mathcal{P}$ we have $|X|=2$. We usually represent these chords with chord diagrams such as

A linear chord is called non-crossing if a chord diagram with non-overlapping chords can be drawn.

Notice that the set of all non-crossing linear chords of length $n$ is the same as the set of balanced brackets of length $2n$. Using this fact, today I am going to write a common lisp program that lists all non-crossing linear chords.

A First Implementation

I am not going to explain the code below. It is a heavily modified version I took from Geeks for Geeks.

(defun ncc (n &optional result xs stack (position 0) (begin 0) (end 0)) (if (= n end) (cons xs result) (let () (if (> begin end) (setf result (ncc n result (cons (list (car stack) position) xs) (cdr stack) (1+ position) begin (1+ end)))) (if (< begin n) (setf result (ncc n result xs (cons position stack) (1+ position) (1+ begin) end))) result)))

NNC

Here are some examples:

(format nil "~{~a~%~%~}~%" (loop for i from 1 to 5 collect (nnc i)))

(((0 1))) (((0 3) (1 2)) ((2 3) (0 1))) (((0 5) (1 4) (2 3)) ((0 5) (3 4) (1 2)) ((4 5) (0 3) (1 2)) ((2 5) (3 4) (0 1)) ((4 5) (2 3) (0 1))) (((0 7) (1 6) (2 5) (3 4)) ((0 7) (1 6) (4 5) (2 3)) ((0 7) (5 6) (1 4) (2 3)) ((6 7) (0 5) (1 4) (2 3)) ((0 7) (3 6) (4 5) (1 2)) ((0 7) (5 6) (3 4) (1 2)) ((6 7) (0 5) (3 4) (1 2)) ((4 7) (5 6) (0 3) (1 2)) ((6 7) (4 5) (0 3) (1 2)) ((2 7) (3 6) (4 5) (0 1)) ((2 7) (5 6) (3 4) (0 1)) ((6 7) (2 5) (3 4) (0 1)) ((4 7) (5 6) (2 3) (0 1)) ((6 7) (4 5) (2 3) (0 1))) (((0 9) (1 8) (2 7) (3 6) (4 5)) ((0 9) (1 8) (2 7) (5 6) (3 4)) ((0 9) (1 8) (6 7) (2 5) (3 4)) ((0 9) (7 8) (1 6) (2 5) (3 4)) ((8 9) (0 7) (1 6) (2 5) (3 4)) ((0 9) (1 8) (4 7) (5 6) (2 3)) ((0 9) (1 8) (6 7) (4 5) (2 3)) ((0 9) (7 8) (1 6) (4 5) (2 3)) ((8 9) (0 7) (1 6) (4 5) (2 3)) ((0 9) (5 8) (6 7) (1 4) (2 3)) ((0 9) (7 8) (5 6) (1 4) (2 3)) ((8 9) (0 7) (5 6) (1 4) (2 3)) ((6 9) (7 8) (0 5) (1 4) (2 3)) ((8 9) (6 7) (0 5) (1 4) (2 3)) ((0 9) (3 8) (4 7) (5 6) (1 2)) ((0 9) (3 8) (6 7) (4 5) (1 2)) ((0 9) (7 8) (3 6) (4 5) (1 2)) ((8 9) (0 7) (3 6) (4 5) (1 2)) ((0 9) (5 8) (6 7) (3 4) (1 2)) ((0 9) (7 8) (5 6) (3 4) (1 2)) ((8 9) (0 7) (5 6) (3 4) (1 2)) ((6 9) (7 8) (0 5) (3 4) (1 2)) ((8 9) (6 7) (0 5) (3 4) (1 2)) ((4 9) (5 8) (6 7) (0 3) (1 2)) ((4 9) (7 8) (5 6) (0 3) (1 2)) ((8 9) (4 7) (5 6) (0 3) (1 2)) ((6 9) (7 8) (4 5) (0 3) (1 2)) ((8 9) (6 7) (4 5) (0 3) (1 2)) ((2 9) (3 8) (4 7) (5 6) (0 1)) ((2 9) (3 8) (6 7) (4 5) (0 1)) ((2 9) (7 8) (3 6) (4 5) (0 1)) ((8 9) (2 7) (3 6) (4 5) (0 1)) ((2 9) (5 8) (6 7) (3 4) (0 1)) ((2 9) (7 8) (5 6) (3 4) (0 1)) ((8 9) (2 7) (5 6) (3 4) (0 1)) ((6 9) (7 8) (2 5) (3 4) (0 1)) ((8 9) (6 7) (2 5) (3 4) (0 1)) ((4 9) (5 8) (6 7) (2 3) (0 1)) ((4 9) (7 8) (5 6) (2 3) (0 1)) ((8 9) (4 7) (5 6) (2 3) (0 1)) ((6 9) (7 8) (4 5) (2 3) (0 1)) ((8 9) (6 7) (4 5) (2 3) (0 1)))

A Second Implementation

As I was finishing the implementation above, I remembered that the set of balanced brackets of length $n$ is bijective to the set of Dyck Words, and I already implemented a lisp function that returns the set of all Dyck words of a given length. I just need a function that converts a Dyck word into a non-overlapping linear chord.

(defun dyck-words (n &optional (a 0) (acc '(()))) (labels ((insert (i xs &optional (m 1)) (let ((y (loop repeat m collect i))) (mapcar (lambda (x) (append y x)) xs)))) (if (= a n) (insert 0 acc n) (append (dyck-words n (1+ a) (insert 1 acc)) (if (> a 0) (dyck-words (1- n) (1- a) (insert 0 acc))))))) (dyck-words 4)

DYCK-WORDS ((0 0 0 0 1 1 1 1) (0 1 0 0 0 1 1 1) (0 0 1 0 0 1 1 1) (0 0 0 1 0 1 1 1) (0 0 0 1 1 0 1 1) (0 0 1 0 1 0 1 1) (0 1 0 0 1 0 1 1) (0 0 1 1 0 0 1 1) (0 1 0 1 0 0 1 1) (0 0 0 1 1 1 0 1) (0 0 1 0 1 1 0 1) (0 1 0 0 1 1 0 1) (0 0 1 1 0 1 0 1) (0 1 0 1 0 1 0 1))

Here is the conversion function:

(defun convert (xs &optional stack res (pos 0)) (cond ((null xs) (nreverse res)) ((= 0 (car xs)) (convert (cdr xs) (cons pos stack) res (1+ pos))) (t (convert (cdr xs) (cdr stack) (cons (list (car stack) pos) res) (1+ pos)))))

CONVERT

Here are the same set of examples above:

(format nil "~{~a~%~%~}~%" (loop for i from 1 to 5 collect (mapcar #'convert (dyck-words i))))

(((0 1))) (((1 2) (0 3)) ((0 1) (2 3))) (((2 3) (1 4) (0 5)) ((1 2) (3 4) (0 5)) ((0 1) (3 4) (2 5)) ((1 2) (0 3) (4 5)) ((0 1) (2 3) (4 5))) (((3 4) (2 5) (1 6) (0 7)) ((0 1) (4 5) (3 6) (2 7)) ((1 2) (4 5) (3 6) (0 7)) ((2 3) (4 5) (1 6) (0 7)) ((2 3) (1 4) (5 6) (0 7)) ((1 2) (3 4) (5 6) (0 7)) ((0 1) (3 4) (5 6) (2 7)) ((1 2) (0 3) (5 6) (4 7)) ((0 1) (2 3) (5 6) (4 7)) ((2 3) (1 4) (0 5) (6 7)) ((1 2) (3 4) (0 5) (6 7)) ((0 1) (3 4) (2 5) (6 7)) ((1 2) (0 3) (4 5) (6 7)) ((0 1) (2 3) (4 5) (6 7))) (((0 1) (2 3) (4 5) (7 8) (6 9)) ((1 2) (0 3) (4 5) (7 8) (6 9)) ((0 1) (3 4) (2 5) (7 8) (6 9)) ((1 2) (3 4) (0 5) (7 8) (6 9)) ((2 3) (1 4) (0 5) (7 8) (6 9)) ((0 1) (2 3) (5 6) (7 8) (4 9)) ((1 2) (0 3) (5 6) (7 8) (4 9)) ((0 1) (3 4) (5 6) (7 8) (2 9)) ((1 2) (3 4) (5 6) (7 8) (0 9)) ((2 3) (1 4) (5 6) (7 8) (0 9)) ((2 3) (4 5) (1 6) (7 8) (0 9)) ((1 2) (4 5) (3 6) (7 8) (0 9)) ((0 1) (4 5) (3 6) (7 8) (2 9)) ((3 4) (2 5) (1 6) (7 8) (0 9)) ((3 4) (2 5) (6 7) (1 8) (0 9)) ((0 1) (4 5) (6 7) (3 8) (2 9)) ((1 2) (4 5) (6 7) (3 8) (0 9)) ((2 3) (4 5) (6 7) (1 8) (0 9)) ((2 3) (1 4) (6 7) (5 8) (0 9)) ((1 2) (3 4) (6 7) (5 8) (0 9)) ((0 1) (3 4) (6 7) (5 8) (2 9)) ((1 2) (0 3) (6 7) (5 8) (4 9)) ((0 1) (2 3) (6 7) (5 8) (4 9)) ((3 4) (5 6) (2 7) (1 8) (0 9)) ((0 1) (5 6) (4 7) (3 8) (2 9)) ((1 2) (5 6) (4 7) (3 8) (0 9)) ((2 3) (5 6) (4 7) (1 8) (0 9)) ((4 5) (3 6) (2 7) (1 8) (0 9)) ((3 4) (2 5) (1 6) (0 7) (8 9)) ((0 1) (4 5) (3 6) (2 7) (8 9)) ((1 2) (4 5) (3 6) (0 7) (8 9)) ((2 3) (4 5) (1 6) (0 7) (8 9)) ((2 3) (1 4) (5 6) (0 7) (8 9)) ((1 2) (3 4) (5 6) (0 7) (8 9)) ((0 1) (3 4) (5 6) (2 7) (8 9)) ((1 2) (0 3) (5 6) (4 7) (8 9)) ((0 1) (2 3) (5 6) (4 7) (8 9)) ((2 3) (1 4) (0 5) (6 7) (8 9)) ((1 2) (3 4) (0 5) (6 7) (8 9)) ((0 1) (3 4) (2 5) (6 7) (8 9)) ((1 2) (0 3) (4 5) (6 7) (8 9)) ((0 1) (2 3) (4 5) (6 7) (8 9)))

0 notes

kaygun · 2 years ago

Text

Clojure/Python Interop Examples

Description of the problem

Today, I am going to write something that I have been playing around with, and found to be extremely useful and fun: deep clojure and python interop. This is done via libpython-clj. You may find the detailed documentation here. The library is but a small part of a large project called scicloj that aims to expand the use of clojure in data science.

The dependencies and the namespace

Let us start with the dependencies

{:deps {clj-python/libpython-clj {:mvn/version "2.024"}}}

Next, the namespace

(ns cl-py (:require [libpython-clj2.require :refer [require-python]] [libpython-clj2.python :refer [py. py.. py.-] :as py]))

and global imports.

(require-python '[numpy :as np]) (require-python '[pandas :as pd]) (require-python '[matplotlib.pyplot :as plt])

A Simple Visualization Example

Let me start with a simple matplotlib visualization example. I am going to use yfinance to use [Yahoo Finance API] to download the market data for a ticker then visualize it as a time-series. The data will be ingested as a pandas dataframe.

(py/from-import yfinance download) (plt/figure :figsize [12 4]) (-> (download "AAPL" :start "2012-01-01") (py/get-attr :Open) (py/call-attr :plot)) (plt/savefig "result.png")

#'cl-py/download Figure(1200x400) AxesSubplot(0.125,0.2;0.775x0.68)

A More Complicated Visualization

In the following example, I am going to pull passenger data from Istanbul Municipality Data Portal. The specific dataset is about number of passengers taking the sea-route in the year 2022. The columns are 'year', 'month', 'company', 'station' and 'passenger'. I am going to display the monthly sums in order.

(let [months ["jan" "feb" "mar" "apr" "may" "jun" "jul" "aug" "sep" "oct" "nov" "dec"] passengers (as-> "https://data.ibb.gov.tr/dataset/20f33ff0-1ab3-4378-9998-486e28242f48/resource/6fbdd928-8c37-43a4-8e6a-ba0fa7f767fb/download/istanbul-deniz-iskeleleri-yolcu-saylar.csv" $ (pd/read_csv $ :encoding "iso8859-15") (py/call-attr $ :to_numpy) (py/->jvm $) (filter (fn [x] (= (x 0) 2022)) $) ;; select year 2022 (map (fn [x] {(x 1) (x 4)}) $) ;; select month and passenger number (apply merge-with + $) ;; monthly sums (sort $) ;; sort wrt month (map #(% 1) $))] ;; get monthly counts only (plt/figure :figsize [12 6]) (plt/bar months passengers) (plt/savefig "passengers.png"))

An Image Processing Example

In our next example, I am going to work with the Olivetti Faces Dataset. I am going to compute the eigen-face of a given random person.

(py/from-import sklearn.datasets fetch_olivetti_faces) (py/from-import sklearn.decomposition PCA) (def faces (fetch_olivetti_faces :data_home "/home/kaygun/local/data/scikit_learn_data/")) (let [N (* 10 (rand-int 40)) X (-> faces (py/get-attr :data) (py/get-item (range N (+ N 10))) (py/call-attr :transpose)) Y (-> (PCA :n_components 1) (py/call-attr :fit_transform X) (py/call-attr :reshape [64 64]))] (plt/figure :figsize [4 4]) (plt/imshow Y :cmap "gray_r") (plt/savefig "eigen-face.png"))

#'cl-py/fetch_olivetti_faces #'cl-py/PCA #'cl-py/faces

A Decision Tree Model

In our next example, I am going to construct a Decision Tree Model using scikit-learn on the Iris dataset. First, I'll split the dataset into train and test datasets, and after I trained the model on the train set, I'll show the confusion matrix on the test dataset.

(py/from-import sklearn.datasets load_iris) (py/from-import sklearn.model_selection train_test_split) (py/from-import sklearn.tree DecisionTreeClassifier) (py/from-import sklearn.metrics confusion_matrix) (def iris (load_iris)) (let [X (py/get-attr iris :data) y (py/get-attr iris :target) [X-train X-test y-train y-test] (train_test_split X y :test_size 0.2) model (DecisionTreeClassifier)] (py/call-attr model :fit X-train y-train) (->> X-test (py/call-attr model :predict) (confusion_matrix y-test)))

#'cl-py/load_iris #'cl-py/train_test_split #'cl-py/DecisionTreeClassifier #'cl-py/confusion_matrix #'cl-py/iris [[ 9 0 0] [ 0 11 1] [ 0 1 8]]

A Support Vector Classifier

In our next example, I am going to write a support vector classifier using scikitlearn on the iris dataset.

(py/from-import sklearn.svm SVC) (let [X (py/get-attr iris :data) y (py/get-attr iris :target) [X-train X-test y-train y-test] (train_test_split X y :test_size 0.2) model (SVC :max_iter 1000)] (py/call-attr model :fit X-train y-train) (->> X-test (py/call-attr model :predict) (confusion_matrix y-test)))

#'cl-py/SVC [[ 8 0 0] [ 0 17 0] [ 0 0 5]]

0 notes

kaygun · 2 years ago

Text

Graph Algorithms in Clojure with JGraphT

Description of the problem

In this blog, I have implemented many graph algorithms from scratch either in Common Lisp, or in Clojure, or sometimes in Scala. Today, I am going to show you how to use the java graph library JGraphT to apply some of these graph algorithms on random graphs. JGrapjT is similar to iGraph or networkx in its functionality, but it is more flexible in that one can use any java object as a vertex. It is not as extensive as Sage Math's Graph Library, but it is very useful.

Dependencies and the name-space

For today's examples, the only dependency I need is the JGraphT:

{:deps {org.jgrapht/jgrapht-core {:mvn/version "1.5.1"}}}

and the name-space is defined as follows:

(ns jg (:import [org.jgrapht.graph SimpleGraph SimpleWeightedGraph SimpleDirectedGraph SimpleDirectedWeightedGraph DefaultEdge DefaultWeightedEdge] [org.jgrapht.alg TransitiveClosure StoerWagnerMinimumCut] [org.jgrapht.alg.flow EdmondsKarpMFImpl] [org.jgrapht.alg.shortestpath JohnsonShortestPaths DijkstraShortestPath] [org.jgrapht.alg.spanning KruskalMinimumSpanningTree PrimMinimumSpanningTree] [org.jgrapht.alg.clique ChordalGraphMaxCliqueFinder BronKerboschCliqueFinder]))

Random Graphs

I am going to need two functions that will generate random graphs for today's computations. The first one is for creating a random directed graph,

(defn random-graph [n e l] (let [G (SimpleGraph. DefaultEdge)] (doseq [i (range n)] (.addVertex G i)) (doseq [i (.vertexSet G)] (doseq [u (range e)] (.addEdge G i (mod (+ 1 i (rand-int l)) n)))) G))

#'jg/random-graph

and the second is for random directed graphs:

(defn random-directed-graph [n e l] (let [G (SimpleDirectedGraph. DefaultEdge)] (doseq [i (range n)] (.addVertex G i)) (doseq [i (.vertexSet G)] (doseq [u (range e)] (.addEdge G i (mod (+ 1 i (rand-int l)) n)))) G))

#'jg/random-directed-graph

I am also going to need weighted versions of these random graphs:

(defn random-weighted-graph [n e l] (let [G (SimpleWeightedGraph. DefaultWeightedEdge)] (doseq [i (range n)] (.addVertex G i)) (doseq [i (.vertexSet G)] (doseq [u (range e)] (.addEdge G i (mod (+ 1 i (rand-int l)) n)))) (doseq [e (.edgeSet G)] (if (> G KruskalMinimumSpanningTree. .getSpanningTree))

Spanning-Tree [weight=39.0, edges=[(0 : 8), (2 : 7), (27 : 36), (6 : 13), (10 : 19), (14 : 23), (29 : 38), (28 : 33), (31 : 39), (11 : 20), (0 : 9), (26 : 31), (0 : 7), (0 : 3), (10 : 18), (0 : 5), (7 : 15), (8 : 14), (17 : 25), (1 : 10), (19 : 28), (1 : 9), (12 : 21), (1 : 4), (15 : 22), (26 : 34), (23 : 30), (22 : 29), (4 : 12), (6 : 11), (7 : 16), (23 : 32), (19 : 27), (27 : 35), (1 : 6), (19 : 26), (17 : 24), (35 : 37), (9 : 17)]]

You may also use Prim's algorithm:

(let [n 40 d 6 G (random-graph n d 9)] (->> G PrimMinimumSpanningTree. .getSpanningTree))

Spanning-Tree [weight=39.0, edges=[(7 : 13), (9 : 10), (37 : 0), (0 : 5), (0 : 4), (13 : 15), (0 : 7), (13 : 14), (13 : 21), (7 : 12), (2 : 3), (1 : 9), (3 : 9), (3 : 11), (23 : 29), (32 : 1), (7 : 16), (23 : 28), (21 : 27), (13 : 17), (39 : 0), (22 : 29), (21 : 23), (34 : 0), (21 : 26), (24 : 25), (38 : 3), (0 : 3), (23 : 30), (35 : 3), (19 : 23), (31 : 39), (36 : 0), (21 : 24), (12 : 18), (7 : 8), (20 : 21), (33 : 39), (3 : 6)]]

Shortest Path

Next, let us move to Dijkstra's shortest path algorithm. I did not actually did this from scratch, but I used a fancy matrix method here and here that used tropic rings.

(let [n 40 d 5 G (random-graph n d 10) alg (DijkstraShortestPath. G) a (->> (.vertexSet G) (random-sample 0.2) first) b (->> (.vertexSet G) (random-sample 0.2) last)] (.getPath alg a b))

[(8 : 12), (38 : 8)]

While at it, let us apply Johnson's Shortest Path Algorithm:

(let [n 40 d 5 G (random-graph n d 10) alg (JohnsonShortestPaths. G) a (->> (.vertexSet G) (random-sample 0.2) first) b (->> (.vertexSet G) (random-sample 0.2) last)] (.getPath alg a b))

[(37 : 1)]

Maximal Cliques

I implemented Bron-Kerbosch both in Common Lisp and Clojure:

(let [n 40 d 6 G (random-graph n d 9) cliques (BronKerboschCliqueFinder. G)] (->> cliques .maximumIterator iterator-seq (into [])))

[#{7 8 10 13 15}]

Maximal Flow

I did an implementation of Ford-Fulkerson Maximum Flow (which is also known as Edmond-Karp) both in Common Lisp and Clojure.

(let [n 40 d 5 G (random-weighted-graph n d 10) flow (EdmondsKarpMFImpl. G) a (->> (.vertexSet G) (random-sample 0.2) first) b (->> (.vertexSet G) (random-sample 0.2) last)] (.getMaximumFlow flow a b))

Flow Value: 1.1119844227952433 Flow map: {(30 : 32)=0.0, (16 : 25)=0.0, (13 : 15)=0.0, (26 : 31)=0.2074921060959558, (34 : 39)=0.0, (4 : 11)=0.0, (37 : 2)=0.0, (21 : 26)=0.257751382221186, (0 : 1)=0.6539934273958473, (36 : 38)=0.0, (28 : 31)=0.0, (9 : 19)=0.0, (14 : 18)=0.0, (9 : 10)=0.0, (4 : 7)=0.0, (32 : 2)=0.0, (3 : 9)=0.0, (26 : 35)=0.09606035114276479, (11 : 16)=0.0, (13 : 14)=0.0, (10 : 18)=0.0, (6 : 16)=0.0, (23 : 24)=0.0, (24 : 28)=0.0, (38 : 6)=0.0, (8 : 14)=0.0, (16 : 26)=0.0, (27 : 31)=0.17328910441742917, (11 : 20)=0.0, (7 : 10)=0.0, (13 : 20)=0.0, (20 : 21)=0.0, (34 : 4)=0.0, (14 : 15)=0.0, (29 : 30)=0.0, (10 : 13)=0.0, (21 : 23)=0.0, (38 : 1)=0.0, (18 : 22)=0.0, (15 : 24)=0.0, (19 : 22)=0.0, (3 : 12)=0.0, (21 : 27)=0.257751382221186, (23 : 32)=0.0, (39 : 5)=0.0, (37 : 7)=0.0, (28 : 36)=0.2648009224619392, (38 : 0)=0.0, (10 : 19)=0.0, (18 : 21)=0.0, (36 : 1)=0.27321221688246233, (17 : 26)=0.0, (22 : 24)=0.0, (19 : 20)=0.0, (22 : 30)=0.0, (25 : 31)=0.0, (12 : 18)=0.0, (35 : 5)=0.0, (38 : 4)=0.0, (12 : 16)=0.0, (15 : 17)=0.0, (7 : 15)=0.0, (38 : 5)=0.0, (32 : 36)=0.08446227780375681, (30 : 36)=0.0, (35 : 36)=0.09606035114276479, (39 : 3)=0.0, (24 : 25)=0.0, (20 : 28)=0.2648009224619392, (1 : 8)=0.0, (19 : 27)=0.0, (39 : 0)=0.0, (11 : 18)=0.0, (35 : 3)=0.0, (2 : 5)=0.0, (25 : 35)=0.0, (27 : 35)=0.0, (17 : 25)=0.0, (0 : 7)=0.0, (18 : 27)=0.0, (6 : 7)=0.0, (15 : 22)=0.0, (34 : 38)=0.0, (21 : 28)=0.0, (3 : 4)=0.0, (6 : 9)=0.0, (36 : 0)=0.4579909953993959, (32 : 1)=0.0, (18 : 19)=0.0, (24 : 33)=0.0, (4 : 9)=0.0, (25 : 32)=0.0, (13 : 17)=0.0, (5 : 12)=0.0, (32 : 0)=0.0, (23 : 25)=0.0, (15 : 25)=0.0, (28 : 34)=0.0, (31 : 1)=0.380781210513385, (21 : 24)=0.0, (1 : 10)=0.0, (27 : 32)=0.08446227780375681, (31 : 35)=0.0, (8 : 11)=0.0, (25 : 34)=0.0, (5 : 11)=0.0, (31 : 38)=0.0, (33 : 38)=0.0, (37 : 3)=0.0, (8 : 15)=0.0, (2 : 10)=0.0, (13 : 22)=0.0, (8 : 13)=0.0, (7 : 12)=0.0, (15 : 23)=0.0, (26 : 28)=0.0, (29 : 36)=0.0, (14 : 21)=0.0, (19 : 23)=0.0, (28 : 30)=0.0, (16 : 19)=0.0, (33 : 3)=0.0, (34 : 1)=0.0, (20 : 24)=0.0, (26 : 36)=0.28587966087339745, (35 : 39)=0.0, (2 : 12)=0.0, (27 : 37)=0.0, (14 : 23)=0.0, (9 : 11)=0.0, (30 : 35)=0.0, (1 : 6)=0.0, (37 : 0)=0.0, (16 : 20)=0.0, (3 : 13)=0.0, (1 : 5)=0.0, (39 : 9)=0.0, (31 : 32)=0.0, (17 : 24)=0.0, (33 : 37)=0.0, (22 : 32)=0.0, (24 : 34)=0.0, (10 : 17)=0.0, (5 : 13)=0.0, (29 : 35)=0.0, (30 : 31)=0.0, (23 : 30)=0.0, (20 : 26)=0.2648009224619392, (10 : 14)=0.0, (4 : 14)=0.0, (11 : 21)=0.0, (33 : 34)=0.0, (36 : 37)=0.0, (12 : 22)=0.0, (7 : 13)=0.0, (28 : 38)=0.0, (5 : 10)=0.0}

Minumum Cut

I did an implementation of Stoer-Wagner in Clojure. Here is the same algorithm from JGraphT:

(let [n 40 d 15 G (random-weighted-graph n d 30) cut (StoerWagnerMinimumCut. G)] (.minCut cut))

[30]

0 notes

kaygun · 3 years ago

Text

2D-Random Walk

Description of the problem

Yesterday I was looking at the deficit vs exchange rate curve. The curve suspiciously looks very similar to 2D-random walk. Today, I’ll sketch several 2D-random walk curves to see if I can get curves similar to what I had yesterday.

Theory

A discrete 1D-random walk is a sequence of real numbers $(x_n)$ such that

$$ \Delta x_n = x_n - x_{n-1} \sim N(0,\epsilon) $$

for some $\epsilon$. In a 2D-discrete random walk we have 2 of these sequences with possibly different $\epsilon$’s.

Code

Let us start with the libraries

from numpy.random import normal from pandas import DataFrame as df import matplotlib.pyplot as plt

I’ll implement the 1D-random walk. For 2D-random walk, I will call this function twice:

def randomWalk1D(n,epsilon=0.1,m=3): x = 0 xs = [] for i in range(n): x += normal(loc=0, scale=epsilon) xs.append(x) return df(xs).rolling(m).mean()

Let us plot:

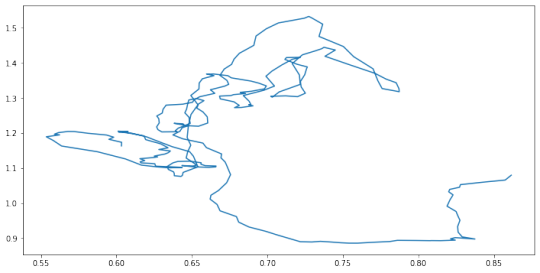
xs = randomWalk1D(250, 0.2, 10) ys = randomWalk1D(250, 0.2, 10) plt.plot(xs,ys) plt.savefig('2d-random-walk.png')

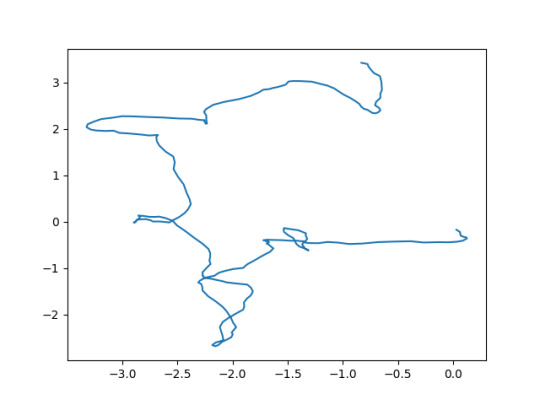
Analysis

Well… The curve I got yesterday looks very similar to these curves. So, really if there is a functional dependence between exchange rate and the trade deficit, it is not easy to see using a simple minded plot of these values against here.

0 notes

kaygun · 3 years ago

Text

Trade Deficit vs Exchange Rate Curve

Description of the problem

I once remember reading an old paper by an economist (whose name escapes me) about relationship between trade deficit and exchange rates. Today, I’ll do a numerical experiment to see if there is a demonstrable relationship.

Data

I am going to pull the data from European Central Bank. Let us start with the libraries:

import json import pandas as pd import numpy as np from matplotlib import pyplot as plt from urllib.request import urlopen

I am going to rehash a function I wrote earlier to pull the data:

def ecbProbe(dataset,name,m): mid = ':'.join(['0' for i in range(m)]) with urlopen(f'https://sdw-wsrest.ecb.europa.eu/service/data/{dataset}?format=jsondata') as url: raw = json.load(url) dates = [x['name'] for x in raw['structure']['dimensions']['observation'][0]['values']] values = [x[0] for x in raw['dataSets'][0]['series'][mid]['observations'].values()] return pd.DataFrame({name: values}, index=dates)

I am going to pull the full data of total imports and exports of EU Area with the US:

country = 'US' df1 = ecbProbe(f'ECB,TRD/M.I8.Y.M.TTT.{country}.4.VAL','imports US',8) df2 = ecbProbe(f'ECB,TRD/M.I8.Y.X.TTT.{country}.4.VAL','exports US',8) deficit = pd.DataFrame(df1['imports US']/df2['exports US']) deficit.plot(figsize=(12,6)) plt.savefig('us-ec-trade-deficit.png')

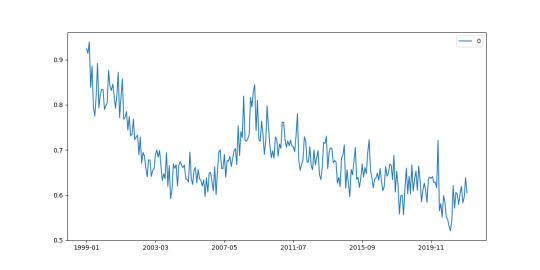
Next, the exchange rate data:

exchangeUStoEUR = ecbProbe('EXR/M.USD.EUR.SP00.A','EURXUS',5) exchangeUStoEUR.plot(figsize=(12,6)) plt.savefig('us-ec-exchange-rate.png')

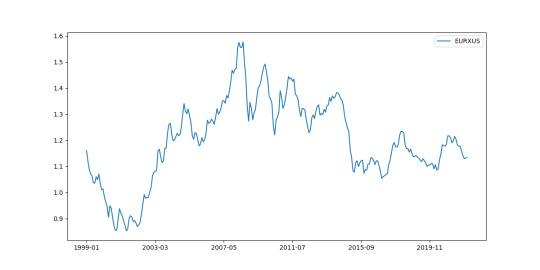
Now, we plot these things against each other. I’ll do a running average of 8 months.

tmp = deficit.join(exchangeUStoEUR,how='inner').rolling(8).mean() plt.plot(tmp.iloc[:,0],tmp.iloc[:,1]) plt.savefig('us-ec-plot.png')

Analysis

Interesting!

0 notes

kaygun · 3 years ago

Text

Working with World Bank Data in Python

Description of the problem

I have been working with European Central Bank data in python. I am teaching two data science classes this semester and I need a good source of real socio-economic data for teaching purposes. World Bank is such a good source. Today, I am going to write two python functions to query the World Bank Data Store.

Implementation

Let me start with the imports:

import pandas as pd import numpy as np import matplotlib.pyplot as plt from io import BytesIO from urllib.request import urlopen from zipfile import ZipFile from xmltodict import parse

My first function pulls the data from World Bank Data store in xml and converts to a hash map:

def queryWorldBank(series): base = 'https://api.worldbank.org/v2/en/indicator/' with urlopen(f'{base}/{series}?downloadformat=xml') as url: zf = ZipFile(BytesIO(url.read())) name = zf.filelist[0].filename return parse(zf.open(name).read().decode('utf8'))

The next function parses the raw xml we pull from the data source:

def parseXML(rawXML, name): res = [] years = [] for x in raw['Root']['data']['record']: y = x['field'] try: res.append({'country': y[0]['#text'], name: float(y[3]['#text'])}) years.append(int(y[2]['#text'])) except: None return pd.DataFrame(res, index=years)

Each data set on World Bank’s Data Store has a unique ID. For example, the store has data that contains the number of air passengers (both domestic and international) carried by the air carriers registered in the country. The unique id for the data set is “IS.AIR.PSGR”. The records indicates that the data came from International Civil Aviation Organization.

raw = queryWorldBank('IS.AIR.PSGR') passengers = parseXML(raw,'passengers') (passengers[passengers['country']=='Turkey'])['passengers'].plot(figsize=(18,6)) plt.savefig('world-bank-data-figure-1.png')

Next, let me pull the gini index data, and I’ll plot the data for Turkey.

raw = queryWorldBank('SI.POV.GINI') gini = parseXML(raw,'gini') (gini[gini['country']=='Turkey'])['gini'].plot(figsize=(18,6)) plt.savefig('world-bank-data-figure-2.png')

Next, I’ll pull the data on the number of years schooling received by 15+ year old women. The ID for that data set is “BAR.PRM.SCHL.15UP.FE”.

raw = queryWorldBank('BAR.PRM.SCHL.15UP.FE') education = parseXML(raw,'level') (education[education['country']=='Turkey'])['level'].plot(figsize=(18,6)) plt.savefig('world-bank-data-figure-3.png')

How about we plot average gini against average year of schooling 15+ year old women get for each country:

ed = education.groupby('country').mean() gi = gini.groupby('country').mean() res = ed.join(gi,how='inner') plt.figure(figsize=(8,8)) plt.scatter(res['level'],res['gini'],c='blue',alpha=0.3) plt.savefig('world-bank-data-figure-4.png')

Do you notice something? The gini index (a measure of economic inequality) reduces as the average number of schooling of women 15+ increases. Something to ponder about.

0 notes

kaygun · 3 years ago

Text

Working with European Central Bank data in python (revisited)

Description of the problem

I have looked at pulling European Central Bank data using lisp, clojure, scala, and python. Today, I am going to revisit my python code and clean it up, and maybe, improve some.

Implementation

Let us start with the imports:

import json import pandas as pd from matplotlib import pyplot as plt from urllib.request import urlopen

Next, our work-horse that will query ECB data warehouse:

def ecbProbe(dataset,name,m): mid = ':'.join(['0' for i in range(m)]) base = 'https://sdw-wsrest.ecb.europa.eu/service/data/' with urlopen(f'{base}{dataset}?format=jsondata') as url: raw = json.load(url) dates = [x['name'] for x in raw['structure']['dimensions']['observation'][0]['values']] values = [x[0] for x in raw['dataSets'][0]['series'][mid]['observations'].values()] return pd.DataFrame({name: values}, index=dates)

There is a specific parameter that I couldn’t figure out. Each dataset has a specific key with specific number of ’0’s. So, I passed the number of these zeros as a parameter m.

Let us look at EU area trade deficit with China (imports divided by exports). For this dataset the parameter m is 8.

df1 = ecbProbe(f'ECB,TRD/M.I8.Y.M.TTT.CN.4.VAL','Imports',8) df2 = ecbProbe(f'ECB,TRD/M.I8.Y.X.TTT.CN.4.VAL','Exports',8) pd.DataFrame(df1['Imports']/df2['Exports']).plot(figsize=(12,6)) plt.savefig('ecb-with-python-trade-deficit.png')

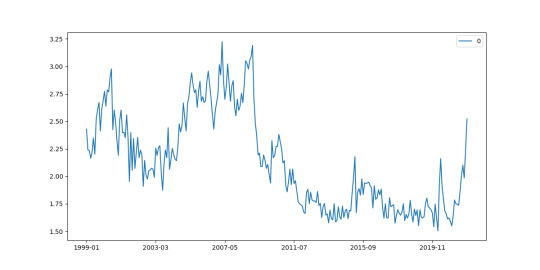
Next, we’ll get the consumer price index for the Euro area:

df = ecbProbe('ICP/M.U2.N.000000.4.ANR','CPI Euro Area',6) df.plot(figsize=(12,6)) plt.savefig('ecb-with-python-cpi.png')

Finally, let us do the labor productivity for the Euro area:

dataset = 'MNA/Q.Y.I8.W0.S1.S1._Z.LPR_PS._Z._T._Z.EUR.LR.GY' df = ecbProbe(dataset,'Labor Productivity',14) df.plot(figsize=(12,6)) plt.savefig('ecb-with-python-labor-productivity.png')

2 notes · View notes

kaygun · 3 years ago

Text

A Clique Analysis of Quakers in early modern Britain (1500-1700)

A description of the problem

Today, I am going to re-implement in clojure a part of a networking analysis done by John R. Ladd, Jessica Otis, Christopher N. Warren, and Scott Weingart titled "Exploring and Analyzing Network Data with Python" at Programming Historian. The original analysis is done with python using networkx. I am going to re-implement the part of the analysis about finding maximum cliques within the network. I am going to use JGraphT which is as extensive as networkx in its functionality. The rest of the analysis can too be repeated within clojure.

Data

The network data is from the Six Degrees of Francis Bacon project. Project aims to show and analyze the social networks of early modern Britain (1500-1700). The dataset composed of pairs of important Quaker figures that know each other. The data is culled from the Oxford Dictionary of National Biography. I collected two files: a list of nodes and a list of edges from Programming Historian.

Here is a small sample from the nodes list:

Name, Historical Significance, Gender, Birthdate, Deathdate, ID Joseph Wyeth, religious writer, male, 1663, 1731, 10013191 Alexander Skene of Newtyle, local politician and author, male, 1621, 1694, 10011149 James Logan, colonial official and scholar, male, 1674, 1751, 10007567 Dorcas Erbery, Quaker preacher, female, 1656, 1659, 10003983 Lilias Skene, Quaker preacher and poet, male, 1626, 1697, 10011152

and a sample from the edge list:

Source, Target George Keith, Robert Barclay George Keith, Benjamin Furly George Keith, Anne Conway Viscountess Conway and Killultagh George Keith, Franciscus Mercurius van Helmont George Keith, William Penn George Keith, George Fox George Keith, George Whitehead George Keith, William Bradford James Parnel, Benjamin Furly James Parnel, Stephen Crisp Peter Collinson, John Bartram Peter Collinson, James Logan

The Code

Preamble

I am going to use JGraphT, and it needs to declared in the list of dependencies. Here's my deps.edn dependencies:

{ :deps {org.jgrapht/jgrapht-ext {:mvn/version "1.5.1"} org.jgrapht/jgrapht-opt {:mvn/version "1.5.1"} org.jgrapht/jgrapht-io {:mvn/version "1.5.1"} org.jgrapht/jgrapht-core {:mvn/version "1.5.1"}} :mvn/repos { "central" {:url "https://repo1.maven.org/maven2/"} "clojars" {:url "https://repo.clojars.org/"}}}

Next, the namespace:

(ns quakers (:require [clojure.set :as s]) (:require [clojure.java.io :as io]) (:import [java.io File]) (:import [org.jgrapht.alg.clique BronKerboschCliqueFinder]) (:import [org.jgrapht.alg.scoring PageRank]) (:import [org.jgrapht.graph DefaultEdge SimpleGraph DefaultEdge]))

Let me start by a utility code that reads the necessary file and converts into a usable sequence:

(defn from-file [file processor] (->> file File. io/reader line-seq (map processor) rest))

#'quakers/from-file

Let us first ingest the nodes. For this analysis, I care only about the names. So, I'll ingest just those. Instead of showing the whole list, I'll show the first 5 names.

(def nodes (from-file "quakers_nodelist.csv" #(-> % (clojure.string/split #",") first))) (->> nodes (take 5) (into []))

#'quakers/nodes ["Joseph Wyeth" "Alexander Skene of Newtyle" "James Logan" "Dorcas Erbery" "Lilias Skene"]

Next, I'll ingest the edges which are pairs of nodes. As before, I'll show only the first 5:

(def edges (from-file "quakers_edgelist.csv" #(-> % (clojure.string/split #",")))) (->> edges (take 5) (into []))

#'quakers/edges [["George Keith" "Robert Barclay"] ["George Keith" "Benjamin Furly"] ["George Keith" "Anne Conway Viscountess Conway and Killultagh"] ["George Keith" "Franciscus Mercurius van Helmont"] ["George Keith" "William Penn"]]

Now, I'll construct the graph.

(def graph (SimpleGraph. DefaultEdge)) (doseq [x nodes] (.addVertex graph x)) (doseq [[x y] edges] (.addEdge graph x y))

#'quakers/graph

Maximal cliques

The next step is to calculate the maximal cliques within the network and list them:

(def result (->> graph BronKerboschCliqueFinder. .maximumIterator iterator-seq (map seq) (into []))) result

#'quakers/result [("Edward Burrough" "George Fox" "John Crook" "William Dewsbury") ("Edward Burrough" "George Fox" "John Crook" "John Perrot") ("James Nayler" "Edward Burrough" "George Fox" "Francis Howgill") ("James Nayler" "Edward Burrough" "George Fox" "Thomas Ellwood") ("James Nayler" "Edward Burrough" "George Fox" "John Perrot") ("William Penn" "George Fox" "George Keith" "George Whitehead") ("Benjamin Furly" "William Penn" "George Fox" "George Keith") ("James Nayler" "Richard Farnworth" "Margaret Fell" "Anthony Pearson")]

There are 8 maximal cliques each with 4 names in them:

[(count result) (map count result)]

[8 (4 4 4 4 4 4 4 4)]

PageRank

In this part of the post, I'll do something different. Let me apply the PageRank algorithm to this network to find the important nodes. As before, I'll display the top 5 nodes.

(def result2 (->> graph PageRank. .getScores (into {}) (sort-by second) reverse)) (->> result2 (map first) (take 5) (into []))

#'quakers/result2 ["George Fox" "William Penn" "James Nayler" "George Whitehead" "Margaret Fell"]

0 notes

kaygun · 4 years ago

Text

Boyer–Moore and Misra-Gries Algorithms in Clojure

Description of the problem

The Boyer–Moore majority algorithm, is a probabilistic algorithm that solves the majority problem for any data stream in a single pass using constant memory. Today, I'll do an implementation in Clojure.

An implementation of Boyer-Moore in clojure

(defn boyer-moore [xs] (loop [ys xs count 0 candidate nil] (cond (empty? ys) candidate (zero? count) (recur (rest ys) 1 (first ys)) (= (first ys) candidate) (recur (rest ys) (inc count) candidate) true (recur (rest ys) (dec count) candidate))))

#'user/boyer-moore

Let us test

(boyer-moore [0 1 1 0 2 2 2 0 0 0 1 0 2 0])

An extension

There is an extension of the Boyer-Moore majority algorithm by Misra and Gries. I'll implement that too.

An implementation of Misra-Gries in clojure

(defn misra-gries [xs k] (loop [ys xs counts {}] (if (empty? ys) (keys counts) (let [y (first ys) zs (rest ys)] (cond (get counts y false) (recur zs (merge-with + counts {y 1})) (< (count counts) k) (recur zs (merge counts {y 1})) true (recur zs (->> (reduce-kv (fn [m k v] (assoc m k (dec v))) {} counts) (filter (fn [[k v]] (> v 0))) (into {}))))))))

#'user/misra-gries

Let us test

(misra-gries [0 1 1 0 2 2 2 0 0 0 1 0 2 0] 2)

(0 2)

0 notes

kaygun · 4 years ago

Text

Tension in Text Plotted

Description of the problem

Sometimes, I’d like to go back to my earlier posts and revisit them see if they still hold up, if I can extend them. Today, I am going to revisit such an old post.

In that post, I posited the hypothesis that in oratory speeches the word overlaps between consecutive sentences is an indicator of pace and tension. In a sense, the plot of these overlaps is an EKG of the speech.

An re-implementaion in Clojure

Let us start with the namespace:

(ns experiment (:import [opennlp.tools.sentdetect SentenceModel SentenceDetectorME]) (:import [opennlp.tools.stemmer.snowball SnowballStemmer SnowballStemmer$ALGORITHM]) (:import java.io.File) (:require [clojure.string :as st] [clojure.set :as s]))

I am going to use Open NLP’s sentence detector and stemmer to process the text into usable tokens. After dividing the text into sentences, I’ll split each sentences into words and then stem them. Then I am going to count the number of common words from one sentence to next.

I need the following function for converting the text into sequence of sentences each of which are sequences of stemmed words.

(let [detector (-> "en-sent.bin" File. SentenceModel. SentenceDetectorME.) clean #(-> % st/lower-case (st/replace #"[^\s\p{IsLetter}]" " "))] (defn bag-of-words [big-string] (->> big-string (.sentDetect detector) (map clean) (map #(->> (st/split % #"\s") (filter (fn [x] (not (= "" x)))))))))

#'experiment/bag-of-words

The following function calculates the overlaps. The overlap is the number of common words divided by the total number of words.

(defn overlaps [stemmer sentences] (let [helper #(into #{} (map stemmer %))] (map (fn [xs ys i] (let [x (helper xs) y (helper ys)] {:sentence (st/join " " ys) :position i :overlap (/ (count (s/intersection x y)) (count (s/union x y)) 1.0)})) sentences (rest sentences) (range))))

#'experiment/overlaps

I am going to export the results into a CSV to plot it via gnuplot:

(defn write-csv [stemmer in-file out-file] (let [data (->> in-file slurp bag-of-words (overlaps stemmer))] (with-open [out (clojure.java.io/writer out-file)] (doseq [x data] (.write out (str (:position x) ", " (:overlap x) "\n")))) (->> data (sort-by :overlap) reverse)))

#'experiment/write-csv

I am going to need a stemmer for English and another for Turkish:

(let [st (SnowballStemmer. SnowballStemmer$ALGORITHM/TURKISH)] (defn ts [x] (.stem st x))) (let [st (SnowballStemmer. SnowballStemmer$ALGORITHM/ENGLISH)] (defn es [x] (.stem st x)))

#'experiment/ts #'experiment/es

Kennedy’s first inaguration speech

My first experiment is on Kennedy’s first inaguration speech

(->> (write-csv es "kennedy-inaguration.txt" "kennedy.csv") (sort-by :overlap) reverse (take 3) (into []))

[{:sentence "but let us never fear to negotiate", :position 27, :overlap 0.5555555555555556} {:sentence "nor will it be finished in the first one thousand days nor in the life of this administration nor even perhaps in our lifetime on this planet", :position 36, :overlap 0.375} {:sentence "my fellow citizens of the world ask not what america will do for you but what together we can do for the freedom of man", :position 49, :overlap 0.36}]

Lincoln’s Gettsyburg address

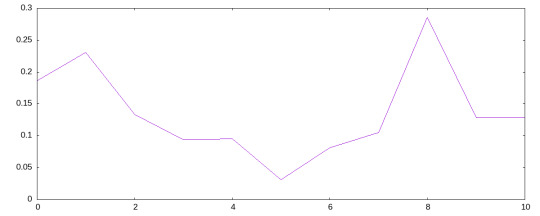
Next, Lincoln’s Gettysburg address.

(->> (write-csv es "lincoln-gettysburg.txt" "lincoln.csv") (sort-by :overlap) reverse (take 3) (into []))

[{:sentence "it is rather for us to be here dedicated to the great task remaining before us that from these honored dead we take increased devotion to that cause for which they gave the last full measure of devotion", :position 8, :overlap 0.2857142857142857} {:sentence "we are met on a great battlefield of that war", :position 1, :overlap 0.2307692307692308} {:sentence "now we are engaged in a great civil war testing whether that nation or any nation so conceived and so dedicated can long endure", :position 0, :overlap 0.186046511627907}]

Atatürk’s presidency inaguration speeches

My new experiments are Atatürk’s first and second presidency acceptance speeches.

(->> (write-csv ts "ataturk-first-inaguration.txt" "ataturk1.csv") (sort-by :overlap) reverse (take 3) (into []))

[{:sentence "son senelerde milletimizin fiilen gösterdiği kabiliyet istidat idrak kendi hakkında suizanda bulunanların ne kadar gafil ve ne kadar tetkikten uzak zevahirperest insanlar olduğunu pek güzel ispat etti", :position 6, :overlap 0.07692307692307691} {:sentence "milletimiz haiz olduğu evsaf ve liyakatini hükûmetinin yeni ismiyle cihan ı medeniyete daha çok suhuletle izhara muvaffak olacaktır", :position 7, :overlap 0.075} {:sentence "türkiye cumhuriyeti cihanda işgal ettiği mevkiye layık olduğunu asarıyla ispat edecektir", :position 8, :overlap 0.07407407407407407}]

(->> (write-csv ts "ataturk-second-inaguration.txt" "ataturk2.csv") (sort-by :overlap) reverse (take 3) (into []))

[{:sentence "istikbale nazarlarımız bu itimat ile müteveccih olduğu halde büyük millet meclisi nin muhterem azasını selamlar ve naçiz bir ferdi olmakla mağrur bulunduğum büyük türk milletine saadetler ve ona hepimiz için güzide ve meşkûr hizmetler temenni ederim", :position 13, :overlap 0.1702127659574468} {:sentence "cumhuriyetin mevcudiyet ve rasanetini ve milletin âli menafiini dahili ve harici herhangi bir kasta karşı her an müdafaaya hazır bulunarak hariçte dostluklara ve sulhcuyane mesaiye müzahir ve vefakâr ve dahilde vatandaşların emn ü asayiş içinde gayret ve inkişafına hadim olmak yeni faaliyet devresinden dahi beklediğimiz asıl gayedir", :position 8, :overlap 0.1428571428571429} {:sentence "üçüncü büyük millet meclisi nin faaliyet devresi hamiyet ve himmetinizle türk milletinin layık ve müstait olduğu faaliyetin yüksek bir merhalesini daha tahakkuk ettireceğine sarsılmaz itimadımız vardır", :position 12, :overlap 0.1428571428571429}]

0 notes

kaygun · 4 years ago

Text

Statistical Distributions using Apache Commons Math in Clojure

Description of the problem

More than often, I need random numbers from standard statistical distributions such as Gaussian, Poisson, T, F, or Beta. Since I like using Clojure so much, I have been looking for a satisfactory solution with as little friction as possible. Then I remember, Apache Commons Math has an excellent statistical sub-library that has all the distributions I need (and more) already implemented. All I need is to form a bridge between Clojure and Apache Commons Math.

Those who are interested in a pure Clojure solution should check out kixi.stats.

Implementation

Let me start with my dependencies in my deps.edn:

{:deps {org.apache.commons/commons-math3 {:mvn/version "3.6.1"}}}

Next, my namespace:

(ns distributions.core (:import [org.apache.commons.math3.distribution BetaDistribution BinomialDistribution CauchyDistribution ChiSquaredDistribution ExponentialDistribution FDistribution GammaDistribution GeometricDistribution GumbelDistribution HypergeometricDistribution IntegerDistribution KolmogorovSmirnovDistribution LaplaceDistribution LevyDistribution LogNormalDistribution LogisticDistribution MixtureMultivariateNormalDistribution MixtureMultivariateRealDistribution MultivariateNormalDistribution MultivariateRealDistribution NakagamiDistribution NormalDistribution ParetoDistribution PascalDistribution PoissonDistribution RealDistribution TDistribution TriangularDistribution UniformIntegerDistribution UniformRealDistribution WeibullDistribution ZipfDistribution]))

I included all distributions in the library in case you'd like to experiment with them later on. Next, some utility functions. I am following R's naming conventions:

(defn quartile [dist x] (.inverseCumulativeProbability dist x)) (defn pdf [dist x] (.density dist x)) (defn cdf [dist x] (.cumulativeProbability dist x)) (defn sample [dist N] (seq (.sample dist N)))

Some tests

Let us test the code. First, the normal distribution with 0 mean and 1.0 variance:

(def ndist (NormalDistribution. 0.0 1.0)) (quartile ndist 0.975) (pdf ndist 12.0) (sample ndist 10)

#'distributions.core/ndist 1.959963984540054 2.1463837356630728E-32 (0.7328831550323387 -1.7564646871411873 0.3036384595319081 -0.6552956779199097 0.09651672484712626 2.100967417766368 -0.3455198591244783 0.4937778023356781 0.44520438525164974 -0.33095042749939735)

Next, the Poisson distribution with p=0.05:

(def pdist (PoissonDistribution. 0.05)) (sample pdist 100)

#'distributions.core/pdist (0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0)

And, finally the T-distribution with 2 degrees of freedom

(def tdist (TDistribution. 2)) (quartile tdist 0.975) (pdf tdist 12.0) (sample tdist 10)

#'distributions.core/tdist 4.302652729698313 5.668533483577864E-4 (0.9571878079111966 0.22544989371671462 -1.4840659295754255 1.1260852156451235 0.38857568503851414 -1.4375968836484603 0.15007647730820867 -1.1068773851595448 0.0021123655126886205 -0.2345292434886456)

1 note · View note