marcilenedamasc-blog

[marcilenedamasc-blog]

Trabalho final - Parte 2 - Marcilene Damasceno

Abaixo o link do vídeo da segunda parte do trabalho final de MAMI

Jogo parte 2:

https://drive.google.com/file/d/1uXo4RmlHiBsSGVfoGyzsBd16CC57uGP1/view?usp=sharing

Fonte utilizada no jogo: https://www.fontsquirrel.com/fonts/amatic

[marcilenedamasc-blog]

Tarefa 17 - Aula 22 - Diagrama da Rosa de Florence Nightingale

Título da tarefa: explicar o Diagrama de Rosa, de Florence Nightingale, destacando o impacto social causado à época de sua criação, e exemplificar o mesmo gerando um modelo baseado em dados reais, à sua escolha

Florence Nightingale  foi uma enfermeira britânica do século XIX responsável pela criação do considerado primeiro gráfico estatístico da história, o Diagrama da Rosa, 1857. Ela desenvolveu esse diagrama para mostrar, de uma forma mais objetiva, a quantidade de mortes de soldados causadas por infecções na Guerra da Crimeia, que foram bem mais numerosas do que o número de mortes em campo de batalha.

Fonte: http://cargocollective.com/desenhosconceito/Tangente-Diagramas

Seu  levantamento estatístico contribuiu para que os hospitais britânicos fossem mais bem planejados, sendo mais bem conservados e limpos. O nome Diagrama da Rosa vem da forma circular irregular do diagrama, que parece com uma rosa. Além de mostrar os dados coletados pela enfermeira, o diagrama foi pensado por ela para ser um formato mais confortável de visualizar informações. Além de informações escritas, as formas irregulares e as cores estabeleceram hierarquias que dividiram informações mas que unificaram uma ideia, uma informação geral.

[marcilenedamasc-blog]

Tarefa 15 - Aula 20 - Média de tons e desvio padrão

Título da tarefa: Crie versões no Photoshop da imagem de einstein.jpg e cinza.jpg com variações de brilho e contraste. Qual impacto ocorreu na média e desvio padrão?

Nessa aula os professores discutiram sobre média de tons e desvio padrão calculado a partir dessa média. Como parâmetros para essa medição a aplicação fez uma leitura de cada pixel, para medir os valores de tons cinza de duas imagens. A média de tons é calculada a partir da soma de todos os valores dividida pela quantidade de pixels da imagem. Já o desvio padrão é um calculo que indica quanto um conjunto de dados é uniforme, ou seja, quanto mais próximo de 0 mais homogêneo é o conjunto de dados. 

Einstein

Original

Média de Tons é: 28.610287; Desvio padrão é:  63.014275

Mais 30% de brilho

Média de Tons é:  33.10823; Desvio padrão é:  70.02935

Mais 50% de Contraste

Média de Tons é  29.458435; Desvio padrão é:  65.74085

Para as aplicações com a imagem do Einstein a variação dos dois cálculos não foram grandes. Como a adição de brilho e de contraste nas duas imagens são aplicadas de forma uniforme, todos os pixels recebem incremento. Isso faz os resultados dos cálculos estarem sempre aproximados.

Cinza

Original

Media de Tons é:  29.0; Desvio padrão é:  0.0

Com mais 30% de brilho

Média de Tons é:  36.0; Desvio padrão é: 0.0

Com mais 50% de contraste

Media de Tons é:  19.0; Desvio padrão é:  0.0

Como resultado dos cálculos feitos para a imagem totalmente cinza vemos uma variação mais significativa para a média de tons, uma vez que todos os pixels receberam incrementos uniformemente. Já o desvio padrão continua 0 para todos os exemplos, uma vez que todos os pixels têm a mesmo tom de cinza. Isso indica que os dados são uniformes.

[marcilenedamasc-blog]

Tarefa 14 - Aula 17 - Modelos natural e matemático de um efeito de transição

Título da tarefa: expor e discutir os modelos natural e matemático, com base na teoria dos conjuntos e nos padrões RGB ou HSB, de uma aplicação que implementa um dos efeitos apresentados em http://goo.gl/KATZjk

O efeito escolhido foi o seguinte, de 0:30 - 0:38

Modelo Natural

Nessa transição existe uma imagem inicial que após alguns segundos é substituída por uma imagem totalmente cinza, formada gradativamente por silhuetas de ovelhas. Após esse preenchimento a tela totalmente cinza vai se desfazendo gradativamente através da animação reversa das ovelhas que preencheram a tela, dando lugar à uma nova imagem.

Modelo Matemático

No modelo matemático desse efeito são consideradas a largura e altura total da tela a receber a transição. Após um determinado período o efeito é acionado e várias formas de ovelhas aparecem na tela até atingirem a altura e largura máxima do espaço da tela, não deixando nenhum espaço aberto, de tal forma que esconde a imagem anterior totalmente. Após toda a região estar preenchida a animação de preenchimento é revertida e uma nova imagem aparece. Escolhi essa transição pois é uma das mais adequadas para observar a utilização de padrões de cores em uma aplicação que fosse tentar implementar esse efeito. Ao ser preenchida a tela com as formas de ovelhas, a aplicação poderia analisar se todos os pixels em determinado intervalo são de determinada cor e, se forem, existiria um contador para o tempo que determinaria quantos segundos a tela continuaria preenchida com essas ovelhas. Após essa condição terminar, após o tempo ser atingido, as ovelhas desapareceriam em uma animação reversa.

[marcilenedamasc-blog]

Tarefa 13 - Aula 16 - Filtros

Título da tarefa: criar e explicar uma aplicação que, empregando variáveis para o controle de valores, realiza o processo abaixo numa imagem à sua escolha:

Imagem de exemplo da tarefa

Nessa aula os professores ensinaram, através de vários exercícios, a criar uma função que consegue ler as informações de cada pixel de uma imagem, guardar as mesmas e modificá-las para um reuso. 

Para isso, uma configuração inicial a ser declarada é o modo de cor da aplicação, que será HSB onde H = Hue (matiz ou “cor pura”) , S = Saturation (saturação) e B =  Brightness (brilho). Com a declaração desse modo de cor, se pode trabalhar e utilizar de várias maneiras esses parâmetros de cor, saturação e brilho.

Assim, para esta atividade escolhi a seguinte imagem para ser trabalhada:

Imagem bem antiga da banda Slowdive

Para produzir os efeitos solicitados na imagem de referência da tarefa, carreguei a imagem original e criei variáveis para todas variações da mesma referentes a sua nova cor e variável para guardar a informação da imagem original, utilizadas na função “processaImage()”.

Além disso, criei uma função “Ruido”, que aplica o efeito de ruído em todas as imagens que, de forma básica, adiciona pixels em posições aleatórias em intervalos declarados do eixo x e y da imagem.

Esses foram os resultados:

Original com ruído

Tons de cinza  (matiz = 0, saturação = 0 e brilho igual ao da imagem original)

Adição de vermelhos  (matiz = 360 com saturação e brilho iguais aos da imagem original)

Adição de amarelos (matiz = 45 com saturação e brilho iguais aos da imagem original)

Este é o código dessa atividade:

PImage imgOriginal; PImage imgDestino = createImage(200, 200, RGB); PImage imgDestino2 = createImage(200, 200, RGB); PImage imgDestino3 = createImage(200, 200, RGB); PImage imgDestino4 = createImage(200, 200, RGB);

color corOriginal, corDestino1, corDestino2, corDestino3, corDestino4; float  red, green, blue;

void setup() {  size(1000, 200);  colorMode(HSB, 360, 100, 100);

 imgOriginal = loadImage("slowdive.jpg");  imgDestino =  loadImage("slowdive.jpg");  imgDestino2 =  loadImage("slowdive.jpg");  imgDestino3 =  loadImage("slowdive.jpg");  imgDestino4 =  loadImage("slowdive.jpg");  image(imgOriginal, 0, 0);  processaImage();  Ruido();  image(imgDestino, 200, 0);  image(imgDestino2, 400, 0);  image(imgDestino3, 600, 0);  image(imgDestino4, 800, 0); } void draw() { } void processaImage() {  for (int i = 0; i<200; i++) {    for (int j = 0; j <200; j++) {      float  h, s, b, result;      corOriginal = imgOriginal.get(i, j);      h = hue(corOriginal);      s = saturation(corOriginal);      b = brightness(corOriginal);      corDestino2 = color(0, 0, b);      imgDestino2.set(i, j, corDestino2);      corDestino3= color(360, s, b);      imgDestino3.set(i, j, corDestino3);      corDestino4 = color(45, s, b);      imgDestino4.set(i, j, corDestino4);    }  } }

void Ruido() {  for (int i = 0; i<7000; i++) {    int x = int(random(200));    int y = int(random(200));    int x2 = int(random(200));    int y2 = int(random(200));    int x3 = int(random(200));    int y3 = int(random(200));    int x4 = int(random(200));    int y4 = int(random(200));    red = int(random(256));    green  = int(random(256));    blue = int(random(256));    corDestino1 = color (red, green, blue);    corDestino2 = color (red, green, blue);    corDestino3 = color (red, green, blue);    corDestino4 = color (red, green, blue);    imgDestino.set(x, y, corDestino1);    imgDestino2.set(x2, y2, corDestino2);    imgDestino3.set(x2, y2, corDestino3);    imgDestino4.set(x2, y2, corDestino4);  } }

[marcilenedamasc-blog]

Trabalho parte 1 - Jogo Casio Airforce Fighter - Marcilene Damasceno

Apresentação

O jogo que escolhi foi o Airforce Fighter, da plataforma Casio CG - 380, de 1987. Nesse jogo o player controla um avião que precisa desviar dos tiros de submarinos. Além disso o avião pode atirar nos submarinos e destruí-los. 

Modelos Naturais

Jogador

- O jogador pode se movimentar em 4 direções: esquerda, direita, para cima e para baixo.

-Para movimentar o avião, o jogador pode utilizar 4 botões direcionais.

-O avião tem uma área específica na qual ele pode se movimentar, não podendo ele sair dos limites horizontais da tela nem entrar na área destinada para as posições do placar nem na área dos inimigos, os submarinos.

-O jogador pode morrer até 3 vezes. Ao atingir esse número de mortes o jogo é encerrado.

-Os tiros do jogador (o avião) é disparados a partir de uma tecla.

-Ao ser atingido, sua posição, assim como a de todos os submarinos voltam para as configurações iniciais.

Os inimigos

- Nesse jogo os inimigos são os submarinos.

- Os inimigos se movem de forma contínua na horizontal.

- A posição Y dos inimigos é randômica.

- A posição Y randômica dos submarinos estão dentro de um limite desse eixo, pois os mesmos não podem entrar na área de outros elementos.

- Os tiros dos submarinos são constantes e os mesmos têm suas coordenadas estabelecidas pelas posições dos seus respectivos submarinos.

- Ao ser atingido, cada submarino volta a sua posição original e some da tela.

Sistema

 - A cada inimigo eliminado o jogador acumula 10 pontos

- A cada tiro recebido pelo jogador uma morte é pontuada

- O jogador só pode ser atingido 3 vezes pelos submarinos. Ao acumular essas 3 mortes o jogo acaba.

Modelos matemáticos

Antes de demonstrar os modelos matemáticos dos elementos, gostaria de dizer que para a obtenção dos mesmo eu trabalhei com proporções visuais, antes de tudo. Como não consegui encontrar a medida correta do aspect ratio da tela da plataforma, eu fiz um print da mesma, levei para um programa de edição de imagens e lá eu criei em cima dela elementos geométricos equivalentes às mesmas proporções, contudo, depois redimensionei a tamanhos maiores para a aplicação no processing. Com esses elementos vi que a tela do jogo se divide em 4 regiões: placar e vidas, frames das nuvens, área do avião e área dos submarinos.

Tela produzida em um programa de edição

Grid simples de proporções

Para essas proporções, busquei guiá-las por um número fechado de resolução e determinar os outros a partir dele. Escolhi então a altura de 720 e aí todas as outras medidas vieram desse valor, todas relacionados a proporção observada. Assim, obtive os seguintes números:

A partir desses números, obtive as seguintes conclusões das movimentações

Jogador

- Só podem se movimentar no intervalo de 0 a 1152 no eixo X

- Só podem se movimentar no intervalo de 152 a 426 no eixo Y

- Se de alguma forma os valores de x e y do avião ultrapassarem essas condições eles retornam para valores válidos.

Submarinos

- Podem se movimentar no intervalo de até -400 a 1152 no eixo X (essa criação com valores negativos nesse eixo permite uma variação de distância entre os submarinos)

- Só podem se movimentar randomicamente dentro do intervalo de 426+25 (o 25 equivale ao raio vertical da elipse) a 720, que é o limite da tela no eixo Y

Placar e nuvens

- Coloquei um contador para o placar que aumenta de 10 em 10

- Nessa parte do trabalho não trabalhei com as posições corretas para esses elementos. Não implementei também as posições das nuvens.

- Para a representação das mortes eu coloquei um contador, mas para segunda parte do trabalho essa representação será visual, como no jogo original.

Modelo computacional

Para a produção desse porte eu utilizei o processing mesmo. Vale dizer que tive muitas dificuldades e que até demorei a começar a construir algo significativo por estar tentando utilizar outras ferramentas de desenvolvimento que, seguindo conselhos, pareciam mais fáceis: Godot e Game Maker. Contudo não tive nenhum sucesso ao tentar utilizá-las pois percebi que eu estava demorando muito mais para entender como ela funcionava do que construindo de fato meu jogo com as informações e as lógicas que eu já estava entendendo.

Comecei a construir melhor meu código a partir da revisão de MAMI e com ela o que eu já estava fazendo ficou melhor e entendi mais o que eu poderia fazer.

No meu código eu determino posições fixas para a criação do elemento no eixo X e Y. Durante o jogo essas coordenadas mudam de formas diferentes. O X e o Y do avião mudam de acordo com a verificação pressionamento das teclas UP, DOWN, RIGHT e LEFT pelo jogador. Já as posições dos submarinos acontecem de forma contínua por funções que incrementam valores nesses eixos para cada inimigo. Além de começarem com posições diferentes de criação, para manter uma distância no eixo X e Y interessantes - Submarino 01 com x igual a -200 e y igual a 451, submarino 02 com x igual a -400 e y igual a 500 e submarino 03 com x igual a -600 e y igual a 600 - dentro de suas funções suas posições no eixo X aumentam de 100 em 100 pixels e suas posições no eixo Y são randômicas entre os números 451 e 680. Assim eles se movimentam sempre em um mesmo sentido uniformemente e estão sempre trocando de posição no eixo Y. 

Já para os tiros do avião e dos submarinos eu criei variáveis próprias para as funções que movem a imagem do tiro. Essas variáveis recebem sempre os valores atualizados das posições x e y de seus respectivos donos, avião ou submarino. Para cada elemento uma função diferente de tiro que utiliza a mesma imagem. Os tiros dos submarinos são constantes e  os tiros do avião surgem com a tecla ESPAÇO pressionada.

Para estabelecer o tempo ideal dos movimentos dos elementos foi muito difícil, pois, para simular uma animação mais quebrada de baixo fps eu tive que pensar muito, uma vez que não bastava só diminuir os frameRate do draw. Diminuindo apenas o frameRate para a animação ficar adequada, a verificação das funções ficava prejudicada, pois a taxa de atualização baixava muito e, por exemplo, ao pressionar a tecla de movimentar o avião o mesmo demorava mais de 1 segundo para responder. Tive outros problemas também com as posições e velocidades do tiro que às vezes ficavam muito rápidas e às vezes lentas demais. Não estava conseguindo equilibrá-las.

A solução foi  recortar o código e determinar fps diferentes para essas partes recortadas. Deixei as funções que precisam ser atualizadas a todo instante dentro de um fps de 60 e as que precisam criar objetos dentro de um fps bem mais baixo.

Um pouco do resultado a baixo:

UP: para cima

DOWN: para baixo

RIGHT: para direita

LEFT: para esquerda

ESPAÇO: atira

Link para download do jogo:

 https://drive.google.com/file/d/1sAY3pokTM15YUZ77AXq1TezTTbkCKbeL/view?usp=sharing

[marcilenedamasc-blog]

Atividade 09 - Tesselação e mapas isométricos

Descrição da atividade: relacionar o conceito de tesselação ao estabelecimento de mapas isométricos, com base no desenvolvimento de uma aplicação que empregue dois ou mais tiles distintos, à sua escolha.

Explicando a Tesselação

Tesselação é, basicamente, o preenchimento de uma superfície por polígonos, de modo que a disposição dos mesmos não se sobreponham, não deixem espaços sobrando e que as medidas individuais de cada um sejam iguais. Além disso, existem alguns grupos de categorização para tipos de tesselação. Seguem alguns exemplos.

Regulares

Semirregulares

Demirregulares

Homogéneas e não-homogéneas

3D

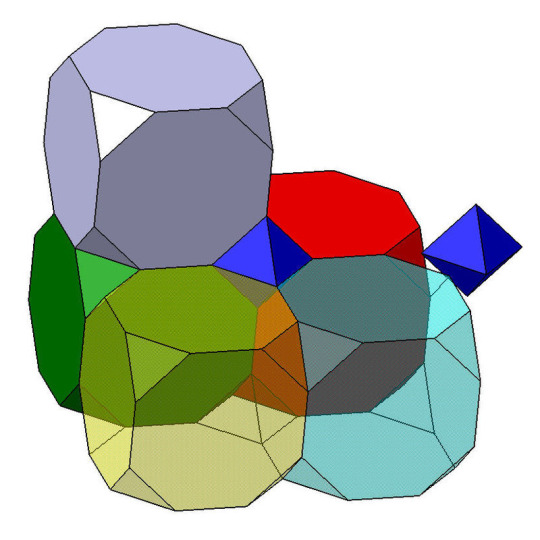
Imagens retiradas do seguinte endereço: https://pt.wikipedia.org/wiki/Tessela%C3%A7%C3%A3o

A atividade

Nessa atividade escolhi os seguintes tiles com as medidas apresentadas a seguir.

Como explicado na aula dessa atividade, criei uma matriz, variável que pode guardar muitas informações. Através de números, “desenhei” o resultado que eu desejava ver no final, na própria matriz, já sabendo que a disposição desses números eu teria que atribuir uma imagem futuramente.

Para isso, dentro do draw, finalmente fiz o for capaz de passar por cada elemento da matriz. Além disso, utilizei também um switch, que identifica qual é o elemento verificado com as coordenadas da matriz. Se o elemento for 1 ele carrega o tile do grama, mas se for 2 ele carrega o tile da chão.

Este é o resultado:

Segue o código:

PImage grama,chao; int posX = 0; int mapa[][] = { {1,1,1,1,1,1},                {2,2,2,2,2,2},                {2,2,2,2,2,2},                {2,2,2,2,2,2},                {2,2,2,2,2,2},                {2,2,2,2,2,2},                {2,2,2,2,2,2},                {1,1,1,1,1,1} };

void setup(){ size(600,400); grama = loadImage("grama.png"); chao = loadImage("chao.png"); }

void draw(){ for(int i = 0; i < 8; i++){   for(int j = 0; j < 5; j++){               switch(mapa[i][j]){       case(1): image(grama,posX,i*26);       break;       case(2): image(chao,posX,i*26);       break;     }     posX += 100;   }   if(i % 2 == 0)     posX = 50;   else     posX = 0;

} posX = 0; }

[marcilenedamasc-blog]

Atividade 08 - Jogo Pong para um jogador empregando a função keyPressed()

Descrição da atividade: reimplementar o jogo Pong para um jogador empregando a função keyPressed() e comparar o uso da mesma em relação ao emprego original da variável de sistema keyPressed.

Explicando o keyPressed() e o keyPressed

A diferença entre essas duas funções é basicamente a forma de como elas verificam se alguma tecla foi pressionada e como elas rodam o código dentro delas. A função keyPressed é uma variável booleana, ou seja, ela é falsa ou verdadeira e ela só se torna verdadeira se a condição que a faz trocar de estado estiver acontecendo num determinado momento. Ou seja, a ação dela não é constante. Ela só roda enquanto a ação da condição estiver sendo realizada. Segue um exemplo:

void draw() {  if (keyPressed == true) {    fill(0);  } else {    fill(255);  }  rect(25, 25, 50, 50); }

Já a keyPressed() não. Ela pode ser explicada como uma função de “efeito” contínuo, uma vez que, se a sua condição de execução for atendida, o código dentro dessa condição roda e fica do jeito que está, sem mudar, a menos exista outra condição para que isso aconteça. Segue um exemplo:

int value = 0; void draw() {  fill(value);  rect(25, 25, 50, 50); } void keyPressed() {  if (value == 0) {    value = 255;  } else {    value = 0;  } }

Para fazer o jogo do Pong de apenas um player, eu utilizei a função keyPressed para fazer a movimentação do retângulo que se movimenta na vertical. Essa função verifica a todo instante, sem precisar que eu atualize alguma variável para que ela volte a verificar, se alguma tecla está sendo pressionada e a partir disso verifica qual é tecla específica. Além disso, nesse código, eu fiz alguns if’s de colisão, para fazer a bola se movimentar em um sentindo contrário e um if específico para fazer o jogo acabar quando a bola ultrapassar um valor x da lateral direita da tela se ele não estiver no intervalo do retângulo que deveria colidir a partir dos comandos do jogador. Segue o resultado.

Segue o código dessa atividade:

OBS.: você pode verificar esse código nesse site, que infelizmente apresentará alguns bugs. Se você quiser jogar sem bugs só no processing mesmo, mas no site serve pelo menos pra entender algumas linhas do código.  https://valentin.dasdeck.com/processing/ 

int bolaY=300; int dY=5; int bolaX=10; int dX=5; int bastaoY = 0; boolean acabou =false;

void setup(){  size(600,600); }

void draw(){  frameRate(60);  background(0);  if (!acabou){  rect (570, bastaoY, 20,100);  ellipse(bolaX,bolaY,20,20);  bolaY=bolaY+dY;  bolaX=bolaX+dX;

  if ((keyPressed == true) && (keyCode==DOWN))  bastaoY = bastaoY +7;

if ((keyPressed == true) && (keyCode==UP))  bastaoY = bastaoY -7;

 if (bastaoY >= 500)  bastaoY = 500;

 if (bastaoY <= 0)     bastaoY = 0;

    if (bolaX>=570){  if (bolaY>bastaoY && bolaY<bastaoY+100){    dX = -dX;  } else acabou=true;}

  if (bolaY<=10)   dY = -dY;   if (bolaX<=10)   dX = -dX;   if (bolaY>=590)   dY = -dY;  }  else text("game over", 220, 300); }

[marcilenedamasc-blog]

Atividade 07 - Reescalar a posição do mouse em retângulo de proporção diferente do tamanho da tela

Descrição da atividade: empregando as funções dist e map do Processing, explicar e exemplificar como a posição do mouse, numa janela com proporção 4:3, pode mover um círculo no interior de uma retângulo com proporção 16:9 centralizado na tela

Explicando como as funções dist e map funcionam

A função dist serve para calcular a distância entre dois pontos, declaradas na mesma por dois conjuntos de coordenadas: x1, y1, x2 e y2. Segue um exemplo de código dessa função: float d = dist(width/2, height/2, mouseX, mouseY);

Já a função map serve para uma adaptação de valores de uma escala específica em outra. Essas duas escalas possíveis são declaradas dentro da função. Segue um exemplo dela:

size(200, 200); float value = 25; float m = map(value, 0, 100, 0, width); ellipse(m, 200, 10, 10);

Nesse exemplo de cima, a função map está verificando a posição 25 de uma escala de 0 a 100 dentro da distancia de 0 até a largura da tela da aplicação. Assim, a ellipse que utiliza essa variável float que recebe o map, aparecerá na posição equivalente ao calculo feito.

Para a resolução dessa atividade específica os valores a serem transformados pelo map foram os do mouseX e mouseY no eixo horizontal e vertical da tela da aplicação, respectivamente. Já a nova escala a ser criada para receber esses valores, será o intervalo da largura e da altura do retângulo 16:9 criado na aplicação. Eis essa parte do meu código como exemplo no qual eu criei 2 círculos em vez de um, para parecer um olho seguindo a posição do mouse:

//circulo maior  float x = map(mouseX, 0, width, dist(0, 0, width/2-640/2, 0)+20, dist(0, 0, width/2+640/2, 0)-20);  float y = map(mouseY, 0, height, dist(0, 0, height/2-360/2, 0)+20, dist(0, 0, height/2+360/2, 0)-20);  //circulo menor  float x2 = map(mouseX, 0, width, dist(0, 0, width/2-640/2, 0)+5, dist(0, 0, width/2+640/2, 0)-5);  float y2 = map(mouseY, 0, height, dist(0, 0, height/2-360/2, 0)+10, dist(0, 0, height/2+360/2, 0)-10);

A aplicação teve as seguintes medidas para cada aspect ratio: 800x600 para a tela da aplicação (4:3) e 640x360 para o retângulo interno (16:9). Segue o resultado.

Segue o código:

/* Se você não tiver o processing no seu computador você pode testar esse código no seguinte site: https://valentin.dasdeck.com/processing/ * /

void setup(){  size(800, 600);  noStroke(); }

void draw(){  background(233, 230, 225);  retangulo();  circulo(); }

void retangulo(){  fill(242,160,182);  rectMode(CENTER);  rect(width/2, height/2, 640, 360); }

void circulo(){  //circulo maior  float x = map(mouseX, 0, width, dist(0, 0, width/2-640/2, 0)+20, dist(0, 0, width/2+640/2, 0)-20);  float y = map(mouseY, 0, height, dist(0, 0, height/2-360/2, 0)+20, dist(0, 0, height/2+360/2, 0)-20);  //circulo menor  float x2 = map(mouseX, 0, width, dist(0, 0, width/2-640/2, 0)+5, dist(0, 0, width/2+640/2, 0)-5);  float y2 = map(mouseY, 0, height, dist(0, 0, height/2-360/2, 0)+10, dist(0, 0, height/2+360/2, 0)-10);  fill(24,89,47);  ellipseMode(RADIUS);  ellipse(x, y, 20, 20);  fill(233,230,225);  ellipseMode(RADIUS);  ellipse(x2, y2, 10, 10); }

[marcilenedamasc-blog]

Atividade 6 - Sequência de Fibonacci e a Proporção áurea

/* Atividade 6 - apresentar e discutir a relação estabelecida entre a sequência de Fibonacci e a noção de proporção áurea e sua respectiva possível contribuição ao Design Gráfico */

Para começar essa atividade, é importante que eu inicie explicando como funciona a Sequência de Fibonacci. Essa sequência se dá pela seguinte regra: os dois primeiros termos são iguais a 1 e os termos seguintes são iguais a soma dos dois números anteriores a ele.

Com base nessa sequência, vários fenômenos naturais podem ser observados em sua constituição, como o crescimento de árvores, o crescimento de uma espécie de animais no decorrer dos anos, etc.

Dessa sequência também pode-se extrair um valor chamado “número de outro”, ou PHI, que se dá pela ração de qualquer número presente na Sequência de Fibonacci pelo seu antecessor. Seu valor é aproximadamente 1,618.

E é a partir desse valor que podemos entender a proporção áurea, esta que tem, por exemplo, esse número na relação entre várias formas geométricas e uma delas é um retângulo que, ao extrairmos um quadrado do mesmo - onde seu lado é tem o valor da menor aresta do retângulo em que eles está inserido - a área restante equivale, em proporções, ao retângulo anterior.

Mas ok, existem todos esses números que se repetem e que aparecem em vários lugares e modelos matemáticos de elementos da natureza e tudo mais. Mas como essa percepção matemática ajuda, colabora, contribui ou constrói estudos e produtos em várias áreas do conhecimento e principalmente no design?

Essa proporção muito antes de ser utilizada hoje pelos designers já foi utilizada para criar obras de artes como Mona Lisa de Leonardo Da Vinci, grandes construções como o templo Partenon, construído pelos gregos para a deusa Atena, entre muitas outras aplicações de artistas e construtores antigos a muitos séculos atrás.

Como esse número de ouro se repete muitas vezes no mundo natural, muitas pessoas consideram válido se utilizar dele, ou de proporções áureas, para embasar a criação de diversos materiais.

Como muitas obras importantes têm a proporção áurea como “grid” e como é muito interessante justificar sua criação mostrando relações matemáticas, proporções e principalmente números, os elementos geométricos que carregam esse número de outro são bastante usados por diversos profissionais principalmente na área da publicidade.

Mas na verdade o seu uso não garante uma harmonia e a certeza de um bom trabalho, uma vez que, para além das disposições de elementos de um projeto gráfico, por exemplo, existem outros fatores que precisam ser muito bem pensados para cada projeto  desenvolvido por um designer, como cor, símbolos, escolha de formas, etc. 

No mais, gostaria de dizer que eu, como designer, nunca utilizei proporção áurea para construir algum material. Fico pensando muito sobre a eficiência dos meus projetos, se estariam melhores ou não utilizando essas regras matemáticas. Não sei, talvez sim, mas de toda forma, acredito que ainda não estou tão preparada para encarar um projeto visual pensando nesses conceitos.

[marcilenedamasc-blog]

Atividade 5 - Bandeira do Brasil

/* Atividade 5 - discutir o emprego das instruções quad, beginShape e endShape, rectMode e ellipseMode do Processing na construção da bandeira do Brasil, considerando a Lei Federal No 5.700. */

Desta vez a tarefa foi criar a bandeira do Brasil no Processing e discutir sobre algumas instruções utilizadas para a produção da mesma. E as instruções são  as seguintes: quad, beginShape e endShape, rectMode e ellipseMode. Acabei não utilizando a rectMode por não saber onde usá-la.

Nessa atividade eu aproveitei muito os exercícios feitos em aula, na qual fizemos a bandeira do Japão e a bandeira da Suíça, estas que aumentam e diminuem de tamanho com relação a posição do MouseX. Quanto maior for o valor da posição do mouse no eixo X maior será a bandeira.

No começo, podemos determinar qualquer valor para o tamanho da janela. Em seguida chamamos a função que cria a bandeira e que recebe como parâmetro o MouseX.

Na função começo a usar de fato as instruções da descrição da atividade, recorrendo antes às referências das mesmas no site do Processing.

Começo com a “beginShape e endShape” para construir a forma retangular verde da bandeira que, diferente da instrução rect - que necessita dos valores x e y para o primeiro vértice superior esquerdo do retângulo, mais os valores da largura e altura respectivamente - pede os valores de x e y de cada um dos 4 vértices da forma. Além disso, no final de sua descrição, ele pode trazer uma espécie de linha de fechamento, a “endShape”, que especifica que a forma criada precisa ser fechada e preenchida com o parâmetro CLOSE. Cada vértice foi determinado a partir de uma fórmula que se utiliza da largura e altura da tela e do valor declarado como  módulo da bandeira, que nesse caso é m = l/20 (onde l é o valor da posição do mouse no eixo X), para determinar seu x, de tal forma que esse valor sempre estará mudando quando a posição do mouse estiver diferente.

Após o retângulo, construí o losango amarelo com a instrução quad, esta que parece com a anterior, no sentido de que os valores que ela recebe também são dos x e y de cada vértice.

Também pude usar a instrução ellipseMode(RADIUS), que pede o x e y da elipse e os dois valores de seu raio, o primeiro da largura e o segundo da algura, que nesse caso é 3.5*m, uma vez que seu diâmetro é 7*m.

Para calcular todos esses valores tive acesso a algumas informações sobre os módulos da bandeira nacional presente na LEI No 5.700, de 1971. A seguir temos uma imagem que exemplifica esses valores de módulos e mais abaixo o link da Lei.

Fonte da imagem:

http://www.inmetro.gov.br/consumidor/produtos/bandeira_nacional.asp

Link da Lei 5.700: http://www.planalto.gov.br/ccivil_03/leis/L5700.htm

Segue o código da atividade e seu resultado.

void setup() {  size (800, 600); }

void draw() {  background(0);  mostraBandeira(mouseX); }

void mostraBandeira(float l) {  float m=l/20.0;  noStroke();  fill(34, 140, 89);  beginShape();    vertex((width-l)/2.0, (height-2*m)/2.0);    vertex(((width-l)/2.0)+20*m, (height-2*m)/2.0);    vertex(((width-l)/2.0)+20*m, ((height-2*m)/2.0)+14*m);    vertex((width-l)/2.0, ((height-2*m)/2.0)+14*m);    endShape(CLOSE);    fill(0, 168, 89);

 fill (255,204,41);  quad (((width-l)/2.0)+1.7*m, (height-2*m)/2.0+7*m, ((width-l)/2.0)+20*m/2.0, (height-2*m)/2.0+1.7*m, ((width-l)/2.0)+(20.0*m-1.7*m),(height-2*m)/2.0+7*m, ((width-l)/2.0)+20*m/2.0, (height-2*m)/2.0+(14*m-1.7*m));

 ellipseMode(RADIUS);  // Set ellipseMode to RADIUS  fill (62,64,149);  // Set fill to white  ellipse((width-l)/2.0+20*m/2, (height-2*m)/2.0+14*m/2, 3.5*m, 3.5*m);  // Draw white ellipse using RADIUS mode

   }

[marcilenedamasc-blog]

Atividade 4

Nessa atividade os professores de MAMI pediram, basicamente, que nós modificássemos um exercício de simulação de lançamento balístico, feito no Processing, de tal forma que fossem apresentados na tela os valores de todas as variáveis utilizadas e, além delas, fosse apresentado também os valores das velocidades instantâneas horizontais e verticais. 

Antes de tudo fui procurar como calcular a velocidade instantânea e encontrei a seguinte fórmula: v = v^0+a*t.

Para a construção do código de lançamento balístico que já tínhamos em sala foram utilizadas duas funções, a de Movimento Retilíneo Uniforme e a de Movimento Retilíneo Uniformemente Variável, a primeira tendo como variáveis a velocidade, a distância e o tempo e a segunda tendo essas mesmas variáveis com o acréscimo da aceleração. 

Então, a solução para essa atividade seria calcular a velocidade instantânea para esses dois movimentos, que representam, respectivamente, a velocidade instantânea horizontal e vertical. Tive, a partir desse novo cálculo inserido no código, que transformar todas as varáveis do Movimento Retilíneo Uniforme em variáveis do tipo float, uma vez que, para o cálculo da velocidade instantânea desse movimento, eu teria que usar o valor da aceleração, que é um número quebrado. Também tive que criar mais duas variáveis para receberem os valores das novas funções criadas: vvAtual (velocidade vertical atual) e vhAtualx (velocidade horizontal Atual).

Além dessas alterações, foi solicitado também, como eu já tinha dito, que nós apresentássemos os valores dessas variáveis na tela. Este é o resultado:

Segue o código:

float tAtual = 0; float vAtual = 100; float aAtual = -9.8; float dAtual; float vvAtual;

float tAtualx = 0; float vAtualx = 20; float dAtualx; float vhAtualx;

void setup(){   frameRate(1);   size(600,600);

   }

void mostraMundo(){  for (int i = 0; i < 12; i++){    line (i*50,0,i*50,600);    line (0, i *50, 600, i *50);  } }

void draw(){   background(255);   mostraMundo();   dAtual = MRUV(vAtual, aAtual, tAtual);   dAtualx = MRU(vAtualx, tAtualx);   //as próximas duas linhas calculam as velocidades instantaneas   vvAtual = velocidadeInstantaneavertical(vAtual, aAtual, tAtual);   vhAtualx = velocidadeInstantaneahorizontal(vAtualx, aAtual, tAtualx);   println(vAtual, tAtual, dAtual);   ellipse(dAtualx, 600-dAtual, 10, 10);   textSize(12);    text("Distância Atual (MRUV):"+dAtual, 10, 30);    text("Distância Atual (MRU):"+dAtualx, 250, 30);    text("Velocidade Atual (MRUV):"+vAtual, 10, 70);    text("Velocidade Atual (MRU):"+vAtualx, 250, 70);    text("Tempo Atual (MRUV):"+tAtual, 10, 140);    text("Tempo Atual (MRU):"+tAtualx, 250, 140);    text("Aceleração Atual (MRUV):"+aAtual, 10, 170);    text("V Instantânea Atual Vertical:"+vvAtual, 10, 200);    text("V Instantânea Atual Horizontal:"+vhAtualx, 250, 200);    fill(0, 102, 153);     tAtual++;     tAtualx++;    }

float MRUV(float v, float a, float t){  // v = 0 m/s, a= 1m/s², t=1  float d;  d = v*t+a*t*t/2.0;  return(d); }

float MRU(float v, float t) {   float d;   d = v*t;   return(d); }

float velocidadeInstantaneavertical(float v, float a, float t){  float vv;  vv = v+a*t;  return(vv); }

float velocidadeInstantaneahorizontal(float v, float a, float t){  float vh;  vh = v+a*t;  return(vh); }

[marcilenedamasc-blog]

Atividade 3 - Mudando fps sem alterar a velocidade de MRU

Nessa atividade os professores pediram que fosse alterado o fps de uma exercício que já tínhamos feito em sala, mas eles queriam que a velocidade do elemento criado no Processing não mudasse. Na tarefa de sala nós fizemos uma bolinha que se deslocava a 10m/s com a configuração de 1 fps.

A primeira etapa para mim foi mudar o fps do MRU, retirando a linha “frameRate(1)” e deixando a quantidade padrão do draw de quadros por segundo, que já é 60 fps.

Após isso sabia que agora a elipse estava muito mais rápida, então alguma variável deveria ser modificada, dividida por 60. Então, sabendo que os números ficariam quebrados agora, transformei todas as variáveis em float.

Após isso, criei um contador como variável global e o usei este para modificar o valor da variável “tAtual”, esta que seria o valor inteiro do contador dividido por 60, fazendo assim a distancia continuar variando a 10m/s, uma vez que a velocidade sempre estaria sendo multiplicada por um número inteiro dividido por 60.

Segue o código dessa atividade:

float tAtual = 0; float vAtual = 10.0; float dAtual; float cont;

void setup(){   //frameRate(1);   size(600,600);

   }

void mostraMundo(){  for (float i = 0; i < 12; i++){    line (i*50,0,i*50,600);    line (0, i *50, 600, i *50);  } }

void draw(){   background(255);   mostraMundo();   dAtual = MRU(vAtual, tAtual);   println(tAtual, dAtual);   ellipse(dAtual, 300, 10, 10);   textSize(32);    text(tAtual, 10, 30);    fill(0, 102, 153);   tAtual=cont/60.0;   cont++;

   }

float MRU(float v, float t) {   float d;   d = v*t;   return(d); }

[marcilenedamasc-blog]

Atividade 2 - Gerando Quadros Randômicos

Nessa atividade os professores pediram a criação de um código no Processign que criasse quadros baseados, visualmente, na obra de arte “Farbstudie Quadrate” de Wassily Kandinsky (1913).

https://www.wassily-kandinsky.org/Farbstudie-Quadrate.jsp

A partir do pequeno código disponibilizado no slide da disciplina, no qual já era criado apenas um conjunto de elementos (quadrado e seus três círculos internos), comecei a pensar que os próximos passos seria imaginar como estruturaria as funções de laços de for, uma vez que eu teria que replicar esse mesmo conjunto várias vezes mas não poderia fazer isso um por um.

No começo fiz o primeiro for, que criava apenas uma linha de sequência de quadrados e seus círculos, ou seja, só recebia variação de valores na variável x. 

Pensando nessa sequência lógica, foi muito mais fácil entender que primeiro se criariam as linhas variando nessa variável x para depois, ao fim de cada linha, a variação acontecer nas variáveis y.

Ao pensar em outro requisito da atividade, que era a existência de variáveis globais, pude ver que não seria ideal determinar valores fixos para x e y, pois esses iriam precisar ser alterados constantemente. 

Então, além de pensar na possibilidade de estruturar o código de uma maneira que o mesmo não se prendesse a valores determinados de x e y, também pensei em possibilitar uma configuração randômica, a partir da criação desses valores como variáveis globais, para o resultado final de cada compilação do código.

Assim, declarei duas variáveis globais chamadas “quantL” e “quantC” para os valores limites da quantidade de linhas e colunas, respectivamente. A primeira variável foi usada no primeiro for, este que chamava o segundo, que trabalhava com a segunda variável para construir todos os grupos de elementos de apenas uma linha. Após criar todos esses elementos, determinados por um número aleatório vindo da variável randômica “quantC”, ele termina e roda o próximo número do primeiro laço, que segue para a próxima linha, variando no eixo y com a variável também randômica “quantL”.

Estes são apenas alguns exemplos de possíveis resultados pois, como as variáveis que determinam a quantidade de linhas e colunas são sempre diferentes, o visual final sempre nunca será igual. Além dessa diferença de composição, as cores também são geradas de forma randômica  a partir de três incrementos baseados no código RGB, uma linha antes de cada elemento.

Segue o meu código:

void setup() { size(1000, 1000); float quantL = random(8); float quantC = random(8); for (int y = 0; y < quantL; y++){  for (int x = 0; x < quantC; x++){    fill(random(256),random(256),random(256));    rect(x*100,y*100,100,100);    fill(random(256),random(256),random(256));    ellipse(x*100+50, y*100+50, 80, 80);    fill(random(256),random(256),random(256));    ellipse(x*100+50, y*100+50, 60, 60);    fill(random(256),random(256),random(256));    ellipse(x*100+50, y*100+50, 40, 40);  } } }

[marcilenedamasc-blog]

Atividade 1 - Modelo matemático do experimento “Shredding a photo”

Nesta atividade é preciso explicar, por meio de um modelo matemático, como acontece um experimento de corte de uma imagem, chamado de “Shredding a photo”, e recriação da mesma a partir de cortes sequenciais apresentado no seguinte vídeo:

A partir do vídeo, podemos observar que existe uma máquina que faz cortes em linha reta perfeita na imagem, de modo que a transforma em vários pedaços retangulares de espessura quase idênticas. Após os cortes a imagem é reorganizada em grupos, que aqui irei categorizar como pedaços pares e ímpares, estes que cabem nessas categorias a partir de suas posições após o corte.

Assim, podemos pensar no modelo matemático da seguinte forma: surge uma relação entre os cortes que cria sempre o dobro de imagens existentes antes de serem modificadas (antes dos cortes). Pode-se representar algebricamente essa relação com potências de 2^n, onde n será o número de cortes feitos. A imagem abaixo tenta exemplificar de forma simples essas relações de corte, mostrando as alterações na quantidade de fotos criadas além de tentar mostrar os grupos ímpares e pares formados a partir dos experimentos.

[marcilenedamasc-blog]

Primeira postagem - Introdução

Bom, bem vindos ao meu blog! Meu nome é Marcilene Damasceno, faço Sistemas e Mídias Digitais desde 2015.1 e adoro Audiovisual. Esse espaço é destinado a compartilhar bastante conteúdo da cadeira de MAMI (Matemática Aplicada à Multimídia).

Ao fazer a disciplina de Projeto Integrado 2, pude conhecer um pouco sobre o universo e design generativo, que me deixou muito animada artisticamente, com todas suas possibilidades de produção e de liberdade criativa. 

Desde então, penso bastante sobre as possibilidades de linguagens que possibilitem o desenvolvimento de produtos legais pro meio artístico e sei que usando o Processing, software utilizado em MAMI, posso descobrir mais e mais sobre essas conversas entre programação, design, audiovisual, etc. Acho muito interessante estudar sobre design generativo, instalações interativas e principalmente video mapping. Digo logo que não entendo muito sobre todos esses assuntos e estou bem atrasada nos estudos com Processing, mas estou muito animada nesse semestre e acho que vai dar tudo certo! ( : v )

Um livro/site legal: http://www.generative-gestaltung.de/

Outro software interessante: https://vvvv.org/