mateideas

[mateideas]

Ecuaciones Cuadráticas

¡Mis matemáticos!

Hoy les traigo un nuevo tema, espero les pueda servir de algo

Recuerda que, una ecuación cuadrática o de segundo grado es toda ecuación en la cual, una vez simplificada, el mayor exponente de la incógnita es 2. Así, ax2 + bx + c = 0 es una ecuación de segundo grado. En esta ecuación La “x” es la variable o incógnita y las letras a, b y c son los coeficientes, los cuales pueden tener cualquier valor, excepto que a = 0.

Te dejo por acá un videito para que puedas ver de una manera gráfica lo que te explico y puedas reforzarte en eso!

Y bueno...¡Nos vemos a la próxima mis matemáticos!

- Yaya

[mateideas]

Ecuaciones Lineales

¡Hola de nuevo mis matemáticos!

El día de hoy hablaremos un poco sobre ¿Qué son las ecuaciones lineales? y eso te lo explicaré a continuación.

Bueno, una ecuación lineal es una igualdad matemática entre dos expresiones algebraicas, denominadas miembros, en las que aparecen elementos conocidos y desconocidos (denominados variables), y que involucra solamente sumas y restas de una variable a la primera potencia. Te dejaré un pequeño ejemplo:

Ej:

Nos vemos!

- Yaya

[mateideas]

Suma y Resta de Fracciones Algebraicas

El procedimiento es el mismo que para sumar o restar fracciones numéricas, es decir, necesitamos tener el mismo denominador para sumar y restar fracciones y cuando no lo tenemos, tenemos que reducir las fracciones a denominador común, con la diferencia de que con las fracciones algebraicas, en vez de números, trabajamos con polinomios.

Suma y Resta de fracciones algebraicas con Igual denominador

La suma de fracciones algebraicas con el mismo denominador es otra fracción algebraica con el mismo denominador y cuyo numerador es la suma de los numeradores.

Ejemplo:

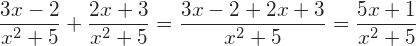
Suma y Resta de fracciones algebraicas con diferente denominador

Si las fracciones tienen distinto denominador en primer lugar se ponen las fracciones algebraicas a común denominador, posteriormente se suman los numeradores.

Pasos:

- Calculamos el común denominador que será el m.c.m. de los denominadores.

- Dividimos el común denominador entre los denominadores de las fracciones dadas y el resultado lo multiplicamos por el numerador correspondiente.

- Quitamos paréntesis

- Realizamos las operaciones en el numerador

- Sacamos factor común 2 en el numerador

- Simplificamos

Dato: La resta se soluciona de igual forma, salvo que el numerador en lugar de componerse de una suma se compone de una resta.

Te dejo de igual manera por acá un video en el cuál te puedas apoyar mejor, es algo largo pero te ayudará a comprender de mejor manera estos casos.

¡Nos vemos!

-Yaya

[mateideas]

División de Fracciones Algebraicas

Hola mis matemáticos, estaremos hablando un poco de las divisiones algebraicas.

Te diré algunas reglas para que puedas dividir.

Se multiplica el numerador de la primera fracción por el denominador de la segunda,(o sea el producto de los extremos); el resultado será el numerador de la fracción resultante.

Se multiplica el denominador de la primera fracción por el numerador de la segunda, (o sea el producto de los medios); el resultado será el denominador de la fracción resultante.

Las multiplicaciones anteriores se dejan indicadas en la fracción resultante, para efectos de poder simplificar la fracción.

Por acá te dejaré este videito para que puedas apoyarte también de esto y comprender de una manera visual y gráfica dicho tema.

¡Nos vemos!

-Yaya

[mateideas]

Multiplicación de Fracciones Algebraicas

Hola mis matemáticos, hoy estaremos viendo la Multiplicación de Fracciones Algebraicas.

Las fracciones algebraicas se multiplican igual que las fracciones numéricas, es decir, se multiplican en línea: numerador por numerador y denominador por denominador, solo que en este caso, en vez de números tenemos polinomios.

Una pequeña recomendación es que, antes de multiplicar descompongamos los polinomios y eliminemos los factores que se repitan en el numerador y el denominador, es decir, que simplifiquemos antes de multiplicar.

Ejemplo:

Al ser una multiplicación de fracciones, multiplicamos en línea, es decir, numerador por numerador y denominador por denominador, pero al ser polinomios, solamente lo dejamos indicado, no los multiplicamos.

Antes de multiplicar, vamos a descomponer los polinomios que se puedan descomponer. Empezamos por el polinomio correspondiente al numerador de la primera fracción.

Descomponemos también el polinomio del denominador de la primer fracción

Sustituimos los polinomios por sus correspondientes descomposiciones

Ahora simplificamos la fracción algebraica, eliminando los factores que se repiten en el numerador y en el denominador

Y nos queda:

Y estos los multiplicamos para obtener el resultado final

Si hubiésemos multiplicado al principio, al final nos hubieran quedado dos polinomios de mayor grado, los cuales hubiera sido mucho más difícil de factorizar.

Siguiendo este procedimiento, llegamos al resultado mucho más directamente.

¡Nos vemos!

-Yaya

[mateideas]

Simplificación de Fracciones Algebraicas

Hola mis matemáticos, hoy aprenderemos un poco sobre la simplificación de fracciones algebraicas.

Para simplificar una fracción algebraica primero se deben factorizar los polinomios del numerador y del denominador, y luego eliminar los factores que tengan en común.

Ejemplo:

Primero de todo, factorizamos los polinomios del numerador y del denominador de la fracción:

Y una vez hemos factorizado los polinomios, eliminamos los factores comunes entre el numerador y el denominador, es decir, quitamos todos los términos que se repiten:

De forma que la fracción algebraica simplificada queda de la siguiente manera:

En este problema factorizamos los polinomios de la fracción algebraica hallando sus raíces, sin embargo, en ocasiones se puede factorizar un polinomio directamente sacando factor común

(método mucho más rápido).

¡Nos vemos!

-Yaya

[mateideas]

Factorización

Debes recordar que factorizar es escribir una expresión como el producto de dos o más factores. Trabajaremos 8 casos: 

Factor común

Se trata de obtener un factor (ya sea numérico o una variable) que sea común a toda la expresión y crear una multiplicación con él.

por ejemplo: 8X + 2Y = 2 * (4X + Y) (En este caso el factor común es 2)

Factor común por agrupación de términos

Este caso es principalmente igual que el anterior, solo que en este caso existen dos factores en común.

Ejemplo: 8XZ +2XY – 12KZ - 3KY = 2X*(4Z + Y) - 3*(4Z + Y) = (2X – 3)*(4Z + Y)

En este caso los factores comunes eran (2X – 3) y (4Z + Y)

 Trinomio cuadrado perfecto

En este caso se tiene un polinomio de grado dos y cuyas raíces están en el campo de los números reales.

por ejemplo: X^2 ± 2*a*X + a^2 = (X ± a)^2

Diferencia de cuadrados

Este es el caso de un producto de dos binomios cuya diferencia es solo el signo del segundo término.  (a + b) * (a – b) = a^2 – b^2

Trinomio cuadrado perfecto por adición o sustracción

Este caso ocurre cuando se posee un trinomio cuadrado perfecto en el que no es posible obtener dos raíces iguales y en el campo de los números reales. Se suma y resta la cantidad necesaria para obtener la forma del trinomio deseado. X^2 + 2X – 5 = (X^2 + 2X + 2) – 2 – 5 = (X + 1)^2 – 7

Trinomio de la forma X^2 + BX + C 

En este caso de factorización se tiene un trinomio que tiene raíces reales pero que no son ni repetidas ni siguen el del caso anterior. Para ello se deben conseguir las raíces del polinomio. X^2 – 5X + 6 = (x – 3) * (x + 2)

Suma o diferencia de potencias

Se trata de descomponer factores que compartan una misma potencia.

X^3 + 27 = X^3 + 3^3 = (X + 3) * (X^2 – 3X + 9)

Trinomio de la forma aX^2 + bX + c

Para este caso se puede factorizar utilizando la ecuación de la resolvente la cual es la siguiente: 

X = - b ± √b^2 – 4*a*c / 2*a 

4X^2 + 12X + 9 

X = - 12 ± √(12)^2 – 4*4*9 / 2*4 

X1 = X2 = -1,5

4X^2 + 12 X + 9 = (X + 1,5) * (X + 1,5)

Por acá te dejo un video para que puedas apoyarte también de eso. 

¡Nos vemos! 

-Yaya

[mateideas]

¡Hola mis matemáticos!

Acaban de unirse a Mate Ideas.

¡Bienvenidos!

Soy Yaya, responsable de este blog, que tiene como objetivo brindarte apoyo en el área de matemática. Si tú eres de esos que les cuesta la mate ¡No te hagas más problemas, con los problemas de la mate! Yo estaré aquí para darte algunos tips y que puedas entender de una manera más clara.

Diariamente, estaré publicando contenido dirigido a niños y adolescentes, para que, en el desarrollo de sus tareas puedan apoyarse de este valioso recurso que he preparado con mucha dedicación y esfuerzo. El contenido interactivo ayudará a desarrollar el nivel de comprensión para los problemas que presenta está materia, que para muchos, se ha convertido difícil y hasta aburrida...

¡Puedes compartir este blog para que tus amigos, familiares, vecinos, etc. Puedan descubrir una manera más fácil y divertida de aprender!

Un abrazo,

-Yaya