mathpy-io

[mathpy-io]

Standard Deviation

In statistics and probability theory, the standard deviation (SD) (represented by the Greek letter sigma, σ) measures the amount of variation or dispersion from the average.

... yup, straight from Wikipedia.

To fully understand this, lets look at the formula, then some code for it.

So, breaking it down, the Standard Deviation is a measure of how spread out numbers are. It is the square root of the Variance. Variance is just the squared differences from the Mean... Yes, the mean is just a fancy way of saying average.

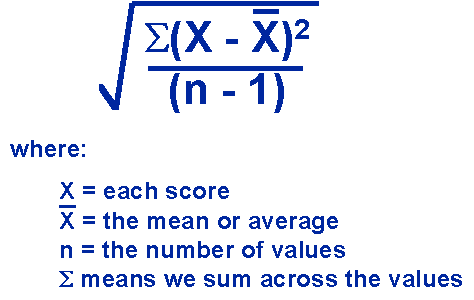
So, let's code this!!!

def stdev(s):     import math     def average(s):        return sum(s) * (1.0 / len(s))     avg = average(s)     variance = map(lambda x: (x - avg)**2, s)     standard_deviation = squareroot(average(variance))     return ("The mean is, ", avg, ". The Standard Deviation is ", standard_deviation)

Like we Said in previous posts, we try to stay away from Python built in functions(the math libraries at least). So, Let's code the Square Root function!!!

def goodenough(g,dvalue):     d=abs(g**2-dvalue)     return (d<0.0001) def average(d,e):     return (d+e)/2.0 def improve(g,dvalue):     return average(g,dvalue/g) def improveloop(g,dvalue):     if (goodenough(g,dvalue)):        return g     else:        return improveloop(improve(g,dvalue),dvalue) def squareroot(f):     return improveloop(1.0,f)

Test in Python2.7.2! I'll soon update it to be compatible with Python 3.*

[mathpy-io]

Permutation and Combination

Permutation and Combination, are fundamental principles of counting. They execute counting using their formulas which includes the factorial operator ("!"). This makes counting possible sets of things much faster than the basic/baby way. In fact, as a programmer or a mathematician, you'll soon know this is basic counting compared to what you'll soon know... ... ... *Don't be scared now!*

The factorial function (symbol: !) just means to multiply a series of descending natural numbers. Examples:

3!= 3*2*1= 6

5!= 5*4*3*2*1= 120

Permutation

where n is the number of things to choose from, and we choose r of them (No repetition, order matters)

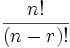
Here's this implemented in python, just for the fun of it!

def nPk(n,k):     print (n, "P", k," is ", ((factorial(n))/(factorial(n-k))), "ways.")

Combination

where n is the number of things to choose from, and we choose r of them (No repetition, order doesn't matter)

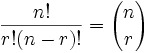
Again, I've implemented this in python, just for the fun of it!

def nCr(n,r):     print (n, "C", r," is ", ((factorial(n))/(factorial(r)*(factorial(n-r)))), "ways.")

**NB:

So, by now you must be wondering, where's the factorial sign.... hmmm Some of you may have decided to use some built in python function and felt like a boss. Well, here, we avoid built in python functions as much as we can!

So, here's how we do factorial!

def factorial(z):     factorial=1     if z < 0:        print("Sorry, factorial does not exist for negative numbers")     elif z == 0:        print("The factorial of 0 is 1")     else:        for i in range(1,z + 1):           factorial = factorial*i        print("The factorial of", z,"is",factorial)        return factorial

[mathpy-io]

Sum Limiter

This script tests simple sumation limits you give it. It repetitively adds your first value until it is the maximum value it can be, to be as close as possible to your second value.

def sumlimiter(x,y):    adder= x    def brain(adder,x,y):       if adder > y:          return "you went beyond your limit"       elif (y-adder) < x:          return adder       else:          return brain(adder+x,x,y)    return brain(adder,x,y)

[mathpy-io]

The lambda

Expanding The Wavelength Of Your Code

>>> def f (x): return x**2

...

>>> print f(8)

64

>>>

>>> g = lambda x: x**2

>>>

>>> print g(8)

64

So, f() and g() do the same thing and can be used in the exact same ways. The Lambda definition, howewever has no "return" statements. as it always contains an expression which gets returned when the parent function is called. You can put a lambda definition anywhere a function is expected, and you don't have to assign it to any variables as lambda is just an inline function. see below for an example which squares any inputed number and multiplies it by pi:

def pi():

   return 22/7.0

def sqrpi(x):

   z= lambda x: (x**2)

   return z(x) * pi()

[mathpy-io]

Loading...