multivarblogs

[multivarblogs]

Chapter 15 ~ Multiple Integrals

Summary

I think I’ve said this for the past three chapters, but this one was the hardest so far. I had trouble with figuring out the bounds for the word problems of the iterated integrals (I had no trouble solving them when the bounds were given). I think that once I was able to visualize the 3D shapes, it was easier to figure out the bounds for the integrals. I did not achieve my goal from last chapter as I had to use a lot of the videos in order to complete the problems. Overall, I think I was able to grasp the main ideas of the chapter, but I still have trouble with some specific topics. 

Work

15.1-2

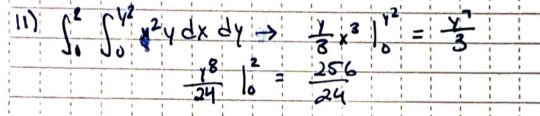
Iterated integrals were a main idea in this chapter, as most problems involved them-- whether it was two or three variables. This problem in particular is simple because it was an intro to iterated integrals and already gave you the bounds of integration for x and y. All you have to do it integrate first with respect to x, and then with respect to y.

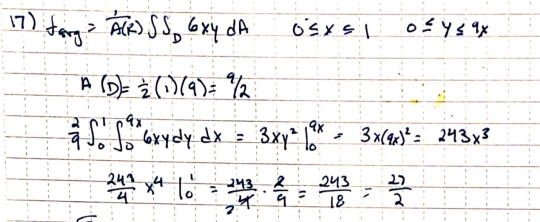
This problem was tricky at first because I didn’t realize that the upper bound for y was a function of x, since it’s a triangle. After that, however, it was relatively straight forward as you just have to evaluate the integral and multiply it by 1/A(R).

15.3-5

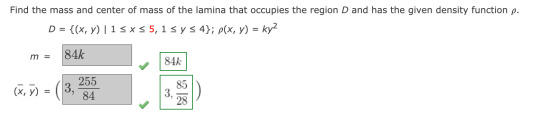
To find the mass, I just took the iterated integral with x going from 1 to 5 and y from 1 to 4 and the density function ky^2. For the center of mass, I took the iterated integral of the density function times x and multiplied it by 1/m and did the same thing for y.

15.6-8

In this unit, we began doing iterated integrals with 3 variables, so this problem is similar to the last one, but it has 3 variables instead of 2. The algebra was very tedious in this problem because of all the ‘a’s being multiplied when the bounds were substituted in. Other than that, however, the same strategies as the last problem can be applied here as long at you remember to include an extra step for z.

This section was difficult because I had trouble figuring out the right bounds, especially for phi. However, I am now able to visualize the angle that phi is making and how it goes from 0 to pi. Rho is just the radius, which goes from 0 to 3 and then, because its a sphere, theta goes from 0 to 2pi. I got rho^4 through the equation x^2 + y^2 + z^2 = rho^2. After that I just evaluated the iterated integral.

Goal

My goal is to finish the year strong by getting above an 85% on the last Webassign.

[multivarblogs]

Chapter 14 ~ Partial Derivatives

Reflection

I think the second half of this chapter was probably the most difficult for me so far. The beginning was also hard because I had trouble grasping the idea of partial derivatives, but they were also a big clicking point for me. At first I constantly messed them up because my brain couldn’t comprehend that the other variable was a constant, but eventually I realized that I barely even had to think when I was asked to do a partial derivative! The most confusing part of this chapter was the Lagrange Multipliers because at first I didn’t really understand why they were necessary, but now I see that they are very useful for finding the local minima and maxima. I achieved my goal of getting two or less  problems wrong for all the Webassigns except for one which was the one about Lagrange Multipliers since I found them difficult.

Problems

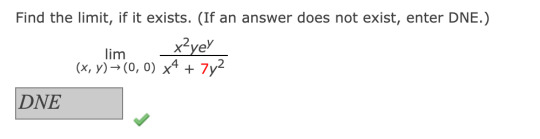
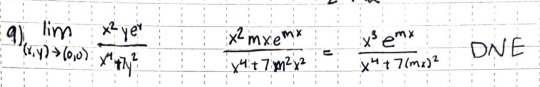
This problem asks you to find the limit, which I knew how to do before, but there are two variables instead of one. By using the equation, y = mx, I was able to put the limit all in terms of x and found that it did not exist.

Partial derivatives can be tricky if you forget to make one of the variables a constant or mess up which variable you are using for the derivative. This problem was really helpful because I had to take two partial derivatives and was able to practice taking the partial derivative off x and y, respectively, and practice making sure I was taking the right one.

The chain rule with multiple variables is complicated because you have to take both a normal and partial derivative. I thought this problem helped bring everything together because I was able to practice remembering the difference between a partial and normal derivative. It was tricky making sure all the algebra was right, but the derivatives were relatively straight forward.

This problem (and other Lagrange problems) was really tedious because you have to write out all of the possibilities for the extrema. Additionally, I had to find the maximum and minimum values, and not just the points.

Goal

My goal is to attempt all the Webassign problems without having to use the “Watch It” feature.

[multivarblogs]

Chapter 13 ~ Vector Functions

 Reflection

I think the hardest part of this chapter was remembering all the equations and when to use what. However, as I began to get a better grasp of what exactly things like a unit tangent vector were, I was able to better remember the when I understood how they worked. I’m proud that I was able to eventually find normal and binormal vectors without thinking twice. I think this finally clicked when I realized that T, N, and B all built off of each other because that helped me remember how to find them and what exactly they meant. I was also able to achieve my goal of getting above a 90% on the Webassigns.

Problems

In finding the curve of intersection, I solved for x and then substituted it into the equation for the cylinder. Vector valued functions were a main part of this unit and this problem helps emphasize the idea of splitting up the function into the x, y and z components. 

The curvature (K) is a measurement of how fast a curve is changing direction at a given point and I found it using the equation above. It can also be found by dividing the magnitude of the derivative of T(t) by the magnitude of the derivative of r(t).

An normal plane is a plane perpendicular to T(t) and an osculating plane is a plane perpendicular to B(t) so to find them I first had to find each of their equations and plug in the t value that does through the points.

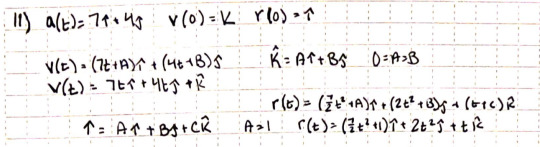
a(t) = v’(t) = r’’(t) so to find v(t) and r(t) you need to take the antiderivative of a(t) and v(t), respectively. It is important to remember to add the initial velocity/position when you take the antiderivative.

Goal

My goal for this unit is to not get more than two problems wrong on the Webassigns.

[multivarblogs]

Chapter 12 ~ Vectors and the Geometry of Space

Reflection

For me, the most challenging part of this unit wasn’t the math, but having to wrap my head around the idea of 3D space. Since I have always done math in 2D, it was difficult to imagine lines and planes in 3D space instead. Specifically, visualizing 3D surfaces was difficult, and my inability to draw definitely did not help. I’m proud that I expanded my understanding of vectors. I took an online quantum computing course this summer where we were introduced to linear algebra, so I was already familiar with vectors and the dot and cross products. However, this unit definitely made me a lot more comfortable with them and I was able to deepen my understanding.

~~~~

Problems

12.1 - 12.2

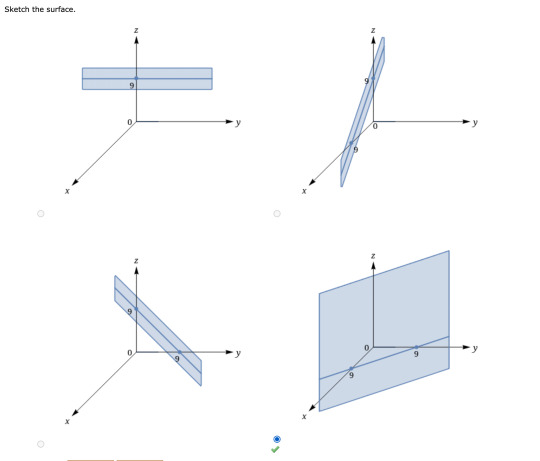
This problem demonstrates an important understanding of planes and surfaces. The idea of the dimensions being represented by R^x is very important to know and knowing how to visualize a plane based on the equation is something that is fundamental to understanding other parts of this unit.

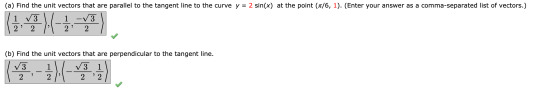
Finding vectors that are parallel and perpendicular to lines was important for later in the chapter when we incorporated orthogonal vectors and finding normal vectors for planes.

12.3 - 12.4

Other than just 0 or 90 degrees, we also learned how to find the angle between vectors, which is not straightforward because the vectors are in 3D space instead of on a 2D plane. 

Direction angles show the angle the vector makes with each axis, which is important for real life applications of problems such as finding the force at an angle.

12.5 - 12.6

Vector equations were a major part of this last section as they incorporate a point as well as the vector for the direction. This problem also includes parametric equations which split the vector equations into the x, y, and z components.

This incorporates two points from this section. One is finding a point of intersection between two lines and the other is finding a plane from two lines. Both of these build on concepts from earlier in the section.

~~~

Goal

My goal for next unit is to get above a 95% on the all the Webassigns.

[multivarblogs]

Chapter 10 ~ Parametric Equations and Polar Coordinates

My Reflection:

This unit was not too hard for me considering a lot of it was review from last year. Polar coordinates especially have always come pretty easily to me. In particular, I’m proud that I actually understood the conic sections section well since I found them very confusing in precalc. I think since we reviewed conics and learned about them through a calculus lens, I was able to understand the terms (directrix and the specific definitions of the various sections) a lot better. Some of the problems where we had to apply the information to real-world situations were challenging to me, but I was usually able to figure them out once I reviewed my notes and took some time to think about them. 

~~~~~~

Problems:

10.1-2: Parametric Equations

This problem was one that I ended up having to get help for, but after getting help I understood it and realized I had been on the right track when I was doing it by myself.

I chose this problem because it was one that completely threw me for a loop at first, but I was later able to figure it out. It looked really complicated at first, but when I took some time to think about it I realized it wasn’t that hard.

~~~~~~

10.3-4: Polar Coordinates

This problem was pretty straightforward, but it helped me refresh finding the area for polar curves. I was excited that I was able to get the right bounds on the first try because I always got confused with the bounds in calc last year.

This was another problem that I was originally very confused by, but then I was able to figure it out completely on my own! 

~~~~~~

10.5-6: Conic Sections

None of the problems in the conics section were super complicated. This second problem, though, was frustrating at first because I forgot to switch the x and y and I couldn’t understand why I was getting it wrong. Then, I realized that the focus and vertex are in line on x=3, so the parabola had to be vertical.

~~~~~~

Goal:

My goal for next unit is to work on the Webassigns early so that I have a chance to ask questions during X-block on Monday before they’re due.