pierres-musings - Tumblr blog

pierres-musings · 1 month ago

Text

Why pain needs better math

Epistemic status: just trying. Please don't be mad at me.

Imagine rating experiences on a scale from 1 to 10. Eating a delicious burger might rate a solid 7, while your first experience with MDMA (profound joy and deep connection, your whole body felt like it was made of pure love) would clearly score a 10. On this scale, MDMA appears only three points better, roughly 30% more enjoyable. Yet intuitively, the difference feels dramatically larger.

The problem with linear scales is straightforward: they assume each step represents an equal increase in intensity. But human experiences don't actually work that way. Severe pains and profound pleasures aren't merely stronger versions of milder ones, they often feel qualitatively different in intensity. Clearly, a linear scale doesn't capture reality well.

Numbers matter!

Before exploring alternatives, let me clarify why we even need a scale at all. Ethical and practical decisions rely on clear comparisons:

Healthcare funding: How much should we spend on migraine treatment vs on cluster headache research?

Policy decisions: Medical triage, insurance coverage, and pharmaceutical research, etc, all depend on explicit measures of suffering.

Even if initial numbers are rough estimates, having a clear numerical starting point is essential to improving our decisions over time. As they say: "all models are wrong, but some are useful."

Let's assume you are a top health policy advisor in RandomCountry. If you assume pain scales are linear and only know very basic math, you might do this:

1,000,000 of your citizens suffer from a minor headache (2/10 pain) for an hour every month = 1,000,000×2×1/30 = 66.7k pain units/day on average.

100 people suffer from cluster headache (10/10 pain) for 10 hours every month = 100×10×10/30 = 333 pain units/day on average.

Finding a cure for minor headaches may be 200 times more important than solving cluster headaches in your country.

This simplified calculation illustrates the problem: linear assumptions can lead to counterintuitive priorities that don't match our moral intuitions about severe suffering.

Introducing QRI and the logarithmic idea

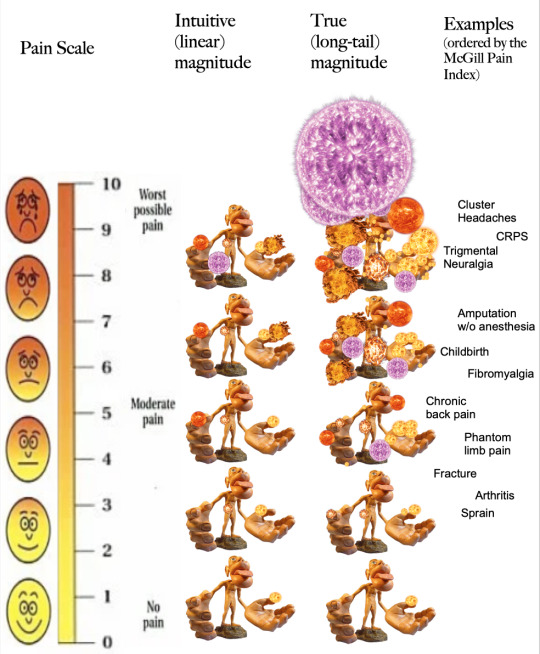
The Qualia Research Institute (QRI) proposes that experiences like pain and pleasure might follow logarithmic or heavy-tailed distributions. Simply put, each step up their scale multiplies intensity rather than adding a fixed amount. This means a pain rated 10 wouldn't just be slightly worse than a 9; it could be exponentially worse.

This intuition aligns somewhat with existing pain scales, such as the Schmidt Pain Index, famously used to rank insect stings. On Schmidt's scale, each increment represents a significant leap in pain intensity: for instance, a bullet ant sting (rated 4) isn't merely twice as painful as a bee sting (rated 2)—it's many times worse.

Their approach, based on countless hours of investigating and surveying the phenomenology of extreme experiences is simple but extremely important. If the pool of pain is truly deeper than what linear scales lead us to believe, we may be live in a world full of quiet ethical tragedies.

Be careful with the log

Yet taking strict logarithmic scaling to human experiences quickly leads to improbable scenarios. Suppose each step on a 10-point pain scale multiplies intensity by 10. In that case, a cluster headache (rated around 10) would be millions of times worse than childbirth (rated around 7). While cluster headaches are horrifically painful, sufferers don't describe them as millions of times worse, only significantly so.

Crucially, people describing cluster headaches use comparisons like "being stabbed multiple times with a burning hot knife" or "like someone drilling into my eye socket." These descriptions show the pain is still comparable to other experiences, not in some incomprehensible other dimension. If cluster headaches were truly hundreds or thousands of times worse than childbirth, we'd expect far higher suicide rates and much more severe psychological trauma than we observe. The pain is horrific, but it's within the realm of human experience, not beyond it.

Pure logarithmic scaling fails to capture these nuances accurately. Now, I know that QRI don't genuinely believe that the scale is purely logarithmic (they prefer the term "heavy tails of valence" nowadays). However, I believe it is important to choose our words and our math carefully when discussing important ethical problems.

Power-law scaling

A more realistic alternative is power-law scaling, capturing significant but plausible differences between experiences and allowing us to get "absolute" numbers (units of pain). The goal is to transform these linear ratings into something that better matches how people actually experience and compare different pains.

Here is a possible formula:

Pain Units = 1000 × (Pain Score ÷ 10)^5

Why the power of 5? I tested different exponents against phenomenological reports and this feels the most intuitively true. However, I wouldn't be surprised if the real exponent is different.

Cluster headache sufferers describe their pain as "several times worse than childbirth" (anecdotes here on Reddit for example) not "thousands of times worse." The power of 5 produces ratios in these ranges.

Before deciding for this formula, I tested different ones (including sigmoid and piecewise functions), but I think the power-law is the strongest one. It's simple to calculate, produces plausible ratios that match reported experiences, and avoids the plateau problem of sigmoid functions. While future research may refine the exact exponent, this provides a workable starting point that's orders of magnitude better than linear assumptions.

Interestingly, power laws are often used in neuroscience. Stevens' psychophysical law demonstrated that sensory perception follows power laws: the subjective magnitude of sensations scales as a power function of stimulus intensity. Even memory follows power laws: the famous Ebbinghaus forgetting curve shows memory retention decreases as a power function of time.

"But wait, your formula says that 10/10 pain is 100,000 times worse than a 1/10 pain. That still seems high."

What you need to understand is that most people never experience the true extremes. When someone rates their broken leg as "10/10," they likely haven't experienced worse. Their "10" might be an absolute 7 or 8.

But: 10/10 pain fundamentally breaks human consciousness. Read any account of cluster headaches or severe burns. People don't just say it hurts, they describe being unable to form coherent thoughts, banging their heads against walls to knock themselves unconscious, begging for death (cluster headaches are not called "suicide headaches" for no reason).

If people trade their entire future (infinite life-years) to escape pain, then 100,000× seems almost conservative.

Conclusion: the moral weight of extreme suffering

Cluster headaches, described as “worse than death” and endured even by children are real moral emergencies. Linear scales obscure this. They treat childbirth and cluster headaches as a 7 vs 10: close, manageable, comparable. But the truth, phenomenologically and ethically, is that the gap might be 5×, 10×, or more. That difference matters. A world that sees it is a world more likely to fund research, develop treatments, and take suffering seriously.

This is where QRI's insight shines: extreme experiences aren’t marginal, they’re dominant. But to act on that insight, we need numbers. Rejecting pure logarithmic scaling doesn't diminish the reality of extreme pain. I just thought it deserved a try at something more concrete. Maybe power-law or sigmoid curves aren’t exact. Maybe our estimate that 10/10 pain is 100,000× worse than 1/10 will one day be replaced. But until then, even rough models can guide better decisions than pretending each point on a scale is equal.

0 notes