Don't wanna be here? Send us removal request.
Text
Unlock Your Study Abroad Journey: Expert Counseling, Test Prep, and Country Selection
Dreaming of studying abroad? It’s an exciting journey, filled with unique opportunities and valuable life experiences. However, navigating the process—from test preparation to selecting the perfect destination—can feel overwhelming. Here, we’ll explore how expert guidance, focused test preparation, and personalized country selection can make your study abroad dreams come true.
1. Why Study Abroad?
Studying abroad offers an enriching experience that extends beyond academics. It allows students to immerse themselves in new cultures, broaden their perspectives, and gain a global network. Plus, international experience can be a valuable asset in today’s job market, enhancing your career prospects.
2. Personalized Test Preparation
Many top universities require exams like the SAT, GRE, GMAT, IELTS, or TOEFL for admission, and scoring well can significantly impact your application. Tailored test preparation not only boosts your scores but also builds confidence.
Our Approach to Test Prep: We assess your current level and create a study plan tailored to your goals. With experienced tutors and practice materials, you can master key concepts and strategies that help you achieve your target scores.
3. Expert Counseling for Streamlined Planning
Applying to universities abroad involves several steps, including selecting programs, preparing documents, and meeting deadlines. This process can feel complex, but professional counselors simplify it. They help you understand admission requirements, manage timelines, and make well-informed decisions about your future.
Counseling Benefits: Our counselors work one-on-one with you to understand your academic goals, interests, and budget, helping you navigate the admissions process with ease. From crafting a strong application to preparing for interviews, our support is designed to give you an edge.
4. Choosing the Right Country and University
Selecting the best country and university is critical. Factors like tuition fees, cultural fit, career opportunities, and language requirements should all be considered. Studying in the U.S., for example, is ideal for those seeking diverse programs and extensive research facilities, while the U.K. is known for its shorter, intensive degree programs.
Tailored Country Selection: We provide detailed insights into popular study destinations, helping you weigh your options based on your goals. Whether it’s Canada’s welcoming policies or Australia’s hands-on learning approach, we guide you toward the ideal choice.
Conclusion
Embarking on a study abroad journey is thrilling yet challenging. With expert counseling, focused test preparation, and personalized country selection, you can navigate this path with confidence. Start planning today and turn your dreams of studying abroad into a reality!
you can visit our wesbite for more details.
https://theproeducator.com/
0 notes
Text
Lawn and Turf Supplies in Sydney's North Shore & Northern Beaches
https://www.acelandscapes.com.au/products-services/turf-supplies/
0 notes
Text
घर पर Green Tea कैसे बनाएं: लाभ, रेसिपी, और टिप्स
उस देश में जहां चाय का महत्व अत्यधिक है, क्या आपने कभी Green Tea का स्वाद चखा है? Green Tea सामान्य चाय की तुलना में कई स्वास्थ्य लाभ प्रदान करती है। इस विस्तृत गाइड में, हम घर पर Green Tea कैसे बनाएं, इसके लाभ, और इसे कब पीना चाहिए इसका विवरण करेंगे।
Green Tea क्यों पीना चाहिए:
रेसिपी पर दिखाई गई बातों से पहले, Green Tea क्यों एक स्वस्थ विकल्प है, यह समझना महत्वपूर्ण है। रोजाना 2-3 कप Green Tea पीना, विशेषकर शाम को, एक सक्रिय और स्वस्थ जीवनशैली के लिए सहायक हो सकता है।
Green Tea के लिए सामग्री:
- 2 कप पानी
- 1 इंच कटा हुआ अदरक
- इलायची
- 2-3 पुदीने की पत्तियां
- 2-3 तुलसी की पत्तियां
- 1 चमच नींबू का रस
Green Tea बनाने की विधि:
1. एक पतीले में 2 कप पानी उबालें।
2. उबलने पर, पानी में कटा हुआ अदरक, इलायची, पुदीने की पत्तियां, और तुलसी डालें।
3. उबलने वाले पानी में एक चमच या एक चाय बैग Green Tea डालें।
4. इसे 2-3 मिनट के लिए पकने दें। ज्यादा पकाने से कड़वाहट आ सकती है।
5. पकने के बाद, गैस बंद करें और नींबू का रस डालें।
6. यदि चाय बैग का उपयोग किया गया है, तो इसे पतीले से निकालें। यदि चाय पत्तियों का उपयोग किया गया है, तो मिश्रण को छानें।
7. अच्छी तरह से मिलाएं और मजा करें।
Green Tea के लाभ:
Green Tea वजन घटाने, पाचन को मजबूत करने, कैंसर के खतरे को कम करने, मानसिक तनाव को कम करने और त्वचा को स्वस्थ और चमकदार बनाए रखने जैसे विभिन्न लाभ प्रदान करती है।
Green Tea के साइड इफेक्ट्स:
Green Tea का अत्यधिक सेवन नींद की कमी, सिरदर्द, मतली, पाचन संबंधी समस्याएँ, और लिवर क्षति जैसे साइड इफेक्ट्स का कारण बन सकता है। इसलिए, यह महत्वपूर्ण है कि हरी चाय का सेवन मात्रित्व में किया जाए और किसी भी गंभीर स्वास्थ्य समस्या के मामले में डॉक्टर से परामर
0 notes
Text
Classification and Properties of Triangles - Turito
A triangle is a geometric figure with three sides and three corners. Remember the polygon with the fewest number of sides? Hmm, a triangle. Polygons are simple closed curves. Consists of line segments. Can a single line segment create a closed curve? The answer is no. If you try to create a curve with two line segments, it won't work. Therefore, we need to create three segments and intersect them to form a closed curve, or triangle. A triangle is therefore a closed curve consisting of three line segments. A square consists of 4 lines of equal length and 4 right angles. Creating triangles is easy because there are no rules. If you connect the three line segments in any way, you get a triangle.
Let's take a look at the different types of triangles we get.
Activity
This activity will help you understand how to classify triangles at a basic level.
• Take pictures of different triangles from the internet.
• Then print them.
• Measure the various sides and angles of a given triangle using a protractor and ruler.
• Are all sides and angles of different triangles equal? The answer is no.
• Different triangle sides and angles have different measurements.
• This difference in the sides and measurements of the various triangles helps classify them.
• Also note that if all angles of a triangle are equal, then its sides are also equal.
• If all sides of a triangle are equal, then it’s angles are also equal.
• A triangle with two equal sides also has two equal angles, and a triangle with two equal angles also has two equal sides.
• If the angles of any triangle are unequal, then the sides are unequal.
• If all three sides of a triangle are unequal, then all three angles are also unequal.
• After going through the whole discussion, we will be able to classify each triangle according to its angles and sides.
Properties of triangles
• A triangle has 3 sides, 3 corners, and 3 vertices.
• The sum of all the interior angles of triangle is equal to 180 degrees.
• The sum of the two sides of the triangle must be greater than the other side.
• The largest side of the triangle is the one opposite to the largest angle
• Adding the three exterior angle values of a triangle gives the result 360 degrees.
Type of angle based on measurement
Before classifying triangles by angle, we need to understand the types of angles. It helps to understand the discussion of how to better classify triangles.
• Angle whose measure are less than 90 degrees are called acute angles.
• An angle whose measurement equals 90 degrees is called a right angle.
• Angles which are greater than 90 degrees and less than 180 degrees are called obtuse angles.
How to classify triangles in terms of their angles
A triangle has three corners. Adding all three angles of a triangle gives 180 degrees.
Just as we categorized types of angles by the same criteria, we can categorize triangles into different types.
• Acute Triangles: A triangle with all three acute angles is called an acute triangle.
• Right Triangles: Triangles with right angles are called right triangles. A triangle can only have one right angle and not more than one. The sum of all the three angles of the triangle must be equal to 180 degrees. Therefore, if one angle equals 90 degrees, the sum of the other two angles must equal 90 degrees. If you try to construct a triangle with two right angles, you cannot assume that the third angle is 0. In this case, the third side of the triangle overlaps the other two sides and cannot form a triangle. Therefore, it is not possible to create a triangle with multiple angles equal to 90 degrees. The other two corners of a right triangle must be acute.
• Obtuse Triangle: Such a triangle has one angle greater than 90 degrees and less than 180 degrees. Now, can we say that an obtuse triangle has one obtuse angle? Yes. The sum of the three angles in a triangle must equal 180 degrees, so the other two angles in an obtuse triangle must be acute.
How to classify triangles in terms of their sides
A triangle consists of three sides. The three sides of the triangle can have the same or different dimensions.
• Isosceles Triangle: An isosceles triangle is a triangle that has two sides with exact measurements, but a third side with different measurements.
• Irregular Triangles: Odd triangles are triangles that have different measurements on all three sides.
• Equilateral Triangle: An equilateral triangle is a triangle with all the three sides of equal length. The same sides of a triangle are called congruent sides. Therefore, all sides of an equilateral triangle are congruent.
Exterior angle of triangle:
Extending the sides of a triangle creates corners on the outside of the triangle. This angle is known as the exterior angle of the triangle. The exterior angle theorem provides this concept. To better understand this concept, let's create a triangle with exterior angles.
• Draw a triangle ABC and extend one of its sides, say BC, as shown. Observe the angle ACD formed by point C. This angle is outside triangle ABC.
• It can be said that it is the exterior angle of the triangle ABC formed by the angle C.
• Corner BCA is the corner adjacent to corner ACD.
• The remaining two angles of the triangle, angle A and angle B, are called the two diagonal interior angles or the two far interior angles of the angle ACD.
• The any one exterior angle of a triangle is equal to the sum of its opposite interior angles.
Application of triangles in our day to day life
A triangle is the basic unit of all polygons. The concept of triangles has been widely used since ancient times. Triangles appear in many aspects of our daily lives, including engineering, mathematics, architecture, carpentry, astronomy, navigation, and physics. This shape can be seen everywhere. A triangle is the strongest shape that forms a strong base.
• Architecture: It's not uncommon to find triangular structures when constructing buildings. The application of the triangle concept in building construction can be seen in the form of the Egyptian pyramids. Another such example is the historic Eiffel Tower. The triangular shape makes these historic buildings look unique and attractive. It also strengthens the base of the tower. A triangle derives its strength from its shape, distributing the force evenly on its three sides. Square structures are also very common. This is because squares stack easily. Triangular buildings are more difficult to construct, but the resulting structures are more stable.
• Most houses have triangular roofs. In areas where it snows, you can see many houses with triangular roofs. • The triangular roof creates a slope that allows snowfall and prevents water from accumulating on the roof.
• A sailboat has a triangular sail. In the past, sailing ships had square sails, but now most have triangular sails. Their shape helps the boat go upwind. This method is called tucking.
• Mountains are triangular. Determine the height of the hill or pole using the concept of right triangle properties. You can also use the triangle concept to find the distance from the tower to the ship.
• Triangles are used to build bridges. This shape helps distribute weight without affecting proportions evenly. Incorporating triangles into the structure of the bridge made it stronger and able to withstand more weight.
• Knowledge of right angles is used in the construction of stairs. The ladder also becomes a triangle when it is leaned against the wall. This position is held firmly. Many foods are triangular, including sandwiches, pizza, and packaged snacks. This shape makes it more attractive and easy to handle. Children prefer triangular sandwiches to sandwiches of other shapes.
• A similar triangle is used to determine the height of objects that are difficult to measure manually. For example, skyscrapers, towers, etc.
• The slope forms a triangle with the ground. Makes loading and unloading easier. You've probably heard packages being unloaded from planes on hillsides. It makes the job easier.
• Traffic signs are triangles. Make them easily identifiable.
• Geometric instruments like protractors are triangles. It helps you draw parallel, vertical and other diagonal lines with precision.
0 notes
Text
A polygon is a plane figure characterised by a finite number of straight line segments connected to form a closed polygonal chain (or polygonal circuit). A bounded planar area, a bounding circuit, or both together are sometimes called polygons in Euclidean geometry.
Some important terms and information about Polygon:
Sides - segments of polygonal circles
vertex - the point where two sides of a polygon meets
body - interior of polygon
A "gon" refers to a side of a polygon. A quadrilateral is a quadrilateral.
A polygon is a two-dimensional figure. The aposem (sometimes abbreviated as apo) of a regular polygon is the line segment from the center to the midpoint of one of the sides.
Interior angle: The angle formed by the vertices of a polygon within the area enclosed by the polygon.
Center point of a regular polygon: The point inside the polygon where all the vertices of the polygon are equidistant.
Congruent Polygons: Polygons with all congruent sides
Exterior angle: The angle formed by the vertices of the polygon outside the area enclosed by the polygon.
Calculating side lengths, diagonals, and angles of regular polygons, bisectors, perimeters, and areas are part of the survey and geometry curriculum.
Common polygon names (by number of sides) and some of their properties:
Monogon - Not commonly recognized as a polygon, but the term is sometimes used in some fields such as graph theory.
Number of sides = 1.
2. Digon - is not commonly recognized as a polygon in the Euclidean plane, but may exist as a spherical polygon.
Number of sides = 2.
3. Triangle (or Trine) - The simplest polygon that can exist in the Euclidean plane. You can align planes. Number of sides = 3.
4. Rectangle (or Rectangle) - The simplest polygon can intersect itself. The simplest polygon that can be concave. The simplest polygons cannot cycle. You can align planes.
Number of sides = 4.
5. Pentagon - The simplest polygon can exist as a regular star. The star pentagram is known as the pentagram or pentagram.
Number of sides = 5.
6. Hexagon - planes can be tiled.
Number of sides = 6.
7. Heptagon (or heptagon) - The simplest polygon is such that a compass and ruler cannot create a regular shape. However, it can be constructed using the noisis structure.
Number of sides = 7.
Polygons can be classified according to their convexity type
• Convexity means that a line drawn through the polygon (not touching its sides or corners) hits its boundary exactly twice. Therefore, no interior angle exceeds 180°. On the other hand, line segments with endpoints on the boundary only pass through points inside between the endpoints.
• Concave: Straight instead of convex. At least one interior angle should exceeds 180°.
• Simple: The boundary of the polygon does not intersect itself. All convex polygons are simple.
• Star polygons - Star polygons are regularly intersecting polygons. A polygon cannot be both a star and a star shape. The difference between this and the next is something to keep in mind when trying to find the area of a regular polygon.
• Star: From at least one point, the entire interior is displayed without intersecting edges. Polygons must be simple and can be either convex or concave. All convex polygons are stars.
• Non Convex: Finds lines that touch the boundary more than once. A line segment is between two boundary points outside the polygon.
• Simple: The boundary of the polygon does not intersect itself. All convex polygons are simple.
• Concave: Straight instead of convex. At least one interior angle should exceeds 180°.
• Self-intersecting: The boundary of the polygon is self-intersecting. The term complex is sometimes used as opposed to simple, but this can confuse the notion of complex polygons that reside in a complex Hilbert plane and have two complex dimensions. .
According to the equality and symmetry aspect
• Equal Angles: means that all angles have equal angles.
• Equilateral: “ Equi “ stands for equal and “ lateral “ stands for sides This means that all sides are of equal length.
• Regular: Equilateral and equiangular shapes.
• Circular: All four corners lie on a single circle known as the circumscribed circle. Another way of defining regularity is that a polygon is regular if it is both equilateral and equilateral, or if it is both periodic and equilateral. A regular polygon is a non-convex regular polygon.
• Coordination or Edge Transitivity: All sides share the same symmetry orbital. Also, polygons are tangential and tangential.
• Tangent: This means that all sides of the circle are tangent. Equiangular or Corner Transition: All corners are on the same symmetrical trajectory. Polygons are also periodic and equiangular.
How did you find the area of a regular polygon?
The area of a regular polygon is represented by the area enclosed by the sides/boundaries of the polygon. Therefore, we can say that to find the area of a regular polygon, we need to calculate the area it occupies.
Difference between perimeter and area of a regular polygon
Perimeter and area are often confused. However, their only similarity is that the area and perimeter do not depend on the interior angles of the polygon. Rather, they depend on the length of the sides. First, to clear up the confusion between these two measurable identities, we need to understand the fundamental differences.
PERIMETER
Definition - It is defined as the total length of a polygon's boundary, obtained by adding the lengths of all its sides.
Formula - Perimeter of polygon = length of side 1 + length of side 2 + … + length of side N (for N-sided polygons)
Units - meters, centimeters, inches, feet, etc.
AREA
Definition - It is defined as the area of space enclosed by any polygon.
Formula - The area of a polygon is whether the polygon is regular or irregular.
Units - (meters)2, (centimeters)2, (inches)2, (feet)2,
Some formulas for known regular polygons are given below.
• Area of triangle = (1/2) * height * base
You can also use Heron's formula to find the area of a triangle if you know the side lengths.
Area = √s(s-a)(s-b)(s-c)s(s a)(s−b)(s−c), where s = perimeter/2 = (a + b + c)/2, a, b, c are the side lengths.
• Area of rectangle = (length) x (width)
• Area of Parallelogram = (height) x ( base)
• Area of trapezoid = (1/2) x (total length of parallel sides or base) *!height
• Area of rhombus = (1/2)x (product of both the diagonals).
How can you find the area of a regular polygon if you know the number of sides?
The area of a regular polygon = (number of sides × length of sides × aposem)/2, where the length of the aposem is given as l/(2tan(180/n)). where l is the side length and n is the number of side of a regular polygon.
In terms of the perimeter of a regular polygon, the area of a regular polygon = (perimeter x length)/2, where perimeter = number of sides x length of side It is.
Example: Find the area of a 5-sided regular polygon with a side length of 10 cm
As we understood in the discussion above, all we need to solve this problem is the side length. The applicable formula is – 1/4×√5(5+2√5)×(side)2
So 1/4*√5(5+2√5)*(10)2= 172.05 square centimeters.
Example: Find the area of a regular polygon with 6 cm sides and 10 cm height
Since it is a triangle here, the triangle formula for finding area is used.
1/2 x base x height
So ½ x base x height = ½ x 6 x 10 = 30 square centimeters
In these examples, the implementation of the basic formulas given makes it much easier to find the area of regular polygons. I'm talking about polygons. This covers the basics of finding the area of regular polygons.
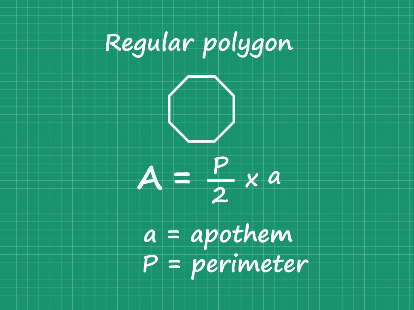
0 notes
Text
Addition of Integers: Formula, Rules, Examples | Turito
Adding Integers: Definition and Examples
An integer is a number written without fractions. For example, 3, 71, 902, -66, -877 - these are all integers. The simplest way to define an integer is to consist of an absolute value and a positive or negative sign.
The digit Zero (0) is neither a positive nor a negative integer. Positive natural numbers are called positive integers (1, 2, 3, etc.) and additive reciprocals are called negative integers (-1, -2, -3, etc.). This is very easy to see by adding an integer.
Arithmetic main features:
Arithmetic is one of the most basic and fundamental parts of mathematics. Basic knowledge also allows you to understand various applications and studies such as algebra, trigonometry, measurement, geometry and other related topics. The foundations of arithmetic are the driving force behind all other aspects of mathematics.
Some common basic problem statements about integers are how to add and subtract integers and how to add integers of the same sign. These, along with several other functions, form the basis of mathematics
The basic operations of arithmetic operations are:
Addition(Sum; `+`)
Subtraction (difference; `-`)
Multiplication (product; `x`)
Division (÷)
How to add integers is explained in detail in this article. In the meantime, let's take a quick look at the other three features.
Subtraction
The arithmetic operation of subtraction shows the difference between two numbers. The symbol "-" represents it. Subtraction is primarily used to find out what is left when things are removed. That is, one number is subtracted from another.
For example, I had 10 apples. Two apples are taken from me. Now we have (10-2) = 8 apples.
Multiplication
Repeated addition is called multiplication. The symbol "x" represents it. Multiplication as an arithmetic operation is useful for finding sums when a number is repeated several times. Example: 3 times 4 is 12. Mathematically, we can write 3 × 4 = 12. Multiplicand and multiplier are terms used in the multiplication process. Product is the term we use for the result of multiplying a multiplicand by a multiplier.
Example: I ate 2 apples every day for 3 consecutive days. So there were 2 x 3 = 6 apples.
Division
Dividing something into equal parts or groups is called division. One of the four basic arithmetic operations that produce an evenly distributed fair result. The inverse of multiplication is division. The symbol "÷ represents that".
Example: For me, Andrew and Michael split his 12 mangoes evenly between us. So there were 12 ÷ 3 = 4 mangoes each.
How to add an integer
Addition is one of four basic operations: arithmetic, subtraction, multiplication, and division. In general, adding two positive integers yields a positive integer. Adding two negative integers yields a negative integer. Adding a negative integer and a positive integer yields the integer containing the greater value between the two negative numbers. You can read more about how to add integers here. Append represents a value added to an existing value. For example, if I had 3 of his pens and 4 more were added to this list, the addition would result in a total of 7 pens. Addition is affected by both irrational and rational numbers. Therefore addition applies to both real and complex numbers.
In summary, how do you add like and opposite integers?
Adding two positive integers always results in a positive integer.
Adding two negative integers always results in a negative integer.
When adding a positive integer to another negative integer, the larger of the two integers determines the sign.
Basic example:
14+15=29
7 + 5 = 12
(-3)+3 = 0 [Addition of two equal inverse integers always results in zero]
(-50)+4 = (-46)
10 + (-1) = 9
(-20) + (-10) = (-30)
Properties of Integer Addition and MultiplicationClosure property : x + y is an integerAssociative property : x + (y + z) = (x + y) + zCommutative property : x + y = y + xExistence of identity element: x + 0 = xExistence of inverse: x + (−x) = 0Distributive law: x × (y + z) = (x × y) + (c × z)Closure propertyThe sum of two integers is results into an integer. If a and b are two integers, their sum is also an integer.Examples: 5 + 6 = 11 ; -5 + 8 = 3.Commutative lawThe commutative law of addition states that the order of terms does not affect the result. Also, changing the conditions does not affect totals or products.Examples: 2 + 4 = 4 + 2 ; -6 + 8 = 8 + (-6)Associative propertyThe associative property of addition states that it makes no difference how the numbers are grouped. the result is the same. Anyway, the answer is the same.Example: 2 + (3 + (-4)) = 1 = (2 + (−4)) + 3Distributive PropertyThe distributive law describes how mathematical operations within one parenthesis should be distributed among other parentheses. It is either the law of distributive addition or the law of distributive subtraction. In this case, the integer is added or subtracted first, then multiplied or divided by each number in brackets, and then added or subtracted. Example: −5 (3 + 2) = −25 = (−5 × 2) + (−5 × 3)How to add an Integers using the number lineThe following principles apply to adding integers on the number line.• To add positive numbers, move the cursor to the right (or positive side) of the number line.• Adding negative integers is done by moving them to the left (or negative) side of the number line. • Each specified integer is a starting point for movement on the number line.Examples and step-by-step guides can be found here:The first step is to choose a scale for the number line. For example, whether a number is expressed as a multiple of 1, 5, 10, or 50 depends on the integer specified. For example, if you need to add 10 and 20, you can use a number line with a scale of 10.If you need to add -4 and 9, you can take the number scale starting at 1.The next step is to find any integer on the number line. A larger absolute value is desirable. For example, if you need to add 3 and 22, first find 22 and then jump right twice is better than first finding 3 and then jumping right twenty two. The final step is to jump left or right and add a second integer to the number from the previous step. This depends on the number whether it is positive or negative.Practical implementation of integer addition and subtractionI had 10 cookies. I borrowed 5 from my father. How many cookies do I currently have?A: The answer is 10 + 5 = 15 (real example of how to add like-signed integers)The temperature in the room is 20 degrees Celsius. My mother asked me to go up three times. What will be the final temperature of the room when it rises?A: 20 + 3 = 23.Mike got -3 points in the pre-final quiz competition. He scored 10 more points to qualify for the final. What was his total score?A: Add integers. -3 + 10 = 7 (integer addition and subtraction example)
0 notes
Text
Adding and Subtracting Mixed Numbers - Turito
0 notes
Text
Radius of the Circle: Definition, Formula with Solved Examples - Turito
0 notes
Text
Multiplication Arrays with Real-life Examples - Turito
0 notes
Text
Additive Identity Property: Definition with Examples - Turito
0 notes
Text
Subtracting Integers: Properties, Rules with Solved Examples
0 notes
Text
Subtract Fractions with Unlike Denominators - Turito
0 notes
Text
Mathematical Modeling: Definition, Classifications - Turito
0 notes