priscilanicolete-blog

[priscilanicolete-blog]

Criando um Blockmodels

Podemos modelar e explorar Blockmodels através do software Pajek. Para isso, primeiramente precisamos criar um arquivo (em um Bloco de Notas, por exemplo) com os nomes dos atores da rede e a indicação de relação entre esses autores (Figura 1).

Na indicação de relação entre os autores, deve-se indicar o grau de relação que essas pessoas possuem, ou seja, escala de intensidade dessa relação, utilizando o número “2” quando o laço pode ser considerado forte (pessoas que se conhece muito bem) e o número “1” para indicar um laço fraco (pessoas que apenas se conhecem).

O último passo para organizar a sua rede é realizar o levantamento de alguns atributos que nos ajudarão a analisar a rede depois do processamento realizado no software. Como mencionado no poste anterior, um Blockmodel pretende identificar subgrupos em uma rede, portanto, este momento é realizado a classificação dos atores através de seus atributos. Esses atributos vão variar conforme sua necessidade, o que você está querendo analisar (exemplos de atributos: nacionalidade, sexo, ambiente de convívio (trabalho, estudo, religioso) e etc.). Essa classificação deve ser feita em um arquivo separado, utilizando um planilha (.excel por exemplo). 

Bom, agora que já temos nosso arquivo vamos colocado no Pajek para identificar nossos Blockmodels.

Depois, devemos exportar a nossa rede em uma matriz em formato EPS, para isso, nesse mesmo local (figura acima) execute: 

File > Network > Export as Matrix to EPS > Original.

Agora vamos criar nossas partições e permutações:

Network -> create Partition – Degree – all

Network – create Permutation – core + degree

Nesse momento teremos os seguintes documentos:

Agora devemos ativar a Permutação de Matrizes no Pajek: Ative uma partição como os grupos de referencia para permutação. 

Partition > Make Permutation.  Aqui o Pajek irá ativar o compartimento Permutations.

E então exporte matriz em formato EPS considerando a permutação e a partição criada: 

File > Network > Export as Matrix to EPS > Using Permutation + Partition 

Nesse momento já temos uma rede de Blockmodels. Se visualizarmos no software XnView teremos uma rede como a apresentada abaixo. Os pontos pretos indicam um laço forte entre dois autores, os pontos cinzas um laço fraco e ausência de cor indica que não há ligação entre os autores.

Como podemos ver, na matriz acima o Pajek criou diversos subgrupos (cada linha em azul está dividindo um subgrupo). Alguns deles com apenas um ou dois autores. Agora então devemos realizar a análise de aglomerados hierárquicos por similaridade das relações. Para isso vamos criar nossos cluster através do Pajek.

Criando um cluster completo: Cluster > Create Complete Cluster. Aqui você cria o cluster do tamanho da rede.

Identificar aglomerados de atores similares nas suas relações:  Operations > Network + Clusters > Dissimilarity > Network based > d1 > All. O índice d1 irá comparar a semelhança dos vértices baseado no compartilhamento de seus vizinhos. Quanto mais vizinhos dois vértices compartilham, mas serão considerados similares. O Pajek irá gerar um dendrograma e uma hierarquia. Ambos mostra o grau de falta de similaridade dos atores.

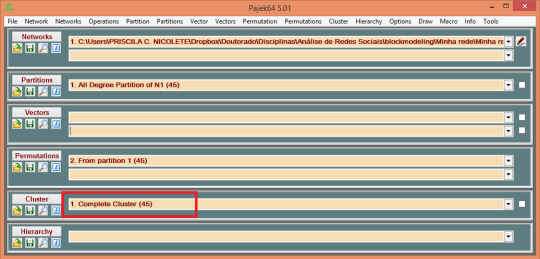
Agora crie uma partição com classes de atores similares a partir da hierarquia.

File > Hierarchy > View/Edit 

Aqui você pode ver o grau de similaridade entre os aglomerados. Com isso, pode definir um grau que expresse a menor falta de similaridade, isto é, um valor próximo de zero. Procure garantir que o seu valor de corte não vai produzir muitos aglomerados pequenos com 2 ou 3 atores. Clique uma vez em cima do aglomerado identificado e execute o comando:

Edit > Change Type.

Repita esse procedimento para todos os grupos identificados. Feche a hierarquia e Execute: 

Hierarchy > Make Partition. 

Uma nova partição foi criada. Cada classe contém os atores mais similares em suas relações.

Agora vamos visualizar a relação entre os aglomerados hierárquicos: 

Ative a rede que está sendo analisada. 

Ative a partição criada a partir da hierarquia. 

Exporte a matriz e analise no software VnView e analise as relações entres os aglomerados identificados.

Gerando então nosso Blockmodel final:

[priscilanicolete-blog]

Blockmodels - Análise de redes sociais

O blockmodel (modelo de bloco) em redes sociais, é uma estrutura simplificada que molda a rede maior a partir da qual o modelo foi construído. Ou seja, em vez de enfatizar ligações entre atores, como feito nas análises de centralidade, densidade, coesão e etc., a análise de blockmodels considera as similaridades entre as redes dos atores em estudo, analisando os papéis, as posições e a equivalência estrutural e regular dos atores. (DOREIAN, 2000). Assim, esta técnica é utilizada para encontrar subgrupos (blocos) em uma rede e estudar as relações entre eles.

Conforme Nelson (1984), “White e Boorman, da Universidade de Harvard, desenvolveram as técnicas de blockmodeling baseando-se no princípio de que as semelhanças nas estruturas de redes individuais são mais importantes do que as ligações reais entre pessoas no estudo da estrutura social”. Assim, os blockmodels procuram agrupar as pessoas cujos contatos, uns com outros e com outros grupos, sigam o mesmo padrão (NELSON, 1984).

Atores que tenham a mesma estrutura nas suas redes sociais são agregados em "blocos" e as matrizes originais contendo os dados são reduzidas para formarem "matrizes-imagem" (que mostram a existência de ligações dentro e entre agregados). Isto fornece uma representação gráfica das relações existentes entre blocos de atores que são "estruturalmente equivalentes". (NELSON, 1984).

A imagem abaixo apresenta uma exemplificação dos estudos que podem ser realizado através do blockmodels. Nesse caso é apresentado duas redes de pais e filhos e o modelo à direita é um modelo de bloco em que atores estruturalmente equivalentes foram agrupados.

Figura 1

Fonte: (DOREIAN, 2000)

Equivalência estrutural e Equivalência regular

Quando falamos em blockmodels, podemos analisar dois tipos de equivalência: equivalência estrutural (como mostrado na figura 1) e equivalência regular.

No primeiro caso, dois atores são estruturalmente equivalentes se estiverem conectados do mesmo modo ao resto da rede. No caso da Figura 1, c1 e c2 são estruturalmente equivalentes na rede pois estão conectados a um outro nó (p1), assim como c3, c4 e c5 são estruturalmente equivalentes na segunda rede. Porém, não podemos dizer que c1 e c2 são equivalentes estruturalmente com c3, c4 ou c5.

Já na equivalência regular, podemos dizer que dois atores sociais são regularmente equivalentes se estiverem conectados de forma equivalente a atores equivalentes. A figura 2 apresenta duas redes com os dois conjuntos de pais que estão conectados de maneira equivalente aos dois conjuntos correspondentes de filhos. Nesse caso, na equivalência regular os pais {f1, m1, f2, m2} ocupam a posição Pais enquanto as crianças {c1, c2, c3, c4, c5} ocupam a segunda posição Filhos.

Figura 2

Fonte: (DOREIAN, 2000)

Modelando os blocos

Agora que entendemos as diferenças entre equivalência estrutural e regular, podemos resolver que em um blockmodel os blocos (subgrupos) são classes de atores estruturalmente ou regularmente equivalentes. Assim, utilizando a técnica em uma rede maior, teremos como resultados os subgrupos da qual pode-se investigar a correspondência entre as posições na rede e os papéis sociais dos atores.

Para a modelagem de um blockmodel iniciamos com uma Matriz de Adjacência (figura 3) contendo todos atores e relações de uma rede. E ao final deverá ter uma Matriz Permutada (figura 4) que divide/organiza os atores por alguma característica, criando os blocos.

Figura 3: Matriz de Adjacência 

Figura 4: Matriz Permutada

Fonte: 

NELSON, Reed. O uso da análise de redes sociais no estudo das estruturas organizacionais. Rev. adm. empres.,  São Paulo ,  v. 24, n. 4, p. 150-157,  Dec.  1984 .   Disponível em: <http://www.scielo.br/scielo.php?script=sci_arttext&pid=S0034-75901984000400025&lng=en&nrm=iso>. Acesso em:  13  Nov.  2017.

DOREIAN, Patrick D. Una introducción de carácter intuitivo a la modelización en bloques («blockmodeling»). Política y Sociedad, n. 33, p. 113-113, 2000.

[priscilanicolete-blog]

Livro: Conectados de Nicholas A. Christakis y James H. Fowler

Os estudos de Nicholas e James apresenta evidências de como as redes sociais modelam e afetam nossas vidas, impactando desde como nos sentimos, como e o que escolhemos, e até mesmo como adoecemos. 

Vivemos em uma sociedade em rede, com isso, os autores defendem que, nessas redes, podemos ser afetados em até três graus de influência. Ou seja, podemos ser incentivados a perder peso porque o amigo do amigo perdeu peso, ou então parar de fumar porque o amigo do amigo parou de fumar. 

Para os autores, a vida em redes possui 5º regras básicas:

1º - Modelamos nossa rede: “Homofilia, a tendência consciente ou inconsciente de se associar a pessoas que se parecem conosco (amar um igual)”    

2º - Nossa rede nos modela: “A transitividade pode afetar tudo, desde encontrar um(a) parceiro(o) sexual até cometer suicídio”.

3º - Nossa rede nos afeta: “Nosso amigos nós influenciam”

4º - Os amigos de nossos amigos nos afeta: “As pessoas não copiam apenas seus amigos. Elas também copiam os amigos de seus amigos, e os amigos dos amigos de seus amigos” - Três graus de Influência.

5º - A rede tem vida própria: “As redes socais podem ter propriedade e funções que nem são controladas e nem percebidas. Essas propriedades só podem ser entendidas ao se estudar o grupo inteiro.”

Abaixo segue um link para um vídeo de Nicholas Christakis falando sobre a influência oculta das redes sociais. A palestra foi ministrada no TED2010, e pode ser um ótimo complemento ao livro.

TEDTalks: Nicholas Christakis - A influência oculta das redes sociais

[priscilanicolete-blog]

Redes por afiliação

Rede por afiliação é um tipo de rede de modo-duplo, na qual existe um conjunto de atores e um conjunto de grupos (entidades). Os atores e grupos não possuem uma conexão direta, mas se dois atores pertencem a um mesmo grupo então estão conectados indiretamente, da mesma forma, dois grupos podem estar conectados entre si se possuírem um ator em comum (WATTS, 2009). “Dois nós, em uma rede por afiliação, podem ser considerados afiliados se participarem do mesmo grupo, mesmo contexto”. (WATTS, p. 81, 2009).

Redes por afiliação são uma classe importante de rede social, não só porque afiliações formam a base para outros tipos de relações sociais, como amizades ou laços comerciais, mas também porque surgem em uma ampla gama de aplicações em redes não sociais que, apesar disso, são econômica e socialmente interessantes. Por exemplo, quando entramos na Amazon.com para comprar um livro e, na parte de baixo da tela, vemos listas como “pessoas que compraram este livro também compraram...”, isso é uma rede por afiliação. Ela consiste em dois elementos – grupos (livros) e atores (pessoas). (WATTS, p. 81, 2009).

A melhor maneira de representar uma rede por afiliação é através de uma rede bipartida ou bimodal. Em uma rede bipartida, dois conjuntos de nós são representados separadamente, e apenas nós de tipos diferentes podem ser conectados, através de uma relação que podemos interpretar como “pertence a”. (WATTS, 2009). Por meio de uma rede bipartida pode-se gerar duas redes unimodais, que representam afiliações entre os atores ou intersecções entre os grupos, como apresentado na figura abaixo.

Figura 1 - Exemplo de rede bipartida

Fonte: (WATTS, 2009)

Assim, pode-se analisar duas principias informações nas redes de afiliação: Distribuição de tamanho de grupos; Distribuição de quantos grupos pertence cada ator.

Redes por afiliação no Pajek              

Imagine uma rede por afiliação na qual pretende-se analisar a relação entre universidades e pesquisadores, analisando as universidades que estão integradas à rede pelas ligações que mantêm com os pesquisadores e os pesquisadores que possuem vínculo por meio de suas ligações com as universidades. A matriz abaixo (quadro 1) apresenta as configurações das ligações universidade-pesquisador, no qual tem-se 0 e 1 indicando ausência ou presença de relação, respectivamente.

Quadro 1 – Matriz universidades-pesquisadores 

Fonte: (TOMAÉL; MARTELETO, 2013)

A partir dessas informações podemos criar nossa rede no software para análise de redes sociais Pajek.    

a) Para a criação de uma rede bipartida no Pajek, primeiramente deve-se criar a base de dados em um arquivo tipo texto (.txt) no padrão esperado pelo Pajek, como a figura abaixo.

b) Agora abra o arquivo no Pajek.

c) Após abrir a rede, precisamos particionar nossa rede em 2 modos: 

*Network -> 2-model network -> Partition into 2 modes

d) Selecione a nova rede e clique no “lápis” para visualizar a rede.

e) Gere as duas redes unimodais – rede de pesquisadores (atores) e rede de universidades (grupos)

*Network -> 2-model network -> 2-model to 1-model -> rows

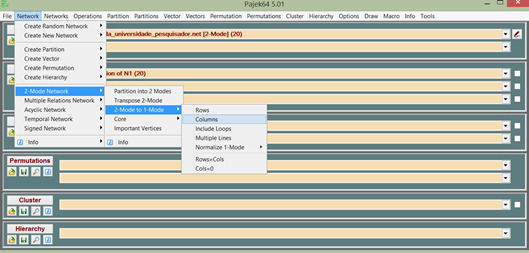
*Network -> 2-model network -> 2-model to 1-model -> columns

Referências

RIBEIRO, Antônio Carlos. Entrada e Visualização de dados nos Softwares Pajek e Ucinet. Belo Horizonte. 2013.

TOMAÉL, Maria Inês; MARTELETO, Regina Maria. Redes sociais de dois modos: aspectos conceituais. Transinformação-ISSNe 2318-0889, v. 25, n. 3, 2013.

WATTS, Duncan J. Seis graus de separação: a evolução da ciência de redes em uma era conectada. São Paulo: Leopardo, 2009.

[priscilanicolete-blog]

Seis graus de separação - Parte 1

Aula do dia 26/09/2017

WATTS, Duncan J. Seis graus de separação: a evolução da ciência de redes em uma era conectada.  São Paulo: Leopardo, 2009.

Primeira parte do debate sobre o livro de Duncan Watts sistematizada pelos alunos @alinedecampos​, @igoryepes​, @marciobigolin​, @priscilanicolete​.

Continuar lendo

[priscilanicolete-blog]

Aula 12/09

Método, aplicação em estudo com a Profa. Dra. Cristiane Koehle.

No estudo apresentado pela Profa. Dra. Cristiane Koehle foi realizado uma análise de grupos de estudos que atuavam na rede social Facebook. Entre os tipos de conexões possíveis de análise (Interação Social, Relações Sociais e Laços Sociais), a professora Cristiane apresentou a análise das interações sociais, através do recurso “curtir”. Para isso, foi utilizado em aula o software para análise de redes Pajek. Pajek é um programa de uso livre desenvolvido pelos pesquisadores eslovenos Andrej Mrvar e Vladimir Batagelj. 

Imagem da página inicial do software Pajek:

Imagem gerada pelo Pajek - Análise da centralizada -> Grau(Degree) -> Todos(Input e Output):

Referências:

KOEHLER, Cristiane. Interação social em redes e nas redes: contributos para uma educação em rede. Tese de Doutorado. Programa de Pós-Graduação em Informática na Educação. Universidade Federal do Rio Grande do Sul. 2016.

RIBEIRO, Antônio Carlos. Entrada e Visualização de dados nos Softwares Pajek e Ucinet. Belo Horizonte. 2013.

[priscilanicolete-blog]

Aula 05/09

[priscilanicolete-blog]

Alguns conceitos sobre a ARS:

25/08

Recursos

*Qualquer bem que posso usar pra trocas. *Recurso é “algo que eu quero”. 

Recursos sociais – usufruir de recursos de meus amigos, tais como: bens, empregos, likes e etc. -> Capital Social.

Recursos pessoais – religião, educação, ocupação.

ARS é um paradigma e não um método

Teoria ou teorias – conceitos

Método, técnicas, procedimentos

Conjunto de pesquisas empíricas

Análise Estrutural

Tipologia da rede

Configuração da rede

Estrutura – ordenamentos estáveis, regularidade instituídas. -> regras, leis, comportamentos comuns.

Análise Ego centrada  

Parte de um ponto – de um ego – e analisa a relação desse nó com outros nós. 

Alters – os nós relacionados com o ego.

Resistência da rede 

É quando mesmo retirando um nó a rede se mantêm. 

Pode significar, também, uma alta coesão – >maior densidade da rede maior coesão. 

Uma rede coesa é uma rede mais fechada.  

Artigos estudados: 

SILVA, Marcelo Kunrath e JR., Rui Zanata. “Diz-me com quem andas, que te direi quem és": uma breve introdução à análise de redes sociais REVISTA USP, n. 92, p. 114-130,  2011-2012. 

FIALHO, Joaquim Manuel Rocha. Análise de redes sociais: princípios, linguagem e estratégias de ação na gestão do conhecimento. Perspectivas em Gestão & Conhecimento, v. 4, n. v.Número Especial, p. 9-26,  2014.   

Efeito Lúcifer - Milgram - Obediência à Autoridade https://www.youtube.com/watch?v=Y-_NDk8HCi0

[priscilanicolete-blog]

[priscilanicolete-blog]

Mapa conceitual do artigo Proposições e controvérsias no conectivismo.

CARVALHO, Marie Jane Soares. Proposições e controvérsias no conectivismo. RIED, v. 16, n. 2, p. 09-31,  2013. Disponível em: <https://ried.utpl.edu.ec/propociciones-controversias>.