questioning-my-identity-element

[questioning-my-identity-element]

lyubashenko's coend for braided finite tensor categories has a hopf algebra structure. the construction of the operations require explicit use of the coend's universal property.

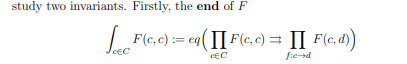
I really wish there was a more intuitive name than end and coend for these sorts of things.

[questioning-my-identity-element]

Do you have any recommendations for learning about algebra beyond high school level? I'm in calculus right now and we just hit definite integrals, if that helps.

sure, ill give a handful of answers depending on your goals.

i would categorize "beyond high school algebra" into linear algebra (which is lower-div college level) and abstract algebra (which is upper-div college level). one could argue that linear algebra is a subfield of abstract algebra, but i am not going to.

linear algebra: lines, planes, hyperplanes, etc can all be fit into essentially the same framework of linear (or affine) equations. think of y=mx+b, except y, x, and b are vectors and m is a matrix. linear algebra is essentially just the study of problems like these and structures that are relevant to their study (e.g., vector spaces). this is inarguably the most important field of mathematics.

abstract algebra: this is a very broad subject which broadly studies structures and the way they interact with other structures. it is hard to get a good feel for abstract algebra without actually doing it, so here is a blog post from my website. you may not be familiar with the notation, but you can find hopefully everything important on the Wikipedia page for sets and functions.

my answer to the question is under the cut. i would encourage other mathblrs to add their opinions though

(A) you want to learn some (but not all) cool algebra without the painful detail

while abstract algebra can be touched with your background, there are certain topics which depend deeply on linear algebra. broadly, this is because linear algebra underlies almost all math. this splits my answer into two parts depending on if (A) you want to learn some (but not a lot of) cool algebra without the painful detail or (B) you want to deeply understand algebra.

try some general audience videos, like from numberphile. generally, videos by good presenters are amazing at teaching you the cool stuff. if you find this to be too little, pick up a lecture series on group theory for undergrads and try your best to follow along. if you can't keep up but still want to pursue it, go to (B).

(B) you want to deeply understand algebra

this is my recommended plan of action:

(1a) pick up some textbook on "discrete math and intro to proofs" (example) and work through a few problems in each section. abstract algebra in general has many prerequisites, and discrete math fills in the vast majority. the topics you should look out for are: proof techniques such as induction, functions and relations, and some basic combonatorics/counting.

(1b) pick up a textbook on "linear algebra and applications" (example) and do the same. i encourage taking a textbook directed at sciences for a few reasons: it's easier, applications can sometimes spark other interests, and most importantly applications give a deeper intuition for the meaning of the math. where possible, try to use your new proof skills to prove the things discussed!

(2) pick up a more serious book on abstract algebra and/or linear algebra and do as many exercises as possible (as in attempt every problem in every section). the standard reference for abstract algebra is dummit and foote but i prefer jacobson. for linear, i would just suggest linear algebra done right

[questioning-my-identity-element]

maybe bings house needed 3 rooms...

[questioning-my-identity-element]

wait good point. im an idiot.

Poll time, but this time linear algebra.

Arguments for any position appreciated!

[questioning-my-identity-element]

there is a standard formula for the determinant given as follows:

for a 0x0, this sum is empty. empty sums evaluate to 0.

edit: no it's not empty you dumbass

Poll time, but this time linear algebra.

Arguments for any position appreciated!

[questioning-my-identity-element]

maybe bings house needed 3 rooms...

[questioning-my-identity-element]

Math enthusiasts of tumblr. What math subjects have you studied and which ones were your favorite? Which ones were your least favorite? Which ones were the hardest?

[questioning-my-identity-element]

bringing this back for those curious about khinchin's constant. i made a post a few years ago.

Let's talk about my favorite constant!

The constant is called Khinchin's constant K_0≈2.685.... Because tumblr isn't LaTeX integrated, I will have to keep the symbolic math to a minimum. It's about continued fractions. I won't go into the proof because it would be too symbolic and make this post even bigger than it already is. I'm gonna try to assume very little going into this. If stuff is unclear, please ask questions. If I am being too obvious, tell me.

So, let's say you had a real number x between 0 and 1. Then, x has a continued fraction 1/(a_1+1/(a_2+1/(a_3+...))), where all of the a_i are positive integers. What can be said about the terms a_i in the continued fraction? One might think...you can't say anything because you don't know what x is. You would be right. So, let's rephrase that question. What can usually be said about the terms in the continued fraction? To which, you may feel inclined to give the same response. But! there's actually a lot you can say about "most real number's continued fractions." So, what properties hold...usually?

Khinchin's constant! Khinchin proved that, if you take a real number x and consider its continued fraction sequence, then the geometric mean of the terms in the continued fraction sequence is usually K_0. That is to say, (a_1*a_2*a_3*...*a_n)^(1/n) usually converges to the same number K_0, and K_0 is Khinchin's constant. This property is perfectly fine to talk about for numbers outside of the interval (0,1) because we just ignore the first integer term outside of the fraction; we still use the same limit when we look at x=a_0+1/(a_1+1/(a_2+...)).

So, what do we mean by usually? For those with some knowledge of measure theory, we are talking about almost everywhere. For those with some probability theory background, we are talking about probability 1. For those without those backgrounds, think about the following. You take a dart and you throw it onto a square dartboard. No matter how well you throw (assuming you don't somehow have perfect aim), the probability that the x-coordinate satisfies the Khinchin's constant property is 1. That doesn't mean that it is always true though! There are an uncountable number of those x coordinates so the probability of hitting say x=1/2 or x=1/3 is 0. What's weirder is that there are an uncountable sets that will be hit with probability 0, like the Cantor set. We say that the sets with probability 0 of being hit almost never occur and those with probability 1 almost always occur.

Okay, so now that we know that this is almost always true. Let's look at some examples of it being true. uh. hm. wait. well, it can't work for rational numbers because that limit isn't even defined because there are only finitely many of those a_i's. It, um, isn't true for e, or quadratic irrational numbers because they have some symmetries that prevent it. Well, how about π? Everybody loves π? Well, frankly we don't know. Fine! It must at least work for Khinchin's constant itself! Actually though, mathematicians haven't proven that the property holds for literally any number beyond those specifically constructed to work. Yet, it's still true for almost all of them.

Okay, fine. It almost always works...but...wait a minute...

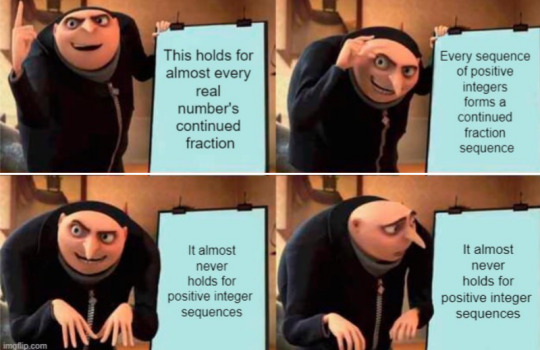
It's true! The probability of a real number having this Khinchin's constant property is 1, but! The probability of a sequence of positive integers having the Khinchin's constant property is typically 0 by the Law of Large Numbers (unless your integer random variable just so happens to satisfy E[log(X)]=log(K₀)). This means that real numbers have some hidden structure that almost guarantees this property.

Now, finally, about that subscript: it does actually mean something. A more general result says that ((a_1^r+a_2^r+...+a_n^r)/n)^(1/r) as n goes to infinity almost always converges to the same constant K_r. It just so happens that as r approaches 0, this becomes a geometric mean and you get Khinchin's constant!

Btw, that Gru meme is from a presentation I made about this. PM me if you want the pdf from the presentation.

[questioning-my-identity-element]

khinchin's constant

do you have a favorite number?

[questioning-my-identity-element]

good point. in that case, i feel like there isn't a good answer to this question, as a straw is in between an annulus and a 2-punctured sphere, which have colloquially a different number of holes.

I’m really into internet discourse but only pointless and stupid internet discourse like how many holes there are in a straw (it’s 2)

[questioning-my-identity-element]

for orientable surfaces with boundary, you can get away with saying the number of 1d holes is n if the first homology is Z^n. you could also ask that the fundamental group is Fn, the free group on n generators. by classification of surfaces, this is fine. both of these are topological (and homotopy) invariants

since the straw is homotopic to a circle, it has no higher dimensional holes. for a straw, n=1.

I’m really into internet discourse but only pointless and stupid internet discourse like how many holes there are in a straw (it’s 2)

[questioning-my-identity-element]

dimension is not preserved under homotopy. straws are essentially very slightly thickened annuli and can be deformation retracted to one of their boundary circles

I’m really into internet discourse but only pointless and stupid internet discourse like how many holes there are in a straw (it’s 2)

[questioning-my-identity-element]

1 is right, but a straw is homotopic to a circle, not a torus. a torus is the surface of a donut, without the inside, which is not the same as a straw.

I’m really into internet discourse but only pointless and stupid internet discourse like how many holes there are in a straw (it’s 2)

[questioning-my-identity-element]

join this if you like math

Mathblr Discord Server

Hi, friends!

@vacuously-true and I found out that there were two Mathblr discord servers recently. While both of these servers still exist, we decided that there should be a single, overarching server for te community.

Therefore, without further ado, introducing:

Least Common Mathblr (LCM)

link: https://discord.gg/JfRj3wxcwX

A discord server for all math enthusiasts on tumblr! Join today!

[questioning-my-identity-element]

i should add: someone on the mathblr discord found a proof that such a ring *DOES NOT* exist when you use normal addition and multiplication, if R is an uncountable field. idk their tumblr username tho.

goal: find a ring (with identity) structure on the set of all finite dimensional matrices over a ring R.

rules:

must somehow be matrix-y

you cannot add things to the set (ie no infinite matrices, no formal linear combinations)

equivalence classes are okay so long as it still satisfies the main goals.

you can choose R as long as it's not a boring choice, but ideally it is generalizable

help

[questioning-my-identity-element]

those functions dont preserve addition

goal: find a ring (with identity) structure on the set of all finite dimensional matrices over a ring R.

rules:

must somehow be matrix-y

you cannot add things to the set (ie no infinite matrices, no formal linear combinations)

equivalence classes are okay so long as it still satisfies the main goals.

you can choose R as long as it's not a boring choice, but ideally it is generalizable

help

[questioning-my-identity-element]

there is an issue with this one i believe. ive tried to make it work. if i remember correctly,

if you quotient out by removing zero rows and columns, then addition is not well-defined.

if you don't quotient out, then multiplication is not well-defined.

goal: find a ring (with identity) structure on the set of all finite dimensional matrices over a ring R.

rules:

must somehow be matrix-y

you cannot add things to the set (ie no infinite matrices, no formal linear combinations)

equivalence classes are okay so long as it still satisfies the main goals.

you can choose R as long as it's not a boring choice, but ideally it is generalizable

help