randomforst

[randomforst]

Social Networks: Theory and Implementation Series Part1

Hi, WTF I have my 3 last exams of my Master’s Degree in AI and one of them is about Social Networks: Theory and Implementation. Or a cooler way to call it: How to hack Tinder(?)

Anyway you can understand how pages rank other webpages, profiles, songs, etc. Lets say NODES.

We can say that the node or page with more recommendations, i.e. better reputation, should be more important than another one with fewer recommendations. If the page with a high reputation recommends another one, then the reputation of this other one will increase and so on. This last page can recommend the first one forming a circularity.

The circularity can be undone with the idea of eigenvalues in which the highest ranked nodes have the highest number of inputs because they are better connected.

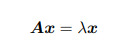
The original PageRank formula

The creators of this idea summarised the PageRank equation of a page (let's call it r(Pi) as the sum of all PageRanks pointing to PiSo we get the following formula, quite simple (for the moment xd).

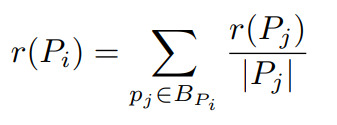
Bp refers to the set of pages pointing in Pi

But the problem is that the value of r(Pj) is unknown and therefore an iterative formula was developed in which r of k+1 (Pj) is taken into account, which corresponds to the PageRank of the page in iteration k+1.

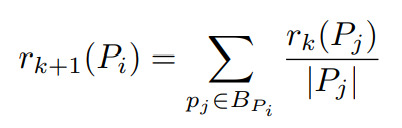
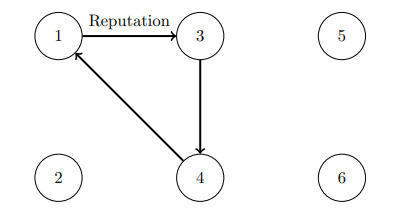
And this equation is usually presented as a Matrix  H. The following graph is represented by the example matrix:

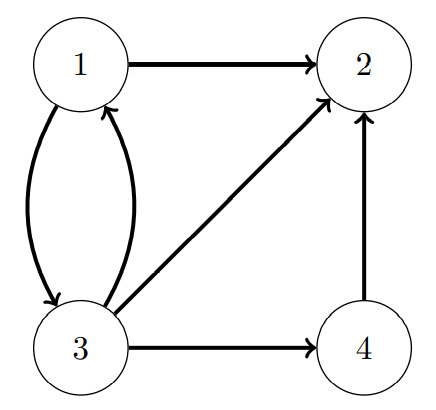
And therefore, we can define the equation as: 

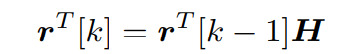
Markov Chains and the Random Surfer

Markov Chains used here. They are a stochastic process where the probability of an event depends exclusively to the previous event. But the main problem is the called dangling node. The dangling nodes are the nodes in network that have no connections and therefore, creates 0 rows. The non-danglin nodes create stochastic rows so the Matrix H is called sub-stochastic matrix.

The Random Surfer is the way the creators of PageRank describe the dangling problem. Where there is a surfer who is going from a page of the internet, and when we arrives to a webpage, he randomly chooses a hyperling and arrives to a new page. He do this process indefinitely. Finally the surfer gets caught when he enters to a dangling node, and as we know the Internet is full of dangling node pages, such as images or pdf files.

To solve this problem, matrix S is defined. A matrix that substitutes H matrix called stochastic matrix S. This matrix S substitutes all the zero rows by 1/n where n is the dimension of the matrix. This guarantees that S is stochastic and then it is the transition probability matrix for the Markov chain.

Finally the S matrix cannot guarantee the convergence result desired. It does not take into account Isolated Convergences and therefore, It is not a primitive matrix.