Don't wanna be here? Send us removal request.
Text
Week 2 - Machine Learning for Data Analysis - Running a Random Forest

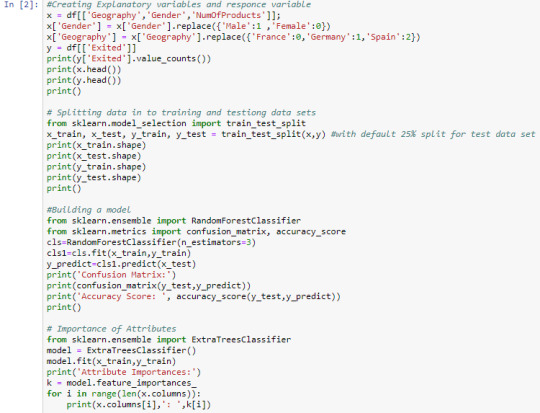
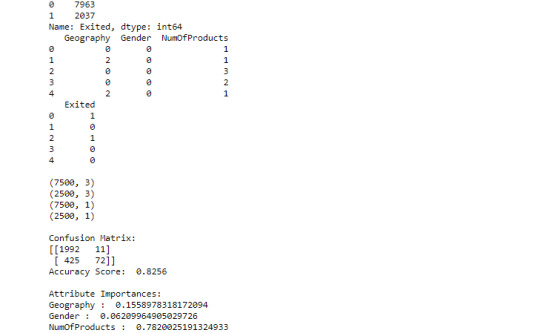
Observations: I built the forest with 3 trees using default 'Gini' criterion. And got the accuracy score around 82%. And also displayed importance of explanatory variables in the forest, which shows the attribute NumOfProducts is having most importance with score 0.79 and Gender is having least importance with score 0.05.
0 notes
Text
Week 1 - Machine Learning for Data Analysis - Running a Classification Tree




Building a model using two explanatory variables



Building a model using three explanatory variables



0 notes
Text
Week 4 - Regression Modeling in Practice - Test a Logistic Regression Model




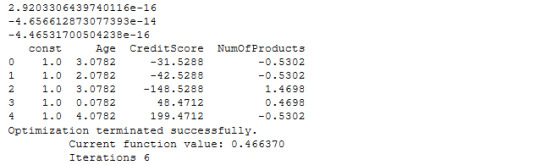





0 notes
Text
Week 3 - Regression Modeling in Practice - Testing a Multiple Regression Model






















0 notes
Text
Week 2 - Regression Modeling in Practice - Test a Basic Linear Regression Model


Testing the association between explanatory variable 'R&D Spend' and response variable 'Profit'.



Observations:
F- Statistic is large and p-value is less than 0.05 so that we can reject null hypothesis and say there is significant association between R&D spend and Profit.
Based on the parameters obtained from the model Profit = 0.8543 * R&D Spend + 112000.
From R-squared value we can say around 94% variability can be observed in response variable Profit.
Testing the association between explanatory variable 'Marketing Spend' and response variable 'Profit'.



Observations:
F- Statistic is large and p-value, 4.38e-10 is less than 0.05 so that we can reject null hypothesis and say there is significant association between R&D spend and Profit.
Based on the parameters obtained from the model Profit = 0.2465 * R&D Spend + 112000.
From R-squared value we can say around 56% variability can be observed in response variable Profit.
0 notes
Text
Week 1 - Regression Modeling in Practice - Writing about Data
Sample: The Iris flower data set or Fisher's Iris data set is a multivariate data set introduced by the British statistician and biologist Ronald Fisher in his 1936 paper ‘The use of multiple measurements in taxonomic problems as an example of linear discriminant analysis’. It is sometimes called Anderson's Iris data set.
Procedures: Edgar Anderson collected the data to quantify the morphologic variation of Iris flowers of three related species. Two of the three species were collected in the Gaspé Peninsula "all from the same pasture, and picked on the same day and measured at the same time by the same person with the same apparatus".
Measures: The data set consists of 50 samples from each of three species of Iris (Iris setosa, Iris virginica and Iris versicolor). Four features were measured from each sample: the length and the width of the sepals and petals, in centimeters. Based on the combination of these four features, Fisher developed a linear discriminant model to distinguish the species from each other.

0 notes
Text
Week 4 - Data Analysis Tools - Exploring Statistical Interactions




Observations: Now we can say that in both the states, New Yark and California, there is a strong positive statistically significant association between R&D Spend and Profit.






Observations: In both the cases we got high chi square value and P-value << 0.05, means that both the tests are statistically significant. And also from means and graphs we can say that the moderator variable does not have any influence on the relation between two variables.







Observations: In both the cases we got high F-statistic value and P-value << 0.05, means that both the tests are statistically significant. And also from graphs we can say that who choose Cardio exercise and diet chart 0 will have good weight loss and who choose weights exercise and diet chart 1 will have good weight loss. That means in the association between Diet chart and Weight Loss, type of Exercise acts as a moderator.
0 notes
Text
Data Analysis Tools - Week 3 - Pearson Correlation
Data set: 50-Startups.csv
Code book:

Hypothesis:
Null Hypothesis H0: There is no association between the quantitative response variable Profit and quantitative explanatory variables R&D Spend, Administration and Marketing Spend.
Alternate Hypothesis Ha: There is a association between the quantitative response variable Profit and quantitative explanatory variables R&D Spend, Administration and Marketing Spend.
Python code:


Observations: Here since Pearson correlation coefficient r = 0.97 and P-value << 0.05 we can say there is a very strong positive statistically significant relation between R&D spend and profit. Since r2 = 0.94 there is a 94% of variability in profit can be predicted by R&D spend.

Observations: Here since Pearson correlation coefficient r = 0.2 and P-value > 0.05 we can say there is a weak positive relation between Administration spend and profit. Since r2 = 0.04 there is only 4% of variability in profit can be predicted by Administration spend

Observations: Here since Pearson correlation coefficient r = 0.74 and P-value << 0.05 we can say there is strong positive statistically significant relation between spend and profit. Since r2 = 0.56 there is a 56% of variability in profit can be predicted by Marketing spend
0 notes
Text
Data Analysis Tools - Week 2 - Chi square Test
Data Set: Churn-modelling.xlsx
Code book:

Hypothesis 1: Explanatory Variable with two levels
Null Hypothesis H0: There is no relation between gender and the customer churn i.e., the variables Gender and Exited are independent.
Alternate Hypothesis Ha: There is a relation between Gender and the Customer churn i.e., the variables Gender and Exited are dependent.
Code:



From the result of chi-square test it is clear that χ2 > 3.84 and P < 0.05 we can reject the null hypothesis and can say the customer churn is statistically related to gender of the customer.
Hypothesis 2: Explanatory variable with more than two levels
Null Hypothesis H0: There is no relation between the number of products holding and the customer churn i.e., the variables NumOfProducts and Exited are independent.
Alternate Hypothesis Ha: There is a relation between number of products holding and the Customer churn i.e., the variables NumOfProducts and Exited are dependent.
Code:


From the result of chi-square test it is clear that χ2 > 3.84 and P < 0.05 we can reject the null hypothesis and can say the customer churn is statistically related to Number of products that customer holds.
Since our explanatory variable NumOfProducts has 4 levels need to go with post hoc test to know which groups are statistically different.



comp1v2 1.0 2.0
Exited
1 1409 348
0 3675 4242
comp1v2 1.0 2.0
Exited
1 27.714398 7.581699
0 72.285602 92.418301
Chi-square value: 656.4492571317394
P-value: 8.841692150752575e-145
comp2v3 2.0 3.0
Exited
1 348 220
0 4242 46
comp2v3 2.0 3.0
Exited
1 7.581699 82.706767
0 92.418301 17.293233
Chi-square value: 1366.5872147076109
P-value: 3.829666674972014e-299
comp3v4 3.0 4.0
Exited
1 220 60
0 46 0
comp3v4 3.0 4.0
Exited
1 82.706767 100.0
0 17.293233 0.0
Chi-square value: 10.695787090007627
P-value: 0.0010737977930260988
comp1v3 1.0 3.0
Exited
1 1409 220
0 3675 46
comp1v3 1.0 3.0
Exited
1 27.714398 82.706767
0 72.285602 17.293233
Chi-square value: 358.3728983487756
P-value: 6.36623788337487e-80
comp1v4 1.0 4.0
Exited
1 1409 60
0 3675 0
comp1v4 1.0 4.0
Exited
1 27.714398 100.0
0 72.285602 0.0
Chi-square value: 148.35121066056206
P-value: 3.975197582728242e-34
comp2v4 2.0 4.0
Exited
1 348 60
0 4242 0
comp2v4 2.0 4.0
Exited
1 7.581699 100.0
0 92.418301 0.0
Chi-square value: 620.4847809929802
P-value: 5.865690173058868e-137

0 notes
Text
Data Analysis Tools – Week 1 – ANOVA
Data Set: diet_exercise.xls
Code Book:

Hypothesis 1:
Null Hypothesis H0: There is no association between type of exercise and amount of weight loss (Means are significantly equal i.e., μcardio = μweights).
Alternate Hypothesis H1: There is a significant association between type of exercise and weight loss (Means are not significantly equal).
Hypothesis 2:
Null Hypothesis H0: There is no association between type of diet chat and amount of weight loss (Means are significantly equal i.e., μA = μB = μC = μD).
Alternate Hypothesis H1: There is a significant association between type of diet chart and weight loss (Means are not significantly equal).
Python Code:




From the OLS Regression Results F-statistic = 16.58 and P-value = 0.000221.
Since p-value << 0.05 we can reject null hypothesis.
That is there is a significant association between type of exercise and weight loss.


From the OLS Regression Results F-statistic = 9.477 and P-value = 0.0038.
Since p-value << 0.05 we can reject null hypothesis.
That is there is a significant association between type of diet chart and weight loss.
Tokay’s Honesty Significant Difference Post Hoc Test:

From above table we can say there is a significant difference between μA and μB & μA and μC i.e., μA ≠ μB and μA ≠ μC. And means of diet charts B and C are not much significantly different. Statistically both B and C charts results approximately same weight loss.
0 notes
Text
Week 4 Assignment - Visual Analysis
Data Set: Churn_modelling.csv
Research Question: What are the customer related factors associated with customer churns of the bank?
Importing Libraries and Reading Data Set:

Checking for missing data:

Uni-variate Analysis:




Observation: Above distribution is uni-modal and skewed right. From the histogram we can clearly say that there are more number of middle aged persons present in the bank.


Observation: Bank is having slightly more male customers than female customers.


Observation: Above analysis says that the bank is holding more number of customers from France.


Observation: CreditScore distribution is Unimodal and left skewed as there are higher frequencies at greater credit scores (Right side).


Observation: Here we can say that the bank is having a good number of customers with 5+ years of tenure.


Observation: Estimated salary is having Uniform distribution.
Bi-variate Analysis:
Here the response Variable ‘Exited’ is Categorical and coded with 0 and 1.
Since the response variable is having two possible values as per requirement steps to be considered are
Step 1: Convert the response variable as type number.
Step 2: If exploratory variable is not categorical perform the binning for it.
Step 3: Display Categorical Vs Categorical chart.



Observation: Female customer churn is more than male customer churn.


Observation: Old aged people are more likely to leave the bank.


Observation: Customer churns are more in Germany.
0 notes
Text
Week 3 Assignment
For week 3 assignment i have selected a new data set and framed a new research question as this data set is having more scope to explore
Data Set: Churn_modelling

Research Question: Is Customer churn is associated with Customer personal information such as age, Gender, geography, tenure, Salary and number of products he is holding in bank?
My Program:
Cell 1: Importing pandas, reading data set and displaying all variables in the data set.

Cell 2: Checking for missing data in the data set.

Cell 3: Frequency Distributions of some of selected variables

Cell 3 output:
Geography Frequency Distribution Germany 2509 France 5014 Spain 2477 Name: Geography, dtype: int64 Gender Frequency Distribution Male 5457 Female 4543 Name: Gender, dtype: int64 Tenure Frequency Distribution 2 1048 1 1035 7 1028 8 1025 5 1012 3 1009 4 989 9 984 6 967 10 490 0 413 Name: Tenure, dtype: int64 Age Frequency Distribution 24 132 32 418 40 432 48 168 56 70 64 37 72 21 80 3 88 1 25 154 33 442 41 366 49 147 57 75 65 18 73 13 81 4 18 22 26 200 34 447 42 321 50 134 58 67 66 35 74 18 82 1 19 27 27 209 35 474 43 297 ... 60 62 68 19 76 11 84 2 92 2 21 53 29 348 37 478 45 229 53 74 61 53 69 22 77 10 85 1 22 84 30 327 38 477 46 226 54 84 62 52 70 18 78 5 23 99 31 404 39 423 47 175 55 82 63 40 71 27 79 4 Name: Age, Length: 70, dtype: int64
Cell 4 and 5: Creation of secondary variable and its frequency distribution

Cell 6 and 7: Grouping Age variable and its frequency distribution.

0 notes
Text
Week - 2 Assignment
My Program:

Output:



As the value_counts() function is having dropna = Flase, if the data set has any null values it might been shown in the output. Then we can say the data set does not have any missing values.
The class values are having equal frequency distribution. Each class has 50 observations.
0 notes
Text
Data Set Selection, Research Question and Hypothesis.
Step 1:
Data set selected: Iris Data Set.
Step 2:
Topic of Interest: Species of iris flower.
Step 3:
Code book for selected topic:

Step 4:
Second topic: Length and Width of the Sepals and Petals.
Step 5:
Addition of the second topic variables to code book

Step 6:
Literature Review:
The Iris flower data set or Fisher's Iris data set is a multivariate data set introduced by the British statistician and biologist Ronald Fisher in his 1936 paper ‘The use of multiple measurements in taxonomic problems as an example of linear discriminant analysis’. It is sometimes called Anderson's Iris data set because Edgar Anderson collected the data to quantify the morphologic variation of Iris flowers of three related species. Two of the three species were collected in the Gaspé Peninsula "all from the same pasture, and picked on the same day and measured at the same time by the same person with the same apparatus".
The data set consists of 50 samples from each of three species of Iris (Iris setosa, Iris virginica and Iris versicolor). Four features were measured from each sample: the length and the width of the sepals and petals, in centimeters. Based on the combination of these four features, Fisher developed a linear discriminant model to distinguish the species from each other.

Step 7:
Research Question:
Is Iris Species is associated with length and width of the Sepals and Petals?
Hypothesis:
The Iris species type is associated with length and width of the Sepals and Petals.
1 note
·
View note