sparseposter

[sparseposter]

intuition for the central limit theorem

the central limit theorem is a frankly magical theorem. i'll assume everyone reading this post is familiar with it, i'm speedrunning out my thoughts, i don't want to spend too much time on this. but basically yeah why should everything add up to the normal distribution? why should the mean of basically everything be normal?

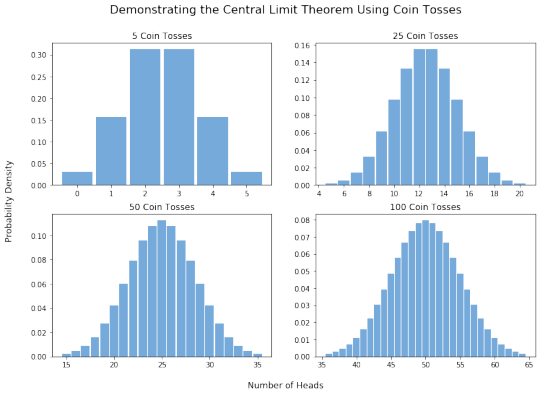
so this bothered me for a long time, it was always kinda insane. i learned about it, and then a while later i learned how to prove it, but i still didn't get it. but then i watched some 3B1B videos (all kudos to them btw) and then specifically i saw this one comment on a video and it all clicked.

basically: what's so special about the normal distribution? like, why *that* one in particular?

well, there's this other property of normal distributions, which may seem unrelated at first but is actually the key to the whole thing: if you add two normal distributions, you get another normal distribution.

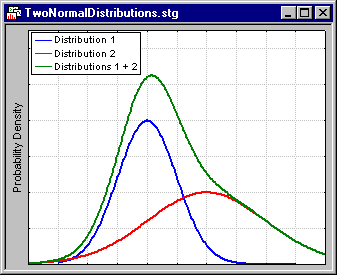
and this is the key to the whole thing! because it means that, when you're doing sums of random variables, normal variables are a *fixed point*.

so at least for me this instantly finally made everything click - things converging to fixed points is just so incredibly natural, it comes up everywhere. to go into a little more detail, distributions where if you add two of them together you get a third one of the *same type* are called stable distributions, and it turns out that the normal distribution is special among stable distributions because it's the unique one with finite mean and variance - all the others, Cauchy, Levy, etc. don't satisfy this condition. i don't understand why but yeah. so then it makes intuitive sense that - if you keep averaging lots and lots and lots of variables which have finite means and variances together and converge to anything at all - it *must* be to the only fixed point which has finite mean and variance: the normal distribution.

[sparseposter]

mission statement

ramble about random mathematics infrequently, to-do