#Trigonal trapezohedron
Explore tagged Tumblr posts
Text

0 notes
Text
Polyhedron of the Day #140: Truncated triangular trapezohedron


The truncated trapezohedron is the first in an infinite series of triangular trapezohedra. It has 8 faces (6 pentagons, 2 triangles), 18 edges, and 12 vertices. It is also known as Dürer's solid, as it appears in Albrecht Dürer's engraving Melencolia I (1514). It is obtained by truncating two opposite vertices of a cube (distorted through stretching to have rhombic faces), trigonal trapezohedron, or parallelepiped. Its dual is the gyroelongated triangular bipyramid.
Image created by Tomruen, CC BY-SA 4.0, https://upload.wikimedia.org/wikipedia/commons/a/a3/Triangular_truncated_trapezohedron.png.
Weisstein, Eric W. "Dürer's Solid." [Image] From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/DuerersSolid.html.
15 notes
·
View notes
Text
Skew dice
The OpenSCAD code is on GitHub.
Background
Henry Segerman had some skew dice at his talk at the Mathematics Insitute in Oxford in January.

He talks about them in this video: https://www.youtube.com/watch?v=OI5njPo7zC0 and this one https://www.youtube.com/watch?v=uAnCL3vhVIs
Although they look weird, the dice are fair because the shape is isohedral (and equidistant from the centroid) so the chance of landing on any face is the same.
Net work
The solid is a trigonal trapezohedron and the net of the dice is composed of 6 identical quadrilaterals with two adjacent equal sides eg: (Wikipedia)

I started by seeing if I could at least generate the net. For the net, the common face can be defined as a perimeter. The only constraint on the perimeter of the quadrilateral is that two adjacent sides have the same length [otherwise the net cannot be folded because side lengths won’t match]. With this constraint, only three parameters define the shape, eg 2 angles and a side. This function solves the quadrilateral by closure:
function trapezium(B,C,c) =
let (p = [[1,B],[1,C],[c,0]]) let (t= peri_to_tile(p,true)) tile_to_peri(t);
The net can be constructed by creating a pair of tiles and tesselating three of these units. The net defined by B=80, C=90 and c=1.3 is

This net is more symmetric than the one in wikipedia and shows the 2 tile rep unit which tesselates:

The parameterisation reduces to more symmetric forms:
(A,180-A,1) - rhombic face constructing a trigonal trapezohedron (rhombic hexahedron)

(90,90,1) - a cube

The code to create an SVG net is on Github. It turns out that a different net configuration is easier to assemble. However, when I printed and folded up a skewed net like the one below, the faces are curved. Clearly there is the additional constraint that the faces of the solid are planar but I couldn’t see what added constraint on the perimeter was needed. A discussion on the OpenSCAD Forum helped me see that the curved faces of the apparently well-formed solid were due to the elasticity of the sheet material under small deviations from the geometry. The resultant objects were quite interesting however and I spent some time making them from mirror card. I’d like to make one from polished metal.


Even with a planar net, I still have the problem of an algorithm for folding it up to a solid. I have code to generate the net of a polyhedron from the solid and the code also folds and unfolds the net, but to do that I need the dihedral angles between the faces.
Solid geometry
So I gave up and looked around on the web some more and finally found the geometry on Reddit from Dr Paul Matthews of Nottingham University. Cast into OpenSCAD :
// Initial point x0 = 1; y0 = 0.9; z0 = 0.7;
m1= [[1,0,0], [0,-1,0], [0,0,-1]]; // 180 rotation about x axis t=2*180/3; c=cos(t); s=sin(t); m2= [ [c,s,0], [-s,c,0], [0,0,1]]; // 120 rotation about z axis
p0= [x0,y0,z0]; //Ensure 4 face points are coplanar z = z0*(-s*x0+(c-1)*y0)*x0/((c-1)*x0+s*y0)/y0;
p1= m2 * p0; p2= m2 * p1; p3= m1 * p0; p4= m2 * p3; p5= m2 * p4; p6 = [0,0,z]; p7 = [0,0,-z]; unit_vertices = [p0,p1,p2,p3,p4,p5,p6,p7];
Initial openSCAD code creates the basic shape, this one printed in bronze PLA. It looks like the faces are not planer but they are.

I was stalled for a while on arranging the pips evenly on the face, but finally realised that instead of trying to fit a rectangular array of pips to the skew face, I could compute the pip positions in relation to the corners of each face: the seven pips being the centroid, intermediates between the four corner and the centroid, and between pairs of these new corners. Parameters determine the size of a pip, their inset from the outer edge and the depth of indentation.

Code on Github
The values of the initial point determine how skewed the die is. I rather think it looks more interesting if it is just noticably off-cube, only just wrong, eg.(1,0.5,0.4)

I put an entry on Thingiverse but the customiser doesn’t work.
I look forward to printing a pair when I’m back at home.
Padstow Harbour, August 2020
7 notes
·
View notes
Text
The arrived and the d5 isn't as interesting as I thought it might be, it's just a triangular prism rounded to fit a sphere, I'm not entirely sure if it's going to be fair though, this video found by trial and error a fair dice with triangular side length of 20mm and rectangle length of 12.5mm, while mine has ~30mm and 17mm respectively, which would make it slightly shorter (should be 18.75mm proportionally) and give the 5 and 1 higher chances, however I don't know what the rounding will do to that now the faces are 5 circles that look like they're the same size as each other.
The d7 is a weird shape, I'm pretty sure it's a variant of a diminished trigonal trapezohedron (see below), which has 3 deltoid faces and 4 triangular ones, again intersected with a sphere to make the faces circles. I sort of expected it to be chiral from the picture on amazon but no it does have symmetry.

I actually think the weirdest shape is the d16 though, I have no idea what it's called but it seems to have 4 equilateral triangle, 4 rhombus, and 8 irregular pentagon faces unless an edge has gone missing in the rounding somewhere.
The others are all pretty regular shapes so they should be fine. Also I was right about the d24, most of them are tetrakis hexahedra, while this one a deltoidal icositetrahedron, which I think is a much better shape for a dice because it's more round and the vertices are less different to each other.
Ok I saw this on amazon for cheap and had to get it

I particularly want to see how that truncated d8 and rhombic d12 roll compared to the standard ones, I also can't tell what d24 they're using, most of them seem to be tetrakis hexahedra, but this looks like it could be a deltoidal icositetrahedron.
The d5 and d7 are... interesting lets say, I roughly know the method of approximately finding 5 or 7 equally spaced points on a circle and flattening at those points, but it's still weird, I want to check their fairness. (I guess the same method goes for the d100, I can't think of any 100-sided isohedra)
4 notes
·
View notes
Photo






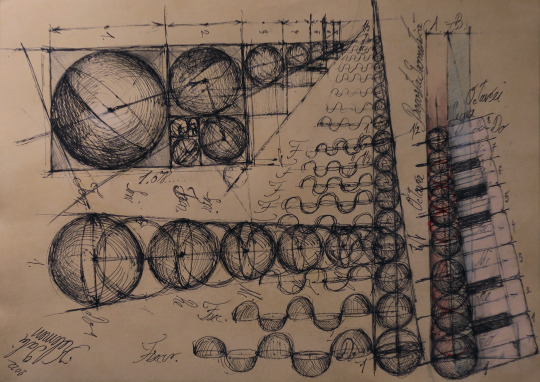
Flower of life pentagon octave
#Trigonal trapezohedron#Polyhedral cosmic octave#cosmic octave#KLMN CODEX#Flower of life pentagon octave#The Universal Hermetic Harmony Principle#harmonic series
4 notes
·
View notes
Photo

Flower of life pentagon octave
2 notes
·
View notes
Photo

Trigonal Trapezohedron octave secret
2 notes
·
View notes
Text
Skew die net
Following the post on the skew die, I thought I should make a net version to allow the die to be constructed from paper. Perhaps not a very practical die to throw but it would be simple to make. I also plan to use the net (or one of its isohedral faces) as a pattern for an asymmetric trigonal trapezohedron in glass or acrylic.
The OpenSCAD script is on Github. It’s a bit long-winded to use because the svg for the net is output as text to the console, so you have to set the parameters, run the script, copy the svg text, paste to a file, save and then view in a browser - sorry :)
Here is a typical parameterization:
x0 = 1; y0 = 0.7; z0 = 0.4; scale=8; pip_size=5; pip_inset_ratio = 0.4; line_width=0.1;
and its net: (also as SVG)

and this is the die assembled:

I was initially surprised by the dihedral angles: 6 of one value, 3 of another and 3 of a third. I expected them to be more symmetric but of course two sides are the same length, so I guess these edges have the same angle.
0 notes

