#Trigonometric Expression sin(pi-x)

[sstonki]

Exponential graph equation maker

Note that the first function is sin(a*x). You can also enter an exact value into the box at the top of the slider, followed by the GRAPH button or the Enter key.įor example, in the chart above, press 'reset'. When you enter your equations, you can refer to up to four variables that are controlled by sliders.Īnd you can adjust the value of each variable by moving the slider up or down. However, if you change the axis limits, this may no longer be true. The initial range of values on the x and y axes are in the same ratio, so a graph of y = x will be at 45°,Īnd circles would be round, not squashed into ellipses. The aspect ratio (ratio of width to height) of the graph window is exactly 4:3. GFE will check to ensure that the lower value is at the bottom of the y axis or the left of the x-axis. To change them, simply edit them in place and press GRAPH or the Enter key again. If you enter a value that is off the graph, the cursor will not show,īut the values of the functions for that x value will be displayed correctly.Īt each end of the x and y axis is a box containing the end values. You can enter the x value for the cursor manually into the text box in the upper left.Īfter entering a value press "Graph" or the enter key. It shows the values of each function where the cursor intersects that function. If you click on "show cursor", a thin vertical line appears. If left unchecked, each function is shaded in a different color. This allows you to more easily see where complex functions overlap, since the more overlap there is, the darker the shading. If this is checked, the shaded areas for all three functions are all the same light gray. When plotting inequalities, the "monochrome shading" checkbox can be used. The area of the graph where y is greater than the function value is shaded. The function will be plotted as a line as usual. GFE can be used to plot inequalities by changing the relational operator in the pull-down menu to the left of the function. It is best to always enter the correct expression yourself. It will add two extra closing parentheses so they balance and evaluate it as 2+(sin(x)) Note: This may not always produce the desired result. When you press GRAPH or enter, it will automatically add enough closing parentheses to balance them. You may have meant it as one over 2sin(x). Since there are no parentheses, it is executed from left to right so it sees it as one half of sin(x). For example if you enter 1/2sin(x) GFE inserts a multiply between the 2 and the sin. It will not work if the function is preceded by a variable name. For exampleģcos(2.1) will be automatically treated as if you entered 3*cos(2.1): three times the cosine of 2.1. If a function (such as sin() ) is preceded by a number, GFE assumes you want to multiply them. See PI definition for more.įor example you could enter sin(pi) or e^2.1 There are two constants you can refer to. Returns the smallest integer greater than or equal to x Returns the highest integer less than or equal to x Returns x rounded off to the nearest whole number Returns the absolute value of x (always positive or zero) The power to which you must raise e to get x.Į (approx 2.718) raised to the power of x. The power to which you must raise the 10 to get x. The trigonometry cotangent function, x in radians. The trigonometry cosecant function, x in radians. The trigonometry secant function, x in radians. The trigonometry tangent function, x in radians. The trigonometry cosine function, x in radians. The trigonometry sine function, x in radians. The function names are not case sensitive.Īll trigonometric functions operate in radians. GFE has the following built-in functions.

[sanguinarysanguinity]

Navigatio Britannica: Planar Trigonometry

Chapter 4: Of Trigonometry, Sections I - V

The first half of this chapter is Planar Trigonometry, which I learned in high school and have used on-and-off ever since; the second half of this chapter is Spherical Trigonometry, which I know nothing about. Consequently, I’m dividing this chapter into two parts -- before we let John Barrow attempt to teach me spherical trig (wish me luck!), I want to do a fast recap of what he has to say about planar trig...

Section I: Definitions

Everything is defined geometrically, on the unit circle, via a diagram that I have yet to find in this scan. (Also, even if I do find the page, I don’t have much hope that it will have been scanned correctly, since Google’s scanning machine can turn pages but not unfold them.) Happily, Barrow is pretty good about describing his figures in enough detail that I can reconstruct them as I go, which is the only reason I was able to understand anything in this chapter.

Not many surprises here, although I did learn that cosine, cotangent, and cosecant are the sine, tangent, and secant of the complementary angle, and likewise that the tangent of an angle is called the tangent because its physical instantiation lives on a line tangent to the circle. Also, Barrow defines the Verse-Sine, which was new to me: geometrically, it is the part of the radius that isn’t the cosine. (Algebraically, it is 1 - cosine.) Wikipedia says the versine was important to navigation, so I assume it will come up later.

Section II: Geometrical Constructions of the Tables of Sines, Tangents, Secants, &c.

In which we are instructed to build ourselves a unit circle, mark it off in 1-degree intervals, and construct ourselves a... well, it’s gonna look a bit like a ruler, but it’s going to measure 1 to 90 degrees, on several parallel scales: chords, sines, versed-sines, tangents, etc. To make this thing, you use your compass and measure the length of a chord for a 10-degree angle, then mark it on your chords-scale, and label it “10 deg.” Repeat for the other 89 degrees, and ta-dah, you have a chords-scale! Then do it again for sines, versed-sines, tangents, and so on. When we get to actually solving trig problems, how to use this scale is one of the three standard methods that Barrow is going to teach us.

Section III: Arithmetical Constructions of the Tables of Sines, &c.

First off, Barrow reassures us this is going to be easy-peasy, no need to panic -- which is our first cue that panicking will be required before we’re done.

But true to his word, Barrow starts out easy, using similar triangles to prove all the basic trigonometric identities: tan = sin/cos, sec = 1/cos, etc. All well and good, except it’s all done in proportions and nothing is called out by name, only by referring to various line-segments in his nowhere-to-be-found unit circle diagram. All of which makes it difficult to absorb at a glance, but once you finish decoding everything this is basically just SOHCAHTOA.

Then he proves two variants on the standard trigonometric sum/difference formulas (although he expresses them as proportions and via verbal descriptions, talking about the means of equi-different angles and the differences between them): 

cos x = (1/2) (sin y + sin (y + 2x)) / sin (y + x)

sin x = (1/2) (sin (y + 2x) - sin y) / cos (y + x)

You can verify those via the standard trigonometric sum/difference identities if you want. (I did.) But they’re also pretty straightforward geometrically, if you take the time to very carefully reconstruct what his diagram must have been: in the end, it’s all just similar triangles. He then proves several corollaries -- which in hindsight are simple enough (just straightforward algebraic manipulations, multiplying everything by two, or both sides by the denominator), but sadly, I lost MANY HOURS to a rash of typos in them.

Then. 

Oh, then.

All hell breaks loose as he endeavours to prove that a semi-circle has an arc-length of pi. I admit to not following this bit: I haven’t seen Newton’s notation for calculus since I was seventeen, when that one weirdo physics professor used it in lectures, and I didn’t really feel like re-teaching it to myself for this. Nor did I really want to get into re-teaching myself binomial expansions. Also, the type-face on all the fractions in the expansions was super-squinchy to read, and you know what, fuck it, I think it’s well-established that a semi-circle has an arc-length of pi, let’s move on.

The point of establishing that a semi-circle has an arc-length of pi is so that we can calculate the arc-length of one minute (simply divide pi by 10,800 minutes, easy-peasy), which we will then use as an approximation of the sine of one minute. ... Which, okay, I suppose if your angle is small enough and your applications are practical enough you can get away with that? But it makes the mathematician in me cry, I’m just saying. (Even as I admit that you really can get away with it for most purposes: according to my handy-dandy TI-84 Plus, pi/10800 differs from sin(1′) in the ninth significant digit. But Dr. Roberts and Dr. Chrestenson would never have let me get away with that shit, never mind that I also have an engineering degree and thus should be okay with this kind of ruthless practicality. In my soul there is a mathematician and an engineer battling to the death over questions like these, you simply don’t know how much shit like this wounds me.)

Anyway, once I finally got over my fit of vapours...

Now that we have an approximation for the sine of one minute, we can calculate the cosine of one minute via the pythagorean trigonometric identity, and then...

And now I want to cry again, because now we get to build our table of sines (and along with it, our table of cosines), minute by freaking goddamn minute, by using the above equations like so:

2 cos (1′) sin (1′) - sin (0′) = sin (2′)

2 cos (2′) sin (2′) - sin (1′) = sin (3′)

2 cos (3′) sin (3′) - sin (2′) = sin (4′)

...

Continue until I cry blood and the seas boil dry.

(At one point Barrow admits that it’s possible to build this table in 5-minute increments and interpolate the intervening minutes when you need them. While this reduces the task to 1/5th of the original, I still want to hug and rock myself and cry.)

Happily, I don’t need to cry, because Barrow includes these tables in the book? But someone cried blood to make those tables, and John Barrow wants us all to know it.

Section IV: Actual Trigonometry Problems, At Long Last!

A ton of sample problems, all worked three ways:

Geometrically: Basically, use a compass and straight edge and your scale-thingie of chords/sines/secants that you made earlier, and draw a triangle of  the correct proportions. Then just read/measure your answer right off the actual triangle in question, ta-dah! No abstract math required, just pretty pictures!

Arithmetically: What you learned in high-school, using the tables that someone cried blood over but without calculators (although you can use logs if you want to skip ahead to chapter five for them!) God, it looks miserable and grindingly awful, and I admit I don’t have the strength of character to follow any of these calculations through to the end.

Magic, I mean, Gunter’s Scale: The instructions here are amazingly low-key -- use your chart-dividers (what tumblr calls a pointy-leg-man what it likes to make walk on tippy-toes across charts) to measure off an interval on one scale, and then drop that same interval across the appropriate second scale, and voila! You have found your answer!

Of course I wanted to know what this magical tool is!

Apparently it was a slide rule without the slidey parts -- you used your dividers to accomplish what the slidey bit does on a slide rule -- but with some extra scales especially chosen for the convenience of navigators. 

Apparently these things were so common among navigators that they were simply called Gunters, and I WANT ONE SO BAD. Here’s a nifty article about them, complete with pictures, and did I say? I WANT ONE SO BAD. I collect old-school mathematical tools and I WANT ONE SO BAD.

Ahem.

Anyway, Section V is more trig homework, except now we’re no longer dealing with right triangles. I admit it, I skimmed this like fuck.

And ta-dah! That’s Planar Trigonomometry, according to John Barrow in Navigatio Britannica, or, A Complete Guide to Navigation, pub. 1750!

Up next: Section VI - Spherical Trigonometry, what makes William Bush cry. Do I have the fortitude to teach myself spherical trig? PLACE YOUR BETS NOW.

[jadagul]

I sometimes forget how common the "simplify your answers" mantra is in math classes.

My students are always so confused when I tell them I don't want them to "simplify" their derivatives after taking them.

I think requiring simplification is often defensible in a few situations. The big advantage is that it forces practice on the steps involved in the simplification---that is, requiring all answers to be "simplified" forces people to practice doing basic algebraic manipulations.

And for that reason, when I teach calculus I require trigonometric and logarithmic expressions to be simplified, so that people get used to knowing what ln(e^3) and sin(pi/3) mean.

Second, sometimes it's useful to require people to jump through formatting hoops just to learn how to: the ability to deliver exactly what your boss/client/whatever asked for is actually pretty useful in life. But this also doesn't need to be every assignment.

Third, simplifying answers can in some cases make problems easier to grade, because it requires everyone to put the answers into the same format.

But there are a few reasons I don't like requiring simplification in most cases. One is that it often feels like busywork---if I'm testing your ability to take a derivative, and you can take the derivative, I don't want to find myself taking off points because you didn't describe it the way I want. (I'd really like my students to internalize the idea that (x-3)(x-2) and x^2-5x+6 are the same thing).

Second and related, "simplification" is often fairly arbitrary. The exemplar here is the high-school rule that you can't have any radicals in the denominator. Is (sqrt(5)+1)/4 really simpler than 1/(sqrt(5)-1)? So if you're docking points for lack of simplification

And third is the counterpoint of the third argument above: sometimes simplification makes things harder to grade. If you leave your derivative unsimplified it's easy for me to check what you did and where you might have screwed up. I'd way prefer to grade quotient rules left in the form (x dy - y dx)/y^2 to grading ones with those things multiplied out and factored and canceled, because that reflects your actual thought processes and work better.

And god forbid I ask anyone to simplify answers to the massive seven-layer-deep chain rule problems I like to give.

[mathematicianadda]

Simplify $\tan^{-1} ( \frac{x-\sqrt{1-x^2}}{x+\sqrt{1-x^2}} )$ with trigonometric substitution https://ift.tt/eA8V8J

I will explain my approach, help me with the last step please! $$ \tan^{-1} {\left(\frac {x - \sqrt {1-x^2}}{x + \sqrt {1-x^2}}\right)}$$

substituting x = $\sin \theta$ (as learnt from book) and solving 1-$\sin^2 \theta$ = $\cos^2 \theta$ $$ \tan^{-1} {\left(\frac {\sin \theta - |\cos \theta|}{\sin \theta + |\cos \theta| }\right)}$$

For solving modulus, it was important to determine range of $\theta$ , therefore I defined it (as it is my variable,i can define it my way) for [-$\pi$/2 , $\pi$/2] so that sine covers all values from $-1$ to $1$ (as , $ -1 \le x \le 1 \,$ , from domain ) and $\cos \theta$ is positive , and hence $|\cos \theta| = \cos \theta$.

$$ \tan^{-1} {\left(\frac {\sin \theta - \cos \theta}{\sin \theta + \cos \theta }\right)}$$ = dividing by $\cos \theta$ $$ \tan^{-1} {\left(\frac {\tan \theta - 1}{\tan\theta + 1 }\right)}$$

= by formula of $\tan (\theta - \pi/4)$ $$ \tan^{-1}( \tan{\left(\theta - \pi/4\right)})$$

That's where I am stuck ,as according to the identity,$\quad$ $tan^{-1} ( \tan \alpha) = \alpha$ $\quad$ only when $\, -\pi/2 <\alpha < \pi/2$ . But here $$ -3\pi/4 \le \,(\theta-\pi/4) \, \le \pi/4 $$ Therefore, I am not going to get ($ \,\theta - \pi/4 $) out of the expression. What i get will be based on that graph of $\bf {\tan^{-1} (\tan x)}$ . $$ (\theta - \pi/4) +\pi \,$$ for $\,-3\pi/4 \le \, (\theta -\pi/4) \, < -\pi/2 \,\,$ and

$$\theta -\pi/4$$ for $\,-\pi/2 < \, (\theta -\pi/4) \, \le \pi/4 \,\,$

My teacher just cancelled arctan and tan and wrote $\theta - \pi/4$ and he didn't even include that modulus function over $\cos \theta$.

So what will be the exact answer because if everyone decide $\theta$ as per they like then there will not be a finite answer. Everyone will have their own answers and in each answer they have multiple cases as I just discussed above.

So please help me, very hopefully I signed up in stackexchange!

Found Solution :-

I was confused because I was thinking that there can be many solutions differing person to person, but even if you choose any value of $\theta$ , you are going to get two solutions which are in the asked question above. The problem resolves when we write $\theta$ in terms of $sin^{-1} x$ as then we would not simply write like $$ \theta = \sin^{-1} x $$ we would write an equation,$$ \sin^{-1} x = \sin^{-1} (\sin \theta)$$, now if $\theta$ is not in range of $-\pi/2$ and $\,\pi/2$ , then there would be some constant in $\pi$ (like , $\pi/4 , 2\pi$ etc. we would have to add or subtract according to the graph of 'sin inverse sin' and when we would put that value of $\theta$ , we would end with the solutions as answered by people. (I write the answer in this edit to help anyone who will reach here after searching web , thanks to everyone for answers)

from Hot Weekly Questions - Mathematics Stack Exchange Aryaman from Blogger https://ift.tt/32uV1PE

[enetarch-math]

Chapter 7.1 & 2 - Trigonometry

Triangles are everywhere. They are the worlds strongest structure. They form boxes and circles; cubes and spheres.  They are used to represent the location of 3 objects in relationship to each other.  So, in this next segment of the Math blog, we will look at how algebraic equations use trigonometric functions.

Let’s start by reviewing the basics on trigonometry.

Triangles

A triangle always has 3 sides.  Always!

The sum of the interior angles of a triangle always equal 180 degrees.

There are 3 special types of triangles:

Right Triangles .. A triangle with a 90 degree corner

Isosceles Triangles .. 2 angles and 2 sides are the same.

Equilateral Triangles .. 3 angles and 3 sides are the same.

Acute and Obtuse triangles are not special, as they can be turned into 2 right triangles.  They describe how a triangle is viewed, and state that one of the angles in the triangle has an angle greater than 90 degrees.

An acute triangle’s longest edge is displayed as the base.

An obtuse triangle’s longest edge is not the base.

The length of any side of a right triangle can be found as long as you have 2 things

The lengths of 2 sides of a triangle

A length of a side and an angle

All 3 angles created by the legs of a triangle can be found with 2 pieces of information.

The lengths of 2 sides of a triangle

A length of a side and an angle

The angles from 2 corners

Terminology

As mentioned, a triangle has 3 sides (or 3 segments).  These sides have specific names and letter abbreviations.  They are most often used in right triangles to describe the angle and sides being worked with.

Hypotenuse .. (h) .. is the longest edge along a right triangle.

Opposite Side .. (o) .. is the edge opposite the angle in a right triangle. 

When drawn on graph paper, this segment of a triangle runs along the (y-axis).

Adjacent Side .. (a) .. is the edge that runs adjacent to the angle in a right triangle.

When drawn on graph paper, this segment of a triangle runs along the (x-axis).

The right angle is represented by a box in the bottom right corner of the triangle.

The angle we will be considering through this series of posts, is in the bottom left corner, represented as a pie slice or wedge.

Equations

Before we get into the functions of triangles, let’s look at some basic equations that are used with right triangles.

The equation of a line:

y = mx +b

(m) represents the (rise / run) of line (or segment) drawn as the hypotenuse (h) of the triangle.

(x) represents that length or run of the adjacent (a) side of a right triangle.

(y) represents the height or rise of the opposite (o) side of a right triangle.

Pythagorean’s Theorem states that you can find the length of the hypotenuse (h) if you know the lengths of the adjacent (a) and opposite (o) sides of a triangle.

h^2 = a^2 + o^2

These equations describes a circle and an ellipse respectively:

r^2 = (x - i)^2 + (y - j)^2 1 = ((x - i)^2) / a^2 + ((y - j)^2) / b^2

Note: if you look closely at these equations and pythagorean’s theorem, you will see how the a^2 and o^2 have been extended.  Example: a^2  = (x - i)^2

These equations are they hyperbolic functions of a circle and ellipse respectively:

r^2 = (x - i)^2 - (y - j)^2 1 = ((x - i)^2) / a^2 - ((y - j)^2) / b^2

Note: the only difference is the ( - ) minus sign in the equation.

Functions

There are 3 types of functions that work on triangles. And, each function returns a value between 0 and 1.

n = Sin (angle) 

n = Cos (angle) 

n = Tan (angle) 

Note: a function takes 1 value and returns 1 value.  It can’t return 2 values, otherwise, it’s not a function.  Example: y = F(x)

Note: There are other functions, but they are versions of these 3 functions.  They will be covered briefly, while most of the time is spent reviewing these 3 functions.

These 3 functions  take in a value (angle) which is a number  

between 0 and 359 degrees 

between 0 and 2 PI 

between 0 to 99 radians

Note: these numbers describe a relationship  between two segments that construct a triangles adjacent (a) and opposite (o) sides.  More on this in a minute.

When you see a right triangle, it is suggested that you draw it as shown. Eventually, your brain will comprehend its parts no matter how the triangle is rotated, reversed, or inverted. So, for now, we will discuss right triangles from this orientation.

Sin (angle) = o / h

Cos (angle) = a / h

Tan (angle) = o / a

It is recommended that you memorize these relationships.

Exercises

1) Create 4 right triangles

Take a piece of letter size paper (8.5 x 11) and create a square.

Fold 1 corner of the paper to the opposite of the paper to create a triangle.  

Actually you have 2 triangles, one on top of the other.

Crease the paper

Fold the remaining piece of paper, that creates a rectangle vs a square, and tear it off.

When you unfold the 2 triangles to form a square.

Take the rectangle and crease it between 2 opposite corners

Seperate all the triangles

2) Mark the 90 degree angle on a triangle

3) Mark the hypotenuse, adjacent and opposite edges on 1 triangle

4) Write the measurements of the angles of 2 different triangles (one from the square, one from the rectangle) in the corner on their respective triangles.

Do they add up to 180 degrees?

Does one of the triangles have a 45 degree angle?

Which triangle is an Isosceles triangle?

Are any of the triangles obtuse or acute?

5) Write the measurements of the sides of 2 different triangles (one from the square, one from the rectangle), and perform the following algebraic expressions with their values.

h^2 = a^2 + o^2

does the sin (angle) = o / h

does the cos (angle) = a / h

does the tan (angle) = o / a

does the o = h * sin (angle)

does the a = h * cos (angle) 

does the o = a * tan (angle)

6) Using graph paper, and a ruler, create 10 different triangles where the adjacent (a) and opposite (o) sides add up to 15 centimeters.  Then use the equations above to figure out what the hypotenuse (h) and angle would be.

7) using graph paper and a ruler, create 10 different triangles where the hypotenuse (h) is 10 centimeters long.  Then use the equations above to figure out what the adjacent (a), opposite (o) and angle would be.

[rowanstree-blog]

Day #167

          Today I started with a math class on the graphs of the trigonometric functions, sine, cosine and tangent. I started the lesson of with a video on the graph of the sinusoidal function, y=sin(x). I started with a question asking what the domain of the sinusoidal function was. The domain is all sets of valuable inputs for the function. I used the unit circle and a y, theta graph to wrote and plot the sinusoidal equation. Once I did all of that, I concluded that the domain of this function is (-1,1) including -1 and 1. I then watched a video on how to construct the graph of y=tan(x). I concluded that the graph would have a vertical asymptote every five radians and approach positive snd negative infinity while doing so. Considering the tangent of theta is the slope of the terminal ray, I just had to take the sin of theta over the cosine of theta to find out the tangent of several pi radians. I then watched a video on intersection points of y=sin(x) and y=cos(x). In this video, I wrote terms of the table in terms of radians for both the cosine of theta and the sine of theta on the unit circle and graphed accordingly. After that, I watched a video on basic trigonometric entities involving symmetry. In the lesson, I drew several terminal rays in all four quadrants of a graph in a unit circle. I then wrote down which sine and cosine functions were equivalent and then followed it up with a video on tangent identities which is the proportion of a sin function over its equivalent cosine function. Next, I watched a video on sine and cosine identities involving symmetry in which I took random sine and cosine functions and determined if they were equal to each other. I then watched a video on tangent identities periodicity. In this video, I did pretty much the same thing except I determined if its slope, or tangent was equal to 1/2. After all of that, I took an Algebra 1 class on the Quadratic equation sample problems as a refresher. I then took a French lesson on Duolingo followed by a Chemistry class on how to fill in an ICE table according to the equilibrium constant expression of a reaction. I stands for initial concentration which should be given in order to calculate E which stands for equilibrium concentration which can be found after adding or subtracting I and C which stands for change in concentration. First, you must write all of your initial concentrations If your equilibrium constant is larger than or equal to 10^4, then your products are favored. If Kc is less than or equal to 10^-2, then your reactants are favored. This information can help you figure out which side is equal to zero which will later determine how you fill in your ICE table. Depending on which side is favored, you must add or subtract the molecules stoichiometric coefficient of x. Add, subtract and solve for x to find out your equilibrium constant. After that, I took a space science class on a simulation video of Earth’s tilt and rotation which determines its season. This information can contribute to the reasoning behind why the equator doesn't have seasons. It is because it is never turned away from the sun, like us hence our four seasons as we turn towards and away from the sun. I then took an environmental science class on various studies launched and questions asked on the transgenic contamination of Mexican maize. Even though there have been both false positives and false negatives in order to protect and expose the firms causing this transgenic contamination. It is true that transgenic contamination is becoming more and more abundant and the effects are still unknown. I then did a quick exercise followed by an hour long lunch. After that, I took a women’s history class on Mary Harris “Mother” Jones who was a labor organizer who played an outspoken role in the world that was mislead by her appearance. She was a passionate and resilient woman that fought for what she believed in and due to that, became known as “the most dangerous woman in America.” I then took an economics class on Allocatice efficiency which is when the marginal cost is equal to the marginal benefit and I did an example that showed this both literally and graphically. Next, I took a grammar class on commas and introductory elements which are followed by a comma and are placed in the beginning of a sentence. After that, I read some of “The Beauty Myth” on how markets rely so much on feminine appearance more that the actual product to “appeal” to the reader while they are actually making them more self conscious.

[mathandnumberystuff]

How to calculate exact trig values, part 3

11th roots of unity

This is my third post about calculating exact trigonometrical values based on roots of unity. I am giving the examples for prime roots of unity.

My previous post showed that the 7th roots of unity had square roots and cube roots in their formulas, because 7 - 1 = 2*3. Since 11 - 1 = 2*5, the 11th roots of unity will have square roots and 5th roots in their expression, namely, a sum of 4 fifth roots, each of formulas involving the fifth roots of unity.

Before we start, I want to make a correction to something I said earlier. In my last post I stated that a1 + a2 + a3 + r1*(a1 + r1*a2 + r2*a3) + r2*(a1 + r2*a2 + r1*a3) = 3*r1, and a1 + a2 + a3 + r2*(a1 + r1*a2 + r2*a3) + r1*(a1 + r2*a2 + r1*a3) = 3*r2. In fact, the first left-hand expression equals 3*r2 and the second equals 3*r1. This is the corrected expression for the 7th root of unity:

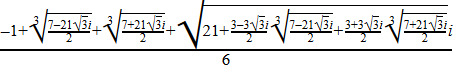
Now on to the current calculation.

Here are the 11th roots of unity:

1, x1, x2, x3, x4, x5, x6, x7, x8, x9, x10

Let’s try to find a power cycle that goes through each 11th root of unity once, except for 1, starting with x1.

Let’s try squaring each term. Since x(n) is just x1^n, and x1^11 = 1, then x(a)*x(b) = x((a + b) mod 11). This is axiom 2 from the first post.

x1, x2, x4, x8, x5, x10, x9, x7, x3, x6, x1...

This gives us a cycle of 10, like we wanted. Now to find each root of unity, we are going to be solving a quadratic equation and a quintic equation. Let’s first find the roots of the equation by summing together every fifth term of the cycle, starting from the first, second, third, and fourth, and fifth terms:

x1 + x10 = a1

x2 + x9 = a2

x4 + x7 = a3

x8 + x3 = a4

x5 + x6 = a5

To find each of these values, we will need to find the following values, where r1, r2, r3, and r4 are the four 5th roots of unity not equal to 1, r1 has a polar angle of 2*pi/5, and r(n) = r1^n:

a1 + a2 + a3 + a4 + a5 = s0

a1 + r1*a2 + r2*a3 + r3*a4 + r4*a5 = s1

a1 + r2*a2 + r4*a3 + r1*a4 + r3*a5 = s2

a1 + r3*a2 + r1*a3 + r4*a4 + r2*a5 = s3

a1 + r4*a2 + r3*a3 + r2*a4 + r1*a5 = s4.

Then we can find the five roots by taking the inverse Fourier transform:

s0 + s1 + s2 + s3 + s4 = 5*a1

s0 + r4*s1 + r3*s2 + r2*s3 + r1*s4 = 5*a2

s0 + r3*s1 + r1*s2 + r4*s3 + r2*s4 = 5*a3

s0 + r2*s1 + r4*s2 + r1*s3 + r3*s4 = 5*a4

s0 + r1*s1 + r2*s2 + r3*s3 + r4*s4 = 5*a5

We already know that s0 = x1 + x10 + x2 + x9 + x4 + x7 + x8 + x3 + x5 + x6 = -1, by axiom 1, but s1, s2, s3, and s4 must be calculated via their fifth powers as sums of 5th roots of unity.

The algebra required to solve for s1^5 is so long-winded that it took 2 whole years since I started writing this post before I finally managed to concentrate on it long enough to solve it. There are 3125 values, of 70 different types, to sum in the expanded expression. Each term consists of a product of 5 values of the form a(n), multiplied by a 5th root of unity, each of which need to be expanded into a pair of x(n) values. Here is the result:

(a1 + r1*a2 + r2*a3 + r3*a4 + r4*a5)^5 = -196 - 130*r1 + 255*r2 - 20*r3 + 90*r4.

After substituting into this expression the respective values for r1, r2, r3, and r4 that we calculated way back in the first post, it becomes:

s1 = -979 - 275*√5 - 220i*√(10 - 2√5) + 275i*√(10 + 2√5)

Amazing! I always get a feeling of wonder when I see such large and arbitrary-looking numbers in a formula for such an easy to define value. The only patterns I can see in these numbers are that -979, -275, -220, and 275 are all multiples of 11 - the degree of the roots we are calculating - and that -275, -220, and 275 are all multiples of 5 as well. The divisibility by 5 occurs because all the terms containing a value r(n) could have their a(n) values cyclically permuted to make 5 different terms having the same value, forcing the total number of r(n)-containing terms to be a multiple of 5 for each value of n.

The expressions for s2^5, s3^5, and s4^5 can be found by substituting out powers of r1 for the corresponding powers of r2, r3, and r4 respectively. Their values are:

s2^5 = -979 + 275*√5 - 220i*√(10 + 2√5) - 275i*√(10 - 2√5)

s3^5 = -979 + 275*√5 + 220i*√(10 + 2√5) + 275i*√(10 - 2√5)

s4^5 = -979 - 275*√5 + 220i*√(10 - 2√5) - 275i*√(10 + 2√5)

Now we need to take 5th roots of each of these expressions. The trouble here is in finding out which 5th root to use. As I said in my first post on roots of unity, I am defining c^(1/n) to be the value x having a polar angle equal to 1/n that of c, such that x^n = c, and therefore x has an angle between 0 and 2*pi/n radians. For the other nth roots of c, it needs to be multiplied by one of the nth roots of unity. But we don’t know what s1's polar angle is, so we don’t know if it’s 1, r1, r2, r3, or r4 times (s1^5)^(1/5).

I haven’t found any pattern in which 5th root to choose when, but a calculator can check that:

s1 = r1*(-979 - 275*√5 - 220i*√(10 - 2√5) + 275i*√(10 + 2√5))^(1/5)

s2 = r1*(-979 + 275*√5 - 220i*√(10 + 2√5) - 275i*√(10 - 2√5))^(1/5)

s3 = r4*(-979 + 275*√5 + 220i*√(10 + 2√5) + 275i*√(10 - 2√5))^(1/5)

s4 = r4*(-979 - 275*√5 + 220i*√(10 - 2√5) - 275i*√(10 + 2√5)^(1/5)

Now we can calculate our a(n) values:

a1 = (-1 + r1*(-979 - 275*√5 - 220i*√(10 - 2√5) + 275i*√(10 + 2√5))^(1/5) + r1*(-979 + 275*√5 - 220i*√(10 + 2√5) - 275i*√(10 - 2√5))^(1/5) + r4*(-979 + 275*√5 + 220i*√(10 + 2√5) + 275i*√(10 - 2√5))^(1/5) + r4*(-979 - 275*√5 + 220i*√(10 - 2√5) - 275i*√(10 + 2√5)^(1/5))/5

a2 = (-1 + (-979 - 275*√5 - 220i*√(10 - 2√5) + 275i*√(10 + 2√5))^(1/5) + r4*(-979 + 275*√5 - 220i*√(10 + 2√5) - 275i*√(10 - 2√5))^(1/5) + r1*(-979 + 275*√5 + 220i*√(10 + 2√5) + 275i*√(10 - 2√5))^(1/5) + (-979 - 275*√5 + 220i*√(10 - 2√5) - 275i*√(10 + 2√5)^(1/5))/5

a3 = (-1 + r4*(-979 - 275*√5 - 220i*√(10 - 2√5) + 275i*√(10 + 2√5))^(1/5) + r2*(-979 + 275*√5 - 220i*√(10 + 2√5) - 275i*√(10 - 2√5))^(1/5) + r3*(-979 + 275*√5 + 220i*√(10 + 2√5) + 275i*√(10 - 2√5))^(1/5) + r1*(-979 - 275*√5 + 220i*√(10 - 2√5) - 275i*√(10 + 2√5)^(1/5))/5

a4 = (-1 + r3*(-979 - 275*√5 - 220i*√(10 - 2√5) + 275i*√(10 + 2√5))^(1/5) + (-979 + 275*√5 - 220i*√(10 + 2√5) - 275i*√(10 - 2√5))^(1/5) + (-979 + 275*√5 + 220i*√(10 + 2√5) + 275i*√(10 - 2√5))^(1/5) + r2*(-979 - 275*√5 + 220i*√(10 - 2√5) - 275i*√(10 + 2√5)^(1/5))/5

a5 = (-1 + r2*(-979 - 275*√5 - 220i*√(10 - 2√5) + 275i*√(10 + 2√5))^(1/5) + r3*(-979 + 275*√5 - 220i*√(10 + 2√5) - 275i*√(10 - 2√5))^(1/5) + r2*(-979 + 275*√5 + 220i*√(10 + 2√5) + 275i*√(10 - 2√5))^(1/5) + r3*(-979 - 275*√5 + 220i*√(10 - 2√5) - 275i*√(10 + 2√5)^(1/5))/5

Unfortunately, since Unicode lacks a fifth root symbol (that I am aware of), I had to write the 5th root of x as x^(1/5).

Anyway, we now know the values of x1 + x10, x2 + x9, x3 + x8, x4 + x7, and x5 + x6.

Since x1 and x10 are complex conjugates, (x1 + x10)/2 is the real part of x1. This is the same value as cos(2*pi/11), and it is just a1/2.

Here is an image of what the expression for cos(2*pi/11) actually looks like when written out (with fifth-root symbols in place of x^(1/5)), just to show you how long it gets.

To figure out the value of, say, x1, we will be needing both x1 + x10 and x1 - x10. We already know the x1 + x10 = a1. Let’s call x1 - x10 = t1.

t1^2 = (x1 - x10)^2 = x2 + x9 - 2 = a2 - 2

So, t1 = √(a2 - 2). And just like a1 = 2*cos(2*pi/11), t1 = 2i*sin(2*pi/11).

So:

sin(2*pi/11) = √(2 - a2)/2 = √(55 - 5*(s1^5)^(1/5) - 5*r4*(s2^5)^(1/5) - 5*r1*(s3^5)^(1/5) - 5*(s4^5)^(1/5))/10.

If written out in full, this expression would look similar to the one given above except that:

the numerator is under a square-root sign

it starts with 55 instead of -1 and then subtracts the 5th roots instead of adding them

All of the 5th roots are multiplied by 5

The 1st and 4th ones don’t get multiplied by r(n) values.

The sines and cosines of 4*pi/11, 8*pi/11, 6*pi/11, and 10*pi/11 can be found by doing operations on a1, a2, a3, and a4 respectively.

--------------------------------------

Whew! That was way more complex than the formula for the 7th roots of unity. Next up is the 13th roots of unity, and I don’t think they will be nearly as hard.

[mathematicianadda]

Exact expression of a trigonometric integral

Let $a>2$ be a real number and consider the following integral $$ I(a)=\int_0^\pi\int_0^\pi \frac{\sin^2(x)\sin^2(y)}{a+\cos(x)+\cos(y)} \mathrm{d}x\,\mathrm{d}y $$

My question. Does there exist a closed-form expression of $I(a)$?

Some comments. Since $a-2<a+\cos(x)+\cos(y)<a+2$ and $\int_0^\pi \int_0^\pi \sin^2(x)\sin^2(y)\ \mathrm{d}x\, \mathrm{d}y=\frac{\pi^2}{4}$, we have the following bounds $$ \frac{\pi^2}{4(a+2)} < I(a) < \frac{\pi^2}{4(a-2)}, $$ however I didn't manage to find an exact expression for $I(a)$. Any help is welcome!

from Hot Weekly Questions - Mathematics Stack Exchange from Blogger https://ift.tt/2WFEXrm