#its just an assignment of an integer to each n-simplex

[positively-knotted]

Great explainer! Very meta point though - isn't this sort of a cyclical way to define a hole, at least to someone who wants to insist that a straw has two holes?

In essence, we're finding holes by taking non-bounding loops (great), and saying two loops bound the same hole if they bound some other 2-simplex. Which like. is kinda what the debate is about.

Idk, find it slightly easier to see in the manifold. H_1 is generated by embedded S¹s, modulo the relation that the boundary of a pair of pants is zero, and an the boundary of an annulus=straw is zero. So a straw only having one hole is part of the definition of homology.

Why Straws Have One Hole: An Introduction to Homology Part 2

In this post I'll discuss simplicial complexes and how we can use them to make our test for holes simpler and motivate the definitions for simplicial homology! The post is more technical but I have tried to motivate each step.

Simplicial Complexes:

A common theme in topology is to build up our spaces from smaller, simpler spaces. One way of doing this is to use simplices! These are generalisations of triangles to all dimensions:

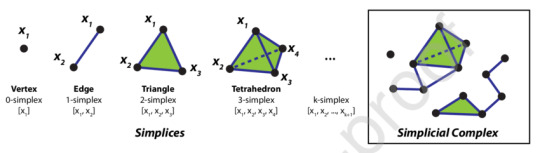
Image is taken from here

An n-simplex has n+1 verticies and is denoted by its vertices in square brackets: <e₀,...,eₙ>. A simplicial complex is made by gluing simplices together such that the intersection of two simplices is also a simplex that is included in the complex. We also require that any n vertices can define at most one n-simplex in the complex. If some vertices e₀,...,eₙ in a simplicial complex, K, define an n-simplex <e₀,...,eₙ> that is in K, we call <e₀,...,eₙ> an n-face of K.

An example of a simplicial complex is a square where each vertex of the square is a 0 simplex and each edge is a 1-simplex. If instead we considered a solid square, we wouldn't automatically get a simplicial complex because the 2 dimensional part isn't made up of 2-simplices. We fix this by adding an addition 1-simplex bewteen one pair of diagonal points which gives us a simplical complex with four vertices, five 1-simplices and two 2-simplices:

We can construct a great number of spaces using simplices! This construction is only up to homeomorphism but that's all we care about! A simplicial complex that is homeomorphic to a space is called a triangulation of that space. Importantly we can triangulate a straw:

This is the simplest triangulation because having fewer simplices would lead to us having different simplices described by the same vertices.

Simplicial Homology

So why do we care about triangulations? The key here is to notice that the boundary of an n-simplex is a simplicial complex made up of (n-1)-simplices. For example, the boundary of a 2-simplex is a simplicial complex made of three 1-simplices. The idea is to modify our test to only involve simplices because then we only have to check finitely many things! This is where things start to get a bit more technical but I will try my best to motivate each step!

Firstly, we need to introduce a convention in the way we describe simplices. We pick an order for the vertices in our complex to be listed, e.g. for the triangulation of the straw we could pick the order a,b,c,d,e,f. Then any time we write a simplex we must list the vertices in that order. For example, with the order above, <a,b,d> is how we describe the left most 2-simplex. The reason we need this is we are about to start thinking about simplices in a more abstract way and we need a systematic way of writing them.

Now for arguably the weirdest (but most powerful) step. We want a way to talk about the boundary of a simlicial complex as one object and we want a way to say when a particular simplicial complex has no boundary. The motivation for this is we want to talk find the analogue of a loop that we can use to test for holes, that is we want a one dimensional object that doesn't have a boundary. Since we eventually want to count things, it might be prudent to somehow assign numbers to things. As mentioned above, the boundary of an n-simplex can be thought of as the union of (n-1)-simplices and unions of sets are kind of similar to a kind of sum. The idea is to talk about "sums" of simplices. It doesn't really make sense to add simplices but we can sort of just fudge it. This fudging is known as "formal sums" and this is when we say "okay, we don't know what a sum of these things actually is but we study it anyway".

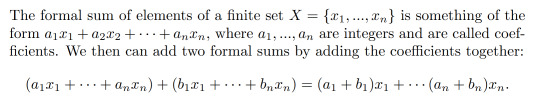
We say the elements of X generate these formal sums.

We then consider the set Cₙ(K) of all the formal sums of n-simplices in a simplicial complex K and we call it the nth simplicial chain group of K and we call elements of Cₙ(K) n-chains. We say that the rank of Cₙ(K) is the number of elements of X. Note that the sum or difference of two chains is again a chain.

The rank of C₂(K) is 1 and the rank of C₁(K) and of C₀(K) is 3.

We can now also give meaning to a simplex that is written in a different order to our chosen order. Given an ordered list of vertices, we can swap two elements around to get a different ordered list. If n is the number of swaps it takes to get an ordered list of vertices into our chosen order, we say that the simplex with vertices written in a different order is equal to the element of Cₙ(K) given by (-1)ⁿ times the simplex with the vertices written in our chosen order.

Now we want to figure out how to represent the boundary as a map from Cₙ(K) to Cₙ₋₁(K) since the boundary of an n-simplex is made up of (n-1)-simplices.

The full representation of this map is a bit detailed so I will stick to the case when n is less than or equal to 2 since that's all we need. The definition of this boundary map only depends on what it does to the simplices because it comes from considering their boundaries. So we will say that the boundary map applied to a formal sum is just the formal sum of the map applied to each simplex, for example

where ∂ is denotes the boundary map. So we just need to define ∂ on simplices.

To motivate the definition, we consider a 2-simplex <x,y,z> with the order x,y,z. Starting at x, we can think of the boundary as a loop that goes from x to y, then from y to z then from z back to x:

So we could represent the boundary as the formal sum <x,y>+<y,z>+<z,x>. Then written in our chosen order, the boundary is <x,y>+<y,z>-<x,z>. That is ∂(<x,y,z>)=<y,z>-<x,z>+<x,y>. In the first term, we remove the first vertex, in the second term we remove the second vertex and multiply by -1, and in the third term we remove the third vertex and multiply by -1 twice. So it would seem sensible to that the pattern here is the nth term in the boundary of a k-simplex is the simplex where the nth vertex is removed and we mutlipy by (-1)ⁿ⁻¹.

So the boundary of a 1-simplex <x,y> is <y>-<x>. But the boundary of a 0-simplex is always 0 since 0-simplices are just points and have no boundary!

We also have that the boundary of the boundary of a 2-simplex is 0. This makes intuitive sense since the boundary itself has no points at the edge of it but we can show this still works in our abstraction to formal sums:

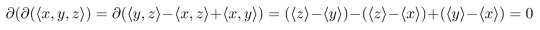
Now we have two special types of formal sums: those that have no boundary and those that are the boundary of something else. We call an n-chain that has no boundary an n-cycle and we call an n-chain that is the boundary of an (n+1)-chain an n-boundary. We can extend the first above argument to show that boundaries are always cycles, i.e. the boundary of a boundary is always 0. 1-cycles are what replace loops in our earlier test, that is we want to find 1-cycles that aren't 1-boundaries! An obvious yet important example of a boundary is 0, 0 is the boundary of 0 (we'll use this fact later). Two other important facts are the sum of n-cycles is also an n-cycle and the sum of n-boundaries is also an n-boundary. If c and c' are both cycles, then ∂(c+c')=∂c+∂c'=0+0=0 and if c=∂b anf c'=∂b', then c+c'=∂b+∂b'=∂(b+b').

Let's take a step back to summarise what we have so far. We have found a test for holes in a space but it didn't really allow for easy calculation of the number of holes in a space. So we restricted our view to simple spaces and have found a way of abstractly representing the building blocks of those spaces. This abstraction has allowed us to reframe our test for holes into a purely algebraic question!

But how can we be sure this test still works? Let's consider a circle. Using our first test, we can just take a loop around the circle. Then this loops isn't the boundary of anything since it bounds a disc of the same radius but this disc isn't part of the circle. So the circle has a hole. Now we triangulate the circle using three vertices and 3 edges, i.e. a triangle. If we label the vertices as <x>, <y> and <z> we already know an example of a cycle: <y,z>-<x,z>+<x,y>. Even though this calculation was done for a 2-simplex, it only involves the 1-simplices so it is valid in this situation too! But in this case, we don't have any 2-simplices in our space so this cycle can't be the boundary of anything! Conversely, suppose we get a positive result using our simplicial hole test, i.e. we've found a cycle that isn't the boundary of anything. Then we can construct a loop in the space using this cycle and this loop wouldn't be the boundary of anything so the first test would also be positive!

The final step that actually lets us count things is to define the homology groups! What we want to do is find cycles that aren't boundaries. Algebraically, we do this by considering cycles to be "the same" if their difference is a boundary. That is, we say two n-cycles c and c' are homologous if there is some (n+1)-chain b such that c-c'=∂b. We have that all n-boundaries are homologous to each other. Say both c and c' are n-boundaries and that b and b' are (n+1)-chains such that c=∂b and c'=∂b', then c-c'=∂b-∂b'=∂(b-b'). The since b and b' are (n+1)-chains, b-b' is an (n+1)-chain so c and c' are indeed homologous. In particular, 0 is a boundary so every boundary is homologous to 0. So now suppose that c is a cycle that is homologous to 0, then there exists an (n+1)-chain b such that c-0=∂b. So c=∂b and hence c is also an n-boundary. This means that a cycle is a boundary if and only if it is homologous to 0. So now if we want to find cycles which aren't boundaries, we look for cycles which aren't homologous to 0.

We define the homology class of a cycle c to be the set of all the cycles which are homologous to c and we denote it [c]. For example, the homology class of 0, [0], is the set of all boundaries! We can also define a notion of addition of homology classes: [c]+[c']=[c+c']. That is, the sum of two homology classes of two cycles is the homology class of their sum. We call the set of all homology classes of a cycles of a simplicial complex K, the (first) homology group of K and write H₁(K). If H₁(K) only has one element, i.e. H₁(K)={[0]} every cycle must be a boundary and K would have no holes. But if K has a hole, H₁(K) would have more than one element.

We are actually now quite close to being able to count the number of holes a space has! Let's come back to the example of a circle. Intuitively, a circle has 1 hole and we've already seen that we have one cycle which isn't a boundary: <y,z>-<x,z>+<x,y>. But by the way we defined the boundary, we also have that

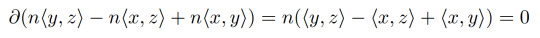
for any integer n. So for any non-zero integer n, we can find a cycle that is not a boundary. In particular, if m doesn't equal n, then n(<y,z>-<x,z>+<x,y>) is not homologous to m(<y,z>-<x,z>+<x,y>) since their difference is (n-m)(<y,z>-<x,z>+<x,y>) which is not a boundary unless n-m=0, which is not the case here since n doesn't equal m. Moreover, I claim that any cycle in a circle must be of this form. Remember, this cycle represents the loop going around the triangulation of the circle once. The only way we can get loops in the circle are obtained by going around the circle a whole number of times (where going in the opposite direction gives us a "negative" loop). Any other path you try to take will end up with not having the same start and end point and so would have a boundary! So there is a homology class of the circle for each integer. Moreover, adding these cycles represents going around a loop n+m times so adding the homology classes together is somehow the same as the regular addition we know for the integers! In formal terms, we say that H₁(circle) is isomorphic to the integers. Like how homeomorphism is the notion of "the same" for topologists, isomorphism is the notion of "the same" for algebrists! The important part of this is that all of the homology classes can be expressed as an integer multiple of [<y,z>-<x,z>+<x,y>] just like how an integer can be thought of as an integer multiple of the number 1. In this sense, we say that [<y,z>-<x,z>+<x,y>] generates H₁(circle), i.e. H₁(circle) has 1 generator. This cycle came about as a loop around the hole in the circle so it is sensible to guess that the number of generators corresponds to the number of holes!* This is how we will go about showing that a straw has 1 hole in the next part! That is, we shall figure out what the first homology group of a straw is and find out how many generators it has!

*technically, we actually count the free generators of H₁ since the torsion elements represent something else but it won't matter for what we're doing. Alternatively, we could have defined homology over a field to get vector spaces which naturally don't have any torsion but this doesn't feel quite as natural as doing homology with integral coefficients.