yusugomori

[yusugomori]

機械学習・深層学習の基礎体力測定②

前回は、線形回帰・ロジスティック回帰および（シンプルな）ニューラルネットワークの出力の式を理解するところまでを考えてみました。今回はその続きを考えていきます。

一番基本的な式は線形回帰の \[ y = wx + b \] 

という直線の式でしたが、では、この傾き \(w\) と切片 \(b\) はどのように求めればいいでしょうか？

これら \(w\)、\(b\) が、いわゆるモデルのパラメータになります。このパラメータを最適化する（＝きちんと求める）ことで、線形回帰が引く直線は、「データの関係性を最もよく表す直線」になるわけです。

この式が \(y = \boldsymbol{w}^T\boldsymbol{x} + b\) になっても、あるいはロジスティック回帰の \(y = f\left(\boldsymbol{w}^T \boldsymbol{x} + b\right) \) という式になっても、考えるべきことは同じです。ここでは \( \boldsymbol{w} \) と \(b\) がそれぞれ “傾き” “切片” になるわけですね。

機械学習ではこの “傾き” のことを重み、“切片” のことをバイアスと呼びますが、なんのことはない、「もともと直線の傾きと切片だったもの」と考えれば話はシンプルです。

それでは、具体的に重みとバイアスをどう求めていくかを考えてみましょう。ここで大事なのは、機械学習が前提としているのは

「実際の値と、予測の値が一致することを目指す」

であるということです。文章で見ると当たり前のことを言っているようにしか見えないのですが、ここを意識するとしないとでは、機械学習の基礎体力に大きな差がでてきます。

さて、ではこの「機械学習の大前提」を実現するにはどうすればいいでしょうか？

実際の値と予測の値が一致するということはすなわち、それぞれの値の「誤差をなくす」ということになります。

ということは、この「誤差を表す関数を定義し、その関数を最小化させること」を考えれば、数学的に解くことができるのではないでしょうか。この関数が、まさしく誤差関数と呼ばれるものになります。

モデルの出力（予測値）を \(y\) で見てきたので、手元にある (入力, 出力) の組み合わせになっているデータの値を \((x, t)\) とおいて考えていきましょう。もう少し細かく書くと、実際のデータが \(N\) 個あったとして、そのうちの \(n\) 番目のデータを \((x_n, t_n)\) で表していきます。すると、例えばロジスティック回帰における予測値は

\[ y_n = f\left(\boldsymbol{w}^T \boldsymbol{x}_n + b\right) \]

となります。各データにおいて、この \(y_n\) と \(t_n\) が一致する、すなわち誤差がなくなるようにすればいいので、「各データの誤差の２乗和」を誤差関数とするのが一番素直そうです。ということで、誤差関数 \(E\) は下式となります。

\[ E = \sum_{n = 1}^{N} \left(y_n - t_n\right)^2 \]

この誤差関数 \(E\) を最小化すればいいことになりますが、「関数の最小化」と言えば何でしょうか？…微分ですね。

例えば「 \(f(x) = x^2\) を最小とするような \(x\) と求めよ」という問題があったら、\(f’(x) = 2x\) を求め、\( 2x = 0 \iff x = 0\) と答えるでしょう。ですので、誤差関数を微分すればいいことになります。

では、先ほどの誤差関数 \(E\) に対して、\(f(x)\) の \(x\) に該当するものはどれでしょうか？

これはつまり \(E\) は何の関数でしょうか？と聞いていることになりますが、最適化すべき値を思い出してみると、重みとバイアス、すなわち \( \boldsymbol{w} \) と \( b \) が答えになります。

よって、誤差関数 \(E(\boldsymbol{w}, b)\) に対して、それぞれの偏微分

\[\frac{\partial E}{\partial \boldsymbol{w}}, \frac{\partial E}{\partial \boldsymbol{b}}\]

がゼロになるような \( \boldsymbol{w}, b \) を求めればいいということになります。

「実際の値と、予測の値が一致することを目指す」

という当たり前のことを突き詰めただけですが、これがあらゆる手法で共通しているアプローチと言っても過言ではありません。体系的な理解をしておくことで、しっかりと基礎体力がついたのではないでしょうか。

さて、こうした話を深層学習まで書いているのが拙著「詳解ディープラーニング」になります。ロジスティック回帰をはじめとして、ニューラルネットワーク（とその応用）について、数式と実装がしっかりと書いてありますので、参考にしてみてください。

あるいは、実装がなく完全に数式のみの書籍としては、深層学習はタイトルの通り「深層学習」、機械学習全般に関しては「パターン認識と機械学習」があります。これらに関しては相当詳しく理論について書かれていますが、その分ボリュームもかなりありますので、気合をいれて読んでみましょう。

最近、エンジニアかどうかを問わずよく「人工知能 / 機械学習を勉強するのにオススメの書籍を教えて」と聞かれるので、今度まとめてみようかと思います。

[yusugomori]

機械学習・深層学習の基礎体力測定①

久しぶりのブログ更新です。今回は、ますます活発に研究されている深層学習分野が、その活発さ故に引き起こされてしまっている下記の問題をテーマに、記事を書いていきたいと思います。

「簡単に深層学習の手法が実装できるライブラリが出てきたことによって、実装はできるけれど実は数式部分、すなわち理論背景についてはよく知らない場合が多い」

これは個人的には非常にもったいないと思っていて、「機械学習に対する体系的な理解」ができていないことに端を発する問題だと考えています。

「体系的な理解」なんて書くとエラそうに聞こえてしまうかもしれませんが、ここで書いていくものは、「こうやって理解すると、少しはスッキリするんじゃない？」くらいの提案として受け取ってもらえれば幸いです。タイトルで「基礎体力」と書いたのもそのためです。

じゃあ具体的には何を理解すればいいの？となるわけですが、ここでひとつ、簡単な問題を考えてみましょう。まずは機械学習の中でも、一番単純とも言える「線形回帰」を取り上げてみます。

例えば下の散布図のような \(x\) と \(y\) の関係性を示すデータがあったとします。

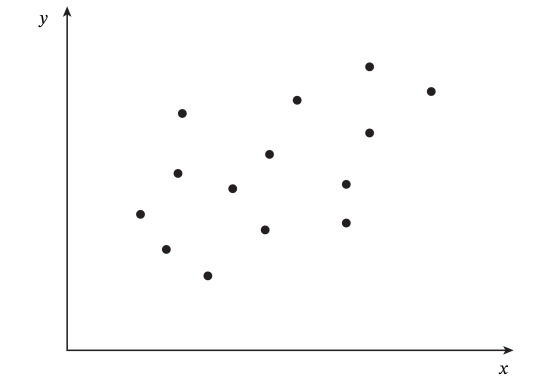
これに対し、線形回帰が目指すのは下図の破線のような、「\(x\) と \(y\) の関係性を表す直線」を引くことですが、この直線は式で書くと \(y = \) 何と表せるでしょうか？

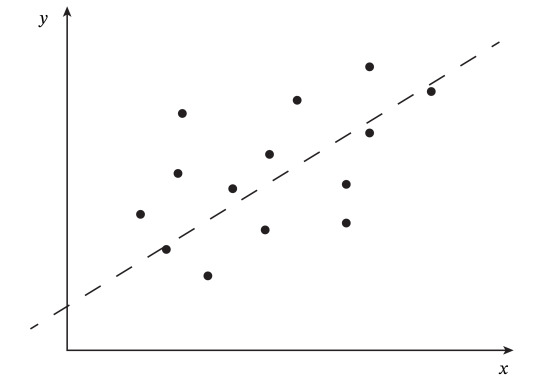
文字の置き方は自由ですが、直線なので傾きを \(w\)、切片を \(b\) とおくと、以下の式で表せます。

\[ y = wx + b \]

ここまでは全く難しくないと思います。では次に進んでいきます。今見た線形回帰の問題は予測値 \(y\) が任意の実数であり、「回帰問題」に分類されますが、それに対し予測値が \(\{0, 1\}\) といった、「分類問題」の場合は、先ほどの式をいじらないと表現することはできません。具体な手法として「ロジスティック回帰」を考えてみましょう。どういう式で表せるでしょうか？

これは下記のように表すことができます。

\[ y = f(wx + b) \]

ここで導入した関数 \(f\) は、シグモイド関数になります。シグモイド関数は

\[ f(x) = \frac{1}{1 + \exp(-x)} \]

で表される関数で、図示すると下のようになりました。

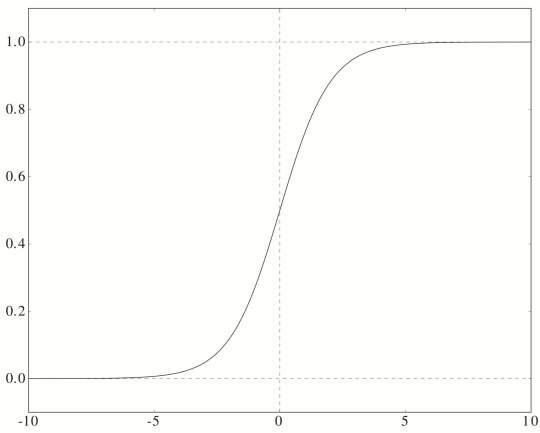
見て分かる通り、任意の実数を 0 から 1 に写像しています。

もともと \(f\) の引数となっている \(wx + b\) は任意の実数をとるものでした。それを 0 から 1 に写像するので、分類問題を解くことができるようになったわけです。

ここまでは \(x\) がスカラ、すなわち特徴量が１つの場合を見てきましたが、特徴量が複数になっても土台となる式は全く変わりません。\(w, x\) がそれぞれベクトルになるだけなので、線形回帰が

\[ y = \boldsymbol{w}^T \boldsymbol{x} + b \]

ロジスティック回帰が

\[ y = f\left(\boldsymbol{w}^T \boldsymbol{x} + b\right) \]

となります。ロジスティック回帰は分類問題用の手法なのに「回帰」という名前がついているのは、もともとは線形回帰だった式を無理やり \(\{0, 1\}\) にフィット、すなわち回帰させるようにした手法だからかもしれません。

さて、一方でニューラルネットワークの考えはどうだったかを見ていきましょう。下図のような入力層・出力層だけのシンプルなモデルを考えます。

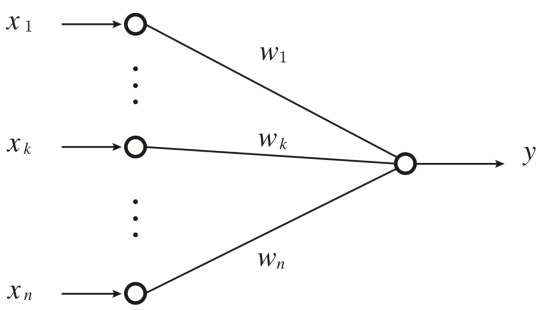
出力層部分のニューロンに着目すると、前の層から伝播してきた電気信号のパターンをそのまま出力する場合、式としては下式のようになります。

\[ y = \boldsymbol{w}^T \boldsymbol{x} + b \]

線形回帰と同じ式に行き着きました。では出力層部分のニューロンが、「ある一定の電気がたまると発火し、たまらなければ発火しない」という性質をもっていたらどうでしょうか。今度は下式のようになります。

\[ y = f\left(\boldsymbol{w}^T \boldsymbol{x} + b\right) \]

ロジスティック回帰と同じですね。 （※厳密には言葉どおりに関数 \(f\) を表そうとすると、シグモイド関数ではなくステップ関数になるわけですが、本質的には変わりません。）

ということで、出発点は全く違うものの、最終的に行き着いた式は同じとなりました。結局のところ、機械学習は「各特徴量に対する重みはどれくらいにすべきか」を考えるものなので、行き着く式は同じになる、というわけですね（ですので、ロジスティック回帰はニューラルネットワークの手法のひとつとして紹介されていますし、ニューラルネットワークとして理解しておくのがよいと思います）。

さて、ここまで特別何も思うことなく、「そんなの当たり前じゃないか」と思った方は、理論的背景をきちんと理解したうえで実装に取り組まれている方だと思います。 しかし、色々な方に線形回帰の式やロジスティック回帰の式などを質問してみると、実際に「仕事で機械学習・深層学習やってきました」という方でも、予想以上に多くの方がきちんと答えることができませんでした。

数式面の理解を置いてけぼりにしてしまうと、応用手法がどんどんでてきたときに、ついていけなくなってしまう可能性が高くなってしまうので、ここで書いた基本的なことはしっかりと理解しておくとよいと思います。

また、機械学習にはニューラルネットワークに以外にもたくさんの手法がありますが、「ニューラルネットワーク以外はやったことない」という方も多く見かけます。そうした方はこちらの「Pythonではじめる機械学習」というオライリーの書籍がオススメです。ランダムフォレストやブースティング、SVM、PCAなど知っておいたほうがよい手法が一通り載っていますし、sklearn の Pipeline など、便利だけど意外と知られていないAPIを使った実装なんかも載っています。

[yusugomori]

JavaScriptによるDeep Learningの実装（Long Short-Term Memory 編）

RNNに引き続き、LSTM (Long Short-Term Memory)をJavaScriptで実装してみました。今回もsin波の予測を行っています。RNNを含むコード全体はこちらのリポジトリを���覧ください。また、理論・数式はこちらにまとめていますので、参考にしてみてください。

https://gist.github.com/yusugomori/0ac7f62b22a6f179e84206c51a377837

最もシンプルなLSTMの実装ということで、LSTMブロックに続く出力層部分も同時に実装しているなど、少し簡略的に書いているところもありますが、全体の流れとしては数式に沿って書いてあります（なので、実装的には冗長になっているところもあります）。

このLSTMクラスを利用して、sin波の予測を行うのがこちら。

https://gist.github.com/yusugomori/92cecfec899f079c74f88ecf9a2acd49

実験用に seedrandom を用いていますが、 Math.random をそのまま用いても問題ありません。

$ npm install $ node main.js

により、sin波の予測が行われているのが確認できるかと思います。

[yusugomori]

JavaScriptによるDeep Learningの実装（Recurrent Neural Networks 編）

久しぶりの更新となりました。これまでいくつかの言語で、代表的なDeep Learningの手法を実装をしてきましたが、今回はリカレントニューラルネットワーク（Recurrent Neural Networks: RNN）を実装してみたいと思います。言語は、初となるJavaScriptでトライしてみました。 完成したコードはGitHubのこちらのリポジトリにまとめてあります。 また、数式は以前にこちらにまとめましたので、理論部分についてはそちらを参考にしてください。

ではコードを紹介します。まずは核となる rnn.js から。

https://gist.github.com/yusugomori/85589717a98447d26f660c61e2275d88

さて、ここで肝心なのが、冒頭にある math です。これは Python で言うところの numpy のような挙動を目指すべく、いくつか線形代数計算で必要となるところの実装をまとめたものです。リポジトリ内の math ディレクトリに色々メソッドを書いています（ただし、まだまだWIPなところも多いです）。 似たようなライブラリには math.js がありますが、Matrix Object が個人的に扱いづらく、あくまでもPure Arrayで計算処理を行いたかったので、自分で実装しています。 math.array.zeros や math.dot, math.outer など、 numpyっぽい書き方で線形代数演算が行えるようになるので、 RNNクラス の各メソッドも、割りと数式通りにスッキリ書くことができています。

また、出力層の活性化関数はsoftmax/sigmoid部分をコメントアウトして、単純な線形活性を用いていますが、これは今回予測したいタスク（後述）に合わせる形となっています。

さて、今回予測するのは、sin波です。Qiitaの記事でも見かけますが、手っ取り早くRNNの予測を試すにはうってつけのタスクです。0...t の sin波 が与えられたときに、t+1 のsin波を予測します。 ただし、単純なsin波ではなく、-1 ~ 1 の一様分布に係数0.1をかけたノイズを波に足しています。これで予測を行ったのが下記のコード。

https://gist.github.com/yusugomori/41bcef42e4a1697b75393e01ee71032f

こちらは特段説明が必要なところはないかと思いますが、main の最後の部分の出力を可視化してみると、きちんと（ノイズがまあまあ取り除かれた）sin波が描かれるのが分かるかと思います。

今回はとても単純なRNNをJavaScriptで実装しました。

$ npm install $ node main.js

と実行すると結果が得られますが、せっかくJSで実装しているので、ブラウザで経過が見られるように変えていこうと思っています（他の手法も実装していきたい）。

また、現在CTOを務めているMICINという会社では、Angular2 や ReactNative でウェブ・アプリ開発をしており、こちらも js, ts 実装をしていますので、記事化していけるところはしていきたいと考えています。

[yusugomori]

数式で書き下す Maxout Networks

Maxoutは、他のディープラーニングの手法とは異なり、活性化関数自体を学習するという、少し特殊な手法です。論文にも示されている通り、実験による精度は人気の活性化関数である rectifier (ReLU) よりも高い結果が得られていますが、そのとっつきにくさからか、敬遠されがちな気がしています。そこで、前回のCNN記事と同様、数式で Maxout function を書き下してみたいと思います。 （ちなみに、CNNはpythonで実装したものの、これまでのコードをかなり変える必要があったり、python向けに最適化できていなかったりするため、devブランチに置いています。ソースコードはこちらからご覧ください。）

さて、Maxout を数式で表すために、以下の graphical model に沿って説明したいと思います。Maxoutは図の真ん中の部分で、図の左端は入力層、右端はもしdeepになっていなければ出力層となります。

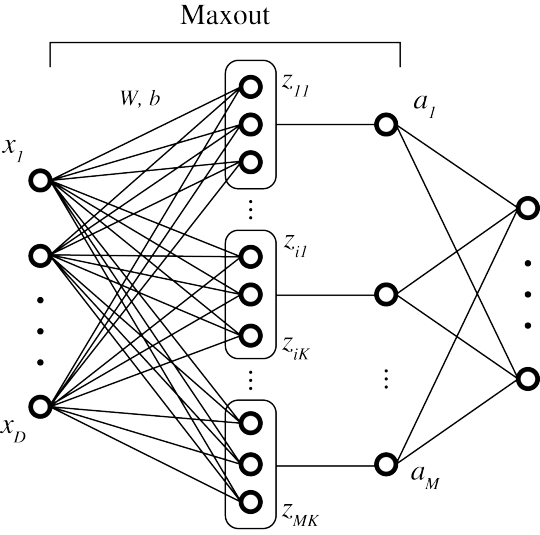
ここで、モデルのパラメータは、重み\(W \in \mathbb{R}^{D \times M \times K} \)、バイアス \(b \in \mathbb{R}^{M \times K} \) となります。すると、まず下記の式が得られます：

\[ z_{ij} = \sum_{k=1}^{K}\sum_{d=1}^{D} w_{dik} \, x_{d} + b_{ij}\]

\[ a_{i} = \max_{j \in [1, K]} z_{ij}\]

以上が順伝播の式となります。特段難しいことはありません。

次に逆伝播となりますが、モデルのパラメータの学習するために、それぞれの勾配を求める必要があります。まず\(W\)の勾配を計算すると、下記のようになります：

\[ \begin{align} \frac{\partial E}{\partial w_{dik}} &= \displaystyle\sum_{j=1} ^{K} \frac{\partial E}{\partial z_{ij}} \frac{\partial z_{ij}}{\partial w_{dik}} \nonumber \\\ \nonumber \\\ &= \displaystyle\sum_{j=1}^{K} \frac{\partial E}{\partial z_{ij}} x_{d} \end{align} \]

ここで、

\[ \begin{eqnarray} \frac{\partial E}{\partial z_{ij}} = \begin{cases} \displaystyle\frac{\partial E}{\partial a_{i}} & \, if \,\, a_{i} = z_{ij} \nonumber \\\ \, & \, \nonumber \\\ 0 & \, otherwise \end{cases} \end{eqnarray} \]

であるため、上記の\(W\)の勾配は前のレイヤーから逆伝播してきた誤差を用いて計算することができることが分かります。同様に\(b\)の勾配は下記のように求めることができます：

\[ \frac{\partial E}{\partial b_{ij}} = \frac{\partial E}{\partial z_{ij}} \frac{\partial z_{ij}}{\partial b_{ij}} = \frac{\partial E}{\partial z_{ij}} \]

これでモデルパラメータの勾配を求めることができました。ディープな層を考える場合、更に前の層（図だと入力層）に伝える誤差も求める必要があります。これは下記のようになります：

\[ \begin{align} \frac{\partial E}{\partial x_{d}} &= \displaystyle\sum_{i=1}^{M}\sum_{j=1}^{K} \frac{\partial E}{\partial z_{ij}} \frac{\partial z_{ij}}{\partial x_{d}} \nonumber \\\ \nonumber \\\ &= \displaystyle\sum_{i=1}^{M}\sum_{j=1}^{K}\sum_{k=1}^{K} \frac{\partial E}{\partial z_{ij}} w_{dik} \end{align} \]

以上でMaxoutを書き下すことができました。実際にこの関数を使う場合は、dropoutと組み合わせるなどしないといい精度が得られませんが、これは上記の式に binary mask をかければよいだけなので、簡単に理解できると思います。数式に間違いがありましたらご連絡ください。

[yusugomori]

数式で書き下す Convolutional Neural Networks (CNN)

CNNは画像認識の分野で驚異的な精度を誇るディープラーニングのアルゴリズムのひとつであるものの、ぱっと見がとても複雑な構造をしているため、実装するのも大変そうです。 実際、ネットや文献上で見られる多くのCNNの実装は、Theano (pythonのライブラリ)の自動微分機能を使っていたり、MATLABの組み込み関数を使っているものがほとんどです。 そのためか、きちんと forward propagation & backpropagation を数式で書き下している文献はないように思いました。（もちろん、楽に実装できるならばそれはそれで素晴らしいことです。） そこで、どうすれば CNN を実装するための数式を書き下せるのか、レイヤーごとに分けて導出していきたいと思います。

まず、CNN がどんな層に分解できるのかについて。これは、下記の３つで表せるでしょう。

Convolution Layer： 畳み込みレイヤー

Activation Layer： 活性化レイヤー

MaxPooling Layer： プーリングレイヤー

この３層をひとつのセットとして、ディープラーニングの場合はこのセットを積み重ねていくのが基本形です。（プーリングレイヤーは、Max PoolingがデファクトスタンダードなのでMaxPooling Layerと書いています。また、モデルの最後に付く通常の多層パーセプトロン層はここでは省いています。）

しかし、この順番は特に決まっているわけではなく、研究によっては Convolution → MaxPooling → Activation で実験していたり、Convolution → Activation → MaxPooling で実験していたりと様々です。数式では違いはほとんど出ないのですが、ここでは後者を前提として数式を考えてみます。

複雑に見えるCNNですが、この３つのレイヤーの feed-forward と backpropagation を数式で表してしまいさえすれば、どんな言語でも実装が可能になるはずです。

では、順番に見ていきましょう。まずは畳み込みレイヤーから。 まずはと言いつつ、この層はカーネルの学習があったり、複数チャネルの場合があったりと一番煩雑になるため、簡単のために最初は画像が１チャネル（グレースケール）の場合にどうなるかを考えてみます。

・Convolutional Layer (1 channel)

さて、理解しやすくするために、下の図に則って数式を表わしていくことにします。

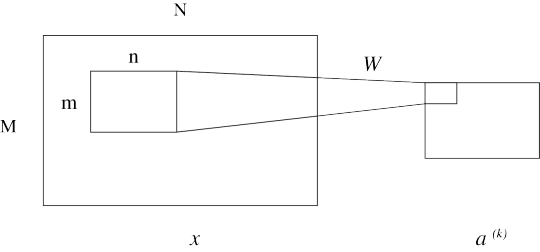
\( M, N \) はインプット画像のサイズ、\( m, n \) はカーネル（畳み込みフィルター）のサイズ、 \( k \) はカーネルのインデックス番号を表しており、 また、 \( x \) は入力画像データ、 \( a^{\,(k)} \) は、畳み込みレイヤーを通した後の２次元データを表しています。理解のしやすさのために、 カーネル \( \, k \, \) に対応しているんだぞ、ということを明記しています。 すると、畳み込みは以下の式で表すことができます：

\[ a_{ij}^{(k)} = \sum_{s = 0}^{m - 1} \sum_{t = 0}^{n - 1} w_{s\,t}^{(k)} \,x_{(i + s)(j + t)} + b^{(k)} \]

ここで、\(w^{(k)}\) はカーネルを、\(b^{(k)}\)はバイアスを表しています。これで、畳み込みレイヤーの feed-forward は書き下すことができました。 続いて、backward (backpropagation) について考えてみます。学習すべきモデルのパラメータは \( w^{(k)} \)および\( b^{(k)} \)であるため、 誤差関数を\( E \) で表したとすると、それぞれの勾配は次のように書くことができます：

\[ \begin{align} \frac{\partial E}{\partial w_{s\,t}^{(k)}} &= \sum_{i = 0}^{M-m} \sum_{j = 0}^{N-n} \frac{\partial E}{\partial a_{ij}^{(k)}} \frac{\partial a_{ij}^{(k)}}{\partial w_{s\,t}^{(k)}} \nonumber \\\\\ \nonumber \\\\\ &= \sum_{i = 0}^{M-m} \sum_{j = 0}^{N-n} \frac{\partial E}{\partial a_{ij}^{(k)}} \, x_{(i+s)(j+t)} \nonumber \\\\\ \nonumber \\\\\ \nonumber \\\\\ \frac{\partial E}{\partial b^{(k)}} &= \sum_{i = 0}^{M-m} \sum_{j = 0}^{N-n} \frac{\partial E}{\partial a_{ij}^{(k)}} \frac{\partial a_{ij}^{(k)}}{\partial b^{(k)}} \nonumber \\\\\ \nonumber \\\\\ &= \sum_{i = 0}^{M-m} \sum_{j = 0}^{N-n} \frac{\partial E}{\partial a_{ij}^{(k)}} \end{align} \]

ここで、バックプロパゲーションの誤差

\[ \delta_{ij}^{(k)} := \frac{\partial E}{\partial a_{ij}^{(k)}} \]

は、前のレイヤー（feed-forwardでは次のレイヤー）から逆伝播してきているはずなので、上式を用いてモデルパラメータを更新することができることになります。

Convolution Layer から更に逆伝播が必要なとき（すなわちディープな層になっているとき）は、 畳み込み層の誤差

\[ \frac{\partial E}{\partial x_{ij}} \]

を求める必要があるので、こちらも書き下してみましょう。次のように表すことができます：

\[ \begin{align} \frac{\partial E}{\partial x_{ij}} &= \sum_{s = 0}^{m - 1} \sum_{t = 0}^{n - 1} \frac{\partial E}{\partial a_{(i-s)(j-t)}^{(k)}} \frac{\partial a_{(i-s)(j-t)}^{(k)}}{\partial x_{ij}} \nonumber \\\\\ \nonumber \\\\\ &= \sum_{s = 0}^{m - 1} \sum_{t = 0}^{n - 1} \frac{\partial E}{\partial a_{(i-s)(j-t)}^{(k)}} \, w_{s\,t}^{(k)} \end{align} \]

ここで注意すべきなのは、\( i - s < 0 \) または \( j - t < 0 \) となり得る場合があるということです。このときは

\[ \frac{\partial E}{\partial a_{(i-s)(j-t)}^{(k)}} = 0 \]

として計算をすることになります。 誤差の式を見ると、カーネル \( w \) を flip した（行・列ともにひっくり返した、すなわち180°回転した）フィルターとの畳み込みになっていることがわかるでしょう。 畳み込みを逆伝播するのでflipの畳み込みになっている、という様に解釈できるでしょうか。これで、次のレイヤー（feed-forwardでは前のレイヤー）に伝播すべき誤差を求めることができます。

・Activation Layer

続いて、活性化レイヤーです。最近のトレンドとして、sigmoid関数やtanh関数を使うよりも、ReLU (Rectified Linear Unit) を使うことが多いので、ReLUでの式を書いてみます。 これは全く難しくありません。まずは feed-forward から：

\[ a_{ij} = {\rm ReLU}\,(x_{ij}) = {\rm max} \,(0, x_{ij}) \]

また、 backward は次のように表せます：

\[ \begin{eqnarray} \frac{\partial E}{\partial x_{ij}} = \begin{cases} \frac{\partial E}{\partial a_{ij}} & \, if \,\, a_{ij} \geq 0 \nonumber \\\\\ \, & \, \nonumber \\\\\ 0 & \, otherwise \end{cases} \end{eqnarray} \]

・MaxPooling Layer

Max Pooling については、フィルターが正方形でなくても適用はできるものの、 正方形にしてもしなくても大差はないので、計算が簡単になる正方形で表すのが普通です。 この層も、学習すべきパラメータはないので、feed-forward, backward ともに 前後のレイヤーにつなげる式を書くだけで終わりです。 feed-forward は次のようになります：

\[ a_{ij} = {\rm max}\, ( x_{(li+s)(lj+t)} ) \,\, {\scriptstyle where \,\, s \in [0, \,l], \,\, t \in [0, \,l] } \]

ここで、 \( l \) はフィルタのサイズを表しています。 また、backward (backpropagation) は次のようになります：

\[ \begin{eqnarray} \frac{\partial E}{\partial x_{(li+s)(lj+t)}} = \begin{cases} \frac{\partial E}{\partial a_{ij}} & \, if \,\, a_{ij} = x_{(li+s)(lj+t)} \nonumber \\\\\ \, & \, \nonumber \\\\\ 0 & \, otherwise \end{cases} \end{eqnarray} \]

これで３つの層の feed-forward, backpropagation の導出ができました。 しかし、カラーの画像やディープラーニングに対応するためには、畳み込みレイヤーで複数チャネルの場合を考えなくてはなりません。 こちらについても考えてみましょう。

・Convolutional Layer (multi-channel)

複数チャネルの場合を図にすると、下のように表すことができます。

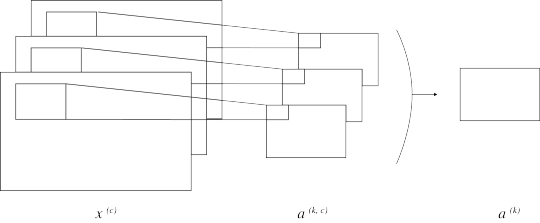
１チャネルのときに比べ、新しくチャネル\(c\) というパラメータが増えました。 そのため、伝播の式もそれぞれチャネルの分、ループが増えることになります。 feed-forwardの式を書いてみると次のようになります：

\[ \begin{align} a_{ij}^{(k)} &= \sum_{c} a_{ij}^{(k, c)} \nonumber \\\\\ \nonumber \\\\\ &= \sum_{c} \, \sum_{s = 0}^{m - 1} \sum_{t = 0}^{n - 1} w_{s\,t}^{(k, c)} \,x_{(i + s)(j + t)}^{(\nonumber c)} + b^{(k)} \end{align} \]

ここで、バイアスは畳み込み後に加えられる項のため、 \(b^{(k)}\) は \( c \) に依存しないことに注意しましょう。 すると、モデルパラメータの更新式は下記のように表すことができます：

\[ \begin{align} \frac{\partial E}{\partial w_{s\,t}^{(k, c)}} &= \sum_{i = 0}^{M-m} \sum_{j = 0}^{N-n} \, \frac{\partial E}{\partial a_{ij}^{(k)}} \frac{\partial a_{ij}^{(k)}}{\partial w_{s\,t}^{(k, c)}} \nonumber \\\\\ \nonumber \\\\\ &= \sum_{i = 0}^{M-m} \sum_{j = 0}^{N-n} \, \frac{\partial E}{\partial a_{ij}^{(k)}} \,x_{(i+s)(j+t)}^{(\nonumber c)} \nonumber \\\\\ \nonumber \\\\\ \nonumber \\\\\ \frac{\partial E}{\partial b^{(k)}} &= \sum_{i = 0}^{M-m} \sum_{j = 0}^{N-n} \, \frac{\partial E}{\partial a_{ij}^{(k)}} \end{align} \]

見た目はだいぶごちゃついていますが、基本的にはチャネルごとの和をとる項が増えたにすぎません。 同様にバックプロパゲーションも下記のように導出することができます：

\[ \frac{\partial E}{\partial x_{ij}^{(\nonumber c)}} = \sum_{k} \, \sum_{s = 0}^{m - 1} \sum_{t = 0}^{n - 1} \frac{\partial E}{\partial a_{(i-s)(j-t)}^{(k)}} \, w_{s\,t}^{(k, c)} \]

これで、複数チャネルの場合にも対応することができるようになりました。 \( \sum \)が多いことからも、実装するとforループが何重にもなることがわかります。 マシンの処理能力が高くないとCNNを走らせるのは難しいでしょう。 CNNの実装はまだしていませんが、できたらまた公開する予定です。 数式に誤りがありましたらご連絡ください。

[yusugomori]

JavaによるDeep Learningの実装（Dropout + ReLU 編）

前回のpythonに引き続き、今回はjavaでDropout + ReLUを実装したコードを紹介します。package名は”DeepLearning”としました。下記の４つのファイルで構成されています。

・Dropout.java ・HiddenLayer.java ・LogisticRegression.java ・utils.java

ReLU以外の活性化関数にも対応できるよう、ラムダ式を用いて”activation”という変数に関数を入れています。 そのため、JDK 1.8 以上のみの対応になります。コードは下記です。

[ Dropout.java ]

https://gist.github.com/yusugomori/fdc1d8a5f050caad01c2

[ HiddenLayer.java ]

https://gist.github.com/yusugomori/dfc1d37c07bc80740233

[ LogisticRegression.java ]

https://gist.github.com/yusugomori/fa37fa32df4153940ee6

[ utils.java ]

https://gist.github.com/yusugomori/54040c9292851a253764

GitHubリポジトリも参考ください。

[yusugomori]

PythonによるDeep Learningの実装（Dropout + ReLU 編）

久しぶりのブログ更新となります。 今回は、Dropout + ReLU のコード（python）を紹介します。

最近の Deep Learning 界隈は、もっぱらDropoutと新しい活性化関数の組み合わせが多いみたいですね。 しばらく触れないでいる内に、以前は最前線だった Deep Belief Nets や Stacked Denoising Autoencoders がすっかり下火になってしまったようで…。

Dropout + ReLU や Dropout + Maxout などが流行っているみたいですが、これは結局、いかに疎な（sparseな）ニューラルネットワークを構築できるかが学習の鍵になっている、ということなのでしょう。シンプルが一番というべきなのでしょうか…。 ともあれ、Dropoutは実装が難しくないのは嬉しい限りです。 ReLU (Rectified Linear Units) もとても簡単です。（活性化関数自体は本当は Rectifier です。念のため。）

ソースコードは下記になります。いつもの通り、Githubリポジトリはこちらから。 ※ ちなみに、こちらのコードではHinton氏の論文で用いられているMomentumなどは使っていません。予めご了承ください。

https://gist.github.com/yusugomori/cf7bce19b8e16d57488a

Dropoutで注意すべきは、バックプロパゲーションのときにも Dropout Mask をかけるのを忘れないようにすることでしょうか。

同じ素子がDropoutされたニューラルネットワークで学習しなければならない、という意味を考えると当たり前と言えば当たり前ですが…。 また、テスト・予測のときには、Dropoutの代わりにDropout確率（p=0.5が多い）をネットワークのパラメータにかけ、平滑化のような処理をかませることでDropoutの代替をします。

バグ・誤りなどありましたらご連絡ください。

[yusugomori]

GoによるDeep Learningの実装（Stacked Denoising Autoencoders 編）

GoによるDeep Learning実装シリーズ。今回はStacked Denoising Autoencoders（SdA）になります。

https://gist.github.com/9cf389915dd9dcfea518

これまで、Python, C, C++, Java, Scala, Goと実装してきましたが、同じアルゴリズムを違う言語で書くと、それぞれの特徴が（何となく）つかめていいですね。

つい最近公開された「Streem」も気になるところです…！

[yusugomori]

GoによるDeep Learningの実装（Deep Belief Nets 編）

前回に続き、GoでDeep Learningの実装をしてみました。今回はDeep Belief Nets (DBN) です。

$ go run DBN.go で実行、もしくは

$ go build -o DBN.out DBN.go でコンパイルしてから試してみてください。

https://gist.github.com/a3572642a82f02a7b7a6

C言語に近い書き方になりますが、GoだとSliceが使える分、多次元配列の受け渡しが楽でいいですね。

[yusugomori]

GoによるDeep Learningの実装（Logistic Regression 編）

Golangをはじめたので、練習がてらDeep Learningシリーズの実装をしてみました。 まずはロジスティック回帰（Logistic Regression）から。 Goにはクラスがないので、C言語のように構造体をつかってオブジェクト指向っぽく書いています。

https://gist.github.com/be00f0e02b826d6c4477

今後、他の手法もアップデートしていく予定です。

※これまで実装したコードは、githubリポジトリにまとめてあります。 また、Deep Learning実装シリーズ記事は、こちらからご覧ください。

[yusugomori]

ScalaによるDeep Learningの実装

Deep Learning 実装シリーズ。今回は、Scalaです。いつもの通り、Deep Belief Nets と Stacked Denoising Auto-encoders を掲載しています。

Scalaはコンパイルしないでも実行することはできる言語ではありますが、実装したものは、一度 scalac でコンパイルしないと何も結果が出力されない作りとなっています。

https://gist.github.com/yusugomori/6668887

  SdA.scala

https://gist.github.com/yusugomori/6668922

ソースコードはgithubでも公開してますので、そちらも参考にしてください。 （気付いたらStar数が350超、Fork数ももうすぐ200という数になっていて、驚いています…。）

[yusugomori]

JavaによるDeep Learningの実装（Deep Belief Nets, Stacked Denoising Autoencoders 編）

これまでPythonやC/C++でDeep Learningを実装してきましたが、Javaでも同様に実装しましたので、コードを紹介しようと思います。

実装したものは、DBN（Deep Belief Nets）およびSdA（Stacked Denoising Autoencoders）となります。

コードの掲載順序は下記のようになっています。

DBN.java

RBM.java（Restricted Boltzmann Machine，制約付きボルツマンマシン）

SdA.java

dA.java（Denoising Autoencoders）

LogisticRegression.java（ロジスティック回帰）

HiddenLayer.java（ニューラルネットワークの隠れ層を表すクラス）

RBMはDBNの教師なし学習部分、dAはSdAの教師なし学習部分となるクラスであり、LogisticRegressionおよびHiddenLayerは両者に共通のクラスです。

DBN.java

https://gist.github.com/yusugomori/5211633

RBM.java

https://gist.github.com/yusugomori/5211631

SdA.java

https://gist.github.com/yusugomori/5211606

dA.java

https://gist.github.com/yusugomori/5211614

LogisticRegression.java

https://gist.github.com/yusugomori/5211626

HiddenLayer.java

https://gist.github.com/yusugomori/5211629

[yusugomori]

JavaScript＋コマ画像によるFlashレスなアニメーションの作成

PCでもモバイルでも動作するアニメーションをウェブページに付ける場合、簡単な動きならばCSS3やJavaScriptを用いることで容易に作成することができると思います。 一方で、複雑なアニメーションを実現するのはCSS3やJavaScriptでは難しく、モバイルでもFlashが使えたらなあ…と感じることが多々あるのではないでしょうか。

今回はこうした問題を解決するために、JavaScript＋コマ画像を使うことにより、どんなに複雑なアニメーションでもFlashなし（およびムービーファイルなし）で作成する方法を紹介したいと思います。 サンプルはこちらです。「START」ボタンをクリックすると、画面真ん中にある三角形の画像がズームするアニメーションが開始されます。Flashは使っていませんので、モバイルでも動作が確認できるかと思います。

では、Flashレスなアニメーションの作成方法について順に説明していきます。と言っても、一番大変なのはコマ画像を用意するところだと思いますが…（笑） JavaScriptによる実装のTipsとしては、$.Deferred( )と画像のプリロードの関連についてが挙げられます。

コマ画像の用意

コマ画像は、画像サイズにも依りますが、1秒あたり5〜20フレームを目安にするとアニメーションがスムーズに動きます。 下の画像は、最初の５フレーム、およびその後５フレームごとのものを表しています。

画像のプリロードの実装

アニメーションをスムーズに行うには、予めコマ画像の全てがキャッシュされている必要があります。そこで、以下のようなコードにより、画像のプリロードを行います。

https://gist.github.com/yusugomori/5193467

preload メソッドを実行することにより、画面には表示されない <img />タグが生成されます。その src をコマ画像のパスとすることで、画像がキャッシュされます。

しかし、上記のコードのみでは画像のリクエストを投げるのみで、画像が完全に取得されてから次の処理が行われる保証はありません。 そこで、jQueryの $.Deferred を用いて、画像の読み込みが完全に行われてから次の処理が行われるようにします。

https://gist.github.com/yusugomori/5193581

preload が dfd.promise() を返すので、.then や .fail を用いて画像読み込み後の処理を実装できるようになります。以下がそのサンプルです。

https://gist.github.com/yusugomori/5193623

アニメーションのコマ画像のように、複数画像の読み込みに対応させるには、 以下のように .when を使います。これで、画像のプリロード処理ができました。

https://gist.github.com/yusugomori/5193668

アニメーションの実装

画像のプリロードは完了しているので、同じ<img />タグ内で画像を連続で切り替えていくことにより、アニメーションは実装できます。コマ送りには、setTimeout を用います。

https://gist.github.com/yusugomori/5193874

コード内の refreshRate がコマ送りの間隔となりますが、この値を小さくしすぎると、処理が追いつかずにアニメーションがスムーズに行えなくなる可能性があります。 コードのように refreshRate = 200 とすると、 fps = 1000 / 200 = 5 となりますが、先ほども触れたように、fps = 20 くらいがスムーズなアニメーションを実現する上限だと思います。

プリロードとアニメーション全体のコードは以下のようになります。

https://gist.github.com/yusugomori/5193969

  サンプルページでは図形の拡大という簡単なアニメーションであったため、CSS3だけでも実現できると思いますが、より複雑な動きが必要な場合は、今回紹介した方法が役に立つのではないでしょうか。 例えば、Yahoo! JAPAN インターネット クリエイティブアワード 2012 に応募した作品のひとつである「根菜爆弾」（残念ながら落選してしまいましたが…）では、コマ画像を使ったアニメーションを採用しています。 （タッチイベントやシェイクイベントを取得していますので、モバイル端末などで動作を確認してください。） ページ上部のバナーをタップすると、人参に導火線がついた画像が出てきますが、この導火線に点いた火を動かすのにコマ画像を使っています。

また、コマ画像を使う利点として、この根菜爆弾のようにアニメーションを途中で止める必要がある場合、簡単に処理を実装できることが挙げられます。 アニメーションは setTimeout によるループ処理なので、ループさせているメソッドにイベントを監視するフラグを渡しておき、イベントが感知された時点でループを止めてしまえば、アニメーションが停止することになります。

複雑なアニメーションの場合、コマ画像を用意する必要があるという点についてはFlashなどと同じですが、マルチプラットフォームで動作するアニメーションの手段として、JavaScript＋コマ画像を検討してみてはいかがでしょうか。

[yusugomori]

C/C++によるDeep Learningの実装（Deep Belief Nets, Stacked Denoising Autoencoders 編）

これまで、PythonでDeep Learningを実装したコードを紹介してきましたが、今回はCおよびC++で実装したコードを紹介したいと思います。 実装したものは、Deep Belief Nets（DBN）、Stacked Denoising Autoencoders（SdA）となります。 コード量が多いので分かりにくいかもしれませんが、

DBN.c

SdA.c

DBN.cpp

SdA.cpp

の順番で掲載しています。 C言語での実装は、こちらの、C言語によるオブジェクト記述法を参考にさせて頂きました。

  DBN.c

https://gist.github.com/yusugomori/5003420

  SdA.c

https://gist.github.com/yusugomori/5003435

  DBN.cpp

https://gist.github.com/yusugomori/5003457

  SdA.cpp

https://gist.github.com/yusugomori/5003473

[yusugomori]

PythonによるDeep Learningの実装（Stacked Denoising Autoencoders 編）

Deep Learningの実装に関する記事が連続していますが、今回はStacked Denoising Autoencoders（SdA）について紹介します。 SdAは、前回の記事で実装したDenoising Autoencoders（DA）の層を組み合わせていくことで特徴抽出を行い、 最後の層でロジスティック回帰を用いて教師あり学習を行います。一応、SdAはDeep Belief Netsよりも画像認識では高い精度が得られているみたいです。

https://gist.github.com/yusugomori/4721355

PythonによるDeep Learningの実装シリーズは、githubのリポジトリもご参照ください。 誤り・訂正がありましたら、コメント等、宜しくお願いいたします。

[yusugomori]

PythonによるDeep Learningの実装（Denoising Autoencoders 編）

今回は、Deep Learningに用いられているDenoising Autoencoders （DA)）のコードを紹介したいと思います。 細かな説明や数式の導出については前回の記事で紹介してありますのでそちらも参考にしてください。 今回も、Pythonで実装しており、numpyのみを使っています。（sysはstderrへの出力に用いているのみなので、なくてもよい）

https://gist.github.com/4700792

DAは、Deep Belief Nets（DBN）で言うところの、制約付きボルツマンマシン（Restricted Boltzmann Machine, RBM）の部分に対応しています。

（DBNの記事はこちら、RBMの記事はこちら。）

DAの層を積み重ねたDeepなニューラルネットワークは、Stacked Denoising Autoencodersとなりますので、そちらも近々、実装してみたいと思います。