#Logarithm of Complex Number

[9nid]

✅ Check Point 02: Complex Numbers Questions Practice – JEE Main ke liye Full Concept Recap

Hello JEE Aspirants!Aaj ke is blog mein hum cover kar rahe hain Complex Numbers ke sabhi important topics through 18 conceptual questions. Agar aap JEE Main ya Class 11 Maths padh rahe ho, to yeh ek perfect revision aur practice checkpoint hai. Hum basic se lekar advanced tak sab kuch revise karenge practical examples ke through. Conjugate of a Complex NumberAgar koi complex number z = a + ib…

[edusquaremaths]

✅ Check Point 02: Complex Numbers Questions Practice – JEE Main ke liye Full Concept Recap

Hello JEE Aspirants!Aaj ke is blog mein hum cover kar rahe hain Complex Numbers ke sabhi important topics through 18 conceptual questions. Agar aap JEE Main ya Class 11 Maths padh rahe ho, to yeh ek perfect revision aur practice checkpoint hai. Hum basic se lekar advanced tak sab kuch revise karenge practical examples ke through. Conjugate of a Complex NumberAgar koi complex number z = a + ib…

[thedemises]

im surprised that algebra II is usually taught in 11th grade

[math-journal]

Cheat Sheet

Shortcut to basic concepts that I might need to review in future.

[mathmedicine]

ALEVEL PURE MATHEMATICS 3 (PAPER 3)

PURE MATHEMATICS 2/3 (2002-2010) C1 Algebra C2 Logarithmic and Exponential Functions C3 Trigonometry C4 Differentiation C5 Integration C6 Numerical Methods C7 Vectors C8 Differential Equations C9 Complex Numbers

[bobacupcake]

Can you do one about the Sea of Thieves water?

OK

so . there was a biiig long talk about this at siggraph one year!! you can watch that here if you'd like . in the time between me getting this ask and me fully recreating the water, acerola also released a great video about it . the biiig underlying thing they do and the reason why it looks so good is they are making a Really Detailed Ocean Mesh in realtime using something called an FFT (fast fourier transform) to simulate hundreds of thousands of waves, based on a paper by TESSENDORF

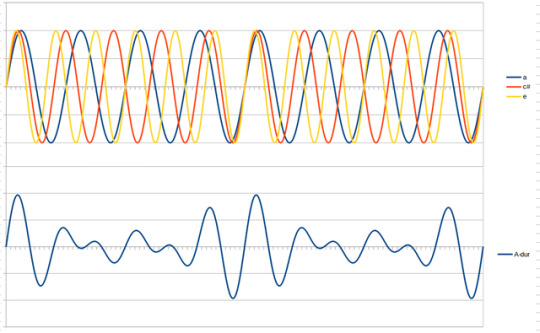
WHAT IS AN FFT - we'll get to that. first we have to talk about the DFT - the discreet fourier transform. let's say you have a SOUND. it is a c chord - a C, an E, and a G, being played at the same time. all sounds are waves!!! so when you play multiple sounds at the same time, those waves combine!!! like here: the top is all 3 notes playing together, so they form the waveform at the bottom!!

now if someone handed you the bottom wave, could you figure out each individual note that was being played? how about if someone handed you a wave of One Hundred Notes. you would think it would be very hard. and well, it would be, if not for the Discreet Fourier Transform.

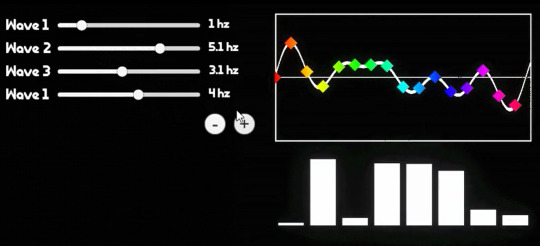
essentially, there is a way to take a bunch of points on a waveform comprised of a bunch of different waves, add them all together, do some messed up stuff with imaginary numbers, that will spit back out at you what individual waves are present. i made a little test program at the start of all this: the left are the waves i am putting into my Big Waveform, the top right is what that ends up looking like, and all the little rainbow points on it are being sampled to spit out the graph at the bottom right: it shows which frequency bands the DFT is finding (here it is animated)

this has enormous use cases in anything that deals with audio and image processing, and also,

THE OCEAN

tessendorf is basically like, hey, People Who Are Good At The Ocean say that a buuuunch of sine waves do a pretty good job of approximating what it looks like. and by a bunch they mean like, hundreds of thousands to millions. oh no.... if only there was a way we could easily deal with millions of sine waves..........

well GREAT news. not only can you do the DFT in one direction, but you can also do it in REVERSE. if you were to be given the frequency graph of a noise for example, you could use an INVERSE DFT to calculate what the combined wave graph looks like at any given time. so if you were to have say, the frequency graph of an oceaaaan, for example, you could calculate what the Ocean wave looks like at any given time. and lucky for us, it works in two dimensions. and thats the foundation of the simulation !!!!!

BUT WAIT

as incredible as the DFT is, it doesn't scale very well. the more times you have to do it, the slower it gets, exponentially, and we are working with potentially millions of sine waves here

THE FAST FOURIER TRANSFORM here we are . the fast fourier transform is a way of doing the discreet fourier transform, except, well, fast. i am Not going to explain the intricacies of it because its very complex, but if you want to learn more there are a ton of good 30 minute long videos on youtube about it . but essentially, due to the nature of sine waves repeating, you can borrow values as you go, and make the calculation Much faster (from exponential growth to logarithmic growth which is much much slower, and scales very well at higher numbers). it's, complicated, but the important part is it's so much faster and the diagram kind of looks like the shadow the hedgehog story plot

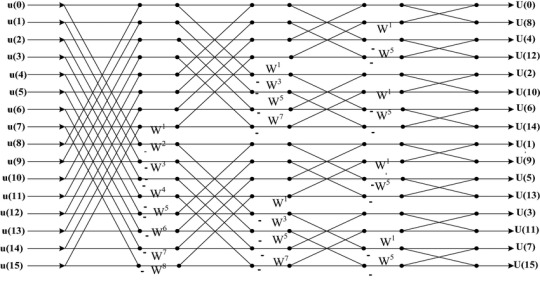
so if we use the inverse FFT on a graph of a rough estimate of what frequency of waves in the ocean (called a spectrum, basically tells us things like how many small waves, how many big waves, how different waves follow the wind direction. sea of thieves uses one called the phillips spectrum but there are better ones out there!!) now we have our waves !!!!!!! we can also use another inverse FFT to get the normals of the waves, and horizontal displacement of the waves (sharpening peaks and broadening valleys) through some derivatives . yayy calculus

OK MATH IS OVER. WE HAVE OUR WAVES!!! they are solid pink and look like pepto bismol. WHAT NOW

i cheated a bit here they look better than not being shaded because i am using the normals to reflect a CUBEMAP to make it look shiny. i think sea of thieves does this too but they didnt mention it in their talk. they did mention a FEW THINGS THEY DID THOUGH

FIRST OFF - SUBSURFACE SCATTERING. this is where the sun pokes through since water is translucent. SSS IS REALLY EXPENSIVE !!!!!! so they just faked it. do you remember the wave sharpening displacement i mentioned earlier? they just take the value where the waves are being sharpened and this will pretty naturally show off the areas that should have subsurface scattering (the sides of waves). they make it shine through any time you are looking towards the sun. they also add a bit of specular ! sss here is that nice blue color, and specular is the shiny bits coming off the sun. the rest of the lighting is the cubemap i mentioned earlier, i dont know if thats what they use but it looks nice !!!!!

then the other big thing that they do is the FOAM !! sorry i lied. there's more math. last one. you remember the wave sharpening displacement i Just mentioned. well they used that to find something called the JACOBIAN and well im not even going to begin to try and explain what it means but functionally what it does, is when the jacobian is NEGATIVE it means waves are clipping into eachother. and that means we should draw some foam!!! we can also blur and fade out the foam texture over time and continuously write to it to give it some movement, and bias this value a bit to make more or less foam. they do both of these!!!

YAYYYYY !! OK !! THAT'S SEA OF THIEVES WATER!!!!! THANKS FOR WAITING ALL THIS TIME. you can see my journey here if you would like to i have tagged it all oceanquest2023

thank you everyone for joining me :) i had fun

[vedalkensamurai]

For a given complex number c, what is the behavior of the iterative sequence z_(n+1) = e^(z_n) + c, where z_0 = 0 and e is the base of the natural logarithm? Experimenting with a few random values, I noticed that the sequence often converges, either to a single value or a repeating loop of values. I wondered if there was any pattern to how quickly it converges, so I wrote a program to systematically check.

In the image above, each pixel represents a complex number ranging from -5.12 - 5.12i to 5.12 + 5.12i, with a distance of 0.04 between neighboring pixels. At each point the program iterates until it reaches a value it's seen before at that point (within a tolerance of 10^-10), then colors that point accordingly: red if it reaches it very quickly through magenta if it gets there slowly, and black if it never repeats in 256 iterations. (This is much slower to calculate than the Mandelbrot set, since it needs to check each z against all previous zs, whereas the Mandelbrot set only checks against a constant escape threshold.)

The other question I had about these sequences was, when they do converge to loops, how long are those loops? My early experiments showed a variety of periods. So of course I wrote a program to check the period lengths too. In the image below, the brightest purple corresponds to single-point convergence, and as the loops get longer the purple gets darker. Once again, black is where no repetition was found. Here I only did 128 iterations per point to save time, so the black area is a bit bigger than above.

I'm interested in the borders between the different purples, as it looks like there is some complexity in the shapes there. I'll be doing some zoomed-in images of those areas next.

[otesunki]

where can i find information on {0|0}. on *. i'm obsessed

colossal infodump incoming

alright there's this Very Very Good Book called Winning Ways for Your Mathematical Plays which explains combinatorial game theory and how they link into surreal numbers in what can only be described as an Unreasonable level of detail, including how it ties into Surreal Numbers oh God surreal numbers is just as loaded of a term Okay let me take a brief detour into That

so surreal numbers are like. imagine defining every number as a pair of sets of other numbers. a set of numbers Less than it and a set of numbers Greater than it. and we write this as foo = {less than foo|greater than foo}. so like. 0 = {|}, 1 = {0|}, 2 = {1|}, 1/2 = {0|1}, -1 = {|0}, that type of thing

the reason why surreal numbers are mindmelting is the fact that they happen to be the Largest Totally Ordered Proper Class and they contain Literally Every Other Totally Ordered Number System inside of them. totally ordered here means that any two numbers are related by < > or =. so like. complex numbers and quaternions aren't included. surreal numbers also behave just like real numbers in that you can do arithmetic on them exactly how you'd do arithmetic with any other real number. and for the surreal numbers that are also real numbers the classic laws of commutativity and associativity hold.

however the surreal numbers are. a.

a bit bigger than just all the real numbers. because there are also numbers that are infinitely big or small and you can make infinitely-bigger-than-infinte numbers and the arithmetic operations still work and also have you ever wanted to take the logarithm base infinity of a number too bad that's defined now

games are what happens when you look at the surreal numbers and go that's for rookies and decide that actually yes {1|-2} makes sense what are you Talking about. why Can't on = {on|} that's a perfectly sane definition also over = {0|over} also Also actually you can define a number that's Even Closer To Zero than over is and if you churn through the calculations you can literally Prove that 0 < tiny < over Yes the number is called tiny

right okay so what is star? in fact if x = {A|B} then -x = {-B|-A} and because A and B are both just the set { 0 } and 0 is {|} you can trivially prove that negating star gives you back star, it's not greater than zero because it has zero in the right hand side, it's not less than zero because it has zero in the left hand side, and it's not Equal to zero because playing a game with a value of zero means that the first player Loses but a game with a value of Star means that the first player Wins which means neither player has an advantage but it's a balanced game in a different way to how 0 is balanced and this is reflected in the Thermograph of star which is a way to draw what star looks like when you Heat it up and Heating a number basically means moving its left and right hand sides closer together in value until eventually they meet up

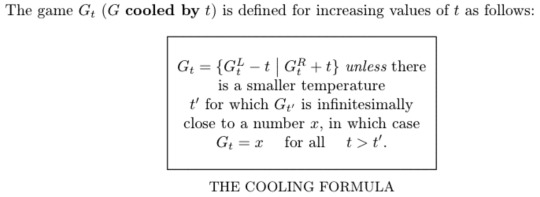
so Zero because both of its sets are empty is just a vertical line at x=0 because it can't heat up nor cool down but Star on the other hand stays at 0 when it is cooled down but if you Heat it up (make t negative) then actually the two zeroes in it begin Diverging and going in opposite directions

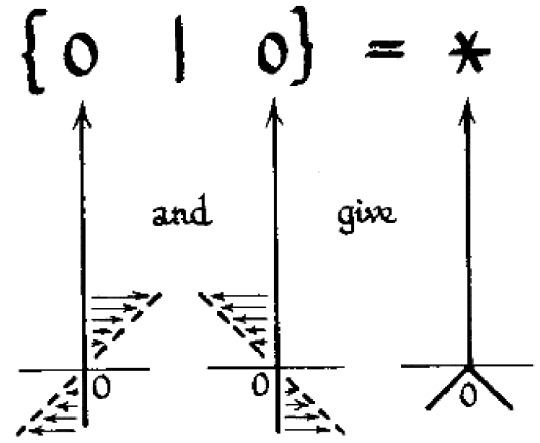
but because the whole thing is Horizontally symmetric it means that the number is its own negative because negating a number is equivalent to a horizontal flip. also if you thought thermographs couldn't get more complicated and involved you're wrong

so. That's. what. star is.

so have you ever wondered what would happen if you had a bunch of numbers that are all mutually recursive and not defined in terms of anything el-

[lectronicproot]

I said this on Bluesky and I really should link these two accounts in a pinned post or some but eh, but basically I’m world building and I saw this video

I knew the relation between this three but it never came across my mind that it would be possible to make the relation between the three more transparent lol.

In my worldbuilding project the species I’m focusing on rn develops pretty complex math a while before most other civilizations and I wonder if it would seem natural to have their math notation have this relation be clearer

I wonder if it could be reflected in their language too, maybe the words for using powers is related to something like “folding”, since when you fold something the creases form an exponentially growing amount of segments.

Rooting could be unfolding, straightening, flattening, something like that. The whole paper analogy kinda depends on whether they discover paper though… they’re in a rainforest, and while it’s possible to make paper from trees, without modern technology they would specifically have to use soft wood, and I don’t know if rainforest trees are soft or hard lol, tho things like plant fibers are also possible materials

Log is harder, but something like just “finding the fold” would suffice, considering my conlang is kinda Chinese like with verb-noun compounds being grammaticalised into their own words. Maybe something like fold scale or something would work.

I feel like I’m focusing too much on the whole paper etymology though. My civilization is one that can naturally fly and are traders. Maybe exponents could be “reaching to the sky” by the exponent amount? Rooting is maybe descent then? Or maybe finding a root is finding what a number is “anchored” or “tied down” to. And logarithm is referred to as the “shadow” of these two?

Conlanging is always hard for more abstract concepts but I find it really interesting to try and do regardless lol. If anybody else has any ideas of other ways a culture could refer to these functions then I’d like to hear them!

[geometrymatters]

Tatyana O. Sharpee’s work in the realm of geometric cognition—a field dedicated to understanding how the brain interprets and represents spatial information—has yielded groundbreaking insights into how our minds map the world around us. Continuing her previous argument for hyperbolic geometry in neural circuits, the recent paper, co-authored with Huanqiu Zhang, P. Dylan Rich, and Albert K. Lee, sheds light on the hyperbolic geometry of hippocampal spatial representations.

The hippocampus, a crucial part of the brain involved in memory and spatial navigation, houses ‘place cells’—neurons that fire when an animal is in a particular location. The geometry of these spatial representations, however, has remained largely unknown. Breaking new ground, Sharpee and her team reveal that the hippocampus does not represent space according to a linear geometry, as might be expected. Instead, they discovered a hyperbolic representation.

We investigated whether hyperbolic geometry underlies neural networks by analyzing the responses of sets of neurons from the dorsal CA1 region of the hippocampus. This region is considered essential for spatial representation and trajectory planning.

Imagine holding a map of your city. A linear representation would be akin to the map’s scale, where an inch on paper corresponds to a fixed number of miles in reality. A hyperbolic representation, in contrast, changes the scale depending on where you are on the map. The implications of this discovery are profound. A hyperbolic representation provides more positional information than a linear one, potentially aiding in complex navigation tasks.

This hyperbolic representation isn’t static—it dynamically expands with experience. As an animal spends more time exploring its environment, the spatial representations in its brain expand. The expansion is proportional to the logarithm of time spent exploring, suggesting our brains continually refine our spatial maps based on our experiences. As we spend more time in an area, our mental map of that area becomes more detailed and expansive. This dynamic updating could be crucial for efficiently navigating familiar environments.

Continue Reading

[staplerpinheart]

Week 1: Day 2

Progress:

Maths: 10 questions of Complex Numbers from Exemplar and theory of Logarithm

Physics: Theory of Motion in Plane and cleared doubts and did some examples

Chemistry: Revision of Structure of Atom and Some Basic Concepts of Chemistry and cleared doubts

Notes:

Today was kinda slow, I wasn't as productive as I wanted, but it was fine, hoping to get more done tommorw! Made appam in the morning, and paired it up with maths. Left one class halfway though, but I did make it up by studying chem and the drank masala chai! Also my exam got postponed, but I'm kinda miffed about that.

time: 6 hours 15 minutes

[mathsinfluencer]

Did You Know the Math Simulation Software Desmos Graphing Calculator? 📊✨

Mathematics can be a daunting subject for many, but thanks to the incredible Desmos Graphing Calculator, the world of numbers, equations, and graphs has become more accessible and engaging than ever before! 🌟 Whether you’re a student, teacher, or math enthusiast, Desmos offers a fantastic tool that brings equations to life in a visually stunning way. Let’s dive into what makes this graphing calculator so special! 🚀

A User-Friendly Interface 🖥️😊

One of the first things you’ll notice about the Desmos Graphing Calculator is its clean and intuitive interface. You don’t need to be a tech genius to start plotting graphs. The layout is simple, making it easy for users of all ages to navigate through the various features. Just type in your equation, and watch as it instantly appears on the graph! ✍️➡️📈

Dynamic and Interactive Graphs 📉✨

Gone are the days of static and boring graphs. With Desmos, you can interact with your graphs in real-time. Want to see how a parabola shifts when you change the coefficient? Or how a sine wave stretches with different frequencies? Desmos lets you adjust parameters on the fly, showing you the immediate impact on the graph. It’s like having a math laboratory right at your fingertips! 🧪🔍

Supports a Wide Range of Functions 📚🔢

From basic algebraic equations to complex calculus functions, Desmos has got you covered. It supports a wide range of mathematical functions including trigonometry, logarithms, and even piecewise functions. This versatility makes it a valuable tool for both high school and college-level math. 📏🔍

Perfect for Teachers and Students 🧑‍🏫👩‍🎓

For educators, Desmos is a game-changer in the classroom. It allows teachers to create interactive lessons that can be shared with students, making learning more engaging. Students can experiment with equations and visualize concepts in a way that textbooks simply can’t match. Plus, the Desmos community is a treasure trove of shared graphs and activities, perfect for enhancing the learning experience. 📚📝

Accessibility and Collaboration 🤝🌍

Desmos is committed to accessibility. It’s available on any device with a web browser, and it’s free! Plus, with the collaborative features, students and teachers can work together on projects, making it a fantastic tool for group studies and classroom activities. The ability to save and share graphs means you can continue learning and exploring, anytime and anywhere. 🌐💡

Beyond Math: Creative Uses 🎨🌈

While Desmos is a powerhouse for mathematical graphing, its utility doesn’t stop there. Many users have found creative ways to use Desmos for art and design. By manipulating equations and parameters, you can create beautiful and intricate patterns. Who knew math could be so artistic? 🎨🖌️

Conclusion: Math Made Magical ✨🔮

The Desmos Graphing Calculator is more than just a tool; it’s a gateway to understanding and appreciating the beauty of mathematics. Its user-friendly interface, dynamic graphing capabilities, and vast range of functions make it an indispensable resource for anyone interested in math. Whether you’re solving complex problems or simply exploring the world of equations, Desmos makes the journey enjoyable and enlightening. So why wait? Dive into the world of Desmos and let the magic of math unfold before your eyes! 🌟📐🧮

[gweniala]

The Lost Marble

Short fanfiction, recounting nearly scene for scene a dream I had a few days ago. It's basically the creation myth but with maths.

The Lost Marble

Once upon a time, Quater made the first man in his garden. He made him out of wire, so he could test how he moved and talked before moving on with his design. The wire man lived happily in the garden. One day, Quater brought a bag of marbles to him.

“Look,” Quater said, pouring the marbles out into his palm. They were white, red, yellow, blue and black. “I made this for you. With these marbles, you can count. You can add numbers,” he showed the wire man how, “and subtract them. You can use them to multiply and divide, like so. This is how you perform exponentials and logarithms. You can handle singularities and complex numbers as well. Anything you desire.” Deftly he demonstrated everything to the wire man. “With these marbles, you can prove any mathematical theorem. Anything you can think of, you will be able to prove it or disprove it conclusively, once and for all. This is because each of the marbles is a universal truth, and together they make up all the knowledge in creation.”

The wire man watched in wonder. Quater took his right hand and made flesh on it from the marbles. The new hand had white skin and black fingers, and it was the hand of God. It was a hand that, if it took a pen, would write the direct words of Father. It was a hand which, if it took a brush, would create wonderful art. The wire man observed his new hand in amazement.

Quater took the flesh off and turned it back into marbles. He put them on a bench and said to the wire man: “I made this all for you. From these marbles, you will make the flesh of your entire body. They will constitute a brain which can name anything it observes, and a heart which can praise Father with the right words. Do you like it?”

The wire man cried out with delight and rushed to hug Quater. He knocked his creator over, so Quater fell on his butt right in the middle of the marbles. The white, red, yellow, blue and black orbs flew to all sides.

“Now look what you’ve done!” Quater cried out. “Come, gather the marbles up.”

The wire man did his best, but he was only wire. In the end, Quater had to find most of the marbles. By the evening, he counted them and sighed. “One red marble is missing,” he said. “Well, no matter. We will find it eventually. My son, make do with these marbles for now. Make your flesh and brain and heart out of them. You can add the last marble later when it is found.”

The wire man took the marbles bashfully. They were still magnificent truths, after all.

So it happened that when Quater exiled the first man from his garden, the last red marble had still not been found. The man left his creator’s bosom incomplete and unfinished. All people descended from this man, and that is why we feel like there is something missing from our lives. We stumble and err and cannot agree on the most basic of things. We are all missing that last, lost marble. With it, we would be complete. We would know the truth of the universe. Without it, we spend our lives searching the garden of Quater for the marble which would make us entire.

[kiskisur]

Lambert W Function, W(x)

In mathematics, the Lambert W function, also called the product logarithm, is a multivalued function, namely the branches of the converse relation of the function f(w) = we^w, where w is any complex number and e^w is the exponential function.

For each integer k there is one branch, denoted by W[k](z), which is a complex-valued function of one complex argument. W[0] is known as the principal branch. These functions have the following property: if z and w are any complex numbers, then

we^w = z, which holds if and only if

w = W[k](z) for some integer k.

When dealing with real numbers only, the two branches W[0] and W[-1] suffice: for real numbers x and y the equation

ye^y = x

can be solved for y only if x ≥ −1/e.

; we get y = W[0](x) if x ≥ 0 and the two values y = W[0](x) and y = W[-1](x) if −1/e ≤ x < 0.

The Lambert W relation cannot be expressed in terms of elementary functions. It is useful in combinatorics, for instance, in the enumeration of trees. It can be used to solve various equations involving exponentials.

For example, The maxima of the Planck, Bose–Einstein, and Fermi–Dirac distributions)

It also occurs in the solution of delay differential equations, such as y′(t) = ay(t − 1).

In biochemistry, and in particular enzyme kinetics, an opened-form solution for the time-course kinetics analysis of Michaelis–Menten kinetics is described in terms of the Lambert W function.

mahal is this u..

[reasoningdaily]

Psychology Today: Consciousness and Intrinsic Brain Information

Does consciousness arise exclusively from complex interactions in brain tissue (materialism)? Or does consciousness originate in some more fundamental level of reality (dualism)? Many nuanced philosophical versions of these positions have surfaced in recent years. The new science of consciousness remains consistent with established physical laws, while fully embracing the knowledge barriers and "hidden reality" imposed by modern physics.

Computer science contributes to this debate through developments in artificial intelligence (AI). A substantial blurring of distinctions between materialism and dualism may be in the works. One source of shifting viewpoints stems from a deeper appreciation of the role of information in both the physical and biological sciences. Information and consciousness appear to be close relatives, some even view them as marriage partners. Prominent scientists and philosophers may claim that “consciousness is just brain-wide information sharing.” But just what is this enigmatic entity “information,” a label often embraced with more enthusiasm than critical scrutiny?

Scientists naturally search for ways to identify, and hopefully even measure, some well-defined “intrinsic information content” of brains. One of today’s leading theories of consciousness was discussed briefly in my post of December 13, 2021, Consciousness and Integrated Information Theory (IIT), a controversial idea with plenty of supporters and detractors. One major issue for any information-based theory is that the meaning of “brain information” is generally subjective and context-dependent.

Information processing may involve multiple levels of organization, ranging from protein molecules, including the tiny microtubules, to cellular scales, to brain-wide cell assemblies to global fields of synaptic action. These nested structures can form and dissolve in fractions of seconds, changing their organizations and mutual alliances at the speed of thought. Brain structures are often loosely labeled as “neural networks,” but their relationships to AI networks might be anything from genuine physical analogs to loose metaphorical similarities. My purpose in this new series of posts is to examine possible relations between information and consciousness, starting at the most basic level so that the discussion is easily available to any interested reader.

Let’s first visit the “binary world” of information. Binary numbers are physically convenient. Bones placed on the ground, beads sliding on sticks, and punched holes in paper tapes have long been used to store and manipulate binary information. Punch cards were the standard means of inputting binary data to early computers. When punched properly, each card location either has a hole or no hole. A famous example of binary misuse involved the “hanging chads” of the 2000 U.S. presidential election. The world of binary information has taken on deep scientific significance—in the second law of thermodynamics, quantum mechanics, biological systems, and more.

Some Information Basics

Paul L. Nunez

Imagine sand buckets placed in a straight line on a beach. Empty buckets are designated 0 and sand-filled buckets are designated 1; fractional fills are not allowed. I adopt the symbol T (after computer scientist Alan Turing) to indicate the number of buckets in the line. As shown in my first figure, a T-bit binary number can represent base-10 integers up to the maximum number W = 2T – 1. Solving this equation for T yields the minimum number of bits (buckets or binary digits) needed to store the number W: T = Log2W. The right side is read, “the base 2 logarithm of W”. This equation has no fixed scientific meaning; it is simply the rule for transforming any base-10 number W into a binary number T, analogous to a simple mathematical rule like A x B = B x A. The binary transformation rule adopts the ceiling function of computer science, the provision that non-integer values of T are to be rounded up to the nearest integer. Thus, for example, ceiling function (6.2) = 7 bits or buckets; no partly filled buckets or hanging chads are allowed.

State Information

A system’s state is the collection of features that describe its condition, at a fixed time or, more likely, over a specified time average. This simple definition masks an extensive assortment of subtle issues that must be faced head-on in the quest to better understand consciousness. State information may be defined simply by the number of possible states of a system, let’s say water, which can be found in the states of solid, liquid, or gas. Economies, forests, and ant colonies can exist in different states. Brains can occupy many mental states—awake, dreaming, Alzheimer’s disease, planning a bank robbery, or thinking great thoughts. Neuroscience seeks relationships between mental states and measurable physical states. Such relationships are labeled the neural correlates of consciousness.

Let’s begin our discussion of states with simple die systems. If a single cubical die is placed or tossed on a surface, the six possible states of the system are 1 through 6. A polyhedron die is a three-dimensional object with W flat surfaces. If, for example, W = 128, each system state can be unequivocally labeled by a single positive integer in the range 1 through 128. This state description is independent of the causes or probabilities of occurrence of each state, which might be the result of a simple die toss, deliberate placement by an intelligent being, or some hidden process. We only require that the system be found in one of the 128 discrete states, independent of the cause or means of observation. The size of state information is defined simply as W, the number of distinct states that the system can be in. To be more precise, we may call W the size of the die's macro-state to distinguish it from the micro-states, which are determined by the locations and velocities of the elementary particles forming the die. State size can also be expressed by T, the number of bits corresponding to W.

Shannon Entropy

State information is often confused with Shannon information (or entropy) developed in modern communication theory. According to Shannon information, a message consists of a sequence of M symbols selected from an alphabet consisting of N symbols. For example, the 7-bit computer code ASCII can contain up to N = 128 symbols. Consider the message, “The Bird is cruel!”, which probably means nothing much to the reader unless he or she has read science fiction by Robert Heinlein. The message consists of M = 18 symbols, including letters, spaces, and an exclamation point. In the common practice of sending messages, meaning is supplied by both the message content and prior knowledge of the receiver. In contrast, the central goal of communication theory is to provide quantitative measures of the information content of messages, independent of meaning.

A message’s Shannon information is defined in terms of the probability of occurrence of each symbol produced by the sending system (whether human or machine). For example, the letter E is more likely to occur than other letters in English text. The information transmitted by each symbol involves a degree of receiver surprise; the letter Z conveys more information than the letter E and so forth. Shannon information is, by definition, additive. Each additional symbol received adds more information, but the additional information varies in size, depending on symbol probabilities in the chosen alphabet. Shannon entropy H is the average number of bits of information per transmitted symbol. If an entire alphabet were to contain only a single symbol, Hwould be zero. On the other hand, if all symbols were to have an equal probability of occurrence, Shannon entropy takes on its maximum value: H = Log2M. More generally, the Shannon entropy H of any collection of symbols, including but not limited to alphabets, lies in the range between zero and Log2M, depending on the probability distribution of the alphabet. H may or may not have any relationship to the intrinsic properties of the sender.

Provocative Equations of Information

Paul L. Nunez

Three major kinds of information are defined in figure 2: T (Turing buckets), H (Shannon entropy), and S (Boltzmann entropy). The three equations are nearly identical but express very different physical processes. The discovery of entropy in the mid 1800s was followed by the development of statistical mechanics in the late 1800s and Shannon’s communication theory in 1949. Many seem to have fallen for the fallacy that T, H, and S are the same creature because they satisfy (essentially) the same equation. In this regard, note that mechanical and electrical systems are often described by identical differential equations, providing the basis for analog computers.

Widespread confusion about information and entropy also originates from their inherently abstract nature, mixed interpretations of the symbols H and S, and the births and on-going maturation of many new informational siblings. For example, Boltzmann's sharp distinction between the macro and micro-states in classical statistical mechanics is not fully adequate to describe complex systems.

Brains other complex systems operate at multiple intermediate scales, leading to multi-scale entropy measures. The confusion continues to this day, especially with the advent of AI, quantum computing with quantum bits (qubits), quantum superposition of states, black hole entropy, cellular information processing, and much more. In future posts, I will discuss other kinds of information that appear to be related to consciousness.

Several efforts to find better-defined measures of intrinsic brain information have tentatively adopted Shannon entropy by interpreting the symbols of the Shannon message (M) as measured brain states (W), adopting Shannon entropy (H) as an approximation of the brain’s intrinsic information. One obvious problem with this approach is that the contents of a message may tell us almost nothing about the internal states of the sender. If the sender is a very simple system, like our 128-face die, its message may provide much of the die’s intrinsic macro-scale information. However, in brains as well as other complex systems, the relationships between the system messages (often obtained from experimental data) and the intrinsic information of the system is tenuous at best. I will look into these issues in more depth in my next post.

[darker-than-darkstorm]

... this is amusing. I probably could solve it, but I'd have to dig up some equations somewhere.

The burger is 6, easy. The fries are easy but the concept is difficult: it's the imaginary number i, which doesn't exist and cannot exist (fries x fries has to equal -1 for the second equation to work, and the no real number multiplied by itself can ever equal a negative number. Hence, imaginary numbers, which do have that property)

Now, let's call the glass x to simplify matters, you have x to the power of i, minus x, equals 3. By definition, x to the power of i is equal to e to the power of (i ln x), and by further definition, that equals (cos ln x+i sin ln x).

(ln is the natural logarithm function, e is a transcendental number similar to π with a lot of applications in more complex forms of mathematics, including the natural logarithm function. I won't explain further, but there's a button on most scientific calculators for both of them. There's also buttons for cosine and sine)

So now we're looking at solving the much simpler equation "cos ln x + i sin ln x - x = 3", and ... oh, look, dinner is almost here, so I'm going to stop there. But I'm sure you can easily solve it from there. Good luck!