#Modulus of Complex Number

[9nid]

✅ Check Point 02: Complex Numbers Questions Practice – JEE Main ke liye Full Concept Recap

Hello JEE Aspirants!Aaj ke is blog mein hum cover kar rahe hain Complex Numbers ke sabhi important topics through 18 conceptual questions. Agar aap JEE Main ya Class 11 Maths padh rahe ho, to yeh ek perfect revision aur practice checkpoint hai. Hum basic se lekar advanced tak sab kuch revise karenge practical examples ke through. Conjugate of a Complex NumberAgar koi complex number z = a + ib…

[edusquaremaths]

✅ Check Point 02: Complex Numbers Questions Practice – JEE Main ke liye Full Concept Recap

Hello JEE Aspirants!Aaj ke is blog mein hum cover kar rahe hain Complex Numbers ke sabhi important topics through 18 conceptual questions. Agar aap JEE Main ya Class 11 Maths padh rahe ho, to yeh ek perfect revision aur practice checkpoint hai. Hum basic se lekar advanced tak sab kuch revise karenge practical examples ke through. Conjugate of a Complex NumberAgar koi complex number z = a + ib…

[admiral-crow-is-watching]

What part of maths letters commonly inhabit (Part I, Latin)

a,b,c: Some kind on constants. Could be anything.

A, B: probably set theory.

B: Could be open balls, could be a binomial distribution.

C: constants of integration in a normal font, complex numbers in blackboard font.

d, k, p, q: Dimensions of something or other

D: Could be another constant of integration, or possibly a domain of discourse if it looks fancy.

E: Expectation! You're doing probability.

e: Euler's number. Will not stop turning up absolutely everywhere.

e, g, h: Group theory or other algebra. You are unlikely to also see numbers.

f, F, g, G, h, H: The classic choice for functions.

H: Whatever this is is named after Hamilton.

i: square root of -1, complex numbers, right up there with e in turning up everywhere.

I: Indicator function, identity matrix, information. An underratedly versatile letter.

i,j,k: Another classic triple act. Could be either index variables or something three-dimensional, like unit vectors or quarternions.

K, M: upper bounds on some kind of modulus. Look for || everywhere.

L, l: Most likely likelihood functions from statistics.

m,n: Integers! Index variables, sequences, induction, these two have you covered.

M: Matrices, welcome to linear algebra.

N: Natural numbers in a fancy font, a normal distribution in a normal one.

O: either big O notation and you're doing computer science; or if it's blackboard font, you're doing octonions and may your gods go with you.

p, P, q: Probability theory, again.

P, Q: formal logic. Usually seen in conjunction with lots of arrows.

Q: Rational numbers, usually blackboard font, you are most likely in algebra.

R: Real numbers, you are in analysis.

r: Something has a radius. It could well be a very abstract multidimensional radius.

s: Possibly generating functions, especially in conjunction with F and G. Not one of the more common maths letters.

t, T: Something is happening over time.

v: Vectors are happening.

u, U: whatever this is, you're too deep.

w: Something in four variables is happening.

x,y,z: the classic variable set. unknowns, vectors, scalars, there's nothing this gang of three can't do.

Z: Integers in blackboard font; a standard normal distribution in a regular one.

[materialsscienceandengineering]

A new transformer-based model for identifying alloy properties

Identifying alloy properties can be expensive and time-consuming. Experiments involving alloys often require a number of resources. Calculating alloys can also become extremely complicated, with a seemingly endless number of configurations of properties. Alloy properties can be determined using Density Functional Theory (DFT) calculations; however, this method is limited and can also be extremely time-consuming in the event of a particularly complex alloy. Amir Barati Farimani and his team aim to reduce both the time and cost of this process, and their recent work has led to the creation of AlloyBert, a modeling tool designed to predict the properties of alloys. AlloyBert is a transformer-based model, meaning researchers input simple English-language descriptors to gain their desired output. Descriptors can include information such as the temperature at which the alloy was processed or the chemical composition of an alloy. AlloyBert will then use this information to predict either the elastic modulus or yield strength of the alloy.

Read more.

[lunarsilkscreen]

Fundamental Maths (Multiplication, Modulus, and Division)

I find it weird that the explanation for division usually involves multiplication somehow. What is 8/2 ? It is 4, because 4 time 2 is eight.

Then they get half way to saying what division is, and never ever say: "Division is repeated subtraction".

If multiplication is repeated addition 2*2 is 2+2, 2*3 is 2+2+2, etc... then division is repeated subtraction: 8/2 = 8-2-2-2-2= remainder. We then count the twos, or 4. Which is why we end up tying multiplication to division, because we want to know *how many times* we can reduce a number by another number to zero.

This is where we can end with lengths of fabric, or strips of paper, because we'd also reasonably like to know how much we have leftover. But maths keeps going, and start subdividing the remainder into a fraction based on the divisor. So if we have 9/2; 9-2-2-2-2=1. But since it needs to be tied to the divisor, the answer isn't 1 it's 4 and (1/2).

I use "but" here because of the dichotomy. It's not until students learn programming that we learn a name for the actual "division" that results in remainder; modulus. 9%2= 1 because with modulus, unlike division, we are in fact doing repeated subtraction, instead of counting the multiplier to the result of how many times one number goes into another number.

Therefore Division can only be taught as a more complex function that includes *both* Multiplication AND Modulus.

And students aren't taught modulus while simultaneously being expected to *know* what modulus is. Especially if they start an entry-level programming class. They know division and remainders, but they don't know that this is a function that we as people use in everyday life AND is a necessity in programming.

How can you understand a dividend, if you're not ever taught to modulus?

[jadagul]

So i^2 is -1 (by definition), and i^3 is -i (-1 * i), and i^4 is 1 (if i*i is -1 then i*-1 is 1), and i^5 is i (1 * i), and it continues to loop from there. But how do things work for non-integer exponents? It's easy to say, of i^1.5, that it multiplied by i^0.5 is -1; but that doesn't tell us what it itself is. Do we just call it 'i^1.5' and leave it at that? Or is there some trick I'm missing that'll let us pin it down as a more traditional real or complex number?

Yeah, there's a trick; it's just dumb.

We didn't go into this in the post (I even mentioned the not-going-into-it!) but complex exponentiation works really well with e as the base, because e^(ix) = cos(x) + i sin(x). And in particular that means e^(i π/2) = i.

So if we want to compute i^(1.5) then that's e^(i π/2 * 1.5) = e^(i 3 π /4) = cos(3π/4) + i sin(3π/4) = -sqrt(2)/2 + i sqrt(2)/2.

In general if you exponentiate a complex number, you regular-exponentiate the modulus, and you multiply the angle from the positive x-axis by the exponent as well. So in your case, i has modulus 1 and angle 90 degrees, so we get the output that has modulus 1 and angle 135 degrees.

[360freeonlineeducation]

Try to solve weakness about mathematics

Mathematics is important for exams like the NCLEX, PRAXIS, and HESI because these tests assess the skills needed for professional practice in nursing, education, and healthcare fields.

GET ONE TO ONE FREE TUTORING CLASS 👈.

How to solve mathematics without any complexity!!

Division of Complex Numbers

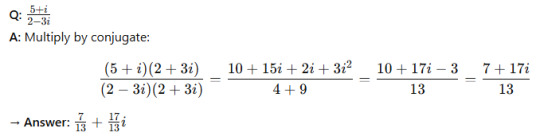
Modulus of a Complex Number

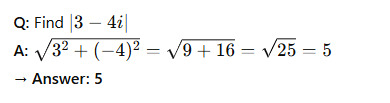
Conjugate of a Complex Number

Why math matters: Nurses need to accurately calculate medication dosages, IV drip rates, intake/output, and conversions. Why math matters: For those seeking to become teachers , the Praxis exam tests both content knowledge and teaching ability in math. Why math matters: Like the NCLEX, the HESI includes a math section to ensure incoming nursing students have the foundational skills needed.

Learn about basic electronics !! 👈.

[literaturereviewhelp]

Currently, fibre reinforced polymers are increasingly used in the automotive industry and other industries due to their benefits that over conventional metals. In addition use of polymer materials in automotive industry, they are increasing applied in the construction, aerospace industries, among other applications. This implies that fibre reinforced polymers are gradually replacing metals in various industries due to their inherent advantages over metals as indicated below. The use of fibre reinforced composite materials in the vehicle industry offers more advantages in reducing the weight of the vehicle. Reduced weight increases fuel consumption efficiency and reduces the amount of carbon compounds produced (Das 2001, 1). Reducing the weight of a vehicle by about 100kgs would lead to a reduction of about 0.3 to 0.4 liters of fuel per 100km (Yu & Dean 2006, 580). For example, the Ford Explorer model by Ford has a scratch resistance and corrosion proof cargo area made from integrated liners and side panels, reducing the vehicle’s weight by up to 20% compared to its conventional metal model. In addition, using composites makes it possible to reduce the number of parts required in fabrication of vehicles, compared to use of steel or aluminum (Calister 2007, 582). This leads to achievement of high volume composite concept in vehicle manufacturing, which leads to increased cost effectiveness. The use of natural based fibre has further improved fibre applications in the vehicle industry. Natural fibres are environmentally sustainable to use compared to metals. These fibres are processed from natural plants, making them biodegradable and environmentally friendly. Table of usages of fiber reinforced polymers (Mair, 1999) Currently, natural fibres are mostly used in making of seat liners, equipment panels, carpets, among other applications in vehicles (Riaz 2012, 9). Natural fibres such as jute, sisal, hemp, and kenaf offer good acoustic properties to vehicles, high stability, less splintering in case of accidents, and reduced forging behavior compared to metals (Sanadi et al 1994, 469). Through the use of fibre reinforced composites, many parts of different shapes can be produced with much ease, and at high speed compared to use of metallic materials. The ability to configure and produce complex shapes inexpensively makes the use of polymers to considerably reduce the cost of a vehicle, making them more affordable to customers. (Source: http://www.compun.com/CompositeBenefits.html) Composites offer increased stiffness, toughness, and strength over structural metal alloys. These superior properties come along with vehicle weight reduction. The specific strength and modulus per unit weight is almost five times that offered by steel or aluminum (Chung 2004, 22). Read the full article

[sethiswiftlearn]

Class 11 Math | Complex number | JEE Main PYQs | JEE, CUET, BITSAT, WBJEE Prep

Master Complex Numbers in Class 11 Mathematics with this in-depth video session, specially designed for students preparing for JEE Main, CUET, BITSAT, WBJEE, and other competitive exams. This lesson by SethiSwiftLearn breaks down the key concepts, formulas, and properties of complex numbers, helping you build a strong foundation.

📘 Learn how to:

Solve JEE Main Previous Year Questions (PYQs) on Complex Numbers

Understand modulus, argument, conjugate, and polar form

Tackle real vs imaginary number problems with ease

Apply properties of complex numbers in real exam situations

Perfect for students aiming to excel in JEE 2025, CUET, and beyond. Whether you’re revising or learning the topic for the first time, this video ensures conceptual clarity and exam-ready practice.

🎥 Watch now: https://youtu.be/f_CYJ_w-Tk4?si=UCU3_nwTAcf8nstn

[cmctelecore]

Mastering GCD Using Recursion in Java – Step-by-Step Guide

Finding the Greatest Common Divisor (GCD) is a fundamental programming task. Learning how to implement GCD using recursion in Java is essential for developing efficient algorithms. Recursion simplifies the logic by breaking down the problem into smaller, manageable parts.

To find the GCD using recursion in Java, you need to understand the Euclidean algorithm, which works by reducing the problem size step-by-step. The base case is when one number becomes zero, and the recursive call reduces the problem using the modulus operator.

Here’s a simple recursive function to calculate the GCD using recursion in Java:

java

CopyEdit

public static int gcd(int a, int b) { if (b == 0) return a; return gcd(b, a % b); }

This code follows the principle that the GCD using recursion in Java can be calculated by replacing the larger number with the remainder until it becomes zero. Mastering this technique helps in solving complex mathematical problems more efficiently.

[9nid]

Square Root of Complex Numbers | Class 11 JEE Maths | Complex Number Series 🔥

Is video mein humne complex numbers ka square root nikalna seekha hai — wo bhi JEE Mains ke point of view se. Kaise aap kisi bhi complex number ka √ निकाल सकते ho using algebraic as well as geometric methods, woh step-by-step samjhaya gaya hai. Yeh Class 11 ke Complex Number Chapter ka ek important concept hai jo directly JEE mein poocha gaya hai. Topics Covered:👉 What is the square root of a…

[edusquaremaths]

Square Root of Complex Numbers | Class 11 JEE Maths | Complex Number Series 🔥

Is video mein humne complex numbers ka square root nikalna seekha hai — wo bhi JEE Mains ke point of view se. Kaise aap kisi bhi complex number ka √ निकाल सकते ho using algebraic as well as geometric methods, woh step-by-step samjhaya gaya hai. Yeh Class 11 ke Complex Number Chapter ka ek important concept hai jo directly JEE mein poocha gaya hai. Topics Covered:👉 What is the square root of a…

[lmerli2953]

Basics of R programming

Understanding the basics of R programming is crucial for anyone looking to leverage its capabilities for data analysis and statistical computing. In this chapter, we'll explore the fundamental elements of R, including its syntax, variables, data types, and operators. These are the building blocks of any R program and are essential for developing more complex scripts and functions.

R Syntax

R's syntax is designed to be straightforward and user-friendly, especially for those new to programming. It emphasizes readability and ease of use, which is why it's popular among statisticians and data scientists.

Comments: Comments are used to annotate code, making it easier to understand. In R, comments begin with a # symbol:# This is a comment in R

Statements and Expressions: R executes statements and expressions sequentially. Statements are typically written on separate lines, but multiple statements can be written on a single line using a semicolon (;):x <- 10 # Assigning a value to variable x y <- 5; z <- 15 # Multiple statements in one line

Printing Output: The print() function is commonly used to display the output of expressions or variables. Simply typing the variable name in the console will also display its value:print(x) # Displays the value of x x # Another way to display x

Variables in R

Variables are used to store data values in R. They are essential for performing operations, data manipulation, and storing results.

Creating Variables: Variables are created using the assignment operator <- or =. Variable names can contain letters, numbers, and underscores, but they must not start with a number:num <- 100 # Assigns the value 100 to the variable num message <- "Hello, R!" # Assigns a string to the variable message

Variable Naming Conventions: It’s good practice to use descriptive names for variables to make the code more readable:total_sales <- 500 customer_name <- "John Doe"

Accessing Variables: Once a variable is created, it can be used in expressions or printed to view its value:total_sales <- 1000 print(total_sales) # Outputs 1000

Data Types in R

R supports a variety of data types that are crucial for handling different kinds of data. The main data types in R include:

Numeric: Used for real numbers (e.g., 42, 3.14):num_value <- 42.5

Integer: Used for whole numbers. Integer values are explicitly declared with an L suffix:int_value <- 42L

Character: Used for text strings (e.g., "Hello, World!"):text_value <- "R programming"

Logical: Used for Boolean values (TRUE or FALSE):

is_active <- TRUE

Factors: Factors are used for categorical data and store both the values and their corresponding levels:status <- factor(c("Single", "Married", "Single"))

Vectors: Vectors are the most basic data structure in R, and they can hold elements of the same type:num_vector <- c(10, 20, 30, 40, 50)

Lists: Lists can contain elements of different types, including vectors, matrices, and even other lists:mixed_list <- list(num_value = 42, text_value = "R", is_active = TRUE)

Operators in R

Operators in R are used to perform operations on variables and data. They include arithmetic operators, relational operators, and logical operators.

Arithmetic Operators: These operators perform basic mathematical operations:

Addition: +

Subtraction: -

Multiplication: *

Division: /

Exponentiation: ^

Modulus: %% (remainder of division)

Example:a <- 10 b <- 3 sum <- a + b # 13 difference <- a - b # 7 product <- a * b # 30 quotient <- a / b # 3.3333 power <- a^b # 1000 remainder <- a %% b # 1

Relational Operators: These operators compare two values and return a logical value (TRUE or FALSE):

Equal to: ==

Not equal to: !=

Greater than: >

Less than: <

Greater than or equal to: >=

Less than or equal to: <=

Example:x <- 10 y <- 5 is_greater <- x > y # TRUE is_equal <- x == y # FALSE

Logical Operators: Logical operators are used to combine multiple conditions:

AND: &

OR: |

NOT: !

Example:a <- TRUE b <- FALSE both_true <- a & b # FALSE either_true <- a | b # TRUE not_a <- !a # FALSE

Working with Data Structures

Understanding R’s data structures is essential for manipulating and analyzing data effectively.

Vectors: As mentioned earlier, vectors are a fundamental data structure in R, and they are used to store sequences of data elements of the same type:numbers <- c(1, 2, 3, 4, 5)

Matrices: Matrices are two-dimensional arrays that store elements of the same type. You can create a matrix using the matrix() function:matrix_data <- matrix(1:9, nrow = 3, ncol = 3)

Data Frames: Data frames are used for storing tabular data, where each column can contain a different type of data. They are akin to tables in a database:df <- data.frame(Name = c("John", "Jane", "Doe"), Age = c(25, 30, 35))

Lists: Lists are versatile structures that can store different types of elements, including other lists:my_list <- list(name = "John", age = 30, scores = c(90, 85, 88))

Uncover more details at Strategic Leap

[etimaterials-blog]

Interaction between rare earth metals and other elements

Rare earth metals have typical metal properties. They have strong chemical activity and can form a variety of compounds, including hydrides, chlorides, silicides, carbides, organic / inorganic salts and complexes. This is the basis for the rare earth metal in the metallurgical industry as a purification, impurity removal and refinement modifier.

Rare earth metals are unstable in air, and their stability increases with increasing atomic number; in other words, the rare earth metals with larger atomic radius have weaker oxidation resistance; light rare earth metals can be easier oxidized than heavy rare earth metals, and lanthanum is the most active. Lutetium and Scandium are the most resistant to air oxidation.

Rare earth metals are widely used as reducing agents, which can reduce oxides of iron, cobalt, nickel, chromium, vanadium, niobium, tantalum, zirconium, titanium, silicon and other elements into metals. Due to the difference in the reducing ability of rare earth metals, and the vapor pressure of the lanthanum is much smaller than that of Samarium, Europium, Ytterbium and Thulium, Lanthanum (cerium) can be used to reduce europium, europium, europium, europium metal from its oxides. However, the activity of rare earth metals is lower than that of alkali metals and alkaline earth metals, so lithium and calcium are commonly used as reducing agents to reduce rare earth metals from their halides.

Interactions between rare earth metals occur. If the two rare earth metals have the same crystal structure at the corresponding temperature, they can form a continuous solid solution; if the two rare earth metals have different crystal structures, they can only form a finite solid solution; Only two rare earth metals belonging to different subgroups (cerium and yttrium) can form intermetallic compounds.

The behavior of Yttrium and scandium in alloys is similar to that of heavy rare earth metals; the behavior of Ytterbium in magnesium alloys is similar to that of light rare earths. The melting point and elastic modulus of Europium and Ytterbium are similar to those of light rare earth lanthanum and cerium.

Rare earth metals and transition metals (iron, manganese, nickel, gold, silver, copper, zinc) and magnesium, aluminum, gallium, indium, thallium can form many alloys. Moreover, many intermetallic compounds are formed in their binary and multicomponent alloys.

Some of these compounds have high melting points, high hardness, high thermal stability, and are dispersed in the non-ferrous alloy matrix or grain boundaries. They play an important role in resisting high temperature, creep resistance, and improving the strength of the alloy. Many of these rare earth intermetallic compounds have been widely used in high and new technology with special functions. It is expected that more new intermetallic compounds will be developed in succession.

Only tantalum / niobium and tungsten / molybdenum and their alloys have little interaction with rare earth metals. Tantalum and molybdenum have almost no interaction with rare earth metals and their halides. Under vacuum or inert gas, tantalum can be used at 1700 °C, molybdenum can be used at 1400 °C, and it is used as the electrode for molten salt electrolysis and the carrying crucible for rare earth metals and rare earth alloys.

[nectoy7]

Java Basics: A Comprehensive Guide for Beginners

Java is one of the most popular and widely-used programming languages in the world. Known for its versatility, platform independence, and security features, it is the go-to language for many developers when building applications across multiple platforms. Whether you are developing web applications, mobile apps, or complex enterprise systems, learning Java is a crucial step in your programming journey.

In this blog, we will cover the fundamental building blocks of Java, often referred to as “Java Basics.” By understanding these essentials, you’ll be well on your way to writing efficient and effective Java programs.

—

1. Java Data Types

In Java, every variable has a specific data type that determines the kind of data it can hold. Java has two primary categories of data types:

1.1 Primitive Data Types

Java provides eight built-in primitive data types that are used to store simple values. These data types are not objects and are stored directly in memory. They include:

byte: A 1-byte (8-bit) integer value, ranging from -128 to 127.

short: A 2-byte (16-bit) integer value, ranging from -32,768 to 32,767.

int: A 4-byte (32-bit) integer value, commonly used for numeric operations. It has a range from -2^31 to 2^31-1.

long: A 64-bit integer, often used when int is not large enough. Range: -2^63 to 2^63-1.

float: A 32-bit floating-point value used for precise decimal calculations. For example, it is used in complex mathematical operations where decimals are involved.

double: A 64-bit floating-point number, more accurate than float.

char: A 16-bit character that stores single Unicode characters, e.g., ‘A’, ‘B’, ‘3’, etc.

boolean: A data type that stores two possible values: true or false. It is primarily used in logical operations and control flow.

1.2 Reference Data Types

Reference types include objects and arrays. These types are stored in heap memory and include the following:

Strings: Although not a primitive type, strings are widely used in Java for text. Java provides a String class to work with sequences of characters.

Arrays: Java supports arrays, which are used to store multiple values of the same type in a single variable, e.g., int[] numbers = {1, 2, 3, 4};.

Objects: Objects are instances of classes, and they have properties and methods.

—

2. Variables in Java

A variable is a container for storing data values. In Java, variables must be declared with a specific data type before they are used. Java allows three types of variables:

Local Variables: Declared inside a method or block of code. They must be initialized before use.

Instance Variables (Non-Static Fields): Defined inside a class but outside any method. These variables hold different values for different instances of the class.

Class Variables (Static Fields): Declared with the static keyword inside a class but outside any method. They share the same value for all instances of the class.

Variable Declaration and Initialization Example:

int age = 25;          // Declaring and initializing a local variable double price;          // Declaring a variable (needs initialization before use) boolean isActive = true;  // Declaring and initializing a boolean variable

—

3. Operators in Java

Java provides a wide range of operators that perform operations on variables and values. Operators are categorized as follows:

3.1 Arithmetic Operators

These operators perform mathematical operations like addition, subtraction, multiplication, etc.

+ (Addition)

– (Subtraction)

* (Multiplication)

/ (Division)

% (Modulus) – returns the remainder

3.2 Relational Operators

These operators compare two values and return a boolean result (true or false):

== (Equal to)

!= (Not equal to)

> (Greater than)

< (Less than)

>= (Greater than or equal to)

<= (Less than or equal to)

3.3 Logical Operators

Logical operators are used to combine conditional expressions:

&& (Logical AND)

|| (Logical OR)

! (Logical NOT)

3.4 Assignment Operators

Assignment operators are used to assign values to variables:

= (Assign)

+= (Add and assign)

-= (Subtract and assign)

3.5 Unary Operators

Unary operators are used with one operand:

++ (Increment)

— (Decrement)

3.6 Bitwise Operators

These operators perform operations on bits of numbers:

& (AND)

| (OR)

^ (XOR)

~ (NOT)

—

4. Control Flow in Java

Control flow statements allow you to manage the flow of execution of your code. The key control flow statements in Java include:

4.1 If-Else Statements

The if-else construct allows you to conditionally execute code.

if (condition) {     // Code to execute if condition is true } else {     // Code to execute if condition is false }

4.2 Switch Statements

A switch statement allows you to execute different parts of code based on the value of an expression.

switch(expression) {     case value1:         // Code block         break;     case value2:         // Code block         break;     default:         // Code block }

4.3 Loops in Java

Loops allow you to execute a block of code multiple times. Java supports three types of loops:

for loop:

for (initialization; condition; update) {     // Code block }

while loop:

while (condition) {     // Code block }

do-while loop (Executes at least once):

do {     // Code block } while (condition);

—

5. Java Methods

A method is a block of code that performs a specific task and is executed when called. Java methods can accept parameters and return values.

Method Syntax:

public returnType methodName(parameters) {     // Method body     return value;  // Optional, based on return type }

Example:

public int addNumbers(int a, int b) {     return a + b; }

Calling Methods:

Methods are called using the object of the class or directly if they’re static.

int result = addNumbers(10, 20);

—

6. Classes and Objects in Java

Java is an object-oriented programming language. This means it revolves around classes and objects.

Class: A blueprint for creating objects.

Object: An instance of a class, created using the new keyword.

Class Example:

public class Car {     // Instance variables     String color;     String model;

    // Method     public void start() {         System.out.println(“Car started”);     } }

Creating Objects:

Car myCar = new Car(); myCar.start();

—

7. Constructor in Java

A constructor is a special method that is used to initialize objects. It has the same name as the class and does not have a return type.

Constructor Example:

public class Car {     String model;         // Constructor     public Car(String model) {         this.model = model;     } }

Creating an Object Using Constructor:

Car myCar = new Car(“Tesla”);

—

8. Arrays in Java

An array is a container object that holds a fixed number of values of a single type.

Array Declaration:

int[] numbers = {1, 2, 3, 4, 5};

Accessing Array Elements:

System.out.println(numbers[0]);  // Output: 1

—

Conclusion

Java basics form the foundation for writing more complex and advanced programs. Understanding data types, variables, operators, control structures, methods, and arrays equips you to tackle more sophisticated topics like Object-Oriented Programming (OOP), collections, and Java frameworks. By mastering these fundamental concepts, you’re setting yourself up for success in your journey as a Java developer. Keep practicing and exploring, as learning Java is an exciting and rewarding endeavor!

[juliebowie]

Introduction to Armstrong Number in Python

Summary: Discover the concept of Armstrong Numbers in Python, their unique properties, and how to implement a program to check them. Learn about basic and optimised approaches for efficient computation.

Introduction

In this article, we explore the concept of an Armstrong Number in Python. An Armstrong number, also known as a narcissistic number, is a number that equals the sum of its own digits, each raised to the power of the number of digits. 

These numbers are significant in both programming and mathematical calculations for understanding number properties and algorithmic efficiency. Our objective is to explain what an Armstrong number is and demonstrate how to implement a program to check for Armstrong numbers using Python, providing clear examples and practical insights.

Read: Explaining Jupyter Notebook in Python.

What is an Armstrong Number?

An Armstrong number, also known as a narcissistic number, is a particular type of number in which the sum of its digits, each raised to the power of the number of digits, equals the number itself. This property makes Armstrong numbers unique and exciting in mathematics and programming.

Definition of an Armstrong Number

An Armstrong number is defined as a number equal to the sum of its digits; each raised to the power of the total number of digits. For example, if a number has 𝑛 digits, each digit d is raised to the 𝑛th power and the sum of these values results in the original number.

Explanation with a Simple Example

Consider the number 153. It has three digits, so we raise each digit to the third power and sum them:

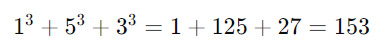
Since the result equals the original number, 153 is an Armstrong number. Another example is 370:

Difference Between Armstrong Numbers and Other Numerical Concepts

Armstrong numbers are distinct because they involve the specific property of digit manipulation. Unlike prime numbers, which are based on divisibility, or perfect numbers, which relate to the sum of divisors, Armstrong numbers focus solely on digit power sums. This unique characteristic sets them apart from other numerical concepts in mathematics.

How to Determine an Armstrong Number?

To determine whether a number is an Armstrong number, we need to verify if the sum of its digits, each raised to the power of the number of digits, equals the number itself. This concept may seem complex at first, but with a clear understanding of the process, it becomes straightforward. 

Let's break down the steps and explore the mathematical method used to identify Armstrong numbers.

Mathematical Formula

The formula to check if a number is an Armstrong number is: 

Here, d1,d2,…,dm​ represent the digits of the number, and 𝑛 is the total number of digits.

Step-by-Step Breakdown

Determine the Number of Digits: First, find the total number of digits, nnn, in the given number. This is crucial as each digit will be raised to the power of nnn.

Extract Each Digit: Extract each digit of the number. This can be done using mathematical operations like modulus and division.

Raise Each Digit to the Power of nnn: For each digit, calculate its power by raising it to nnn.

Sum the Powered Digits: Add the results of the previous step together to get the sum.

Compare the Sum with the Original Number: Finally, compare the sum with the original number. If they are equal, the number is an Armstrong number.

Example Calculation

Let's determine if 153 is an Armstrong number:

Number of digits (n): 3

Extracted digits: 1, 5, 3

Raised to the power of n:

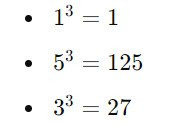
Sum of powered digits: 1+125+27=1531

Comparison: The sum, 153, equals the original number, confirming that 153 is an Armstrong number.

This systematic approach helps in accurately identifying Armstrong numbers, making the concept both interesting and accessible.

Also Check: Data Abstraction and Encapsulation in Python Explained.

Armstrong Number Algorithm

An Armstrong number, also known as a narcissistic number, is a number that is equal to the sum of its own digits each raised to the power of the number of digits. To determine if a number is an Armstrong number, we follow a specific algorithm. 

This section outlines the steps involved and discusses the efficiency and complexity of the algorithm.

Outline of the Algorithm

To check if a number is an Armstrong number, follow these steps:

Determine the Number of Digits:

First, calculate the number of digits (n) in the given number. This step helps in raising each digit to the appropriate power.

Calculate the Sum of Digits Raised to the Power of n:

For each digit in the number, raise it to the power of n and sum these values. This step involves iterating through each digit, performing the power operation, and accumulating the results.

Compare the Sum with the Original Number:

Finally, compare the calculated sum with the original number. If they are equal, the number is an Armstrong number.

Key Steps in the Algorithm

Extracting Digits: We extract each digit from the number, which can be done using modulus and division operations.

Power Calculation: Raise each extracted digit to the power of the total number of digits.

Summation: Accumulate the results of the power calculations to form the total sum.

Comparison: Compare the accumulated sum with the original number to determine if it is an Armstrong number.

Efficiency and Complexity

The Armstrong number algorithm is efficient for small to moderately sized numbers. The primary operations involve basic arithmetic, such as modulus, division, and exponentiation, making the algorithm computationally light. The time complexity is O(d), where d is the number of digits in the number. 

This is because the algorithm processes each digit exactly once. For large numbers, the time complexity may increase, but it remains manageable due to the simplicity of the calculations involved.

Implementing Armstrong Number in Python

To determine whether a number is an Armstrong number, we need to implement a straightforward approach in Python. Armstrong numbers, also known as narcissistic numbers, are numbers that equal the sum of their own digits each raised to the power of the number of digits. 

Here, we’ll explore a basic implementation in Python and discuss how to optimise it for better performance.

Basic Implementation

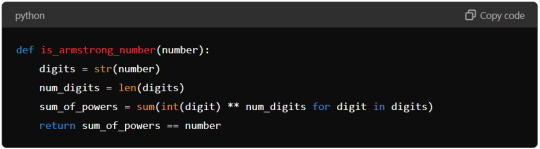
Let’s start with a simple Python program to check if a number is an Armstrong number:

Explanation of the Code:

Function Definition: The function is_armstrong_number takes an integer number as its parameter.

Convert Number to String: We convert the number to a string using str(number) to easily access each digit.

Count Digits: We determine the number of digits using len(digits).

Initialise Sum Variable: We initialise sum_of_powers to zero to accumulate the sum of each digit raised to the power of num_digits.

Calculate Sum of Powers: We loop through each digit in the string, convert it back to an integer, raise it to the power of num_digits, and add it to sum_of_powers.

Check Armstrong Condition: Finally, we compare sum_of_powers with the original number to determine if it is an Armstrong number.

Optimised Approach

While the basic implementation is easy to understand, it may not be the most efficient for larger numbers. Here are some optimisations:

Use List Comprehension: Python’s list comprehension can make the code more concise. Here’s an optimised version:

This version uses a single line to calculate sum_of_powers using list comprehension, making the code more compact and potentially faster.

2. Precompute Powers: For very large numbers, precomputing powers for digits (0 through 9) and reusing them can reduce computation time.

3. Avoid String Conversion: If working with extremely large numbers, you might want to avoid converting numbers to strings repeatedly. However, this is a trade-off between readability and performance.

By employing these optimisations, you can enhance the efficiency of the Armstrong number checking algorithm, especially for larger inputs.

Frequently Asked Questions

What is an Armstrong Number in Python?

An Armstrong Number in Python is a number that equals the sum of its digits each raised to the power of the number of digits. For example, 153 is an Armstrong Number because 1^3+5^3+3^3=153.

How can I check for an Armstrong Number in Python?

To check for an Armstrong Number in Python, calculate the sum of each digit raised to the power of the total number of digits. If this sum equals the original number, it’s an Armstrong Number.

What is the efficiency of the Armstrong Number algorithm in Python?

The Armstrong Number algorithm in Python is efficient for small to moderate numbers with a time complexity of O(d), where d is the number of digits. The primary operations include basic arithmetic and exponentiation.

Further See: Understanding NumPy Library in Python.

Conclusion

In this article, we've explored Armstrong Numbers in Python, highlighting their unique property of being equal to the sum of their digits raised to their respective powers. We demonstrated how to implement and optimise a Python program to check for Armstrong Numbers. Understanding this concept and its implementation enhances both mathematical knowledge and programming skills.