#adding and subtracting decimals

[presswoodterryryan]

Alice’s Super Fun Guide to Big Sister Ariel’s AMAZING Paper on Decimals! ✨🔢🎉

By Alice Hi, friends! It’s me, Alice! 🐰💡 And guess what? My big sister Ariel wrote another brilliant paper—this time, it’s all about adding and subtracting decimals! 🧮✨ Now, before you think, “Decimals? That sounds tricky!”—WAIT! Ariel showed me that decimals are everywhere, and knowing how to use them can help you in real life! From figuring out how much money you have in your piggy bank to…

[nectardaddy]

I see yalls messages I stg 😭😭 if I feed the delulu I won't catch up please 💀

[er-cryptid]

Adding and Subtracting Significant Figures

Patreon

[dr-vrat1o]

professor what are fractions and how do I multiply them?? I moved schools at third grade, my first school taught them in 4th and the second school caught them in 3rd so I never actually learned them

-very confused critter

Fractions

Fractions are parts of a whole. To put it simply, imagine a pizza, divide it into 8, then you have 8/8 parts. Take 1 part away, and you have 7/8 of the pizza left. So on, so forth.

Fractions can also be seen as division.

More explanation can be seen under the cut.

Parts of a Fraction

Normal fractions are written like this:

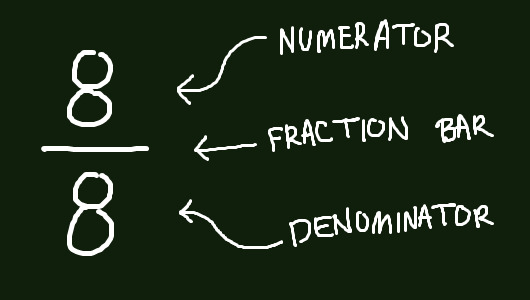
Or, as I had written earlier: 8/8.

As mentioned, fractions are also division. 8 is being divided by 8. The denominator is the divisor, and the numerator is the dividend.

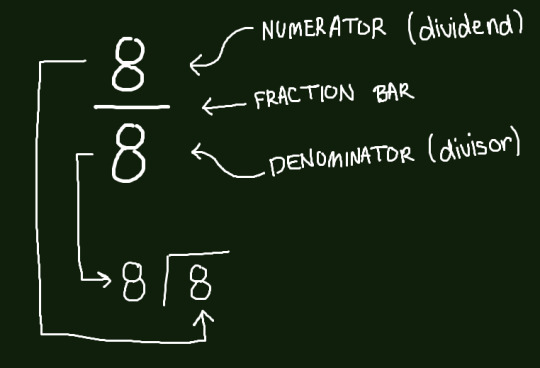
Whole Numbers, Improper Fractions, & Proper Fractions

8/8 = 1, because if you divide 8 by 8, you get the quotient of 1. Same with other numbers. 3/3 = 1. Now, imagine we have 16/8. That's basically 16 divided by 8, which is 2.

Improper fractions are fractions where the numerator is greater than the denominator. Such as 9/8. What do we do if we have 9/8? Obviously, we cannot easily divide 9 by 8. Well, if you recall the lesson of remainders during division, that is what we do here.

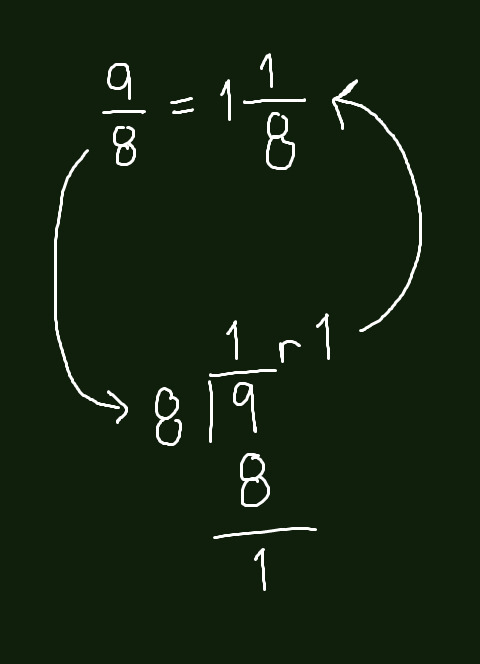
To turn a proper fraction into an improper fraction, we simply multiply the denominator by the whole number & add the value with the numerator.

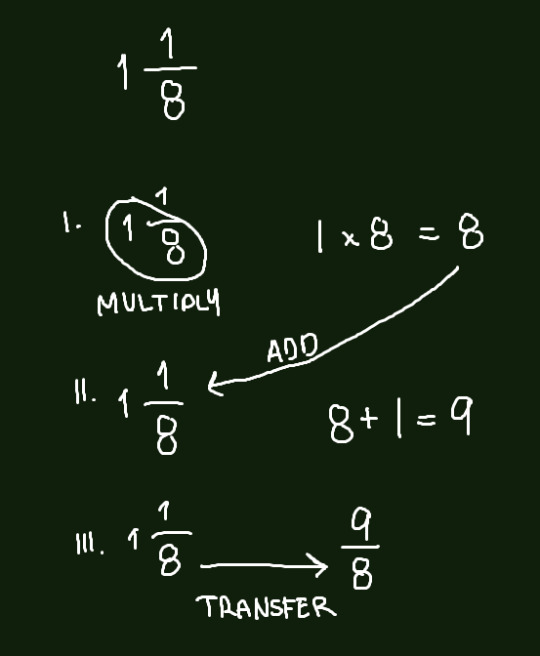
Whole numbers can also be turned into decimals. 1/1 = 1, 2/1 = 2, so on so forth. To put it into perspective:

Simplifying & Fractions -> Decimals.

Fractions can be simplified, by being divided by a greatest common factor (GCF) . Let's imagine 4/8, where their greatest common factor is 4.

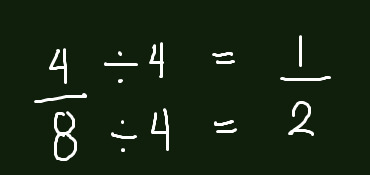
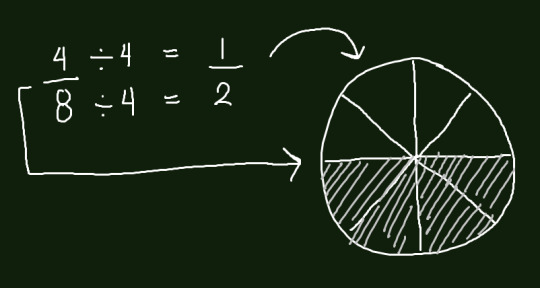
4/8 when simplified is 1/2. Putting this into diagram, we can find that this is true.

Can 3/8 be simplified? Of course not. But it would be a great example for how we can turn fractions into decimals. As mentioned earlier, fractions are division, instead of having "remainders" during division, you will end up with decimals.

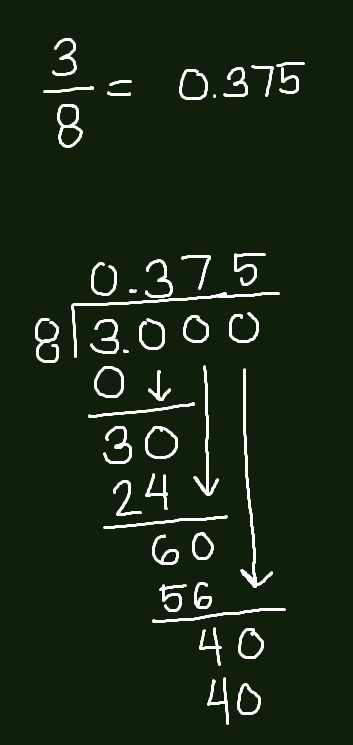
To explain how to turn a decimal into a fraction, let's use a simple number, 0.25. You should know the places of decimals, the digit on the rightmost is on the hundredths place. Which means we will be multiplying our number by 100.

As you know, whole numbers can be made into 0.25/1, so we will be starting from there.

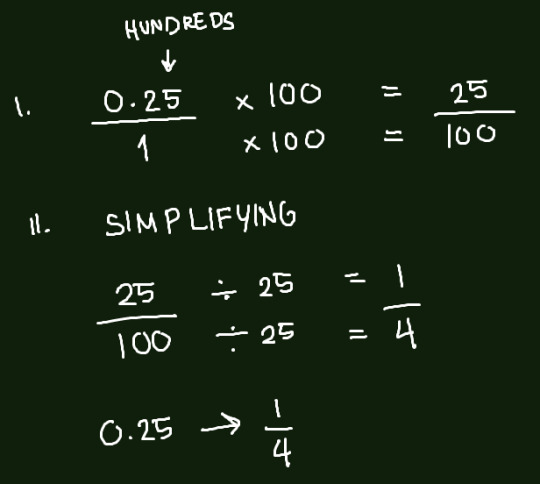
Operations with Fractions

Addition

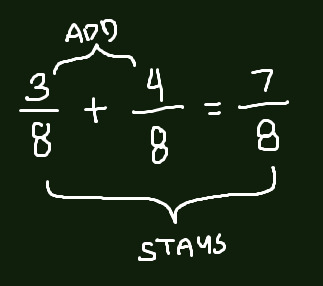
When adding fractions, the numerators are the values you will be adding together, while the denominators stay the same. For example, 3/8 + 4/8.

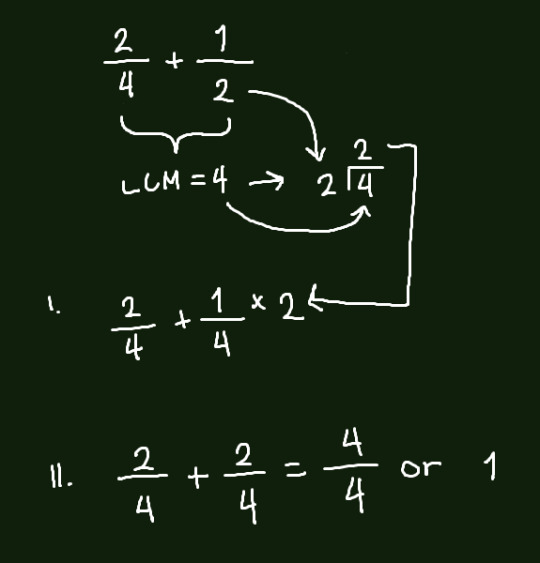
What if their denominators are different, however? You can use multiple methods, however I am much more adept with using the LCM (Least common multiple) method.

In the LCM method, you have to find their least (smallest) common multiple. You divide the multiple by the denominator and multiply the quotient to the numerator. For example:

Subtraction

Subtraction works almost similar to addition, the only difference being that you subtract the numerators.

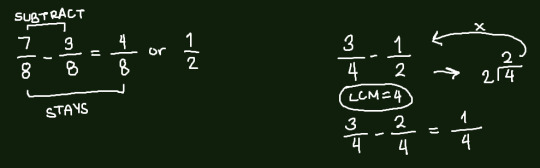
Multiplication

Multiplication is very simple, you multiply both the numerators and the denominators by one another.

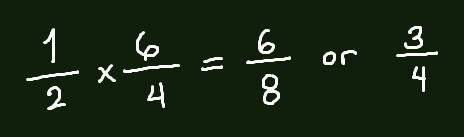
Looking at the equation, you can still simplify the answer. Rather than coming up with two final answers, you can simplify the equation instead. But you may only do this with diagonal values. For example:

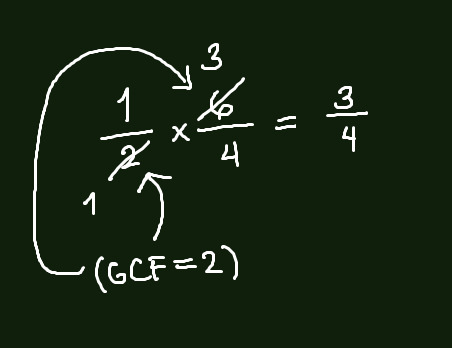
I am aware that you can simplify 6/4, which is an option as well. If the fraction can be simplified, then go ahead.

This applies with 2+ fractions.

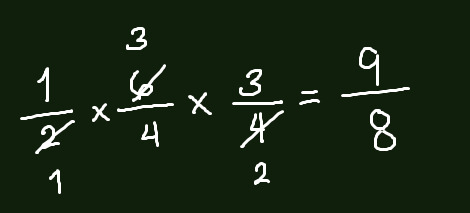
Division

Division uses the operation of multiplication, however it has a few steps. There's a popular method to use for division of fractions, called the KCF (Keep-Change-Flip) method.

Keep the first fraction, change the sign from division to multiplication, and flip the 2nd (or more) fraction.

For 2+ fractions:

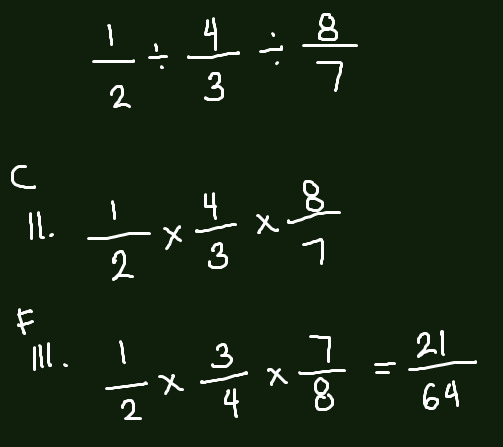
Conclusion

[apple-onigiri]

DISTANCE IN VAUGARGE (revamped edition)

IMPORTANT: this post was deleted and made again to make edits and not spread misinformation (because i made a stupid mistake and took earth's entire circumference and accidentally treated it like it was only half of it! it's really funny because i did think that this feels way too big of a distance... happens i guess! especially at 4am lmao but it did uh, increase all the numbers by a whole Two so. unfortunate! gotta fix it!!)

@cyten0 (sorry to tag you again just figured you'd like an update and an actual correct answer, and you're still the one who inquired about this) asked if i could provide more information about my calculations for traveling across vaguarde, and since it seems too long for a reblog and i want to categorize it properly on my blog, here it is in a whole separate post!

this honestly started out as a curiosity about what climate the northern island could've had given its distance from the equator compared to earth's countries and uh. spiraled into me thinking about this. don't ever think about anything guys

TL;DR (for people who don't want the super fun math part): it's 1111.4 km/690.59 miles from dormont to bambouche in a straight line and somewhere in the ballpark of 250 hours of constant travel by foot to cross the distance. with a bonnie-ordained preteen-friendly tempo of around 5 km/h (3.1 ish mph) and eight hours of travel per day from 8am until 1pm and then 3pm to 6pm to set up camp properly early, it'd take around a month or so to make the trip, not counting any and all longer stays to refill supplies and any irregularities caused by going to a town and not having to set up camp or pack it back up.

ok quick geography lesson: the lines on the globe running horizontally are the latitude. they go up to 90 in each direction from the equator, which is 0, so there's a 180 in total. obviously for specific locations you'd use decimals but who caressss

longitude is important too here - the vertical lines - but less so. they go up to 180 on each side of the latitude's version of the equator, the prime meridian, as well but it really doesn't matter where that meridian is placed here, the only thing that matters is that the lines are in a correct distance to each other.

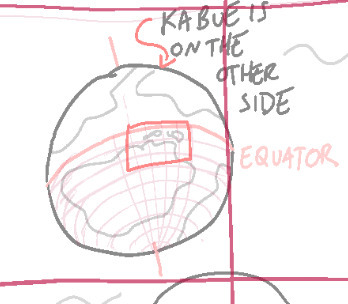
here's the globe id5, in her infinite wisdom, bestowed upon us (i'm completely normal about the existence of any and all maps. in the original post i said can be trusted with them but that is! clearly not the case!) that i added all the southern hemisphere latitude lines onto, as well as the longitude needed for my insane needs (math)

i obviously assumed the planet is the same size as the earth because i genuinely see no reason why it couldn't be other than to make my life sad and hell also. the general distance from one pole to another is 20,000 ish kilometers. (if you for some reason want the planet to be smaller or bigger, cool trick, literally just multiply the 20,000 by it. want it to be one third of its current size? multiply by 0.3. two-and-a-half times bigger? 2.5!) so what i did was draw out the lines onto the actual map and measure the estimated distance based on how big of a chunk it is out of this 20k.

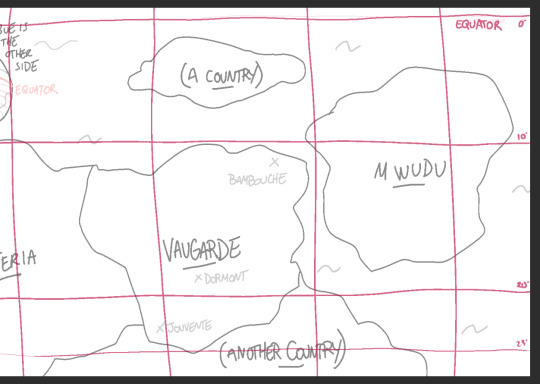
it seems dormont is at about 19 degrees, while bambouche is at 11. easy here!

just divide the whole distance by 180 and you get 111.(1) km (that 1 in a bracket telling you that that one goes on foreeeeever if you let it). since we're looking for the distance of 8 degrees, and we've got a distance of one, you can either multiply it by 8 or subtract the one degree times 2 to get 889. ish. any decimals are the enemy here at this point.

you do the same for the other direction - both bambouche and dormont seemed to be about 2 degrees from the longitude lines, so you do the process with just multiplying by 6 at the end or subtracting the one degree times 4 and get 1333. ish.

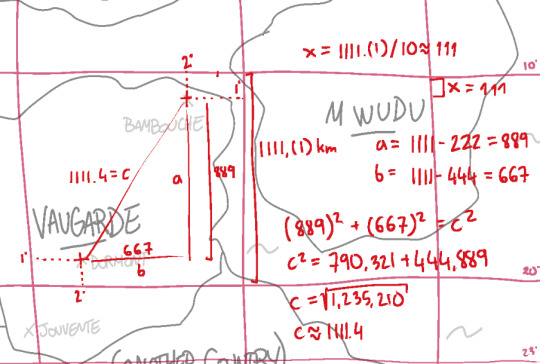
it's pythagorean theorem time!! it looks like a lot of big numbers but they do that only to get added nicely, it's okay, they're not that scary and they don't bite pretty promise with a cherry on top, and you get the resulting distance of 1111.4 kilometers like that!

here's how it measures up in reality for some scale:

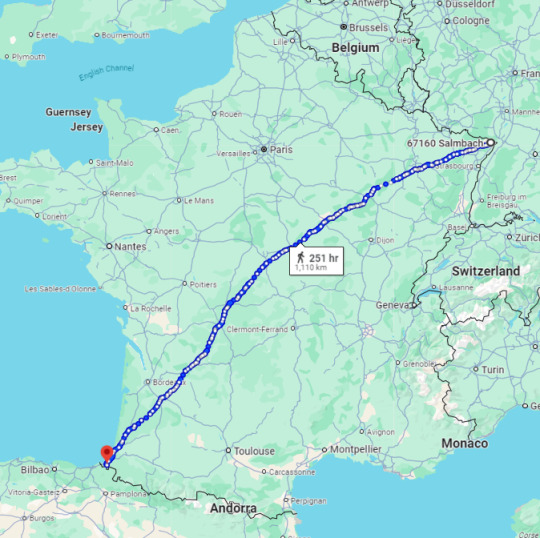
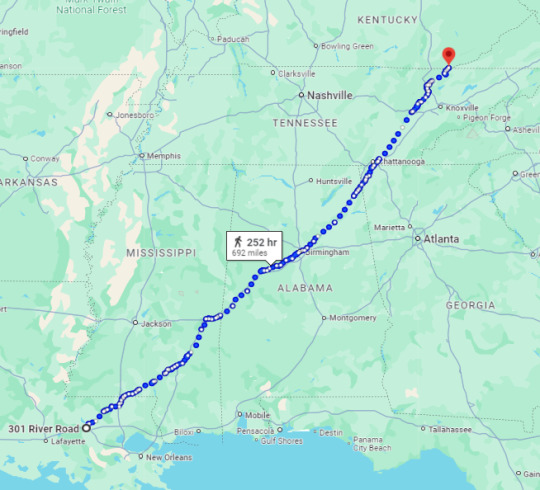
(hey it fits into all of france now!!)

the average recorded speed of a preteen - which the party logically must move at most of the time - is about 5 kilometers per hour (3.1 ish miles). with a travel plan of 4 hours of travel since 9am until 1pm, a two hour break, and another 3 hours until 6pm, because you need to set up camp and things like that need time, it's safe to assume they'd be crossing around 35 km/h a day. and this is still a really good pace!!! very endurance-heavy! divide the total distance by that and you get an estimated time of travel in days, which here is 31; just around a month.

this is, while less than my initial busted calculations, still a lot! lots of walking. so i uphold my statement that they better have sent a letter to nille ahead of them and that the vaugarde postal system is robust enough to deliver it in a timely manner right after the entire country defrosted, to keep her from worrying to death!

[serpentface]

What's Wardi math like? What base is their number system and is it a place-value system? Is there a concept of mathematical rigor? For the classes with formal education, what level of proficiency in math is expected?

I'm not the most math brained so this isn't Super fleshed out tbr

The number systems in use in the present day I Think counts as biquinary and uses sign value additive notation rather than place value. This system does not account for decimal fractions (it Conceptualizes these integers as divisions of measurements but does not have a discrete means of depicting them), and does not have a well-defined mathematical concept of Zero that can be used in calculations, though does use visual placeholders to Indicate the concept of a lack of numerical value. There is no recognition of negative numbers whatsoever.

For people not familiar with the concept of place value vs sign value (because I don't Think this is super common knowledge?):

If you're reading this, there's a high chance you use the Hindu-Arabic numeral system, which uses place value notation. In this system, 326 and 623 represent different numerical value even though they're written with the same combination of numerals. Their position indicates what they must be multiplied by to determine their value (623 is 6 x 100 + 2 x 10 + 1 x 1)

The Wardi numeral system (and that of most of their regional contemporaries) uses sign value additive notation. A symbol's value remains fixed regardless of its position, the number is determined by adding its facets together.

This is what the numeral system looks like as of now. This is developed out of older tally systems and some pictograms, the latter having been simplified beyond recognition into blocky shapes.

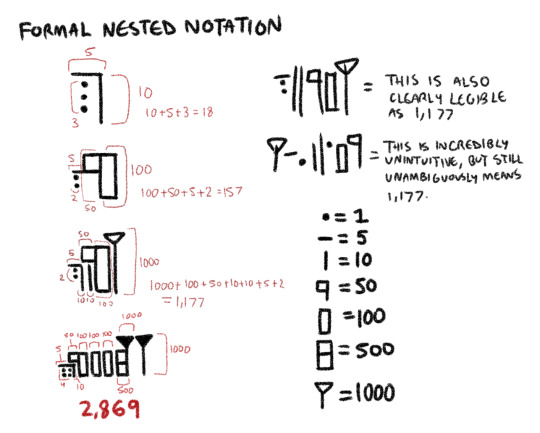
There are stylistic conventions to improve ease and clarity of reading. Numbers are usually written right to left from the highest to lowest symbol integers, which is intuitive for the broader right-left writing system. The 5, 50, 500, etc signifiers are usually connected to their nearest 10, 100, 1000, etc as a matter of visual simplification (ie combining the 100 and 50 symbols will be instantly read as 150, thus and speeding up the mental math).

However, writing them the wrong way does not imply a need for subtraction or otherwise change the numerical value, it's just substantially less intuitive to read. You can write a number with its parts completely out of order and it will mean the same thing, it will just take significantly longer to read and people will think you're a jackass for it.

The 'nesting' mentioned here refers to the smaller integers being nested at a smaller size within their nearest master, causing the scale to decrease from right to left. This convention was inherited from older Burri numerical systems and is utilized in formal record keeping, though is rarely used elsewhere and is broadly falling out of favor (in large part due to jarring heavily with aesthetic conventions in formal Wardi script).

You'll also see numbers written in abstracted form with modified logograms or pictograms (the latter shown here)

This is completely abstracted, lacks clarity, and doesn't convey any internal information beyond Resembling the shapes and positions of the number characters being represented. This is related to the de-stylization of certain logograms in written poetry (ie fully illustrating a cow rather than the typical heavily stylized vague cow shape for the character 'Gan'), and is an artistic convention for beautifying certain texts, functionally Adjacent to the practice of illuminated manuscripts.

You'll also see this form of stylization used in sympathetic magic and some ritual contexts, where shaping numbers into the subject of your rite is a matter of emphasis of what EXACTLY you want accomplished.

---

I have the measurement system better fleshed out so I'll go over that a little.

The smallest standard unit of measurement is the wan (literally 'thumb'), which is associated with the length of the distal phalynx on the thumb and its joint (I didn't actually intend for this, but that's pretty close to an inch on average).

'Hands' (the word is 'un') are the unit of measurement for height/length at human scales, associated with the width of a closed fist (this averages around 4-4.25 inches). These are clumped into larger measurements still referred to with the 'hand' value, with the 'five-hand' being the next base (approximately 20 inches).

In most cases the average person does not have to measure small heights with great accuracy, so they will describe it rounded to the nearest hand base. IE:

I would describe my height (5'2") as 15 hands, or 3 five-hands (rounded down by a couple wan).

I would describe my dad's height (6') as 18 hands, or 3 five-hands and 3.

The five-hand is the base for longer measurements, having similar function to the meter or foot. It tends to be Associated with the length from the tip of the middle finger to the elbow (though is generally longer), and is often approximated as such for low-stakes everyday use.

'Ten five-hands' is the basis of measurement for distances. (approximately 17 ft). (I haven't decided on the in-universe terms for these btw, 'five-hand' probably is spoken how it's written but the 'ten five-hands' unit would have its own discrete word).

The biggest unit of measurement is a mile (no Wardi name yet), composed of 200 'ten five-hands'. (This is a little over a kilometer).

In everyday life most people are just using their own bodies for reference of the 'hands' unit, so measurements in hands can vary TREMENDOUSLY. There have been attempts to standardize these units and divorce them from the length of the body parts of individuals, which is what is usually used in official capacities.

The standardization of these measurements worked backwards from the preexisting established units. The length of the wan was given a set value and established as the smallest unit of measurement from which other measurements derived. 5 standard wan is one hand, a five-hand is 25 standard wan or 5 standard hands, and so on up the scale.

You'll see solid yardstick type tools for small measurements, but most larger scale measurements are performed with knotted lengths of cord, prepared referencing a standardized model cord. Fully beaded measurement cords like this are somewhat of a status symbol- they require a lot of beads and are EXTREMELY time consuming to produce and repair while maintaining accuracy.

People also measure in 'paces', though this one has not been adopted into standardized systems. It colloquially refers to the average length of a single stride at a normal walking pace. You say 'twenty paces from here' to give an approximation of distance in an intuitive way, not when you want to accurately measure a space.

---

You aren't expected to have high proficiency in math unless you're entering a field that requires it, but educated classes/all nobility is expected to have Proficiency. The act of reading numbers in of itself requires you to know at least Basic addition.

Every child who gets any form of formal education learns arithmetic as part of their core studies. Most public education for commoners keeps this pretty basic, you'll learn addition and subtraction thoroughly and will be taught how to multiply and divide small numbers, but it's unlikely that you'll be working with particularly large sums or getting into any algebra or more than basic geometry. It's potentially important knowledge for every member of society, both for basic utility and in managing finances and taxes.

Nobility get much more advanced education in mathematics. Most nobility are landowners who receive a the majority take of crops and livestock from peasants on their land. Much of this will be owed in taxes, but most will still end up with a large surplus Far beyond what their household can consume. Having a good grasp on math is important for wealth management in this context.

Male nobility in particular get thorough educations as part of the broader purpose of grooming them for official positions or priesthood. Anyone involved in the taxation system needs to have a rigorous understanding of mathematics, and the ability is also important for astrological observations performed by priests. Female nobility Usually get a more basic training adjacent to that of commoners, with any additional depth mostly being framed around home economics.

The MOST complex math education tends to be received in formal training as a scribe, which is generally a servant position occupied by members of the commoner class. Most scribes will double as accountants and the like, and working with large numbers with rigorous accuracy is vital to the job. Specialist craftsmen and merchants in the coastal guilds also frequently receive more in-depth math education during mentorships, particularly architects and shipbuilders.

[trash-raccoon]

headcanon on some genshin characters and how they do math. mostly on the men. under read more bcs it got long.

kaeya

can do quick math in his head on the fly. knows some tricks to use his hands to help count to keep track with bigger numbers. give him paper and pen and he can do impressive calculations super fast

diluc

slower with counting than kaeya but better with big numbers. can do rough estimates quickly but needs to write things down to make sure things are accurate.

jean

somehow manages to have the bros' skills combined. good at estimates, can do quick math in her head, big numbers are no problem. they all disappear when she's out of coffee.

zhongli

math whomst. he can make money appear in his hands, he doesn't need math. it gets worse since childe starts footing his bills. he can do math but he won't be happy about it.

childe

god of math. he's an overachiever who thinks that since he's basically posing as a banker in liyue, he HAS to be a good banker, which means he has to be better at math. already good at math to begin with but now he can do big numbers in his head no problem. who needs pen and paper if you have your noggin

keqing

can probably do math in her sleep if she wants to. probably already does that in her dreams tbh.

alhaitham

smart as fuck. cannot do math to save his life. there's a reason why he goes into haravatat. he can grasp concepts but can't do numbers.

kaveh

another god of math. he needs to be accurate with numbers because of his job. king of decimals. somehow his math abilities goes up in smoke when money is involved

collei

hilariously, better at math than she is at her other studies. other forest rangers in training are jealous. "counting is easier than spelling bcs you just keep adding." sure jan.

xingqiu

math whomst, i got lots of mora, i don't need to count.

chongyun

the one doing math for xingqiu

xiangling

can't do math, unless cooking or food is involved. "xiangling what's two plus two?" idk. "xiangling we want to make 77 servings of almond tofu, how many liters of milk do we need" miraculously comes up with the correct answer in 2 seconds

yun jin

can do simple math but is in no way an expert at it. can count the number of her audience accurately in just a glance somehow

kamisato siblings

both are decent at math, but they turn to thoma when it comes to accurate calculation on big numbers. dude's not in childe's levels but he's still calculator on legs

yoimiya

multiplication is easy! somehow, subtraction elude her.

itto

what's math?? that's what shinobu is for!!

kuki

has to be good at math bcs itto is too big of a himbo to realize what addition even is. bless him but pray for her sanity.

layla

has math anxiety. akademiya leaves its marks in different ways in everyone.

furina

can memorize entire scripts in 10 seconds flat. needs calculator to check 1+1

neuvilette

math on legs. he judges he counts he subtracts. we stan a king

lyney

decent at math but lynette has to check his work bcs she's more meticulous

wriothesley

wasn't the best at math but picks it up when he became the warden. sigewinne tutored him and is very very proud of his progress

sigewinne

typically can't be bothered but she does need to calculate meds doses

navia

asks his subordinates to check her work. they usually end up doing the math themselves. save my queen she's good in many things but not math

clorinde

girl's decent at math. she can do her taxes no problem and that's enough for her.

sethos

probably the one who does the accounting for his tribe tbh he has that vibes

[t1d-culture-is]

t1d culture is learning basic decimal adding/subtracting wayyyy before your peers (or knowing what decimals are in general) bc that's how you figured out bolus calculations / how your pump displays them

(or for some, how they read their blood sugar, if I recall?)

★

[leslie-redirects-here]

Roman Numerals Crash Course

As the name suggests, Roman numerals are a numbering system devised by the ancient Romans. Unlike the Hindu-Arabic numerals most commonly used by English-speakers, Roman numerals do not use a decimal system and do not have individual symbols for numbers 0 - 9. Instead, Roman numerals have a small set of symbols that are combined to make a specific number.

Think of the way we write English. The alphabet we use - funnily enough, called the Latin alphabet, though that's misleading - doesn't have a symbol for every word. Instead, we have a set of letters that we then combine to make whatever word we want. It's similar with Roman numerals: you mash them together to make any number that doesn't have its own individual symbol.

Because every suit in a typical tarot deck has fewer than thirty cards, we only need to worry about the first three Roman numerals: I, V, and X.

I = 1 V = 5 X = 10

Let's use the Major Arcana as an example. The first card in the suit is The Fool, who either doesn't have a number or is the number 0. The first numbered card in the suit is The Magician.

The Magician's number is one, so the card is numbered I.

The second numbered card in the Major Arcana is The High Priestess; this card is numbered two. But in Roman numerals, there is no symbol for two. So how is two written? By adding one and one: II.

The same goes for The Empress, numbered three: we add one plus one plus one to get III.

So far so much like tally marks. Four must be four ones, right? Wrong! That'd be too easy or something. Never let it be said the ancient Romans did anything linguistic or numerical the easy way. No, we only do addition for one, two, and three. For four we switch over to subtraction. This is kind of confusing, but bear with me.

Right. So the symbols we have at our disposal are I (1) and V (5). We've already written II (2) and III (3), so now we're only one more number away from the next individual symbol we've got: V (5). So instead of taking four of the smaller symbol (I) and adding them together, instead we're going to take the larger symbol (V) and subtract one from it.

How do we show we're doing subtraction, though? Well. In the same way that there's no + symbol for II or III, there also isn't a - symbol for this next one. What matters is the order the numerals are written in. Numerals of equal value written side-by-side are added together. If a smaller numeral is written to the left of a larger numeral, the smaller numeral is subtracted from the larger one. If a smaller numeral is written to the right of a larger numeral, then the smaller numeral is added to the larger one. Make sense? No? That's fine; it's confusing. We need some more examples.

To get four, we're going to subtract one from five. To do that, we have to write the one to the left of the five: IV.

And that's how we get IV for The Emperor, numbered four:

The next card, The Hierophant, is numbered five, and fortunately five has its own symbol: V.

And now for The Lovers, numbered six! For six we need a five and a one, and for addition we need the smaller numeral to the right of the larger numeral, so for six we get five plus one: VI.

We follow the same pattern to get seven, The Chariot: five plus one plus one, with the smaller numerals to the right of the larger numeral so we know to add them all together: VII. Same for eight, Strength: five plus one plus one plus one, the smaller numerals to the right of the larger numeral: VIII.

And we are on a roll!

But now! We are once again coming up to a new symbol: X (10). The same as before (the rules for Roman numerals are, if confusing, at least consistent), for the last number before the new symbol, we are going to do subtraction instead of addition. And to do subtraction, we write the smaller numeral to the left of the larger numeral. In this case, to get nine for The Hermit, we need to subtract one from ten, so we're going to put a one to the left of the ten, like so: IX.

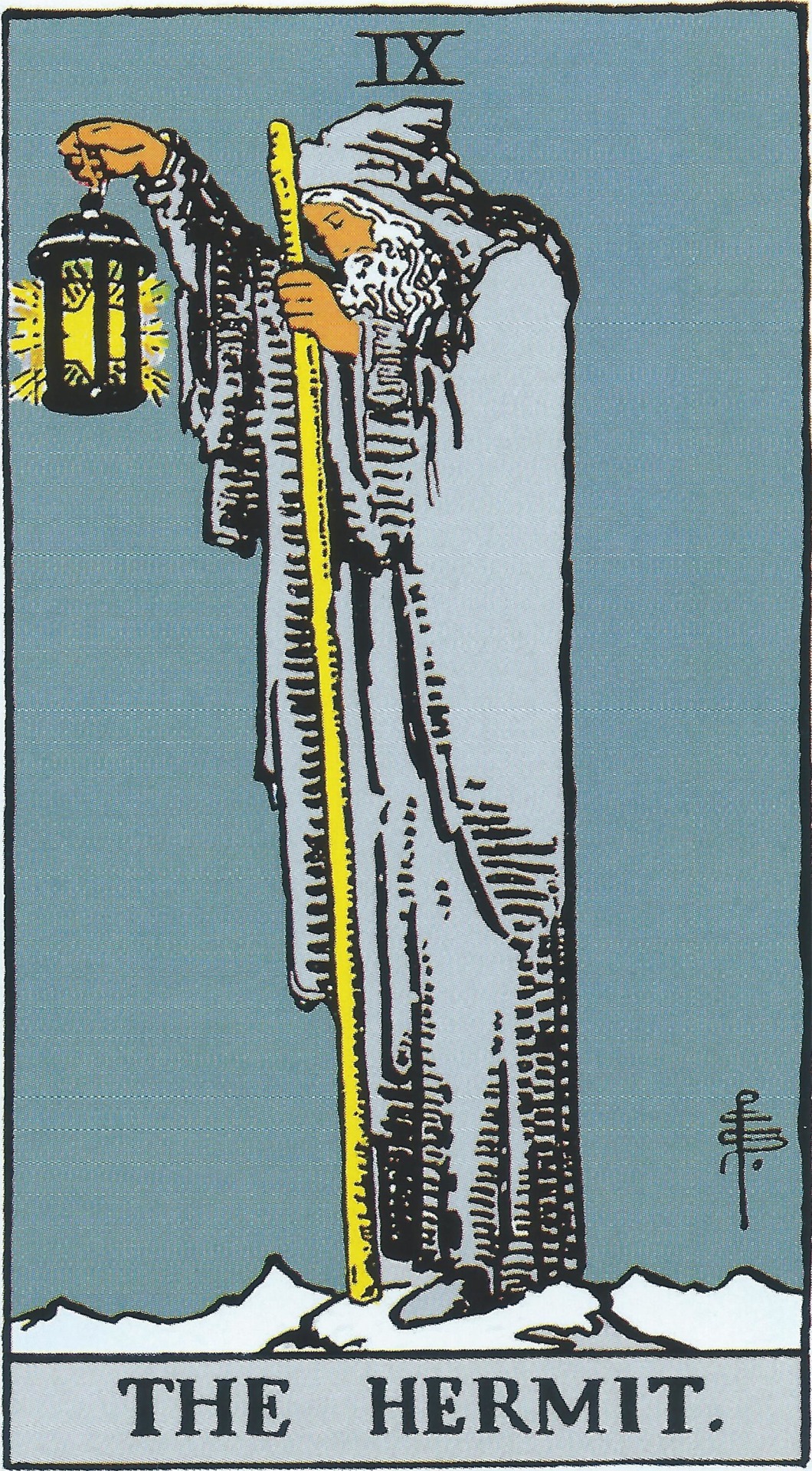
We're doing it!

The Wheel of Fortune is numbered ten, and since ten has its own symbol we don't need to do any addition or subtraction, it's just X.

We can keep following the pattern to get eleven for Justice (ten plus one: XI), twelve for The Hanged Man (ten plus one plus one: XII), and thirteen for Death (ten plus one plus one plus one: XIII).

But what about fourteen? There is no symbol for four, and the last time we made four we did it by using subtraction. So how are we going to use subtraction to get four while also using addition to get fourteen?

My children: we are going to use addition and subtraction at the same time.

To make this a little easier, we're actually going to make fifteen and sixteen before we tackle fourteen. Just roll with it.

Let's look at the rules real quick one more time: if two numerals of the same value are written next to each other, we add them together. If a smaller numeral is written to the left of a larger numeral, we subtract the smaller one from the larger one. If a smaller numeral is written to the right of a larger one, we add them together. And now we're going to add one more rule: subtraction comes before addition.

The numerals we have at our disposal are I (one), V (five), and X (ten). Using these, we can get fifteen by adding ten and five, putting the five to the right of the ten so we know we're adding: XV.

To get sixteen, we need ten plus five plus one. Since we're doing addition we need the smaller numerals to the right of the larger numerals. The largest numeral is ten (X), so that one comes first, furthest on the left. Five (V) is larger than one (I), so next comes five (V), and since one (I) is the smallest it goes furthest right. So sixteen, ten plus five plus one, is: XVI.

And now we're going to do fourteen.

To get four, we subtract one from five. Since we want to subtract, we put the smaller numeral to the left of the larger numeral: IV.

To get fourteen, we add four to ten. Since we want to add, we put the smaller numerals to the right of the larger numeral: XIV.

Here's the thing. XI is ten plus one, which is eleven, right? And if you have XIV, wouldn't that be ten plus one plus five, which is sixteen?

Nope. That does make sense, but that's not how the ancient Romans rolled. Because remember: subtraction comes before addition. So smaller numerals are subtracted before they're added. If you have XIV, ten one five, the one is subtracted from the five and not added to the ten, because subtraction comes first.

Another way to remember is: in theory, yes, you could write sixteen as either XIV or XVI. But the only way to write fourteen is XIV. So XIV has to be fourteen, because there are no other options.

(If it's still confusing or you're not sure you'll be able to remember, that's fine. The more you look at your tarot cards, and the more often you practice using Roman numerals, the easier it will be.)

So! To get fourteen for Temperance, we subtract one from five and get four (IV) and then add that to ten: XIV.

Like we've already seen, fifteen for The Devil is ten plus five (XV), and fortunately the next three numbers are also only addition: sixteen for The Tower is ten plus five plus one (XVI), seventeen for The Star is ten plus five plus one plus one (XVII), and eighteen for The Moon is ten plus five plus one plus one plus one (XVIII).

But what about nineteen for The Sun? Ten plus nine, right? Except the way we wrote nine before was one subtracted from ten. Are we going to write nine that way again?

Yep! Nineteen is ten plus nine, and nine is one subtracted from ten. So we start with ten (X), and add one subtracted from ten (IX), giving us: XIX.

Judgement is numbered twenty, and there is no individual symbol for twenty. In the same way that two is one plus one, so also twenty is ten plus ten: XX.

The final card in the Major Arcana is The World, numbered twenty-one. This one, too, is just addition: ten plus ten plus one, so XXI.

And there we have it! Roman numerals for all the Major Arcana!

Below are some cheat sheets (both text and image).

If you're interested in numbering systems, and how what numbers we had at our disposal has affected machines and technology, I really strongly recommend reading Code: The Hidden Language of Computer Hardware and Software by Charles Petzold.

0 N/A zero 1 I one 2 II two 3 III three 4 IV four 5 V five 6 VI six 7 VII seven 8 VIII eight 9 IX nine 10 X ten 11 XI eleven 12 XII twelve 13 XIII thirteen 14 XIV fourteen 15 XV fifteen 16 XVI sixteen 17 XVII seventeen 18 XVIII eighteen 19 XIX nineteen 20 XX twenty 21 XXI Twenty-one

N/A 0 zero I 1 one II 2 two III 3 three IV 4 four V 5 five VI 6 six VII 7 seven VIII 8 eight IX 9 nine X 10 ten XI 11 eleven XII 12 twelve XIII 13 thirteen XIV 14 fourteen XV 15 fifteen XVI 16 sixteen XVII 17 seventeen XVIII 18 eighteen XIX 19 nineteen XX 20 twenty XXI 21 Twenty-one

Learning tarot | Daily Tarot so far | the Rider-Waite deck | the Aquarian deck | Tarot crash-course | Tarot vocab | main blog

[tumbleringismycopingmechanism]

Also, the solution to struggling is not "let AI do it". I saw a mother complain in a reel on Instagram today that adding and subtracting decimals is practically impossible and not even adults can do it and that therefore her 4th grade kid shouldn't have to do it either and be instead allowed to just ask ChatGPT to do it.

What actually would help would be to try and figure out what exactly the problem is (could be several root causes, e.g. dyscalculia, a general problem with addition and subtraction, a general problem with decimals etc.) and then try to eliminate the problem. That would take time and energy (and most likely money) though.

And sure, not everyone has to be an expert on everything, but school is not there to turn you into an expert – not even remotely. It's there to teach you logical and critical thinking in various areas, and to give you a relatively broad field of things to see if you may be interested in them and to see how capable you are, so that ideally by the end of it you have a vague idea of what you wanna specialize in for the rest of your life. And you can't learn those skills and figure those things out by outsourcing everything to fucking AI

[adaminou]

Cours des maths.Adding, Subtracting, Multiplying, and Dividing Decimals.6th Grade

Description

● Decimals have a decimal point, and we can do math with them like adding, subtracting, multiplying, and dividing. ● When adding or subtracting decimals, line up the decimal points and add or subtract like with whole numbers. ● When multiplying decimals, multiply like whole numbers and then count the total number of digits after the decimal points in the original numbers to place the decimal point in the answer.

Check it now from here

[edugamingappworld]

Interactive Math Games for Children – A Smarter, More Playful Way to Learn

In an era dominated by touchscreens and digital learning, the traditional classroom is no longer the sole arena for education. Today’s young minds are growing up in a world where learning must be engaging, immersive, and responsive. That’s where Interactive Math Games for Children steps in—an app designed to turn numbers, logic, and problem-solving into a delightful journey.

Now available on Google Play, Interactive Math Games for Children is not just another educational app—it’s a dynamic, interactive, and child-focused tool created to blend learning with fun. Whether you're a parent seeking quality screen time or a teacher looking for reinforcement activities, this app has the potential to revolutionize the way your child experiences math.

Why Interactive Math Matters in Childhood Learning

Mathematics forms the foundation of logical thinking, analytical reasoning, and problem-solving. But for many children, math can feel dry or intimidating. That’s exactly why interactive math games are essential—they break down complex ideas into playful, easy-to-grasp activities that build confidence, encourage curiosity, and foster love for learning.

By gamifying traditional math concepts like counting, addition, subtraction, multiplication, division, patterns, and shapes, children can absorb information naturally and joyfully. Interactive Math Games for Children uses smart design to keep kids engaged while reinforcing key concepts through repetition and exploration.

What Makes "Interactive Math Games for Children" Stand Out?

Developed with early learners in mind, this app on Google Play is more than a digital workbook. It offers a fully immersive experience by combining vibrant visuals, fun audio, intuitive controls, and adaptive learningthat grows with your child’s skill level.

Key Features Include:

🎮 Multiple Game Modes – Matching, fill-in-the-blanks, drag-and-drop, and quick challenges.

📊 Level Progression – From basic counting to more advanced arithmetic.

🧠 Logical Puzzles – Stimulates brain development beyond numbers.

🏆 Stars and Rewards – Motivates children through achievements.

👨‍👩‍👧‍👦 Family-Friendly Design – Ad-free, safe, and simple interface.

Skill Development Through Play

Children learn best when they are actively involved. That’s the essence of interactive learning—it ensures children participate, respond, and engage, instead of just watching or memorizing. This app targets several core skills:

🔢 Numerical Fluency

From simple number recognition to mastering addition and subtraction, the app covers all bases with colorful visuals and progressive challenges.

🧮 Problem Solving

With games that require decision-making and pattern recognition, children enhance their critical thinking and spatial awareness.

🎯 Focus and Patience

Timed games and strategic puzzles teach children how to think calmly under pressure, encouraging focus and discipline.

🤝 Collaboration

Some features are designed to allow for co-play, which promotes healthy competition and teamwork when siblings or friends join in.

Designed

Whether your toddler is just starting to explore numbers or your older child needs extra support with math homework, Interactive Math Games for Children meets them where they are.

For Preschoolers:

Colorful counting games

Shape matching

Basic addition puzzles

For Early Elementary:

Two-digit math

Time-based challenges

Multiplication memory games

For Older Kids:

Fractions, division, and decimals

Logic-based math puzzles

Real-world math scenarios

Safe and Screen-Time Smart

Parents are rightfully cautious about what their children engage with online. That’s why Interactive Math Games for Children was built withsafety and quality at its core.

✅ No intrusive ads

✅ No in-app purchases for children

✅ No data tracking

✅ Frequent updates with new games

Every element is carefully designed to ensure your child enjoys a secure, age-appropriate experience that aligns with educational standards.

Why Parents and Educators Love This App

“We tried several math apps, but this one truly keeps my son interested. The reward system and different games help him stay motivated.” – Rachel T., Parent

“I use it in the classroom for warm-ups before math lessons. It’s fun, but more importantly, it’s effective.” – Ms. Lopez, 2nd Grade Teacher

“This is now part of our daily screen time routine. I’m amazed at how much my daughter has improved her addition speed!” – Daniel W., Parent

Available Now on Google Play

Whether your child is just starting their math journey or needs extra practice to reinforce classroom concepts, Interactive Math Games for Children is ready to help. Available for download now on Google Play, this app is compatible with most Android devices and offers a user-friendly experience from the first tap.

📲 Download Interactive Math Games for Children on Google Play

Learning Can Be Fun—And It Should Be!

The days of flashcards and repetition without engagement are over. With Interactive Math Games for Children, education meets entertainment. This app makes math relatable, repetitive in the best way, and play-based, which means kids learn not out of obligation—but because they truly enjoy it.

As digital natives, today’s children deserve more than chalkboards and textbooks. They thrive when presented with material in interactive formats that encourage exploration. By downloading Interactive Math Games for Children, you’re giving your child access to a world of math learning that’s lively, colorful, and cognitively enriching.

From preschool basics to elementary-level equations, this app keeps children engaged, educated, and entertained. And with the trust and expertise of an experienced developer team behind it, parents can rest easy knowing their child’s time is well spent.

[surajkumasblog]

How to Write a Simple Calculator Program in C Using Switch Case

write a simple calculator program in c using switch case way to understand control structures and user input handling in C. This program will allow users to perform basic arithmetic operations like addition, subtraction, multiplication, and division. Below is a step-by-step guide along with the complete code.

Understanding the Program Structure User Input: The program prompts the user to enter two numbers and select an arithmetic operation. Switch Case Logic: The program uses a switch statement to determine which operation to perform based on user input. Display Result: The computed result is displayed. C Code for Simple Calculator Using Switch Case c Copy Edit

include

int main() { double num1, num2, result; char operator;// User input printf("Enter first number: "); scanf("%lf", &num1); printf("Enter an operator (+, -, *, /): "); scanf(" %c", &operator); // Space before %c to handle newline issues printf("Enter second number: "); scanf("%lf", &num2); // Switch case to perform calculation switch (operator) { case '+': result = num1 + num2; printf("Result: %.2lf\n", result); break; case '-': result = num1 - num2; printf("Result: %.2lf\n", result); break; case '*': result = num1 * num2; printf("Result: %.2lf\n", result); break; case '/': if (num2 != 0) printf("Result: %.2lf\n", num1 / num2); else printf("Error! Division by zero is not allowed.\n"); break; default: printf("Invalid operator! Please use +, -, *, or /.\n"); } return 0;

} Explanation of the Code The program takes user input for two numbers and an operator. The switch statement checks which operation the user selected. The corresponding case executes the mathematical operation and prints the result. The default case handles invalid operators. For division, the program ensures the denominator is not zero to prevent runtime errors. Key Takeaways switch case improves code readability and structure. Using %.2lf in printf ensures the result is displayed with two decimal places. Always check for division by zero when performing division. This simple calculator demonstrates how switch cases can be used effectively in C. You can enhance this program by adding a loop to allow multiple calculations without restarting the program.