#exponent section
Explore tagged Tumblr posts
Text
Solving Ohms


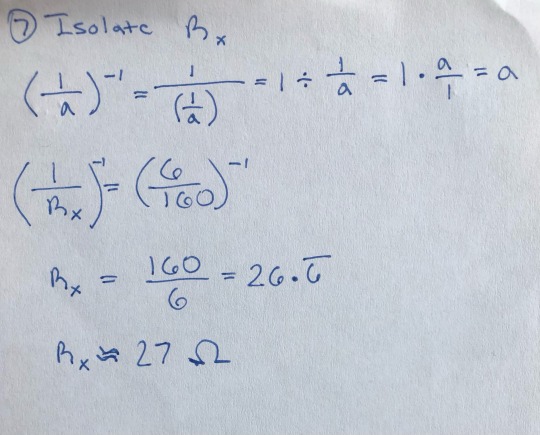
#sept24#exponent section#fraction#ohm#ohms#fractions#exponent#exponents#application problem#application problems
0 notes
Text
Dealing Out Agony Within - E.M Short
Hurt/No Comfort - Any gender (I think)
Please reblog with hastags! It helps a bunch! 💗

You held the aged envelope in your hands. Every year you looked at it with the intent to finally gather up the courage to open it. But you never did. Try as you might, the pain, like a lake, would whirlpool beneath you and drag you under. Until you put the letter back in the box. Back under your bed. Waiting for the same time next year. But this year it remained in your hold, your glossy eyes looking at the haphazardly scribbled letters of your name, slightly smudged, mostly worn.
The rain, the thunder, it seemed to claw and howl at your window just like it did back then. Perhaps a sign. Now was the time to summon up all that courage. That strength. See what Eddie had left you.
The letter had come after you heard of his death. It was bittersweet. A final gift. The last of a long collection of letters between you both. You were both so young. You were just nineteen then. 39 years later and you still sat there just as fragile as you had then.
You took a breath. You gently turned the envelope around and carefully, so carefully opened it. Taking your time. Bracing yourself. Once you had opened it, there was no going back, there was no undoing the last bit of Eddie you had been holding onto. As if he were still here. Unable to accept the truth.
As you pulled out the letter, you saw something else tucked within, but you turned your attention to the letter first. The bad handwriting, the scribbled doodles, the change in pen when clearly one had run out.
"OK. First off you're wrong about Critters. It was a cool movie and you don't give it enough credit. And I don't want to hear how I'm wrong and how it was, by your words, "an unconvincing comedy horror that could barely keep a kid entertained". - again. And I didn't just enjoy it because I have the humour of a child. I know that's what you would say and you're wrong."
You scoffed at his words but enjoyed them nevertheless. Seeing at the end of that section there was a drawing of a face with his tongue out. It wasn't a bad movie, you had just loved to wind him up and annoy him.
"Fun fact from Professor Munson-! The Longest length of sword able to be "swallowed" by a practiced exponent, after a heavy meal, is 27 inches". Or at least according to the Guinness book of world records from 1978. I found it at a yard sale. Now I have way more facts to give than you.
...and I could swallow more than 27 inches, I'm sure. wink wink."
He was always so immature but you found yourself cringing and laughing at the comment. You unfolded the last bit and noticed how he had changed his pen for a red ink.
"I know you probably thought I forgot but unfortunately, for you, I am still holding you to your promise. So pack your bags! Metallica Damage, Inc Tour; here we come! And only the legend himself. OZZY OSBOURNE is also playing. Keep hold of the tickets for me. Wayne doesn't know. Our secret!
Catch you next month for movie night
- your humble servant, the awesome, the one and only, Eddie Munson of the no.1 touring band in the world- Corroded Coffin!"
And in the envelope sat tickets. Two. For a show played 39 years ago. You didn't get to see it with Eddie. But you sure as hell know he was watching from above. And rocking out.
You had long left Hawkins behind but every year you felt a tug to go back. Perhaps you owed Eddie a trip. At least, one last time. Make amends for wasting those tickets.
#eddie munson#writing#fanfic#fanfiction#eddie munson imagine#eddie munson x reader#eddie munson fanfiction#eddie munson fanfic#eddie munson imagines#eddie munson hurt/no comfort#eddie munson season 4
29 notes
·
View notes
Text
Did you know if a number is divisible by 3, you can add all the digits of the number and the sum is divisible by 3? For example, 327 is divisible by 3 and 3+2+7 = 12, which is divisible by 3.
For the Proof on why this is, click Read More
Prerequisite Knowledge
Numbers
Yes, I need to explain how numbers work for this proof.
Let's go back to elementary school. You're being taught basic addition of multi-digit numbers. You're given the number 54,321. 54,321 = 50,000 + 4,000 + 300 + 20 + 1
Let's expand that a little.
54,321 = 5*10,000 + 4*1,000 + 3*100 + 2*10 + 1
Now I''m going to take an aside and mention exponents, just in case.
Normal notation for exponents are a base number with a smaller number floating on the top right corner of your base value. Since Tumblr can't support that notation, I'll use a^b as the notation.
When you have an exponent, you have to multiply the base number by itself however many times the exponent number is. For example, 3^4 = 3*3*3*3 = 81.
Also, if the exponent value is 0 or smaller, you start dividing by the base number instead. So 3^0 = 3/3 = 1.
Now that I've explained that, let's go back to earlier.
54,321 = 5*10,000 + 4*1,000 + 3*100 + 2*10 + 1
Each digit in 54,321 is beling multiplied by an exponential power of 10.
54,321 = 5*10^4 + 4*10^3 + 3*10^2 + 2*10^1 + 1*10^0
This expanded form of an arbitrary number is going to be necessary for the proof.
Modulo and Equivalence
Let's go back to elementary school again. Remember how in division, you'd give a remainder as part of your answer? 12 / 5 = 2 remainder 2.
The modulo operator returns the remainder when you divide two numbers. In programming, % is used for modulo so I'll use that for notation. So 12 % 5 = 2.
An expansion of modulo is equivalence. Two numbers are equivalent under a modulo value when both numbers have the same remainder when divided by the modulo value. Under modulo value 5, 7 and 12 are equivalent because 7 % 5 = 2 and 12 % 5 = 2.
The normal notation for equivalence is the equal sign with 3 lines instead of 2. I'll use == for the notation here.
Since 7 and 12 are equivalent under mod 5, the notation is 7 == 12 (mod 5)
If a number is evenly divisible by a modulo power, it's equivalent to 0. 5 / 5 = 1, therefore 5 % 5 = 0, therefore 5 == 0 (mod 5)
There are some special rules about numbers that are equivalent. We'll let a, b, c, and m be arbitrary numbers.
If a == b (mod m), then a+c == b+c (mod m) If a == b (mod m), then a*c == b*c (mod m) If a == b (mod m), then a^c == b^c (mod m)
The Proof
Now let's move onto the proof.
Let's say we have some arbitrary whole number X which is divisible by 3. That means there is some whole number c such that X = 3*c. So if X is 327, c would be 109 because 109*3 = 327.
Now let's rewrite X into the expanded form from the Numbers section. We'll let d(0) refer to the least significant digit (The one at the far right). d(1) will be the next least significant digit and so on until we reach d(n), the most significant digit.
X = d(n)*10^n + d(n-1)*10^(n-1) + ... + d(1)*10^1 + d(0)*10^0
Since X is divisible by 3, that means the long form of X is equal to 3c.
d(n)*10^n + d(n-1)*10^(n-1) + … + d(1)*10^1 + d(0)*10^0 = 3*c
Now let's start doing some modulo.
10 == 1 (mod 3)
By the earlier rules mentioned in the Modulo section, we can multiply and exponentiate each term (The parts between the +) and they're still equivalent. So now we'll replace each term with an equivalent term under mod 3.
d(n)*10^n + d(n-1)*10^(n-1) + ... + d(1)*10^1 + d(0)*10^0 == d(n)*1^n + d(n-1)*1^(n-1) + … + d(1)*1^1 + d(0)*1^0 (mod 3)
1 exponentiated to any power is 1 so
d(n)*10^n + d(n-1)*10^(n-1) + ... + d(1)*10^1 + d(0)*10^0 == d(n) + d(n-1) + … + d(1) + d(0) (mod 3)
Meanwhile 3*c == 0 (mod 3). Since 3*c = X, then anything equivalent to X is equivalent to 0.
d(n) + d(n-1) + … + d(1) + d(0) == 0 (mod 3)
At this point we can say the sum of all the digits of X can be divided by 3 because the sum would have no remainder.
So in conclusion, if the sum of all the digits of a number can be divided by 3, then the number can be divided by 3.
195 notes
·
View notes
Text
Pilot
Chapter 1 of They Act As One
Summary: Akashi meets a girl in the library and makes a sudden decision that Seijuro disapproves of.
next

"You're gonna have to rush again. Wake up," Akashi called out to the other side of the room, fixing his tie in front of a mirror. There was no response.
"Oi." he hissed, grabbing a pillow and throwing it to the bed opposite his. A hand shot up from the sea of blankets that covered him, catching the pillow with perfect precision despite being turned away.
"I'm awake enough, I don't need your bickering. You sound like mom." Seijuro groaned, adding the pillow to his sea of blankets and hugging it tight.
"Then get your ass up to get ready for school."
"Mooom."
"Suit yourself." Akashi retorted, walking out of the room and closing the door behind him.
Seijuro took a deep sigh, sitting up from his bed. Wiping his face with his hand, he did his best to wake himself up.
They say the state of your bedroom is the same as the state of your mind. Theirs was divided, the twins liked to keep their side according to their own tastes. As such, Seijuro had his achievements and medals displayed, and so was some of his favorite books and a shogi set. Akashi on the other hand kept it simple, mostly small trinkets displayed and instead had pictures on the walls of his friends. Aside from the regular desk and bed that a bedroom needs, I dare say there was only one thing in common that the two sides shared. A picture of the twins, side by side with their mother.
Always they took the same route as they were dropped off at the front entrance of the school. Walking side by side in the middle of the way. The crowds instinctively parted, intimidated by their presence. Typical. Two was more dangerous than one.
Akashi had since smiled at the rest of their classmates in case of eye contact. Seijuro on the other hand, ignored them.
"I'd like to visit the library this morning. Before the Student Council meeting." the older boy announced to his brother.
"How unusual." Seijuro muttered under his breath.
"Is it?"
"We have a much larger library. It is unusual. And unnecessary."
"Well I merely want a change of scenery." Seijuro just rolled his eyes, following him to the library anyways. From there they went their separate ways, Seijuro browsing a different section despite his disapproval.
"A-Ah, Seijuro-sama! Glad to see you here for the first time... Is there anything in particular you are looking for?" one of the student librarians immediately bowed to the younger redhead, quite panicked from his presence.
"I’m merely browsing at the moment."
As he roamed the shelves, Akashi found himself in the presence of a girl on one of the tables. It was clear from the expression on her face that she was struggling, her face scrunched up as she wrote vigorously on her notebook. The redhead subtly peeked at her book as he passed behind her.
"Cubed, not squared."
"What?"
"Your exponent, you've made an error." the girl reread her equations and slammed her hand on the table.
"Shit- you're right! Thanks Akashi," the girl smiled up at him.
He was rather surprised, not quite noticing that he was staring at her.
"Um... are you good?" her question snapped him out of his trance.
"Ah, yes. Apologies... I was caught off guard," Akashi chuckled apologetically.
"By... what?"
"Never you mind," Akashi said, sitting down in front of her.
"Your name is?"
"Sevia."
"Oh yes, you're the transfer student." The girl nodded.
"I do hope I am not interrupting you. You see-"
"Akashi," Seijuro appeared out of nowhere, looking down at his brother and glancing at the girl.
"Come, we will be late."
"Ah... another time, then," Akashi stood up, the girl smiling back and nodding.
"See you," the girl called back to them, waving her hand.
When they were finally out of earshot and alone in the hallways, (Seijuro looked around to make sure) he scolded his brother.
"Hey- what the fuck was that? What happened to just looking in the library?"
"What, I'm not allowed to talk to people now?"
"You are, but to the point that you basically almost forgot about the meeting? Usually you're the one saying we always need to get there early!"
Akashi pouted and turned away, defeated.
"Fine, fine... sorry," he said, his apology half-assed.
"But... she's kinda pretty, isn't she?"
A teacher suddenly exited the classroom, and in the blink of an eye, it was as if the two put on a mask, instantly behaving. They walked straight as they usually do, side by side.
"Good morning Akashi, Seijuro,"
"Good morning, Toshio-sensei." the twins said in perfect unison, as if it was only one voice echoing through the halls.
Seijuro let out a soft sigh, shaking his head slightly.
"Bakashi..." he muttered under his breath.
"How vulgar, Seijuro. We are in public," he scolded his brother playfully, Seijuro ignoring him. Though, he couldn't help but comment.
"It is quite peculiar..."
"Mmh."
It was something the twins were born with. Such curses came with being born an Akashi, born to Masaomi specifically. The inherent burden of being perceived as nearly a god by those around you, and especially by those who worked with you. Those who bow down to them without a single thought was just like everyone else. And they despised it.
"But... rather refreshing, don't you think?"
"Agreed."
"Then it's decided. I'll court her."
Seijuro forced a laugh.
"I'm serious."
Seijuro did not laugh this time. They stopped in front of the Student Council office.
"We will talk about this later."

#kuroko no basket#kurokosbasketball#the basketball which kuroko plays#kuroko's basketball#akashiseijuro#kurokos basketball#kuroko’s basketball#akashi seijuro#knb#akashi seijirou#knb akashi#seijuro akashi#akashi seijuurou#akashi#akashi twins#oreshi#bokushi#They Act As one#taao
12 notes
·
View notes
Text
A rootless people are one asking to be conquered by nefarious forces.
Even those who reside in a polity that views it as “exceptional” would be wise to never forget their roots. The story of American conservatism over the last century has been one of embracing creedal nationalism, wherein conservative adherents believe America “is an idea” — a proposition nation of sorts that is “exceptional” among nations due to its commitment to free enterprise, the rule of law, and limited government.
The essence of this can be found in the section of the Declaration of Independence where it spells out “all men are created equal.” For the exponents of the American universalist project, the Union’s triumph over the Confederacy during the Civil War, the U.S.’s victories in the two world wars in the 20th century, and its social engineering projects spanning the New Deal to the Great Society are viewed as ventures to advance the country’s founding principle of equality.
Once the U.S. reached its unipolar moment in the 1990s, American punditry embraced an imperial smugness that would make ancient emperors blush. They viewed the rest of the world, especially the ethnostates of the globe (save Israel of course), as primitive backwaters driven by parochial nationalism and outdated cultural practices.
9 notes
·
View notes
Text

Soo today I decided to look further into whathever happened to the I Giacobini screenplay - buckle in, I did my best to include as much info as I could find!!
"I Giacobini" (the jacobins) is an Italian screenplay from 1962 based on Federico Zardi's homonymous drama and it is, as of today, a lost media.
The cause for the disappearance of the screenplay from the RAI (Italian national public broadcasting company) archives is either reconduced to the lack of care for the preservation of medias at the time or to the theory which believes the cause to be due to political circumstances.
According to Wikipedia (eh):

...while Italy was in the hands of the Democrazia Cristiana, RAI for the first time broadcast to the public a screenplay «practically entirely aligned with the left and in which Robespierre doesn't come off as a bloody monster but rather like a Che Guevara of reason»
The Democrazia Cristiana or DC (Christian Democracy) was a centrist christian democratic political party in Italy.
The screenplay became largely appreciated by the public, as well as receiving praises from Palmiro Togliatti, exponent of the PCI (Italian communist party) - which happens to be one of the DC 's political opponents at the time.

(source)
Palmiro Togliatti on "Rinascita" wrote that television was bringing a change, since «for the first time it brought a representation of the French revolution inside Italian households»
I went ahead and looked through the archives of Rinascita but found this.
Here I found Togliatti's comment on the screenplay - the below image is a section of it:

The screenplay I Giacobini can be considered an important event of national culture. [...] What matters is that for some weeks a few billions of Italians, have seen and have had in front of their minds a revolution, have been brought to think about about it and to discuss it, seeing it as a political, social and human conflict.
It's then necessary to understand the political contexts of the time both within and outside of Italy:

(source)
...In 1962, under the threat of the cold war, a few months before the Cuban Missile Crisis, a screenplay remarked positively by the leader of a communist party in a NATO country could've raised any kind of reaction.
Thus, the mystery surrounding the disappearance of the screenplay is believed to be caused by some archivist involved with the democristian party.
While this is widely believed to be the reasoning behind it there's not much clear evidence and it's likely impossible to investigate since so much time has passed.

About the screenplay: it was broadcast in 6 episodes, of 90 minutes each, between 11th March - 15th April of 1962 (with a rerun in 1963 after which the tapes disappeared).
It originally featured La Marseillaise, La Carmagnole and Ça ira as well as 4 songs produced for the theater play by Gino Negri.
Audio Recording
In 2012 a man came forward with a (illegally) recorded copy of the audio from the screenplay and sent it over to the Rai archives. The studio managed to recover and digitalize the audios of the six episodes - sadly the video recording is still missing.
Funnily enough, the archive page on which the audios were supposedly made public is gone as of today - but I have found YouTube uploads here: [1] [2] [3] [4] [5] [6]
Also here's a doc that wast broadcast on Italian television on the 11th March of 2012, in honor of the 50 years since the first run of the screenplay - (it's in Italian, if anyone's interested I'll gladly sub it/provide a translation)



In short - bless that viewer for pirating the audio in 1962 and lots of hate to whoever lost the tapes..
Maybe I Giacobini was the friends we made along the way 🍊
#Hope this is good enough if I find more I'll add to this post :p#french revolution#frev#I giacobini (1962)#I giacobini#Frev lost media
45 notes
·
View notes
Text
hwevent18 starter for chu wanning & aequa claudius // @masqce
Chu Wanning looks over the sheet of parchment with a critical eye, quill poised to make any corrections; she's progressed far beyond arithmetic to algebraic geometry, which is what today's lesson has been focusing on. Aequa has proven to be a diligent-- if somewhat demanding-- student. And on all of today's problems, there are no mistakes, beyond one, which he points to sharply. "In the last step of this problem, the number in front must be multiplied before you consider the exponent." But it was just a single slip-up, compared to the many problems she'd completed successfully. Neatly, he writes a replacement equation underneath it, of the same structure but with different numbers substituted in, so she can give it a second try. The repeat problem is likely unnecessary, he doesn't doubt that she won't make the same mistake twice, but he's equally certain she'd want the opportunity to demonstrate her mastery anyway. "Your next task will be to take notes on book three of Euclid's Elements. Pay attention to the section on Thales's theorem; the next time we meet, we'll do work to prove it." The outcome and application of the principles of geometry itself is not the most relevant topic to any noble's life; but the problem-solving techniques and academic resilience it builds can be.

3 notes
·
View notes
Text
I think I found the most unintentionally funny website
So there's this website called https://exponentiations.com/
It's a website that's designed to show up in search engines when you search for an exponent, amidst the bible verses.

I decided to check it out, mainly out of curiosity. It begins with a table of contents.

I'm not sure why a table of contents is necessary for a question that can be answered with five digits. But then it's clear that this site is written to pad its own length.

The first section is the Calculator, with a like button and a tweet link bigger than the result. (Interestingly, they use the word tweet for this link, but refer to X in the sidebar)

In several rounds of redundancy, repeating the question, and saying the same thing repeatedly, we eventually get to the answer, restated.

The next section is complete nonsense. At first I thought this was AI-generated, but I later found evidence against this.

This is just more redundancy. I think the redundancy is just there for search engine optimisation.

Then there's this conclusion and self-promotion. Inexplicably, the conclusion uses scientific notation.
15 notes
·
View notes
Text
Whence Fabulous Faulhaber?
should I promise not to make this a habit?
Dear Mr. Haran, I'm grateful to you and correspondent Eischen (and Conway) for putting the name of Faulhaber on a calculation which heretofore I'd only known quoted, without attribution, by Heinrich Dörrie in Triumf der Mathematik---(which I've only read in translation). However, I'm most frustrated that neither Dörrie nor Eischen give any satisfying motivation for why the postulate should work.
For bystanders still catching up, this postulate is that if one defines a sequence of numbers $B_k$ "by expanding" $$(B-1)^{k+1} = B^{k+1}$$ and transcribing exponents to subscripts... one finds that the differences $$ (n + B)^{k+1} - B^{k+1} $$ similarly treated are equal to cumulative power sums, $$(k+1) \sum_{j \leq n} j^k$$
So the calculation is doable. My Beef is Dilemmimorphic: Either the notational abuse of $(n + B)^k$ suggests that $B$ should be Some Kind Of Linear Operator, in which case what is it? Or else there's an Amazing Coincidence being Overlooked!
It's a comparative Triviality that the power sums $\sum_1^N n^k$ should be polynomials of $N$, and that the leading term be $\frac{1}{k+1} N^{k+1}$ , so indeed it is perfectly reasonable to consider coefficients $B_{k,j}$ defined by $$ \sum_1^N n^k = \frac{1}{k+1} \sum \binom{k+1}{j} B_{k,j} N^{k+1-j} $$ BUT WHY SHOULD WE ASSUME that in fact $B_{k,j}$ depends only on $j$? That's STAGE MAGIC, and the fact that indeed it somehow works does not explain "where it comes from" (Eischen's favourite phrase on the matter).
So, in my customary way of starting with the actual problem and throwing at it what seems to me the minimum of thought, let's first explicate that "comparative triviality": the sequence of polynomials $p_k(j) = \binom{j+k}{j}$ are integral generators for the Integral-valued polynomials, and are recursively definable as iterated cumulative sums of the constant polynomial $p_0 \equiv 1$: $$\binom{j+k+1}{j} = \binom{j+k}{j} + \binom{j+k}{j-1}$$. Hence, cumulative sums of any polynomial, written in the binomial basis, can be obtained just by incrementing: $$\sum_{j=1}^N \sum a_n p_n(j) = \sum a_n p_{n+1}(N)$$
Next, cumulative sums are themselves defined by induction: $"\sum_{j=1}^0" P(j) = 0$ and $\sum_{j=1}^{N+1} P(j) = P(N+1) + \sum_{j=1}^N P(j)$, or said differently, by the Difference equation $$ SP(N+1) - SP(N) = P(N+1).$$ In other words we are trying to solve the Difference Equations $$ S_k(N) - S_k(N-1) = N^k,$$ but in the basis of Monomials $N^j$ instead of Binomials $p_j(N)$.
The binomial theorem, $$ (x+y)^k = \sum \binom{k}{j} x^{k-j} y^j $$ makes the Taylor-MacLaurin formula a Theorem for polynomials $$ (x+y)^k = \sum y^j \frac{1}{j!} \frac{d^j}{dx^j} x^k $$ which is fruitfully abbreviated $$ P(x+y) = e^{y\\, d/dx} P(x) $$ the Backwards Difference, then, is similarly $$ P(x) - P(x-1) = (1 - e^{- d/dx}) P(x) $$
Shall we say, The kernel of the Backward Difference is reasonably well understood? The differential operator is the retract of the Integral operator $\int_0$, so the Taylor-MacLaurin formula provides us also a section for the Forward Difference operator, $$ 1-e^{-x} = \frac{d}{dx} + A\frac{d^2}{dx^2} $$ where, for now, the main point is that the unbounded-degree differential operator $A$ commutes with $d/dx$, so that, for example $$ (1 - e^{-d/dx}) \left(\int_0 \sim dx - A + A^2 \frac{d}{dx} - A^3\frac{d^2}{dx^2} + - \cdots \right) P(x) = P(x)$$
Of course, there are various paths to the power series, other than via expansion of the powers of $A$, but there is a (Laurent) power series $$ \frac{1}{1-e^{-t}} = \frac{1}{2}\coth(\frac{t}{2})+\frac{1}{2} = \frac{1}{t} + \sum \frac{B_j}{j!} t^{j-1} $$ where $B_j$ are the faBulous Bernoulli numbers.
In any case, applied to simple powers, $$ \left( \int_0 \sim dx + \frac{1}{2} + \sum_{j=2}^{\infty} \frac{B_j}{j!} \frac{d^{j-1}}{dx^{j-1}} \right) x^k = \frac{1}{k+1} x^{k+1} + \sum_{j=1}^{k} \frac{k!}{j!(k-j+1)!} x^{k-j+1} B_j \\\\ {} = \frac{1}{k+1} \sum_{j=0}^{k} \binom{k+1}{j} B_j x^{k+1-j} $$ Finally, the power sum polynomials $S_k$ vanish both at zero (formally an empty sum) and at $-1$ (since $S_k(0) - S_k(-1) = 0^k$), so that in particular, $$ \sum_{j=0}^k \binom{k+1}{j} B_j (-1)^{k-j} = 0$$ THAT'S WHERE THIS IS COMING FROM.
3 notes
·
View notes
Text
Exponent Practice


0 notes
Text
Free Online SAT Math Classes & US Citizenship Support with India Houseinc
In today's interconnected world, individuals often harbor dual aspirations: the pursuit of higher education and the dream of establishing a new life in a foreign land. For many, particularly those with ties to diverse global communities, these paths frequently intertwine, requiring meticulous preparation and reliable guidance. Navigating the complexities of standardized tests like the SAT for college admissions, or the intricate processes involved in applying for U.S. citizenship, can be daunting without the right support. This is precisely where organizations like India Houseinc emerge as invaluable pillars, providing comprehensive assistance for both educational advancement and crucial immigration milestones. We understand these multifaceted challenges, and our mission is to empower individuals by offering essential resources, including Free Online SAT Math Classes, and expert guidance for those looking to apply for American citizenship.
The road to achieving significant life goals, whether academic or civic, demands not only dedication but also access to accurate information and effective tools. For students, excelling in standardized examinations like the SAT is often a critical gateway to their desired universities in the United States. For immigrants, understanding every nuance of the American citizenship application process is the key to a smooth transition and achieving full civic participation. India Houseinc is steadfastly committed to bridging these gaps, ensuring that individuals from all backgrounds are equipped with the knowledge and support necessary to realize their dreams and forge a successful future.
Conquering the SAT Math Challenge: Your Path to Academic Excellence
The SAT (Scholastic Assessment Test) remains a pivotal component of the college application process for most universities in the United States. A strong performance, particularly in the Math section, can significantly enhance a student's profile and improve their chances of admission to their preferred academic institutions. However, high-quality test preparation often comes with a substantial financial burden, creating a significant barrier for many talented and deserving students. This is a crucial challenge that India Houseinc directly addresses by proudly offering Free Online SAT Math Classes.
Our Free Online SAT Math Classes are meticulously designed to provide comprehensive and accessible preparation, covering all essential topics rigorously tested on the SAT Math section. These include:
Heart of Algebra: Covering linear equations, inequalities, functions, and systems of linear equations.
Problem Solving and Data Analysis: Focusing on ratios, percentages, rates, proportional reasoning, statistical concepts, and interpreting graphical data.
Passport to Advanced Math: Delving into quadratic equations, polynomials, rational exponents, exponential functions, and complex numbers.
Geometry and Trigonometry: Revisiting fundamental concepts of area, volume, angles, triangles, circles, and basic trigonometric principles.
What truly distinguishes our Free Online SAT Math Classes and makes them exceptionally effective is their dual emphasis on accessibility and unwavering quality. Students benefit immensely from the flexibility of learning at their own pace, the ability to revisit challenging concepts as often as needed, and the utilization of premium resources that would otherwise be financially prohibitive. The online format offers unparalleled flexibility, enabling students from diverse geographical locations to benefit without the logistical or financial burdens of physical commutes. This initiative is a powerful step towards democratizing access to superior test preparation, fostering academic excellence irrespective of socio-economic background.
Furthermore, these SAT Math classes online extend beyond mere content review. They strategically focus on:
Effective Test-Taking Strategies: Imparting crucial techniques for managing time efficiently, identifying common question traps, and approaching various question types with confidence.
Extensive Practice and Mock Tests: Providing abundant opportunities to apply newly acquired concepts, hone problem-solving skills, and simulate the actual test environment through full-length mock examinations.
Profound Conceptual Clarity: Breaking down even the most complex mathematical concepts into easily digestible and understandable segments, thereby building a robust foundational knowledge that transcends rote memorization.
By offering these invaluable SAT Math classes online, India Houseinc empowers students to confidently approach one of the most significant examinations of their academic lives, thereby opening wide the doors to prestigious higher education opportunities across the United States.
Navigating the Path to a New Beginning: The American Citizenship Application
For individuals who have established their lives in the United States as lawful permanent residents, the next pivotal step is often the deeply significant milestone of becoming a U.S. citizen. The process to apply for American citizenship, formally known as naturalization, is a profound achievement that grants full civic participation, including the invaluable rights to vote, run for public office, and travel with a U.S. passport. However, the American citizenship application process can be intricate and lengthy, involving multiple forms, comprehensive interviews, and specific civic knowledge requirements that can feel overwhelming without proper guidance.
India Houseinc provides indispensable support for individuals looking to apply for American citizenship. We are committed to simplifying this complex journey by offering comprehensive guidance and assistance at every stage. Our support includes:
Eligibility Assessment: Helping applicants meticulously understand if they meet all the stringent criteria based on continuous residency, physical presence, demonstrating good moral character, and proficiency in English language skills.
Form N-400 Preparation Assistance: Guiding applicants through the accurate and complete preparation of the Application for Naturalization (Form N-400), a comprehensive document requiring detailed personal, residential, and employment history.
Document Gathering Support: Advising applicants on systematically collecting all necessary supporting documentation, such as Green Cards, marriage certificates, tax returns, and international travel records.
Biometrics Appointment Preparation: Explaining in detail what to expect during the crucial fingerprint and photograph appointment.
Citizenship Interview Coaching: Providing essential resources and extensive practice for both the civics and English language components of the naturalization interview. This often includes practicing the 100 civics questions and preparing for common interview scenarios to build confidence. We also help individuals understand their interactions at the Application Support Center Houston TX, which is where biometrics appointments typically take place.
Oath of Allegiance Ceremony Information: Guiding applicants on the final, ceremonial step where they formally pledge their allegiance and become U.S. citizens.
The journey to apply for American citizenship can indeed be daunting, often perceived as an arduous path filled with legal jargon and extensive paperwork. Our pivotal role at India Houseinc is to provide utmost clarity, ensure absolute accuracy in documentation, and offer compassionate, unwavering support throughout every single stage. We tirelessly strive to make the American citizenship application process as smooth, transparent, and stress-free as possible, thereby enabling individuals to achieve their dream of becoming fully integrated and contributing members of American society. Our understanding of the local infrastructure, including the role of the Application Support Center Houston TX, further enhances our practical assistance.
India Houseinc: Integrated Support for Your Aspirations
India Houseinc is far more than just an organization; it is a vibrant community dedicated to fostering success, facilitating seamless transitions, and empowering individuals. Our unwavering commitment stems from a deep and empathetic understanding of the unique challenges faced by students aiming for higher education and immigrants building new lives.
Our unique value proposition lies in our integrated approach:
Unparalleled Accessibility and Affordability: Our Free Online SAT Math Classes exemplify our profound dedication to making quality educational resources accessible to everyone, regardless of their financial circumstances, breaking down traditional barriers.
Expert and Reliable Guidance: We provide accurate, up-to-date information and highly personalized assistance for the complex American citizenship application process, ensuring that every step is handled with precision and care, including preparation for visits to the Application Support Center Houston TX.
Holistic Community Support: We recognize that both academic success and immigration processes are intrinsically interconnected parts of a larger, profound life journey. Therefore, we provide a comprehensive suite of resources and support that addresses both aspects, fostering overall well-being.
Trust and Proven Track Record: Our stellar reputation is built upon years of consistent, reliable service and successful outcomes for countless individuals who have achieved their dreams with our guidance.
Whether you are embarking on your academic journey, meticulously seeking to enhance your SAT scores, or taking the monumental step to apply for American citizenship, India Houseinc is unequivocally here to guide you. We firmly believe in empowering individuals with the essential knowledge, practical tools, and unwavering support they need to achieve their aspirations and meticulously build a truly successful and fulfilling future.
Embark on your definitive path to success today. Explore our Free Online SAT Math Classes or reach out for expert assistance with your American citizenship application. Visit India Houseinc to learn more and begin your transformative journey!
0 notes
Text
1518 SANCTUS THOMAS SUPER ANIMA By Tommaso D'Aquino Good Christianity
1518 , SANCTUS THOMAS SUPER ANIMA Sancti doctoris By Tommaso D'Aquino Thomas Aquinas (Roccasecca, between 1224 and 1226 - Piperno, 7 March 1274) was an Italian religious man, theologian and philosopher. A Dominican friar, the main exponent of Scholasticism, he was already called Doctor Angelicus by his contemporaries. He was proclaimed a saint by Pope John XXII in 1323 and since 1567 he has been listed among the doctors of the Church. In 1880 he was declared patron saint of Catholic universities and study centers. Thomas represents one of the main theological and philosophical pillars of the Catholic Church, also being the point of connection between Christianity and classical philosophy, which has its foundations and masters in Socrates, Plato and Aristotle, and then passed through the Hellenistic period, especially in authors such as Plotinus. He developed a theory of law that had a large following in the following centuries. Illustrated By: Format: Vellum, Language: Latin Dust Jacket: No Jacket, Dust Jacket Condition: No Jacket Published By: Lucantonium de Giunta florentini, Venice Imperial octavo (8vo 8+1⁄4 × 11+1⁄2 210 × 292),Pages 176 ISBN: This valuable edition of 1518 presents the commentaries of St. Thomas Aquinas on Aristotle's work "De Anima". The "Angelic Doctor" offers here a profound philosophical analysis of the soul, intertwining Aristotelian doctrine with Christian theology. Thomas Aquinas, a central figure in medieval philosophy, is known for his ability to reconcile Christian faith with Aristotelian reason. His commentaries on Aristotle's work are considered fundamental to understanding his philosophy and theological thought. P. Camerini, Annali dei Giunti, I.1, p. 178. Only one copy available in the library of Francesco della Vigna. On the Soul (Ancient Greek: Περὶ ψυχῆς; Latin: De Anima) is a writing by Aristotle. The treatise is probably a collection of notes taken by the philosopher himself (in fact they are concise and concise) that he would later develop in his school. In fact, Aristotle does not dwell so much on its definition but describes its functioning, and focuses, therefore, on its faculties (functions). For Aristotle, the soul is not only the formal and driving cause of the living but also the final cause and therefore the primary condition of the immanent finalism of the world of life. Plants and animals act unconsciously for the universal, for the continuity of the species and for the conservation of their form. Man lives consciously for the universal, he values life up to the highest levels of activity. The soul is the essence or substantial form of the living, and the faculties are accidental forms. The definition of the soul as substance as form means that the soul, in general, is not substance in and of itself but the form of the living. The substantialist vision of the soul must therefore be integrated with the examination of the concrete ways in which the activity of the soul is expressed in different living beings. SKU: BTETM0002558 Approximate Package Dimensions H: 12.5, L: 30, W: 25 (Units: cm), W: 2Kg
Good - Folio. Parchment binding. Interesting illustrated diagrams in the text. Spine with signs of wear, later binding in stiff parchment, red page edges, splits top and bottom of spine and the back cover text block firm. Initials and Giunti Lily on the colophon, rubricated in red. Text in two columns in Gothic character, text of Aristotle in Latin, woodcut initials, water stain, slight defect on the internal margin of the first sections. Overall good state of preservation of the work. PP. (2); 172; (2). With the text of Aristotle in Latin. - Gothic. Text in two columns. Numerous woodcut initials - Occassional ink margenelia Please see photos as part of condition report
0 notes
Text
A Trump Outreach Administrator provides the information they will find as a new part
Entrant Assistant to President of President of President Expon is willing to keep a new section to confirm President Donald Trump Heaves his promises for promises to spread in refuge, Latino and others in customs received the last options from the last November. Sitting down for a unique discussion that “My feelings in lara trump“On Saturday, she pointed out what changes she was determined to…
0 notes
Text
A Trump Outreach Administrator provides the information they will find as a new part
Entrant Assistant to President of President of President Expon is willing to keep a new section to confirm President Donald Trump Heaves his promises for promises to spread in refuge, Latino and others in customs received the last options from the last November. Sitting down for a unique discussion that “My feelings in lara trump“On Saturday, she pointed out what changes she was determined to…
0 notes
Text
The first part of this discussion deals with the tenets, criticism and appraisal of the natural semantic metalinguage theory. The second part is the explication of Swahili interjections while the last section explicates the English emotion expression is disgusted with. 1.1 Claims of the natural semantic metalanguage (NSM) The theory of natural semantic metalanguage (NSM), postulated by Wierzbicka and her co-researchers, posits the lexicalization of a set of semantic primes the in all natural languages. As such, each primitive has an exponential equivalence in every language. The following table exemplifies this concept with English, French or Slovene primes. EXPONENTS PRIMITIVES English French Slovene SOMEONE someone quelqu’un nekdo SOMETHING something quelque chose nekav WANT want Vouloir hoteti Wierzbicka (1996, 110) estimates the number of semantic primes at one hundred. The current entries are 65 (see Appendix 1). These words, according to the proponents of NSM, are translatable into every language without loss or addition of meaning. Wierzbicka (1996, 19) further explains that these primes can combine to form canonical sentences with basic syntactic structures. These constructions are not only the product of universal syntactic rules but also, importantly, the result of verifiable intuitive patterns for combining primitive concepts. In her view, lingua mentalis, “the language of the human mind” is the real originator of syntactic and semantic structures. In a nutshell, the basic core of the natural semantic metalanguage (NSM) lies in identifying semantic primes and combining them within basic syntactic frames (canonical sentences) useful in defining all words in a language. Natural semantic metalanguage (NSM) is useful in cross-cultural translation. According to Wierzbicka (1996, 137), words are the best expression of a society’s cultural values and assumptions. She, however, finds lexicographical definitions inaccurate, classical decomposition of meanings restrictive and the prototype approach inadequate. She, therefore, proposes the natural semantic metalanguage (NSM) as an effective device for identifying ethnosyntactic phenomena useful in cross-cultural translation. Culturally-specific words are translatable through the universal semantic primes. This approach, it is argued, eliminates residual effects and deficits in translation of words. Some widely cited semantic explications done through this approach include the ones for a Japanese word of emotion, amae, and the Polish word szczęśliwy which this approach proves to be more intense than its English equivalence, happy (Wierzbicka 1996, 215, 239). 1.2 Nick Riemer’s Critique of the NSM Riemer (2006) puts to question both methodological and theoretical constructs of NSM. The NSM’s principle that a definition must be simpler and more intelligible than the utterance being defined is dismissed as a misrepresentation of the nature of semantic explanation. This criticism is unfounded. The theorists’ position should be upheld; the only rider should be that there could be exceptions but NSM has provided for semantic molecules to suffice when the primes are ineffective. Canonical sentences or contexts as a means of semantic explication are another tenet of NSM that attracts criticism. Riemer finds some of the primes listed such as move, feel et cetera ambiguous and questions the sense of the words that warrants their inclusion. Multiple ambiguities are resolvable by disambiguation through definition but this would nullify one of NSM’s maxims that some words must remain indefinable. This criticism is valid. The theorists should provide a more conclusive criterion for selecting primes other than translatability and indefinability. The other aspects of NSM theory critiqued have to do with substitution and polysemy. Riemer applies the substitutability test to validate the extent to which NSM’s paraphrases Read the full article
0 notes
Text
COP 3223 Homework 8 Solution
You are creating a program to help you understand some important math concepts: factorials and exponents. Since you are focused on understanding the concepts, you will not use the math library (math.h). One of those sections will be the function to calculate a factorial. Your function will take in a single non-negative integer (n) and you’ll calculate n! or n factorial. To calculate n! you would…
0 notes