#fermat's principle

[todays-xkcd]

Of course you get an ice cream cone for the swimmer too! You're not a monster.

Path Minimization [Explained]

Transcript Under the Cut

Cueball stands on a beach. At a roughly forty-five degree angle to him a ways away is a swimming presumably in distress, and straight ahead of him and roughly the same distance is an ice cream stand.

Path that minimizes distance [A straight line from Cueball to ocean swimmer, bearing about 135]

Path that minimizes time [A line from Cueball to the waterline closer to horizontal, bearing about 120, then angling towards swimmer, bearing about 150]

Path that minimizes swimming [A line from Cueball to the waterline closest to swimmer, bearing about 115, then angling toward swimmer, bearing 180]

Path that minimizes time until you get ice cream [A line from Cueball to an ice cream stand manned by Ponytail, bearing about 90, then angling toward swimmer, bearing about 190]

Path that maximizes time [A line from Cueball away from the shore, bearing 0, fading and disappearing at the top of the panel, and reappearing at the bottom of the panel directly below swimmer]

[squeakadeeks]

theres been a few times now where ive had a student run into my cosplay work randomly before, and aside from the bonkers whiplash that gives me personally, its insane to think about seeing some guy playing dress up in his house online, and then some number of months later that same guy ends up inexplicably teaching you fermat's principle

[oqmemphis]

John Gabriel and Mathematical Ignorance

Have you ever watched a flat earth conspiracy video? If not, the usual format is pretty straightforward: the presenter rambles, unscripted and unedited, into a cheap microphone while using some shitty screen recording software to film themselves drawing lines on top of random jpegs in paint.net for five to ten minutes, before sitting back and proudly claiming that their unmatched genius has proven all human knowledge from the last several millennia to be hopelessly fraudulent.

John Gabriel is a flat earther for mathematics.

Mr. Gabriel writes and speaks at great length about an invention which he calls "the New Calculus", a theory most briefly described as an attempt to reformulate all of mathematics starting from (what he perceives to be) the base principles used by the Ancient Greeks. He believes that mathematics as a field of study has been practiced almost exclusively by idiots for approximately the last two thousand years, or nine hundred, or a hundred and fifty (the exact time at which things went to shit seems to vary a lot; he rejects much of Euler and Fermat, but also calls Cantor "the father of all cranks") and claims that only he can understand numbers "properly".

Whenever a popular maths YouTube channel makes a video about infinity (see Numberphile on -1/12 or Vsauce on transfinite ordinals), there are inevitably people in the comments arguing that the video's premise is misleading, wrong, unnecessary or incoherent, or that the concept of doing mathematics with infinite sets is fundamentally invalid. Mr. Gabriel takes this finitist view to its logical extreme.

In his 152-page tirade against modern academia, he argues that any "infinite process" is outright unmathematical and should not be allowed; his definition of "infinite process" includes convergent limits, such as the unending decimal expansion required to express irrational numbers. A significant basis of his work is that irrationals like π and √2 are not numbers, but rather "constants" or "incommensurable magnitudes". Why this is a useful distinction, given that these "constants" behave like numbers in nearly every regard, is never explained. He additionally claims that 0 is not only not a number, but is "not even required at all in mathematics". He spends the entire first half of the book re-deriving all of arithmetic and algebra based entirely on principles of Euclidean geometry, while repeating, mantra-like, that only integer ratios are numbers and that anyone who claims otherwise is an ignorant buffoon. I wonder if he writes RPF of himself throwing Hippasus into the sea.

He has then taken this idiosyncratic worldview as a starting point from which to reinvent calculus.

He is straightforwardly wrong.

Mr. Gabriel frequently complains that his critics mindlessly hurl insults at him without seriously engaging with his work, so as a show of absurdly generous good faith I will engage with it now. Any fellow masochists reading this are invited to take a look at Mr. Gabriel's manuscript - specifically his demonstration of how to take a derivative without the use of limits - and try and figure out where the problem is.

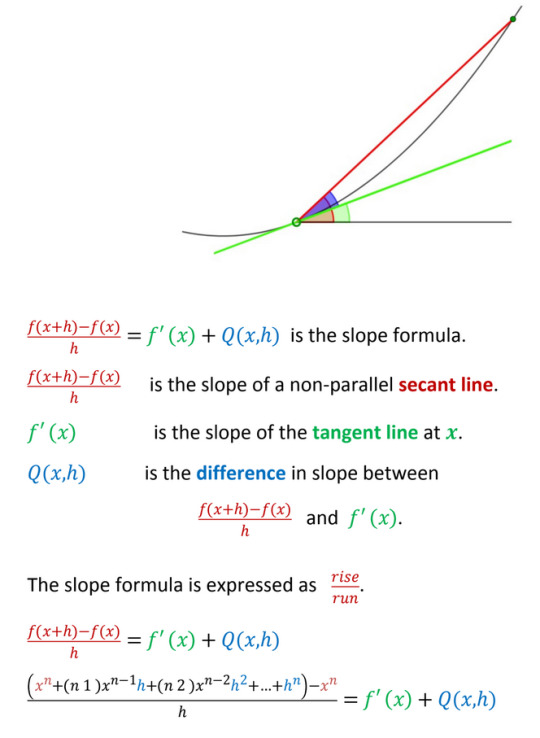
Ignoring Mr. Gabriel's apparent inability to find the subscript button in Microsoft Word, he has taken an nth-degree polynomial (which could contain many terms), and transformed it into a single term of degree n-1. This, you will be astounded to learn, is not the correct result when taking the derivative of anything more complicated than f(x) = x^p. Notably, he never attempts to do this.

In fairness, the above demonstration is not actually the New Calculus. Mr. Gabriel explains that he has helpfully preceded his earth-shattering revelations with a less rigorous, more geometrically-derived formulation. I'm sure we'll get some real mathematics in a minute.

What we get is him complaining that the Encyclopaedia Britannica does not provide sufficient intuition for the work of Newton and Leibniz, before claiming that his New Calculus is "the first and only rigorous formulation of calculus in human history". He uses this exact phrasing (or nearly) at least four other times in his PDF; if he is unhappy with the Britannica, I might politely advise him to try reading Roget's Thesaurus instead.

Finally, on page 120 of 152, we are given an explanation of the epiphany to which the entire monograph has been building.

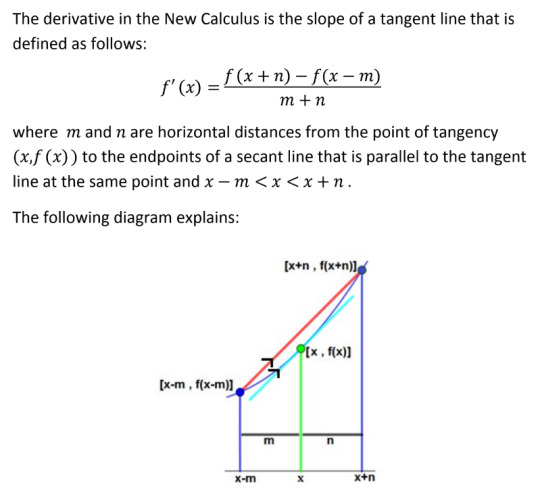
"Left as an exercise for the reader" is a phrase used by cowards (and to his credit, John Gabriel is not a coward), so I will point out the slight issue here: it is not possible to calculate values for m and n unless you already know the tangent slope. In his example of how to compute the derivative of sin(x), he expresses the function in its Taylor series form (so much for shunning infinite summations), and then simply replaces said series with the one for cos(x) without comment; he then manages to successfully determine his secant intersection values, and then calculates the value of the derivative function he just shoved into his pile of equations a few lines further up. Thus, his bafflingly circular logic is enabled almost invisibly.

This is it. This is all that this book is. John Gabriel's magnum opus, the thing he has been building up to for 119 pages amid paragraphs of bluster about the idiocy of irrationals and his own vaunted genius, is the ability to compute the derivative of a function as long as you know the derivative of the function. And as long as that derivative is not a zero found at one of the function's inflection points, because apparently that doesn't count as drawing a tangent line (for reasons that I'm sure are unrelated to the fact that Mr. Gabriel's secant method fails for such points).

I don't want to go deep into personal insults here - that's John Gabriel's job - but this is not useful mathematics. The logic is circular, the motivation is worthless, and it enables no new insights not already achievable with the current mainstream understanding of calculus. No statement is proven that has not already been shown to be true within the framework of Newton and Leibniz; there are only restatements of existing theorems based on the shaky-at-best logic of these new principles. So what is it for?

This is a question I kept coming back to while reading Mr. Gabriel's PDF. What is this for? What is gained by stubbornly insisting that π and e are not numbers, but rather "constants of incommensurate magnitude"? How does rejecting the usual definition of division as a multiplicative inverse in favour of some guff about "measuring in equal parts of an abstract unit" expand the horizons of mathematical knowledge? Of course, it doesn't.

John Gabriel, ultimately, is not important. There are thousands of other flat-earthers and similar grifters just as laughable as him, and to my knowledge there is roughly nobody who takes him seriously. (And if anyone does, the chance of some random guy on Tumblr convincing them otherwise is vanishingly small.) But I find his writing fascinating precisely because of the way in which he is wrong. He seems firmly rooted in the idea that mathematics is all discovery and no invention; that we can derive mathematical truths out of absolutely nothing. He rejects the notion of logical axioms as a starting point for derivation, instead seeking answers grounded in reality (by proxy, via "pure geometry"), and he is incensed when people ignore his demands.

But mathematics is not physics. Mathematical objects don't exist independent of their definitions, but they do exist independent of the real world. The rules of mathematics are defined by mathematicians only; if we want π to be a number, all we have to do is say "let π qualify as a number"; if we want to define an infinite sum as being equal to its limit, we can. If the rules disallow something, nobody can stop us picking different rules, reality be damned. John Gabriel has in fact done this too, even if he doesn't realise it - it's just that his starting axiom around which the rest of his theory is based is "I am the greatest mathematician in the world, and everyone who has come before me is a moron". I do not exaggerate when I say this; a pinned comment under one of his recent videos reads:

I, the GREAT JOHN GABRIEL explained why calculus works and I defined NUMBER correctly for the FIRST TIME in human history. For this, I am called a crank by your ignorant, incompetent and incorrigibly stupid mainstream math professors and teachers. I shall keep reminding students of your venom and your hatefulness towards me. You are vile, disgusting excuses for human beings. The longer you deny me as the greatest mathematician, the more shit will accumulate in your diapers.

If Mr. Gabriel objects to logical premises that are rooted in fiction, I have some suggestions for ideas he might want to discard.

[materialsscienceandengineering]

Determining refractive index at relativistic speeds

If you studied advanced physics at high school, there's a good chance that you remember Snell's law, which states how a ray of light bends when it crosses a boundary between two media. According to this law, the ratio of the sines of the incident and refracted angles is a non-universal constant, later understood as the relative refractive index of the refracting medium with respect to the incident one. The theoretical formulation of the law of optical refraction was initiated by Descartes in the early 17th century. He introduced a metaphysical form of an optical-mechanical analogy, suggesting a conceptual parallel between trajectories in classical mechanics and wavefronts in optics. Descartes considered the conservation of the tangential component of the velocity of a particle, as well as light, as it crosses a boundary between media. He determined the relative refractive index as the ratio of the speed of light in the two media. Later this century, Descartes' metaphysical theory was rejected by Fermat by introducing the "least time principle" that was named after him. He also determined the relative refractive index as the ratio of the speed of light in the two media.

Read more.

[gook54-blog]

If light, electrons, photons and cells theme explore multiple paths is there actually any constant in the universe ?

Light explores every possible path due to the principle of least action and quantum mechanics. In classical physics, light seems to travel in a straight line or follow the path of least time (Fermat's Principle). However, in quantum mechanics, Richard Feynman's path integral formulation shows that light (or any quantum particle) actually takes all possible paths, but interference effects cause only certain paths to contribute significantly.

How Does Light Explore Every Path? Wave Nature of Light: Light behaves like a wave and interferes with itself. If you calculate all possible paths, the ones that reinforce each other are the most probable, while others cancel out. Feynman's Path Integral: Every possible path of light is summed up as an amplitude, and only the paths that constructively interfere (which often approximate the classical least-time path) dominate. Double-Slit Experiment: A photon can go through both slits at once, interfering with itself as if it took multiple paths. How Does This Apply to Electrons? Quantum Superposition: Like photons, electrons exist in a superposition of all possible paths until observed. Tunneling: Electrons do not follow fixed paths but have a probability of appearing on the other side of a barrier they should not classically cross. Orbital Behavior: Electron clouds around atoms are the result of all possible paths combining into probability distributions (orbitals). How Does This Apply to Cells? Biophotons and Quantum Coherence: Cells emit weak light (biophotons), which may follow similar quantum rules. Enzyme Reactions and Quantum Tunneling: Some enzyme reactions involve quantum tunneling, where particles like protons or electrons take multiple paths to find the most efficient reaction route. Photosynthesis Efficiency: Quantum coherence in chlorophyll allows energy to explore multiple pathways and find the most efficient route to the reaction center.

Essentially, at a fundamental level, all particles—including those in living cells—follow quantum rules where every possible path is explored, but interference determines the most probable outcomes.

By deduction there cannot be any constant , only observation!s!!

[integrating-sphere]

Analytical optical detector - colorimeter, glossmeter

The colorimeter and glossmeter developed and produced are optical testing instruments. The reason why these instruments can measure the color difference, gloss, chromaticity, and image clarity of various products is due to the optical principles of their internal design. Learning optical knowledge is very helpful for the use and analysis of color difference meters and glossmeters. People can see that color and light density are inseparable. Only in the visible spectrum can we clearly see color through the naked eye. Generally, the wavelength of visible light that the human eye can feel is 400 nm (purple) to 700 nm (red), and the visible spectrum is a small part of all electromagnetic spectrum. There are thousands of colors in the world, among which red, green, and blue are known as the three primary colors. Changes in the ratio of red, green, and blue can produce multiple colors, and equal mixing of the three can reproduce white. The concept of complementary color: The color formed by subtracting color X from white is called the complementary color of color X. White red=cyan cyan White Green=Magenta magenta White blue=yellow yellow White Red Green Blue=Black Complementary color characteristics: When we use an X complementary color filter, we will find that the primary color corresponding to the complementary color will be filtered out. Names of primary colors and corresponding complementary colors: There are two ways to achieve color reproduction: Primary color addition: All three primary colors are added to form white, and any two primary colors are added to form complementary colors that do not participate in the synthesis. Subtraction of primary colors: All three complementary colors are added to form black, and any two complementary colors are added to form a primary color that does not participate in the synthesis. In these two methods, the addition of primary colors is relatively simple, which is the addition of other colors formed by the addition of primary colors. However, this method is rarely used in practical life; The primary color subtraction method is to subtract the corresponding primary color from white to form other colors, which is to use complementary colors to superimpose to form other colors. It is relatively common in applications. We have introduced the knowledge of color above, but in fact, color definitions and concepts are not widely used in chromatic aberration meters, glossmeters, and other instruments. At most, they are optical concepts. Below, we will briefly explain optical knowledge. The law of linear propagation of light: Light travels in a straight line in a uniform medium. Fermat's law is the first consideration in the development of glossimeters. The so-called Fermat's law refers to the fact that when a beam of light propagates in vacuum or air, medium A transmits to the interface of medium B, it is generally divided into two types of light beams: reflection and refraction. Reflection law: The reflection angle is equal to the incident angle, and i (reflection angle)=i '(incident angle). The brightness of the mirror surface depends on the viewpoint, and the surface brightness varies with the viewing angle. This is why the current glossmeter is divided into 20 °, 60 °, 85 °, 120 °, and other angles. In fact, the measurement principle of a glossmeter is an ideal diffuse surface that reflects incident light uniformly in all directions, and its brightness is independent of the viewpoint and is a constant. Refraction law: n1 sin i=n2 sin r The refractive index of any medium relative to vacuum is called the absolute refractive index of the medium, referred to as the Index of Refraction. In the formula, n1 and n2 represent the refractive indices of the two media, respectively. The phenomenon of light refraction is caused by the different propagation speeds of light in different media. The refractive index depends on the properties of two different media and the wavelength of light. The absolute refractive index of a medium in an ideal vacuum is: n=c/v (c is the speed of light in the vacuum, and v is the speed of light in the medium) From the above formula, we can see that in a medium with a large refractive index, the speed of light is relatively low; In a medium with a small refractive index, the speed of light is relatively high. Diffraction of light: During the propagation of light, when light encounters obstacles, it will deviate from the straight line, which is called diffraction of light. Due to the short wavelength of light, it is difficult to detect diffraction phenomena in daily life. Diffraction not only causes the geometric shadow of an object to lose its clear outline, but also produces a series of bright and dark lines at the edges. Relatively complex optical knowledge is commonly used in our colorimeters. We all know that colorimeters are an optical color detection device developed using optical principles and color detection optics. This instrument has a very complex internal structure and is a precision instrument. There are many applications of optical theory. We can see these from "Analysis Principle of Chromatograph". Focus When light rays parallel to the optical axis enter a convex lens, the ideal lens should be that all the light rays converge at a point and then spread out in a conical shape. This point where all the light rays converge is called the focal point. Circle of dispersion Before and after the focal point, light begins to gather and diffuse, and the image of the point becomes blurred, forming an enlarged circle called a diffusion circle. Different manufacturers and film areas have different numerical definitions of allowable circle of diffusion diameter. The image perceived by the human eye is greatly related to magnification and viewing distance. The allowable dispersion circle for a 35mm photographic lens is about 1/1000 to 1/1500 of the diagonal length of the negative. The premise is that the image is enlarged to a 5x7 inch photo with a viewing distance of 25-30cm. Depth of field There is an allowable dispersion circle before and after the focal point, and the image blurring presented on the bottom surface is within the allowable range of the dispersion circle. The distance between these two diffusion circles is called depth of field, that is, the depth of field where the image still has a clear range before and after the subject (focus). The depth of field varies with the focal length, aperture value, and shooting distance of the lens. For fixed focal lengths and shooting distances, the smaller the aperture used, the greater the depth of field. Based on the camera holder, the distance from the focal point to the near allowable dispersion circle is called foreground depth, and the distance from the focal point to the far allowable dispersion circle is called back depth of field. The larger the lens aperture, the smaller the depth of field; The longer the focal length of the lens, the smaller the depth of field; The shorter the focal length, the greater the depth of field; The closer the shooting distance, the smaller the depth of field. Compared to instruments with relatively complex internal results such as colorimeters and glossometers, it is relatively simple to use color light boxes and transmission light boxes. The main optical principles they apply are the color temperature, wavelength, and illuminance of light. Combining these factors, color comparison is performed. Gloss meters AGM-580 are mainly used in the surface gloss measurement for paint, plastic, metal, ceramics, building materials. It conforms to the DIN67530, ISO2813, ASTM D523, JIS Z8741, BS 3900 Part D5, JJG696 standards and so on. Portable Colorimeter/Chroma Meter is an innovation color measuring tool with powerful configuration to make color measurement easier and more professional; It support Bluetooth to connect with Android and ISO devices, Portable Colorimeter/Chroma Meter will take you into a new world of color management; It can be widely used to measure color value, color difference value and find similar color from color cards for printing industry, paint industry, textile industry, etc. Lisun Instruments Limited was found by LISUN GROUP in 2003. LISUN quality system has been strictly certified by ISO9001:2015. As a CIE Membership, LISUN products are designed based on CIE, IEC and other international or national standards. All products passed CE certificate and authenticated by the third party lab. Our main products are Goniophotometer, Integrating Sphere, Spectroradiometer, Surge Generator, ESD Simulator Guns, EMI Receiver, EMC Test Equipment, Electrical Safety Tester, Environmental Chamber, Temperature Chamber, Climate Chamber, Thermal Chamber, Salt Spray Test, Dust Test Chamber, Waterproof Test, RoHS Test (EDXRF), Glow Wire Test and Needle Flame Test. Please feel free to contact us if you need any support. Tech Dep: Service@Lisungroup.com, Cell/WhatsApp:+8615317907381 Sales Dep: Sales@Lisungroup.com, Cell/WhatsApp:+8618117273997 Read the full article

[ajay511]

Unraveling the Beauty of Mathematics: A Journal of Mathematical Wonders

Introduction

Welcome to our Journal of Mathematics, where we embark on a journey through the enchanting realm of numbers, equations, and the boundless wonders of mathematical concepts. In this journal, we will explore various aspects of mathematics, from its historical roots to its modern applications, aiming to shed light on the fascinating world of mathematical theory and its practical relevance.

Table of Contents

The Beauty of Mathematical Abstraction

   Mathematics is Journal of mathematics  as the universal language of nature. Dive into the world of abstract mathematical concepts, from numbers and sets to functions and structures. Discover how mathematicians use abstraction to understand complex phenomena.

Mathematics through the Ages: A Historical Perspective

   Trace the evolution of mathematics from its humble beginnings in ancient civilizations to the cutting-edge research of today. Explore the contributions of mathematicians like Euclid, Pythagoras, and Gauss, and how their work shaped the mathematical landscape.

The Elegance of Mathematical Proof

   Mathematics is built on the foundation of rigorous proofs. Learn about the importance of proof in mathematics, famous theorems like Fermat's Last Theorem, and the role of proof in advancing mathematical knowledge.

Mathematics in Nature: The Golden Ratio and Fractal

   Discover the mathematical patterns hidden in the natural world. Explore the Golden Ratio, Fibonacci sequence, and fractals, and learn how they appear in everything from seashells to galaxies.

Algebra: The Language of Equation

   Delve into the world of algebra, the branch of mathematics that deals with equations and variables. Uncover the fundamental algebraic principles used in solving real-world problems.

Geometry: The Study of Shapes and Space

      Explore the world of geometry, where we study shapes, sizes, and the properties of space. Learn about Euclidean geometry, non-Euclidean geometries, and their applications in fields such as physics and art.

Calculus: The Mathematics of Change

   Understand the concept Journal of mathematics which deals with rates of change and accumulation. Explore the fundamental ideas of differentiation and integration and their significance in science and engineering.

Statistics: The Science of Data Analysis

   In a data-driven world, statistics plays a crucial role. Explore the basics of statistical analysis, including data collection, probability, hypothesis testing, and regression analysis.

Modern Mathematics: From Number Theory to Cryptography

   Discover the diverse branches of modern mathematics, including number theory, graph theory, and cryptography. Learn how these fields impact our daily lives and technological advancements.

Mathematics in Action: Real-World Applications

    Explore how mathematics is applied in various fields, from engineering and finance to computer science and healthcare. See how mathematical modeling and algorithms solve complex problems.

The Future of Mathematics: Unsolved Mysteries and Frontier Research

    Peek into the exciting frontiers of mathematical research and the unsolved problems that continue to challenge mathematicians. Learn about the Clay Millennium Prizes and their million-dollar challenges.

Mathematics for Everyone: Resources and Learning Opportunities

    Conclude your journey by discovering valuable resources and tips for learning and enjoying mathematics. Find out how to make mathematics accessible and enjoyable for all.

Conclusion

As we embark on this mathematical journey, we invite you to explore the depths of a subject that has intrigued and inspired scholars for centuries. Mathematics is more than just numbers and equations; it is the foundation of our understanding of the world. Whether you are a seasoned mathematician or a curious beginner, join us in this Journal of Mathematics as we uncover the beauty, elegance, and practicality of this timeless discipline.

Hyderabad Telangana

[yesthatsatumbler]

I'm reminded of the Letters from the Future project.

OK, so you probably wouldn't have heard about it. TL/DR: in 2002, there was a website where people could send messages to... um... let's say a girl from the future (...also from some kind of weird AU where her adventures happened in the 2170s and not the 2070s as the usual descriptions would have it), and get answers from her, for a while. The project functioned in this manner only for a few months; then the interaction part closed down (there were some vaguely-related fanworks posted on the same site later) but the existing letters remained up (I just checked and they're still up as I write this).

I found the site as an impressionable teenager in 2007, very much liked it, and for a while legitimately believed that the letters must have been arriving from some kind of future. Until I found the Fermat's Last Theorem comment.

Slightly paraphrasing: she said that Fermat's Last Theorem was still unsolved in her time, and that there was a strong suspicion that it was actually unprovable [in the Gödelian sense], but the attempts to prove that hadn't succeeded yet either.

Now, I could plausibly assume that an author in 2002 would have been unaware of Wiles, and/or, semi-equivalently, that by the 2180s some kind of error would have been found in his proof. (I think I knew about the DS9 joke/retcon by then; if not, I'd have read about it shortly afterwards.)

The part that made absolutely no sense to me in an "actual letters from a smart future girl" context was the suggestion that 1) FLT could have been unprovable; and, more importantly, 2) that this in turn is something that could be proved.

You can't prove that FLT is unprovable. It's absolutely, mathematically impossible. And this is still true even if you don't accept (or know about) the Wiles proof; it's a pretty simple argument that only requires relatively simple math.

...OK, now I should probably do the actual math.

Suppose that - theoretically - FLT was false. If so, it would mean that there was a solution to a^n+b^n=c^n with the usual restrictions on the variables (I don't recall the exact restrictions offhand).

In that case, you could prove that falsity simply by providing such a solution (and explaining why it worked).

If FLT was unprovable [again, in the Gödelian sense], it would mean that there was no proof of its falsity either. But, by the previous argument, it would imply that it was not false.

Consequently, any proof of FLT's unprovability would be trivially extended into a proof of its truth. Contradiction.

[Note that this argument does not depend in any way on the existence of a proof for FLT, and indeed quite easily extends to some still-unsolved problems, such as Goldbach's conjecture.]

...anyway, the above argument was something that I was sure a smart girl from the 2180s (or indeed the 2080s) could probably quickly work out in her head, and consequently I would not have expected her to phrase the response that way. [Actually, now that I checked the actual phrasing for the first time in many years, turns out it wasn't quite as clear-cut as that, but it definitely didn't sound like "maybe it's unprovable, but if so we'll never know" either.]

So the only explanation that matched the evidence was the normal one: someone (who presumably wasn't as good at math) must have been making up the answers in her name.

[The aforementioned answer also mentioned that they did determine, at least, that Fermat was mistaken when he thought he had a proof.

My headcanon is that Fermat's proof was based on the same principles as the 1847 proof by Gabriel Lamé, and that Fermat, just like Lamé, had failed to notice the rather arcane failure of factorization which invalidated that proof.]

It's a funny and unfortunate coincidence that in S2E12 of Star Trek: TNG (aired 1989) they talk about Fermat's Last Theorem as this untractable problem that even hundreds of years into the future people are still trying to crack. Fermat wrote down the conjecture around 1637, so when the episode aired it had been an open problem for 352 years. Little did they know that Wiles would finish the proof in 1994!

[jadedelcinismo]

Greetings my fellow SanSan fans,

I wrote a thing.

I suck at writing abstracts but the story can be best described as an AU Sansa interacting with a Canon Sansa in which they discover disturbing truths of their respective realities. Along that journey they explore their feelings for Sandor Clegane and their roles as individuals who wish to change the Realm they inhabit—Stark legacy or otherwise.

Hope you’ll give it a peek :)

[intelligentliving]

New communication technologies could be the outcome of a new class of laser beam that scientists have recently created, which defy long-held laws of light physics. These new beams, dubbed “spacetime wave packets,” follow different rules of refraction than any known light beam. The speed of light alters depending on...

[and-then-there-were-n0ne]

Years ago, Russiagate enthusiast David Klion really uncorked one.

It’s incredible how many years I wasted associating complexity and ambiguity with intelligence. Turns out the right answer is usually pretty simple, and complexity and ambiguity are how terrible people live with themselves.

This was handy to me, in the sense that it perfectly encapsulated the exact opposite of everything I believe. I remember reading this and turning it around in my head, over and over; I imagine a sociopath viewing it the way Patrick Bateman viewed that business card. It’s perfect. I mean, the sentiment behind it is utterly demented, but it’s still perfect, beautiful in the same way a virus is beautiful under a microscope.

I don’t even really know how I’d go about defending the essential concepts of complexity and ambiguity in the abstract. I guess I would point to the indisputable existence of chronic and intense complexity in our world. Like the complexity inherent to the proof for Fermat’s Last Theorem, primogeniture in the British aristocracy, the relationship between extradimensional geometries and the potential for reconciling general relativity and quantum mechanics, the linguistic dynamics of the Voynich manuscript, microtonal music, the geopolitical conditions that led to the Yemen-Saudi Arabia conflict and the tangle of alliances involved, Brownian motion, the anthropology of the Kula ring, programming a physics engine for a 3D video game, technical architecture involving uneven distribution of load-bearing elements in a limited space, escaping saṃsāra, parsing the various levels of linguistic etiquette in the Korean language, solving the Riemann hypothesis, rendering realistic computer-animated human faces in variable lighting, the history of anarchism and its various schools, the line of succession for the office of Holy Roman Emperor, Hungarian language case structure, Bernoulli’s principle, Microsoft Excel, black holes, the internal politics of the Chinese Communist Party, the legacy of brutalism in contemporary architecture, Finnegans Wake, cricket, Heiddegger’s dasein, making the perfect pizza dough, and literally every other thing that has ever crossed the human mind. You can wash your hands of nuance all you like; you live in a world that will always defy your clumsy, reductive efforts. Life’s complexity is irreducible.

But it’s not just that complexity is ubiquitous and inevitable. It’s that complexity is good. Complexity is what makes life interesting, and complexity is what makes art enjoyable. We have brains that have developed an exquisite ability to parse complicated, multivariate information - the fact that you are reading these words right now and understanding them is a miracle of raw processing - and we crave the opportunity to exercise them. We create all manner of strange hobbies specifically because they’re intellectually taxing, like those guys who do Rubic’s cube-style puzzles that have dozens of blocks. Overly simplistic games like Tic Tac Toe quickly bore us, and we go looking for deeper challenges. We inject our art with symbolism and reference in order to connect with it on a deeper and more satisfying level. Recently, the dominance of simplistic stories of good heroes and bad villains has robbed movies of some of their essential power. The injection of absurd rules into what stories can be told in Young Adult literature has rendered the genre a wasteland. Morally, the ability to traffic in complexity is absolutely essential, as the basic task of ethical development lies in expanding the moral imagination, and you can’t achieve that unless you’re willing to imagine that there are things about another person that go beyond your simplistic impressions, that they suffer under problems that are too (yes) complex for you to fully understand. Life would be powerfully boring without complexity.

Ambiguity, meanwhile, is just the state of most of life. We’re ambivalent, about most things, most of the time. I think that’s good, but either way - it just is.

I was inspired to remember Klion’s little koan by this bizarre piece of therapy-speak nonsense from Adam Grant in the New York Times. Grant is one of those 21st-century hucksters who peddle pseudo-psychology to unhappy people, dressing up everything they already want and think and feel in a patina of legitimacy derived from self-help ideology. The modern American cult of therapy takes a useful and necessary medical practice, meant for specific contexts and purposes, and generalizes its habits to the entirety of human life. Its folklore exists to justify what insecure people can’t justify for themselves. Narcissistic personality disorder is thought to occur in less than 1% of adults, and yet every ex-boyfriend in this country suffers from it. Curious! But not actually curious, given that an army of opportunists have built careers out of telling people just that kind of story - everyone you don’t like is a sociopath; every time you don’t get everything you want, you’re experiencing trauma; every conflict you get into, about anything, ever, is evidence of a toxic personality in the other person. Are you sure your boss is just another human being with legitimate pressures and needs, and your disagreements the product of the inevitable friction that results from a universe where friction is inevitable? Or could they be operating under the influence of the Dark Triad??? Sure. Why the fuck not. This is what therapeutic rhetoric has become, in this culture, an excuse architecture for every spare selfish impulse you ever have. And people like Grant get rich peddling it.

(That word, toxic - I think it’s a fallen soldier, at this point, a write-off. It has been applied so liberally, and so witlessly, that it no longer has any value. I’m sure I’ll still use it, out of habit, but today it suffers from a uniquely intense combination of lack of meaning and relentless overuse.)

Grant’s concern today is, I’m not kidding, the evil of ambivalent relationships. He presents several studies that show that, when we traffic in ambiguous interactions with other people, the stress takes a physical toll. He writes, “The most toxic relationships aren’t the purely negative ones. They’re the ones that are a mix of positive and negative.” Puzzlingly, Grant does not define what the actual boundaries of an ambiguous relationship might be; how would such a thing be quantified? InterPersonal Ambivalence Units (IPAUs)? I’m torn here, because taken literally that line means that the most toxic relationships are those that do not fall clearly into a binary of perfect affection or perfect enmity. Which, of course, is a category that includes every human relationship, ever, in the history of human relationships. To read more generously, we might take it that Grant means that relationships that don’t pass a particular threshold of certainty when it comes to friend or enemy status are the most toxic. But where is that threshold? If we’re going to be justifying all of this with reference to scientific research, shouldn’t there be some level of scientific precision in the essential question of what relationships are actually toxic? The studies here don’t inspire me with confidence; they’re exactly the kind that keep failing to replicate, and when you check how they’re operationalized, it’s always some sort of dubious self-reported scale. I don’t know. I’m confused as to who and how this helps.

The notion that human relationships fall simplistically and reliably onto a linear spectrum of “positive” and “negative” is so fundamentally contrary to my lived experience that I don’t really know how to begin here. We have multivariate, inscrutable, often unknowable personalities; these personalities are shaped by innumerable Byzantine internal forces and by a relentless stream of formative experiences. The notion that any two personalities are going to interact with each other in some kindergarten polarity of positivity and negativity seems farcical, just mathematically. And, personally, I find that ambiguous relationships can be among the most stimulating. In particular, they can be very sexy - when you’re first getting to know someone who might be (but might not be) a potential romantic interest, that ambiguity, that not knowing, is one of the best parts. Of course, sometimes the way that not knowing plays out is that you’re interested in them and they’re not interested in you, and it hurts. But that’s how it goes; it’s precisely the chance for failure that makes success sweeter. [...]

I would like to summon a charitable reading here, but there’s a kind of too-cute maximalism that makes it hard. Grant writes that “Even a single ambivalent interaction can take a toll.” Even a single ambivalent reaction! My God! What are we to take from this information? I’m not sure if this is common knowledge, but we are a mortal species with finite lives that evolved by chance on an indifferent rock in a universe devoid of transcendent meaning, cursed to watch those we love die around us until we die in turn. We exist on a planet where our genetic endowment compels us to be selfish in pursuit of food, sex, and status, and there are 7 billion of us, all competing for limited resources and jockeying for status in competitions that are often inherently zero-sum. I’m going to go ahead and suggest that never having a single ambivalent interaction is perhaps an unrealistic expectation for anyone. And this gets to this paradox of self-help woowoo that I’ve talked about before: the vision of healthy human life becomes so unattainable that people end up developing guilt and shame over their inability to live without guilt and shame. Being “self-actualized” is just another unfair expectation nobody can reach. Which is perverse! I genuinely cannot comprehend what supposedly-therapeutic purpose is served by telling people that even a single ambivalent interaction is going to “take a toll.” Who is this helping?

Ambivalence is an invitation for rumination.

Well, yes, Adam. Yes it is. You’ve got me there. So, how could rumination be bad?

We agonize about ambiguous comments, unsure what to make of them and whether to trust the people who make them. We dwell on our mixed feelings, torn between avoiding our frenemies and holding out hope that they’ll change.

Again, this is presented as though what’s discussed is obviously something that we must try to avoid at all costs. But why? Is agonizing over things really that bad? I think I’ve done a lot of growing by agonizing over things in my life. That’s just part of the endowment of being a person, agonizing over things. Why are mixed feelings unhealthy? In a world this complicated, with relationships that are so full of interlocking and unconscious dynamics, aren’t mixed feelings unavoidable and ultimately benign? And why are we assuming that our “frenemies” are the ones who have to change? Is there really no chance at all that we’re the ones who should change? This gets to another point of mine about all this weird “everything is therapy all the time” self-help horseshit: life is full of zero-sum interactions between people with competing and legitimate interests. [...] This whole world of pop psychology insists that the individual is sacrosanct, that anyone who deals with insecurity or anxiety or self-doubt is the victim of injustice, and they are entitled to do whatever they want to self-actualize. But what do we do when two people are trying to self-actualize in ways that conflict with each other? I have no idea, and I don’t think these gurus know either. [...]

And, as I so often do, I have to say to this general ideology: the purpose of human life is not to feel comfortable all the time, bad and dark feelings are an essential part of being a person, and while you are entitled to having your physical self protected, your material needs met, and your basic autonomy respected, you aren’t entitled to never feel pain, sadness, insecurity, anxiety, self-doubt, or that you’re “invalid.” Society could never accommodate such an entitlement, and it’s a bad goal anyway.

[aorish]

wikipedia disagrees with me on the local maximum thing, and I don't want to re-work out the proof because it's been a solid decade since I've done any calculus of variations, but i'm pretty sure they're interpreting the source they're citing (Born and Wolf) incorrectly?

At any rate Born and Wolf doesn't have a proof either way, they just cite Carathéodory's Geometric optics:

Weird, this is far from a rigorous proof, and also makes a stronger claim than either wikipedia or born and wolf? because it would rule out all stationary points that aren't local minima, something i've definitely heard repeated over and over by various physics professors! and i'm also not sure this accounts for the possibility of a non-uniform index of refraction, where a deviation from the geometrically shortest path might decrease the time.

I don't know enough math to rigorously prove it either way, though.

But maybe it's all just a common misconception among physicists, and it's that misunderstanding Fermat's principle makes being a mathematical Platonist seem appealing. idk

i could see how a study of optics could turn someone into a mathematical platonist. like no light doesnt always take the *minimum* time to get somewhere, it only cares that the derivative is zero, it *can* be a local maximum or another stationary point.

[uuuuuhhhhhhhhhhhhhhhhhh]

When banned from using "trivially" in a proof...

“Hello all. In a fellow mathposter's topology class they were not allowed to use the word "trivially" or any synonym thereof his proofs. The person presenting his work then crossed out "trivially" and wrote instead "indubitably." This inspired him to write a program that will insert condescending adverbial phrases before any statement in a math proof. Trivially, this is a repost. Below is the list--please come up with more if you can!

Obviously

Clearly

Anyone can see that

Trivially

Indubitably

It follows that

Evidently

By basic applications of previously proven lemmas,

The proof is left to the reader that

It goes without saying that

Consequently

By immediate consequence,

Of course

But then again

By symmetry

Without loss of generality,

Anyone with a fifth grade education can see that

I would wager 5 dollars that

By the contrapositive

We need not waste ink in proving that

By Euler

By Fermat

By a simple diagonalization argument,

We all agree that

It would be absurd to deny that

Unquestionably,

Indisputably,

It is plain to see that

It would be embarrassing to miss the fact that

It would be an insult to my time and yours to prove that

Any cretin with half a brain could see that

By Fermat’s Last Theorem,

By the Axiom of Choice,

It is equivalent to the Riemann Hypothesis that

By a simple counting argument,

Simply put,

One’s mind immediately leaps to the conclusion that

By contradiction,

I shudder to think of the poor soul who denies that

It is readily apparent to the casual observer that

With p < 5% we conclude that

It follows from the Zermelo-Fraenkel axioms that

Set theory tells us that

Divine inspiration reveals to us that

Patently,

Needless to say,

By logic

By the Laws of Mathematics

By all means,

With probability 1,

Who could deny that

Assuming the Continuum Hypothesis,

Galois died in order to show us that

There is a marvellous proof (which is too long to write here) that

We proved in class that

Our friends over at Harvard recently discovered that

It is straightforward to show that

By definition,

By a simple assumption,

It is easy to see that

Even you would be able to see that

Everybody knows that

I don’t know why anybody would ask, but

Between you and me,

Unless you accept Gödel’s Incompleteness Theorem,

A reliable source has told me

It is a matter of simple arithmetic to show that

Beyond a shadow of a doubt,

When we view this problem as an undecidable residue class whose elements are universal DAGs, we see that

You and I both know that

And there you have it,

And as easy as ABC,

And then as quick as a wink,

If you’ve been paying attention you’d realize that

By the Pigeonhole Principle

By circular reasoning we see that

When we make the necessary and sufficient assumptions,

It is beyond the scope of this course to prove that

Only idealogues and sycophants would debate whether

It is an unfortunately common misconception to doubt that

By petitio principii, we assert that

We may take for granted that

For legal reasons I am required to disclose that

It is elementary to show that

I don’t remember why, but you’ll have to trust me that

Following the logical steps, we might conclude

We are all but forced to see that

By the same logic,

I’m not even going to bother to prove that

By Kant’s Categorical imperative,

Everyone and their mother can see that

A child could tell you that

It baffles me that you haven’t already realized that

Notice then that

Just this once I will admit to you that

Using the proper mindset one sees that

Remember the basic laws of common sense:

There is a lovely little argument that shows that

Figure 2 (not shown here) makes it clear that

Alas, would that it were not true that

If I’m being honest with you,

According to the pointy-headed theorists sitting in their Ivory Towers in academia,

We will take as an axiom that

Accept for the moment that

These are your words, not mine, but

A little birdie told me that

I heard through the grapevine that

In the realm of constructive mathematics,

It is a theorem from classical analysis that

Life is too short to prove that

A consequence of IUT is that

As practitioners are generally aware,

It is commonly understood that

As the reader is no doubt cognizant,

As an exercise for the reader, show that

All the cool kids know that

It is not difficult to see that

Terry Tao told me in a personal email that

Behold,

Verify that

In particular,

Moreover,

Yea verily

By inspection,

A trivial but tedious calculation shows that

Suppose by way of contradiction that

By a known theorem,

Henceforth

Recall that

Wherefore said He unto them,

It is the will of the Gods that

It transpires that

We find

As must be obvious to the meanest intellect,

It pleases the symmetry of the world that

Accordingly,

If there be any justice in the world,

It is a matter of fact that

It can be shown that

Implicitly, then

Ipso facto

Which leads us to the conclusion that

Which is to say

That is,

The force of deductive logic then drives one to the conclusion that

Whereafter we find

Assuming the reader’s intellect approaches that of the writer, it should be obvious that

Ergo

With God as my witness,

As a great man once told me,

One would be hard-pressed to disprove that

Even an applied mathematician would concede that

One sees in a trice that

You can convince yourself that

Mama always told me

I know it, you know it, everybody knows that

Even the most incompetent T.A. could see,

This won't be on the test, but

Take it from me,

Axiomatically,

Naturally,

A cursory glance reveals that

As luck would have it,

Through the careful use of common sense,

By the standard argument,

I hope I don’t need to explain that

According to prophecy,

Only a fool would deny that

It is almost obvious that

By method of thinking,

Through sheer force of will,

Intuitively,

I’m sure I don’t need to tell you that

You of all people should realize that

The Math Gods demand that

The clever student will notice

An astute reader will have noticed that

It was once revealed to me in a dream that

Even my grandma knows that

Unless something is horribly wrong,

And now we have all we need to show that

If you use math, you can see that

It holds vacuously that

Now check this out:

Barring causality breakdown, clearly

We don't want to deprive the reader of the joy of discovering for themselves why

One of the Bernoullis probably showed that

Somebody once told me

By extrapolation,

Categorically,

If the reader is sufficiently alert, they will notice that

It’s hard not to prove that

The sophisticated reader will realize that

In this context,

It was Lebesque who first asked whether

As is tradition,

According to local folklore,

We hold these truths to be self-evident that

By simple induction,

In case you weren’t paying attention,

A poor student or a particularly clever dog will realize immediately that

Every student brought up in the American education system is told that

Most experts agree that

Sober readers see that

And would you look at that:

And lo!

By abstract nonsense,

I leave the proof to the suspicious reader that

When one stares at the equations they immediately rearrange themselves to show that

This behooves you to state that

Therefore

The heralds shall sing for generations hence that

If I’ve said it once I’ve said it a thousand times,

Our forefathers built this country on the proposition that

My father told me, and his father before that, and his before that, that

As sure as the sun will rise again tomorrow morning,

The burden of proof is on my opponents to disprove that

If you ask me,

I didn’t think I would have to spell this out, but

For all we know,

Promise me you won’t tell mom, but

It would be a disservice to human intelligence to deny that

Proof of the following has been intentially omitted:

here isn’t enough space in the footnote section to prove that

Someone of your status would understand that

It would stand to reason that

Ostensibly,

The hatred of 10,000 years ensures that

There isn’t enough space in the footnote section to prove that

Simple deduction from peano’s axioms shows

By a careful change of basis we see that

Using Conway’s notation we see that

The TL;DR is that

Certainly,

Surely

An early theorem of Gauss shows that

An English major could deduce that

And Jesus said to his Apostles,

This fact may follow obviously from a theorem, but it's not obvious which theorem you're using:

Word on the streets is that

Assuming an arbitrary alignment of planets, astrology tells us

The voices insist that

Someone whispered to me on the subway yesterday that

For surely all cases,

Indeed,

(To be continued)

[t4tbruharvey]

11 and 19 :)

11 - what non-fiction books do you like if any?

OH BOY OH BOY so i really like maths pop-sci books (fermat's last theorem + math without numbers + hello world are my faves and they fucking BANG) and also in theory i like autobiographies i think the style is really interesting, so like smth that may shock and discredit you is brilliant, but i only got halfway through the rise the fall and the rise, which tbh i don't care about the fall as a band that much so the bit about her childhood in LA was the most interesting bit for me, and that part was really well written. oh and also i'm obsessed w sebag's stalin book that lois and i share custody of because we're studying him (simon) like a bug

19 - most disliked popular books?

i hate sarah j maas on principle. same w sally rooney. that i've read? i found both great expectations and gone with the wind incredibly boring and i didn't finish them. i HATE the crucible, which is a play but i read it physically so it counts, and that's a whole other rant. i also really don't like heartstopper and loveless i think that they're way more popular than they should be and alice oseman has MUCH better works.

[majorproblems77]

Me right now but instead of neuro its Fermat's principles

We suffer together my friend

@skyloftian-nutcase good luck with studying Buddy!!

You’re gonna do great tomorrow❤️

Enjoy Twi and Wars studying together, while War’s sanity starts slipping away

[caprice-nisei-enjoyer]

Tagged by @algernon-charles-swinburne. I love these!

Name: Okay, I'll bite. What's a "name"?

Age: Oh man, for a few months I thought I was 28 for some reason. I'm not.

Height: Literally 5 feet. No inches.

Where do you call home? The San Francisco Bay Area, although that's changing as we speak

Any tattoos or piercings? Nope!

Last song you listened to? The Greatful Dead - Looks Like Rain

Last movie you watched? Promising Young Woman

Last book or fanfic you read? Prince of Persusasion by Scarlett Scott

Do you collect anything? I have ADHD. That's a dangerous question! I have enough messes as it is!

Morning person or night owl? A morning person in principle. I just can't keep myself from staying up too late.

Are you an optimist, a pessimist, or a realist? I'm an optimist, which is to say I'm a realist and everyone else is a pessimist :P

A quote you live by? "Get a job." - my dad, when asked if he'd ever given me any good advice

Are you an introvert, an extrovert, or an ambivert? Again, I'm an extrovert in principle but I moved like once a year from 2016 to 2021. So it's been hard to keep friends.

Do you believe in an afterlife? No, our best evidence about the universe doesn't leave much room for the supernatural.

A weird or fun fact about yourself: I have no idea what other people find weird or fun. I have a lifelong vendetta against seagulls. The first time I ate a Babybel cheese, I ate the wax wrapper with it. I have listened to (part of) The Nutcracker Suite hundreds of times. I was concieved, born, and raised in three separate cities (thousands of miles apart). I've had this blog since probably 2013 but I've only been active since 2019. I once rescued a person who jumped off the Golden Gate Bridge. I'm a habitual liar, especially on the Internet.

If you could have coffee with anyone, dead or alive, who would it be? Dead seems like the way to go. If we're bending the laws of the universe, might as well bend them as much as we can, right? Would be cool to sit down with Fermat and get an idea of how he proved his Last Theorem. But ultimately I think I'd pick Trevor, a young man I knew who died when we were both young.

As always people who want to be tagged in this should consider themselves tagged. But I'm betting @max1461 and @squareallworthy would have a good time with this.