#introduction to Derivative Calculus

[golearners]

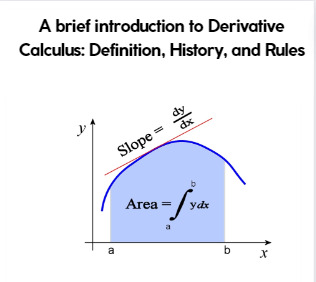
A brief introduction to Derivative Calculus: Definition, History, and Rules

A brief introduction to Derivative Calculus: Definition, History, and Rules In mathematics, finding the instantaneous rate of variation in a function based on specified factors is known as the derivative procedure. In Calculus, a derivative is a fundamental concept. In simpler terms, a derivative is a contract between two parties that specifies the conditions under which payments are to be made…

[theapollospectrohelioscopic]

Hello. This is an introduction post.

I am TheApolloSpectrohelioscopic, but I mainly go by the names Apollo and Spectro.

Other names I go by include:

Apollon

Mind

Apollinariya

Polina

Helio

Helios

Lux

Sun

Xanthus

Ash/ASh/ASH/Ashs/AShs

Basically any name related to the sun or to sunshine or to light or to Mind from CCCC

Some names related to the colour blue or to the colour yellow

Honestly I don’t really care what you call me just don’t be a third derivative of displacement

Well, also make sure it is obvious that you are referring to me.

Oh and if you are my irl friend you can call me Lemonade but only if you are my irl friend. Or, well, if you are in on the joke you can call me Lemonade.

I use all pronouns.

I am a minor.

My birthday is the tenth of July.

I am primarily in the CCCC fandom (if you couldn’t already tell), but I am also in the OSC and Hermitcraft/Life Series fandoms as well. I also might somewhat be in the CRK and PJSK fandoms as well.

Yes, spectrohelioscopic is a real word (at least, according to some sources, autocorrect says it isn’t a real word).

I have diagnosed ADHD and autism.

I am genuinely baffled by the fact that there are people who hate Mind.

I am not the greatest at drawing, but I might occasionally post drawings of primarily Mind, but on occasion other characters.

Aquatic creatures are cool, my favourite being squids, octopodes (yes that is a correct pluralisation of octopus), and jellyfishes.

Foxes are my favourite animal. Fun fact: A group of foxes is called a skulk.

I live in Australia.

I prefer cats to dogs.

I have way too many aus that I never write stuff down about.

I suck at telling if questions are directed towards me.

I may ramble at any time.

My favourite movie is Colorful Stage! The Movie: A Miku Who Can’t Sing.

I fucking adore Mind.

If my tags ever seem to not fit it is because I don’t know what tags I should use and because I honestly don’t really care.

I have an overabundance of Mind headcanons, and very few for Heart and Soul.

I enjoy mathematics, and think calculus is cool.

I have a quite spectacular vocabulary, but if you were to give me a vocabulary test, I would most likely do not so spectacularly, for those tests use words like “jocular”, whereas I know words like “idolatry”, “autophagy”, and “defenestration”.

Despite said good vocabulary, I often use plain and ordinary language.

Anyways that’s enough random facts about me.

DNI: Basic stuff I guess I don’t know all the different words and I also don’t want this to take up 17 duotrigintillion rows.

I will not answer donation asks!

List of tags I may use and what they mean:

“uh oh apollos rambling again” - I go on a ramble about something.

”tag rambling” - I ramble in the tags.

“apollo rambles somewhat” - I go on a short ramble, one that isn’t full length.

“oh yeah i reblog stuff sometimes” - I reblog something.

“oh wait polls are a thing” - I make a poll.

More tags may be added to this list, and I may not be consistent with my usage of these tags.

[frank-olivier]

From Knots to Quantum: A Cultural and Mathematical Transformation

Shiing-Shen Chern was born in Jiaxing, China, in 1911, during a time of great change and upheaval in his homeland. From an early age, he displayed a remarkable aptitude for mathematics, and his journey in the world of differential geometry began at Nankai University and Tsinghua University, where he laid the foundation for his future academic endeavors. Chern's education took him to Germany, where he pursued his graduate studies at the University of Hamburg under the mentorship of Wilhelm Blaschke. It was here that Chern's passion for geometry flourished, and his doctoral research on the theory of webs marked the beginning of a brilliant career in mathematics.

Chern's contributions to differential geometry are vast and profound. He made significant advancements in the calculus of variations, the theory of differential forms, and the study of characteristic classes. His most celebrated achievement, the Chern-Weil theory, provides a powerful framework for constructing and understanding characteristic classes, which are essential tools in algebraic topology and differential geometry. The introduction of Chern classes revolutionized the study of complex manifolds and algebraic varieties. These classes capture the topological and geometric intricacies of these spaces and have become indispensable in various branches of mathematics. Chern's proof of the generalized Gauss-Bonnet theorem further solidified his place among the greatest geometers.

Beyond his mathematical prowess, Shiing-Shen Chern played a pivotal role in fostering mathematical exchange and collaboration between China and the Western world. In the mid-20th century, as China emerged from a period of isolation, Chern became a key figure in re-establishing mathematical connections with the international community. Upon his return to China in the 1980s, he took on the task of revitalizing mathematical research and education. Chern founded the Mathematical Research Institute of the Chinese Academy of Sciences, which became a hub for mathematical excellence and international collaboration. His vision and leadership attracted mathematicians from around the world, fostering a vibrant and diverse intellectual environment.

Chern's dedication to nurturing the next generation of mathematicians is evident in his establishment of the Nankai Institute of Mathematics at Nankai University and his later contributions to Zhejiang University. Through these institutions, he inspired and mentored countless students, many of whom became leading mathematicians.

Shiing-Shen Chern's influence extends far beyond pure mathematics, significantly impacting the field of Topological Quantum Theory (TQFT). TQFT is a fascinating area of mathematical physics that explores the connections between topology, geometry, and quantum mechanics, and Chern's contributions have been instrumental in its development.

Chern-Simons theory stands as a testament to the deep interplay between geometry and quantum theory. Named after Shiing-Shen Chern, Simon Donaldson, and James Simons, this topological quantum field theory is a masterpiece in mathematical physics. Chern-Simons theory assigns complex amplitudes to manifolds and knots, relying on the Chern-Simons form, a differential form derived from the curvature of connections on principal bundles. The Chern-Simons action functional, a central object in the theory, captures the geometric and topological aspects of manifolds, providing a powerful tool for understanding quantum systems. This theory finds applications in various areas of physics, including knot theory, quantum gravity, and condensed matter physics, offering insights into topological phases of matter.

Chern's work on characteristic classes, particularly the Chern classes, has been instrumental in the study of topological invariants, which are crucial in TQFT. These invariants remain unchanged under continuous deformations of manifolds and play a vital role in classifying topological phases. Chern classes, along with other characteristic classes, provide a rich toolkit for constructing and analyzing these topological invariants. The Chern-Simons invariant, derived from Chern-Simons theory, is a prime example with far-reaching implications. It distinguishes different 3-manifolds and connects to knot invariants like the Jones polynomial, which are of great interest in TQFT.

Chern's contributions to differential geometry have also influenced the study of quantum states and their geometric properties. The geometry of the space of quantum states, known as the projective Hilbert space, has become an important research area in mathematical physics. Chern's work on complex geometry and Kähler manifolds provides valuable insights into the structure of these spaces and their associated geometric invariants. Additionally, the concept of Berry phases in quantum mechanics, arising from the geometric properties of quantum state spaces, is connected to Chern's work on connections and curvature. These geometric phases find applications in quantum computing and quantum information theory.

The interplay of mathematics, history, and cultural exchange is captured in the documentary "Taking the Long View" by George Paul Csicsery. The film portrays Chern's life, his enduring legacy, and the tapestry of his contributions to mathematics and the cultural exchange between East and West.

Taking the Long View - The Life of Shiing-shen Chern (George Paul Csicsery, 2000)

Knots have been an integral part of human civilization for thousands of years, dating back to ancient times when they were used for practical purposes such as sailing, fishing, and weaving. However, the systematic study of knots as a mathematical discipline is a relatively modern development that has evolved over the centuries, intertwining with various scientific and intellectual pursuits.

In ancient civilizations like Egypt, Greece, and China, knots were used for practical purposes, such as securing objects, creating fishing nets, and recording information. The ancient Inca civilization in South America even developed a sophisticated system of recording information called "quipu," which used knotted strings to encode numerical data and possibly even more complex information.

During the Renaissance, knots continued to play a role in various crafts and trades, but the mathematical study of knots as a distinct field was not yet established..

The 19th century saw significant advancements in mathematics and physics, and it was during this time that knot theory began to take shape as a mathematical discipline. One of the pioneering figures in this field was the Scottish physicist and mathematician Peter Guthrie Tait. In the 1870s, Tait and his colleagues, including Thomas Kirkman and C.N. Little, embarked on a project to classify all possible knots with a given number of crossings. This effort, known as the "Tait Conjecture," aimed to create a table of knots and links, which would serve as a foundation for understanding their properties.

Tait's work laid the groundwork for the systematic study of knots, and he is often considered one of the founders of knot theory. He introduced the concept of "alternating knots" and developed techniques for distinguishing and classifying knots based on their diagrams.

In the early 20th century, mathematicians continued to build upon Tait's work and made significant contributions to knot theory. James Waddell Alexander II, a prominent American mathematician, introduced the concept of "knot invariants," which are mathematical quantities that remain unchanged under various deformations of a knot. These invariants provided a powerful tool for distinguishing and classifying knots.

Another influential figure during this period was Max Dehn, a German mathematician who made important contributions to the study of three-dimensional manifolds and knot theory. Dehn introduced the concept of "Dehn surgery," a technique for modifying three-dimensional spaces by cutting out and gluing back solid tori, which has deep connections with knot complements and the topology of three-dimensional spaces.

The mid-20th century witnessed a revolution in physics with the development of quantum mechanics. Surprisingly, this new branch of physics would have profound implications for knot theory. In the 1980s, the discovery of the Jones polynomial by Vaughan Jones, a mathematician working in the field of operator algebras, marked a significant turning point.

The Jones polynomial is a knot invariant that assigns a Laurent polynomial to each knot or link. It was initially discovered in the context of von Neumann algebras and subfactors in quantum physics, but its significance for knot theory was quickly recognized. The Jones polynomial provided a powerful tool for distinguishing knots and led to the development of other knot polynomials, such as the HOMFLYPT polynomial, which further enriched the theory.

The connection between knot theory and quantum physics deepened with the emergence of topological quantum field theories, mathematical models that describe the behavior of quantum systems in terms of topological and geometric properties. Edward Witten played a pivotal role in this development.

Edward Witten's foray into knot theory began in the late 1980s, a period marked by significant advancements in mathematical physics. Witten, already renowned for his contributions to string theory and quantum field theory, turned his attention to the intricate world of knots and links, seeking to understand their topological and geometric properties. Witten's interest in knot theory was not merely academic; he sought to uncover the deep connections between knot theory and quantum physics.

Shiing-Shen Chern's work in differential geometry and topology provided a crucial foundation for Witten's exploration of knot theory. Witten's groundbreaking insight was to relate Chern-Simons theory to knot invariants, such as the Jones polynomial. He showed that the Jones polynomial could be obtained from Chern-Simons theory, providing a physical interpretation for this important mathematical object.

Witten's exploration of knot theory has led to a deeper understanding of the role of knots and links in quantum field theory. He has studied the behavior of quantum fields in the presence of knotted configurations, revealing the intricate interplay between topology and quantum phenomena. This research has opened up new avenues for understanding the mathematical structure of quantum field theories and their connection to knot invariants.

Witten's research has explored the geometry of quantum state spaces, known as projective Hilbert spaces. He has used geometric and topological concepts, such as Kähler manifolds and Berry phases, to understand the structure and behavior of quantum systems in these spaces. This work builds upon Chern's contributions to differential geometry and topology, particularly in the study of complex manifolds and their geometric properties.

By building upon Chern's mathematical foundations, Witten has revealed the deep connections between geometry, topology, and quantum phenomena, opening up new avenues for research and a deeper understanding of the mathematical structure of the physical world.

Prof. Edward Witten: Knots and Quantum Theory (Institute for Advanced Study, April 2012)

Wednesday, October 9, 2024

[omegaphilosophia]

The Philosophy of Arithmetic

The philosophy of arithmetic examines the foundational, conceptual, and metaphysical aspects of arithmetic, which is the branch of mathematics concerned with numbers and the basic operations on them, such as addition, subtraction, multiplication, and division. Philosophers of arithmetic explore questions related to the nature of numbers, the existence of mathematical objects, the truth of arithmetic propositions, and how arithmetic relates to human cognition and the physical world.

Key Concepts:

The Nature of Numbers:

Platonism: Platonists argue that numbers exist as abstract, timeless entities in a separate realm of reality. According to this view, when we perform arithmetic, we are discovering truths about this independent mathematical world.

Nominalism: Nominalists deny the existence of abstract entities like numbers, suggesting that arithmetic is a human invention, with numbers serving as names or labels for collections of objects.

Constructivism: Constructivists hold that numbers and arithmetic truths are constructed by the mind or through social and linguistic practices. They emphasize the role of mental or practical activities in the creation of arithmetic systems.

Arithmetic and Logic:

Logicism: Logicism is the view that arithmetic is reducible to pure logic. This was famously defended by philosophers like Gottlob Frege and Bertrand Russell, who attempted to show that all arithmetic truths could be derived from logical principles.

Formalism: In formalism, arithmetic is seen as a formal system, a game with symbols governed by rules. Formalists argue that the truth of arithmetic propositions is based on internal consistency rather than any external reference to numbers or reality.

Intuitionism: Intuitionists, such as L.E.J. Brouwer, argue that arithmetic is based on human intuition and the mental construction of numbers. They reject the notion that arithmetic truths exist independently of the human mind.

Arithmetic Truths:

A Priori Knowledge: Many philosophers, including Immanuel Kant, have argued that arithmetic truths are known a priori, meaning they are knowable through reason alone and do not depend on experience.

Empiricism: Some philosophers, such as John Stuart Mill, have argued that arithmetic is based on empirical observation and abstraction from the physical world. According to this view, arithmetic truths are generalized from our experience with counting physical objects.

Frege's Criticism of Empiricism: Frege rejected the empiricist view, arguing that arithmetic truths are universal and necessary, which cannot be derived from contingent sensory experiences.

The Foundations of Arithmetic:

Frege's Foundations: In his work "The Foundations of Arithmetic," Frege sought to provide a rigorous logical foundation for arithmetic, arguing that numbers are objective and that arithmetic truths are analytic, meaning they are true by definition and based on logical principles.

Russell's Paradox: Bertrand Russell's discovery of a paradox in Frege's system led to questions about the logical consistency of arithmetic and spurred the development of set theory as a new foundation for mathematics.

Arithmetic and Set Theory:

Set-Theoretic Foundations: Modern arithmetic is often grounded in set theory, where numbers are defined as sets. For example, the number 1 can be defined as the set containing the empty set, and the number 2 as the set containing the set of the empty set. This approach raises philosophical questions about whether numbers are truly reducible to sets and what this means for the nature of arithmetic.

Infinity in Arithmetic:

The Infinite: Arithmetic raises questions about the nature of infinity, particularly in the context of number theory. Is infinity a real concept, or is it merely a useful abstraction? The introduction of infinite numbers and the concept of limits in calculus have expanded these questions to new mathematical areas.

Peano Arithmetic: Peano's axioms formalize the arithmetic of natural numbers, raising questions about the nature of induction and the extent to which the system can account for all arithmetic truths, particularly regarding the treatment of infinite sets or sequences.

The Ontology of Arithmetic:

Realism vs. Anti-Realism: Realists believe that numbers and arithmetic truths exist independently of human thought, while anti-realists, such as fictionalists, argue that numbers are useful fictions that help us describe patterns but do not exist independently.

Mathematical Structuralism: Structuralists argue that numbers do not exist as independent objects but only as positions within a structure. For example, the number 2 has no meaning outside of its relation to other numbers (like 1 and 3) within the system of natural numbers.

Cognitive Foundations of Arithmetic:

Psychological Approaches: Some philosophers and cognitive scientists explore how humans develop arithmetic abilities, considering whether arithmetic is innate or learned and how it relates to our cognitive faculties for counting and abstraction.

Embodied Arithmetic: Some theories propose that arithmetic concepts are grounded in physical and bodily experiences, such as counting on fingers or moving objects, challenging the purely abstract view of arithmetic.

Arithmetic in Other Cultures:

Cultural Variability: Different cultures have developed distinct systems of arithmetic, which raises philosophical questions about the universality of arithmetic truths. Is arithmetic a universal language, or are there culturally specific ways of understanding and manipulating numbers?

Historical and Philosophical Insights:

Aristotle and Number as Quantity: Aristotle considered numbers as abstract quantities and explored their relationship to other categories of being. His ideas laid the groundwork for later philosophical reflections on the nature of number and arithmetic.

Leibniz and Binary Arithmetic: Leibniz's work on binary arithmetic (the foundation of modern computing) reflected his belief that arithmetic is deeply tied to logic and that numerical operations can represent fundamental truths about reality.

Kant's Synthetic A Priori: Immanuel Kant argued that arithmetic propositions, such as "7 + 5 = 12," are synthetic a priori, meaning that they are both informative about the world and knowable through reason alone. This idea contrasts with the empiricist view that arithmetic is derived from experience.

Frege and the Logicization of Arithmetic: Frege’s attempt to reduce arithmetic to logic in his Grundgesetze der Arithmetik (Basic Laws of Arithmetic) was a foundational project for 20th-century philosophy of mathematics. Although his project was undermined by Russell’s paradox, it set the stage for later developments in the philosophy of mathematics, including set theory and formal systems.

The philosophy of arithmetic engages with fundamental questions about the nature of numbers, the existence of arithmetic truths, and the relationship between arithmetic and logic. It explores different perspectives on how we understand and apply arithmetic, whether it is an invention of the human mind, a discovery of abstract realities, or a formal system of rules. Through the works of philosophers like Frege, Kant, and Leibniz, arithmetic has become a rich field of philosophical inquiry, raising profound questions about the foundations of mathematics, knowledge, and cognition.

[occultboyscout]

What does it mean to be a Hermeticist for you personally? I’m curious about the core beliefs and practices you follow, I don’t know much about hermeticism

Feel free to ignore this if you don’t feel like answering :)

Hey! This is a great question!

It's harder to answer than it probably should be lol, but I will do my absolute best.

Ultimately Hermeticism is a lot of things to a lot of different people. That can come down to how hard or soft you are on its use and definition. I'm *somewhere* in the middle between a couple extremes.

For me, Hermeticism means that -I believe in a single divine entity I call God. Although their being a single divinity does not preclude them from having aspects or segments which are derived from them (the Nous or the word being one example). -I believe that the natural world is a reflection of that divinity, and that divinity is not created by the natural world -I believe that closeness to that divinity, and the freedom there, is found through knowledge, through noesis. -I believe that the natural world, even if it is derived from demiurgic forces (I frame this in my own way, but the Poimandres cites a fiery demiurge) is wholly good, and that the act of love and the will to propagate is wholly good. -I believe that there is value in autonomy and that autonomy is claimed through knowledge. -I believe the universe is describable, and that scientific and mathematic achievement do not distract from the divine but describe it directly.

Most of those things are pulled from the most firmly Hermetic documents we have access to, the Corpus Hermeticum. I'll include a link to the Salaman Clement translation of the Corpus below.

I also draw from the Emerald Tablets, another foundational and notably Hermetic document.

There's a Hermetic interpretation that discredits the holiness with which I treat the material world. It's a pretty valid interpretation and the ideas were certainly present (at the time of main body hermetic texts creation) that the material world is dirty and flawed, and the holy act is to transcend to achieve closeness with the divine.

I don't like that take quite as much, and there is textual evidence contradicting it. But you can find a summary of that mainline interpretation here:

My Hermeticism is not the *only* Hermeticism, of course. The Hermetica saw a reawakening in the Renaissance along with the advent of a Christianized form of Hermetic thought. I do describe myself as a Christian Hermeticist, primarily because I am culturally Christian, and because my primary magical work comes from Christian sources (like the majority of the Grimoires). But my Hermetica differs a little from how the Renaissance thinkers incorporated it. We saw another reawakening of the Hermetica with Newton and his translation, which I love (well, I love that it's a thing we know exists. There's less available about Newton's occultism than I would like). I'm obsessed with Newton and I think his use of the Hermetica is one the best in modern times. I mean, it gave us Calculus guys. Like, come on. (Special shoutout to Gottfried Leibniz who also invented Calculus you deserve the credit too dude but you didn't do a translation of the Hermetica so bummer for you no wizard points.) And Newton's Hermetica and mine might look a little more similar.

My Hermetica has nothing at all to do with modern texts like the Kybalion, which I strongly dislike (it's a baby of the New Thought movement and is essentially pulling the title of Hermetic for clout, which doesn't necessarily discredit it as a text but hard to approach in good faith). And especially nothing to do with texts spouting that Thoth the Atlantean stuff. I really hope people aren't reading that shit with any seriousness it's so... fanfiction-y.

"What if Thoth was an Atlantean God King and he wrote the Emerald Tablets and..." fuck off dude.

Ultimately I call myself a Hermeticist to place me in a tradition stemming from the man turned syncretic "god", Hermes Trismegistus. We are called to follow, like the initiatory structure of the Poimandres, to seek knowledge and to find the Divine there.

I place myself in the tradition of people like Newton, Boyle, Yates, Ficino, Paracelsus...

And no I'm not an egoist why do you ask?

I mean I inform what I do by the things these people wrote and thought and created. And I strive to be a little better, a little closer to divinity, every single day.

That's my Hermetica I suppose.

That was a really really long answer and I apologize for inflicting it upon you lol. I truly appreciate being able to talk about this sort of thing long form. I hope some of this was helpful, or at least passing interesting.

[shielddefenceacademy24]

NDA Syllabus 2025 PDF download – Maths and GAT Syllabus

NDA Syllabus 2025 PDF download – Maths and GAT Syllabus

Are you dreaming of joining the Indian Armed Forces through NDA in 2025? Then buckle up, because understanding the NDA syllabus 2025 is the first step toward success. Whether you’re aiming for the Army, Navy, or Air Force wings, the syllabus is your ultimate guide to cracking the NDA written exam.

Let’s break it all down for you — subject by subject, topic by topic. Ready? Let’s dive in.

Introduction

What is the NDA Exam?

The National Defence Academy (NDA) entrance exam is conducted by the Union Public Service Commission (UPSC) twice a year. It’s your gateway to a life of honor, discipline, and adventure in the Indian Armed Forces.

Why Knowing the NDA Syllabus Matters?

You wouldn’t go into battle without knowing the terrain, right? Similarly, you can’t ace NDA without knowing the NDA syllabus 2025 inside-out. It helps you plan, prepare, and perform better.

Overview of NDA Syllabus 2025

Structure of the NDA Exam

The exam consists of two papers:

Mathematics – 300 Marks

General Ability Test (GAT) – 600 Marks

Each paper is of 2.5 hours duration and both are conducted on the same day.

Subjects Covered

The NDA syllabus 2025 focuses on:

Mathematics: Designed to test your problem-solving and logical abilities.

GAT: Evaluates your command over English and General Knowledge.

NDA Mathematics Syllabus 2025

Here’s what you need to conquer:

Algebra

Sets, Venn diagrams

Complex numbers

Quadratic equations

Arithmetic and geometric progression

Logarithms and their applications

Matrices and Determinants

Types of matrices

Operations on matrices

Determinants and their properties

Inverse of a matrix

Solution of simultaneous equations

Trigonometry

Trigonometric ratios

Identities and equations

Heights and distances

Inverse trigonometric functions

Analytical Geometry of Two and Three Dimensions

Cartesian coordinates

Distance formula

Equation of a line and circle

Direction cosines and direction ratios

Plane and line in 3D space

Differential Calculus

Functions and limits

Continuity and differentiability

Derivatives and applications

Integral Calculus and Differential Equations

Indefinite and definite integrals

Area under curves

First-order differential equations

Vector Algebra

Addition and multiplication of vectors

Scalar and vector products

Applications in geometry

Statistics and Probability

Mean, median, mode

Variance and standard deviation

Probability theories and distributions

NDA GAT Syllabus 2025 (General Ability Test)

Let’s break this 600-mark section down further.

English Section (200 Marks)

Your command over English will be tested through:

Grammar and usage

Spotting errors

Synonyms and antonyms

Vocabulary usage

Comprehension passages

Sentence improvement

General Knowledge Section (400 Marks)

Covers a wide range of topics:

Physics

Motion and laws

Heat and Thermodynamics

Light, Sound, Electricity

Nuclear physics

Chemistry

Physical and chemical changes

Atomic structure

Acids, bases, and salts

Carbon compounds

General Science

Human body and nutrition

Biotechnology

Environmental science

History, Freedom Movement, etc.

Ancient, Medieval, and Modern History

Indian National Movement

Constitution of India

Geography

Earth structure and atmosphere

Climate and vegetation

Rivers and mountains

Demography

Current Affairs

National and international events

Awards, sports, and culture

Marking Scheme for NDA 2025

Mathematics: 300 marks (Each question = 2.5 marks, -0.83 for wrong answers)

GAT: 600 marks (Each question = 4 marks, -1.33 for wrong answers)

You need to be accurate — guesswork can cost you.

Best Tips to Cover NDA Syllabus Efficiently

Make a Study Plan

Break the syllabus into daily goals. Focus on weak areas but don’t ignore your strengths.

Practice Mock Tests

Time-bound mock tests simulate real exam pressure. Analyze mistakes and improve.

Refer to NCERT Books

NCERT books from class 9 to 12 are the holy grail, especially for Maths and Science.

Focus on Time Management

Don’t spend too much time on a single question. Practice makes perfect!

Recommended Books and Resources

For Maths

NDA Pathfinder by Arihant

NCERT Maths (Class 11 & 12)

R.S. Aggarwal for basics

For GAT

Wren & Martin (English Grammar)

Lucent’s GK

Current affairs magazines like Pratiyogita Darpan

Importance of NDA Syllabus for SSB Preparation

While the SSB is a different stage, your understanding of current events, logical reasoning, and communication—covered in the NDA syllabus—plays a vital role in your SSB interview.

Changes in NDA Syllabus Over the Years

While the core structure remains the same, the paper pattern and emphasis areas evolve. For instance, recent papers are heavier on applied mathematics and current affairs.

Mistakes to Avoid While Preparing

Ignoring English or GAT

Relying solely on coaching

Not analyzing previous year papers

Poor time management

Final Thoughts

If you’re serious about NDA 2025, your first mission is to decode the NDA syllabus 2025. It’s your blueprint to success. From solving matrices to mastering military history, every topic brings you closer to that dream uniform. Stay consistent, stay curious — and victory will follow.

Conclusion

Cracking NDA isn’t just about hard work, it’s about smart work. And smart work begins with mastering the NDA syllabus 2025. Whether it’s complex numbers or the history of the Indian freedom struggle, every topic holds the key to your dream career in the armed forces.

So grab that syllabus, make your plan, and start today. The parade ground awaits you!

FAQs

Q1. What are the main subjects in the NDA syllabus 2025? A1. The main subjects are Mathematics and General Ability Test (GAT), which includes English, General Knowledge, Science, and Current Affairs.

Q2. Is there any change in the NDA Maths syllabus for 2025? A2. No major changes are expected. However, UPSC may increase the complexity or pattern of some topics.

Q3. How to prepare for the NDA GAT paper? A3. Read newspapers daily, revise NCERT Science & History, and practice English grammar regularly.

Q4. Are NCERT books enough for NDA Maths? A4. Yes, they form the base. You can complement them with practice books like Arihant or Pathfinder.

Q5. What is the level of difficulty for NDA Maths? A5. It’s moderate to high. Basic concepts from Class 11 and 12 are tested in a tricky manner, so conceptual clarity is vital.

[callofdutymobileindia]

Machine Learning Syllabus: What Mumbai-Based Courses Are Offering This Year

As Artificial Intelligence continues to dominate the future of technology, Machine Learning (ML) has become one of the most sought-after skills in 2025. Whether you’re a data enthusiast, a software developer, or someone looking to transition into tech, understanding the structure of a Machine Learning Course in Mumbai can help you make informed decisions and fast-track your career.

Mumbai, a city synonymous with opportunity and innovation, has emerged as a growing hub for AI and ML education. With a rising demand for skilled professionals, leading training institutes in the city are offering comprehensive and job-focused Machine Learning courses in Mumbai. But what exactly do these programs cover?

In this article, we break down the typical Machine Learning syllabus offered by Mumbai-based institutes, highlight key modules, tools, and career pathways, and help you understand why enrolling in a structured ML course is one of the best investments you can make this year.

Why Machine Learning Matters in 2025?

Before diving into the syllabus, it’s essential to understand why machine learning is central to the tech industry in 2025.

Machine learning is the driving force behind:

Predictive analytics

Recommendation engines

Autonomous systems

Fraud detection

Chatbots and virtual assistants

Natural Language Processing (NLP)

From healthcare to fintech and marketing to logistics, industries are deploying ML to enhance operations, automate decisions, and offer personalized services. As a result, the demand for ML engineers, data scientists, and AI developers has skyrocketed.

Overview of a Machine Learning Course in Mumbai

A Machine Learning course in Mumbai typically aims to:

Build foundational skills in math and programming

Teach practical ML model development

Introduce deep learning and advanced AI techniques

Prepare students for industry-level projects and interviews

Let’s now explore the typical modules and learning paths that top-tier ML programs in Mumbai offer in 2025.

1. Foundation in Programming and Mathematics

🔹 Programming with Python

Most courses start with Python, the industry-standard language for data science and ML. This module typically includes:

Variables, loops, functions

Data structures (lists, tuples, dictionaries)

File handling and error handling

Introduction to libraries like NumPy, Pandas, Matplotlib

🔹 Mathematics for ML

You can’t master machine learning without understanding the math behind it. Essential topics include:

Linear Algebra (vectors, matrices, eigenvalues)

Probability and Statistics

Calculus basics (gradients, derivatives)

Bayes’ Theorem

Descriptive and inferential statistics

These foundations help students grasp how ML models work under the hood.

2. Data Handling and Visualization

Working with data is at the heart of ML. Courses in Mumbai place strong emphasis on:

Data cleaning and preprocessing

Handling missing values

Data normalization and transformation

Exploratory Data Analysis (EDA)

Visualization with Matplotlib, Seaborn, Plotly

Students are often introduced to real-world datasets (CSV, Excel, JSON formats) and taught to manipulate data effectively.

3. Supervised Machine Learning

This core module teaches the backbone of most ML applications. Key algorithms covered include:

Linear Regression

Logistic Regression

Decision Trees

Random Forest

Naive Bayes

Support Vector Machines (SVM)

Students also learn model evaluation techniques like:

Confusion matrix

ROC-AUC curve

Precision, recall, F1 score

Cross-validation

Hands-on labs using Scikit-Learn, along with case studies from domains like healthcare and retail, reinforce these concepts.

4. Unsupervised Learning

This segment of the syllabus introduces students to patterns and grouping in data without labels. Key topics include:

K-Means Clustering

Hierarchical Clustering

Principal Component Analysis (PCA)

Anomaly Detection

Students often work on projects like customer segmentation, fraud detection, or market basket analysis using unsupervised techniques.

5. Model Deployment and MLOps Basics

As real-world projects go beyond model building, many Machine Learning courses in Mumbai now include modules on:

Model deployment using Flask or FastAPI

Containerization with Docker

Version control with Git and GitHub

Introduction to cloud platforms like AWS, GCP, or Azure

CI/CD pipelines and monitoring in production

This gives learners an edge in understanding how ML systems operate in real-time environments.

6. Introduction to Deep Learning

While ML and Deep Learning are distinct, most advanced programs offer a foundational understanding of deep learning. Topics typically covered:

Neural Networks: Structure and working

Activation Functions: ReLU, sigmoid, tanh

Backpropagation and Gradient Descent

Convolutional Neural Networks (CNNs) for image processing

Recurrent Neural Networks (RNNs) for sequential data

Frameworks: TensorFlow and Keras

Students often build beginner deep learning models, such as digit recognizers or sentiment analysis tools.

7. Natural Language Processing (NLP)

With AI’s growing use in text-based applications, NLP is an essential module:

Text preprocessing: Tokenization, stopwords, stemming, lemmatization

Term Frequency–Inverse Document Frequency (TF-IDF)

Sentiment analysis

Named Entity Recognition (NER)

Introduction to transformers and models like BERT

Hands-on projects might include building a chatbot, fake news detector, or text classifier.

8. Capstone Projects and Portfolio Development

Most Machine Learning courses in Mumbai culminate in capstone projects. These simulate real-world problems and require applying all learned concepts:

Data ingestion and preprocessing

Model selection and evaluation

Business interpretation

Deployment and presentation

Example capstone projects:

Predictive maintenance in manufacturing

Price prediction for real estate

Customer churn prediction

Credit risk scoring model

These projects are crucial for portfolio building and serve as talking points in interviews.

9. Soft Skills and Career Preparation

The best training institutes in Mumbai don’t stop at technical skills—they invest in career readiness. These include:

Resume building and portfolio review

Mock technical interviews

Behavioral interview training

LinkedIn optimization

Job referrals and placement assistance

Students also receive guidance on freelancing, internships, and participation in Kaggle competitions.

A Standout Option: Boston Institute of Analytics

Among the many training providers in Mumbai, one institute that consistently delivers quality machine learning education is the Boston Institute of Analytics.

Their Machine Learning Course in Mumbai is built to offer:

A globally recognized curriculum tailored for industry demands

In-person classroom learning with expert faculty

Real-world datasets and capstone projects

Deep exposure to tools like Python, TensorFlow, Scikit-learn, Keras, and AWS

One-on-one career mentorship and resume support

Dedicated placement assistance with a strong alumni network

For students and professionals serious about entering the AI/ML field, BIA provides a structured and supportive environment to thrive.

Final Thoughts: The Future Is Machine-Learned

In 2025, machine learning is not just a skill—it's a career catalyst. The best part? You don’t need to be a Ph.D. holder to get started. All you need is the right course, the right mentors, and the commitment to build your skills.

By understanding the detailed Machine Learning syllabus offered by Mumbai-based courses, you now have a roadmap to guide your learning journey. From Python basics to deep learning applications, and from real-time deployment to industry projects—everything is within your reach.

If you’re looking to transition into the world of AI or upgrade your existing data science knowledge, enrolling in a Machine Learning course in Mumbai might just be the smartest move you’ll make this year.

[sunenajain-blog]

IGCSE Math vs IB Math: What Changes and How to Adapt

For many students, the transition from IGCSE Mathematics to IB Mathematics (AA/AI, SL/HL) can feel like stepping into a new world of complexity, abstraction, and independence. While both programs aim to build strong mathematical foundations, the IB Math curriculum demands significantly more from students in terms of conceptual depth, real-world application, and critical thinking.

In this article, we’ll explore the key differences between IGCSE and IB Math, how to adapt successfully, and how platforms like IBGram can support that academic leap.

📊 Key Differences Between IGCSE Math and IB Math

CategoryIGCSE MathIB Math (AA/AI)Curriculum StyleProcedural, focused on problem-solvingConceptual, emphasizes real-life applicationLevel of RigorModerateHigh (especially at HL level)Assessment StyleShort questions, straightforward answersMulti-step, analytical problemsTechnology UseMinimalEssential (e.g., GDC calculators)Internal AssessmentsNoneIncludes IA (Internal Assessment essay)Focus AreasAlgebra, geometry, number theoryStatistics, calculus, modeling

🔁 What Changes: From IGCSE to IB Math

1. Complexity of Concepts

IGCSE introduces foundational topics with relatively straightforward methods.

IB Math delves deeper, especially in Calculus, Vectors, and Statistics, where derivations, justifications, and applications matter more.

2. Application Over Memorization

IB emphasizes understanding over rote learning. You’re expected to justify your reasoning, not just show correct answers.

3. Internal Assessment (IA)

A major shift is the introduction of the Math IA—a 12–20 page investigation where you explore a math concept of personal interest using real-world data or modeling.

4. Course Options: AA vs AI

Applications and Interpretation (AI) leans towards statistics, modeling, and real-world use.

Analysis and Approaches (AA) is more abstract and proof-based, ideal for students pursuing engineering, physics, or math-intensive fields.

5. Use of Technology

IB Math requires use of graphical display calculators (GDCs) and sometimes tools like Desmos, GeoGebra, or spreadsheets.

🧠 How to Adapt Successfully

✅ 1. Build Strong Algebraic Fluency

Algebra is the backbone of both IB AA and AI. Master equations, inequalities, and functions early.

✅ 2. Practice Real-World Problems

Start applying math to real-life situations—model the height of a basketball shot, or use statistics to analyze survey results.

✅ 3. Understand, Don’t Memorize

Ask why something works—not just how. This is especially crucial in IB assessments.

✅ 4. Get Comfortable with Your GDC

Know how to use functions like graph plotting, regression analysis, and probability simulations.

✅ 5. Start Prepping for the IA Early

Explore math topics that interest you and try simple investigations in your IGCSE years.

🤝 How IBGram Supports the Transition

IBGram is a trusted learning platform tailored to the unique needs of IB students, and it plays a vital role in helping students bridge the gap between IGCSE and IB Math.

🚀 What IBGram Offers:

Transition Modules: Designed specifically for students entering IB from IGCSE, covering advanced algebra, trigonometry, and precalculus.

IA Support: Step-by-step IA guidance, example investigations, and one-on-one mentorship.

Concept Videos: Bite-sized explainer videos focused on AA/AI topics.

Live Doubt Sessions: Weekly Q&A with experienced IB tutors.

GDC Tutorials: Learn your calculator through practical walkthroughs.

📈 Student Impact:

Students who use IBGram during their transition report:

Faster adaptation to IB-style questions

Higher engagement with the Math IA process

Improved scores in formative assessments and mock exams

📝 Final Tips for New IB Math Students

Don’t underestimate IB Math—it’s a major leap from IGCSE, even for high achievers.

Choose the right course (AA vs AI) based on your future aspirations.

Don’t wait until term 2 to seek help—start early with resources like IBGram to build confidence.

📌 Summary

Key AreaWhat to Focus OnCore SkillsAlgebra, functions, calculator usageMindsetConceptual learning > memorizationAssessment PreparationPractice IB-style questions earlySupport SystemUse IBGram’s structured resources

[sathcreation]

Expert IIT Mathematics Teacher at Gritty Tech

Introduction to IIT JEE Mathematics Excellence

The journey to cracking the prestigious IIT JEE begins with mastering one of its most challenging components – Mathematics. At Gritty Tech, we understand the intensity and depth required to succeed in this subject. That's why we offer specialized coaching under the guidance of expert IIT Mathematics teachers who not only know the syllabus but also understand the psychology and strategy behind high-stakes exams For More…

Our teaching is not just about covering topics. It’s about building a solid mathematical foundation, developing analytical thinking, and fostering a problem-solving mindset.

Why Expert Teachers Make a Difference

IIT JEE Mathematics is not about rote learning. It demands creativity, speed, accuracy, and deep conceptual understanding. An expert IIT Maths teacher brings all these elements to the table. At Gritty Tech, our instructors are selected through a rigorous process. Each of them has years of experience in mentoring toppers, with proven results across multiple batches.

Key Attributes of Our Expert Maths Faculty:

In-depth Subject Knowledge: Every teacher at Gritty Tech has a mastery over the entire JEE syllabus including Algebra, Calculus, Coordinate Geometry, Trigonometry, Probability, and more.

Strategic Teaching Methods: They know how to break down complex problems into simpler steps and highlight shortcuts that save time in exams.

Focus on Conceptual Clarity: Instead of encouraging memorization, our approach ensures students understand the 'why' behind every formula.

Real Exam Insight: Teachers share insights from previous year papers, trends, and changing patterns in JEE to keep students one step ahead.

Individual Mentorship: Every student is different. Our experts provide personal guidance to overcome weaknesses and build on strengths.

A Curriculum Built for Success

At Gritty Tech, the Mathematics curriculum is not generic. It is crafted specifically for IIT JEE aspirants, keeping in mind the latest trends, difficulty levels, and expected question formats. Our curriculum is reviewed and refined every year by a panel of experts.

The Core Topics Covered Include:

Algebra: Quadratic equations, Complex numbers, Matrices & Determinants, Permutations & Combinations

Calculus: Limits, Continuity, Differentiability, Application of Derivatives, Integrals, Differential Equations

Coordinate Geometry: Straight lines, Circles, Conic Sections

Trigonometry: Identities, Equations, Inverse Trigonometric Functions

Vectors and 3D Geometry

Probability and Statistics

Each topic is taught from the ground up, beginning with theory and moving into solved examples, practice sheets, test series, and revision strategies.

Teaching Methodology at Gritty Tech

What truly sets Gritty Tech apart is not just the content we teach, but how we teach it.

Interactive Concept Classes

Our sessions are designed to be interactive. Teachers use smart boards, real-life analogies, and visual aids to explain abstract mathematical ideas. Every class ends with a set of practice problems that help reinforce the day’s learning.

Doubt Resolution in Real-Time

Students never have to wait till the end of the week to clear their doubts. With dedicated doubt-solving sessions and availability of the faculty even outside class hours, learning continues seamlessly.

Regular Testing and Feedback

Frequent quizzes, weekly tests, and full-length mock exams are conducted to ensure students are exam-ready. After each test, teachers provide personalized feedback and performance analysis.

Adaptive Learning

Not every student learns the same way. Our experts use adaptive learning techniques to identify the learning style of each student and modify their approach accordingly.

[fractalmathematics]

1: INTRODUCTION TO DIFFERENTIATION

Calculus: the branch of mathematics that deals with how things change. It's split into two main areas—differentiation and integration. In this introduction, I'll be focusing specifically on differentiation, which is all about understanding rates of change and the slope of curves.

Unlike a normal rectangle (attached below), whose area can be quantified by the product of the length and width, real-world shapes are more complex. They aren't always so straightforward.

Think of the arc of a thrown basketball: it most certainly will not have a constant slope by virtue of projectile motion. This is where differentiation comes in, making it easier to calculate the instantaneous rate of change.

At its core, differentiation is the process of finding the derivative of a function. The derivative tells us how a function is changing at any given point. In more visual terms, it's the slope of the tangent line to a curve at a particular point. Let's see this manifest a solved problem:

[edgythoughts]

Why Is Zero So Powerful in Math 2025

Why Is Zero So Powerful in Math 2025

📘 Book-Level Answer (University-Level – Mathematics & History) Zero, represented as “0,” is not just a placeholder or a symbol for "nothing"—it is a cornerstone of modern mathematics. The introduction and understanding of zero fundamentally reshaped arithmetic, algebra, calculus, computer science, and even philosophical reasoning in mathematics. 🔢 Mathematical Power of Zero 1. Zero as an Identity Element In arithmetic, zero is the additive identity, which means: a+0=afor any real number aa + 0 = a quad text{for any real number } a This property is foundational to number theory and linear algebra, especially when defining vector spaces and algebraic structures like groups and rings. 2. Zero in Algebra - Roots of equations: Solving for when an equation equals zero helps us find key points like intercepts and turning points. - Zero-product property: If ab=0ab = 0, then either a=0a = 0, b=0b = 0, or both — a crucial principle in factoring and solving equations. 3. Zero in Calculus - Limits and continuity: Zero plays a key role in limits. For example, lim⁡x→0sin⁡xx=1lim_{x to 0} frac{sin x}{x} = 1 - Derivatives: The rate of change is often zero at maximum or minimum points. 4. Zero in Coordinate Systems Zero gives us the origin in a Cartesian coordinate system (0,0)(0, 0), a reference point from which we measure all other positions in geometry and physics. 5. Zero in Computer Science Binary code (the language of computers) is built using only two digits: 1 and 0. Zero represents the “off” state in logic gates and digital signals.

📜 Historical Significance of Zero - Ancient Origins: Zero was developed independently in ancient India (by Brahmagupta in the 7th century) and Mesoamerica (by the Mayans). - It revolutionized counting systems—especially the place-value system—making arithmetic operations like multiplication and division practical and scalable. 💡 Easy Explanation (Understanding Zero for Everyone) Imagine you're playing a game where you score points. If you have “0 points,” you haven't scored yet—but that still means something. Zero tells you where you are, even if it's at the starting point. Why is zero powerful? - It’s not just nothing—it’s a marker. A starting line. - Without zero, we couldn’t write big numbers like 1,000. You’d be stuck figuring out whether 1 is ten or a hundred! - It balances equations. If you want to keep things fair on both sides, you often use zero. In everyday life: - Bank account: If you have ₹0, you know exactly how much you have—not unknown or empty, but zero. - Temperature: Zero degrees is the point between freezing and not freezing—it's important! 🧠 Summary: - Zero is the additive identity. - It makes equations solvable and systems like calculus work. - It marks origin points in math and space. - It powers computer logic. - It revolutionized number systems and mathematical thinking. ⚠️ Disclaimer: The easy explanation is just to help you understand the concept in simple terms. For academic or exam purposes, always rely on the detailed explanation. If you score less for using this simplified version, we're not responsible—we're just here to make things clearer for learning purposes. 🔗 Related Reading from Our Blog: - How Does Quantum Entanglement Work 2025 https://edgythoughts.com/how-does-quantum-entanglement-work-2025 - How Do Gravitational Waves Affect Space-Time 2025 https://edgythoughts.com/how-do-gravitational-waves-affect-space-time-2025 🔗 External Source: - https://en.wikipedia.org/wiki/0 Read the full article

[allsaeasonsvaleters]

Mastering Advanced Placement Prep in Dubai: Your Guide to AP Success

The journey to academic success in Advanced Placement (AP) courses can be both exciting and challenging, especially for students in Dubai, where AP programs have gained immense popularity. Advanced Placement programs are an excellent way for high school students to experience college-level courses, helping them earn college credits early and stand out on university applications. Among the various AP subjects, AP Calculus stands out for students pursuing fields in STEM (Science, Technology, Engineering, and Mathematics). Preparing effectively for AP courses can make a difference, and Dubai’s education sector offers a wealth of resources to aid students in Advanced Placement Prep in Dubai.

In recent years, the UAE has experienced a surge in students opting for AP courses, making Advanced Placement Prep in Dubai a high-demand service. AP courses are recognized internationally, making them an ideal choice for students who may pursue higher education abroad. Advanced Placement Prep in Dubai offers a structured approach to mastering AP subjects and prepares students for the AP exams that take place each May. These exams are pivotal since many universities use them to gauge a student’s readiness for college-level studies and may award college credits based on scores. As the demand for AP courses has increased, so too has the need for specialized tutoring and prep courses that guide students through AP courses, particularly challenging ones like AP Calculus.

Calculus, a fundamental area in AP courses, is often seen as intimidating but is crucial for those interested in advanced fields of science, technology, and engineering. AP Calculus, available in two forms – AB and BC – covers topics ranging from limits and derivatives to integrals and differential equations. Mastering these topics through effective ap calculus preparation not only boosts exam scores but also sets students up for success in higher education. By providing a rigorous introduction to calculus concepts, AP Calculus builds a strong foundation for students’ future studies.

Students in Dubai aiming for AP excellence can benefit greatly from enrolling in local and online Advanced Placement Prep in Dubai. In these courses, students receive guidance from experienced instructors, many of whom have a background in AP courses and exam preparation. They offer strategies on how to approach the AP Calculus curriculum, ensuring students fully grasp calculus concepts. With Dubai’s diverse international student body, these prep courses often incorporate a variety of teaching methodologies to cater to students from different educational backgrounds.

Preparing for AP exams demands a structured study plan. Students focusing on AP Calculus should begin by identifying areas where they need the most improvement, whether it’s in understanding complex calculus theorems or practicing problem-solving techniques. Students are advised to start their Advanced Placement Prep in Dubai months before the exam date. Doing so allows ample time to reinforce key concepts and practice under timed conditions, which is vital for performing well on AP exams. Working with tutors can further streamline this process, as they provide personalized feedback and clarify any doubts.

For students aiming to maximize their AP scores, taking practice exams is essential. Practicing under exam conditions familiarizes students with the format of AP exams and enables them to manage time effectively. This is especially relevant for AP Calculus, where students need to solve problems quickly and accurately. By incorporating practice exams into their Advanced Placement Prep in Dubai, students can track their progress and build the confidence needed to excel on exam day.

In summary, AP courses, particularly AP Calculus, present an incredible opportunity for students in Dubai to gain advanced knowledge and earn college credits. Through consistent effort, focused Advanced Placement Prep in Dubai, and guidance from experienced tutors, students can navigate the challenges of AP courses. With dedication, a well-structured study plan, and the right resources, excelling in AP courses is an achievable goal for any motivated student in Dubai.

[abhijitdivate1]

Comprehensive Breakdown of a Data Science Curriculum: What to Expect from Start to Finish

Comprehensive Breakdown of a Data Science Curriculum: What to Expect from Start to Finish

A Data Science course typically covers a broad range of topics, combining elements from statistics, computer science, and domain-specific knowledge. Here’s a breakdown of what you can expect from a comprehensive Data Science curriculum:

1. Introduction to Data Science

Overview of Data Science: Understanding what Data Science is and its significance.

Applications of Data Science: Real-world examples and case studies.

2. Mathematics and Statistics

Linear Algebra: Vectors, matrices, eigenvalues, and eigenvectors.

Calculus: Derivatives and integrals, partial derivatives, gradient descent.

Probability and Statistics: Probability distributions, hypothesis testing, statistical inference, sampling, and data distributions.

3. Programming for Data Science

Python/R: Basics and advanced concepts of programming using Python or R.

Libraries and Tools: NumPy, pandas, Matplotlib, seaborn for Python; dplyr, ggplot2 for R.

Data Manipulation and Cleaning: Techniques for preprocessing, cleaning, and transforming data.

4. Data Visualization

Principles of Data Visualization: Best practices, visualization types.

Tools and Libraries: Tableau, Power BI, and libraries like Matplotlib, seaborn, Plotly.

5. Data Wrangling

Data Collection: Web scraping, APIs.

Data Cleaning: Handling missing data, data types, normalization.

6. Exploratory Data Analysis (EDA)

Descriptive Statistics: Mean, median, mode, standard deviation.

Data Exploration: Identifying patterns, anomalies, and visual exploration.

7. Machine Learning

Supervised Learning: Linear regression, logistic regression, decision trees, random forests, support vector machines.

Unsupervised Learning: K-means clustering, hierarchical clustering, PCA (Principal Component Analysis).

Model Evaluation: Cross-validation, bias-variance tradeoff, ROC/AUC.

8. Deep Learning

Neural Networks: Basics of neural networks, activation functions.

Deep Learning Frameworks: TensorFlow, Keras, PyTorch.

Applications: Image recognition, natural language processing.

9. Big Data Technologies

Introduction to Big Data: Concepts and tools.

Hadoop and Spark: Ecosystem, HDFS, MapReduce, PySpark.

10. Data Engineering

ETL Processes: Extract, Transform, Load.

Data Pipelines: Building and maintaining data pipelines.

11. Database Management

SQL and NoSQL: Database design, querying, and management.

Relational Databases: MySQL, PostgreSQL.

NoSQL Databases: MongoDB, Cassandra.

12. Capstone Project

Project Work: Applying the concepts learned to real-world data sets.

Presentation: Communicating findings effectively.

13. Ethics and Governance

Data Privacy: GDPR, data anonymization.

Ethical Considerations: Bias in data, ethical AI practices.

14. Soft Skills and Career Preparation

Communication Skills: Presenting data findings.

Team Collaboration: Working in data science teams.

Job Preparation: Resume building, interview preparation.

Optional Specializations

Natural Language Processing (NLP)

Computer Vision

Reinforcement Learning

Time Series Analysis

Tools and Software Commonly Used:

Programming Languages: Python, R

Data Visualization Tools: Tableau, Power BI

Big Data Tools: Hadoop, Spark

Databases: MySQL, PostgreSQL, MongoDB, Cassandra

Machine Learning Libraries: Scikit-learn, TensorFlow, Keras, PyTorch

Data Analysis Libraries: NumPy, pandas, Matplotlib, seaborn

Conclusion

A Data Science course aims to equip students with the skills needed to collect, analyze, and interpret large volumes of data, and to communicate insights effectively. The curriculum is designed to be comprehensive, covering both theoretical concepts and practical applications, often culminating in a capstone project that showcases a student’s ability to apply what they've learned.

Acquire Skills and Secure a Job with best package in a reputed company  in Ahmedabad with the Best Data Science Course Available

Or contact US at 1802122121 all Us 18002122121

Call Us 18002122121

Call Us 18002122121

Call Us 18002122121

Call Us 18002122121

[usaq22]

(1) March 2024 Journal (Joniaux).

(2) Table of Contents =

Table of Contents. (Newest iMAGE Search All iNTERESTiNG Words!).

Welcome to March 2024! (48/671 MiT Calculus).

Picture Folder Organization.

Wolfram|Alpha: Entering iNPUT Math Student iNTRODUCTiON.

Wolfram|Alpha: Managing Computations iN NoteBooks. 

Large Language Model Programming.

Get Code Definitions by Highlighting & Option Clicking.

Wolfram|Alpha: Free-Form & External iNPUT.

Kinetic Learning Types.

Note On “Accordion Style” (Collapsible List) Format.

Fractions & Decimals (Wolfram|Alpha).

Variables & Functions (Wolfram|Alpha).

Algebra (Wolfram|Alpha).

Plots iN 2D (Wolfram|Alpha).

Geometry (Wolfram|Alpha). 

Trigonometry (Wolfram|Alpha).

Polar Coordinates (Wolfram|Alpha).

iF > Documentation Search [SingleWord] ⮚Then > Return “SubjectWordList” 1st [Before Singular Word Definitions’.

Exponentials & Logarithms (Wolfram|Alpha).

Limits (Wolfram|Alpha).

Derivatives (Wolfram|Alpha).

Integrals (Wolfram|Alpha).

Trace and Zoom (MiT 48/671).

Sequences, Sums, and Series (Wolfram|Alpha).

Recursive Sequence (Google).

Recurrence Table (Wolfram|Alpha).

Wolfram|Mathematica Documentation Center WebPage Suggestions:

A Note About “LinkLines”.

March 7th 2024.

More Plots iN 2D (Wolfram|Alpha).

Plots iN 3D (Wolfram|Alpha).

MultiVariate Calculus (Wolfram|Alpha).

Vector Analysis & Visualization (Wolfram|Alpha).

Differential Equations (Wolfram|Alpha).

Ordinary Differential Equation [ODE] (Google).

Partial Differential Equation [PDE] (Google).

Delay Differential Equation [DDE] (WikiPedia). 

iNTERPOLATE (Oxford).

iNTERPOLATiNG Function (Google).

Parametric (Dictionary.Com).

Product ∏ Notation (WikiPedia).

Learning Algorithm (Joniaux).

CoProduct ∐ Notation (WikiPedia).

Complex Analysis (Wolfram|Alpha).

Matrices & Linear Algebra (Wolfram|Alpha).

Discrete Mathematics (Wolfram|Alpha).

Probability (Wolfram|Alpha).

Statistics (Wolfram|Alpha).

Data Plots & Best-Fit Curves (Wolfram|Alpha).

Group Theory (Wolfram|Alpha).

Math Puzzles (Wolfram|Alpha).

iNTERAVTiVE Models (Wolfram|Alpha).

Mathematical TypeSetting (Wolfram|Alpha).

Color Text iS Necessary for Documentation, but NOT for Note Taking (Joniaux).

Chapter 2: Derivatives (MiT) — 2.1 The Derivative of a Function.

The Derivative of [1/t] (Mit).

2.2 Powers and Polynomials (MiT) [57/671].

Derivatives of Polynomials (MiT) [59/671].

A Look at Differential Equations (Find [y] from [dy/dx]) {MiT} <60/671>.

Marginal Cost and Elasticity iN Economics (MiT) [61/671].

iT Was Books, but Now  iT iS Simulators, Computers, and Programs (Joniaux).

2.3 The Slope and the Tangent Line (MiT) [65/671].

The Equation of a Line (MiT) [65/671].

March Summary (Joniaux).

[sathcreation]

Vedic Maths Teacher: Transforming Mathematics Learning at Gritty Tech

Introduction to Vedic Maths

Vedic Maths is an ancient Indian system of mathematics that simplifies arithmetic operations, algebra, geometry, and calculus. It is based on 16 Sutras (aphorisms) and 13 sub-sutras derived from the Vedas, the sacred Hindu scriptures. This technique enables students to solve complex mathematical problems faster and more efficiently compared to conventional methods For More…

Gritty Tech proudly offers comprehensive Vedic Maths courses, aiming to empower students, teachers, and enthusiasts with exceptional mental math skills. The programs are meticulously designed to enhance cognitive abilities, foster analytical thinking, and boost confidence in tackling mathematical challenges.

Why Learn Vedic Maths?

Vedic Maths offers a host of benefits:

Speed and Accuracy: Students can perform calculations 10 to 15 times faster than traditional methods.

Mental Agility: Enhances mental computation skills, reducing dependency on calculators.

Reduces Math Anxiety: Simplifies complex problems, making math enjoyable.

Applicable Across Levels: Useful for school students, competitive exam aspirants, and professionals alike.

Enhances Memory and Concentration: By stimulating brain activity, it improves memory retention and focus.

At Gritty Tech, we believe that with the right teaching, every learner can unlock the joy of mathematics.

Vedic Maths Teacher Training at Gritty Tech

We offer a specialized Vedic Maths Teacher Training Program designed for individuals who wish to become certified Vedic Maths instructors. The program covers both the theoretical foundations and practical teaching methodologies.

Key Features:

Certified Program: Receive a globally recognized certification upon completion.

Experienced Trainers: Learn from experts with years of teaching and training experience.

Interactive Learning: Engage in live sessions, workshops, and hands-on problem-solving.

Flexible Schedule: Options for weekend, weekday, and self-paced learning.

Comprehensive Curriculum: Covers basic to advanced concepts.

Eligibility:

Anyone passionate about teaching and mathematics can enroll. Prior experience in teaching or a background in mathematics is an advantage but not mandatory.

Curriculum Overview

Introduction to Vedic MathematicsHistory and originsImportance and relevance today

The 16 Sutras and 13 Sub-SutrasDetailed explanations and applications

Basic Arithmetic Using Vedic TechniquesAddition, subtraction, multiplication, division

Advanced CalculationsSquares, cubes, square roots, cube roots

Algebraic ApplicationsSolving equationsFactorization and expansions

Geometry and Trigonometry BasicsQuick methods for calculation

Calculus IntroductionBasic concepts simplified with Vedic methods

Teaching MethodologyHow to teach Vedic Maths effectivelyDesigning lesson plans and activities

Assessments and Certifications

At Gritty Tech, every module is taught with clarity and hands-on exercises, ensuring complete understanding.

Teaching Methodology at Gritty Tech

We believe that learning is most effective when it is engaging and interactive. Our methodology includes:

Live Classes: Real-time interaction with instructors.

Workshops: Practical sessions focusing on specific topics.

Assignments and Projects: Regular practice to reinforce learning.

Peer Learning: Collaborative problem-solving and discussions.

Assessments: Regular quizzes and final evaluation.

Our teachers use modern pedagogical strategies to ensure that every learner, irrespective of their background, can grasp and apply Vedic Maths principles with ease.

Benefits of Becoming a Vedic Maths Teacher

Career Growth: Open new avenues in schools, coaching centers, and online education.

Entrepreneurship: Start your own Vedic Maths training center.

Skill Enhancement: Improve your own mathematical abilities.

Make a Difference: Help students overcome math phobia and develop love for numbers.

Gritty Tech provides post-certification support including guidance on setting up classes, marketing strategies, and continuous upskilling workshops.

Who Should Enroll?

School teachers

Tuition center owners

College students

Homemakers looking for a flexible career

Retired professionals

Anyone with a passion for teaching and mathematics

Whether you want to upskill yourself or start a fulfilling teaching career, Gritty Tech’s Vedic Maths Teacher Training Program is your perfect launchpad.

Why Choose Gritty Tech?

Proven Track Record: Hundreds of successful alumni.

Comprehensive Learning Materials: Access to exclusive ebooks, video tutorials, and practice sheets.

Personal Mentorship: Get personalized guidance throughout your journey.

Global Recognition: Certification that adds value to your professional portfolio.

Community Access: Lifetime membership to the Gritty Tech Vedic Maths community.

Our commitment at Gritty Tech is to build confident educators who can revolutionize mathematics education.

Success Stories

Our alumni have:

Established successful Vedic Maths coaching centers.

Enhanced their teaching methods in schools.

Helped thousands of students excel in competitive exams.

Built online teaching businesses reaching global students.

These achievements underline the effectiveness of the training provided at Gritty Tech.

Frequently Asked Questions (FAQ)

Q: How long is the Vedic Maths Teacher Training Program? A: The program duration is typically 3 months, but fast-track options are available.

Q: Is there any final exam? A: Yes, you must pass a final assessment to receive certification.

Q: Can I start teaching immediately after certification? A: Absolutely! Our training prepares you thoroughly to start teaching right away.

Q: Is the course online or offline? A: We offer both online and offline options to suit your convenience.

Q: What support will I receive after certification? A: You will get lifetime access to resources, mentorship, and community support.

Enrollment Details

Ready to embark on your journey as a Vedic Maths Teacher? Join Gritty Tech today!

Website: www.grittytech.com

Contact: +91-XXXXXXXXXX

Email: info@grittytech.com

Limited seats available. Enroll now to transform your career and inspire the next generation of math enthusiasts!

Conclusion

Becoming a Vedic Maths Teacher with Gritty Tech is more than just a professional certification. It is a transformative experience that empowers you with skills to inspire and educate. Whether you want to teach professionally, start your own educational venture, or simply enhance your own math skills, Gritty Tech provides the perfect platform.

Embrace the power of Vedic Maths. Shape the future. Start your journey with Gritty Tech today.

[mathsminds]

Feature of Math

Mathematics

Content of Mathematics

Course Overview:

This course aims to provide a comprehensive understanding of fundamental mathematical concepts and techniques. Through a combination of theory, problem-solving exercises, and practical applications, students will develop critical thinking skills and mathematical proficiency necessary for success in higher-level mathematics and related fields.

Module 1: Number Systems

Understanding the properties of real numbers

Integers, rational numbers, irrational numbers, and their properties

Introduction to complex numbers and their operations

Exploring number patterns and sequences

Module 2: Algebraic Expressions and Equations

Simplifying algebraic expressions

Solving linear and quadratic equations

Factoring polynomials and solving polynomial equations

Graphing linear and quadratic functions

Module 3: Functions and Relations

Understanding the concept of a function

Identifying types of functions: linear, quadratic, exponential, logarithmic, etc.

Analyzing graphs of functions and their transformations

Solving systems of linear equations and inequalities

Module 4: Geometry

Exploring geometric shapes and properties

Understanding angles, lines, and polygons

Calculating area, perimeter, and volume of geometric figures

Introduction to trigonometry: sine, cosine, tangent, and their applications

Module 5: Probability and Statistics

Understanding basic concepts of probability

Calculating probabilities of events and outcomes

Introduction to descriptive statistics: mean, median, mode, and range

Analyzing data sets and making statistical inferences

Module 6: Calculus

Introduction to limits and continuity

Understanding derivatives and their applications

Calculating rates of change and optimization problems

Introduction to integrals and their applications in finding area and volume

Module 7: Discrete Mathematics

Exploring combinatorics and counting principles

Introduction to sets, relations, and functions

Understanding logic and proof technique

Exploring graph theory and its applications

Module 8: Mathematical Modeling

Understanding the process of mathematical modeling

Formulating mathematical models for real-world problems

Analyzing and interpreting mathematical models

Evaluating the effectiveness and limitations of mathematical models

Module 9: Applications of Mathematics

Exploring interdisciplinary applications of mathematics in science, engineering, finance, and other fields

Case studies and real-world examples demonstrating the relevance of mathematical concepts

Ethical considerations and implications of mathematical applications

Module 10: Review and Final Assessment

Reviewing key concepts and techniques covered in the course

Solving comprehensive problem sets and practice exam

Final assessment covering all topics and skills learned throughout the course.