#mathematical model

[raffaellopalandri]

My life in three years from now?

Daily writing promptWhat will your life be like in three years?View all responses In three years, my life will be both a continuation of my current path and a testament to the accumulated wisdom of that journey. Photo by Ricky Esquivel on Pexels.com Even though I don’t create elaborate plans for a future date as distant as three years, I trust that my principles and the habits I cultivate…

[in-sightpublishing]

Conversation with Tomáš Perna on AI and ANN: Member, World Genius Directory (4)

                      Publisher: In-Sight Publishing Publisher Founding: March 1, 2014 Web Domain: http://www.in-sightpublishing.com Location: Fort Langley, Township of Langley, British Columbia, Canada Journal: In-Sight: Independent Interview-Based Journal Journal Founding: August 2, 2012 Frequency: Three (3) Times Per Year Review Status: Non-Peer-Reviewed Access: Electronic/Digital & Open…

[calicojack1718]

What Happens Post Trump: There's Good News but Mostly Bad News

Reading time: 5 minutes Even while Trump fades into the criminal justice system, we still have the GOP gunning for our democracy, trying to saddle us with an oligarchy of elites. What is likely to happen as we continue down this road to rack and ruin?

Trump, Narcissism, Indictments, Election Loss, and the August Insurrection: Some Predictions I2I4, the rotund, dull-orange, short-fingered, vulgar Star Wars inept larceny bot, will win the Republican nomination no matter what happens. He doesn’t need to campaign. He doesn’t need to run commercials. He doesn’t need to debate. He just needs to be on the ballot. The MAGA base will take care of the…

[catgirl-lucy]

Ultrafilters & Ultrapowers

Hey! Call me Lucy. I might make an introduction blog later, but I first wanted to make a blog-post about ultrapowers.

Ultrafilters are a concept from set theory, I'll try my best to explain what they are and why they're defined as they are.

First, a quick overview of what we will do: we will extend the real number line by adding new numbers through the use of an ultrapower, these new numbers are called "hyperreals". Roughly, this means that we will have infinite sequences [a₀,a₁,a₂,...] of real numbers representing hyperreal numbers, where similar sequences are regarded as equal. We will also show a surprising theorem: although there are seemingly more hyperreals than reals, hyperreals look the same as real numbers "from within".

If we have a sequence of reals like this: [0,1,1/2,1/3,1/4,...] (I'll call this sequence "ε"), the hyperreal that it represents can be viewed as the "limit" of the sequence. Since a large number of entries of this sequence is smaller than any positive real number r > 0, ε will be smaller than any positive real number r, but since also a large number of entries is larger than 0, ε will be larger than 0. ε is thus an infinitesimal hyperreal number. This is mostly just intuition though, so don't worry if you don't entirely get it.

Two hyperreal numbers x = [x₀,x₁,x₂,...] and y = [y₀,y₁,y₂,...] are equal if x_i = y_i for a large number of indices i. But what does "large" mean in this context?

Well, that's where the ultrafilter comes in. Ultrafilters split a family of sets into sets that are "large" and sets that are "small". In this case, we split sets of natural numbers (numbers 0, 1, 2, 3, etc) into large sets and small sets, so we have an ultrafilter on ℕ, the set of natural numbers. Ultrafilters are identified by the family of large sets: if some set A is in an ultrafilter U, then it is large, and if it's not, then it is small.

We do want our notion of "large sets" and "small sets" to make sense: for example, a hyperreal should always be equal to itself, so we want the whole set of natural numbers, {0, 1, 2, 3, 4, ...} (which is the set of indices for which a sequence is equal to itself), to be large.

Obviously, it would make sense that if a set A is large and B is larger than A, then B is also large. Thus, if A ∈ U is a member of an ultrafilter U ("∈" is the membership symbol), and if B ⊃ A contains everything A contains too ("⊃" is the superset symbol), then B ∈ U is a member of the ultrafilter as well.

We also want hyperreal equality to be transitive, thus if [x₀,x₁,x₂,...] = [y₀,y₁,y₂,...] and [y₀,y₁,y₂,...] = [z₀,z₁,z₂,...], then we want [x₀,x₁,x₂,...] = [z₀,z₁,z₂,...]. If A = {i ∈ ℕ | x_i = y_i} is the set of points at which x and y are equal and B = {i ∈ ℕ | y_i = z_i} is the set of points at which y and z are equal, then C = {i ∈ ℕ | x_i = z_i}, the set of points at which x and z are equal, includes the set A ∩ B = {i ∈ ℕ | x_i = y_i ∧ y_i = z_i}, the set of points at which x is equal to y and y is equal to z. It thus makes sense to have our ultrafilter be closed under intersections: if two sets A and B are large, then the set of points that are both in A and in B, called the "intersection" of A and B (denoted A ∩ B), is a large set as well (and thus also in the ultrafilter).

It would also make sense that, if two hyperreal numbers are nowhere equal, then they aren't equal. So the empty set, {} = ∅, is small.

The five axioms above describe a filter:

A filter F on κ is a family of subsets of κ.

A filter F on κ must contain the whole set κ.

A filter F on κ must be upwards closed, thus for every large set A ∈ F, and every larger set B ⊃ A, B ∈ F is large as well.

A filter F on κ must be downwards directed, thus for every large set A ∈ F and every large set B ∈ F, the intersection of A and B, A ∩ B ∈ F, is large as well.

A filter F on κ may not contain the empty set.

However, these are the axioms of a filter, and not of an ultrafilter. Ultrafilters have one additional axiom.

Suppose we have the hyperreal [0,1,0,1,0,1,...]: an alternating sequence of 0's and 1's. Is this equal to 0 = [0,0,0,0,...], or to 1 = [1,1,1,1,...], or is it its own thing? (Note: the 0 in 0 = [0,0,0,0,...] is a hyperreal and the 0's in 0 = [0,0,0,0,...] are real numbers, so they're different (kind of) numbers both called "0"). If it is its own thing, then is it smaller than 1? If it is smaller than 1, then it must be smaller on a large set of indices, meaning it's equal to 0 on a large set of indices, meaning it's equal to 0. If it's not smaller than 1, well, it can't be larger, so it'd only make sense if it's equal to 1, but no axiom about filters says it should! That's why we have this last axiom for ultrafilters, which makes them "decisive": for every set A, it is either large (thus, A ∈ U), or small, meaning that its complement, Ac = {i | i ∉ A}, the set of all points that aren't in A, is large.

And so we have our six axioms of an ultrafilter:

An ultrafilter U on κ is a family of subsets of κ, these subsets are called "large sets".

κ is large.

U is upwards closed.

U is downwards directed.

∅ is not large.

For every set A ⊂ κ, either A ∈ U or Ac ∈ U.

But we're still missing one thing. We can take our ultrafilter U to be the set of all sets of natural numbers that contain 6. ℕ is large, as it contains 6. It is upwards closed: if A contains 6 and B contains everything that A contains and more, then B also contains 6. U is downwards directed: if both A and B contain 6, then the set of all points that are in both A and B still contains 6. The empty set does not contain 6, and every set either does contain 6 or does not contain 6. With this ultrafilter, two hyperreals x and y are equal simply when x₆ and y₆ are equal, so we don't get cool infinitesimals and infinities, and that makes me sad :(

These kinds of boring ultrafilters are called principal ultrafilters. Formally, a principal filter on κ is a filter F on κ for which there is some set X ⊂ κ so that any set A ⊂ κ is large only if it contains everything in X. This filter is often denoted as ↑X. If you want a principal filter U to be an ultrafilter, X needs to be a singleton set, meaning it only contains a single point x. Proving this is left as an exercise for the reader.

Let U be a non-principal ultrafilter on ℕ. This post is getting a bit long, so I won't show why such an ultrafilter exists. Now, we can take the ultrapower of ℝ, the set of real numbers, by U. This ultrapower is often denoted as ℝ^ℕ/U. Members of this ultrapower are (equivalence classes of) functions from ℕ to ℝ, meaning that they send natural numbers/indices to real numbers (the sequence [x₀,x₁,x₂,...] maps the natural number i to the real number x_i). These functions/sequences/equivalence classes are called hyperreal numbers. Two hyperreal numbers, x and y, are equal if {i ∈ ℕ | x(i) = y(i)}, the set of points at which they are equal, is large (i.e. a member of U). We can also define hyperreal comparison and arithmetic operations: x < y if {i | x(i) < y(i)} is large, (x + y)(i) = x(i) + y(i) and (x · y)(i) = x(i) · y(i). Every real number r also has a corresponding hyperreal j(r), which is simply [r,r,r,r,...] (i.e. j(r)(i) = r for all i).

In general, if M is some structure, κ is some set and U is some ultrafilter on κ, then we can take the ultrapower M^κ/U, which is the set of equivalence classes of functions from κ to M, where any relation R in M (for example, "<" in ℝ) is interpreted in M^κ/U as "R(x₁,...,xₙ) if and only if {i ∈ κ | R(x₁(i),...,xₙ(i))} ∈ U is large" and any function f in M (for example, addition in ℝ) is interpreted in M^κ/U as "f(x₁,...,xₙ)(i) = f(x₁(i),...,xₙ(i)) for all i ∈ κ".

A quick note on equivalence classes: in M^κ/U, points aren't actually functions from κ to M, but rather sets of functions from κ to M that are all equal on a large set of values. Given a function f: κ → M, the equivalence classes that f is in is denoted [f]. In this way, if f and g are equal on a large set of values, then [f] and [g] are actually just equal.

The hyperreal [0,1,2,3,4,...], which sends every natural number i to the real number i, is often called ω.

This part of the blog will get a bit more technical, so be warned!

In the beginning of this blog-post, I mentioned that hyperreals look the same as real numbers. I'll make this statement more formal:

For any formula φ that can be built up in the following way:

φ ≡ "x = y" for expressions x and y (expressions are variables and "a + b" and "a · b" for other expressions a and b)

φ ≡ "x < y" for expressions x and y

φ ≡ "ψ ∧ ξ" (ψ and ξ are both true) for formulas ψ and ξ

φ ≡ "ψ ∨ ξ" (ψ or ξ is true (or both)) for formulas ψ and ξ

φ ≡ "¬ψ" (ψ is not true) for an formula ψ

φ ≡ "∃x ψ(x)" (there exists a value for x for which ψ is true) for a variable x and an formula ψ

φ ≡ "∀x ψ(x)" (for all values of x, ψ is true) for a variable x and an formula ψ

We have that ℝ ⊧ φ (φ is true when evaluating equality, comparison and expressions from within ℝ, where variables can have real number values) if and only if ℝ^ℕ/U ⊧ φ (φ is true when evaluating equality, comparison and expressions from within ℝ^ℕ/U, where variables can have hyperreal number values).

In other words: ℝ and ℝ^ℕ/U are elementary equivalent.

So, how will we prove this? Well, we will use induction: "if something being true for all m < n implies it being true for n itself, then it must be true for all n (where m and n are natural numbers)". Specifically, we will use induction on the length of formulas: we will show that, if the above statement holds for all formulas ψ shorter than φ, then it must also hold for φ.

However, we won't use the exact statement above. Instead, we will use the following:

Given a formula φ(...) and hyperreal numbers x₁,...,xₖ, ℝ^ℕ/U ⊧ φ(x₁,...,xₖ) if and only if {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} is large.

Now, why does this imply the original statement? Well, when k = 0, {i | ℝ ⊧ φ} can only be ∅ or ℕ. It being ∅ is equivalent to φ being false in ℝ and, if the statement is true, also equivalent to φ being false in ℝ^ℕ/U. And it being ℕ is equivalent to φ being true in ℝ and, again, if the statement is true, it is also equivalent to φ being true in ℝ^ℕ/U. We thus have that φ being true in ℝ is equivalent to φ being true in ℝ^ℕ/U.

Note: M ⊧ φ simply means that the formula φ is true when interpreted in M.

Now, why do we need this stronger statement? Well, it makes induction a lot easier: given that this statement holds for all ψ shorter than φ, it's easier to prove it also holds for φ.

Now, we can actually do the induction.

First, if φ ≡ "x = y", then we need to show that (1) ℝ^ℕ/U ⊧ φ(x,y) iff (2) {i | ℝ ⊧ φ(x(i),y(i))} is large. This follows immediately from the definition of equality in ℝ^ℕ/U, the same holds for "<".

Now, if φ(x₁,...,xₖ) ≡ "ψ(x₁,...,xₖ) ∧ ξ(x₁,...,xₖ)", we have that {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} = {i | ℝ ⊧ ψ(x₁(i),...,xₖ(i)) ∧ ℝ ⊧ ξ(x₁(i),...,xₖ(i))} = {i | ℝ ⊧ ψ(x₁(i),...,xₖ(i))} ∩ {i | ℝ ⊧ ξ(x₁(i),...,xₖ(i))}. Since {i | ℝ ⊧ ψ(x₁(i),...,xₖ(i))} is large iff ψ(x₁,...,xₖ) is true in ℝ^ℕ/U, and {i | ℝ ⊧ ξ(x₁(i),...,xₖ(i))} iff ξ(x₁,...,xₖ) is true in ℝ^ℕ/U, and U is closed under intersections, we have that {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} is large iff φ holds in ℝ^ℕ/U. A similar argument works for ∨.

If φ(x₁,...,xₖ) ≡ "¬ψ(x₁,...,xₖ)", then we can just use the ultraness of the ultrafilter.

If φ ≡ "∃y ψ(y,x₁,...,xₖ)", then {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} = {i | ℝ ⊧ ∃y ψ(y,x₁(i),...,xₖ(i))} = {i | ∃y ∈ ℝ. ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} = ∪_{y ∈ ℝ} {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))}. We have that the set {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} for y ∈ ℝ is large iff ℝ^ℕ/U ⊧ ψ(j(y),x₁,...,xₖ). If this set is large for some y ∈ ℝ, and thus if ℝ^ℕ/U ⊧ φ(x₁,...,xₖ), then ∪_{y ∈ ℝ} {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} is larger than that set, so it is large as well. For the converse direction, if ∪_{y ∈ ℝ} {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} is large, then we can create a hyperreal z where ψ ⊧ ψ(z(i),x₁(i),...,xₖ(i)) for all i for which ℝ ⊧ ∃y ψ(y,x₁(i),...,xₖ(i)), and we have ℝ^ℕ/U ⊧ ψ(z,x₁(i),...,xₖ(i)), and thus ℝ^ℕ/U ⊧ φ(x₁(i),...,xₖ(i)). Again, a similar argument works for ∀.

(Sorry if you couldn't follow along, I'm not good at explaining these things in an intuitive way.)

This result can be extended to show that M^κ/U is elementary equivalent to M for every structure M, every set κ and every ultrafilter U on κ.

Now, this result might be surprising, as we have a new number ω in ℝ^ℕ/U. Surely, there is a formula that states the existence of this number, right?

Well, it turns out, such a formula does not exist! You can try something like "there is no natural number n so that 1+...+1 w/ n 1's is greater than ω", but ω+1 is a natural number in the hyperreals, so such a natural number does exist. Similarly, any formula you can come up with, as long as it is created using the rules above (using conjunction, disjunction, negation, qauntification, etc), cannot state the existence of an infinite number ω.

But if ℝ^ℕ/U and ℝ are seemingly indistinguishable, might there already be an undetectable infinite real number in ℝ? Well, maybe~ :3 But it's undetectable anyways, so you don't have to worry about it.

Before I end this blog-post, I want to give some more intuition on what filters & ultrafilters actually are. To me, ultrafilters, and filters in general, are like "limits of sets". The principal filter ↑X has X as limit, while non-principal filters and ultrafilters have limits that aren't really sets, but look like ones. For example, you might have the set of prime numbers in your filter, and then the limit of that filter will be a "set" in which all numbers are prime numbers. And if your ultrafilter is non-principal (so for every n, there is a set A ∈ U in the filter that does not contain n), then the limit of that ultrafilter will be a "set" in which all numbers don't actually exist. In the case of filters, this "set" can be any "set" (though it still isn't really a set), but in the case of ultrafilters, this limit looks like a singleton set (i.e. it only has one "element": ω).

I don't know if my intuition of filters and ultrafilters will help anyone, tho, but I think it's cool!

That's all I had to say.

Bye!~ Have a nice day.

[pv1isalsoimportant]

(Semi-regularly updated) list of resources for (not only) young mathematicians interested in logic and all things related:

Igor Oliveira's survey article on the main results from complexity theory and bounded arithmetic is a good starting point if you're interested in these topics.

The Complexity Zoo for information on complexity classes.

The Proof Complexity Zoo for information on proof systems and relationships between them.

Computational Complexity blog for opinions and interesting blog posts about computational complexity and bunch of other stuff.

Student logic seminar's home page for worksheets on proof complexity, bounded arithmetic and forcing with random variables (great introduction for beginners).

Eitetsu Ken's list for resources on proof complexity, computational complexity, logic, graph theory, finite model theory, combinatorial game theory and type theory.

Jan Krajíček's page is full of old teaching materials and resources for students (click past teaching) concernig logic, model theory and bounded arithmetic. I also recommend checking out his books. They are basically the equivalent of a bible for this stuff, although they are a bit difficult to read.

I also recommend the page of Sam Buss, there are downloadable versions of most of his articles and books and archive of old courses including resources on logic, set theory and some misc computer science. I especially recommend his chapters in Hnadbook of Proof Theory.

Amir Akbar Tabatabai's page for materials on topos theory and categories including lecture notes and recordings of lectures.

Andrej Bauer's article "Five stages of accepting constructive mathematics" for a funny and well-written introduction into constructive mathematics.

Lean Game Server for learning the proof assistant Lean by playing fun games.

[myfairkatiecat]

So I was thinking about the whole elves-being-naturally-prettier-than-humans thing because that was always sort of weird to me when I FINALLY think I figured it out.

Humans used to know about the elves, and there are some things they still remember—hence myths about Atlantis and such. Reality is, humans and elves resembled each other in a lot of ways, but elves put themselves on a pedestal as better than every other species (that’s, like, canon, and better be addressed more fully at some point?) and that’s probably a part of the reasons humans “betrayed” the elves—they got sick of hearing that elves were better.

But it was just sort of implanted in their minds, though they weren’t fans of the idea, and elves didn’t go to great lengths to erase that idea from their minds. So humans remember myths and some things about elves, and Atlantis being the underwater city………and beauty standards.

It’s not that elves are naturally prettier than humans. It’s that human beauty standards are shaped around the natural looks of elves.

Thanks for coming to my ted talk

[unnonexistence]

one of my friends is a biologist & i was really amused hearing some of her stories yesterday because they put into context just how believable newt's kaiju drift is as Shit A Biologist Would Do. like my friend has personally met both a guy who got infected with a botfly larva and didn't do anything to remove it (because he just didn't mind), and another guy who identified a tapeworm species by intentionally exposing himself to it (he had it narrowed down to 2 species and needed to know if it was the one that would infect humans) (it was)

[autistobrat]

Info Dump: Parallelohedron

Parallelohedra are 3D shapes that can tile space completely by translation only (no gaps, no rotations, just copying and sliding the shape in 3D). Think of them as the 3D equivalents of those 2D tiles that make up bathroom floors. But more... unhinged.

There are 5 types of parallelohedra in 3D Euclidean space:

1. Cube

The most vanilla parallelohedron.

All sides are squares, all angles 90°, and it tiles 3D space like Lego blocks.

Honestly, it’s the only shape here with a healthy work-life balance.

2. Hexagonal Prism

hexagon faces on top and bottom, and rectangles for the sides.

This can tile space like a stack of honeycomb columns.

Why the torment? Probably because visually it looks deceptively “neat,” but tiling 3D space with it can get complicated fast, especially with face alignments. Also, the symmetry is seductive and a lie.

3. Rhombic Dodecahedron

12 rhombus-shaped faces.

It perfectly fills space— actually, it’s the Voronoi cell of the face-centred cubie lattice (used in crystal structures).

No right angles. Everything’s off, slanted, almost symmetrical but not quite. A Kafkaesque cube.

4. Elongated Dodecahedron

Also known as the elongated rhombic dodecahedron.

Looks like a rhombic dodecahedron that’s been stretched, with even more awkwardness.

Tiling with it is more rare in nature. It's a shape you force into space-filling through desperation.

5. Truncated Octahedron

8 hexagonal faces, 6 squares.

A true space-filler that tiles 3D space perfectly, and forms the Voronoi cells of the body-centred cubic lattice.

[djskiskyskoski]

CT scanner in Blender almost working now.

Leftmost image is the source I'm using. Center image is the 'xray' image that I created from the source. With enough 'xray' images from different angles the source object should be recreatable, and that what the rightmost image is suppose to be.

My previous attempt used 250 cubes rotates around with volume shaders to produce a fog of the object. This causes some problems as the fogs dont really 'add' in blender and was hitting some limits in the depth cause not enough information to come through.

This new method uses geometry nodes. Instead of creating the fogs through the shader and rendering it is done using geometry nodes at runtime.

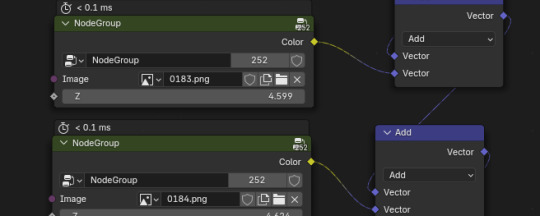
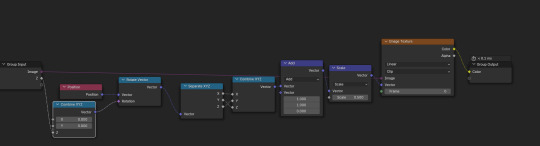
each node holds a small instruction set that adds the image at a small rotation. Each node was created by hand, as geo nodes scripting is a little different from shader nodes scripting and this process really wasnt that difficult to do (mostly just me remembering how many nodes I need to create as I can copy paste blocks).

With this being done in geo nodes I can also do more to the object. Something I see from CT scanners is slicing up the created object to view slices.

With geo nodes this is quite easy and in theory I should be able to start pulling internal data if I had any to begin with.

I think at this point its a problem with the 'xrays' I made. There should be a way to make them better as it was something I made in 20 minutes after a job interview about Tomography. But thats for later, my back hurts and I'm starting to see grid lines from all those nodes.

Shoutout to that one weirdo who told me to continue. You understand.

[liuisi]

guys not gonna lie this toxico class is kinda sucking out my will to live

[m---a---x]

Inspired by all the newly created communities i have also created one about the topic closest to my heart: Foundational Mathematics

It is inteded for all types of posts about and from people of all kinds of backgrounds interested in the topic.

Please share with anyone you think might be interested. If you want to be added comment on this post, so I can add you.

[oakdll]

i love that math nerds spend so much time emulating real world physics, like they really just decided “no i’m not gonna go outside i’m gonna create the outside realistically on my computer”

[calicojack1718]

What Happens Post-Trump: The Path of Political Disintegration, Part 1

They tell us the economy is good, but everybody feels so bad. Trump is indicted, but everybody is so anxious. What is going to happen next? Peter Turchin's Cliodynamics model helps us understand our current situation.

SUMMARY: Trying to envision the future of American democracy is proving to be difficult and despairing. Peter Turchin’s cliodynamics model of nation formation and dissolution is used mathematically model the national cycles of political integration and disintegration. It can help us understand the current state of American politics and where we might go after Trump exits the political stage.…

[p-isequalto-np]

I found a book specifically for finite model theory that contains like 80% of all the things that interest me in math... Let's just say my motivation is back.

[pv1isalsoimportant]

Professors will skip a nontrovial part of a proof and then write this

like thank's for reminding me of what \aleph_0^+ is i guess.

[algebraic-dualist]

Whenever I see someone using ultraproducts outside of model theory there is a certain surprise and shock and vague outrage as part of my brain says "Those are my methods, what are you doing with them?" Every other thing I use in my subfields I enjoy seeing other fields use, but for some reason I feel territorial about ultraproducts. To be clear, I am working on that, I'm not saying it is good to be this way.