#mathsblr

[uuuuuhhhhhhhhhhhhhhhhhh]

"contrapositives are for cowards"

[autistobrat]

Info Dump on Graham's Number

This is by far my favourite so enjoy :D

(update: this is the info dump on hypercube)

Graham's number is mind-bendingly large you literally can’t write it down in the observable universe. Not because your hand would get tired (sure it will), but because even if you turned every atom in the universe into ink and paper, you wouldn’t have enough to express it in normal notation.

It is born from Ramsey theory, a field where mathematicians say: “If you have enough stuff, patterns happen whether you like it or not.” Ronald Graham, legendary mathematician/juggler, needed an upper bound for a problem about colouring edges of a hypercube (I'll info dump on this sooner or later but not now). He didn’t just pick big numbers. He went full “hold my beer” and gave the world something too large.

Let me break it down for you:

To even talk about Graham’s number, we need a special notation called Knuth up-arrow notation:

3↑3 = 3³ = 27 3↑↑3 = 3^(3^3) = 3^27 = 7,625,597,484,987 3↑↑↑3 is already incomprehensibly big.

Graham’s number starts with something even worse:

G₁ = 3↑↑↑↑3 G₂ = 3↑^(G₁) 3 (with that many arrows) ... G₆₄ = Graham’s number

Each step uses the previous beast to decide how many arrows the next operation has. That happens 64 times. Yes, that’s 64 recursive levels of arrow hell :D

So why do people even care about a number so big we can't write?

Because it’s in a real proof. I'm not joking, and I will never wish it to be. Guinness Book of World Records listed it as the largest number ever used in a serious proof in 1980. Mathematicians later found smaller numbers to solve the same problem, but Graham’s number stayed famous because it’s basically math’s middle finger to practicality (and efficiency but at least it's cool).

Can we visualize It? Nope. Even the number of digits in Graham’s number is so huge it can’t be represented in the physical universe. Like, if you converted every particle in existence into an atom-sized digit, you’d still fall short. (There are 10⁸⁰ atoms in this observable universe by the way)

Thanks to modular arithmetic, we actually know that the last few digits of Graham’s number are 7262464195387. Here is the modular arithmetic breakdown (if anyone was wondering).

The powers of 3 repeat last digits every 4 steps:

3¹ → 3 3² → 9 3³ → 7 3⁴ → 1 → cycle repeats. Cycle: (3 → 9 → 7 → 1).

Now, the last digit of 3ⁿ depends on n mod 4:

n ≡ 1 (mod 4) → last digit = 3 n ≡ 2 (mod 4) → last digit = 9 n ≡ 3 (mod 4) → last digit = 7 n ≡ 0 (mod 4) → last digit = 1

Graham’s number = 3^(huge exponent)

We don’t need “huge exponent.” We just need huge exponent mod 4. And that “huge exponent” is itself a power tower of 3’s.

Powers of 3 mod 4 are simple: 3 ≡ -1 (mod 4)

(-1)^odd = -1 → 3 (mod 4) (-1)^even = 1 → 1 (mod 4)

Tracing the parity of the tower shows it’s odd, therefore:

exponent ≡ 3 (mod 4)

QED. The ultimate incomprehensible number ends in 7.

But how did mathematicians figure out 7262464195387 these?

It's not actually rocket science. We want last 13 digits which mathematically means G mod 10¹³ (i.e., what remains when you divide by 10¹³).

We are going to use these mates for this:

Modular arithmetic: we only care about certain digits, not the whole number Euler’s Totient Theorem and Carmichael Function: they will help with giant exponents. Pattern cycles of powers of 3 for mod 2^n and mod 5^n separately (because 10¹³ = 2¹³ × 5¹³). Chinese Remainder Theorem (CRT): for combining results mod 2¹³ and mod 5¹³ back into one result

We will first split 10¹³ into factors: 2¹³ and 5¹³.

Now we can work out last 13 digits separately in base-2 and base-5 worlds.

2¹³ = 8192.

For powers of 3 mod 2¹³, there’s a repeating cycle because 3 and 2 are coprime.

The cycle length = Carmichael function λ(2¹³) = 2¹¹ = 2048

So exponent mod 2048 decides result mod 2¹³.

5¹³ = 1220703125.

The cycle length = 4 × 5¹² = 4 × 244140625 = 976562500

So exponent mod 976562500 decides result mod 5¹³.

The “exponent” of the top-level 3 is itself a tower of 3’s (from all those recursive arrows). Now reduce that tower mod the cycle lengths from above, which collapses ridiculously fast because patterns repeat at small moduli. After multiple reductions, the exponent collapses into manageable values.

Now we know:

Result mod 2¹³ = some number A. Result mod 5¹³ = some number B.

Chinese Remainder Theorem gives one number mod 10¹³ which is unique because 2¹³ and 5¹³ are coprime.

After doing all that, we can know that

the last 13 digits = 7262464195387

The beauty is: we don’t need to know the full value of Graham’s number; just its exponent mod relatively small cycles is enough. The computation is heavy but finite and actually doable on a computer (unlike writing the whole number).

[saphi-maths]

Is it just me or is tableau the sexiest word ever

like mmmmm

Tableau

[autisticaroace]

A spooky calculation I thought of 🧮

Choose four distinct single digits.

Form all three-digit numbers possible using three distinct digits from those you picked

Divide the sum of the three-digit numbers found by the sum of the four distinct digits.

You'll always get 666, but why?

[hapless-studyblr]

exam season's coming

[i-am-a-woman-in-stem]

november 3rd: 29/100 days of productivity

took note for my analysis class

start reviewing exercises of my probability class

I'm back in my hometown for my autumn break. I missed my cat so much it was nice to see him

[uncontrolledfission]

The search for dark matter

Post #6 on Physics and Astronomy, 06/10/23

Welcome back. 

This time, I’m going to be talking about how astronomers and physicists have made an effort to detect and provide evidence for the existence of dark matter. 

To recap from my first issue, it’s worth talking about what dark matter actually is. It’s a type of matter estimated to make up about 80% of the Universe’s matter. To date, it hasn’t been detected. Light passes straight through, it is assumed, however we infer the existence of such a substance due to its gravitational influence. 

We can take an example from the Bullet Cluster. This is a pair of galaxy clusters that collided head-on a while ago. That pink mist you see in the photo is hot gas, and within it most of the regular matter. The blue mist, on the other hand, is dark matter, and where most of the mass of these two galaxies were in this photo. 

Vera Rubin and Kent Ford

Vera Rubin and Kent Ford were two astronomers who had worked together to observe the Andromeda Galaxy, more specifically the rotational velocities of concentric regions from the center. The prediction was that, the further you looked from the center, the less the velocity of the stars within that region, since a greater centripetal force would be required to maintain a high-velocity orbit. This, however, was not the case. 

It was observed that the velocity remained nearly constant the further you went out. Wait a minute, though, this didn’t make sense–that velocity was high enough, in theory, to make the stars fly off into space. But they weren’t.

These findings matched those of Fritz Zwicky. He was a Swiss astronomer who had studied the Coma galaxy cluster. He made the same observation–the speeds were so high that the stars should just have been flung off into space. His findings, however, were ignored.

Experiments to detect dark matter

So far, experiments to detect dark matter have been largely unsuccessful. Some of these include PICASSO, LUX-ZEPLIN, EURECA, FUNK, KIMS, DarkSide, Edelweiss, DARWIN, and DAMA/LIBRA, which is what I’m exploring next. 

This detector in particular, introduced promising results which ended up the subject of dispute. DAMA/LIBRA, which hoped to capture activity from WIMPs (Weakly Interacting Massive Particles), returned a signal with a period of one year. This looked to be one step closer to affirming dark matter’s existence–however, COSINE-100, an experiment set up to mirror that of DAMA/LIBRA, could not reach those same results, which led to the belief that the signal detected could be from some other factor.

The search for dark matter is one that interests me very much. It’s like telling someone in the Stone Age that metal exists, and they should go find it. Except, dark matter is seemingly even more impossible to find, since we can’t perceive it, with the human eye or the best of our current technology. Which, I guess you could argue, would be exactly how the Stone Age person would have felt, but you understand my point.

That said, it’s something I’m eagerly watching. The day we find something promising? You’ll hear it first from me.

[a-lesson-you-never-asked-for]

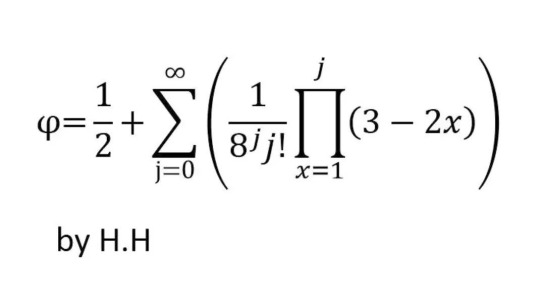
a fascinating identity found on facebook (not all facebook is bad it seems)

[yanderehiro]

Don't get on the wrong side of a set theorist, because they could construct the set of all sets that contain your inevitable demise

[autisticaroace]

This reminds me of when one of my moots who wasn't into math thought that Golden Ratio is just a fancy term for Eurocentric Beauty standards. Definitely an understandable misconception due to how much of that number's hype in beauty filters, designs, and nature is cherry-picked or factually incorrect.

Here's a good video on the topic:

[uuuuuhhhhhhhhhhhhhhhhhh]

[saphi-maths]

(Not) Daily Problem: The first polygon (3)

Yet more pretty geometry questions

(Can you tell that I like geometry?)

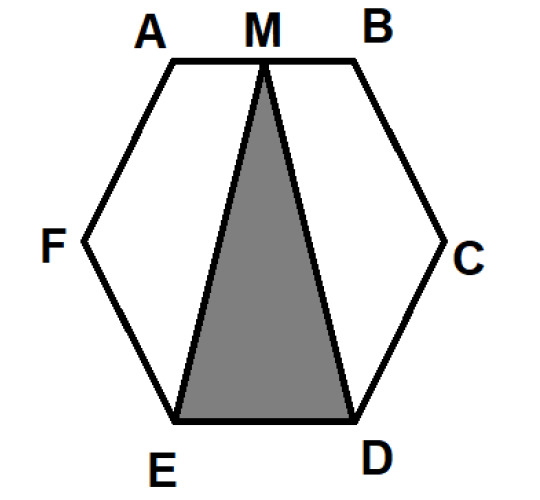
ABCDEF is a regular hexagon M is the midpoint of AB What fraction of the hexagon is shaded by the triangle EMD?

Give it a go! Consider the shapes, perhaps the sheer transformation of them in your mind might help :P (<- hint)

Hint explanation and answer under the cut:

The first step to solving this question, is to use a shear transformation :P

Move the point M across to A, the area of the triangle still remains the same, since its base and perpendicular height don't change

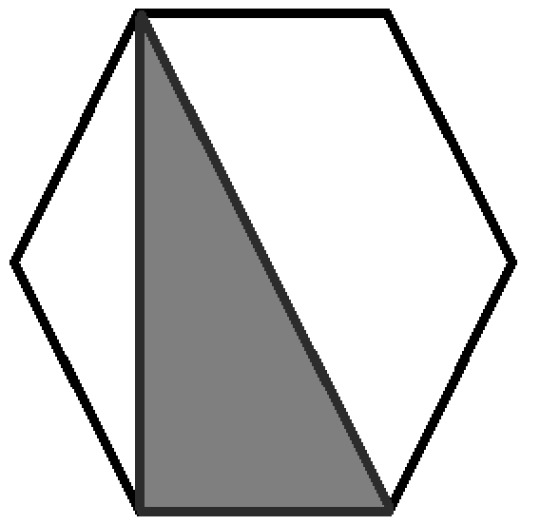
From here, you have a few options that work, but my personal favourite, and I think the simplest, is to split the hexagon into many shapes, like so:

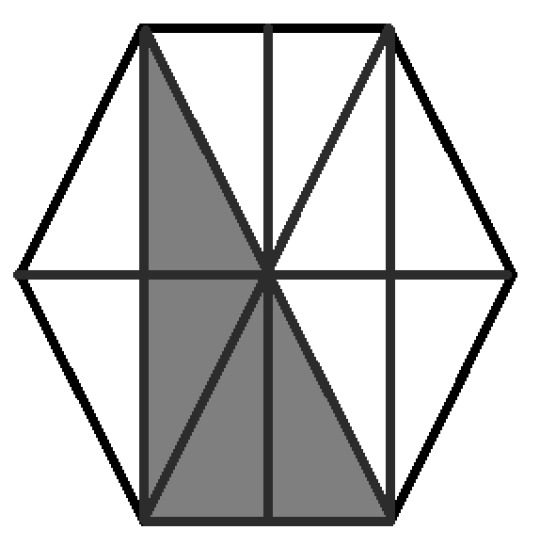
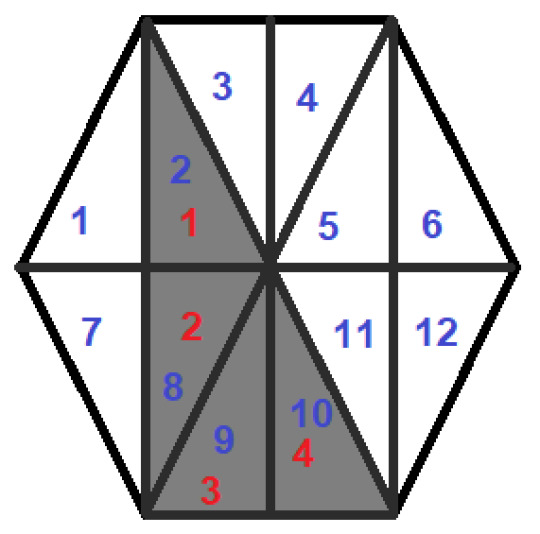
and suddenly it becomes a lot easier to count :P

So the fraction of the hexagon shaded is:

⁴⁄₁₂ = ⅓

and that is your answer ^w^

You can prove that all the triangles are the same (and therefore that this answer is correct) using the fact that a hexagon is made up of 6 equilateral triangles. We then cut the triangles in half and use that grid to measure the fraction of the shape that is shaded. This means that all the smaller right angled triangles must be equal in area, and therefore that our answer holds ^w^

(You can also solve this using trig, but I find that more boring :P)

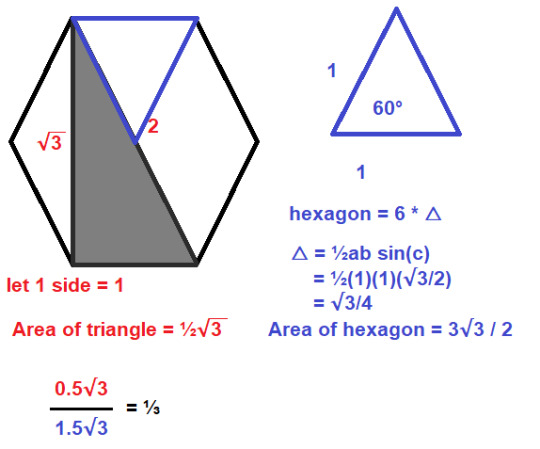
Thanks for reading ^w^

[autisticaroace]

Here's a math problem related to the current year:

[autistobrat]

I will somehow figure it out :D

i figured out what ails me. it is, in fact, less fun to learn math by doing "trust me bro this works" and then finding out later why it works, and more fun to learn math by building up to the theorems without already expecting them at the start, i think

[hapless-studyblr]

electric circuit fundamentals + coffee

[i-am-a-woman-in-stem]

12th october : 10/100 days of productivity

create a quizz with basics probability law

finish studying class notes of my probability class

review some old exercises of my probability class

It's been a while since I updated the challenge, but I am still going at it!

I did take a break during one weekend because exam season is starting for me and I needed it before the rush haha.