#theta持って出かけよう

[kanakitoblr-blog]

鶴岡八幡宮 #theta360 #thetagram #thetaのある生活 #theta持って出かけよう #thetaを持って出かけよう #ricohtheta #thetas #360度カメラ #360photo #360camera #360photography #littleplanet #tinyplanet #torii #kamakura #tsurugaokahachimangu #shrine #鶴岡八幡宮 #寺社巡り #鎌倉 #鎌倉八幡宮 (Tsurugaoka Hachimangū)

[folkboys]

🌹バラの惑星🌹 美しいと棘は我慢出来ますか？ #richo #thetas #theta360 #littleplanet #リトルプラネット #360度カメラ #360camera #360 #360degree #theta360contest #thetaのある生活 #シータのある生活 #thetaを持って出かけよう https://www.instagram.com/p/ByJZFKzAfqs/?igshid=1dwt45t0m7agc

[shin-kackey]

夜が更けて空が快晴になりました。 おりひめ星とひこ星見れましたよ！。。。多分(笑) 我が家は田舎ですけど、天の川が見える程真っ暗で空気が澄んだな田舎じゃ無いのでこんなもんです。(^^;) 願い事はカープが。。。あっ！ダメだっ💦思い出した。(>o<) もう少しハッピーな気持ちになる願い事。。。うーん。。。 そんな七夕の夜。 明日からまた一週間が始まる。。。どんどん思い気持ちになるw #theta #ricoh #thetaのある生活 #七夕 #夜空　#ricohtheta #thetasc #おりひめ星　#ひこ星　#願い事出来ず　#もやもやしたまま　#星空 #星空撮影 https://www.instagram.com/p/BznqR2QBqTM/?igshid=1b1r2z7e0ha3h

[white7s]

K-1 II Silver Edition

買っちった。

去年から RICOH は元気ですね。GR や THETA を筆頭に、色々発売されています。

今回の Silver Edition は K-1 の Limited Edition とは違い、シャッターボタンとホットシューが黒くなり、よりメリハリが出てきました。昔はデジカメの銀色って野暮ったく見えるなと思っていたのですが、気がつくと Silver Edition の虜になっていました。全世界1000台中の1台が我が家に・・・。

そして、勢いに乗って、全世界 600 本限定の D FA☆ 50mm F1.4 も同時購入しました。

レギュラーモデルとは違い、金環はありません。落ち着いた銀と黒で構成され、マウント付近の緑ラインがいいアクセントになっています。

K-1 II Silver Edition との組み合わせは最高です。 まさか D FA☆ レンズまで銀装になるとは思ってもみませんでした。

私は 2016年発売の K-1 から PENTAX を使っています。しかもアップグレードサービスを利用したので実質 mark II です。

K-1 は私的にとても使いやすく、いろいろ旅に出て色々な風景を撮って来ました。その模様は「ph音（ふぉと）」にも不定期にあげています。

もちろん D FA☆ 50mm も買って、PENTAX 最高の高画質を楽しんでいました。

では、なぜ今回 Silver Edition を購入したのか。

いくつか理由はありますが 「PENTAX の作ったシルバーモデルはかっこいいから」 というのが一番の理由��す。まだ手に馴染んでないからか、グリップの革の質感や、ボタンの感触が新鮮です。

さて、手元には K-1 改 と K-1 II があります。D FA☆ 50mm も2本。我ながらどうかしていると思いますが、RICOH さんには今後も一眼レフ開発を頑張って欲しいと思っています。

レギュラーモデルについては併用するか入れ替えるか、もう少し検討します。Silver Edition 購入翌日に撮影に出かけたのですが、2台持ちは大変撮影が捗りました。ボディは残そうかな・・・

ということで、これからも PENTAX と写活を楽しみたいと思います。

（こう見ると、MX がおもちゃに見えますね・・・）

[jf3nka]

AlphaGo Zero: Learning from scratch

　私たちが聴きとったニューラルネットワークの懇願は、どうやら空耳ではなかったようだ。

　AlphaGo Zero。

　Nature 550 (19 October 2017) に掲載された “Mastering the game of Go without human knowledge” と題するDeepMindの新論文は、ヒトの知識に依拠しない、文字通り「ゼロ」からの機械強化学習による取り組みだった。（日本語要約）

　ヒトの棋譜を教師として学習したAlphaGoの前バージョン（イ・セドル、柯潔など世界の強豪を退けたもの）を遙かに凌ぐ実力を示すことが報告されている。また、学習の過程においてヒトが長年を費やして見出してきた囲碁の定石も再発見したが、これとは別に見つけた新定石の方を好む傾向があること、 ヒトの思考とは異なる戦略を学習している可能性があることなども報告されている。

　実装レベルでは、従来のAlphaGoが備えていたふたつの深層ニューラルネットワークの機能をひとつのネットワークに統合。また従来版が対局時に併用していた線形識別器による高速ロールアウトを廃し、ニューラルネットワークの推論のみによって打ち進めるとしている。

　以下は論文の概要メモ。

背景/AlphaGo Zeroの特徴

　人工知能の進歩の多くは、専門家の決定を再現するように訓練された教師付き学習システムとしてもたらされた。一方、以下の難点もあった。

教師データセットのコスト高、入手難、低信頼性

教師自体がシステム性能のボトルネックになってしまう可能性

これに対し、強化学習システムは自分の経験のみによって訓練され、ヒトの能力を超えることを可能にし、ヒトの専門知識が不足している領域でも高い性能を発揮できると期待される。

事実、近年は強化学習によって訓練された深層ニューラルネットワークを用いたシステムが、この目標に向かって急速に進歩している。

　従来のAlphaGoは囲碁の領域でヒトの能力を凌駕した初のプログラムとなった。2015年にFan Hui（ファン・フイ）に勝った「AlphaGo Fan」は、ふたつの深層ニューラルネットワークを使っていた。

ポリシー・ネットワーク（ある盤面に対し最善手を推論する）

バリュー・ネットワーク（ある盤面に対しどちらが勝つかを推論する）

ポリシー・ネットワークは最初はヒトの棋譜を正確に真似るよう、教師付き学習によって訓練され、続いてAlphaGo同士の自己対戦による強化学習を用いて精度を高めた。バリュー・ネットワーク���、ポリシー・ネットワークによる対戦結果を予測するように訓練された。

訓練が完了すると、これらのネットワークをモンテカルロツリー探索（MCTS）と組み合わせて先読みを行い、ポリシー・ネットワークによって勝つ確率の高い着手を絞り込み、バリュー・ネットワークによる盤面評価を（高速ロールアウト・ポリシーを用いたロールアウト実行と併用して）行う。

このアプローチを適用した 次のバージョン 「AlphaGo Lee」は、2016年3月にLee Sedol（イ・セドル）を破った。

これらの従来版AlphaGoに対し、「AlphaGo Zero」は次の3つの特徴を備える。

ヒトの知識や棋譜を参照せず、ランダムプレイを起点とする自己対戦強化学習のみによって訓練される

盤面の入力として黒石と白石の配置情報だけを用いる1

盤面の評価と着手の決定は、単一のニューラルネットワークによる単純なツリー探索のみによって行う（モンテカルロ・ロールアウトは実行しない2）

AlphaGo Zeroの強化学習

　AlphaGo Zeroに実装された深層ニューラルネットワーク3は、盤面s を入力とし、パラメータθ を用いて以下の出力を得る。

\[(\boldsymbol{p},v) = f_{\theta}(s)\]

　　ｐ：ポリシー・ベクトル （最善手の確率分布。盤面sから着手aを選択すべき確率 　　　　pa = Pr(a|s)として定義されるベクトル値） 　　v：勝利確率 （スカラ値）

このニューラルネットワークは、従来のAlphaGoが備えていたポリシー・ネットワークとバリュー・ネットワークの役割をひとつのアーキテクチャに統合したものである。

AlphaGo Zeroのニューラルネットワークは、自己対戦にによる新たな強化学習アルゴリズムを用いて以下のように訓練される。

Figure 1

Figure1 a　自己対戦中の着手決定 盤面sにおいて、その時点の最新のfθ を使ってMCTS（モンテカルロ木）探索により着手を決定する（Figure2参照）。MCTSは各着手の最善度確率分布πを出力する。終局面sTでは勝利者z が記録される。敢えてニューラルネットワークfθ とは別にモンテカルロ木のπを用いる理由は、訓練が済んでいないfθ よりも良い着手を選択する可能性が高いため。

Figure1 b　ニューラルネットワークの訓練 各盤面st においてニューラルネットワークの出力 (pt, vt) = fθ(st) も評価する。 パラメータθ は、ポリシーベクトルpt とMCTS確率πt との類似性を最大に、予測勝者vt と実際の勝者z との間の誤差を最小にするように更新する（下記式（1）参照）。更新されたパラメータは次の自己対戦に反映され、以降これを繰り返す。

　学習中のニューラルネットワークのパラメータθ の更新は、以下の式で与えられる損失関数l （平均二乗誤差と交差エントロピー損失の合計）を確率的勾配降下法を用いて最小化するように行う。

\[l=(z-v)^{2}-\pi^{T}\\log \boldsymbol{p}+c{\Vert \theta \Vert}^2\qquad (1)\]

ここでc は過学習防止項（L2ノルム）を制御するパラメータである。

以上のように、MCTSは強力なポリシー改善オペレーターの役割を果たし、自己対戦は強力なポリシー評価オペレーターの役割を果たす。

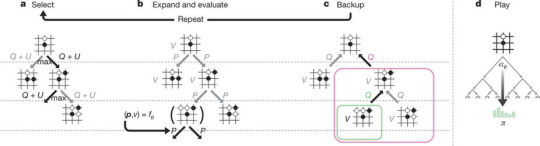
Figure 2

Figure 2 a 　着手の選択 この部分の考え方はAlphaGo Funとほぼ同じである。 探索木の各エッジ(s, a)は、事前確率P(s, a)、訪問回数N(s, a)、及び着手価値Q(s, a)を記憶している。 1回のシミュレーションは、あるルートノードs0 から始まり、時間ステップL 後に到達するリーフノード（未展開のリーフ）sL で終了する。その間 の （t ≤ L）各ステップ毎に Q(s,a)+U(s,a) で計算するUCB（Uppoer Confidence Bound：信頼上限）価が最大となる着手at を選択していく。

\[a_{t}=\mathrm{argmax}(Q(s_{t},a)+U(s_{t},a))\]

なおU(s, a) はPUCTアルゴリズムの変形を使って求める。

\[U(s,a)=c_\mathrm{puct}P(s,a)\frac{\sqrt{\textstyle \sum_{b}N(s,b)}}{1+N(s,a)}\]

cpuctは探索レベルを決める定数。学習の浅い段階では事前確率が高く、かつ訪問回数の少ない着手を優先的に選び（未発見の最善手を効率よく探索するため）、漸進的に高価値の着手に近づける戦略をとる。

Figure 2 b 　ツリーの拡張と盤面評価 リーフノードsL に達すると状態をキューへ登録するが、その盤面はミラー反転(x2)、ローテーション(x4)操作を行った計8通りの対称配置（di, i =1,2,...8）の中から無作為にひとつ���選ぶ。キューが8エントリ（ミニバッチ数）分溜まると、ニューラルネットワークによる盤面評価を起動する。 なお、評価実行中は探索スレッドはインターロックされる。

\[(d_{i}(\boldsymbol{p}),v) = f_{\theta}(d_{i}(s_{L}))\]

リーフノードを下へ拡張し、評価結果の出力ベクトルp を盤面sL から出ていくエッジに格納する。

Figure 2 c　バックアップ シミュレーション期間 (t ≤ L） の各ステップ毎にツリーを逆方向にたどってエッジの統計値を更新する。訪問回数をインクリメントし、

\[N(s_{t},a_{t}) = N(s_{t},a_{t})+1\]

着手価値Q はサブツリーすべての評価結果Vの平均値が反映されるように更新する。

\[Q(s,a) = \frac{\textstyle \sum_{s'|s,a \rightarrow s'}V(s')}{N(s,a)}\]

ここで s,a→s' は局面s から着手a を選択した後、シミュレーションが最終的にs' に到達したことを示す。

Figure 2 d　対戦 探索が完了すると、累積訪問数に比例して、ルートノードs0 に対する最善着手確率πが得られる。

\[\pi(a|s_{0}) = \frac{N(s_{0},a)^{1/\tau}}{\textstyle \sum_{b}N(s_{0},b)^{1/\tau}}\]

ここでT は探索レベルに応じた温度パラメータである。探索木は次の時間ステップで再利用される。今度はそこで選択された着手に対応する子ノードが新たなルートノードとなり、 そのの下のサブツリーが統計値と共に保持され、残りのツリーは破棄される。以降、これを繰り返す。

AlphaGo ZeroのMCTSはいかなるロールアウトも使用ないという点でAlphaGo FanおよびAlphaGo Leeと異なっている。対局時のAlphaGo Zeroはニューラルネットワークによる評価以外の演算を行わない。なお、ここで得られたMCTSのテーブル値は後述の40ブロック版にも流用されている。

学習結果の分析

　訓練は完全にランダムな着手から始めて、ヒトの介入なしで約3日間継続した。その間、MCTS探索毎に1,600のシミュレーションを実行し、490万局の自己対戦を行った。これは一手あたりの思考時間 0.4秒に相当する。

ニューラルネットワークは20ブロックのResNetで構成されている。

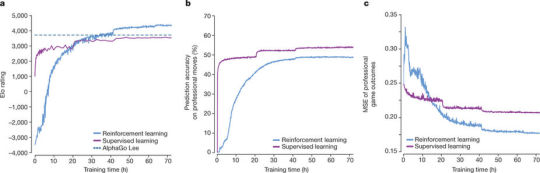
Figure 3

Figure 3 a 自己対戦による強化学習中のAlphaGo Zero（Reinforcement learning）の性能の推移をEloスケールで示している（青色。紫は同一ネットワークに対する教師付き学習の推移）。 AlphaGo Zeroは学習開始から36時間後にAlphaGo Leeを上回った。 72時間の訓練後、AlphaGo LeeとAlphaGo Zeroの対戦評価（持ち時間2時間。その他の条件も��ウルで行われたGoogle-Deepmindチャレンジマッチと同一）を行ったところ、100-0でAlphaGo Zeroが勝利した（棋譜例はExtended Data Fig. 1を参照）。

Figure 3 b KGS囲碁サーバ上の棋譜に対する再現度（ヒトの着手をどのくらい真似できているか）を評価した。教師付き学習（紫）は良い初期性能を達成し、プロ棋士の着手を精度高く予測した。一方、自己学習型のAlphaGo Zero（青）は訓練開始から24時間後には教師付き学習（紫）を破っている。 この事実は、AlphaGo Zeroがヒトの思考とは質の異なる戦略を学習している可能性があることを示唆している。

Figure 3 c 同じ棋譜を用いて各ニューラルネットワークfθi の勝敗予測値vと実際の勝敗結果z との平均二乗誤差を評価した。

Figure 4

Figure 4 a AlphaGo Zeroの性能向上をもたらした要因を調べるために4種類のニューラルネットワークを用意した。

dual-res     p/vネットワーク統合、ResNet （＝AlphaGo Zero）

sep-res      p/vネットワーク分離、ResNet

dual-conv   p/vネットワーク統合、ConvNet

sep-conv    p/vネットワーク分離、ConvNet （＝AlphaGo Lee）

AlphaGo ZeroとAlphaGo LeeのEloレーティング値には約1,200の開きがある。このうち約600（半分）がネットワークを従来のConvolutional型からResidual型へ変えたことの効果、残りの600がポリシー・ネットワーク(p)とバリュー・ネットワーク(v)をひとつのネットワークに統合したことの効果。

Figure 4 b KGS囲碁サーバ上の棋譜に対する再現度（ヒトの着手をどのくらい真似できているか）を評価した。

Figure 4 c 同じ棋譜を用いて各ニューラルネットワークfθi の勝敗予測値vと実際の勝敗結果z との平均二乗誤差を評価した。

AlphaGo Zeroが学んだ知識

　AlphaGoが自己対戦を通じて学び取った囲碁の知識には、ヒトが習得済みのものだけではなく、伝統的な知識の範囲を超える戦略も含まれていた。

Figure 5

Figure 5 a AlphaGo Zeroが5種類の既知の「隅の定石」を見つけた時期をタイムライン上に示している。（時間軸に対する出現頻度はExtended Data Fig.2を参照）

Figure 5 b これらの5種類の隅の定石は、訓練中の異なる段階で高頻度で出現した。学習開始から10時間後には囲碁の形にならない手を好んだ。47時間後には3-3定石が最も多く打たれた。これはプロ棋士も打つ形だが、AlphaGo Zeroはこの後で別のバリエーションを発見し、最終的にはそれを好むようになった。（ 時間軸に対する出現頻度は Extended Data Fig.3を参照）

Figure 5 c 訓練中の異なる段階で行われた自己対戦の棋譜を示している。 学習開始から3時間後にはヒトの初心者���ように相手の石を取ることだけに集中し、19時間後には死活、地合いを理解した。70時間後にはコウを含む複雑な複数の攻め合いを含むバランスの取れた戦いを見せた。 （Extended Data Fig.4も参照）

　AlphaGo Zeroは完全にランダムな動きから学習を始め、より洗練された囲碁の考え方の理解に向けて急速に進歩した。布石、死活、コウ、ヨセ、攻め合い、先手、形、地合い、といった概念も最初の基本原理だけから習得した。 意外にもシチョウ（ヒトが学んだ囲碁の基礎知識のひとつ）の習得だけは遅い段階だった。

AlphaGo Zeroの最終性能 

　最終的にニューラルネットワークの構成を40ブロックのResNetへ拡張し、40日間の学習を行った。その間の自己対戦数は2,900万局である。

Figure 6

Figure 6 a AlphaGo Zero（40ブロック版）の学習曲線を示している。（学習期間中に定期的に行われた自己対戦の棋譜はExtended Data Fig.5を参照）

Figure 6 b 各プログラムのEloレーティング比較。「Raw network」はAlphaGo Zeroの先読み機能を外した状態の参考値。

Alpha Go Zero：5,185

AlphaGo Master：4,858

AlphaGo Lee：3,739

AlphaGo Fan：3,144

 　「Alpha Go Zero」と「AlphaGo Master」の自己対戦結果（持ち時間2時間）は89-11であった。（棋譜の一部はExtended Data Fig.6、棋譜アーカイブを参照）

まとめ

　純粋な強化学習のアプローチが実現可能であることを示した。

　ヒトの知識や指導がなくとも、基本ルールだけに基づいてヒトを超えるレベルにまで訓練することが可能であることが分かった。AlphaGo Zeroはヒトのデータから訓練されたAlphaGo Master（AlphaGoの最も強力な従来バージョン）の性能を大きく凌駕した。

　人類は何千年もの間に行われた無数の対局から囲碁の知識を蓄積し、それを定石、ことわざ、書籍などに蓄積してきた。 AlphaGo Zeroはタブラ・ラーサ（tabula rasa：白紙状態）を起点として、数日間の間にその多くを再発見した。また、この最古のゲームに新たな洞察を付け加える戦略も発見した。

AlphaGo Zeroにおけるニューラルネットワークへの入力情報は「19x19x17」の画像スタック。 19x19：碁盤の座標に対応 x17：座標毎の下記ベクトル情報 　　si=[Xt, Yt, Xt-1, Yt-1, ..., Xt-7, Yt-7, C] 　　　　Xt: 時刻t、座標iにおける対局者Xの石の有無（0:なし 1:あり） 　　　　Yt: 時刻t、座標iにおける対局者Yの石の有無（0:なし 1:あり） 　　　　C: 石の色（0：白 1:黒） 8手分の履歴情報が必要な理由：現盤面だけからでは次の着手を決定できないため��“コウ”の規則） 石の色情報が必要な理由：囲碁のルールが白と黒で非対称なため（“コミ”の規則） これに対し従来版AlphaGoは「19x19x48」の画像スタックを入力しており、その中にはアタリ（取ることができる/取られる石数）、ダメ（呼吸点数）、シチョウ（シチョウアタリ/脱出可能）、禁則手/自殺手などの情報、すなわち盤面の客観情報以外の付帯情報（一定の解釈を帯びた情報）が含まれていた。

従来のAlphaGoはふたつのニューラルネットワーク（ポリシーネットワーク、バリューネットワーク）とは別に、やや精度を犠牲にして推論速度を稼いだロールアウト・ポリシーpπを備えていた。対局時にはこれを用いたロールアウトをバリューネットワークの推論と並行して実行し、両方の結果を盤面評価に使っていた。 （従来版のように精度は高いが計算時間の遅いネットワークと、精度は劣るが計算時間の速いネットワークを併用するシステム仕様は、実戦投入の必要性、すなわち持ち時間制約の有無と計算機資源量、信頼性確保、等々のバランスで決まっていたと想像する。AlphaGo Zeroとても、仮に“絶対に負けられない”実戦へ投入されるとしたら、何らかのダイバーシティ実装（冗長性）が求められるのではないだろうか）

AlphaGo Zeroのネットワーク構成 入力層　 　(1) 3x3（ストライド1）の畳み込みフィルター 256枚 　(2) バッチ正則化 　(3) 活性化関数 中間層 以下のシーケンシャル構成をもつ残差ブロック19個（or 39個） 　(1) 3x3（ストライド1）の畳み込みフィルター 256枚 　(2) バッチ正則化 　(3) 活性化関数 　(4) 3x3（ストライド1）の畳み込みフィルター 256枚 　(5) バッチ正則化 　(6) 残差入力のスキップ接続 　(7) 活性化関数 出力層 中間層の出力が2系統に分岐し、ポリシーヘッドとバリューヘッドへ接続される 。 [ポリシーヘッド] 　(1) 1x1（ストライド1）の畳み込みフィルター 2枚 　(2) バッチ正則化 　(3) 活性化関数 　(4) 全結合（19x19+1=362ノード出力。19x19の碁盤座標と一手パスに対応） [バリューヘッド] 　(1) 1x1（ストライド1）の畳み込みフィルター 1枚 　(2) バッチ正則化 　(3) 活性化関数 　(4) 全結合（256ノード出力） 　(5) 活性化関数 　(6) 全結合 　(7) Tanh関数（勝率を[-1,1]レンジのスカラ値として出力 ） したがって全体のネットワーク深度は以下のようになる。 　20ブロック版 ： 畳み込み x 1層 + 畳み込み x 2層 x 19ブロック = 39層 　40ブロック版 ： 畳み込み x 1層 + 畳み込み x 2層 x 39ブロック = 79層 これにポリシーヘッド系統は2層（畳み込み1層＋全結合1層）、バリューヘッド系統は3層（畳み込み1層+全結合2層）が加わる。

[fxcfdlabo]

トレンドを見極める方法の一つとして、オシレーターでギャンファンを利用してみよう！AXIORYで、Autochartistを利用しよう！！

株式投資や、為替取引をするとき、価格の強気下落中の下降トレンドへの投資は、かなり人気のある長期戦略です。なぜなら、安売りバーゲンセールだからです。日本円を売って米ドルを買うという通貨ペア 「USD / JPY」や、もしくは、長期の強気トレンドにある他の通貨ペアに注目し、下落してジャンプするのを待ちます。通貨ペアが低いときに買い、上昇トレンドが続き、利益確定を待ちます。 しかし、「安く買って高く売ればいい」と口で言うのは簡単ですが、安値で通貨を買って、逆に損失が膨らんだというトレーダーが多いのも現状です。 少しの価格下落が、ストップロス(ロスカット, 損切り)に達するまでどんどん強くなり、ストップロスされ、市場から強制退場させられます。 そして、思ったようにうまくいかない事象は、何でも間違ってしまうという「マーフィーの法則」が発動し、ストップロス(ロスカット, 損切り)された後、上昇し始め、損してしまうトレーダーもたくさんいます。 我々投資家に必要なのは、我々がいつ、通貨を買うという「エントリー」をして、強制ロスカットされることなく強気のトレンドに乗ることができるように、どのくらいの強い相場なのかを把握することです。 このブログの管理人がトレンドを見極めるのに効果的だと思う戦術の1つは、「ギャンファン」と「オシレーター」を組み合わせることです。 これにより、下落相場で通貨を購入する適切なタイミングを、より高い精度で予測できます。

全てのギャンファンには、オシレーターが必要だ

ギャンファンの仕組みは非常に簡単です。 下の図のように、トレンド全体のトレンドラインサポートとしてメインギャンラインを引き伸ばし、「ギャンファン」という概念を使用すると、上下の代替トレンドラインが得られます。 しかし、「ギャンファン」という概念を利用するときの一番の難しいことは、どの代替トレンドラインが実際に保持され、トレンドを継続できるかを判断することです。 「ギャンファン」を利用すると、今までよりもトレンドを見極めやすくなります。 それにもかかわらず、ギャンファンをオシレーターと組み合わせると、ギャンファンは、はるかに正確になります。 ギャンファンと同時に、使用できるオシレーターは、MACD、ストキャスティックオシレーター、移動平均オシレーターなどです。 以下の図を見ると、ギャンファンがトレンド��転換である可能性と思われる3つのポイント「A、B、C」を暗示していることがわかります。 A地点とB地点では、トレンドが上昇すると思われても下降してしまう「だまし」ですが、Cはトレンド転換点です。 C地点でのみ、オシレーターが負から正に移動し、運動量の変化を示唆し、これが真の支持線であることを示します。

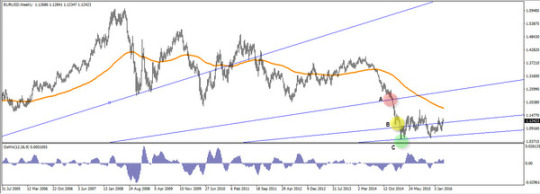
「だまし」を避ける3つのコツとは?

ギャンファンを利用するとき、他のテクニカル分析と同様に、「落とし穴」や「だまし」を見分けるために、最善の注意を払わなければなりません。 最も一般的な「だまし」を回避するためのいくつかのトリックを以下に示します。

ギャンファンのチェック

はじめに確認しなければならないことは、主要トレンドラインの上に「ギャンファン」のメインラインを描いたことです。 トレンドの転換点から、以下の図のようにギャンラインを描く必要があります。これは、以下の図に示すように、上昇トレンドか下降トレンドかを認識するための主な「トレンドライン」を目視して理解するのに役立ちます。

スキャルビングや、数分程度の短期トレードで「ギャンファン」を利用しない

「ギャンファン」を1時間以下の短い間隔で測定することは可能ですが、これらの短期間では、オシレーターの効果ははるかに低くなります。 また、オシレーターと併用することによってギャンファンの精度��向上するので、オシレーターがない短期間では、ギャンファンの精度が大幅に低下します。この場合は、「ギャンファン」は利用せずに、異なるストラテジーとテクニカル分析を使用しましょう。

通貨ペアに注意

オシレーターと親和性のある「ギャンファン」を使って分析する最大のリスクの1つは、トレンドが強気から弱気に変わった場合、ギャンの支持線や抵抗線を突破して価格が動いてしまうことです。 トレンドの変化を見極めることができない場合や、ペアが2〜3回、「ギャンファン」の支持線や抵抗線を上回らなかった場合には、警告サインが表示されます。 これは、ペアの抵抗が大きいことを示しています。 トレンドがまだ強気もしくは弱気であることを少なくとも二重にチェックした方がリスク回避につながります。トレンドの認識に対して確実な確信が持てない場合は、取引を一時期休止して、様子を見ることも必要です。

「ギャンファン」とは?

ギャンファンとは、株式取引やFX取引をするための取引市場の価格が、本質的に幾何学的かつ周期的であるという考えに基づいたテクニカル分析の一つです。 ギャンファンは、「ギャンアングル」と呼ばれる一連の線で構成されます。 これらの角度は、潜在的な支持線と抵抗線を示すために価格チャートに重ねられます。 以下の画像は、トレンドの変換点での、数分という短期間ではない近未来の価格の変化を予測するのに、「ギャンファン」が役立ちます。

ギャンファンの主なポイント

・ギャンファンは、W.D. Gannによって開発されました。 ・ギャンファンはトレンド転換点を原点とする「直線」です。 ユーザーが開始点を選択すると、線が未来に延長されます。 ・ギャンファンは、45°の角度を中心にして、度数法で表されたおおよその角度「82.5°、75°、71.25°、63.75°、26.25°、18.75°、15°、7.5°」を描写。 ・ギャンファンは、低または高ポイントで開始されます。 結果の行は、将来の潜在的なサポートと抵抗の領域を示しています。

ギャンファンがトレーダーに伝える内容とは?

トレンドの方向と強さを判断するために、中央の45度の線の上下に斜めの線が引かれています。 ギャンファンは。「W. D. Gann」によって開発されました。時間と価格のバランスに関する理論に基づいて、トレンドの転換点を原点として、そこから引いた直線から45度の角度がチャート作成に理想的な角度であるとW. D. Gannは、主張しています。 ギャンファンは、指定されたトレンド反転レベルから伸びる中央の45度の角度線から描画されます。トレーダーは反転点でギャンファンを引き寄せ、支持線と抵抗線の位置が、将来に拡大することを確認します。 ギャンファンの45度の角度線は、チャート上の45度の角度に揃える必要があります。 45度の角度を見つけるには、グラフ作成プラットフォームで角度ツールを使用します。

45度の線は1：1の線として知られています。これは、価格が単位時間ごとに1単位上下するときに価格が45度の角度で上下するためです。 ギャンファンファンの他のすべての線は、1：1の線の上下に描かれます。トレーダーは、ギャンファンチャートの1：1の線の上下にさまざまな数の線を使用できます。その他の角度は、2：1、3：1、4：1、8：1と、1：1の線の境にして、1：8、1：4、1：3、1：2の価格設定時間の動きに関連付けられています。 1：1行が主要な指標です。ただし、チャーティストは、独自の裁量で行を追加する選択肢があります。上昇トレンドと下降トレンドの両方で、1：1線は反転を検出するのに役立ちます。下降トレンドでは、1：1線を下回る価格は弱気とみなされます。上昇トレンドでは、1：1ラインを上回ったままの価格は強気と見なされます。したがって、1：1ラインは抵抗線およびサポート線として機能します。

ギャンファンが描かれた追加の線は、抵抗線およびサポート線としても使用されます。ギャンは、価格が1つの角度を移動した場合、次の角度に向かう可能性が高いと考えていました。たとえば、価格が45度の角度（1：1）を下回ると、26.25度の角度（2：1）に下がります。価格が1：1を下回っても、必ずしも全体的な上昇トレンドが終わったわけではありません。価格は2：1でサポートされ、その後上昇し続ける可能性があります。そうは言っても、価格が2：1の線に下がった場合、1：1未満の下落は少なくとも短期的な弱さを示す可能性があります。

ギャンファン利用時の「ギャンアングル」の計算方法

ギャンファンを利用するとき、傾斜角度である「ギャンアングル」\( \theta \)を理解しなければなりません。 \( xy \)平面に置ける格子点に置いて、 正方形の一片を単位時間とすると、その単位時間内に価格が正方形の高さまで上昇する場合、正方形の左下から右上に線を引くことができます。 その線の傾斜度は45°になります。 1つのボックスの高さを上げるのに2つの正方形が必要な場合は、2：1であり、上昇角度は45度よりも平坦になります。 1つのボックスの時間枠が1：2の間で価格が2つのボックスの高さまで上昇する場合は、その角度は45度よりも急な傾きになります。 ギャンファンには、価格と時間の比率の動きに基づく角度が次の比率で組み込まれています。 ・1：8の場合は「82.5°」 ・1：4の場合は「75°」 ・1：3の場合は「71.25°」 ・1：2の場合は「63.75°」 ・1：1の場合は「45°」 ・2：1の場合は「26.25°」 ・3：1の場合は「18.75°」 ・4：1の場合は「15°」 ・8：1の場合は「7.5°」 となります。この角度はテクニカル分析を利用している投資家にはよく知られている角度ですが、この角度は、厳密には違います。つまり、上記の角度は、数学的には、不正確なのです。 トレンド転換点からの単位時間を\( x\)とし、トレンド転換点からの価格を\(y \)とし、ギャンアングルを\( \theta \)とすると、以下の式が成り立ちます。 \[ \tan \theta=\frac{y}{x} \] この\( \theta\)を正確に求める必要があります。正確さこそが、トレンドを正確に測るのに必要だからです。 任意の実数\(x \)に対して、\(\tan x \)は、周期\( \pi \)を持ち、任意の整数\( n\)に対して、\(x= \frac{\pi}{2}+n\pi \)では定義することはできません。そこで、\(-\frac{\pi}{2} \[ \frac{d}{dx}(\tan x)=\frac{1}{\cos^{2}x} > 0 \] が成り立つので、狭義単調増加します。したがって、関数\( f(x)=\tan x \)を表す写像 \[ f: ( -\pi /2, \pi /2 ) \rightarrow ( -\infty, \infty ) \] は、全単射となるので、任意の実数\( y\)に対して、\( y=\tan x \)となる\( x\in ( -\pi /2, \pi /2 ) \)がただ一つ存在します。したがって、\( \tan x \)は、\(-\frac{\pi}{2} すると、トレンド転換点からの単位時間\( x\)と、トレンド転換点からの価格\(y \)に対して、求めるギャンアングル\( \theta \)は、 \[ \theta =\arctan \frac{y}{x} \] となります。よく知られている値は、 \[ \begin{eqnarray} &\arctan 1=\frac{\pi}{4},\ \arctan \frac{1}{\sqrt{3}}=\frac{\pi}{6},\ \arctan \sqrt{3}=\frac{\pi}{3},\ \arctan 0=0&\\ &\arctan (-1)=-\frac{\pi}{4},\ \arctan \left(-\frac{1}{\sqrt{3}} \right)=-\frac{\pi}{6},\ \arctan (-\sqrt{3})=-\frac{\pi}{3}&\\ \end{eqnarray} \] ぐらいです。つまり、任意の実数\( x\)に対して、\( \arctan x \)を具体的に求めるのは、難しいと思われます。そこで、以下の冪級数を利用します。 \[ \arctan x=\int_{0}^{x}\frac{dt}{1+t^{2}}=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{2n+1}x^{2n+1}, \quad (-1\leq x \leq 1) \] しかし、上記の冪級数は、\(-1\leq x \leq 1 \)でしか定義されていないので、\(x \[ \arctan x+\arctan \frac{1}{x}=\frac{\pi}{2} \] が成り立つことを利用すれば、\(x すると、以下のように、比較的に精度の高いギャンアングルが得られます。 \[ \begin{eqnarray} &\arctan \frac{1}{8}=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{2n+1} \left(\frac{1}{8} \right)^{2n+1}=0.1243549945\cdots &\\ &\arctan \frac{1}{4}=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{2n+1} \left(\frac{1}{4} \right)^{2n+1}=0.2449786631\cdots &\\ &\arctan \frac{1}{3}=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{2n+1} \left(\frac{1}{3} \right)^{2n+1}=0.3217505544\cdots &\\ &\arctan \frac{1}{2}=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{2n+1} \left(\frac{1}{2} \right)^{2n+1}=0.463647609\cdots &\\ &\arctan 2=\frac{\pi}{2}-\arctan \frac{1}{2}=1.107148718\cdots &\\ &\arctan 3=\frac{\pi}{2}-\arctan \frac{1}{3}=1.249045772\cdots &\\ &\arctan 4=\frac{\pi}{2}-\arctan \frac{1}{4}=1.325817664\cdots &\\ &\arctan 8=\frac{\pi}{2}-\arctan \frac{1}{8}=1.446441332\cdots &\\ \end{eqnarray} \] となります。ここで注意すべきことは、上記で計算した\( \arctan\)の値が、実数値(弧度法)であり、度数法ではないということです。従って、上記の値に\( 180/\pi\)をかける必要があります。すると、 \[ \begin{eqnarray} &\arctan \frac{1}{8}=0.1243549945\cdots \times \frac{180}{\pi}=7.125016349\cdots ^{ \circ } &\\ &\arctan \frac{1}{4}=0.2449786631\cdots \times \frac{180}{\pi}=14.03624347\cdots ^{ \circ }&\\ &\arctan \frac{1}{3}=0.3217505544\cdots \times \frac{180}{\pi}=18.43494882\cdots ^{ \circ }&\\ &\arctan \frac{1}{2}=0.463647609\cdots \times \frac{180}{\pi}=26.56505118\cdots ^{ \circ }&\\ &\arctan 2=1.107148718\cdots \times \frac{180}{\pi}=63.43494882\cdots ^{ \circ }&\\ &\arctan 3=1.249045772\cdots \times \frac{180}{\pi}=71.56505118\cdots ^{ \circ }&\\ &\arctan 4=1.325817664\cdots \times \frac{180}{\pi}=75.96375653\cdots ^{ \circ }&\\ &\arctan 8=1.446441332\cdots \times \frac{180}{\pi}=82.87498365\cdots ^{ \circ }&\\ \end{eqnarray} \] となります。ギャンアングルの精度がかなり上がりましたが、小数点がずっと続いています。一体、上記の数がどのような数なのかをこの記事ではしっかりと調べていきます。 今、\( s > 0 \), \( t \geq 0 \)を整数として、0以上の整数\( n \)に対して、以下の漸化式を満たす数列\( \{a_{n} \}_{n=0}^{\infty} \)を以下のようにとります。 \[ \begin{eqnarray} &a_{0}=1,\ a_{1}=s&\\ &a_{n+2}-2sa_{n+1}+(s^{2}+t^{2})a_{n}=0& \end{eqnarray} \] また、\( 0 \[ \cos\theta=\frac{s}{\sqrt{s^{2}+t^{2}}}, \quad \sin\theta=\frac{t}{\sqrt{s^{2}+t^{2}}} \] を満たす定数とします。すると、\( s\)と \(t \)は整数なので、上記の漸化式に\( n\)に関する帰納法を適用することによって、\( a_{n}\)はすべての0以上の整数\( n\)に対して、整数となることがわかります。では、上記の漸化式の一般項\( a_{n}\)を求めてみましょう。まず、数列\( \{\boldsymbol{x}_{n} \}_{n=0}^{\infty} \)を以下のようにとります。 \[ \boldsymbol{x}_{n}=\left( \begin{array}{c} a_{n} \\ a_{n+1} \\ \end{array} \right) \] すると、漸化式\( a_{n+2}-2sa_{n+1}+(s^{2}+t^{2})a_{n}=0 \)は、以下のように行列を用いて表されます。 \[ \boldsymbol{x}_{n}=A\boldsymbol{x}_{n-1}\quad (n\geq 1) \] ただし、 \[ A=\begin{pmatrix} 0 & 1 \\ -(s^{2}+t^{2}) & 2s \end{pmatrix} \] です。すると、 \[ \boldsymbol{x}_{n}=A \boldsymbol{x}_{n-1}=A^{2} \boldsymbol{x}_{n-2}= \cdots =A^{n}x_{0} \] となるので、\( A^{n}\)を求めればいいことがわかります。まず、行列\( A\)を対角化(Jordan標準形)してみましょう。今、0でないベクトル\(\boldsymbol{p} \)に対して、 \[ A\boldsymbol{p}=\lambda \boldsymbol{p} \] とおきます。すると、ベクトル\(\boldsymbol{p} \)は0ではないので、行列式 \[ \det (\lambda I -A)=\lambda^{2}-2s\lambda +s^{2}+t^{2}=0 \] を満たします。この式を行列\( A\)の特性多項式と言い、特性多項式の根\(\lambda \)を固有値、\(A\boldsymbol{p}=\lambda \boldsymbol{p} \)となるベクトル\( \boldsymbol{p}\)を固有ベクトルと言います。では、オイラーの公式\( e^{i\theta}=\cos\theta+i\sin\theta\) (ただし、\(i=\sqrt{-1} \) )を利用してこの特性多項式を解くと、固有値は、 \[ \lambda=\sqrt{s^{2}+t^{2}}e^{i\theta},\quad \sqrt{s^{2}+t^{2}}e^{-i\theta}, \] となります。すると、\(\lambda=\sqrt{s^{2}+t^{2}}e^{i\theta} \)に対する固有ベクトルの一つは、 \[\left( \begin{array}{c} 1 \\ \sqrt{s^{2}+t^{2}}e^{i\theta} \\ \end{array} \right)\] となり、\(\lambda=\sqrt{s^{2}+t^{2}}e^{-i\theta} \)に対する固有ベクトルの一つは、 \[ \left( \begin{array}{c} 1 \\ \sqrt{s^{2}+t^{2}}e^{-i\theta} \\ \end{array} \right)\] となります。この2つの固有ベクトルは、互いに一次独立なので、対角化可能となります。したがって、正則行列\( P\)を \[ P=\begin{pmatrix} 1 & 1 \\ \sqrt{s^{2}+t^{2}}e^{i\theta} & \sqrt{s^{2}+t^{2}}e^{-i\theta} \end{pmatrix} \] とおくと、 \[ P^{-1}AP=\begin{pmatrix} \sqrt{s^{2}+t^{2}}e^{i\theta} & 0 \\ 0 & \sqrt{s^{2}+t^{2}}e^{-i\theta} \end{pmatrix} \] となるので、 \[ P^{-1}A^{n}P=\begin{pmatrix} (\sqrt{s^{2}+t^{2}})^{n}e^{in\theta} & 0 \\ 0 & (\sqrt{s^{2}+t^{2}})^{n}e^{-in\theta} \end{pmatrix} \] となります。したがって、 \[ \begin{eqnarray} A^{n}&=&P\begin{pmatrix} (\sqrt{s^{2}+t^{2}})^{n}e^{in\theta} & 0 \\ 0 & (\sqrt{s^{2}+t^{2}})^{n}e^{-in\theta} \end{pmatrix}P^{-1}\\ &=&\frac{1}{\sin\theta}\begin{pmatrix} -(s^{2}+t^{2})^{\frac{n}{2}}\sin((n-1)\theta) & (s^{2}+t^{2})^{\frac{n-1}{2}}\sin(n\theta) \\ -(s^{2}+t^{2})^{\frac{n+1}{2}}\sin(n\theta) & (s^{2}+t^{2})^{\frac{n}{2}}\sin((n+1)\theta) \end{pmatrix} \\ \end{eqnarray} \] したがって、\( \cos\theta=\frac{s}{\sqrt{s^{2}+t^{2}}}, \quad \sin\theta=\frac{t}{\sqrt{s^{2}+t^{2}}}\)の関係と\( \boldsymbol{x}_{n}=A^{n}x_{0} \)の関係から、 \[ a_{n}=(s^{2}+t^{2})^{\frac{n}{2}}\cos(n\theta) \] となります。ここで、すべての0以上の整数\( n\)に対して、\( a_{n} \)が\( \sqrt{s^{2}+t^{2}}\)の整数倍ではないとき、\( \frac{\theta}{\pi}\)は、無理数になります。背理法で示しましょう。実際に、\( \frac{\theta}{\pi}\)が有理数だと仮定します。すると、 \[ \frac{\theta}{\pi}=\frac{q}{p},\quad (ただし、p > 0とqは互いに素な整数) \]とかけます。すると、\( \theta=\frac{q}{p}\pi \)なので、 \[ a_{n}=(s^{2}+t^{2})^{\frac{n}{2}}\cos \left(\frac{nq}{p}\pi \right) \] となります。すると、すべての0以上の整数\( n\)に対して、\( n=kp \)となる整数\(k \)が存在するので、 \[ \cos \left(\frac{nq}{p}\pi \right)=\cos(kq\pi )=(-1)^{kq} \] となり、この時、\( a_{n}=(-1)^{kq}(s^{2}+t^{2})^{\frac{n}{2}}\)となり、\( a_{n}\)は、\( {\sqrt{s^{2}+t^{2}}}\)の整数倍となってしまいます。これは、すべての0以上の整数\( n\)に対して、\( a_{n} \)が\( \sqrt{s^{2}+t^{2}}\)の整数倍ではないという仮定に矛盾します。 まとめると、以下のことが言えます。

\( s > 0 \), \( t \geq 0 \)を整数として、0以上の整数\( n \)に対して、以下の漸化式を満たす数列\( \{a_{n} \}_{n=0}^{\infty} \)を与えます。 \[ \begin{eqnarray} &a_{0}=1,\ a_{1}=s&\\ &a_{n+2}-2sa_{n+1}+(s^{2}+t^{2})a_{n}=0& \end{eqnarray} \] また、\( 0 \[ \cos\theta=\frac{s}{\sqrt{s^{2}+t^{2}}}, \quad \sin\theta=\frac{t}{\sqrt{s^{2}+t^{2}}} \] を満たす定数とすると、 \[ a_{n}=(s^{2}+t^{2})^{\frac{n}{2}}\cos(n\theta) \] となり、すべての0以上の整数\( n\)に対して、\( a_{n}\)は整数となり、特に、\( a_{n}\)が\( \sqrt{s^{2}+t^{2}}\)の整数倍ではないとき、\( \frac{\theta}{\pi}=\frac{1}{\pi}\arctan\left(\frac{t}{s}\right)\)は、無理数になります。言い換えれば、\( \frac{\theta}{\pi}=\frac{1}{\pi}\arctan\left(\frac{t}{s}\right)\)が有理数になる時、\( a_{n}\)が\( \sqrt{s^{2}+t^{2}}\)の整数倍となる0以上の整数\( n\)が存在するということです。

すると、1:1以外の上記のギャンアングルは、すべて無理数であることがわかります。例えば、 \[ \arctan \frac{1}{8}=0.1243549945\cdots \times \frac{180}{\pi}=7.125016349\cdots ^{ \circ } \] を見てみましょう。\(s=8, t=1 \)の場合なので、\(\sqrt{s^{2}+t^{2}}=\sqrt{65} \)となり、 \[ \frac{a_{1}}{\sqrt{65}}=\frac{1}{\sqrt{65}}=\frac{\sqrt{65}}{65}, \quad \frac{a_{2}}{\sqrt{65}}=\frac{8}{\sqrt{65}}=\frac{8\sqrt{65}}{65} \] となり、\( a_{1}, a_{2}\)は共に\( \sqrt{65}\)の整数倍ではありません。そして、\( a_{n}, a_{n+1}\)が共に\( \sqrt{65}\)の整数倍ではないと仮定すると、 \[ a_{n+2}=16a_{n+1}-65a_{n}\equiv 16a_{n+1} \mod \sqrt{65}\mathbb{Z} \] であり、(ただし、\( \mathbb{Z}は整数の集合\)) \[ \frac{16}{\sqrt{65}}=\frac{16\sqrt{65}}{65}\not\equiv 0 \mod\sqrt{65}\mathbb{Z} \] なので、\( a_{n+2} \)は、\( \sqrt{65} \)の整数倍にはなりません。したがって、\( n\)に関する帰納法から、全ての0以上の整数\( n\)に対して、\( a_{n} \)は、\( \sqrt{65}\)の整数倍にはなりません。つまり、\( \frac{1}{\pi}\arctan \frac{1}{8}\)は無理数となります。

Axioryは、真の意味で「無料で」オートチャーティストが使える

オートチャーティストとは、トレードチャンスを自動検知できるメタトレーダーのプラグインツールで、トレーダーに、取引するための正しい判断をもたらしてくれる便利なツールです。Axioryにライブ口座を持つだけで一定以上の金額を入金しなくても、無料で利用できます。 1日24時間、数千ものの金融商品を監視する検索エンジンが、チャート・パターン、フィボナッチ・パターン、キー・レベルの3つの方法で、ユーザーのプラットフォームに取引シグナルをリアルタイムでお届けします。この3つ以外にも、オートチャーティストではボラティリティ分析も提供します。これらの統計情報を元に、トレーダーは自信をもって、利益確定や損切りの設定ができるようになります。そして結果的にリスクとボラティリティのより良い判断につながります。

オートチャーティストを使うメリットとは?

・チャート分析の技術的な能力を身につけられる 大量のデータを分析し、それらをあらゆるチャート・パターン、フィボナッチ・パターン、キー・レベル、およびボラティリティ分析に加工します。それと同時に高度なカスタマイズが可能です。オートチャーティストの多様な利用方法を学ぶには少し時間がかかります。しかし、Axioryでは、オートチャーチスとの使い方を映像で用意しているので、以下の動画をご覧ください。

・チャート分析の時間の節約 オートチャーティストは、取引するタイミングをなるべく早くAxioryのクライアントに通知するので、日々の取引タイミングを決して逃させません。またテクニカル分析にかけていた時間の節約にもなります。

AxioryのAutochartistの詳細はこちらから

Axioryでのオートチャーティストの使い方

Axioryでは、WindowsバージョンとMacバージョンの2種類が用意されています。

・Windowsバージョン

1.　こちらからオートチャーティストの「ダウンロードページ」に入り、［Download Plugin］をクリックしてください。

2.　ファイル［Autochartist MTEA Setup］をダウンロードしてください。 3.　ダウンロードしたファイル［Autochartist MTEA Setup］をクリックして開いて、言語設定［ 日本語（日本）］を選択してください。 4.　【Autochartist MetaTrader Expert Advisor セットアップウィザードへようこそ】というタイトルのセットアップ画面が表示されますので、［次へ(N) ＞ ］をクリックしてください。

5.　使用許諾契約（プライバシーポリシー、免責事項、利用規約）のチェックボックスに✔を入れ同意し［次へ(N) ＞ ］をクリックしてください。 6.　MT4プラットフォームを選択してください。チェックボックスに✔を入れて選択します。（すべて選択の場合は、すべて選択に✔を入れて選択） ※リストに無い場合には追加、表示以外で追加したい場合には次をさらに追加して［次へ(N)＞］をクリックしてください。 ※選択せずに［次へ(N) ＞ ］をクリックされますと、少なくとも1つの保存先フォルダを選択してください。というエラーメッセージが表示されます。 7.　次に下記のページへと移行されます。よろしければ［次へ(N)＞］をクリックしてください。 ※注意：Autochartist MetaTraderプラグインファイルがインストールされる前に、 MetaTraderターミナルはシャットダウンされます。 8.　インストール準備完了と表示されましたら、［インストール(I)］をクリックしてインストールを開始してください。

9.　インストール画面が表示されますので ［Yes］をクリックしてください。 10. インストールが完了しましたらMT4を再起動してください。 パソコン内「non-Unicode Programs」 の設定を日本語に設定ください。 EAのバージョン167かそれ以上のものをお使いの場合、MT4の言語設定も日本語に設定ください。既に英語バージョンをインストールされている方で日本語でのご利用をご希望の場合は、一度オートチャーティストをアンインストールの上、再度日本語バージョンをインストールください。 MT4を立ち上げて頂き、ナビゲーターのエクスパートアドバイザーの下にありますAutochartistよりご確認下さい。

また、毎日の市場予想のメールマガジンを希望の場合は、MT4を立ち上げた際に表示されるメールマガジンの申込フォームへ、メールアドレスを入力してください。メールマガジンを希望しない場合は、表示されているウインドウをクリックしたまま上にドロップして、申込フォームを消去ください。

・Macバージョン

1. こちらからファイルをダウンロードしてください。 2, ターミナルを開いてください（command + space、そこにTerminalと入力してください） 3. 以下のコマンドをTerminalにコピー＆ペーストしてEnterキーを押してください。 ・この時点で、隠しファイルや隠しフォルダが見えるようになるはずです。 4. 「Macintosh HD」→「ユーザー」→「ユーザー名」→「ライブラリ」（右クリックして新しいタブで開くを選択してください）「アプリケーションサポート」→「com.AxioryGlobal.MT4_123456」→「Cドライブ」→「プログラムファイル」→「Axiory MetaTrader 4」→「MQL4」 5. ダウンロードしたファイル「MQL4」を「Axiory MetaTrader 4」フォルダにコピーして貼り付けます（「MQL4」フォルダを新しくダウンロードしたものに置き換えます）。 6. MT4を再起動してください。 7. ナビゲータウィンドウの「エキスパートアドバイザ」の下にオートチャーティストがあります。次の手順に従ってWebリクエストを有効にする必要があります。 8. メニューのToolsをクリックしてください。 9.Optionsをクリックしてください。 10.Expert advisors タブをクリックしてください。 11.「リストされたURLに対するWebRequestを許可する」の横のボックスをクリックします。 12.「新しいURLを追加」をダブルクリックして、次のWebアドレスを貼り付けるか入力します。 http://direct.autochartist.com/aclite/jsp/DirectLogin.jsp https://direct.autochartist.com/aclite/jsp/DirectLogin.jsp https://mt4.autochartist.com/ この段階ではオートチャーティストはMT4で使えるようになっています。この時点で、オートチャーティストがインストールされていますので、確認してください。

AxioryのAutochartistをこちらから利用する

AXIORYは、透明性の高いデータを赤裸々に公開

AXIORYは、スリッページの発生率や約定スピードの分布など、取引するときに、必要なデータをウェブサイトで赤裸々に公開しています。Axioryが顧客の取引を邪魔したり、恣意的にスプレッドを大きくしたりしていないという明確な根拠を示しています。

Axioryの概要

運営会社Axiory Global Ltd設立年2013年7月31日営業拠点No. 1 Corner of Hutson Street and Marine Parade, Belize City, BelizeライセンスIFSC No.IFSC/60/255/TS/19預託証拠金の取り扱い (分別管理、預託金保険)完全信託分別管理(全額保証)最大レバレッジ400:1最小(初回)入金額20,000円, 200USD口座通貨建��EUR, GBP, JPY, USD追証ゼロカット対応なので追証なしマージン・コール50%ロスカット20%約定モデルECN, STP, NDD日本語対応のサポートデスク日本語対応口座タイプスタンダード口座、ナノスプレッド口座 MultiTrader, Multi Account Manager 入出金方法国内銀行送金(by Curfex), 海外銀行送金, クレジットカード(VISA), SticPay, bitpay取扱金融商品CFD取引, FX取引コモディティ (商品取引), 原油 (石油、オイル), 株価指数 (株式指数、Index、Indices), 貴金属(金、Gold)取扱通貨ペアAUD/CAD, AUD/CHF, AUD/JPY, AUD/NZD, AUD/USD, CAD/CHF, CAD/JPY,CHF/JPY,EUR/AUD, EUR/CAD, EUR/CHF,EUR/CZK,EUR/GBP,EUR/HUF, EUR/JPY,EUR/NOK,EUR/NZD,EUR/PLN, EUR/SEK,EUR/USD,GBP/AUD,GBP/CAD, GBP/CHF,GBP/JPY,GBP/NZD,GBP/USD, NZD/CAD,NZD/CHF,NZD/JPY,NZD/USD,USD/CAD, USD/CHF,USD/CZK,USD/HUF,USD/JPY,USD/NOK, USD/PLN,USD/SEK,XAG/USD,XAU/USD 計40ペア (取扱通貨ペア) 取引プラットフォームMetaTrader4(MT4), cTrader, Webトレーダー(by Fortex), MultiTrader ・Fortexによって提供されているWebTraderとcTrader Webは、全てのOSに対応。ソーシャルトレードMultiTrader 10万ドル以上の証拠金の残高がある方限定なので敷居が高い表示桁数5桁取引単位1Lotあたり100,000通貨最小取引単位0.01ロット=1,000通貨

こちらからAxioryのライブ口座を持つ

source http://kaigai-invest.blog.jp/axiory/autochartist/gann_fan

[tak4hir0]

はじめに 千葉県柏市に住む織姫と埼玉県越谷市に住む彦星は恋人同士です. 二人の間には江戸川が流れていますが, 橋は何本も架かっているので, 行き来にこれと言った不便はありません. 至って順調に見える二人の関係でしたが, ある日, 織姫は海外転勤を言い渡されてしまいました... 今日は七夕ということで, 遠距離恋愛を題材に, 「距離」というものについて再考したいと思います. 2点間の距離 2019年3月, 織姫は越谷, 彦星は柏で暮らしていました. 越谷 - 柏 まず, 越谷と柏の間の「距離」をGoogle Mapで調べてみました. ある地点で右クリックをすると"Measure Distance"と出てきます. 結果は「16.87 km」でした. これを経度と緯度から計算することを考えます. Euclid距離 以後, 越谷と柏の座標は次の表で定めます. 経度は東, 緯度は北を正の方向とします. 都市名 経度 $\lambda$ 緯度 $\phi$ 越谷 139.970779 35.862065 柏 139.786040 35.888076 この座標は球面座標表示になっているので, 地球の半径を$R=6378.1 \mathrm{km}$として, 次のように直交座標に変換します(手書きの図で失礼します). \begin{align} x &= R\cos{\phi}\cos{\lambda}\\ y &= R\cos{\phi}\sin{\lambda}\\ z &= R\sin{\phi} \end{align} $p_1=(x_1,y_1,z_1)$と$p_2=(x_2,y_2,z_2)$のEuclid距離は次の式で定めます. $$ D_{Euc}(p_1, p_2) = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2 + (z_1-z_2)^2} $$ Pythonだと次のように書けます. def euclidize(degs): lamda, phi = np.radians(degs) x = R * np.cos(phi) * np.cos(lamda) y = R * np.cos(phi) * np.sin(lamda) z = R * np.sin(phi) return np.array([x,y,z]) def euclidian_dist(pol1, pol2): euc1 = euclidize(pol1) euc2 = euclidize(pol2) diff = euc1 - euc2 return np.sqrt(np.dot(diff, diff)) ori = [139.970779, 35.862065] hiko = [139.786040, 35.888076] euclidian_dist(ori, hiko) 16913.382975766835 結果は16.91kmでした. 測地線距離 越谷を点A, 柏を点B, 地球の中心を点Oとすると, 先ほど求めたEuclid距離は線分ABと対応します. しかし, このように地球を貫く経路は現実的でないので, 実際には弧ABの長さを求めたいです. $\angle \mathrm{AOB} = \theta$とすると, 球面上での測地線距離は次の式で定められます. $$ D_{geo}(R, \theta) = R\theta $$ Pythonで計算します. def geodesic_dist(pol1, pol2): d_euc = euclidian_dist(pol1, pol2) theta = 2 * np.arcsin(d_euc/2/R) return R * theta geodesic_dist(ori, hiko) 16913.387931385758 結果は変わらず「16.91km」でした(少しだけ大きくなりました). 今回は$\theta$が小さかったので, 弧ABは線分ABでよく近似できたということですね. Manhattan距離 Google Mapで2地点間の「道のり」を測ると「20.9km」でした. このような距離の測り方に対応するものとしてManhattan距離があります. Manhattanのような通りが格子状に走っている街で2地点間の「道のり」を表す距離で, 次の式で定められます. 詳しくは[3]をご覧ください. $$ D_{Man}(p_1, p_2) = |x_1-x_2| + |y_1-y_2| + |z_1-z_2| $$ Euclid距離のときに定めた直交座標系に沿って格子状の道が走っていると仮定した場合の越谷 - 柏間のManhattan距離は次のように計算されます(地球サイズのクレーンゲームで越谷から柏にクレーンを移動させるときの軌跡の長さを想像してください). def manhattan_dist(pol1, pol2): euc1 = euclidize(pol1) euc2 = euclidize(pol2) diff = euc1 - euc2 return np.sum([np.abs(d) for d in diff]) manhattan_dist(ori, hiko) 26030.942586314864 結果は「26.03km」でした. Chebyshev距離 座標の各成分の差分の絶対値の最大値をChebyshev距離と呼び, 次の式で定義されます. $$ D_{Cheb}(p_1, p_2) = \max{ (|x_1-x_2|, |y_1-y_2| ,|z_1-z_2|) } $$ Pythonでは次のように計算されます. def chebychev_dist(pol1, pol2): euc1 = euclidize(pol1) euc2 = euclidize(pol2) diff = euc1 - euc2 return np.max([np.abs(d) for d in diff]) chebychev_dist(ori, hiko) 12035.805316988379 結果は「12.03km」でした. Minkowski距離 ここまでに紹介したEuclid距離, Manhattan距離, Chebyshev距離は, すべてMinkowski距離 (Lp距離) の特別な場合と考えることができます. Minkowski距離は次で定められます. $$ D_{Min}(p_1, p_2) = \Bigl(\sum_{i}(|p_{1i}-p_{2i}|^p)\Bigr)^{1/p} $$ $p=1,2,\infty$の場合にそれぞれManhattan距離, Euclid距離, Chebyshev距離となります. 詳しくは[4]をご覧ください. ラバト - 柏 2019年4月, 織姫はモロッコのラバトにあるオフィスに転勤することになりました. 遠距離恋愛の始まりです. 2人の距離はどのくらいになるでしょうか？ 都市名 経度 $\lambda$ 緯度 $\phi$ ラバト -6.855500 34.002235 柏 139.786040 35.888076 前節で定義した関数で計算した結果をまとめて示します. 距離関数 距離[km] 測地線 11519.65 Manhattan ($p=1$) 13335.16 Euclid ($p=2$) 10016.52 Chebyshev ($p=\infty$) 9195.70 同じ座標でも, Lpノルムの$p$の値を大きくすると距離は小さくなることが確認できます. Chebyshev距離で考えれば2人の距離が小さくなるということです！ 確率分布間の距離 少し見方を変えて, 二人がそれぞれ点ではなく確率分布であると考えてみましょう. 12ヶ月のうち, 織姫は2ヶ月を越谷, 9ヶ月をラバト, 1ヶ月を柏で過ごし, 彦星は1ヶ月を越谷, 2ヶ月をラバト, 9ヶ月を柏で過ごすとして, 電子雲のように各地点において分布として存在するイメージです. 確率分布をヒストグラムで表すと次のようになります. # [koshigaya, rabat, kashiwa] ori = np.array([2, 9, 1])/12 hiko = np.array([1, 2, 9])/12 plt.figure(figsize=(8,6)) plt.bar([1,2,3], ori, width=0.4, label='orihime') plt.bar([1.4,2.4,3.4], hiko, width=0.4, label='hikoboshi') plt.xticks([1.2, 2.2, 3.2], ['koshigaya', 'rabat', 'kashiwa']) plt.xlabel('city') plt.ylabel('probability') plt.legend() plt.ylim([0,1]) plt.grid() plt.show() Kullback–Leibler距離 確率分布間の距離を測るための関数として最も有名なのはKullback–Leibler距離 (KLダイバージェンス; KL情報量; 相対エントロピー) でしょうか. 位置を表す確率変数を$X$として, 織姫と彦星の分布関数をそれぞれ$p(x), q(x)$とすると, $p$と$q$のKL距離は次で定められます. $$ D_{KL}(p||q) = \int_{-\infty}^{\infty}p(x)\log{\frac{p(x)}{q(x)}}dx $$ これは$p$と$q$の情報量の差の$p$に関する期待値を取ったもので, 確率値の配列を引数にとる関数として簡単に書けます. def kl_dist(p, q): return sum(p * np.log(p/q)) ただし, KL距離は式の形を見て分かる通り, $p$と$q$に関して非対称です. 実際に計算すると, print('ori-hiko:', kl_dist(ori, hiko)) ori-hiko: 1.06048052956 print('hiko-ori:', kl_dist(hiko, ori)) hiko-ori: 1.33947660183 となります. KL距離は距離の公理 : $D(x,y)\geq0$ (非負性) $D(x,y)=0 \iff x=y$ (同一律) $D(x,y) = D(y,x)$ (対称律) $D(x,z)\leq D(x,y)+D(y,z)$ (三角不等式) のうち対称律と三角不等式を満たさないため, 厳密には距離関数ではありません(そのため「ダイバージェンス」と呼ばれ���す). Jensen-Shannon距離 KL距離の非対称性を克服したものとしてJensen-Shannon距離 (JSダイバージェンス) が提案されています. \begin{eqnarray} m(x) &=& \frac{p(x)+q(x)}{2}\\ D_{JS}(p||q) &=& \frac{D_{KL}(p||m) + D_{KL}(q||m)}{2} \end{eqnarray} こちらも簡単に実装できます. 対称性も確認しましょう. def js_dist(p, q): m = (p+q)/2 return (kl_dist(p,m)+kl_dist(q,m))/2 print('ori-hiko:', js_dist(ori, hiko)) ori-hiko: 0.260817818792 print('hiko-ori:', js_dist(hiko, ori)) hiko-ori: 0.260817818792 JS距離も三角不等式を満たさないため, 厳密には距離関数ではありません. Wasserstein距離 KL距離の定義式を見てみると, $\log{\frac{p(x)}{q(x)}}$に$q(x)=0$になるような$x$があればゼロ除算になってしまいますし, $p(x)=0$になるような$x$があれば$\log0$となってしまうことがわかりますが, これは計算を非常に不安定にします. このような観点からより安定性の高い距離関数として, Wasserstein距離 があります. W距離は直感的には, 確率分布を砂山だとみなし, 砂山$p$を別の砂山$q$に変形させるときにかかる最小コスト(質量×距離)です. earth mover's distance (EMD) とも呼ばれます. W距離は, $p(x)$と$q(x)$のすべての可能な同時分布を$\Pi(p,q)$として, その中での輸送距離の期待値の下限として定められます. $$ D_W(p, q) = \inf_{\gamma \sim \Pi(p, q)} \int_{(x, y) \sim \gamma}| x-y |dxdy $$ これを実装するには最小化問題を解かなければならないため少し厄介です. SciPyにはW距離が実装されているようですが, 球面上で使うのは大変そうだったので, ここはアドホックに解くことにします. 図のように, 越谷とラバトから織姫の余分な砂を柏に持っていけば, 最小コストで彦星と同じ砂山ができます. koshigaya = [139.970779, 35.862065] kashiwa = [139.786040, 35.888076] rabat = [-6.855500,34.002235] earth_koshigaya = ori[0]-hiko[0] earth_rabat = ori[1]-hiko[1] w_dist = earth_koshigaya*geodesic_dist(koshigaya, kashiwa) + earth_rabat*geodesic_dist(rabat, kashiwa) print(w_dist) 6721207.71245 W距離は単位をmとしてもよいでしょう. ということで, 結果は「6721.21km」でした. 測地線距離の平均 もっと素朴なアプローチとして, 2人を動点として2点間の測地線距離の時刻に関する平均をとることもできます. 先程示した確率分布を満たしながら2人がなるべく近くにいられるようにすると, 例えば4月から3月まで ori = [koshigaya, rabat, rabat, rabat, rabat, rabat, rabat, rabat, koshigaya, kashiwa, rabat, rabat] hiko = [koshigaya, kashiwa, kashiwa, rabat, rabat, kashiwa, kashiwa, kashiwa, kashiwa, kashiwa, kashiwa, kashiwa] のように動くことができます. このとき, 測地線距離の平均は, np.mean([geodesic_dist(o,h) for o,h in zip(ori, hiko)]) 6721207.7124540322 結果はW距離と等しい「6721.21km」になりました. 2人の動き方次第でこの値は変わりますが, W距離はこの「測地線距離の時間平均」の最小値を与えています. 確率分布間の距離には他にもL2距離やPearson距離などがあるようですが, 単位をmにできるものは私の知る限りこのくらいです. おわりに 様々な距離関数を考えることで, 織姫と彦星の距離を「11519.65km」から「6721.21km」まで減らすことができました. ひとくちに「遠距離恋愛」といっても, いろいろな距離がありますね. 距離関数 距離[km] 測地線 11519.65 Manhattan ($p=1$) 13335.16 Euclid ($p=2$) 10016.52 Chebyshev ($p=\infty$) 9195.70 Wasserstein 6721.21 七夕なので短冊を飾って本記事の結びとします. 高い目標ではありま��が, 精進を続けて参ります…！ ーーーーーー |　　　数　| |　　　学　| |　を　と　| |　完　コ　| |　全　ン　| |　に　ピ　| |　理　ュ　| |　解　｜　| |　で　タ　| |　き　｜　| |　ま　サ　| |　す　イ　| |　よ　エ　| |　う　ン　| |　に　ス　| ーーーーーー 参考文献 [1] 【Day-23】機械学習で使う"距離"や"空間"をまとめてみた - プロクラシスト いろいろな距離をまとめた表があり, 参考にさせていただきました. [2] 杉山将, "確率分布間の距離推定 : 機械学習分野における最新動向", 日本応用数理学会論文誌, 2013. [3] マンハッタン距離 - Wikipedia Manhattan距離は通りが直交するManhattanでの移動距離にちなんで名付けられたそうです. [4] ノルムの意味とL1，L2，L∞ノルム | 高校数学の美しい物語 単位円の図がわかりやすいです. [5] Lilian Weng, "From GAN to WGAN", 2017. GANの文脈でKL距離, JS距離, W距離の違いを解説したブログで, 非常にわかりやすかったです. [6] 小林昭七, "曲線と曲面の微分幾何", 裳華房, 1995. 球面上でW距離などを考えるのに役立ちそうですが, そこまでたどり着けませんでした. どなたか続きをお願いします笑

[0kuribito]

Theta Network(シータ)仮想通貨とは?取扱取引所での買い方や今後の将来性!

https://www.bulimbaoztag.com/theta-network-cryptocurrency-exchange/

Theta Network(シータ)仮想通貨とは?取扱取引所での買い方や今後の将来性!

テレビよりもYou TubeやNetflixを見る時間が長くなり、テレビ見逃しもTverやAbemaTVなども活用するとスマホやテレビでいつでも見れる時代になりすごく便利ですね♪

「子供の将来の夢のNO1はYouTuber！」と言われ、日本でも人としての多様性（個性）をより活かせて活躍できる時代へと移り変わってきたと思うと「ホッ」としますよね♪

今回は、動画配信の非中央集権化を行うサービスを提供している「Theta Network(シータ)仮想通貨の特徴」や「取り扱い取引所での買い方から今後の将来性」などについてお伝えしていきます。

時代は4Kから「8KやVR」の時代へと移り変わってきている中、視聴者としても演者としてもコストを掛けずに楽しめるシステムをチェツクしてみてくださいね♪

  Theta Network(シータ)仮想通貨の特徴

名称 Theta Network(シータ ネットワーク) 通貨単位 Theta 仮想通貨ランキング 50位（2020.6月現在） プラットフォーム Ethereum タイプ ERC-20 発行日 2018年1月 発行上限数 10億枚（Theta） ホワイトペーパー 開発組織

Theta Labs Inc

特徴

非中央集権的な動画サイトの構築

SILVER.tvとの提携

有名な機関投資家が出資

Theta Network(シータ)とは、Ethereumプラッツフォーム上に構築されたERC20トークン��構成されたストリーミングネットワーク（ビデオ配信ネットワーク）「DNS」です。

プラッツフォーム上の分散型アプリケーション（DApps）を構築し、E-スポーツ・音楽・TV・映画・などのストリーミングを楽しむことができます。

既存プラットフォームとの大きな違いは、視聴者のコンピューターの空き容量を活用して視聴者も「ThataやTFUEL」で報酬を得ながら閲覧でき、提供者（広告主）も報酬を得られる仕組みを提供しています。

広告主（コンテンツ所有者）は、視聴者やストリーミングサイト、インフルエンサーをサポートするためにトークンを消費する

ユーザーはストリーミングを視聴者に中継するためのトークンをマイングする

視聴者も広告主から報酬を受け取るためにマイニング可能で、コンテンツ作成者を応援するためにトークン提供もできる

このようにThataを利用する上で利害関係をもたらすすべての参加者が参加する価値の有る動機があり「4K・8K・VR」時代を活躍できるプラットフォームが提供されているのです。

プロジェクトメンバーも「SilverTVのCEO」や「Twichの共同創業者」などの業界著名人が含まれ信頼性も高いプロジェクトでもあり日本でのThata取り扱いも可能にできるように金融庁とも協議しています。

今後、日本の取引所で取り扱いが決定した暁には、今以上に大きな値動きを見せることでしょう♪

  Theta Network(シータ)仮想通貨チャートから見る今後の将来性

2017年価格推移 11.69円～32.51円（1Theta） 2018年価格推移 7.08円～29.52円（1Theta） 2019年価格推移 4.97円～17.80円（1Theta） 2020年価格推移 5.37円～48.55円（1Theta）

Theta Network(シータ)仮想通貨の将来性は、大手企業やベンチャー企業からの資金調達にも成功していることもありチームの技術力評価も信頼も高いプロジェクトです。

Silverのプロダクト開発を行っている主力メンバーがThataストリーミングプロジェクトを行っているから実現可能な案件のため投資家も資金提供をしやすいからです。

ストリーミング業界に精通したメンバーで構成され技術力も高いからICO前の資金調達にも成功したということですよね！

ブロックチェーン上のゲーム配信プラットフォームのTHATA.TVがサムスン（Samsung）の新型スマートフォンに搭載されていることもあり、需要も今後大きく増えてくる予定で仮想通貨業界にとっての追い風を起こすプロジェクトとなっています！

実現可能性も有効性も実用性も高くプレイや閲覧するすべての人にとってThataトークンが感動を世界中に浸透させる日は近いかもしれませんね♪

  Theta Network(シータ)を取り扱いしている仮想通貨取引所　TOP4

Theta Network(シータ)取り扱い仮想通貨取引所①「OKEX」

名称 OKEX取引所（オーケーイーエックス） 取引の種類 現物取引・レバレッジ取引・先物・C2C取引・スポット取引 最大レバレッジ 10倍 仮想通貨の種類 144種類 通貨ペア 390通貨ペア 手数料 メーカー0.1％・テイカー0.15％ 日本語対応 サポート スマホアプリ

OKEX取引所公式サイト

OKEX取引所の登録方法

https://www.bulimbaoztag.com/okex-register/

取り扱いペア

Theta/USDT・Theta/BTC

  Theta Network(シータ)取り扱い仮想通貨取引所②「Binance」

取引所名 バイナンス（Binance） 取り扱い通貨数 193通貨、取引通貨ペア577種類 取引方法 現物取引、レバレッジ取引 最大レバレッジ 最大125倍 取引手数料 0.1% サポート 日本語対応 IEO通貨取引

バイナンス公式サイト

Binance取引所の登録方法

https://www.bulimbaoztag.com/binance-register-login/

取り扱いペア

Theta/USDT・Theta/BTC・Theta/ETH・Theta/BNB

  Theta Network(シータ)取り扱い仮想通貨取引所③「BKEX」

名称 BKEX取引所 取引の種類 現物取引・OTC取引 仮想通貨の種類 140種類 通貨ペア 193通貨ペア 手数料 メーカー0.15％・テイカー0.2％ 日本語対応 サポート スマホアプリ

BKEX取引所キャンペーン公式

BKEX取引所の登録方法

https://www.bulimbaoztag.com/bkex-exchange-registration-login-bkk-dividend/

取り扱いペア

Theta/USDT・Theta/ETH

  Theta Network(シータ)取り扱い仮想通貨取引所④「HOTBIT」

ホットビット（Hotbit）取引所 取引の種類 現物取引 仮想通貨の種類 500種類 通貨ペア 938通貨ペア 手数料 0.2% 日本語対応 サポート スマホアプリ

Hobit（ホットビット）キャンペーン公式サイト

HOTBIT取引所の登録方法

https://www.bulimbaoztag.com/hotbit-register-login/

取り扱いペア

Theta/BTC・Theta/ETH

  Theta Network(シータ)の買い方（購入方法）

日本国内の仮想通貨取引所の登録「bitFlyer・GMOコイン」がおすすめ

日本国内の仮想通貨取引所で「BTC（ビットコイン）」購入

Theta取り扱いしている海外仮想通貨取引所の登録

海外仮想通貨取引所のKYCや二段階認証設定などを完了させる

「日本国内の仮想通貨取引所」から「海外の仮想通貨取引所」へビットコインを送金する

「Theta／BTC」という組み合わせを探して「BTC→Theta」にかえる

Theta購入完了

①～②国内の仮想通貨取引所の口座開設

https://www.bulimbaoztag.com/bitflyer-register/

③～⑦国外の仮想通貨取引所の口座開設

https://www.bulimbaoztag.com/okex-register/

  Theta Network(シータ)仮想通貨の口コミ・評判

  THETAヤバイ！

THETAとTFUELヤバイなww これぞ仮想通貨って動きしてる

— Glad (@gladeeee78) May 21, 2020

投資すべき銘柄

仮想通貨アルト考察

BTCやXRP以外あまり年間成長率を見てない方が多いですけど、前年度対比ではBTCで5%プラスくらい。

XRPは55%マイナスくらい。

中堅アルトですごいヤツは比較にならないくらいすごい。$LINK $XTZ $THETA

調べてみたら分かりますよ、これが昨年から投資すべき銘柄だったのかと。

— hiro (@uSWyMfHQsbrQ2v2) May 28, 2020

Theta急騰中！

3月の仮想通貨情報 どうにか3末までに 色々やりたいプロジェクトが多い

その中でもちょっと 気になった通貨$THETA と $ZEN どちらも3月はバ��バタしそう 前者は既に急騰中だが 後者は…🧐

— ニイタク@BTCFX (@niizeki_BTC) March 2, 2019

  よくあるQ&A

  SILVER.tvについて詳しく教えて下さい。

eスポーツの動画配信プラットフォーム「SILVER.tv」ではそのサイト構築にThetaのブロックチェーンフォームが活用されています。すでに多くのユーザーによって人気ゲームが配信されており、ios版、android版のアプリも公開されています。

出資している有名な機関投資家とは誰ですか？

日本、アメリカ、EUとイスラエル圏で投資を行うソニーイノベーションファンドが投資家として名が挙げられています。その他にもGREE、韓国からはサムスンが出資しています。

  まとめ

  今回は、次世代ストリーミングプラットフォームを開発提供行っている「Theta Network(シータ)仮想通貨の特徴や今後の将来性」などについてお伝えしてきました。

大手のサムスン社の新型スマートフォンにTHATAプラットフォームが搭載され現実的に仮想通貨プロジェクトが人々の生活の中に浸透させようとする大きな動きが始まっています。

仮想通貨の大きなウネリは、仮想通貨マイニングの企業のオーナーや仮想通貨大口保有者などの世界を動かす影響力を持っている存在によって動かされている側面もありウネリに逆らうことが現実的に不可能な勢力でもあります。

仮想通貨が確実に世界経済を動かす存在に成り代わることは決定していることでもあり、この現実を信じて（先読みして）動いたものが勝者となることでしょう。

あなたは時代のウネリに逆らい今の不自由な生活水準にしがみ付き続けますか？

You Tubeと共存する世界を作るTHATAがもたらす未来に勝者ありですよ♪

[takachan]

4K動画も撮れる3万円台のエントリー360度カメラ「THETA SC2」の実力は？

Engadget 日本版 YouTubeチャンネルより。 最近はVRカメラの高解像度競争が激化していますが、広く普及するためにはお求めやすいモデルも必要ですよね。 今回ご紹介するのは元祖360度カメラTHETAの新しいエントリーモデル「THETA SC2」です。名前の通りTHETA SCの後継機種にあたり、従来のエントリーモデル同様に4色展開。直販価格は税込み3万6800円です。 今回は女性ユーザーをイメージした「ネイルカラー」が採用され、お借りしたブルーの他に、ピンク、ベージュ、ホワイトから選べます。ベージュはエレガントな大人の女性に似合いそうです。 一番大きな違いは上位モデルのTHETA V同等の4K動画記録に対応したこと。ただし最長記録時間は3分までの制限がかかっています。 4K動画に目が行きがちですが、機能面もかなり洗練されてきました。新たにセルフタイマーボタンが追加され、本体のみでオンオフが可能。また状態表示用のOLEDで動作状況がひと目で分かるようになりました。特にバッテリー残量やセルフタイマーのカウントダウンが分かりやすいです。 モードは静止画／動画の他に「プリセット」が追加されました。オートでは難しかったシーンも簡単・綺麗に撮影することができます。用意されているのは「顔／夜景／車窓」の3つのプリセット。 ・顔モード：顔を検出し画像の中心に配置。人物を綺麗に撮影する。 ・夜景モード：ハイライト領域のダイナミックレンジを広げつつノイズを抑��。また顔検出により人物も綺麗に撮影可能。 ・車窓モード：前後カメラの露出／ホワイトバランスを独立して制御し、明るさが大きく異るシーンを撮影。 さらにホワイトバランスに「水中モード」が追加され、ダイビングなどでより自然な印象の撮影が可能となりました。 画像処理エンジンが変更されたこともあり、普通に静止画を撮影してもSCよりも締まった印象です。HDRアルゴリズムも変更され、派手さを抑えた自然な処理になりました。 THETA SC2 車窓モード #theta360 - Spherical Image - RICOH THETA ▲車窓モード THETA SC2 顔モード #theta360 - Spherical Image - RICOH THETA ▲顔モード THETA SC2 夜景モード #theta360 - Spherical Image - RICOH THETA ▲夜景モード THETA SC2 水中モード #theta360 - Spherical Image - RICOH THETA ▲水中モード 無線LAN接続でのスマホへのデータ転送が高速化されただけでなく、Bluetooth接続も可能となり軽快に撮影できるようになりました。Bluetoothリモコンからシャッターを切ることもできるそうです。 これだけ機能強化されながら従来機種と大きさは変わらないので、各種アクセサリー類も共用可能です。気軽に持ち歩いて、サッと取り出して、パッと撮影して、あとでじっくり楽しむ♪そんな使い方に向いているでしょう。 ▲THETA SC2 撮って出し360VR動画 しかし動画のスティッチ精度が悪いですね...今までこんなに悪くなかったので、これは何が原因なのでしょうか？お借りした機材固有の問題なのかは現時点では判明せず、ただいま原因を調査中です。 アップデートで早急に解決してくれることを望みます。それとTHETAの手ブレ補正はやっぱりこの程度が限界なんですかね？これもスティッチソフトのアップデートで精度を向上して欲しいです。 これらの問題点や動画記録時間3分という制限はあるものの、全体的にはTHETA Vよりも使いやすく感じました。ライトユーザーが増えるともっともっと楽しくなりそうです♪ http://j.mp/2M72ewh Engadget Japanese

[tehenisi]

(un)touchable world -ちょっとだけ宇宙に近いところでの話-

(twitterに投稿した、"(un)touchable world"と題した写真にまつわるお話のpart2。撮影したころの日記をベースに、それを振り返っていろいろ補記したものです。)

※part1(きっかけの話)はこちら

山に入るときは、いつもワクワクと恐怖がともにある。夜行となればもっともっとそうだ。自分が日頃どれだけ誠実に生きているかはわからないけれど、「下手したら死ぬ」、という思いは、やっぱり街で暮らしているときよりも山にいる時のほうが断然、敏感にそして大きくなっていると思う。 「怪我はもう完全に良くなっている、はずだし…、体力的にも問題はない、とは思うけれど…」久しぶりの歩きであることには違いないから、そういったちょっとした不安もいくつもあった。

ヘッドランプを灯し、鈴を鳴らしながら、お邪魔しますと山に入る。一応言っておくと、なんというか特別な山道ではない。晴れた日中であれば子ども連れでも登る道らしい。（こういう書き方をすると、少しの油断も許さないやまケイサツに取り締まられそうだが） 向かった山について、少し前にその地方であった荒天のせいで山道が荒れていたらやだなぁと思っていたけれど、そんなことはなかった。これは率直に少し驚いた。もちろん地質とかによるものが大きいとは思うけれど、よく整備された道はこうなのかも知れない、とも思った。

このクラスの山道には不釣り合いな大きなザックを背負って歩く。撮影が目的なので大切な機材も結構詰めてある、あとおやつも多めだ。 そして胸元のサブのスマフォンからは音楽が流れる。これも私にとって大切なアルバムである、POLTAの"SAD COMMUNICATION"。2015年に出会ってから色褪せない、少しひねくれて透明な輝きがある、素晴らしい作品だと思う。他のアルバムももちろん大好きなのだけれど、山行にはこれが合う気もして、ひとりの時はよくかけてる。

・　・　・

無事に撮影のポイントまでついてびっくりした。山にかかる雲が一部赤く色づいている。燃えるようでもあり、上に向かって放射状に広がって、灯台みたいに存在を示すようでもあり。 方角的には東の方だけれど、明らかに日の出にはまだ早いし、明かりの根本は谷っぽい。さすがに山火事とかじゃないよね…。谷間にある町や駅の明かりなのかな。そんな風にちょっとどきっとしたけれど、いそいそとカメラの準備を始めた。

そうしているとふと、向こうの明かりに対して、自分が今ひとりでここに立っていることに改めて意識が向き、「ネガティブな感じじゃない、さみしさ」みたいなものを感じた。うまく言えないけれど。

かつて、POLTAの自主企画"IS CONNECTED"にて、つるうちはなさんがMCで「ひとりでいること」について話していたことを思い出す。 そして、ふとある曲の一節が思い浮かぶ。

　『お祭りの明かりはいつも遠いけど、いつだってそばにいるよ』

私たちはこれからどうなっていくのだろう、最後の最後にはどうしているんだろうな、なんてことも、あんまりシリアスじゃなく、ぼんやり考えたり。しながら、シャッターを切ったりする。…三脚ちゃっちいやつでいいからもう一つ持ってこればよかったな。

この日は空の一部だけに雲がかかっていて、天頂の雲の様子もよく変わっていき、星空もよく見える。「こういうのがたまらないんだよなぁ?」と思わずつぶやいた。（文字にするとニワカオタク感が出ていいすね） 赤く染まる雲、目を上げていくと星空、天の川はちょっと左手。縦に据えた超広角で、それらを全部抱きしめたい。とか思うけれどでもとても遠くて、きれいで、そんなことはできなくて、私はただ、見ているだけなのだけれど。ありがたくお借りします。

雲一つない晴天とよく言うものだけれど、じっくりと写真を撮るようになって、雲が作る表情にも、すごく惹かれることに気付いた。立ち上がりどんどんと姿を変える積乱雲、空高く広く遊ぶ巻雲、ソリッドな雲型に隠れた太陽から鋭く光が漏れてくるところに立ち会うと、自分まで爆発してしまうんじゃないか、とか思う。うろこ雲が遠くまで続いてると「あ?！！！ほんとやめろよ！！！！」って思うしね。夏が終わっちゃうからね。音も立てずにね。（お約束の）

そんな雲、この日はさらに眼下にも雲が広がっている。ちょっとした雲海みたい。こういうのも私は数えるほどしか経験がないのでうれしくなる。敷かれた雲と、向こうの空、その水平線ならぬ雲平線？に目を向けて、だんだんと色づいてくる空すじを、借りる。まぁ山と海は、どっちも好きだよ、泳ぐのは苦手だけれど。

思い付きでカメラのレンズを付け替えたり、THETAで連続写真を撮ったり。（ちなみにこのTHETA SはPOLTAの傑さんが使ってくれたこともある、ちょーいい思い出） "心のシャッター派"の人を否定するつもりはないけれど、いろいろうだうだ考えながらも、ぼんやりしながらも、私はひとりだと撮影についてはいろいろやっちゃうほうかもしれない。

そのうち、薄い雲に霞んだ山かげから日が昇ってくる。日の出は好きだ。物事の締切に追われたりしている状況だと、空が白んでくると焦るものだけれど。 そう考えると、呑気に日の出を見に来られている、この状況は既に平和なんだろうな。 結局日の出後しばらくまで、誰一人上がってこなかった。良い空だった。切なさと喜びがある。今年の空撮りではこないだの江ノ島と並んで指折りかもしれない。山に来れたってのも嬉しい。

時が経てば忘れてしまうのかもしれないけれど、またこういう気持ちになれたらいいな。

お気に入りのTシャツを乾かすオタク

[kanakitoblr-blog]

江ノ島神社⛩ #theta360 #thetagram #thetaのある生活 #theta持って出かけよう #thetaを持って出かけよう #thetas #ricohtheta #mirrorball #360度カメラ #360photo #360camera #360sphere #360photography #insta360 #instagood #instajapan #shrine #torii #enoshima #江ノ島神社 #ミラーボール #寺社巡り #江ノ島 #全天球カメラ #鳥居 #鎌倉旅行

[folkboys]

GW6日目 今日はチューリップの惑星に落ちたみたいだ。 #世羅高原農場 #世羅高原農場チューリップ祭 #richo #thetas #theta360 #littleplanet #リトルプラネット #360度カメラ #360camera #360 #360degree #vr #theta360contest #thetaのある生活 #シータのある生活 #thetaを持って出かけよう https://www.instagram.com/folkboys/p/Bw9m728Bguc/?utm_source=ig_tumblr_share&igshid=13wb5ehdrfa4n

[himatsubushini7]

本当に写真？　“360度自撮り”ブームくるか 　真ん中に球形が浮かぶ、一見イラストに見える写真がある。Instagramで「#littleplanet」と検索すると、似たような「不思議な球形」がずらりと並ぶ。ハッシュタグの通り、小さな惑星に人や建物が立ち並んでいるように見える。画面中央に撮影者自身の姿を収めることもでき、“次世代の自撮り”とでもいえるかもしれない。 【画像：新しい自撮り方法】 　これは、ワンショットで360度写真が撮れるリコーの全天球カメラ「THETA」（シータ）シリーズの写真を加工したもの。本体の前後に付いたカメラで各180度以上を撮影、それらをソフトウェアが自動でつなぎあわせて1つの写真を合成する。専用のスマートフォン向けアプリ（iOS／Android向け、無料。用途別に複数あり）で「リトルプラネット」というアイコンを押すと、一風変わった“丸い写真”��出来上がる（海外では、「#tinyplanet」とも）。Instagramで #littleplanetと検索すると、7月29日時点で8万件以上がヒットする（#tinyplanetは28万件以上）。 　「最初はInstagramで見つけて、斬新で面白い写真だなと。自分でも撮ってみたくなって今年3月にTHETAを買って、今ではいつも持ち歩いてます。広く撮れるから、友達も全員写るし。遊びにきてるのか、写真を撮りにきてるのか分からないくらい撮りますね」――カメラが趣味で、今は特にTHETAの360度写真にハマっているという会社員の渡辺満里奈さん（27）は、そう笑う。 　「360度撮れるから人がたくさんいても全員写るし、加工しながら角度を変えられるから失敗も少ない。カメラが苦手なほどオススメしたい。私の周りで持っている人は全然いなくて、『これいいよ』って友達に勧めたら4人買ってました（笑）」（渡辺さん） 　遠出するときは、iPhone、キヤノンの一眼レフカメラ「EOS Kiss X5」、そして360度写真が撮れる「THETA SC」のほか、100円ショップで買ったビー玉や水晶玉などの小道具も携え、“フル装備”で向かうそうだ。「リュックはすごく重いんですが、Instagramでコメントをもらえたときのうれしさが尋常じゃないんですよね」と話す渡辺さんは「多いときは4～5時間で600～700枚くらい撮ることもあるけど、私ほどガチな子は周りにはいないです」と笑う。 　これまで、自撮り棒、SNOWアプリなど写真に関わる、はやりのものは一通り手にしてきたが、たどりついたTHETAは、その延長線上にあるものという。 　Instagramで「#theta」を検索すると、16万件以上（7月29日現在）の写真がヒットする。渡辺さんも、ハッシュタグのリンクに飛びながら「撮ってみたい」と思う写真を探すという。ビー玉や水晶玉を使う発想もInstagramにアップされている写真から得た。 ●「360度きっかけで自撮り始める」人も 　360度写真や実写VRの撮影を手掛けるベンチャー企業LIFE STYLEの岩嵜和哉マネージャー（VR制作部 360フォトチーム マネージャー）は、THETAを買ってから自撮りをするようになった1人だ。「これまでわざわざ自撮りなんてしなかったけど、THETAはとにかく面白い。プライベートでもよく撮ります」（岩嵜マネージャー。記事冒頭の写真は岩嵜さんのInstagram） 　広く風景を収めたいようなシーンでは、スマホよりもTHETAが活躍する。撮影や加工のコツもスマホとは異なるという。 　「360度写ってしまうので、とにかく背景を気にすること。スタンドを使って遠隔撮影しないと、絶対自分も写ってしまう。左右対称の場所はバランスよくきれいに写ります」（岩嵜マネージャー） 　家族で出かけたときに自撮りをして思い出を残すこともあれば、同じ場所で違う時間帯に定点撮影した画像を編集ソフト「Photoshop」で加工し、「左半分が昼の空、右半分が夜空のlittleplanet」を時間をかけて作ることもあるという。加工はTHETAの醍醐味（だいごみ）の1つ。同じ写真でも角度によって全く違う印象のものに仕上がることもある。岩嵜マネージャーは「夢中になってやっていると、たまに30分以上加工していることもある」そうだ。 　これまで、大人数の自撮りには、自撮り棒やスマホのカメラ部分に装着する外付け魚眼（広角）レンズなどが使われてきたが、同じ用途で360度写真を活用する人も現れ始めている。リコーは13年9月にTHETAを発売して以来、出荷台数などは公表していないが、「#theta360」「#thetaのある生活」「#thetas」など、Instagram上のハッシュタグでは日々写真がアップされている。また、一眼レフやサムスンの「Gear360」、スマホアプリでも360度写真は撮れるが、価格や使い勝手に対する写真のクオリティーの高さ、「カメラ本体のかわいさ」（渡辺さん）などから、THETAを手にする人も少なくないようだ。 　こうした360度写真の盛り上がりは、個人だけにとどまらない。 ●企業が「360度写真」を求める理由 　360度写真は、法人需要も増えてきたという。LIFE STYLEの前元健志さん（管理部 マーケティング課）は「飲食店、不動産、観光、病院などは360度コンテンツ（写真・動画）と相性がいい」と話す。 　「既存の写真や動画では雰囲気が伝わりづらい場合は、360度コンテンツの出番。お客さんが現地に行く前に雰囲気を確かめたいと思う場所と相性が良く、オフィスの紹介をしたい企業から声がかかることもある。屋内の情報のほぼ全てを公開することで、席数や部屋の雰囲気などに関する問い合わせを減らす効果もあった」 　熱狂的なファンが多いコアなジャンルの記録も360度撮影の醍醐味（だいごみ）。例えば、銀座線の車両が丸の内線内を走ったときの様子を360度動画で公開したこともあった。運転台にカメラを置き、運転士の視点を味わえるファン垂涎（すいぜん）の内容だ。 　Facebook、LINEなどのSNSが、“写真をぐるぐると好きな画角に動かせる360度写真の表示に対応したことや、コンシューマー向け製品の普及などに伴い、360度写真を目にする機会は増えてきた。「法人需要でも、他の企業でやっていた事例をまねしたいという声が増えた。施設案内などは漏れなく360度コンテンツになる時代が早いタイミングで来るのではないか」（前元さん） 　渡辺さんは「街中でTHETAを持っていると、あれは何だと通行人が珍しがって見てくる。昔の自撮り棒のような感覚かも」と話す。インパクトのある見た目から、「こんなものが本当にはやるのか？」という声もあったが、これまで自撮り棒は旅行先や宴会などさまざまなシーンで活躍してきた。 　写真に目がない女の子たちに360度写真ブームが訪れる日は来るのか。 （村上 万純） Source: ネットで副業生活！いつでもどこでも

[rhyauc37-blog]

本当に写真？　“360度自撮り”ブームくるか 　真ん中に球形が浮かぶ、一見イラストに見える写真がある。Instagramで「#littleplanet」と検索すると、似たような「不思議な球形」がずらりと並ぶ。ハッシュタグの通り、小さな惑星に人や建物が立ち並んでいるように見える。画面中央に撮影者自身の姿を収めることもでき、“次世代の自撮り”とでもいえるかもしれない。 【画像：新しい自撮り方法】 　これは、ワンショットで360度写真が撮れるリコーの全天球カメラ「THETA」（シータ）シリーズの写真を加工したもの。本体の前後に付いたカメラで各180度以上を撮影、それらをソフトウェアが自動でつなぎあわせて1つの写真を合成する。専用のスマートフォン向けアプリ（iOS／Android向け、無料。用途別に複数あり）で「リトルプラネット」というアイコンを押すと、一風変わった“丸い写真”が出来上がる（海外では、「#tinyplanet」とも）。Instagramで #littleplanetと検索すると、7月29日時点で8万件以上がヒットする（#tinyplanetは28万件以上）。 　「最初はInstagramで見つけて、斬新で面白い写真だなと。自分でも撮ってみたくなって今年3月にTHETAを買って、今ではいつも持ち歩いてます。広く撮れるから、友達も全員写るし。遊びにきてるのか、写真を撮りにきてるのか分からないくらい撮りますね」――カメラが趣味で、今は特にTHETAの360度写真にハマっているという会社員の渡辺満里奈さん（27）は、そう笑う。 　「360度撮れるから人がたくさんいても全員写るし、加工しながら角度を変えられるから失敗も少ない。カメラが苦手なほどオススメしたい。私の周りで持っている人は全然いなくて、『これいいよ』って友達に勧めたら4人買ってました（笑）」（渡辺さん） 　遠出するときは、iPhone、キヤノンの一眼レフカメラ「EOS Kiss X5」、そして360度写真が撮れる「THETA SC」のほか、100円ショップで買ったビー玉や水晶玉などの小道具も携え、“フル装備”で向かうそうだ。「リュックはすごく重いんですが、Instagramでコメントをもらえたときのうれしさが尋常じゃないんですよね」と話す渡辺さんは「多いときは4～5時間で600～700枚くらい撮ることもあるけど、私ほどガチな子は周りにはいないです」と笑う。 　これまで、自撮り棒、SNOWアプリなど写真に関わる、はやりのものは一通り手にしてきたが、たどりついたTHETAは、その延長線上にあるものという。 　Instagramで「#theta」を検索すると、16万件以上（7月29日現在）の写真がヒットする。渡辺さんも、ハッシュタグのリンクに飛びながら「撮ってみたい」と思う写真を探すという。ビー玉や水晶玉を使う発想もInstagramにアップされている写真から得た。 ●「360度きっかけで自撮り始める」人も 　360度写真や実写VRの撮影を手掛けるベンチャー企業LIFE STYLEの岩嵜和哉マネージャー（VR制作部 360フォ��チーム マネージャー）は、THETAを買ってから自撮りをするようになった1人だ。「これまでわざわざ自撮りなんてしなかったけど、THETAはとにかく面白い。プライベートでもよく撮ります」（岩嵜マネージャー。記事冒頭の写真は岩嵜さんのInstagram） 　広く風景を収めたいようなシーンでは、スマホよりもTHETAが活躍する。撮影や加工のコツもスマホとは異なるという。 　「360度写ってしまうので、とにかく背景を気にすること。スタンドを使って遠隔撮影しないと、絶対自分も写ってしまう。左右対称の場所はバランスよくきれいに写ります」（岩嵜マネージャー） 　家族で出かけたときに自撮りをして思い出を残すこともあれば、同じ場所で違う時間帯に定点撮影した画像を編集ソフト「Photoshop」で加工し、「左半分が昼の空、右半分が夜空のlittleplanet」を時間をかけて作ることもあるという。加工はTHETAの醍醐味（だいごみ）の1つ。同じ写真でも角度によって全く違う印象のものに仕上がることもある。岩嵜マネージャーは「夢中になってやっていると、たまに30分以上加工していることもある」そうだ。 　これまで、大人数の自撮りには、自撮り棒やスマホのカメラ部分に装着する外付け魚眼（広角）レンズなどが使われてきたが、同じ用途で360度写真を活用する人も現れ始めている。リコーは13年9月にTHETAを発売して以来、出荷台数などは公表していないが、「#theta360」「#thetaのある生活」「#thetas」など、Instagram上のハッシュタグでは日々写真がアップされている。また、一眼レフやサムスンの「Gear360」、スマホアプリでも360度写真は撮れるが、価格や使い勝手に対する写真のクオリティーの高さ、「カメラ本体のかわいさ」（渡辺さん）などから、THETAを手にする人も少なくないようだ。 　こうした360度写真の盛り上がりは、個人だけにとどまらない。 ●企業が「360度写真」を求める理由 　360度写真は、法人需要も増えてきたという。LIFE STYLEの前元健志さん（管理部 マーケティング課）は「飲食店、不動産、観光、病院などは360度コンテンツ（写真・動画）と相性がいい」と話す。 　「既存の写真や動画では雰囲気が伝わりづらい場合は、360度コンテンツの出番。お客さんが現地に行く前に雰囲気を確かめたいと思う場所と相性が良く、オフィスの紹介をしたい企業から声がかかることもある。屋内の情報のほぼ全てを公開することで、席数や部屋の雰囲気などに関する問い合わせを減らす効果もあった」 　熱狂的なファンが多いコアなジャンルの記録も360度撮影の醍醐味（だいごみ）。例えば、銀座線の車両が丸の内線内を走ったときの様子を360度動画で公開したこともあった。運転台にカメラを置き、運転士の視点を味わえるファン垂涎（すいぜん）の内容だ。 　Facebook、LINEなどのSNSが、“写真をぐるぐると好きな画角に動かせる360度写真の表示に対応したことや、コンシューマー向け製品の普及などに伴い、360度写真を目にする機会は増えてきた。「法人需要でも、他の企業でやっていた事例をまねしたいという声が増えた。施設案内などは漏れなく360度コンテンツになる時代が早いタイミングで来るのではないか」（前元さん） 　渡辺さんは「街中でTHETAを持っていると、あれは何だと通行人が珍しがって見てくる。昔の自撮り棒のような感覚かも」と話す。インパクトのある見た目から、「こんなものが本当にはやるのか？」という声もあったが、これまで自撮り棒は旅行先や宴会などさまざまなシーンで活躍してきた。 　写真に目がない女の子たちに360度写真ブームが訪れる日は来るのか。 （村上 万純） Source: ネットで副業生活！いつでもどこでも

[peanut-sub]

Θ Capsule http://www.nicovideo.jp/watch/sm4603213

ワンポイントアドバイス： One point of advice: 最近θっていう Called the 'modern-day θ' よくないモノが流行ってるらしい It appears bad things are becoming popular 気をつけてくださいね Please be careful

錆付いたポストに久々の手紙　どこからともなく Letters from long ago suddenly appeared in my rusted mailbox 「この街で　一番　景色がきれいな場所の　写真が・・・貼ってあったの・・・」 "Attached are pictures of this town's best... and most beautiful... locations...."

わずかな興味と狂気が　日常の裏側を覗かせるの A little bit of curiosity and insanity peeks out from the other side of the ordinary

退屈な籠と　白黒天井 A boring basket and a monochrome ceiling

発する言葉は　宙に舞い消える Spoken words fly out and flutter in the air before vanishing

絵本と人形　　紙とクレヨンを With my picture book, my doll, paper, and crayons 持って出かけるの　逃げ出してやるのよ...↓ I set off on my journey, I'm running away...↓

☪月気球　追いかけて　旅に出ようよ I chase after the ☪ moon balloon, let's go together 神様がくれた　この世界が大キライだから God gave us this world, so I hate it very much

紳士のおじさんが見せる I saw an older gentleman それは　流行の「シータ」らしいの Who seemed to be into that "theta" fad

差し出されたのは　小さいθ He offered me a small θ (capsule)

甘くて　楽しい　味がしたのかも It seemed to have a sweet, fun flavor

空を飛ぶ魚　泳げる気がした Like a fish flying in the sky, I felt like I could swim 昼が　音も無く　夜へと置き換わる The day silently crossed over into night

一つだけ　願い事　してもいいなら If i could have one single wish 次もまた　次もまた　わたしでありますように I hope this happens to me again and again

手に入れたものは　わずかな安息 With the amount I had, I got a little bit of rest 漆黒の闇が　すべてを飲み込む As the pitch-black darkness swallows everything

空と海が融け　☆が魚へと The sky and sea mix, and the ☆ stars become fish

わたしの体は　ひたすら落ちてゆく My body just keeps sinking

幸福の　♫を詰めた　θシュガー θ Capsule sugar, packed full of happy ♫ sounds 報われた　気がした　ほんの少し遅かったけれど The rewarded feeling was a little late, but

わたし今　幸せ　だよ I'm so happy now だけど　何故　かな But, somehow

「さみしい・・・」 "Lonely..."

気づいたの　やっと I finally realized この世界が　大好きだったと I love this world so much

[omsrkb]

FAN3 参加レポート #02

Vigyan Ashramは、世界最初のファブラボというか、ファブラボという名称がない時に既にそれに近い活動をしていたという伝説の場所なので、いつか行ってみたかった。MITのニール・ガーシェンフェルド教授がここを視察して感銘を受けて、その活動をデジタルファブリケーションで実現するものをファブラボとしてMITに作ったという流れら��く、FabLabの先祖ということで、FabLab0（ゼロ）とも言われる。 とにかくVigyan Ashramは、自分たちで共同生活しながら必要なものを作り上げて活用していく理想郷のような場所で、そこに向かう旅の間は天竺を目指す三蔵法師一行の様な気分。結構遠かった・・・。

朝まだ薄暗い中、キャンバスの集合場所に行くと、まだ数人しかおらず犬が寝ていた。なんだかんだでみんなが集まって、バスが来たのは結構後だった。そして、Vigyan Ashramまでそのバスで何時間かかるのか？２時間という人もいれば３時間という人もいて皆目見当がつかない。とにかくバスは走り出した。

１時間半ほど走ったところで、高速脇のサービスエリアに立ち寄った。日本のそれに比べると、もう少しごちゃごちゃしていて、様々な小さなお店が建物の中に入っている雰囲気。そこでチャイを飲んだり売られているお菓子を食べたりしてみんな興味津々だった。それにしてもチャイにしても、コーヒーにしても小さすぎて飲んだ気にならない。マグカップくらいのサイズでガブガブ飲みたい派なので辛いけど、10ルピーだしそんなものなのかな？上の写真の中央の下の男性が持っているのがチャイ。めちゃ砂糖入っている。

バスは山を登り始め、地平線が見えそうな雄大な景色が広がった。その高速道路に荷物を満載したトラックが苦しそうにゆっくり登っていて、バスはそれらを避けながら進む。景色を見ながら、今まで書籍や誰かのプレゼンテーションでしか見ていないVigyan Ashramという場所は一体どんなところなのだろう？といろいろ想像してしまう。高速を降りて農村の広がる中を抜けて、荒野の様な丘を登って行き、ついにキャンパスを出発してから４時間半ほどで、Vigyan Ashramに到着した。

バスを降りてVigyan Ashramの中に入っていくと、太鼓を叩いて歓迎してくれる。更に各自の額にビンディ（赤い点？）を付けて、白い帽子を被せてくれた。そしてチャイとクッキーで休憩をしてからいくつかのグループに分かれてVigyan Ashramの中の各施設を見学して周りながら説明を受けた。ここにある建物の幾つかは職員やここで学ぶ生徒たちが建てたらしい。自分たちで自分が学ぶ場所自体を作るというのはどういう気分だろう？愛着が湧くだろうな。

Vigyan Ashramに行く前のイメージはこんな感じだった。 ・次々と苦しい農村の課題を解決し続けている清貧的活動。 ・インド各地からここにものづくりを学びに来て故郷に帰って活躍。 ・共同生活と学校でもあるということでちょっと戸塚ヨットスクール的？

実際に来てみて、ここに学びに来ている人たちに話を聞くと、辛い感じはあまりなく楽しんでいて、早く学んで起業したい！というような前向きな話をよくしてくれた。日本で社会課題の解決というと大げさに感じてしまうが、ここでは生活が便利にできるようなものづくりへのハードルが低いのではないか？

自分たち自身で作れる≒安く作れる≒買える人が増える

というような事も考えながら製作しているようだ。中国に行った時も感じたが、日本人が「それ作ってもなあ」「もう他にあるしなあ」などと考え過ぎて何も作らないでいる間に、どんどん作ってスキルや経験を上げていくのだろう。敷地のあちこちにこれまで作られた道具や機械が置かれていた。

Post from RICOH THETA. https://theta360.com/s/jlqU1telI9yhbbwzXxukSKmH6

同行した渡邊先生の情報では、ここでの製作は基本的に、想定顧客がいる事を前提に実施するそうで、故郷の村の人たちでもいいし、どこか自分で見つけてきた、電気のない村のための発電機でもいいが、とにかく顧客がいるという事を重視している。Vigyan Ashramのスポンサーも幾つかの企業や団体がいるそうで彼らのテーマに合わせたものでも良いらしい。

ドーム型の温���を作り、中の湿度や温度を一定に保ち、必要な量だけの水を適当なタイミングで供給するというシステム。丘の上にあるVigyan Ashramでは水は非常に貴重なのだ。その水をどう効率的に活用するのか？そういうテーマが多かった。このドームの中では各作物の根元の土にセンサーがあって、乾燥してくると水が供給される。

外から見た温室。細い鉄骨の組み合わせで多面体を作り、そこにビニールを掛ける形式。このドーム構造が様々な建物で使われていた。

こちらはドーム構造の乾燥室。ビニールではなく、セメントの様なもので覆われている。頂上に空気を抜く部分を設けていて、ドームの基部近くに小さな空気穴がいくつか開けてあり、下から上に空気を流しつつ内部を乾燥させていく。それによって保存食の製作などを行うというもの。 同様のドーム構造で居住施設も作られていて、外から見るとSFの世界のような雰囲気もあった。

他にもここで作られた様々な機械が並んでいた。このべスパ？バジャジ？を改造した機械は、映画「きっとうまくいく」（原題「3 idiots」）のラストシーンで登場するらしい。みんな嬉しそうにこの機械を改造した写真中央の白いシャツのおじさんと記念写真を撮っていた。ちなみに自分はこの映画を観ていないのでみんなの盛り上がりに乗ることができず。Netflixで観れるので今度見てみようと思う。

続いてこちらは、アクアポニックス。高い位置まで組み上げた水を流して段々畑で作物を育てつつ、最後に魚を飼っている池で水を回収、魚の糞などを栄養としてその水をまた畑に戻すという循環型水耕栽培施設。オクラやいくつかの種類の作物を作っているらしい。段々畑の下部にある池には魚がいるそうだが、姿は見ることはできなかった。

女性のグループが３Dプリンターでの義手製作も実施していた。実はつくる〜むでも、exiiのオープンソースの義手を作ってみようとしたんですが、あまりのパーツ数の多さに諦めてしまいました。それを彼らは作って実際に試していた。女の子が使うので、それには結構大きすぎるのでなんとか小さくしたいというのが彼らの願いでしたが、単純に小型化するとサー���などの部品が収まらなくなるしでかなり苦戦しているとのこと。パラメトリックに各部のサイズ、形状、指の長さなどを調整できるようなCADの進化形の様なモノがあれば良いのかも。確か２年くらい前のイベントでexiiの人と話をしたことはあったので、インドの僻地で作った人がいるよ！と報告したいと思ったものの、ほんのちょっと話をしただけで、相手はこちらを覚えていないだろうし、つい最近触覚デバイスを発表して忙しいだろうなとか、社長さん最近辞めてたなとか余計なことを考えて躊躇。

巨大なソーラークッカー。要は連邦がソロモンに対して使ったソーラ・システムと同じで鏡で太陽の光を集めて一点に集めるというもの。集光した部分ではかなりの高温になると云う。試しに壁に反射しているあたりに立ってみたらかなり暑かった。そしてその直後に「危ないだろ！」と注意を受けてしまった。 二個めの画像は集光する部分で、右の丸いモノは温水器で、ここに水を通すことでお湯を作ることができ、この部分はドアの様に動かすことができるので、集光部から外すと、左側に鍋がありますが、料理に光の熱を使うことができる。反射のための鏡部分は太陽の移動に応じて向きを変えることができるのだが、現状は手動でいつか自動化したいとの説明があった。

巨大なCNCにプラズマカッターを付けた試作と、その切断サンプル。加工精度が悪く調整がまだまだ必要とのことだったが、厚み１cm近い鉄を任意の形状に切断できるというのは魅力的だ。施設が大きいこともあり、このようなサイズの加工機を設置し、さらに溶接などもできるので、インド各地から来た生徒たちは様々なスキルを身につけて帰ることができる。3Dプリンターなどのデジタル・ファブリケーションだけでなくアナログな製作手段を組み合わせることが重要なのだと感じた。

彼らの食事をご馳走になった。とても美味しかった。後日Vigyan Ashramで学ぶコストについて聞いてみた。 ・受講料は３ヶ月ごとに2500ルピー ・食事、宿舎でも同じく2500ルピー前後 ・2年、1年など幾つかのコースがある ということの様だった。どんな人が来るのか？というと既存の学校をドロップアウトした様な人が多いと言う。2500ルピーと言うのは日本人からしたらそうでもないけど、インドではそこそこの額なので、それなりの家庭の子が来るイメージなのかな？卒業後は起業するケースが多いらしい。2015年の卒業生のスタートアップをまとめたページを、FAN3後に再度現地を訪ねた高寺さんより教えてもらったので参考に。Vigyan Ashramに寄付をするくらい成長した会社も存在するらしい。社会課題を発見しやすいインドだから出来ることなのか？、日本では同様のことが可能なのか？

Vigyan Ashramに来たことで、更に色々考えてしまった。もし可能ならいつか自分も数か月滞在しながら何かを作れたらいいな。

翌15日は主にMakerMelaの見学です。