ajchm92

[ajchm92]

[ajchm92]

Video grabado en la Isla Taquile - Perú 

Volando con el cuadricoptero DJI mini 2

#drone #lake #laketiticaca

[ajchm92]

Finjo que no duele, pero duele. Me lastima. Pero el tiempo pasa y transforma todo en aprendizaje. Uno madura y percibe que existen varias posibilidades de ser feliz. Cuan bueno es vivir la vida a plenitud. Uno descubre que nuevos amores y nuevas historias nos esperan a cada esquina. Descubrí que los capítulos se acaban, pero el libro continua. Los hombros vuelven a ser leves y uno vuelve a sonreír.

Jacobin 

[ajchm92]

BREVE REFLEXIÓN SOBRE LA VIDA

En tiempos de pandemia es difícil no aventurarse en la imaginación sobre un posible infortunio mundial. Este virus (Sars coV - 2) viene cobrando miles de vidas a nivel mundial y si esto no es controlado las consecuencias serán catastróficas para la raza humana. 

La industria cinematográfica ha mostrado en películas como TERMINATOR 1, 2, 3 e IMPACTO PROFUNDO como el ser humano se adhiere a la supervivencia cuando es amenazado por causas externas fuera de su alcance de su comprensión. 

- “Pero eso es solo una película” tal vez digas. 

Pero imagina: ¿Que pasaría si el virus avanzara, volviendo cada vez mas agresivo  hasta el punto de exterminar a todo humano al ras de la tierra? ¿Que condiciones serian necesarias para  reiniciar la vida?  y si alguien consigue sobrevivir ¿que es lo primero que necesita aprender sobre la naturaleza si no hay bibliotecas ni profesores? 

Quiero terminar esta reflexión con las palabras del físico estadounidense Richard Feynman sobre el conocimiento humano y las leyes de la naturaleza:

“Si, en algún cataclismo, se destruyera todo el conocimiento científico y se transmitiera una sola frase a la próxima generación de criaturas, ¿qué enunciado contendría la mayor cantidad de información en la menor cantidad de palabras? Creo que es la hipótesis atómica de que todas las cosas están hechas de átomos: pequeñas partículas que se mueven alrededor en un movimiento perpetuo, que se atraen entre sí cuando están a poca distancia, pero que se repelen al ser presionadas una contra la otra. En esa oración, verá, hay una enorme cantidad de información sobre el mundo, si solo se aplica un poco de imaginación y pensamiento”.

[ajchm92]

[ajchm92]

LA MATEMÁTICA DETRÁS DEL COVID-19

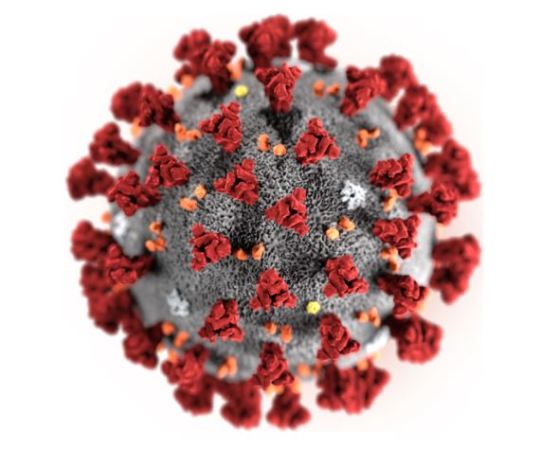
En estos momentos de angustia en torno al infame coronavirus, llegan voces desde distintos campos de la ciencia tratando de echar una mano para entender o mitigar la pandemia. En un mundo de biotecnología parece extraño acudir a las matemáticas para resolver los enigmas que nos plantea el SARS-CoV-2, o comúnmente conocido como COVID-19. Esto se debe a que, normalmente, no se concibe la conexión entre las matemáticas y la realidad más allá de “contar con los dedos” como aprendimos a hacer de niños.

Para probar al lector que esto no es así, seamos osados y ¡contemos con los dedos! Imaginemos que cuando acabe todo fuésemos capaces de determinar quién contagió a quién. El lector podría ser el primer portador del virus y haber estrechado la mano o tosido delante de otras 3 personas que se contagiaron a su vez. Luego, cada una de estas tres personas habrían contagiado a otras 3 (y ya van 1+3+9) que, por avatares de la vida, habrían propagado la infección a otras 3 (es fácil contar: 1+3+9+27). Matemáticamente, esto se conoce como progresión geométrica o, como se repite en los medios estos días, crecimiento exponencial. En epidemiología, ese número 3 se conoce como ritmo (o factor) reproductivo básico, R0, y representa el número medio de contagios propagados por cada persona contagiada. Este número tiene que ser mayor que 1 para que haya epidemia y, como parece natural, cuanto mayor es, más explosiva será la epidemia. Por poner unos ejemplos, el sarampión tiene un valor R0 entre 12 y 18, y el ébola y la gripe común entre 2 y 3. Con R0 no somos capaces de medir cómo de letal es un virus, sólo cómo de infeccioso ha sido en una cierta población. A partir de los datos de China, se observa que SARS-CoV-2 tiene un factor R0 estimado en 2,68 (aunque sospechamos que, en el caso de Italia o España, R0 podría ser mayor).

Las medidas de higiene y distanciamiento social que sufrimos en estos días permiten hacer decrecer R0 y, por tanto, mitigan el impacto de la propagación de SARS-CoV-2. Para cuantificar este impacto, proponemos utilizar un modelo matemático (y sus variantes) ya existente propuesto por el escocés Anderson Gray McKendrick en el año 1926, conocido como modelo SIR de epidemias. Con los términos SIR se hace énfasis sobre los tres estados de un individuo ante la enfermedad – susceptible (sano), infectado (infeccioso con capacidad para contagiar a otros) y removido (recuperado e inmune a nuevas infecciones, o fallecido) –, así como su evolución  S -> I -> R en el tiempo. Los estados dan lugar a tres compartimentos – o subpoblaciones de individuos susceptibles, infectados y removidos – que permiten clasificar a los individuos de la población en cada instante de tiempo.

En términos del modelo SIR, la propagación de SARS-CoV-2 está vinculada al sistema de ecuaciones diferenciales para las proporciones s(t) de susceptibles, i(t)  de infectados y r(t) de removidos respecto al tamaño N de la población (que se asume constante) dado por

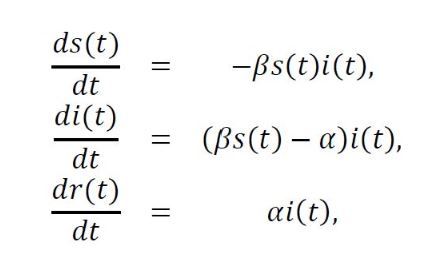
donde β es la tasa de infección y α es la tasa de recuperación, en el supuesto de las proporciones iniciales s(0)= s0 >0, i(0)=1- s0 >0 y  r(0)=0. En lenguaje cotidiano, la primera ecuación nos dice que la velocidad con la que decrece el número de susceptibles es proporcional al producto s(t) i(t), donde este producto se puede interpretar como la probabilidad de que una persona susceptible se encuentre con una infectada y el parámetro β mide la probabilidad de que el contagio sea exitoso. Es interesante entender que β tiene tanto que ver con el número promedio de “encuentros” entre personas susceptibles e infectadas, como con el resultado de esa infección. Como discutiremos más adelante, esto tiene implicaciones en las políticas de aislamiento y de higiene.

Una sencilla interpretación de los signos de las derivadas de  s(t), i(t) y r(t), garantiza que la proporción de individuos susceptibles disminuirá (s(t)≤ s0)  hacia su valor final s∞=   lim t→∞⁡ s(t)  y la proporción de removidos se incrementará hacia un valor final r∞=   lim t→∞ ⁡r(t) mientras que, en ambos casos, existan individuos infectados. Por el contrario, la proporción de infectados aumentará si βs(t)>α  y disminuirá si βs(t)<α.

La principal propiedad del modelo SIR, aplicado a SARS-CoV-2 o a cualquier otro patógeno, es que la propagación de la enfermedad termina con el paso del tiempo (es decir, la enfermedad es no endémica) ya que

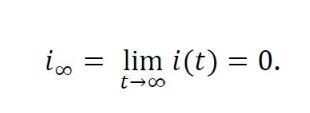
Sin embargo, hay que distinguir dos posibles comportamientos hasta que se produzca la extinción de la enfermedad dependiendo del factor reproductivo básico, que en el modelo SIR se expresa como R0=β⁄α:

-       Cuando R0 < 1 (en promedio, un individuo infectado se recupera antes de transmitir la enfermedad), la relación s(t)≤1<1⁄R0 garantiza que la proporción de infectados disminuye desde el primer momento (i(t)≤1-s0) y la enfermedad desaparece con rapidez. En tal caso, la máxima proporción de infectados durante un episodio de la enfermedad se observa en el instante inicial, imax=1-s0.

-       Cuando R0 > 1 (en promedio, un individuo infectado transmite la enfermedad antes de recuperarse), la proporción de infectados podría decrecer desde el primer momento (i(t)≤1-s0) si s0 < 1/R0, mientras que podría aumentar inicialmente hasta la máxima proporción

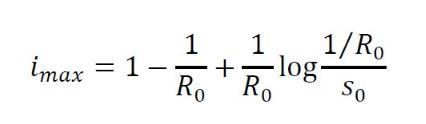
y luego decrecer hasta la extinción cuando s0 > 1/R0. En este segundo caso, tiene sentido hablar de epidemia y el pico de la infección se alcanza cuando la proporción de susceptibles coincide con el umbral crítico α/β, es decir, en el instante de tiempo tmax > 0 que verifica s(tmax) = 1/R0. Como mencionamos con anterioridad, el coronavirus SARS-CoV-2 tiene un valor de R0 próximo a 2,68, por lo que si toda la población fuese susceptible al virus (ésto no sabemos si es así a día de hoy), el virus podría infectar simultáneamente a casi un cuarto de la población si no aplicamos ninguna medida de precaución o control.

La magnitud de  imax  – pequeña o grande – es fundamental para determinar si los recursos sanitarios son suficientes o no ante la propagación de SARS-CoV-2. Para ello, basta traducir la capacidad del sistema sanitario en términos de un número i* que refleje sus limitaciones (por ejemplo, en términos de la proporción de camas hospitalarias en UCI disponibles para atender a una población de  individuos), y concluir que los recursos son suficientes si se tiene  imax ≤ i* o, por el contrario, son insuficientes cuando imax  > i*.

¿Qué hacer si se prevé que los recursos sanitarios no serán suficientes?

Para entender cómo podemos revertir una situación de alarma, imax  > i*, en otra aceptable, imax ≤ i*, es importante hablar de dos conceptos y la relación entre ellos:

La velocidad exponencial de crecimiento

Las medidas de contingencia

Para complementar nuestros comentarios sobre R0 y la noción de velocidad exponencial de crecimiento de una epidemia, nos fijamos en la proporción j(t) = i(t) + r(t) de individuos afectados por la enfermedad hasta el instante t (si se estuviesen realizando tests masivamente en la población, esta proporción debería coincidir con los datos que aparecen en los medios asociada a los “casos confirmados”); a partir de esta proporción, podemos estimar el número acumulado de fallecidos, dado por ρNj(t), donde ρ es el índice de letalidad de la enfermedad. En concreto, el valor ρ=0,023 estimado en China refleja que el porcentaje de fallecidos entre los afectados por SARS-CoV-2 es el 2,3%. Matemáticamente, se puede encontrar una expresión explícita para la fracción de afectados:

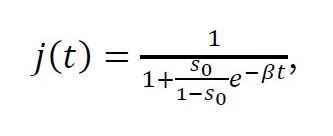
que muestra que la proporción j(t) es inversamente proporcional a e-βt, de manera que el número acumulado de afectados Nj(t) se incrementará a la misma velocidad que el valor de e-βt decrezca cuando el tiempo t se incremente.

Como j(t) es una función creciente del tiempo y sus valores mínimo y máximo son 1-s0 (en el instante de aparición del patógeno) y 1-s∞ (en el instante de extinción), con 0 < 1-s0 < 1-s∞ ≤ 1 , su crecimiento no es siempre del mismo tipo. En concreto, existirá un intervalo de tiempo donde la velocidad del crecimiento de j(t) aumenta hasta alcanzar su valor máximo. Para determinar ese intervalo, traducimos la velocidad de crecimiento de j(t) en términos de su derivada

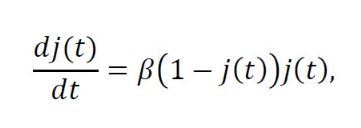
y determinamos su valor máximo como función de j(t), dentro del rango 1-s0 ≤ j(t) ≤ 1 . Desde la Figura 2 es sencillo llegar a la conclusión de que la máxima velocidad de crecimiento se alcanzará cuando j(t) = 1/2 y lo habrá hecho en un instante de tiempo antes del cual la velocidad de crecimiento crece hasta su valor máximo β/4  y, después del cual, la velocidad comienza a decrecer progresivamente.

Figura 2: La velocidad de crecimiento de j(t) (es decir, dj(t)/dt) como función de j(t).

Desde lo anterior, es claro que la curva del número acumulado de afectados  por SARS-CoV-2 no se suavizará hasta que el 50% de la población no se haya visto afectada por la epidemia, siempre que la epidemia no se haya extinguido antes.

En el supuesto de que SARS-CoV-2 siga propagándose, ¿cómo podemos suavizar la curva del número acumulado de afectados? La respuesta se encuentra entre nuestras observaciones anteriores:

Minimizando el valor máximo β/4 de la velocidad de crecimiento.

Eso significa “disminuir la tasa de contacto entre individuos” para hacer posible disminuir la tasa de transmisión β, en el mismo sentido que el factor reproductivo básico R0. En este punto, toman sentido las medidas de distanciamiento social, así como medidas profilácticas (uso de guantes, mascarillas, lavado de manos) dictadas por los Gobiernos de los países afectados por SARS-CoV-2.

Pongamos un ejemplo para poner de manifiesto las repercusiones de una medida de contingencia, como el distanciamiento forzoso de los ciudadanos, ante la enfermedad Covid-19 asumiendo que el valor R0 = 2,68 del factor reproductivo – publicado en la revista científica Lancet– es correcto; en ese caso, la tasa de contagio estimada es  β = 0,19 días -1 y el tiempo medio de transmisión es, aproximadamente, 1/β= 5,26 días. Tomemos cuatro escenarios:

Escenario 1: Sin medidas de contingencia. Representa la propagación de SARS-CoV-2 sin medidas de control, es decir,  β = 0,19 días -1 y R0 = 2,68.

Escenario 2: Medidas de contingencia leves. Se ponen en práctica medidas de control de baja intensidad (β’ = 90%  β) que conducen a R0 = 2,39.

Escenario 3: Medidas de contingencia moderadas. Se ponen en práctica medidas de control de intensidad media (β”= 80%  β)  que conducen a R0 = 2,13.

Escenario 4: Medidas de contingencia severas. Se ponen en práctica medidas de control de alta intensidad (β”’= 50%  β))  que conducen a R0 = 1,33.

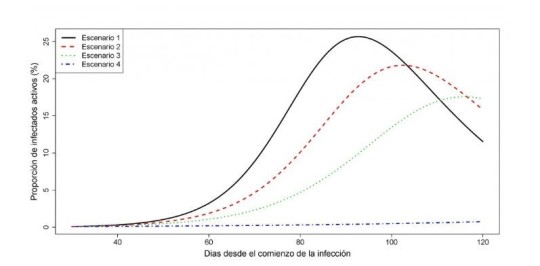
Figura 3: Variación de la proporción de infectados i(t) en función de la intensidad de las medidas de contingencia.

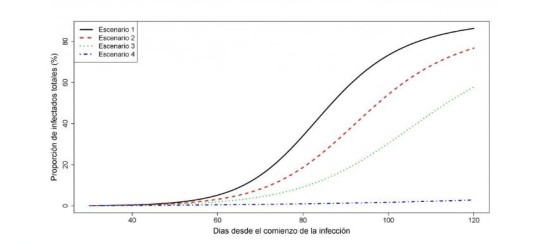
Figura 4: Variación de la proporción de individuos afectados j(t) en función de la intensidad de las medidas de contingencia.

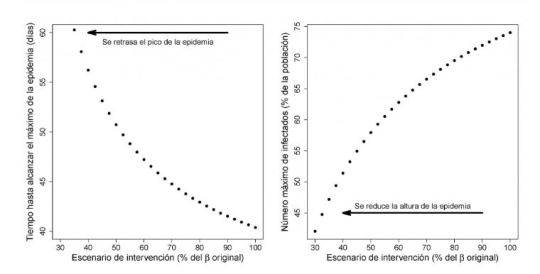
Figura 5: Tiempo transcurrido hasta alcanzar el pico de infección  tmax   y proporción máxima de individuos simultáneamente infectados  imax en función de la intensidad de las medidas de contingencia.

Observando detenidamente las Figuras 3 y 5, es claro que el pico de infección, en términos de la máxima proporción imax de infectados, disminuye a la vez que el instante tmax de ocurrencia del pico de infección se incrementa cuando se ejecutan medidas de control más severas; en tal caso, una adecuada especificación del umbral i*  de capacidad límite de los recursos sanitarios permitirá definir medidas de contingencia concretas, sin que resulten ser excesivas para los ciudadanos. El incremento del número de días desde el inicio de los contagios hasta alcanzar el pico de infección también permite dar cabida al desarrollo de tratamientos paliativos (antivirales) y acercarnos a la fecha en la que una vacuna pueda estar disponible y ayude a poner fin definitivamente a la epidemia.

Además, la imposición de medidas de contingencia más restrictivas hace que la franja [1-s0,1-s∞]  de variación de la proporción de individuos afectados j(t) en la Figura 4 se contraiga, al decrecer su valor límite 1-s∞, lo cual permitirá disminuir el impacto de la enfermedad, medido en términos del número de individuos que se verán afectados.

Es importante observar que la tasa de recuperación α se ha mantenido constante en el ejemplo, reflejando que no existe tratamiento específico o vacuna que permite mejorar el tiempo medio de recuperación. Por ello, todos los esfuerzos de lucha frente a SARS-CoV-2 están orientados hacia la disminución de la tasa de contagio β.

El modelo y sus limitaciones

No queremos engañar al lector: el modelo SIR es un modelo inicial – la comunidad  científica anglosajona usa el término toy model para referirse a un modelo de partida que progresivamente es mejorado – y nuestro anterior ejemplo es ideal. Con seguridad, ambos estarán muy alejados de una realidad que, por ahora y hasta que la pandemia de SARS-CoV-2 se estabilice, no conoceremos con detalle. En ese momento, las estimaciones de las tasas de contagio y de recuperación serán más precisas y el modelo se verá seriamente modificado por la necesidad o no de distinguir entre susceptibles, infectados-asintomáticos, infectados-sintomáticos, recuperados-infecciosos y recuperados (incluyendo a los fallecidos) si se confirman los diferentes indicios epidemiológicos en ese sentido. Incluso el modelo podría ser estructurado por edades y patologías previas para reflejar diferentes niveles de letalidad de la enfermedad, e incluso modificado cuando una vacuna efectiva sea conocida. Otros caminos no tan evidentes y que merecen ser explorados consistirían en asumir que los parámetros del modelo son cambiantes (debido a medidas políticas, al temor de los ciudadanos frente a las noticias, …). O, por poner otro ejemplo, la suposición de que el contagio es proporcional a s(t) i(t) debería modificarse para reflejar la compleja red social de contactos; en particular, se sabe que la mayoría de los ciudadanos se mueven en círculos de contactos pequeños, pero algunos individuos, llamados superpropagadores, son capaces de llevar la enfermedad de una ciudad a otra o, como en el caso de SARS-CoV-2, de un continente a otro.

No nos cabe ninguna duda de que, para conseguir un modelo predictivo suficientemente preciso para el estudio de SARS-CoV-2, será necesario realizar un esfuerzo multidisplicinar entre epidemiólogos, inmunólogos, neumólogos, bioestadísticos y matemáticos, entre otros. Desde el lado de las matemáticas y, en general, de todas las ramas de la ciencia, ya existen algunas iniciativas para desarrollar modelos más precisos que permitan evaluar cuantitativamente el impacto de estas medidas.

Hasta ese momento, los autores esperan haber convencido al lector – inclinado o no hacia las matemáticas- de la importancia de esforzarnos en hacer disminuir la tasa de contagio β, es decir, de respetar el consejo

¡Quédate en casa!

Autores: Mario Castro Ponce,  Manuel de León y  Antonio Gómez Corral

[ajchm92]

EL VIRUS DE ESTE MUNDO ERES TÚ

Traté de advertirte. Varias veces. Grité, rogué, intenté llamar tu atención, pero nunca me escuchaste. Al contrario. Parece que te esforzabas para hacerlo aún peor. Para destruirme más cada día. Cada vez más codicioso. Más egoísta. Cada vez menos humano. Humano, palabra que no existe mas en tu vocabulario. O tal vez nunca supiste lo que significa. Y yo siempre pensé que eras mi inquilino más prometedor. El único capaz de hacer cosas que otros no harían. Qué tonto fui. Porque fue precisamente este privilegio que te cegó. Olvidaste que no vives solo aquí. Que no puedes hacer todo lo que quieras. Que me necesitas y necesitas de todo lo que esta aquí. Como todo padre que aman a su hijo, traté de aceptar tus errores. Todo lo verde que destruiste. Todas las especies que exterminaste. Toda la sangre que se derramó. Di la vuelta a todo lo que pude. Grité y pedí ayuda en forma de terremotos, tornados y tsunamis. Nada de esto te detuvo. El agujero en la capa de ozono no te sobresaltó. Te hiciste la vista gorda con el derretimiento de mis glaciares. Bueno pues, llegamos al punto donde necesitaba detenerte. No pude soportarlo más. Es por eso que esta vez reaccioné con este virus. Lo siento, pero era el arma que tenía. Un virus que te obliga a quedarte en casa y repensar tu comportamiento. Un enemigo silencioso que ha vaciado todo lo que tu avaricia ha construido. No tiene sentido el dinero que has recaudado, ahora que no tienes dónde gastar. ENTIENDE DE UNA VEZ: tú solo no eres nadie, no vales nada. Ahora lo que te queda es estar atrapado por unos días. ¿No es así como su sociedad suele educar a los delincuentes? Pues entonces. Usted allí, atrapado en su casa, y los otros animales libres de usted. Tu especie llora y el resto del mundo celebra. Eres el virus de este mundo, esa es la verdad. Sabes, no te lo mereces, pero aun confió en ti. Creo que esta lección te hará reflexionar y cambiar. Después de eso tendremos mejores días. Espero que si. No querías aprender para bien, espero que aprendas con dolor.

Firmado: Planeta Tierra.

Autor: @precisavaescrever

[ajchm92]

CONSEJOS PARA PREVENIR EL CORONAVIRUS

Amigos voy a darles algunas recomendaciones de cómo proceder para evitar contagiarse del coronavirus.

1.- Si llegaste de la calle: lávate las manos, pasa abundante alcohol entre las palmas de la mano y enciéndete fuego.

2.- Si vas a toser: Cúbrete con el antebrazo, pasa alcohol y amputa el brazo con moto sierra.

3.- Si alguien tosió frente a ti: Pásate abúndate alcohol en ti y en la otra persona y préndele fuego.

4.- Si te frotaste los ojos: Pasa alcohol en el ojo frotado y arráncalo con pinza y deséchalo.

5.- Si pasaste la mano en la boca: Ingiera 1 LITRO de alcohol, haga gárgaras y luego enciéndete fuego.

6.- Si tosiste encima de un niño: Báñalo en alcohol y aléjate del niño (creíste que deberías encenderle fuego al niño? No eso no se hace)

[ajchm92]

HEY JUDE - THE BEATLES.

COVER GUITAR

Este video lo hice en 2016 cuando estaba aprendiendo guitarra con Guitar Pro.

[ajchm92]

Hoy conté a las paredes de mi habitación cosas del corazón. Es mejor que ir un psicólogo. Me escucha y me siento bien

Jacob Sad

[ajchm92]

NOVEMBER RAIN, GUNS N' ROSES  - COVER SOLO

[ajchm92]

Todo inicio tiene un final y el mio llega hasta aquí. Solo me restan palabras de agradecimiento para cada uno de uds por haber compartido esta bonita experiencia que, para mi, fue un honor trabajar a lado de personas cuyas cualidades tanto profesional como humano son dignos de admiración. Les deseo éxitos y ojalá podamos nuevamente coincidir en otros proyectos. ABRAZOS.

[ajchm92]

Ateos

“Los ateos definen su estilo de vida como sigue:

El ateo se ama a sí mismo y a su prójimo en vez de a un dios.

El ateo sabe que el paraíso es algo por lo cual deberíamos trabajar ahora, aquí en la Tierra, para que todos los hombres juntos lo disfruten.

El ateo cree que no puede obtener ayuda a través de la oración, sino que debe encontrar en sí mismo la convicción y la fuerza interna para encontrarse con la vida, aferrarla, someterla y disfrutarla.

El ateo cree que sólo en el conocimiento de sí mismo y de su prójimo puede encontrar el entendimiento que lo ayudará a vivir una vida plena de logros. Por lo tanto, busca conocerse a sí mismo y a su prójimo más que conocer a un dios.

El ateo sabe que debería construirse un hospital en vez de una iglesia.

El ateo sabe que se debe realizar una acción en vez de rezar una plegaria.

El ateo lucha por involucrarse en la vida, no escaparse hacia la muerte. Quiere que la enfermedad sea sometida, la pobreza derrotada, y la guerra eliminada. Quiere que el hombre entienda y ame al hombre. Quiere una forma ética de vida. Sabe que no podemos poner nuestra confianza en un dios, ni enfocar acciones con una plegaria, ni tener esperanza de que los problemas se terminen en el más allá. Sabe que somos los cuidadores de nuestros hermanos y de nuestras propias vidas; que somos personas responsables, que el trabajo se hace aquí y que el momento es ahora.”

- Madalyn Murray, activista atea norteamericana, fundadora de la organización American Atheists.

[ajchm92]

LAS MATEMÁTICAS A TRAVÉS DE UN TÚNEL

La isla de Samos ha pasado a la historia por ser la cuna de Pitágoras en el siglo VI a.C.  Sin embargo, otro hito relacionado con las matemáticas sigue siendo recordado en la actualidad: LA CONSTRUCCIÓN DEL TÚNEL DE EUPALINO.

Samos estaba gobernada por Polícrates, un tirano que había alcanzado el poder tras un golpe de estado tramado junto a sus hermanos, a los cuales hizo desaparecer rápidamente. Según cuenta Herodoto, Polícrates gozó de una alta popularidad, estableció vínculos con Egipto y convirtió la isla en un gran centro religioso y cultural.

Bajo su reinado, Samos recibió a los más grandes artistas y eruditos. “En muy poco tiempo subieron los asuntos de Polícrates a tal punto de fortuna y celebridad que así en Jonia como en lo restante de Grecia se oía sólo en boca de todos el nombre de Polícrates, observando que no emprendía expedición alguna en que no le acompañase la misma felicidad” [Herodoto].

El tirano emprendió tres obras principales: la construcción del templo de Hera, la fortificación de la ciudadela y la excavación de un túnel-acueducto para abastecer de agua a la población. A nivel constructivo, las matemáticas iban a jugar un papel esencial.

La necesidad de agua era acuciante. Sin embargo, el manantial más cercano se situaba al otro lado del monte Kastro, y Polícrates planteó la urgencia de abastecer del líquido elemento a una población en continuo crecimiento. Eupalino, un arquitecto natural de Megara, quedó encargado de construir el túnel-acueducto. Y no era trivial.

La obra debía realizarse lo más rápido posible y debía ser subterránea, a fin de evitar su bloqueo en caso de invasión. Ante tal desafío, el arquitecto acudió al ingenio. Y, ya sabemos que, cuando hablamos de ingenio, suelen aparecer las matemáticas. Eupalino lo vio claro: la única posibilidad era comenzar la construcción desde ambos extremos. Solo había un pequeño problema: Sin conocer la dirección exacta, los obreros podrían pasar años excavando sin encontrarse en el corazón de la montaña.

¿Qué pudo hacer exactamente Eupalino?

Pues bien, nada cierto se conoce debido a que el arquitecto no dejó nada escrito. Solo su obra bajo la montaña. Sin embargo, Herón de Alejandría (s. I a.C.) describe un método que bien pudo ser la clave.

Eupalino de Megara entró en juego una vez los grupos de obreros estaban formados y los consejeros de Polícrates habían señalado los puntos de entrada y salida del túnel (A y B).

Su solución es sencillamente brillante, y es fiel reflejo del potencial de las matemáticas griegas.

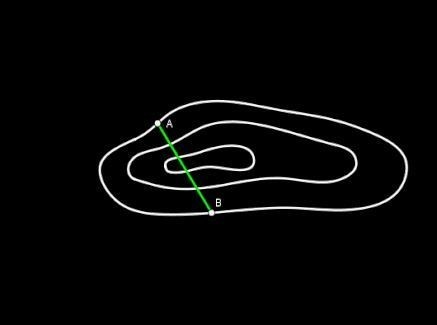
En primer lugar, Eupalino debió fijar una dirección arbitraria desde el punto A (llamémosle AK).

Después, el equipo de trabajo debía bordear el monte, desde A, pasando por K, hasta llegar al punto B, a lo largo de una poligonal con tramos perpendiculares.

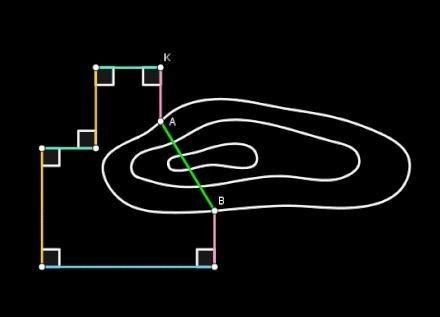
Las longitudes de los tramos de la poligonal permitieron obtener los catetos de un triángulo rectángulo ΔABC cuya hipotenusa AB representaba el túnel (y, por tanto, la dirección que debía seguir la excavación en ambos lados).

Pocos años antes, Tales de Mileto había establecido las reglas para la mayor herramienta de la mente humana: las matemáticas (tal y como las conocemos ahora con el esquema teorema-demostración).

Y estas encontraron en los triángulos la semilla perfecta.

Por tanto, un arquitecto reconocido como Eupalino, mandado llamar por un gobernante exitoso como Polícrates, debía conocer las cuestiones referentes a la semejanza de triángulos (sus longitudes, sus proporciones, sus razones, sus ángulos). 

Así, por ejemplo, Eupalino sabría que:

“Si dos triángulos rectángulos tienen catetos proporcionales, entonces sus ángulos agudos son iguales”.

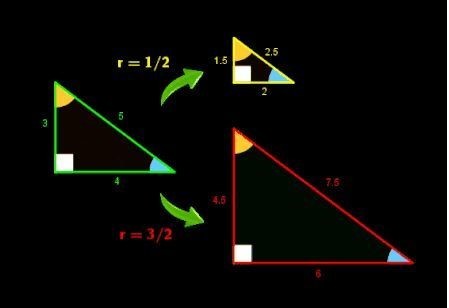
En otras palabras, si ΔABC es un triángulo rectángulo cuya razón entre los catetos es r=AC/BC, entonces es posible construir otro triángulo rectángulo ΔADE con el mismo vértice A y cuyos catetos responden a la misma razón, de forma que las hipotenusas están alineadas.

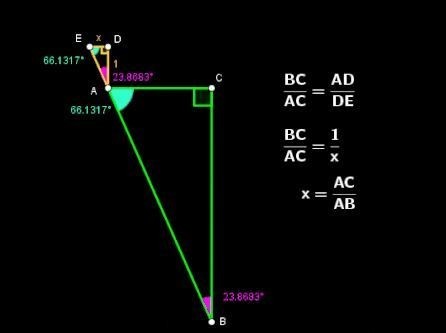
Lo cual, en un lenguaje menos coloquial, da lugar a la siguiente propiedad:

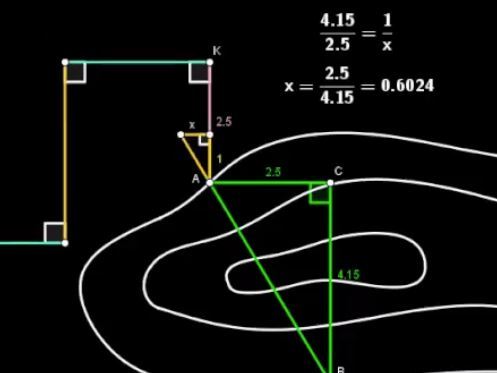
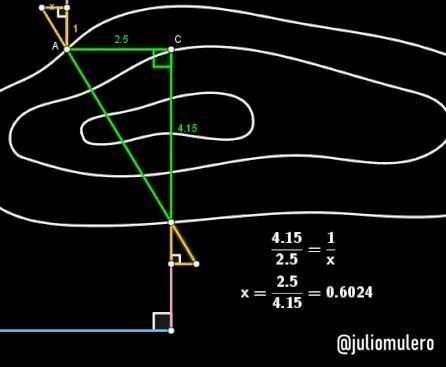
“Si ΔABC y ΔADE son dos triángulos rectángulos con un vértice común A, AC y AD son perpendiculares y, además, BC/AC=AD/DE, entonces las hipotenusas AB y AE están en línea recta”.

Tal y como ya hemos comentado, Eupalino habría calculado la longitud de los catetos del triángulo rectángulo en el que el túnel era la hipotenusa, así que pudo obtener fácilmente la razón entre ellos.

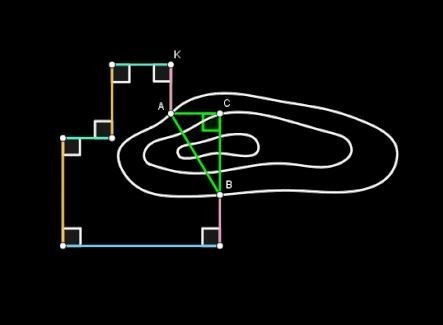
En nuestra figura, r=BC/AC=4.15/2.5=1.66.

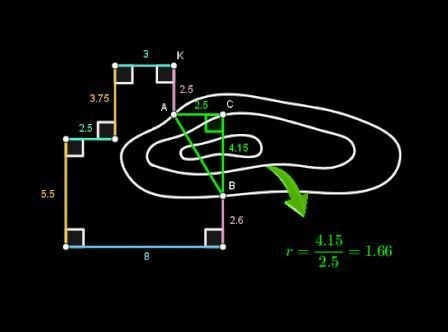
Por último, atendiendo a la propiedad anterior, el arquitecto construyó dos pequeños triángulos rectángulos, con vértices en A y B, cuyos catetos responden a la razón r (1.66) y sean paralelos a los tramos de la poligonal.

Et voilà! ¡La dirección quedaba fijada!

Otras dos cuestiones, o problemas, quedaban por resolver:

1.       Había que asegurar el encuentro de los dos grupos de obreros aproximadamente en la mitad del túnel.

2.       Había que asegurar el flujo de agua el comienzo hasta el final del túnel.

A fin de resolver el primer problema, Eupalino calculó la longitud del túnel mediante la semejanza de triángulos e indicó a cada uno de los grupos que, cercanos a dicha distancia, giraran hacia la izquierda y la derecha convenientemente. El encuentro quedaba así asegurado. 

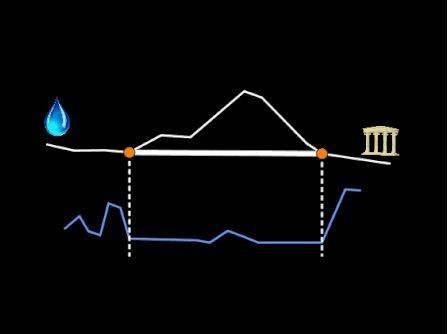
Por otro lado, a fin de asegurar el flujo de agua, Eupalino pudo haber construido un acueducto exterior provisional bordeando el monte (como la poligonal) y obtener la altura exacta del punto de partida y de llegada. 

Como resultado, la ciudadela recibió la tan esperada agua a través del túnel más largo de su tiempo, con 1036 metros de longitud.

El túnel de Eupalino, el Pitagoreo (la ciudadela) y el templo de Hera fueron registrados como Patrimonio de la Humanidad de la Unesco en el año 1992.

Y esta es la historia del túnel de Eupalino. Una historia de ingeniería, de arquitectura y de matemáticas. Una historia en la que las matemáticas entroncan con la leyenda.

¡Muchas gracias por leer este post!

 Written by: Julio Mulero

Coloborador

[ajchm92]

Señor aleja de mi esas ganas de dar un beso en quien no debo.

[ajchm92]

SOMEONE LIKE YOU - COVER FT ADELE 

[ajchm92]

UNA VISTA AL ARCOÍRIS QUE DECIDIÓ SER MONTAÑA

Dicen que las experiencias vividas nadie te los quita, y puedan que tengan razón, hace un par de semanas atrás visite la montaña de colores, que curiosamente, supe de su existencia en una exposición de arte natural que se realizaba en SP-Brasil en 2016. Solo ahora pude realizar el recorrido a dichosa montaña, y que valgan verdades, se ganó un puesto en el “olimpo de paisajes turísticos naturales” del mundo.

El mountain rainbow abre todo su encanto a cuyos ojos tuvieron que llegar por la senda que recorre 6 km a pie para llegar hasta ella. Una vez en la cumbre y al lado opuesto de la misma se observa la magnifica preciosidad que solo podría concluirse que: “un día el arcoíris cansado de ir de aquí para allá decidió tomar un descanso en la cima de la montaña Vinicunca para nunca más abandonarla”.

Sus colores llamativos invitan a soñar, reflexionar y pensar en las cosas que la naturaleza aun esconde a los ojos del hombre y que talvez nunca los revele por causa de que este lo utilice para sus fines egoístas como la de obtener producto rentable solo para saciar su hambre de avaricia.

Dejando el misticismo de lado, cual la explicación técnica de dichos colores en la montaña vinicunca?

Los guías explican que las montañas poseen esos colores debido a los minerales presentes en su composición, pero no saben en qué momento se formaron. Investigando con más calma y de acuerdo con algunos amigos geólogos los colores que adornan la montaña resulta de “una historia geológica compleja, con sedimentos marinos, lacustres y fluviales”.  Esos sedimentos, transportados por el agua que antes cubrían todo el lugar, datan de los periodos terciario y cuaternario, o sea, de 65 millones hasta millones de años atrás.

A lo largo del tiempo, los sedimentos fueron formando capas (con granos de diferentes tamaños) que hoy componen cada una de las fajas de colores de la montaña.

El movimiento de las placas tectónicas de área elevo esos sedimentos hasta que se transformen en lo que es actualmente la montaña, y de a pocos, las diferentes capas fueron adquiriendo sus colores llamativos.

Ellos resultan de la oxidación de los diferentes minerales en virtud de la humedad del área y también de la erosión de los mismos. Cada mineral, en contacto con el oxígeno, ocasiona el aparecimiento de un color único. El óxido de hierro puede dejar la roca más rojiza o con tonos de marrón. El azufre puede tener tonos amarillentos. El cobre tiende a un tono azulado o verde y finalmente el marrón café está compuesto de roca y lodo de magnesio.

Si en el lapso de mi pequeña existencia se me da la oportunidad de ir nuevamente lo haría sin pensarlo dos veces, de hecho, iría cuantas veces sea necesario hasta que mis ojos guarden dichos colores en el fondo de mi corazón.